Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Evaluating the contributions to conductivity in room temperature ionic liquids†
Emily D.
Simonis
 and
G. J.
Blanchard
and
G. J.
Blanchard
 *
*
Michigan State University, Department of Chemistry, 578 S. Shaw Lane, East Lansing, MI 48824, USA. E-mail: blanchard@chemistry.msu.edu; Tel: +1 517 303 1105
First published on 31st May 2024
Abstract
The conductivity of room temperature ionic liquids is not described adequately by the Nernst–Einstein equation, which accounts only for Brownian motion of the ions. We report on the conductivity of the ionic liquid 1-butyl-3-methylimidazolum bis(trifluoromethylsulfonyl) imide (BMIM TFSI), comparing the known conductivity of this RTIL to the diffusion constants of the cationic and anionic species over a range of length scales, using time-resolved fluorescence depolarization and fluorescence recovery after photobleaching (FRAP) measurements of chromophores in the RTIL. Our data demonstrate that the diffusional contribution to molar conductivity is ca. 50%. Another mechanism for the transmission of charged species in RTILs is responsible for the “excess” molar conductivity, and we consider possible contributions.
Introduction
Room temperature ionic liquids (RTILs) have received a great deal of attention because of their unique properties and broad applicability. The physiochemical properties of ionic liquids have been reported widely, but achieving a fundamental understanding of the factors that determine these properties remains a work in progress. Among the issues that serve to complicate our understanding of these materials is the existence of long-range organization, which has been reported over a variety of length scales, ranging from tens of nm to ca. 50 μm.1–17 It is likely that long-range electrostatic forces play an as-yet unresolved role in these observations.17 Several ionic liquids have been studied to determine their conductivity as a function of experimental conditions, such as the impact of water on ionic liquid conductivity, which was found to increase with increasing water content.18 The alkyl chain length of the ionic liquid cation has also been shown to influence conductivity.19–23 In that work, for imidazolium RTILs, conductivity was found to decrease with increasing cation alkyl chain length. Among the properties that are thought to account for RTIL behavior is the ability of the ions within ILs to exhibit translational motion as well as participate in association and dissociation equilibria. An important point to note is that the frequently used property of ionicity24,25 is not necessarily a direct measure of conductivity. The steady state free ion concentration would be directly proportional to ionic conductivity only in the limit that ion diffusion was the sole mechanism of conductivity. The contribution of this equilibrium process to conductivity in RTILs remains to be resolved. The relative importance of translational diffusion of the ions and the dynamics of association and dissociation in determining conductivity is the focus of this work. By determining the relative importance of each mechanism, ionic liquids can be better understood and the applications for which they are best-suited can be developed more fully.In this work, the reported molar conductivity of the ionic liquid BMIM TFSI is compared to translational diffusion data for chromophores dissolved in the RTIL. The experimental conductivity in RTILs has multiple contributions. It is expected that both ion translational diffusion and association and dissociation dynamics will contribute to the overall conductivity of ionic liquids. At the present time, the relative importance of these contributions is not generally known, but they can be evaluated by determining the conductivity expected from diffusional contributions and comparing those results to literature values of conductivity. The molar conductivity, Λ, is related to the ion diffusion constants through the Nernst–Einstein equation.26
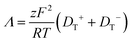 | (1) |
Values for DT+ and DT− are determined over a range of length scales from experimental fluorescence depolarization and FRAP data. The Nernst–Einstein description of conductivity relies on the translational diffusion of the ions, which depend on the viscosity of the medium as shown in the Stokes–Einstein equation,35
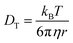 | (2) |
Experimental methods
Materials used
The ionic liquid BMIM TFSI (TCI, >99%) was purchased and then further purified before use. ITO-coated glass slides (Nanocs Inc., IT10-111-25, 10 Ω sq−1) and O-ring spacers made from red silicon (1.6 mm, MSC) were used to make the sample cells for TCSPC measurements. Solvents ethanol (≥99.5%, Sigma-Aldrich), 2-propanol (≥99.5%, Sigma-Aldrich) and ethylene glycol (Macron Fine Chemicals) were used as received. Chromophores included cresyl violet (Eastman), rhodamine B (Sigma-Aldrich, 97%), and nile red (Sigma-Aldrich) were used as received, without further purification. Water used in the cleaning procedures was from a Milli-Q system (Millipore, 18 MΩ-cm).Purification of ionic liquid
To minimize water contamination, all glassware used was oven dried. The ionic liquid, BMIM TFSI (TCI) was prepared according to an established procedure for removing water and other impurities. The BMIM TFSI as received was stored over activated carbon for at least a week in a nitrogen purged glove bag. Using syringe filtration (0.22 μm, Durapore, Mellex), the BMIM TFSI was separated from the charcoal. In a Schlenk vessel in an oil bath the ionic liquid was heated to 85 °C while being sparged with argon for five hours. Karl Fischer titration (Mettler Toledo, C10SD) determined the water content of the purified BMIM TFSI to be less than 50 ppm.Chromophore solutions
Stock solutions of the chromophores cresyl violet (CV), rhodamine B (RB) and nile red (NR) were prepared in ethanol at ca. 5 × 10−4 M. Chromophore structures are displayed in Fig. 1. For TCSPC measurements, the BMIM TFSI and chromophore solution was prepared by pipetting 100 μL of the CV stock solution into a vial and evaporating the ethanol to dryness before adding 1 mL of the purified BMIM TFSI for a final chromophore concentration of ca. 5 × 10−5 M. For the FRAP measurements, RB was used as the chromophore and the RB concentration was ca. 5 × 10−6 M in the BMIM TFSI solution. The neutral chromophore NR was also used for FRAP measurements and was prepared to the same concentration in the ionic liquid. All BMIM TFSI-chromophore solutions were prepared in a N2-purged glove bag. Ethylene glycol was used as a control for both types of measurements and ethylene glycol-chromophore solutions were made to the same concentrations as the BMIM TFSI and chromophore solutions.TCSPC measurements
The time-correlated single photon counting (TCSPC) system used to acquire time-resolved fluorescence depolarization data has been described elsewhere, and we provide a brief description here.39 The light source for the TCSPC system is a passively mode locked Nd:YVO4 laser (Spectra Physics Vanguard), which produces 13 ps pulses at a repetition rate of 80 MHz. The output is 2.5 W average power at both 355 nm and 532 nm, and these pulse trains are used to excite cavity-dumped dye lasers (Coherent 701-3 laser, Coherent 7220 cavity dumpers). For the experiments reported here, 532 nm excitation of pyrromethene 567 dye produced 575 nm output from the dye laser, characterized by 5 ps pulses at a repetition rate of 4 MHz. The output of the dye laser was ported by fiber optic cable to the input of the confocal scanning head (Becker & Hickl DCS-120) that is mounted on an inverted microscope (Nikon Eclipse Ti-U). A 10× microscope objective was used for excitation beam focusing and fluorescence collection from the sample, and the collected fluorescence was passed through a polarizing beamsplitter and sent to two avalanche photodiode detectors (ID Quantique ID100). The output of the detectors and the output of a reference photodiode (B&H PHD-400N) was sent to the TCSPC detection electronics (B&H SimpleTAU 152) and processed using commercial (B&H) software. Separation of the fluorescence signal from excitation light was accomplished using color filters, and the instrumental response function for this system is ca. 100 ps. This instrument was designed to acquire time-resolved imaging data, but when used with a homogeneous sample, all spatial resolution elements can be acquired and averaged rapidly.TCSPC sample cell
Indium doped tin oxide (ITO) coated glass slides were used as ionic liquid sample supports. The ITO-coated supports were cleaned by sonicating in detergent (Fisher Sparkleen 1®) and DI water for 15 minutes, rinsed with Milli-Q water and dried under nitrogen. The cleaned support was then sonicated in Milli-Q water for 15 minutes and in isopropanol (Sigma-Aldrich, ≥99.5%) for 15 minutes. After rinsing with ethanol, the ITO supports were dried at 200 °C for 30 minutes and cleaned by UV-Ozone cleaner for 20 minutes. O-ring spacers made from red silicone (1.6 mm, MSC) were cleaned by sonicating in detergent and DI water for 15 minutes, rinsed with Milli-Q water, and sonicated in Milli-Q water for 15 minutes. The spacer was rinsed with ethanol and dried under N2 before punching a hole through center of the spacer. Using the adhesive side, the spacer was attached to the ITO piece. In a glove bag purged with N2, approximately 60 μL of the IL and chromophore solution was pipetted into the sample mount. A second ITO-coated piece of glass was placed on top with the ITO coated side facing inward so the ITO coated sides were facing each other. The assembly was clamped together to create the sample cell. A schematic of the TCSPC sample cell is shown in Fig. S1 (ESI†).FRAP measurements
Fluorescence recovery after photobleaching (FRAP) measurements were performed using an inverted confocal microscope (Nikon Eclipse TiU) equipped with a three-color imaging detector (Nikon C2) and a laser light source (Nikon LU-N4) operated at 560 nm for the measurements reported here. Commercial software (Nikon Elements 4.30.02) was used to acquire data. Time-resolved recovery data were fitted using software written in-house.FRAP sample cells
Glass microscope slides were cleaned in a similar manner as the ITO pieces. Initially cleaned by sonicating in detergent (Fisher Sparkleen 1®) and DI water for 15 minutes, rinsed with Milli-Q water and dried under N2. Glass slides were then sonicated in Milli-Q water for 15 minutes and in isopropanol for 15 minutes. After rinsing with ethanol, the slides were dried at 200 °C for 30 minutes. Coverslips (Globe Scientific Inc., #1.5) were cleaned in piranha solution (Caution! Strong oxidizer!) for 15 minutes and then rinsed with Mili-Q before oven drying. An adhesive spacer (0.12 mm depth SecureSeal, Sigma Aldrich) with a well was added onto the glass slide. In a glove bag purged with N2, 5 μL of the BMIM TFSI and chromophore solution was added to the well and the coverslip placed on top. A schematic of the FRAP cell is shown in Fig. S2 (ESI†).Results and discussion
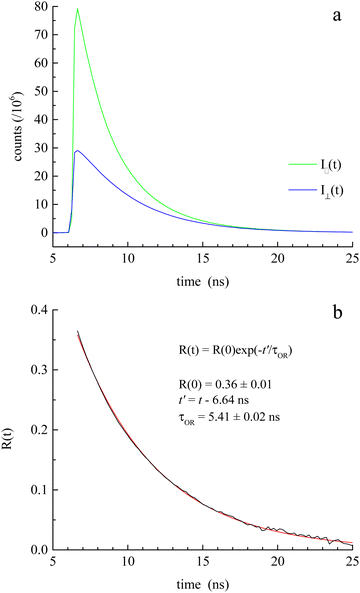
We are concerned with determining the mechanism(s) by which conductivity operates in RTILs. In addition to the fundamental importance of this question, conductivity in RTILs affects the rate at which an induced charge density gradient can develop in these materials. Previous work, that has demonstrated the operation of the direct and converse piezoelectric effects in RTILs, has not addressed the rate at which the induced charge density gradient formed,2–7 but recent data suggests that it forms over several seconds, which is much faster than could be accounted for by diffusion alone. In this work, we compare published conductivity data for BMIM TFSI40–43 to diffusion data for the RTIL constituent species. The difference between the predictions of the Nernst–Einstein equation and the experimental conductivity data points to an additional mechanism by which charge can move in RTILs, and we consider the possible mechanisms by which this can occur. We measure the diffusion constants of the chromophores shown in Fig. 1 by TCSPC (CV) and FRAP (NR, RB). The two measurements are sensitive to different length scales and provide insight into how heterogeneity in the RTILs affects the effective diffusion constants of the constituent species.1,37,38,44–48 We consider the relationship between the rotational and translational diffusion data first.The diffusion constant extracted from the fluorescence depolarization data is the rotational diffusion constant, DR, and the diffusion constant extracted from FRAP data is the translational diffusion constant, DT. DR is described by the modified Debye–Stokes–Einstein (DSE) equation,49–51
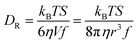 | (3) |
The translational diffusion constant, DT, is given by the Stokes–Einstein equation, eqn (2), which is similar in form to DR, save for the use of the radius rather than the volume of the diffusing entity. Note that the terms f and S are not typically included in eqn (4) because DT is measured over a timescale long enough to include extensive orientational averaging (i.e., S ∼ 1), and the term f is ca. 1 for most polar systems. The relationship between DR and DT is
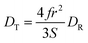 | (4) |
Thus, there should be a direct relationship between the DT values extracted from FRAP and reorientation data. While DR measurements are inherently limited in spatial extent owing to the timescale of the rotational motion, DT can be measured over a range of length scales, determined by the size of the photobleached region of the sample. In homogeneous media, FRAP measurements of different photobleached spot sizes yield the same value of DT. For heterogeneous media, the recovered DT value depends on the size of the photobleached spot, and this phenomenon is termed “frustrated diffusion”. In heterogeneous media, the path of the diffusing molecule is interrupted and altered upon interaction between the diffusing molecule and heterogeneous features. Thus, any spot size-dependence in FRAP data, and change in the relationship between DR and DT, is reflective of heterogeneity in the medium, and DR provides on molecular motion on a length scale shorter than the characteristic dimension of the heterogeneities in the medium.
Measurement of DR
The induced orientational anisotropy function (eqn (5)) contains information on DR.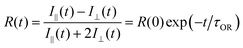 | (5) |
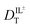 through eqn (6).
through eqn (6).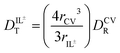 | (6) |
The hydrodynamic volumes and corresponding radii, r, of the species considered in this work are contained in Table 2. Hydrodynamic volumes were calculated using the method of van der Waals increments.35 The quantities 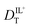 and
and 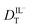 are related to Λ. We use the
are related to Λ. We use the 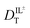 values determined from experimental DR values to calculate an expected molar conductivity, Λ, (eqn (1)).26 The rotational diffusion data yield
values determined from experimental DR values to calculate an expected molar conductivity, Λ, (eqn (1)).26 The rotational diffusion data yield 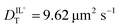 and
and 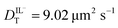 to produce a value of Λ = 7.0 ± 0.06 μm2 s−1 at 293 K (Table 3). Calculating an accurate molar conductivity value for ionic liquids in this manner is challenging because several assumptions and estimations are built into this calculation. However, the value is still significant as it gives a molecularly-based comparison to literature data and to other methods of determining DT.
to produce a value of Λ = 7.0 ± 0.06 μm2 s−1 at 293 K (Table 3). Calculating an accurate molar conductivity value for ionic liquids in this manner is challenging because several assumptions and estimations are built into this calculation. However, the value is still significant as it gives a molecularly-based comparison to literature data and to other methods of determining DT.
| Species | Hydrodynamic volume (Å3) | Radius (Å) |
|---|---|---|
| BMIM | 139 | 3.21 |
| TFSI | 169 | 3.43 |
| Cresyl violet | 217 | 3.73 |
| Rhodamine B | 415 | 4.63 |
| Nile red | 285 | 4.08 |
| D T from DR data (TCSPC) | D T from FRAP data (pure diffusion model) | D T from FRAP data (full reaction-diffusion model) | |
|---|---|---|---|
| D BMIM (μm2 s−1) | 9.62 ± 0.48 | 3.22 ± 0.16 | 5.41 ± 0.33 |
| D TFSI (μm2 s−1) | 9.02 ± 0.25 | 3.01 ± 0.15 | 5.07 ± 0.31 |
| Λ (S-cm2 mol−1) | 0.70 ± 0.06 | 0.23 ± 0.01 | 0.39 ± 0.02 |
Assumptions about the homogeneity of the ionic liquid, the values of the frictional term and shape factor all combine to introduce some uncertainty in the molar conductivity value derived from DR data. Of those sources of uncertainty, perhaps the most serious is the assumption of homogeneity of the ionic liquid, and this is a matter that can be evaluated. The relationship between translational and rotational diffusion constants (eqn (6)) assumes a homogeneous medium, but there is literature evidence suggesting aggregation in ionic liquids.40,58
We consider next the measurement of DT over macroscopic length scales. FRAP is a technique that measures DT. Using RB as the chromophore, a 561 nm laser is used for photobleaching. Initial experiments, using a 20 μm diameter spot size (30 s photobleach time) produced fluorescence recoveries over a timescale of ca. 100 s. The extraction of DT from these data requires normalization and fitting to a model, where the extent and kinetics of association and dissociation within the diffusing medium is taken into account.34,59 We consider next the treatment of the FRAP data to extract DT.
We have chosen to use two chromophores for FRAP measurements, RB and NR (Fig. 3). Our reason for these choices is that RB is a cationic chromophore under these experimental conditions and, as such, is expected to participate in ionic association and dissociation as well as translational diffusion. In contrast, NR is a neutral chromophore and is therefore precluded from participating in ionic association equilibria. The NR data thus serve as a way to characterize the effective viscosity of the RTIL. Fluorescence recovery data are normalized and fitted to one of three possible models. The models, developed by Soumpasis,34 consider whether ionic association and dissociation contribute, and the relative strength of binding of the chromophore. In the model as originally described, the binding sites for ionic species were taken as immobile locations and the issue of import was whether the kinetics of association and dissociation are fast or slow relative to diffusional motion. Another related model is for pure diffusion, where association and dissociation dynamics are not operative and only Brownian motion is considered. These models are termed reaction dominant (strong binding), full-reaction diffusion (both processes contribute on similar time- and length-scales), and pure diffusion (no binding). They were developed originally for biological systems and the interaction of proteins with binding sites, which can be considered analogous to the association and dissociation processes in BMIM TFSI. The model for BMIM TFSI is shown in eqn (7).59
 | (7) |
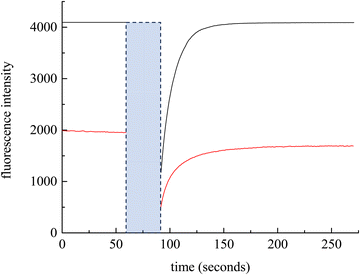 | ||
| Fig. 3 Experimental FRAP data for RB (black) and NR (red). The blue box indicates the photobleach time. | ||
With the reaction dominant model ruled out, there remains the pure diffusion and the full-reaction diffusion models. Because RB is charged, it must participate in association and dissociation processes, and the full-reaction diffusion model is appropriate. This limit assumes that complexation is modest energetically, and the association and dissociation kinetics are competitive with translational diffusion.59,60 We note that the measurements we make sense the interactions of excited chromophores with the RTIL constituents and, in principle, these interactions may be stronger than between the ground state chromophores and the RTIL constituents. We believe this not to be important, however, because of measurements that show little or no difference between ground state and excited state rotational diffusion for the chromophore used in this work.61 The recovery of the FRAP signal is fitted to the equations for each model by MATLAB. Diffusion can be modeled and the diffusion constant, DT, determined by eqn (8) and (9) for pure diffusion,34,59
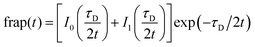 | (8) |
| τD = ω2/DT | (9) |
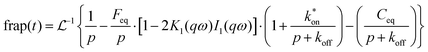 | (10) |
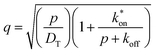 | (11) |
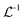 is the inverse Laplace function, and p is the Laplace variable. For this model the modified Bessel functions are of the first kind (I1) and the second kind (K1). The Ceq and Feq functions are related to the rate constants when the system is at equilibrium.
is the inverse Laplace function, and p is the Laplace variable. For this model the modified Bessel functions are of the first kind (I1) and the second kind (K1). The Ceq and Feq functions are related to the rate constants when the system is at equilibrium.
The chromophore NR is neutral, so eqn (8) and (9) apply. FRAP recovery data for NR in BMIM TFSI are qualitatively similar to those for RB, but are characterized by a lower intensity (Fig. 3). This difference is due to the molar absorptivities (NR εmax = 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 M−1 and RB εmax = 106
000 cm−1 M−1 and RB εmax = 106![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 M−1)62,63 and fluorescence quantum yields of the chromophores. To evaluate the DT for NR vs. RB, the bulk viscosity was calculated from eqn (2) using NR data.35,64 NR is used to determine η because it does not participate in complexation with BMIM TFSI. The viscosity recovered in this manner is 129 ± 1 cP, which is somewhat larger than has been reported for BMIM TFSI elsewhere. We note that the range of viscosity values reported for ionic liquids has been comparatively broad, and the values are known to depend on the purity of the ionic liquid. In addition, the viscosity we sense using FRAP data is reflective of interactions between the chromophore and the ionic liquid, and this value may differ from interactions between ionic liquid constituents.65
000 cm−1 M−1)62,63 and fluorescence quantum yields of the chromophores. To evaluate the DT for NR vs. RB, the bulk viscosity was calculated from eqn (2) using NR data.35,64 NR is used to determine η because it does not participate in complexation with BMIM TFSI. The viscosity recovered in this manner is 129 ± 1 cP, which is somewhat larger than has been reported for BMIM TFSI elsewhere. We note that the range of viscosity values reported for ionic liquids has been comparatively broad, and the values are known to depend on the purity of the ionic liquid. In addition, the viscosity we sense using FRAP data is reflective of interactions between the chromophore and the ionic liquid, and this value may differ from interactions between ionic liquid constituents.65
With these data, we are able to compare the molar conductivity values from eqn (1) using 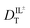 values derived from our measured DR values for CV and the DT values for RB. Conductivity of ionic liquids has been reported previously; however, it is often reported in terms of the electrical conductivity value and not molar conductivity. Using the density and molar mass of BMIM TFSI allows conversion of the literature data to molar conductivity (Table 1).41 BMIM TFSI has an average molar conductivity value of 1.20 ± 0.05 S cm2 mol−1 at 298 K.41 The value of 0.70 ± 0.06 S cm2 mol−1, calculated from the DR measurements at 297 K is 58% of the literature value of bulk molar conductivity and Λ ∼ 0.4 S cm2 mol−1 based on the DT measurements at 293 K is 33%, suggesting contributions to the molar conductivity of ionic liquids other than ion diffusion.
values derived from our measured DR values for CV and the DT values for RB. Conductivity of ionic liquids has been reported previously; however, it is often reported in terms of the electrical conductivity value and not molar conductivity. Using the density and molar mass of BMIM TFSI allows conversion of the literature data to molar conductivity (Table 1).41 BMIM TFSI has an average molar conductivity value of 1.20 ± 0.05 S cm2 mol−1 at 298 K.41 The value of 0.70 ± 0.06 S cm2 mol−1, calculated from the DR measurements at 297 K is 58% of the literature value of bulk molar conductivity and Λ ∼ 0.4 S cm2 mol−1 based on the DT measurements at 293 K is 33%, suggesting contributions to the molar conductivity of ionic liquids other than ion diffusion.
Averaged experimental values of DT for BMIM TFSI based on the pure diffusion and full reaction diffusion models are given in Table 3. The corresponding molar conductivity values determined using the Nernst–Einstein model are also shown in Table 3. There are two important points to be taken from these data. The first is that both the DR and DT results show that the molar conductivity of BMIM TFSI cannot be accounted for solely in terms of ion diffusion, and we consider this matter below. The second point is that the values of DT determined from FRAP data are smaller than would be expected from the DR data. This result indicates that BMIM TFSI cannot be considered as a homogeneous medium, consistent with other reports suggesting heterogeneity in ionic liquids.1,37,38,44–47 Unfortunately, the comparison of DR and DT data do not provide insight into the details of the heterogeneity within the ionic liquid.
The values of DT for BMIM TFSI have been measured by other means and reported elsewhere.19–21 The values we extract from the FRAP data are ca. 5 μm2 s−1 (293 K) for both the cation and anion, and the values from the rotational diffusion measurement are 9.6 μm2 s−1 and 9.0 μm2 s−1 (298 K) for the cation and anion, respectively. Those extracted from NMR measurements are 16 μm2 s−1 for the cation and 11 μm2 s−1 for the anion (303 K), and no uncertainties are provided.20 Given the differences in the techniques and the unknown purity of the RTILs used, these values are in quite reasonable agreement.
It is useful to put these findings into perspective relative to the well-established Walden rule for conductivity as a function of viscosity (Fig. 4). The diffusion data measured in the form of rotational diffusion (DR) or translational diffusion (DT) are related to the viscosities of their microenvironments. We provide the values of DR and DT for the chromophores used and the derived values of h in Table 4. Significantly, all of the data derived from the experimental diffusion constants lies below the Walden rule ideal for KCl, indicating that diffusion alone cannot account for the conductivity reported for BMIM TFSI (Table 1). At the very least, these results point to there being more than one operative mechanism for conductivity in ionic liquids. The fact that the data shown in Fig. 4 depend on the method by which the diffusion measurements were made underscores the heterogeneous nature of ionic liquids. The value of Λ determined from the rotational diffusion data are closest to Walden rule ideal value, suggesting that the local environment experienced by the CV chromophore (and by extension the RTIL species) approaches a homogeneous environment than that experienced by the chromophores used for the FRAP measurements. It is interesting to note that the viscosities recovered by the rotational diffusion measurements and the translational diffusion measurements for the charged chromophore RB are in good agreement despite the difference in characteristic length scales, while the neutral chromophore which does not participate in complexation with the RTIL yields an apparent viscosity that is a factor of two larger. This difference possibly speaks to the relative importance of ionic and dipolar interactions in mediating mobility in RTILs.
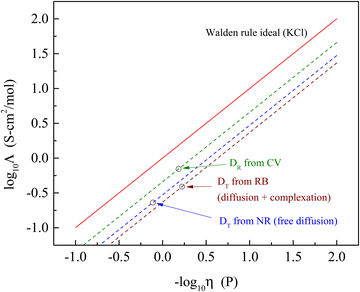 | ||
| Fig. 4 Walden rule plot of the molar conductivity data extracted from diffusion measurements (open circles) and associated Walden-rule lines compared to the Walden rule ideal for KCl (Λ = 1/η). | ||
| Chromophore → | Cresyl violet | Nile red | Rhodamine B |
|---|---|---|---|
| Measurement → | TCSPC | FRAP (diffusion) | FRAP (diff + cplx) |
| Diffusion constant | 3.08 × 107 Hz | 4.09 μm2 s−1 | 7.80 μm2 s−1 |
| η (cP) | 65 | 129 | 60 |
The data on DR and DT demonstrate that there are additional contributions to Λ that remain to be accounted for. There is a possible analogy to other systems where anomalously high conductivity is seen. For small ions in H2O, such as Na+ or Li+, the Nernst–Einstein model is useful in describing molar conductivity, but Λ for H+ is a factor of ca. 4 higher.66 The relative volumes of H+, Na+ and Li+ are not sufficiently different to account for this finding, and the explanation that has been put forth is the so-called Grotthuss mechanism,67 where the mechanism for H+ conductivity involves exchange of protons between water molecules on a comparatively rapid timescale.66 Proton exchange between water molecules allows for charge migration that is largely decoupled from translational diffusion of individual water molecules. Since the analogous process cannot operate for Na+ or Li+, i.e., conductivity based on these ions requires actual translational motion of the ions, proton exchange can translate charge rapidly. We suggest that there is analogy with ionic liquids, where ionic association and dissociation of BMIM+ and TFSI− can give rise to translation of charge by exchange, not involving large scale diffusional motion of ions.68 This mechanism would operate in addition to diffusional contributions to molar conductivity and it may be possible to resolve this contribution using rheo-dielectric spectroscopy.69,70
Conclusions
Comparing diffusion data acquired using fluorescence anisotropy decay (DR) and fluorescence recovery after photobleaching (DT), we have shown that the reported molar conductivity of the ionic liquid BMIM TFSI cannot be accounted for solely in the context of ion diffusion. DR data suggests ca. 58% of the molar conductivity of BMIM TFSI is accounted for by ion diffusion, and DT data recovered from FRAP data suggests ca. 33% of the molar conductivity is accounted for by ion diffusion. The fact that the values of DR and DT do not scale according to eqn (4) for the two methods of measurements underscores the fact that ionic liquids are not simple, homogeneous media. We propose that the unaccounted-for molar conductivity of BMIM TFSI arises from the association/dissociation dynamics of the ionic liquid ions, loosely analogous to the Grotthuss mechanism of proton hopping in water.Conflicts of interest
There are no conflicts to declareAcknowledgements
We are grateful to Michigan State University for support of this work.References
- M. I. Hossain, L. Adhikari, G. A. Baker and G. J. Blanchard, J. Phys. Chem. B, 2023, 127, 1780–1788 CrossRef CAS PubMed.
- K. Ma, R. Jarosova, G. M. Swain and G. J. Blanchard, Langmuir, 2016, 32, 9507–9512 CrossRef CAS PubMed.
- K. Ma, R. Jarosova, G. M. Swain and G. J. Blanchard, J. Phys. Chem. C, 2018, 122, 7361–7367 CrossRef CAS.
- Y. Wang, L. Adhikari, G. A. Baker and G. J. Blanchard, Phys. Chem. Chem. Phys., 2022, 24, 18067–18072 RSC.
- Y. Wang, L. Adhikari, G. A. Baker and G. J. Blanchard, Phys. Chem. Chem. Phys., 2022, 24, 19314–19320 RSC.
- Y. Wang, F. Parvis, M. I. Hossain, K. Ma, R. Jarosova, G. M. Swain and G. J. Blanchard, Langmuir, 2021, 37, 605–615 CrossRef CAS PubMed.
- Y. Wang, G. M. Swain and G. J. Blanchard, J. Phys. Chem. B, 2021, 125, 950–955 CrossRef CAS PubMed.
- R. S. Anaredy and S. K. Shaw, Langmuir, 2016, 32, 5147–5154 CrossRef CAS PubMed.
- R. S. Anaredy and S. K. Shaw, J. Phys. Chem. C, 2018, 122, 19731–19737 CrossRef CAS.
- R. S. Anaredy and S. K. Shaw, J. Phys. Chem. C, 2019, 123, 8975–8982 CrossRef CAS.
- M. A. Gebbie, H. A. Dobbs, M. Valtiner and J. N. Israelachvilli, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7432–7437 CrossRef CAS PubMed.
- M. A. Gebbie, M. Valtiner, X. Banquy, E. T. Fox, W. A. Henderson and J. N. Israelachvilli, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9674–9679 CrossRef CAS PubMed.
- J. Y. Shin, S. A. Yamada and M. D. Fayer, J. Am. Chem. Soc., 2017, 139, 311–323 CrossRef CAS PubMed.
- J. Y. Shin, S. A. Yamada and M. D. Fayer, J. Am. Chem. Soc., 2017, 139, 11222–11232 CrossRef CAS PubMed.
- B. Wu, J. P. Breen and M. D. Fayer, J. Phys. Chem. C, 2020, 124, 4179–4189 CrossRef CAS.
- B. Wu, J. P. Breen, X. Xing and M. D. Fayer, J. Am. Chem. Soc., 2020, 142, 9482–9492 CrossRef CAS PubMed.
- M. A. Gebbie, A. M. Smith, H. A. Dobbs, A. A. Lee, G. G. Warr, X. Banquy, M. Valtiner, M. W. Rutland, J. N. Israelachvilli, S. Perkin and R. Atkin, Chem. Commun., 2017, 53, 1214–1224 RSC.
- E. Hua, Z. Liu and L. Qin, J. Solution Chem., 2021, 50, 503–516 CrossRef CAS.
- H. Tokuda, K. Hayamizu, K. Ishii, M. A. B. H. Susan and M. Watanabe, J. Phys. Chem. B, 2005, 109, 6103–6110 CrossRef CAS PubMed.
- H. Tokuda, S. Tsuzuki, M. A. B. H. Susan, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2006, 110, 19593–19600 CrossRef CAS PubMed.
- S. Tsuzuki, W. Shinoda, H. Saito, M. Mikami, H. Tokuda and M. Watanabe, J. Phys. Chem. B, 2009, 113, 10641–10649 CrossRef CAS PubMed.
- A. Martinelli, M. Marechal, A. Ostlund and J. Cambedouzou, Phys. Chem. Chem. Phys., 2013, 15, 5510–5517 RSC.
- S. Papović, S. Gadžurić, M. Bešter-Rogač and M. Vraneš, J. Chem. Thermodyn., 2016, 102, 367–377 CrossRef.
- K. Ueno, H. Tokuda and M. Watanabe, Phys. Chem. Chem. Phys., 2010, 12, 1649–1658 RSC.
- D. R. MacFarlane, M. Forsyth, E. I. Izgorodina, A. P. Abbott, G. Annat and K. Fraser, Phys. Chem. Chem. Phys., 2009, 11, 4962–4967 RSC.
- M. Dalal, A Textbook of Physical Chemistry, Dalal Institute, Haryana, India, 2020, vol. 1 Search PubMed.
- M. Karagianni, L. Gkoura, A. Srivastava, A. Chatzichristos, N. Tsolakis, G. Romanos, S. Orfanidis, N. Panopoulos, S. Alhassan, D. Homouz, J. Hassan, M. Fardis and G. Papavassiliou, Nat. Commun. Mater., 2023, 4, 1–10 CrossRef.
- C. C. Fraenza and S. G. Greenbaum, ChemPhysChem, 2023, 24, e202300268 CrossRef CAS PubMed (202300261-202300211).
- A. Menjoge, J. Dixon, J. F. Brennecke, E. J. Maginn and S. Vasenkov, J. Phys. Chem. B, 2009, 113, 6353–6359 CrossRef CAS PubMed.
- A. Kaintz, G. Baker, A. Benesi and M. Maroncelli, J. Phys. Chem. B, 2013, 117, 11697–11708 CrossRef CAS PubMed.
- A. Kaintz, G. Baker, A. Benesi and M. Maroncelli, J. Phys. Chem. B, 2014, 118, 5615 CrossRef CAS.
- G. Annat, D. R. MacFarlane and M. Forsyth, J. Phys. Chem. B, 2007, 111, 9018–9024 CrossRef CAS PubMed.
- R. Nanda and K. Damodaran, Magn. Reson. Chem., 2018, 56, 62–72 CrossRef CAS PubMed.
- D. M. Soumpasis, Biophys. J., 1983, 41, 95–97 CrossRef CAS PubMed.
- J. T. Edward, J. Chem. Educ., 1970, 47, 261–270 CrossRef CAS.
- R. K. Cashen, M. M. Donoghue, A. J. Schmeiser and M. A. Gebbie, J. Phys. Chem. B, 2022, 126, 6039–6051 CrossRef CAS PubMed.
- M. I. Hossain and G. J. Blanchard, Phys. Chem. Chem. Phys., 2022, 24, 3844–3853 RSC.
- M. I. Hossain and G. J. Blanchard, J. Mol. Liq., 2022, 367, 120447 CrossRef (120441-120449).
- I. Setiawan and G. J. Blanchard, J. Phys. Chem. B, 2014, 118, 537–546 CrossRef CAS PubMed.
- M. Vraneš, N. Zec, A. Tot, S. Papović, S. Dožić and S. Gadžurić, J. Chem. Thermodyn., 2014, 68, 98–108 CrossRef.
- J. A. Widegren, E. M. Saurer, K. N. Marsh and J. W. Magee, J. Chem. Thermodyn., 2005, 37, 569–575 CrossRef CAS.
- Y. Fu, X. Cui, Y. Zhang, T. Feng, J. He, X. Zhang, X. Bai and Q. Cheng, J. Chem. Eng. Data, 2018, 63, 1180–1189 CrossRef CAS.
- M. Vranes, S. Dozic, V. Djeric and S. Gadzuric, J. Chem. Eng. Data, 2012, 57, 1072–1077 CrossRef CAS.
- O. Russina, F. Lo Celso, N. V. Plechkova and A. Triolo, J. Phys. Chem. Lett., 2017, 8, 1197–1204 CrossRef CAS PubMed.
- O. Russina, M. Beiner, C. Pappas, M. Russina, V. Arrighi, T. Unruh, C. L. Mullan, C. Hardacre and A. Triolo, J. Phys. Chem. B, 2009, 113, 8469–8474 CrossRef CAS PubMed.
- M. Kofu, M. Nagao, T. Ueki, Y. Kitazawa, Y. Nakamura, S. Sawamura, M. Watanabe and O. Yamamuro, J. Phys. Chem. B, 2013, 117, 2773–2781 CrossRef CAS PubMed.
- D. A. Turton, J. Hunger, A. Stoppa, G. Hefter, A. Thoman, M. Walther, R. Buchner and K. Wynne, J. Am. Chem. Soc., 2009, 131, 11140–11146 CrossRef CAS PubMed.
- T. Sonnleitner, D. A. Turton, S. Waselikowski, J. Hunger, A. Stoppa, M. Walther, K. Wynne and R. Buchner, J. Mol. Liq., 2014, 192, 19–25 CrossRef CAS.
- P. Debye, Polar Molecules, Chemical Catalog Co., New York, 1929 Search PubMed.
- C.-M. Hu and R. Zwanzig, J. Chem. Phys., 1974, 60, 4354–4357 CrossRef CAS.
- F. Perrin, J. Phys. Radium, 1934, 5, 497 CrossRef CAS.
- T. J. Chuang and K. B. Eisenthal, J. Chem. Phys., 1972, 57, 5094–5097 CrossRef CAS.
- L. D. Favro, Phys. Rev., 1960, 119, 53–62 CrossRef.
- K. Kinosita Jr., S. Kawato and A. Ikegami, Biophys. J., 1977, 20, 289–305 CrossRef CAS PubMed.
- G. Lipari and A. Szabo, Biophys. J., 1980, 30, 489–506 CrossRef CAS PubMed.
- A. Szabo, J. Chem. Phys., 1984, 81, 150–167 CrossRef CAS.
- T. Tao, Biopolymers, 1969, 8, 609–632 CrossRef CAS.
- M. Iqbal Hossain and G. J. Blanchard, J. Mol. Liq., 2022, 367, 120447 CrossRef CAS.
- B. L. Sprague, R. L. Pego, D. A. Stavreva and J. G. McNally, Biophys. J., 2004, 86, 3473–3495 CrossRef CAS PubMed.
- S. M. Baumler, Diffusional Motion As A Gauge of Interfacial Fluidity And Adhesion Of Supported Model Membrane Films, Michigan State University, 2017 Search PubMed.
- G. J. Blanchard and M. J. Wirth, J. Chem. Phys., 1985, 82, 39–44 CrossRef CAS.
- J. M. Dixon, M. Taniguchi and J. S. Lindsey, Photochem. Photobiol., 2005, 81, 212–213 CrossRef CAS PubMed.
- M. Taniguchi and J. S. Lindsey, Photochem. Photobiol., 2018, 94, 290–327 CrossRef CAS PubMed.
- A. Einstein, Ann. Phys., 1906, 324, 371–381 CrossRef.
- S. Yasmeen, Riyazuddeen and N. Anwar, J. Mol. Liq., 2016, 221, 1207–1217 CrossRef CAS.
- N. Agmon, Chem. Phys. Lett., 1995, 244, 456–462 CrossRef CAS.
- C. J. D. T. von Grotthuss, Ann. Chim., 1806, 58, 54–73 Search PubMed.
- K. Xu, Nat. Energy, 2019, 4, 93–94 CrossRef.
- S. Patil, R. Sun, S. Cheng and S. Cheng, Phys. Rev. Lett., 2023, 130, 098201 CrossRef CAS PubMed.
- S. Cheng, S. Patil and S. Cheng, Phys. Rev. Lett., 2024, 132, 058201 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01218f |
| This journal is © the Owner Societies 2024 |