 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
An atomic layer deposition diffusion–reaction model for porous media with different particle geometries†
Niko
Heikkinen
 *a,
Juha
Lehtonen
*a,
Juha
Lehtonen
 a and
Riikka L.
Puurunen
a and
Riikka L.
Puurunen
 b
b
aVTT Technical Research Centre of Finland, P.O. Box 1000, FIN-02044 VTT, Espoo, Finland. E-mail: niko.heikkinen@vtt.fi; juha.lehtonen@vtt.fi
bDepartment of Chemical and Metallurgical Engineering, Aalto University School of Chemical Engineering, Kemistintie 1, Espoo, Finland. E-mail: riikka.puurunen@aalto.fi
First published on 14th February 2024
Abstract
This work presents a diffusion–reaction model for atomic layer deposition (ALD), which has been adapted to describe radial direction reactant transport and adsorption kinetics in a porous particle. Specifically, we present the effect of three particle geometries: spherical, cylindrical and a slab in the diffusion–reaction model. The reactant diffusion propagates as a unidimensional front inside the slab particle, whereas with cylinder and spherical particles, the reactant diffusion approaches the particle centre from two and three dimensions, respectively. Due to additional reactant propagation dimensions, cylindrical and spherical particles require less exposure for full particle penetration. In addition to the particle geometry effect, a sensitivity analysis was used to compare the impact of the particles’ physical properties on the achieved penetration depth. The analysis evaluates properties, such as the combined porosity and tortuosity factor, mean pore diameter, specific surface area, pore volume, and particle radius. Furthermore, we address the impact of the reactant molar mass, growth-per-cycle (GPC), sticking probability, reactant exposure and deposition temperature on the simulated diffusion and surface coverage profiles. The diffusion–reaction model presented in this work is relevant for the design and optimization of ALD processes in porous media with different particle geometries.
1. Introduction
Atomic layer deposition (ALD) can be used to prepare conformal coatings on porous media, such as aerogels,1 molecular sieving membranes,2 fuel cell components,3 carbon nanotubes4 and catalysts.5 The precise control of reactant deposition inside the porous media is achieved via self-limiting adsorption, regulated by available surface reaction sites, rather than the amount of introduced reactant.6–10 In catalyst preparation, ALD can be used to introduce active metals, promoters and other modifiers with tuneable coating thicknesses and penetration depths inside a porous particle.5,10–17 In order to achieve the desired reactant deposition result with different reactants and porous substrates, diffusion–reaction modelling can be used to design and optimize the ALD process. In the diffusion–reaction model, the particle geometry has an effect on the reactant transport inside the porous particle. Fig. 1 presents the particle geometries discussed in this work, where a spherical particle geometry is relevant for heterogeneous catalyst applications, whereas the slab model could be used for porous membranes (e.g. fuel cell applications) and the cylinder geometry for porous high aspect ratio fibres and monoliths.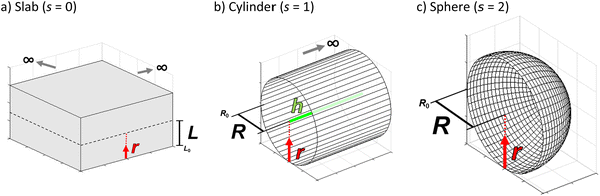 | ||
| Fig. 1 Schematic illustrations of ideal particle geometries: (a) slab with a shape factor s = 0, (b) cylinder (h = nR, n > 100) with a shape factor s = 1 and (c) sphere with a shape factor s = 2. | ||
The literature presents various analytical and computational models for the ALD process in porous materials and well-defined high aspect ratio features. Gordon et al.18 present an analytical model to describe ALD growth inside high aspect ratio holes and trenches, where the reactant exposure required to achieve conformal coating increases quadratically with respect to the aspect ratio. This and other analytical models19–21 have been especially suitable for reactant propagation and surface reaction modelling in a diffusion limited growth setting. Computational models to address ALD conformality can be classified22 as ballistic transport–reaction,23,24 Monte Carlo21,25–28 and diffusion–reaction (sometimes “continuum”) models.1,4,29–31 Monte Carlo and diffusion–reaction models are applicable from continuum flow (Knunden number, Kn ≪ 1) to free molecular flow (Kn ≫ 1) regimes, whereas ballistic transport–reaction models are used in the Knudsen diffusion regime (free molecular flow).24,30,31 Diffusion–reaction models are suitable for simplified particle geometries, while ballistic transport and Monte Carlo models are appropriate for complex structures.22,31
The diffusion–reaction modelling of the ALD process in porous media is based on Fick's law of diffusion.32–34 In this work, we assume homogeneous porosity and tortuosity throughout the particle, where reactant travel begins from the particle outer surface and the reactant diffuses through a tortuous pathway towards the centre of the particle. From the surface to the centre of the particle, the reactant travel is affected by the effective diffusion coefficient (De).35–37 Typically, the effective diffusion coefficient related to porous catalyst particles is determined in a Knudsen diffusion (DKn) regime as De = DKnετ−1.35,36 With a Knudsen diffusion assumption, the effective diffusion coefficient depends on the pore dimensions, temperature and reactant molar mass,10 porosity (ε) and tortuosity (τ). The diffusion coefficient can also be used in a molecular diffusion regime or a combination of Knudsen diffusion and molecular diffusion.35
Simplified particle geometries, which are especially relevant in diffusion–reaction modelling, are well known in the literature related to heterogeneous catalyst particles.35–37 The catalyst regeneration process is a typical example of gas diffusion and reaction in a spherical particle, where carbon formation (fouling) inside the catalyst particle is removed through oxidation.35 Here, oxygen would be analogous to ALD reactant, diffusing into the catalyst pores and reacting with fouled carbon. Due to the spherical particle geometry, the oxygen demand decreases towards the particle centre. The diffusion–reaction regeneration process is commonly described with a shrinking core model (SCM), where the shell volume of a spherical particle decreases towards the particle centre.35,37
In this work, a shape factor is used to determine partial differential equation for the respective particle geometry.36,38 Here, symbol r presents the radial coordinate along the characteristic dimension R. With cylindrical and spherical particles, R is the particle radius, whereas with slab particle geometry R is half of the slab thickness. The radial coordinate r is defined to be zero at the outer surface of a particle, and R at the centre for a sphere/cylinder or half thickness for a slab particle. With the slab particle, the ALD reactant is propagating from under- and upside directions towards the centre of the slab. With the cylinder particle, the reactant propagates in a radial direction, whereas the axial propagation direction is neglected. With the spherical particle, the reactant is propagating from all directions towards the centre. In the literature, the shape factor is determined as the external surface area divided by the particle volume, which is then multiplied by the particle radius R.35,37 The shape factor is a common simplification to describe the effect of the particle geometry on a gaseous and liquid flow through a packed catalyst bed (for example, Thoenes–Kramers mass transfer correlation).35 Furthermore, relevant to our work, the shape factor can be also used to describe particle geometry effect on the intraparticle gas diffusion.37 Most relevant previous work on the particle geometry effect on the intraparticle diffusion, specifically in the ALD process, has been presented by Lee et al.39 They presented a model to address particle geometry effect on the minimum exposure time for the complete ZnO coverage of planar, cylindrical and spherical porous alumina monoliths. Additionally, Elam et al.6 and Detavernier et al.40 have also shown that the spherical particle geometry has a significant effect on the decreasing reactant consumption towards the particle centre.
Our work adapts slab, cylinder and spherical shape factors in an ALD diffusion–reaction model. With partial differential equations for different particle geometries, we demonstrate the effect of the shape factor on the diffusion and surface coverage profiles. We discuss the radial reactant propagation for each particle geometry and evaluate the effect of ALD process parameters and porous material properties on the achieved coating penetration depth. We implement parameters for the growth-per-cycle (GPC, from areal number density of the metal adsorbed), sticking probability, particle porosity and tortuosity, pore diameter, specific surface area, pore volume and particle radius into the coupled partial differential equations. The modelling principles in this work might be relevant also to thin film preparation methods beyond ALD, for example, sequential infiltration synthesis41 and vapor-phase infiltration.42
2. Methods
2.1 Shape factors and diffusion–reaction differential equations
The shape factor (see Fig. 1) is relevant for modelling of diffusion in a porous material, as the modelled reactant consumption profiles vary according to the used shape factors. Eqn (1) presents the diffusion–reaction equation for the volumetric reactant number density (sometimes “particle number density”) with respect to the deposition time for the different shape factors (s = 0, 1, 2).34,37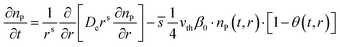 | (1) |
![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) .4 = A0/Vp (m−1) the ratio of specific surface area (m2 g−1) and pore volume (m3 g−1), vth (m s−1) the thermal velocity of the reactant in the gas phase, β0 the reactant sticking probability and θ the surface coverage (fraction of occupied adsorption sites) at time t and position r inside the catalyst particle.
.4 = A0/Vp (m−1) the ratio of specific surface area (m2 g−1) and pore volume (m3 g−1), vth (m s−1) the thermal velocity of the reactant in the gas phase, β0 the reactant sticking probability and θ the surface coverage (fraction of occupied adsorption sites) at time t and position r inside the catalyst particle.
In the eqn (1), the symbol s is the shape factor with a relationship s = a − 1, where factor a has values of one, two and three for a slab, cylinder and sphere, respectively.35–37 The factor a is (APar/VPar)R,35,36 where the particle radius R (m) is multiplied by the ratio of the particle outer surface area (APar, m2) and the catalyst particle volume (VPar, m3). Factor a related to the slab particle geometry is (APar/VPar)L, where L is the half thickness of the slab, corresponding to L = R/2. Table S1, ESI† presents some example calculations to determine the shape factor s for relevant particle geometries. (Note: one should not confuse APar and VPar with the specific surface area (AO, m2 g−1) and pore volume (VP, m3 g−1) of the porous media.) The ratio APar/VPar represents the surface area per volume of a non-porous particle. The adsorption loss term incorporates the self-limiting nature of the ALD process in the diffusion–reaction model.
The effective diffusion coefficient (De, m2 s−1), is derived from the gas phase diffusion coefficient in porous materials, consisting of both molecular diffusion and Knudsen diffusion factors. In eqn (2), according to the Bosanquet relation, the gas phase diffusion coefficient (Di) is a sum of the molecular diffusion coefficient (Dmi) and Knudsen diffusion coefficient (DKn).25
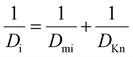 | (2) |
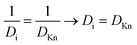 | (3) |
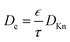 | (4) |
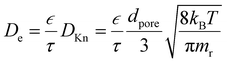 | (5) |
After introducing the corresponding shape factor values to the eqn (1), the final partial differential equations for a slab (eqn (6)), cylinder (eqn (7)) and sphere (eqn (8)) can be written in the form:
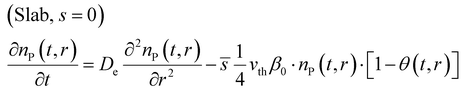 | (6) |
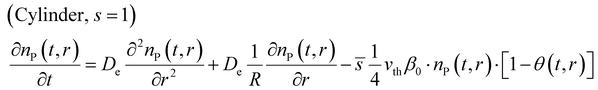 | (7) |
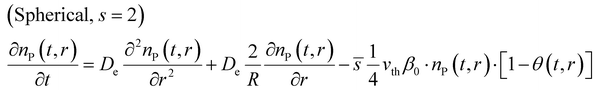 | (8) |
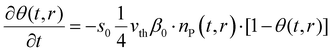 | (9) |
The model initial condition for θ is presented in eqn (10). At time t = 0, θ is zero for all values of the radial distance (r) within the range from 0 to R.
| θ(t = 0, r) = 0, ∀r ∈ [0, R μm] | (10) |
| nP(t = 0, r) = 0, ∀r ∈ [0, R μm] | (11) |
| nP(t, r = 0) = nP0, ∀t ≥ 0 | (12) |
 | (13) |
Partial differential equations (PDEs) were solved in Matlab (MATLAB Version: 9.14.0 (R2023a)) by discretizing the first and second derivatives of the particle radius applying finite differences. For the first derivative, dss004 code was applied using five-point fourth order approximation and for the second derivative, dss044 code using six-point fourth order approximation was used.48 The spatial domain of the radius was discretized typically using 300 points. The formed system of ODEs was solved using Matlab solver ode15s being applicable for stiff ODE systems.
2.2 ALD reactant and catalyst structural parameters
The above presented coupled differential equations (see eqn (6)–(9)) can be used to determine the ALD reactant consumption and surface coverage profiles. The resulting profiles will be influenced by parameters related to the reactant molecule, structural properties of the porous media and the ALD process. Table 1 presents the baseline parameters for the porous media and Table 2 shows the baseline parameters for the ALD process used in the simulations in this work. These baseline parameters were used to compare the effect of particle shape factors on the resulting reactant consumption and surface coverage profiles. While the values do not represent any specific ALD reactant or porous media, they have been inspired by a typical ALD process, such as the trimethylaluminium–water process49 and by mesoporous catalyst supports,50 such as silica or alumina.29| Parameter | Value |
|---|---|
| Porosity, ε | 0.5 |
| Tortuosity, τ | 1 |
| Mean pore diameter, dpore | 2 × 10−8 m |
| Specific surface area, AO | 200 m2 g−1 |
| Pore volume, VP | 6 × 10−7 m3 g−1 |
| Particle radius, R | 3 × 10−4 m |
| Parameter | Value |
|---|---|
| a Estimated from ALD reactant vapour pressure of 100 Pa at 423 K. b Baseline reactant exposure duration marked with bold text. | |
| Reactant molar mass, mR | 100 g mol−1 |
| Initial sticking probability, β0 | 2 × 10−2 |
| Areal number density of metal atoms deposited on each exposure cycle at saturation, σP | 4 × 1018 m−2 |
| Reactant volumetric number density outside the porous material, nP0 (t, r = 0) | 1.71 × 1022 m−3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
| Temperature, T | 423 K |
| Reactant exposure time, t | 100, 500 and 1000 sb |
3. Results and discussion
3.1 The effect of the shape factor on the volumetric reactant number density and surface coverage profiles
The selection of the shape factor has a distinctive effect on the diffusion–reaction model simulation results. Fig. 2 presents simulated profiles for the volumetric reactant number density and surface coverage as a function of radial coordinate r (r is zero at the particle surface and increases until the centre of the particle, where r = R). Here, the coating penetration depth varies according to the particle geometry. The penetration depth (rθ=1/2) in Fig. 2(a) and (b) was 177, 133 and 114 μm for the spherical (s = 2), cylindrical (s = 1) and slab (s = 0) geometries, respectively. In the panel (a), the reactant number density profile for the slab shape factor shows known decreasing linear trend as a function of the penetration depth,18,39 whereas profiles for the cylinder and sphere are curved. In general, for the same exposure, the ALD coating penetrates deeper in the order of sphere > cylinder > slab. In this work, the shape factor s = 1 considers long cylinders, where the dimension h is large with respect to R (see Fig. 1). A cylinder with h = nR, n ≥ 2, the shape factor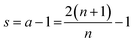 , where the effect of the cylinder bottom and top decrease when n increases.36 With increasing values of n, the shape factor (S) approaches the value 1. If n is small, the shape factor approaches a value of 2 and the partial differential equation ∂np/∂t (eqn (7)) becomes similar to spherical particle geometry (eqn (8)). For values n < 2, the shape factor for cylindrical geometry is not defined.36
, where the effect of the cylinder bottom and top decrease when n increases.36 With increasing values of n, the shape factor (S) approaches the value 1. If n is small, the shape factor approaches a value of 2 and the partial differential equation ∂np/∂t (eqn (7)) becomes similar to spherical particle geometry (eqn (8)). For values n < 2, the shape factor for cylindrical geometry is not defined.36
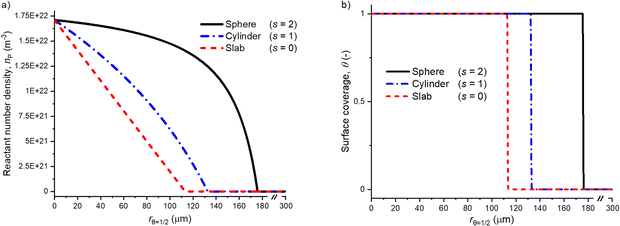 | ||
| Fig. 2 The effect of the shape factor (s) as a function of the radial coordinate r for (a) the volumetric reactant number density and (b) the surface coverage. A list of the used parameters is presented in Tables 1 and 2. | ||
Fig. 2(a) presents the particle geometry effect on the gas-phase reactant number density as a function of the coating penetration depth. The slab geometry demonstrates a linear behaviour as the reactant diffuses through a “plate” with an infinite depth and width, with only one diffusion propagation dimension.35,36 The cylinder profile is curved because of two diffusion propagation dimensions and one indefinite dimension (see Fig. 1). The spherical geometry has no infinite dimensions and the reactant diffusion front approaches the particle centre from all directions. Then, the deposition area per shell volume decreases towards the centre of the porous particle.35
Although the shape factor is not included in the equation for the surface coverage (eqn (9)), the cylinder and spherical particle penetration depth increases in the surface coverage profile compared to the slab in Fig. 2(b). This is due to ∂np(t,r)/∂t and ∂θ(t,r)/∂t equation coupling. Despite the increasing penetration depth for the cylinder and spherical shape factors compared to the slab, all three surface coverage profiles have a similar overall shape and slope at the adsorption front.
3.2 Shape factor and exposure needed for full particle penetration
The shape factor has an impact on the achieved penetration depth (rθ=1/2) for a given exposure. The value for the penetration depth (rθ=1/2) is determined as the position where the surface coverage θ = 0.5.32,51Fig. 3 presents the penetration depths obtained from simulations in which all the parameters remain the same, except that the porous media particle radius R is varied. For example, the penetration depth values from Fig. 1 (177 μm and 114 μm) can be seen in Fig. 3 in red at R = 200 μm (the red sphere marker indicates spherical particle geometry and a red rectangle shows the slab geometry).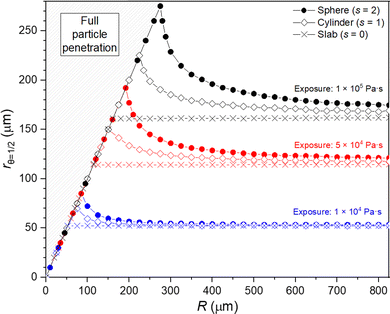 | ||
| Fig. 3 The effect of varying particle size R on the achieved rθ=1/2 (penetration depth) with three different exposures of reactant (1 × 104, 5 × 104 and 1 × 105 Pa s). Three curves for each exposure present the model results for different shape factors: sphere (s = 2), cylinder (s = 1) and slab (s = 0). The simulation parameters are presented in Tables 1 and 2. | ||
Fig. 3 presents the penetration depth results for each shape factor as a function of the particle radius (R). The distinct line starting from the origin is the penetration depth, where the reactant has reached the centre of the particle with a radius R. For example, for a particle with a radius of 50 μm, the penetration depth is 50 μm for all the presented exposures and shape factors. With an increased exposure, larger particles can be fully penetrated by the ALD reactant. In Fig. 3, full penetration is achieved with a 1 × 105 Pa s exposure and a spherical shape factor when R ≤ 275 μm. A reduced particle size can be penetrated with the same exposure with R ≤ 225 μm and ≤ 161 μm for the cylinder and slab particle geometries, respectively. According to Fig. 3, when the particle radius increases, all shape factors result in increasingly similar values for the penetration depth. This behaviour is expected, as the increasing radius of a particle reduces the factor 1/R and 2/R in eqn (7) and (8). Increasing the particle radius R will diminish the effect from the first order partial derivative, resulting in an asymptotically closing equation with respect to the slab geometry (see eqn (6)).
In the example in Fig. 3, the shape factor has a significant effect on the modelled penetration depth when particle radius is <600 μm. However, the model results are not bound to a specific particle size. Instead, the important particle size range depends on the used exposure. Fig. 4 presents the penetration depth difference between slab and spherical geometries. In the figure, the horizontal axis is the normalized penetration depth for sphere, 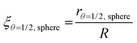 , where the value 1 indicates a full coating (e.g., when particle radius is 200 μm and the reactant has reached the centre of the particle at 200 μm, R = 200 μm and rθ=1/2,sphere = 200 μm). The vertical axis in the figure is the percentage difference between the penetration depths in the slab and spherical geometry. These values can be found in Fig. 3, where for example, a 1 × 105 Pa s exposure resulted in rθ=1/2,sphere of 229 μm and rθ=1/2,slab of 161 μm. In Fig. 4, these values can be found from the vertical axis percentage difference of
, where the value 1 indicates a full coating (e.g., when particle radius is 200 μm and the reactant has reached the centre of the particle at 200 μm, R = 200 μm and rθ=1/2,sphere = 200 μm). The vertical axis in the figure is the percentage difference between the penetration depths in the slab and spherical geometry. These values can be found in Fig. 3, where for example, a 1 × 105 Pa s exposure resulted in rθ=1/2,sphere of 229 μm and rθ=1/2,slab of 161 μm. In Fig. 4, these values can be found from the vertical axis percentage difference of 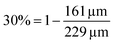 and horizontal axis value
and horizontal axis value 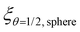 of
of 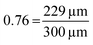 .
.
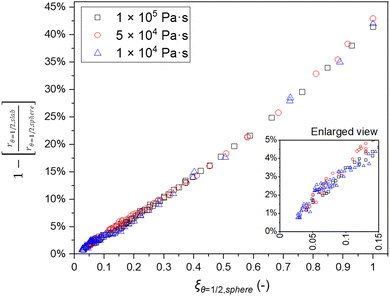 | ||
| Fig. 4 The percentage difference between the penetration depths of the slab and spherical shape factors as a function of ξθ=1/2. The vertical axis is the percentage difference in the penetration depth between the slab and spherical shape factors. The horizontal axis presents the normalized value ξ of penetration depth with the spherical shape factor per particle radius. The small inset is an enlarged view of the same plot. The figure shows the results for 1 × 104, 5 × 104 and 1 × 105 Pa s exposures at 423 K and the particle radius (R) varying from 50 to 3000 μm in 25 μm step intervals. All other parameters are presented in Tables 1 and 2. | ||
Fig. 4 illustrates the difference in the achieved penetration depth between the slab and spherical shape factors. When ξθ=½,sphere ≤ 0.15, the percentage difference in the penetration depth estimate between the slab and spherical shape factors is <5%. In order to achieve a <1% difference, ξθ=½,sphere should be ≤0.05. Increasing the penetration depth with respect to the particle radius, the selection of the shape factor becomes increasingly relevant. At full infiltration, the penetration depth reaches ∼40–45% difference. This finding corresponds to the work by Lee et al.,39 Elam et al.6 and Detavernier et al.,40 in which the spherical particle geometry has a significant effect on the decreasing reactant consumption towards the particle centre.
3.3 Sensitivity analysis: baseline parameters with one varying parameter
A sensitivity analysis was conducted to address the effect of varying a single parameter at a time on the volumetric reactant number density and surface coverage profiles. Fig. 5 presents the volumetric reactant number density profiles for the spherical particle geometry (left) and slab particle geometry profiles (right). In all figures, the solid black line illustrates the baseline parameters and other profiles are for varied parameter values.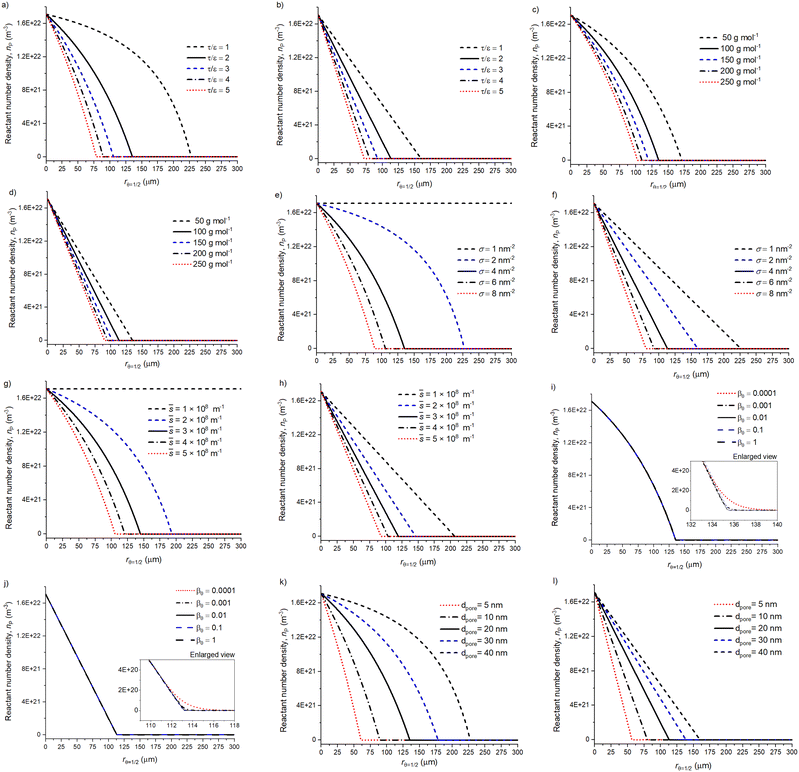 | ||
Fig. 5 Parameter effect on the volumetric reactant number density profile (nP) with a spherical shape factor and slab shape factor. Panel (a) and (b) show the effect of tortuosity (τ) per porosity (ε), (c) and (d) reactant molar mass variation (mr), (e) and (f) show the reactant areal number density (σ, atoms per nm2), (g) and (h) varying ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) = AO/Vp (m−1), (i) and (j) sticking probability (β0), (k) and (l) pore diameter (dpore, m). The parameter effect is addressed by changing one parameter at a time and all other values are baseline parameters with a 500 s reactant exposure duration (see Table 1 and 2). The related surface coverage profiles are shown in Fig. 6. = AO/Vp (m−1), (i) and (j) sticking probability (β0), (k) and (l) pore diameter (dpore, m). The parameter effect is addressed by changing one parameter at a time and all other values are baseline parameters with a 500 s reactant exposure duration (see Table 1 and 2). The related surface coverage profiles are shown in Fig. 6. | ||
Fig. 5 panels (a) and (b) show the effect of tortuosity (τ) and porosity (ε) as a single factor τ/ε for the sphere and slab respectively. The factor τ/ε is a reciprocal value of ε/τ which is present in the effective diffusion coefficient (see eqn (5)). Factor values from 1 to 5 are typical for heterogeneous catalyst support materials, where increasing tortuosity increases the diffusion, i.e. the precursor travel distance inside the porous particle. Similarly, reducing the porosity increases the diffusion resistance due to the retained reactant passage through the porous media. Interestingly, with a restricted diffusion and increasing τ/ε, the achieved rθ=1/2 is increasingly similar between slab and spherical particles. With a decreasing τ/ε the difference between the particle geometries becomes apparent, especially with the shrinking core effect from the spherical particle geometry.35
Panels (c) and (d) in Fig. 5 present the effect of the reactant molar mass on the penetration depth (rθ=1/2). The penetration depth decreases with an increasing reactant molar mass due to the decreasing reactant gas-phase mean thermal velocity vth (m s−1). This observation corresponds to the findings reported by Yim et al.43
Panels (e) and (f) in Fig. 5 illustrate the effect of the areal number density (σP, m−2) of deposited metal atoms upon saturation (directly related to the GPC) on the penetration depth. Here, smaller values increase penetration depth due to decreased amount of reactant adsorption sites. The presented trend is similar to Yim et al.,43 where an increasing σ (nm−2) strongly reduces the achieved rθ=1/2. With σ = 1 nm−2, the spheres have been fully coated.
Panels (g) and (h) in Fig. 5 present the effect of varying ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) = AO/Vp (m−1), a factor found in eqn (6)–(8). Here, increasing the ratio
= AO/Vp (m−1), a factor found in eqn (6)–(8). Here, increasing the ratio ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) increases the surface area compared to the pore volume. Thus, the increased surface area per given volume (increasing
increases the surface area compared to the pore volume. Thus, the increased surface area per given volume (increasing ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ) results in an increased number of surface adsorption sites per volume and a reduced penetration depth.
) results in an increased number of surface adsorption sites per volume and a reduced penetration depth.
Panels (i) and (j) in Fig. 5 present the volumetric reactant number density profiles that appear the same for all varied values of β0. Similar findings have been reported by Keuter et al.34 and Arts et al.,51 where varying the β0 value has no significant effect on the average coating penetration depth. However, the enlarged subplot reveals minute differences in the profiles with varying β0. When the reactant number density approaches zero (reactant depletion), the decreasing sticking probability (β0) reduces the rate of reactant adsorption on the surface, enabling the reactant to travel deeper into the particle. On the other hand, different findings have been reported by Yim et al.,43 where they observed a slight increase in the rθ=1/2, as β0 increased. Yim et al.43 assumed that this would be a result of their analytical model approximation for the reactant partial pressure, resulting in a penetration depth (rθ=1/2) increase, when the β0 value increases.
Lastly, panels (k) and (l) in Fig. 5 present profiles with varied pore diameters. In the presented diffusion–reaction model, the pore diameter is only present in the Knudsen diffusion coefficient (see eqn (5)). A reduced pore diameter restricts diffusion and results in a decreased penetration depth. For both the slab and spherical particle, the rθ=1/2 increases linearly with the pore diameter. However, due to the spherical particle geometry, the rθ=1/2 increases faster. For example, increasing the dpore from 10 to 40 nm will double the rθ=1/2 for the slab. The same increase with spherical particle increases the rθ=1/2 2.5 times.
Fig. 6 presents the surface coverage profiles connected to the volumetric reactant number density profiles in Fig. 5. For example, panels (a) and (b) illustrate the effect of the τ/ε on the surface coverage profile. Panels (i) and (j), show the β0 surface coverage profiles revealing a widening distribution as the β0 decreases. Interestingly, the spherical and slab particle geometries seem to have similar surface coverage profiles with respect to a varied β0, and only the penetration depth is different. Similar surface coverage profiles for the slab and spherical particle geometries with a varying β0 are due to the model using the same ALD process, reactant and particle properties for both the spherical and slab particle geometries. Then, the only difference is the reactant propagation inside the particles. With the spherical particle, the reactant propagation depends on the location (radial coordinate) inside the particle, whereas the slab particle reactant propagation is independent of the location.
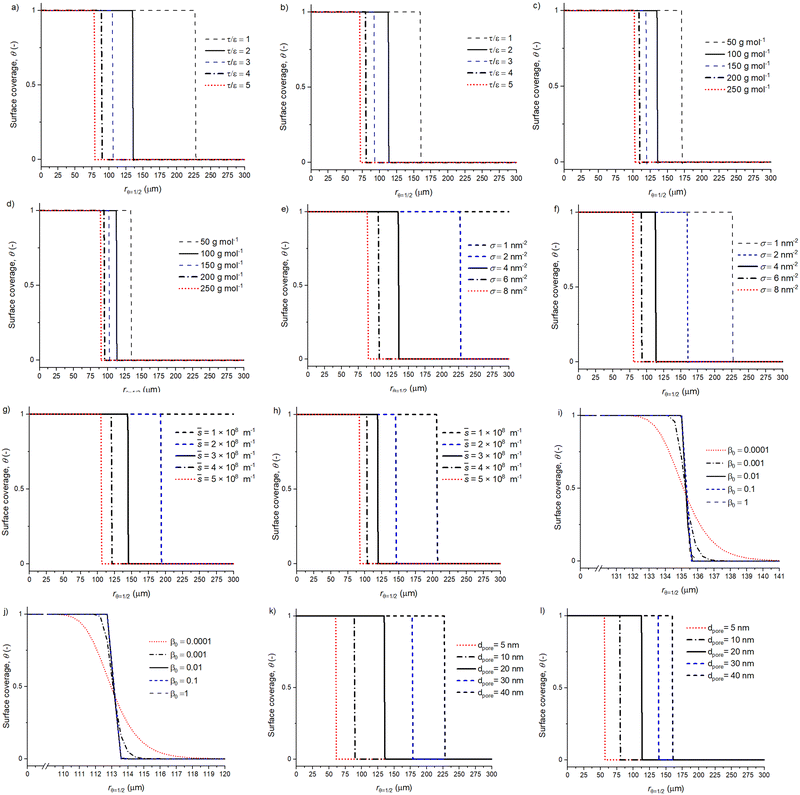 | ||
Fig. 6 The parameter effect on the surface coverage profile with a spherical shape factor and slab shape factor. Panel (a) and (b) present the effect of tortuosity per porosity, (c) and (d) show the reactant molar mass variation, (e) and (f) show the reactant areal number density (atoms per nm2), (g) and (h) show a varying ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) = AO/Vp (m−1), (i) and (j) show the sticking probability β0, while (k) and (l) show the pore diameter (m). The parameter effect is addressed by changing one parameter at a time and all other values are baseline parameters with a 500 s duration reactant exposure (see Tables 1 and 2). The related volumetric reactant number density profiles are presented in Fig. 5. = AO/Vp (m−1), (i) and (j) show the sticking probability β0, while (k) and (l) show the pore diameter (m). The parameter effect is addressed by changing one parameter at a time and all other values are baseline parameters with a 500 s duration reactant exposure (see Tables 1 and 2). The related volumetric reactant number density profiles are presented in Fig. 5. | ||
3.4 The effect of porous media physical characteristics on the coating penetration depth
The physical characteristics related to porous materials, such as the specific surface area, pore volume and pore size have a distinctive effect on the ALD coating penetration depth. Fig. 7 presents the simulation results for the spherical particle geometry and varied porous material properties. Different to the previously presented sensitivity analysis, three parameters are changed at the same time. Typically, with heterogeneous catalyst supports, increasing the specific surface area (AO) will increase the pore volume (VP) and decrease the pore diameter (dpore). The varied values range from AO = 100–1000 m2 g−1, dpore = 3–50 nm, VP = 0.55–0.70 cm3 g−1,![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) = 1.8 × 108–1.4 × 109 (m−1). A full list of parameters and corresponding Knudsen numbers can be found from the ESI† (Table S2). Fig. 7 presents the effect of (a) the specific surface area, (b) pore diameter and (c) pore volume on the achieved penetration depth (rθ=1/2). All panels present results for three particle radius R = 100, 200 and 300 μm. The simulations were conducted with three reactant exposures: 1 × 103, 1 × 104 and 1 × 105 Pa s at 423 K.
= 1.8 × 108–1.4 × 109 (m−1). A full list of parameters and corresponding Knudsen numbers can be found from the ESI† (Table S2). Fig. 7 presents the effect of (a) the specific surface area, (b) pore diameter and (c) pore volume on the achieved penetration depth (rθ=1/2). All panels present results for three particle radius R = 100, 200 and 300 μm. The simulations were conducted with three reactant exposures: 1 × 103, 1 × 104 and 1 × 105 Pa s at 423 K.
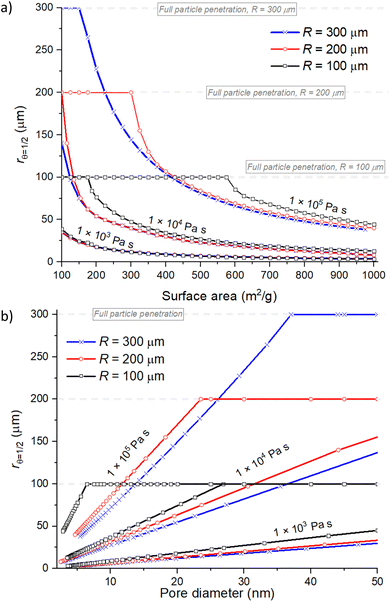 | ||
| Fig. 7 Achieved penetration depth (rθ=1/2) with three varying parameters (a) the surface area (m2 g−1) and (b) pore diameter (nm). The results are shown for particle radiuses of 100, 200 and 300 μm and with reactant exposures of 1 × 103, 1 × 104 and 1 × 105 Pa s at 423 K. Other parameters are baseline parameters and the used shape factor spherical particle geometry. Values used for AO = 100–1000 m2 g−1 and dpore = 3–50 nm. All varied parameters and values for the Knudsen number are presented in the ESI† Table S2. | ||
In Fig. 7(a), the coating penetration depth decreases when the specific surface area (AO) increases. The increasing specific surface area increases the number of adsorption sites per unit volume, resulting in a reduced penetration depth. The pore diameter (dpore) in Fig. 7(b) is included in the Knudsen diffusion coefficient (DKn) (see eqn (5)). Therefore, the pore diameter has significant effect on the reactant travel inside the particle through the Knudsen diffusion coefficient. Increasing the pore diameter increases the Knudsen diffusion coefficient (DKn), which will increase the achieved penetration depth via faster reactant diffusion inside the porous media.
3.5 Temperature effect on the reactant exposure and transport inside porous media
With diffusion–reaction models presented in the literature,1,31,32 the reactant exposure (Pa s) is determined from the partial pressure multiplied by the reactant exposure time. In these previous studies, at least Yim et al.31 and Gayle et al.1 have reported that increasing the deposition temperature reduces the achieved ALD coating penetration depth. Fig. 8 presents simulation results for the effect of varying the temperature on the volumetric reactant number density (nP0) profiles and achieved coating penetration depths.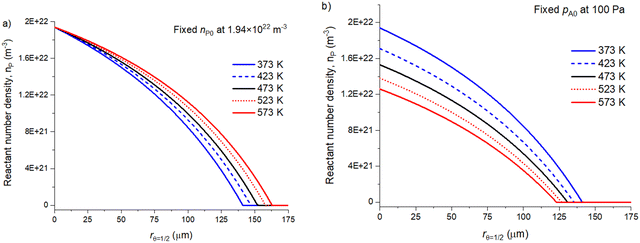 | ||
| Fig. 8 The effect of selecting the volumetric reactant number density (m−3) or partial pressure (Pa) in a diffusion–reaction model as a function of temperature. Panel (a) shows the fixed volumetric reactant number density to 1.94 × 1022 m−3 and (b) shows the fixed partial pressure to 100 Pa as a function of the achieved penetration depth (rθ=1/2). A full list of the simulation parameters and plotted values are presented in the ESI† in Table S4. | ||
Our diffusion–reaction model uses an absolute number of reactant molecules (volumetric reactant number density, nP0) to represent the initial reactant quantity at t = 0. Fig. 8(a) illustrates the simulation results with a fixed initial volumetric reactant number density (1.94 × 1022 m−3). Here, the absolute quantity of reactant molecules is fixed and the reactant partial pressure increases with the increasing temperature. As the absolute reactant quantity remains unchanged, the penetration depth increases due to temperature assisted diffusion and the increasing rate of surface reactions. As the sticking probability (β0) remains unchanged, the increased rate of surface reactions is related to the increased frequency of reactant collisions with the surface.
If a partial pressure (pA0) would be selected for the initial reactant quantity, this value has a temperature dependency. Fig. 8(b) illustrates profiles when volumetric reactant number density is determined from a fixed 100 Pa partial pressure (pA0) at varying temperatures. For example, at a temperature of 373 K, a 100 Pa partial pressure corresponds to nP0 of 1.94 × 1022 m−3 and at a temperature of 573 K, a 100 Pa partial pressure corresponds to 1.26 × 1022 m−3 volumetric reactant number density. Here, the achieved penetration depth decreases as a function of temperature. The decrease is due to the decreasing initial volumetric reactant number density.
4. Conclusions
This work presents a diffusion–reaction model for ALD on porous particles with three different particle geometries: a sphere, cylinder and slab. The particle geometries are presented by means of shape factors (symbol s) for sphere (s = 2), cylinder (s = 1) and slab (s = 0). This work shows that within a spherical porous particle, the reactant diffusion propagates from three radial directions towards the particle centre (three diffusion propagation dimensions) and the decreasing volume towards the centre of a spherical particle results in decreased reactant consumption. Compared to the slab geometry, less reactant is needed to coat spherical and cylindrical particles.By comparing the model results for the slab and spherical particle geometries, we found that when the reactant penetration depth (rθ=1/2) is less than 5% of the particle radius (R), all shape factors result is similar estimates (difference within 1%) for the penetration depth. However, when increasing the penetration depth with respect to the particle radius, the difference between shape factors increases. With the slab shape factor, the penetration depth increases linearly as a function of the square root of the reactant exposure. However, this relationship is different for the spherical particle, where the shell volume available for reactant deposition decreases towards the spherical particle centre as r3, where r is the radial distance from the particle surface.
In addition to the analysis of the shape factors, the presented diffusion–reaction model was used to perform a parameter sensitivity analysis to address the parameter effects on the model results. The varied parameters included porosity (ε), tortuosity (τ), reactant molar mass, areal number density of metal atoms deposited on each exposure cycle upon saturation (σ), the specific surface area (AO), pore volume (VP), sticking probability (β0), and pore diameter (dpore). Furthermore, the single parameter variation was extended to address in detail the combined effect of the specific surface area (AO), mean pore diameter (dpore) and pore volume (VP) on the achieved penetration depth. The general trend was that with a fixed exposure, increasing the specific surface area decreases the coating penetration depth, while increasing the pore diameter decreases the coating penetration depth, and increasing the pore volume increases the coating penetration depth. Lastly, we conceptually compared the effect of the ALD process temperature on the diffusion–reaction model volumetric reactant number density (m−3) and partial pressure (Pa). Our diffusion–reaction model uses the volumetric reactant number density (nP0) to represent the initial reactant quantity. Here, the absolute initial reactant quantity has no temperature dependency, whereas the initial reactant quantity given as the partial pressure (pA0) depends on the temperature. Then, the absolute quantity of initial reactant molecules and the achieved penetration depth decrease as a function of the increasing temperature.
This work presents a diffusion–reaction modelling approach to ALD on porous media with different particle shapes. We used a porous and tortuous heterogeneous catalyst particle as an example substrate. Typically, catalyst particles are simplified as a spherical particle (s = 2). Furthermore, the model can be implemented for the ALD process on many other shapes of porous media, for example, porous membranes (s = 0), high aspect ratio fibres (s = 1) and monoliths (s = 1). The selection of the particle shape factor and corresponding partial differential equation becomes increasingly relevant as the coating penetration depth is approaching the particle centre.
Symbols and abbreviations
| ALD | Atomic layer deposition |
| a | Shape factor; a = s + 1(−) |
| A O | Specific surface area (m2 g−1) |
| A Par | Catalyst particle outer surface area, ideal non-porous sphere (m2) |
| β 0 | Initial sticking probability (−) |
| D e | Effective diffusion coefficient (m2 s−1) |
| D i | Gas phase diffusion coefficient (m2 s−1) |
| D Kn | Knudsen diffusion coefficient (m2 s−1) |
| D mi | Molecular diffusion coefficient (m2 s−1) |
| d pore | Mean pore diameter (m) |
| v th | Mean thermal velocity (m s−1) |
| ε | Porosity (0 ≤ ε ≤ 1) |
| GPC | Growth-per-cycle |
| h | Height (m) |
| k B | Boltzmann constant (m2 kg s−2 K−1) |
| m r | Mass for a single reactant molecule (g) |
| n P0 | Volumetric reactant number density (m−3) |
| p A0 | Partial pressure of component A (Pa) |
| r | Radial coordinate (m) |
| r θ=1/2 | ALD reactant penetration depth (μm) |
| R | Particle radius (m) |
| s | Shape factor for a particle; s = a − 1 (−) |
![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif)
| Ratio of surface area (AO) and pore volume (VP) |
| s 0 | Average surface area of adsorption sites (m2) |
| SCM | Shrinking core model |
| σ | Areal number density of metal atoms deposited on each exposure cycle upon saturation (m−2) |
| t | Time (s) |
| τ | Tortuosity (–) |
| T | Temperature (K) |
| θ | Surface coverage (0 ≤ θ ≤ 1) |
| V P | Pore volume (m3 g−1) |
| V Par | Catalyst particle volume (m3) |
Author contributions
N. H. was the main contributor to interpret results and prepare the manuscript. He also finalized the diffusion–reaction model Matlab code with J. L., who also wrote the original diffusion–reaction model Matlab code and assisted N. H. in the implementation. R. L. P. suggested the initial idea to adapt particle geometries into an ALD diffusion–reaction model and supervised the manuscript writing process.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The work was financially supported by Business Finland project Forest CUMP (Dnro 2158/31/2022), Business Finland project e-Fuel (Dnro 43287/31/2020) and the Academy of Finland ALDI consortium (decision no. 331082). The authors would like to acknowledge Jihong Yim for valuable discussions and kind assistance during the manuscript preparation.References
- A. J. Gayle, Z. J. Berquist, Y. Chen, A. J. Hill, J. Y. Hoffman, A. R. Bielinski, A. Lenert and N. P. Dasgupta, Tunable Atomic Layer Deposition into Ultra-High-Aspect-Ratio (>60000:1) Aerogel Monoliths Enabled by Transport Modeling, Chem. Mater., 2021, 33, 5572–5583 CrossRef CAS.
- A. W. Ott, K. C. McCarley, J. W. Klaus, J. D. Way and S. M. George, Atomic layer controlled deposition of Al2O3 films using binary reaction sequence chemistry, Appl. Surf. Sci., 1996, 107, 128–136 CrossRef CAS.
- T. Keuter, G. Mauer, F. Vondahlen, R. Iskandar, N. H. Menzler and R. Vaßen, Atomic-layer-controlled deposition of TEMAZ/O2-ZrO2 oxidation resistance inner surface coatings for solid oxide fuel cells, Surf. Coat. Technol., 2016, 288, 211–220 CrossRef CAS.
- W. Szmyt, C. Guerra-Nuñez, L. Huber, C. Dransfeld and I. Utke, Atomic Layer Deposition on Porous Substrates: From General Formulation to Fibrous Substrates and Scaling Laws, Chem. Mater., 2022, 34, 203–216 CrossRef CAS.
- B. J. O’Neill, D. H. K. K. Jackson, J. Lee, C. Canlas, P. C. Stair, C. L. Marshall, J. W. Elam, T. F. Kuech, J. A. Dumesic, G. W. Huber, B. J. Oneill, D. H. K. K. Jackson, J. Lee, C. Canlas, P. C. Stair, C. L. Marshall, J. W. Elam, T. F. Kuech, J. A. Dumesic and G. W. Huber, Catalyst design with atomic layer deposition, ACS Catal., 2015, 5, 1804–1825 CrossRef.
- J. A. Libera, J. W. Elam and M. J. Pellin, Conformal ZnO coatings on high surface area silica gel using atomic layer deposition, Thin Solid Films, 2008, 516, 6158–6166 CrossRef CAS.
- J. R. van Ommen, A. Goulas and R. L. Puurunen, Kirk-Othmer Encyclopedia of Chemical Technology, Wiley, 2021, vol. 51, pp. 1–42 Search PubMed.
- S. M. George, Atomic layer deposition: An overview, Chem. Rev., 2010, 110, 111–131 CrossRef CAS PubMed.
- T. Suntola, Atomic layer epitaxy, Mater. Sci. Rep., 1989, 4, 261–312 CrossRef CAS.
- E. L. Lakomaa, Atomic layer epitaxy (ALE) on porous substrates, Appl. Surf. Sci., 1994, 75, 185–196 CrossRef CAS.
- E. Sarnello, Z. Lu, S. Seifert, R. E. Winans and T. Li, Design and Characterization of ALD-Based Overcoats for Supported Metal Nanoparticle Catalysts, ACS Catal., 2021, 11, 2605–2619 CrossRef CAS.
- J. A. Singh, N. Yang and S. F. Bent, Nanoengineering Heterogeneous Catalysts by Atomic Layer Deposition, Annu. Rev. Chem. Biomol. Eng., 2017, 8, 41–62 CrossRef PubMed.
- J. Lu, B. Liu, J. P. Greeley, Z. Feng, J. A. Libera, Y. Lei, M. J. Bedzyk, P. C. Stair and J. W. Elam, Porous alumina protective coatings on palladium nanoparticles by self-poisoned atomic layer deposition, Chem. Mater., 2012, 24, 2047–2055 CrossRef CAS.
- M. Lindblad, S. Haukka, A. Kytökivi, E.-L. Lakomaa, A. Rautiainen and T. Suntola, Processing of catalysts by atomic layer epitaxy: modification of supports, Appl. Surf. Sci., 1997, 121–122, 286–291 CrossRef.
- R. K. Ramachandran, C. Detavernier and J. Dendooven, in Nanotechnology in Catalysis: Applications in the Chemical Industry, Energy Development, and Environment Protection, ed. B. F. Sels and M. Van de Voorde, John Wiley & Sons, Incorporated, Vienna, 2017, p. 1183 Search PubMed.
- A. Arandia, J. Yim, H. Warraich, E. Leppäkangas, R. Bes, A. Lempelto, L. Gell, H. Jiang, K. Meinander, T. Viinikainen, S. Huotari, K. Honkala and R. L. Puurunen, Effect of atomic layer deposited zinc promoter on the activity of copper-on-zirconia catalysts in the hydrogenation of carbon dioxide to methanol, Appl. Catal., B, 2023, 321, 122046 CrossRef CAS.
- H. Zhou, S. R. Docherty, N. Phongprueksathat, Z. Chen, A. V. Bukhtiyarov, I. P. Prosvirin, O. V. Safonova, A. Urakawa, C. Copéret, C. R. Müller and A. Fedorov, Combining Atomic Layer Deposition with Surface Organometallic Chemistry to Enhance Atomic-Scale Interactions and Improve the Activity and Selectivity of Cu–Zn/SiO2 Catalysts for the Hydrogenation of CO2 to Methanol, JACS Au, 2023, 3, 2536–2549 CrossRef CAS PubMed.
- R. G. R. G. Gordon, D. Hausmann, E. Kim and J. Shepard, A kinetic model for step coverage by atomic layer deposition in narrow holes or trenches, Chem. Vap. Deposition, 2003, 9, 73–78 CrossRef CAS.
- J. Dendooven, D. Deduytsche, J. Musschoot, R. L. Vanmeirhaeghe and C. Detavernier, Modeling the Conformality of Atomic Layer Deposition: The Effect of Sticking Probability, J. Electrochem. Soc., 2009, 156, P63 CrossRef CAS.
- N. Yazdani, V. Chawla, E. Edwards, V. Wood, H. G. Park and I. Utke, Modeling and optimization of atomic layer deposition processes on vertically aligned carbon nanotubes, Beilstein J. Nanotechnol., 2014, 5, 234–244 CrossRef PubMed.
- V. Cremers, F. Geenen, C. Detavernier and J. Dendooven, Monte Carlo simulations of atomic layer deposition on 3D large surface area structures: Required precursor exposure for pillar- versus hole-type structures, J. Vac. Sci. Technol., A, 2017, 35, 01B115 CrossRef.
- V. Cremers, R. L. Puurunen and J. Dendooven, Conformality in atomic layer deposition: Current status overview of analysis and modelling, Appl. Phys. Rev., 2019, 6, 021302 Search PubMed.
- A. Yanguas-Gil and J. W. Elam, A Markov chain approach to simulate Atomic Layer Deposition chemistry and transport inside nanostructured substrates, Theor. Chem. Acc., 2014, 133, 1465 Search PubMed.
- R. A. Adomaitis, A ballistic transport and surface reaction model for simulating atomic layer deposition processes in high-aspect-ratio nanopores, Chem. Vap. Deposition, 2011, 17, 353–365 CrossRef CAS.
- P. Poodt, A. Mameli, J. Schulpen, W. M. M. (Erwin) Kessels and F. Roozeboom, Effect of reactor pressure on the conformal coating inside porous substrates by atomic layer deposition, J. Vac. Sci. Technol., A, 2017, 35, 021502 CrossRef.
- M. C. Schwille, J. Barth, T. Schössler, F. Schön, J. W. Bartha and M. Oettel, Simulation approach of atomic layer deposition in large 3D structures, Modell. Simul. Mater. Sci. Eng., 2017, 25, 035008 CrossRef.
- J. W. Elam, D. Routkevitch, P. P. Mardilovich and S. M. George, Conformal Coating on Ultrahigh-Aspect-Ratio Nanopores of Anodic Alumina by Atomic Layer Deposition, Chem. Mater., 2003, 15, 3507–3517 CrossRef CAS.
- H. C. M. Knoops, E. Langereis, M. C. M. van de Sanden and W. M. M. Kessels, Conformality of Plasma-Assisted ALD: Physical Processes and Modeling, J. Electrochem. Soc., 2010, 157, G241 CrossRef CAS.
- N. Heikkinen, J. Lehtonen, L. Keskiväli, J. Yim, S. Shetty, Y. Ge, M. Reinikainen and M. Putkonen, Modelling atomic layer deposition overcoating formation on a porous heterogeneous catalyst, Phys. Chem. Chem. Phys., 2022, 24, 20506–20516 RSC.
- A. Yanguas-Gil, Growth and Transport in Nanostructured Materials, Springer International Publishing, Cham, 2017 Search PubMed.
- J. Järvilehto, J. A. Velasco, J. Yim, C. Gonsalves and R. L. Puurunen, Simulation of conformality of ALD growth inside lateral channels: comparison between a diffusion–reaction model and a ballistic transport–reaction model, Phys. Chem. Chem. Phys., 2023, 25, 22952–22964 RSC.
- M. Ylilammi, O. M. E. Ylivaara and R. L. Puurunen, Modeling growth kinetics of thin films made by atomic layer deposition in lateral high-aspect-ratio structures, J. Appl. Phys., 2018, 123, 205301 CrossRef.
- A. Yanguas-Gil and J. W. Elam, Self-limited reaction-diffusion in nanostructured substrates: Surface coverage dynamics and analytic approximations to ALD saturation times, Chem. Vap. Deposition, 2012, 18, 46–52 CrossRef CAS.
- T. Keuter, N. H. Menzler, G. Mauer, F. Vondahlen, R. Vaßen and H. P. Buchkremer, Modeling precursor diffusion and reaction of atomic layer deposition in porous structures, J. Vac. Sci. Technol., A, 2015, 33, 01A104 CrossRef.
- H. S. Fogler, Elements of Chemical Reaction Engineering, Upper Saddle River, New Jersey, USA, 3rd edn, 2004 Search PubMed.
- T. Salmi, J. Wärnå, J. R. Hernández Carucci and C. A. de Araújo Filho, Chemical Reaction Engineering, De Gruyter, Berlin, 2020 Search PubMed.
- L. D. Schmidt, The Engineering of Chemical Reactions, 1998, vol. 45, p. 536 Search PubMed.
- E. Leonardi and C. Angeli, Transient Diffusion within Spherical Particles: Numerical Resolution of the Maxwell−Stefan Formulation, Ind. Eng. Chem. Res., 2010, 49, 5654–5660 CrossRef CAS.
- H. Y. Lee, C. J. An, S. J. Piao, D. Y. Ahn, M. T. Kim and Y. S. Min, Shrinking core model for Knudsen diffusion-limited atomic layer deposition on a nanoporous monolith with an ultrahigh aspect ratio, J. Phys. Chem. C, 2010, 114, 18601–18606 CrossRef CAS.
- C. Detavernier, J. Dendooven, S. Pulinthanathu Sree, K. F. Ludwig and J. A. Martens, Tailoring nanoporous materials by atomic layer deposition, Chem. Soc. Rev., 2011, 40, 5242 RSC.
- X. Yang, A. B. F. Martinson, J. W. Elam, L. Shao and S. B. Darling, Water treatment based on atomically engineered materials: Atomic layer deposition and beyond, Matter, 2021, 4, 3515–3548 CrossRef CAS.
- A. C. Liapis, A. Subramanian, S. Cho, K. Kisslinger, C. Nam and S. Yun, Conformal Coating of Freestanding Particles by Vapor-Phase Infiltration, Adv. Mater. Interfaces, 2020, 7, 1–6 Search PubMed.
- J. Yim, E. Verkama, J. A. Velasco, K. Arts and R. L. Puurunen, Conformality of atomic layer deposition in microchannels: impact of process parameters on the simulated thickness profile, Phys. Chem. Chem. Phys., 2022, 24, 8645–8660 RSC.
- Y. Yong, X. Lou, S. Li, C. Yang and X. Yin, Direct simulation of the influence of the pore structure on the diffusion process in porous media, Conf. Math. Appl., 2014, 67, 412–423 Search PubMed.
- L. Shen and Z. Chen, Critical review of the impact of tortuosity on diffusion, Chem. Eng. Sci., 2007, 62, 3748–3755 CrossRef CAS.
- R. L. Puurunen, Growth per cycle in atomic layer deposition: Real application examples of a theoretical model, Chem. Vap. Deposition, 2003, 9, 327–332 CrossRef CAS.
- B. E. Rapp, Microfluidics: modeling mechanics and mathematics, William Andrew, Amsterdam, Netherlands, 1st edn, 2017 Search PubMed.
- W. Schiesser, The Numerical Method of Lines – Integration of Partial Differential Equations, Academic Press, 1st edn, 1991 Search PubMed.
- R. L. Puurunen, Surface chemistry of atomic layer deposition: A case study for the trimethylaluminum/water process, J. Appl. Phys., 2005, 97, 121301 CrossRef.
- A. D. McNaught and A. Wilkinson, The IUPAC Compendium of Chemical Terminology, International Union of Pure and Applied Chemistry (IUPAC), Research Triangle Park, NC, 2nd edn, 2019 Search PubMed.
- K. Arts, V. Vandalon, R. L. Puurunen, M. Utriainen, F. Gao, W. M. M. (Erwin) Kessels and H. C. M. Knoops, Sticking probabilities of H2O and Al(CH3)3 during atomic layer deposition of Al2O3 extracted from their impact on film conformality, J. Vac. Sci. Technol., A, 2019, 37, 030908 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05639b |
| This journal is © the Owner Societies 2024 |
