Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Sensitivity of solid phase stability to the interparticle potential range: studies of a new Lennard-Jones like model†
Olivia S.
Moro
 *ab,
Vincent
Ballenegger
*ab,
Vincent
Ballenegger
 a,
Tom L.
Underwood
a,
Tom L.
Underwood
 c and
Nigel B.
Wilding
c and
Nigel B.
Wilding
 *b
*b
aUniversité de Franche-Comté, CNRS, Institut UTINAM, Besançon F-25000, France. E-mail: hn22404@bristol.ac.uk
bHH Wills Physics Laboratory, Royal Fort, University of Bristol, Bristol BS8 1TL, UK. E-mail: nigel.wilding@bristol.ac.uk
cScientific Computing Department STFC, Rutherford Appleton Laboratory, Harwell Campus, Didcot, OX11 0QX, UK
First published on 5th February 2024
Abstract
In a recent article, Wang et al. (Phys. Chem. Chem. Phys., 2020, 22, 10624) introduced a new class of interparticle potential for molecular simulations. The potential is defined by a single range parameter, eliminating the need to decide how to truncate truly long-range interactions like the Lennard-Jones (LJ) potential. The authors explored the phase diagram for a particular value of the range parameter for which their potential is similar in shape to the LJ 12-6 potential. We have reevaluated the solid phase behaviour of this model using both Lattice Switch Monte Carlo and thermodynamic integration. In addition to finding that the boundary between hexagonal close packed (hcp) and face centred cubic (fcc) phases presented by Wang et al. was calculated incorrectly, we show that owing to its finite range, the new potential exhibits several reentrant transitions between hcp and fcc phases. These phases, which do not occur in the full (untruncated) LJ system, are also found for typically adopted forms of the truncated and shifted LJ potential. However, whilst in the latter case one can systematically investigate and correct for the effects of the finite range on the calculated phase behaviour (a correction beyond the standard long-range mean field tail correction being required), this is not possible for the new potential because the choice of range parameter affects the entire potential shape. Our results highlight that potentials with finite range may fail to represent the crystalline phase behavior of systems with long-range dispersion interactions, even qualitatively.
1 Introduction
In a recent paper, Wang et al.1 have proposed a new class of interparticle potential for use in molecular simulation. The new potential, which has received considerable attention, takes the form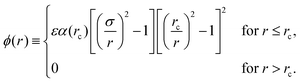 | (1) |
Here σ sets the length scale, and
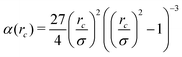 | (2) |
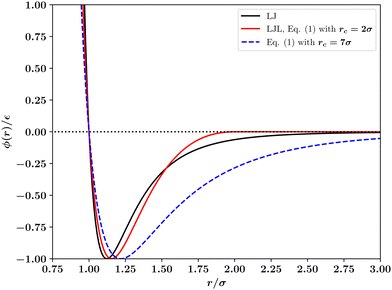 | ||
| Fig. 1 Comparison of the standard 12–6 Lennard-Jones (LJ) interaction potential with the potential of Wang et al.1 (eqn (1)) with range parameters rc listed in the legend. The case rc = 2.0σ is the Lennard-Jones like (LJL) potential. | ||
Wang et al. presented various thermophysical properties of the LJL potential including the phase diagram for the vapor, liquid and crystalline solid phases, all computed from free energy measurements via thermodynamic integration (TI). They rightly stress that their potential is not suitable for use in situations where long ranged interactions can significantly affect the properties of a given system. It is therefore relevant to assess under which circumstances this might be the case. In the present work we have revisited the crystalline solid region of the LJL model using both TI and Lattice Switch Monte Carlo (LSMC). The latter is a powerful method for determining the free energy difference between crystalline phases. Our results reveal an error in the measurement of the phase boundary between hcp and fcc phase presented by Wang et al.1 Furthermore we find that on increasing number density the correct phase diagram for the solid region manifests several reentrant fcc and hcp phases – features that are absent in the full LJ potential. We trace the source of these re-entrant phases to the finite range of the LJL potential i.e., the lack of long ranged dispersion interactions. Our results for the phase behaviour are set out in Section 2 while Section 3 provides a discussion and summarises our conclusions concerning the model.
2 Phase diagram of the Lennard-Jones like model
We have studied the crystalline solid phase behaviour of the LJL model using both Lattice Switch Monte Carlo and thermodynamic integration in conjunction with Molecular Dynamics simulation. We have also performed ground state energy calculations as a function of number density for both the LJL model and a truncated and shifted LJ potential. Implementation details for these methods and the results of our calculations are reported below and in the ESI.† In all cases, numerical values are expressed in dimensionless units, namely reduced temperature T* = kBT/ε, pressure p* = pσ3/ε and particle number density ρ* = ρσ3. For notational simplicity we shall henceforth suppress the superscript * on these quantities.2.1 Lattice Switch Monte Carlo calculations
LSMC2–5 is a well established and powerful simulation technique for determining solid–solid coexistence parameters. Its high precision stems from the fact that it focuses on the difference in the free energy between two candidate stable phases rather than the absolute free energy of each.6 In the course of a LSMC simulation the system repeatedly switches back and forth between two crystalline phases allowing the accumulation of statistics on their relative statistical weight. To enable such switching, the sampling must be biased to visit – on a regular basis – certain ‘gateway’ configurations from which a switch from one phase to the other can be launched. The requisite bias function can be obtained by using the transition matrix method.7,8 The effects of the bias are unfolded from the statistics a posteriori.We have deployed the LSMC method to obtain the crystalline solid phase behaviour of the LJL model using the implementation included within the open source multipurpose MC simulation engine DL_MONTE.9,10 Details regarding the simulations can be found in the ESI.† We investigate in particular the relative stability of hcp and fcc structures‡ as a function of the particle number density ρ = N/V and temperature T. To do so, we work within the isobaric-isothermal (constant-NpT) ensemble for which LSMC provides direct access to the Gibbs free energy difference between the hcp and fcc phases ΔG = Ghcp − Gfcc. This is given by
ΔG = −kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Phcp/Pfcc) ln(Phcp/Pfcc) |
Coexistence state points are defined by ΔG = 0. We located the value of the pressure (p) that corresponds to phase coexistence for a prescribed temperature using a root finding algorithm. Specifically, we applied Newton–Raphson's method to the function ΔG(p) which leads, since dG = VdP, to iterate the pressure according to5
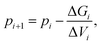 | (3) |
Our LSMC results for the phase diagram are presented in Fig. 2. While we find agreement with the work of Wang et al.1 for the vapor-fluid binodal (which we have determined using separate Gibbs Ensemble Monte Carlo (GEMC) simulations within DL_MONTE), our results for the crystalline region are very different. Specifically, we find at least three separate lines of hcp–fcc transitions, none of which coincide with that of Wang et al. In order to check our findings and throw light on the discrepancy, we have performed TI calculations for the solid region. The results of these calculations are described in the next subsection.
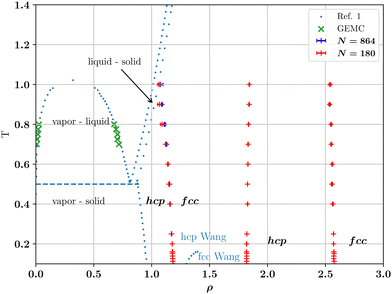 | ||
| Fig. 2 Phase diagram in the density-temperature plane of the LJL system, eqn (1) with rc = 2.0σ. Blue dots are phase boundaries reported in Wang et al.,1 symbols are the present work. Green crosses denote liquid–vapour coexistence densities calculated from GEMC. Our LSMC estimates of the reentrant hcp–fcc coexistence boundaries are denoted by + and were obtained in the reduced temperature range 0 < T ≤ 1 and for the particle numbers N shown in the legend. Note the complete disparity with the single hcp–fcc boundary calculated by Wang et al., as marked by blue dots in the solid region. In all cases, the difference in the coexisting hcp and fcc densities is invisibly small on the scale of the graph. Uncertainties for the coexistence densities were calculated as described in the ESI† and unless indicated by an error bar, do not exceed the symbol size. | ||
2.2 Thermodynamic integration calculations
To elucidate the origin of the discrepancy between our prediction for the hcp–fcc coexistence line(s) based on LSMC calculations and the TI calculations of ref. 1, we have computed absolute Helmholtz free energies of both phases using the MD simulation package GROMACS,†11,12 and the TI method13 for a system comprising N = 768 particles. We selected a number of (T,ρ) state points for which absolute Helmoltz free energies have previously been calculated by Wang et al. and given in their supplementary material (SM).1For our TI calculations we adopted the integration path described by Aragones et al.14,15 to connect the crystalline phase of interest and a known reference state, namely an ideal Einstein crystal that has one atom fixed at its lattice site (state 0)§. The Helmholtz free energy of state 0 is A0 = 3/2(N − 1)ln(βkEΛT2/π) where  is the thermal de Broglie wavelength, β = 1/(kBT) and kE is the spring constant of the (N − 1) harmonic oscillators. The absolute free energy A can be expressed as14,16
is the thermal de Broglie wavelength, β = 1/(kBT) and kE is the spring constant of the (N − 1) harmonic oscillators. The absolute free energy A can be expressed as14,16
| A = A0 + ΔA1 + ΔA2 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln〈e−β(E1−E0)〉0 where the thermal average is over equilibrium trajectories of the ideal Einstein crystal (state 0). Notice that E1−E0 = Epair is merely the sum of the LJ-like pair interactions. To avoid overflows in the exponent, the formula is rewritten as βΔA1 = βEpair(T=0) − ln〈exp(−β(Epair−Epair(T=0)))〉0 where Epair(T=0) is the sum of the pair interactions in the perfect crystal at T = 0. The spring constants were adjusted so that the second term (per particle) − ln〈exp(−β(Epair−Epair(T=0)))〉0/N is close to 0.02, as recommended.14,15 The integral in the contribution
ln〈e−β(E1−E0)〉0 where the thermal average is over equilibrium trajectories of the ideal Einstein crystal (state 0). Notice that E1−E0 = Epair is merely the sum of the LJ-like pair interactions. To avoid overflows in the exponent, the formula is rewritten as βΔA1 = βEpair(T=0) − ln〈exp(−β(Epair−Epair(T=0)))〉0 where Epair(T=0) is the sum of the pair interactions in the perfect crystal at T = 0. The spring constants were adjusted so that the second term (per particle) − ln〈exp(−β(Epair−Epair(T=0)))〉0/N is close to 0.02, as recommended.14,15 The integral in the contribution  where ri(0) is the reference lattice site of the ith particle and the thermal average is over an interacting Einstein crystal with spring constant
where ri(0) is the reference lattice site of the ith particle and the thermal average is over an interacting Einstein crystal with spring constant 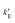 , was computed by using the change of variable13,16
, was computed by using the change of variable13,16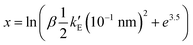 and a Gauss-Legendre quadrature with 15 points.
and a Gauss-Legendre quadrature with 15 points.
The results of our TI calculations are compared in Table 1 with LSMC calculations that we have performed in the canonical (constant-NVT) ensemble. The state points listed are a selection of those also studied by Wang et al.1 (see their SM). At T = 0.1, our LSMC and TI both predict a (first) transition from hcp to fcc around density ρ ≈ 1.18(1) (where ΔA(ρ) changes sign), far removed from the density ρ ≈ 1.29 at which coexistence is predicted in ref. 1. At higher temperatures we find consistency between our canonical LSMC and TI estimates of transition densities on this first hcp–fcc phase boundary, and the constant-NpT LSMC calculations of the full phase boundary reported in Fig. 2. Error bars are straightforward to assess for LSMC (see ESI†) and standard deviations on the LSMC results are reported in the table. Absolute free energies depend on the atomic mass and on Planck's constant via the thermal de Broglie wavelength ΛT, while the free energy difference ΔA does not. Our TI values were computed by setting ΛT = σ, separately at each considered temperature. This standard convention was apparently also used in ref. 1. It leaves out not only Planck's constant17 but also a temperature-dependent contribution to the free energy.
| T | ρ | ΔA = Ahcp − Afcc | Difference LSMC – TI | A (this work) − A (ref. 1) | |||
|---|---|---|---|---|---|---|---|
| LSMC | TI | Ref. 1 | fcc | hcp | |||
| 0.1 | 1.16 | −0.044(4) | −0.021 | −0.228 | −0.02 | 0.02 | 0.23 |
| 0.1 | 1.20 | 0.027(3) | 0.054 | −0.157 | −0.03 | 0.02 | 0.23 |
| 0.1 | 1.24 | 0.106(10) | 0.131 | −0.083 | −0.03 | 0.02 | 0.23 |
| 0.1 | 1.28 | 0.181(17) | 0.206 | −0.012 | −0.02 | 0.02 | 0.23 |
| 0.1 | 1.32 | 0.240(23) | 0.264 | 0.020 | −0.02 | 0.01 | 0.23 |
| 0.204 | 1.2 | 0.0185(17) | 0.036 | −0.168 | −0.02 | 0.02 | 0.22 |
| 0.308 | 1.2 | 0.0147(14) | 0.032 | −0.172 | −0.02 | 0.00 | 0.20 |
| 0.399 | 1.2 | 0.0135(13) | 0.030 | −0.175 | −0.02 | 0.01 | 0.22 |
| 0.503 | 1.2 | 0.0120(13) | 0.026 | −0.178 | −0.01 | −0.01 | 0.19 |
| 0.607 | 1.0 | −0.0107(11) | −0.005 | −0.206 | −0.01 | −0.07 | 0.13 |
| 0.607 | 1.1 | −0.0053(6) | 0.002 | −0.204 | −0.01 | −0.04 | 0.17 |
| 0.607 | 1.2 | 0.0109(11) | 0.028 | −0.181 | −0.02 | −0.02 | 0.19 |
| 0.802 | 1.0 | −0.0046(3) | −0.006 | −0.207 | 0.001 | −0.05 | 0.15 |
| 0.802 | 1.1 | −0.0007(1) | 0.007 | −0.206 | −0.01 | −0.05 | 0.16 |
| 0.802 | 1.2 | 0.0102(10) | 0.018 | −0.187 | −0.01 | −0.03 | 0.18 |
At all densities and temperatures reported in Table 1, the free energy difference ΔA = Ahcp − Afcc that we obtain with TI deviates slightly and systematically from our LSMC results by a shift of the order − 0.02NkBT (see column 6 of the table). This small difference might be due to systematic integration errors in the TI calculations. Much larger discrepancies are observed between our LSMC and TI values for ΔA and those of ref. 1 (compare columns 3 and 4 with column 5 of Table 1 respectively). Comparing separately the free energies estimates of the fcc and hcp phases, we find generally reasonable agreement between our TI results and those of Wang et al.1 for the fcc phase, but a much larger discrepancy for the hcp phase, as reported in the rightmost two columns of Table 1. This shows that the absolute free energies of the hcp phase (at least) have very likely been miscalculated in ref. 1, leading to a very different and incorrect crystalline phase boundary. Since the missing contribution is proportional to the temperature, the hcp–fcc coexistence curve determined in ref. 1 (for ρ ≤ 1.4) deviates increasingly from our coexistence curve. We note that the error in the calculation of the free energy also raises questions regarding the correctness of the estimates of the vapor-solid and liquid–solid phase boundary reported by Wang et al., as shown in Fig. 2, though we have not checked those particular calculations.
2.3 Ground state energy calculations
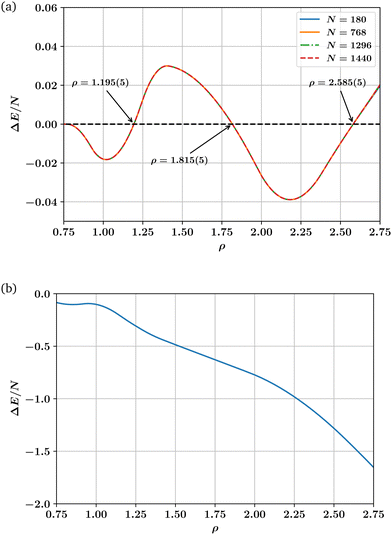
The corrected ρ − T phase diagram for the LJL model displayed in Fig. 2 shows that the boundaries between hcp and fcc phases are almost linear and independent of temperature over a wide temperature range which extends down to very low T. It is thus reasonable to assume that coexistence properties calculated from ground state (i.e., T = 0) energy calculations may aid an understanding of the overall solid state phase behaviour.In the ground state, particles occupy their lattice sites, there are no entropic contributions to the hcp–fcc free energy difference, and energy calculations suffice to determine the phase behaviour. We have used the potential eqn (1) to calculate the ground state energy difference per particle ΔE/N = (Ehcp − Efcc)/N as a function of ρ. The criterion ρ(ΔE = 0) corresponds to hcp–fcc transition points. Note though that while the stability of each phase is correctly predicted by the sign of ΔE, the hcp and fcc phases have slightly different specific volumes. The coexisting densities are then not given merely by the condition ΔE = 0, but by ΔG = ΔE + pΔV = 0. They can be deduced from the curve E(ρ,T = 0) of each phase by performing the common tangent construction, which imposes a common pressure at coexistence. However as the coexistence densities straddle the density ρ(ΔE = 0) and are very close in value to one another – indistinguishably so on the scale of Fig. 2—it is sufficient in the current context to simply determine ρ(ΔE = 0).
Our ground state energy calculations for the LJL model are shown in Fig. 3(a), which plots ΔE/N as a function of ρ. One sees that ΔE = 0 occurs for ρ = 1.195(5) (p = 12.48), which is close to the extrapolation to T = 0 of the first hcp–fcc transition line shown in Fig. 2. The same is true of the second and third transition lines shown in Fig. 2 which our T = 0 calculations place at densities of ρ ≈ 1.815(5) (p = 145.31) and ρ ≈ 2.585(5) (p = 623.81) respectively. Thus our ground state energy calculations are consistent with the phase boundaries found at finite temperatures via LSMC.
Following a suggestion by an anonymous referee, we have also calculated the ground state energy difference between the fcc structure and a body centered cubic (bcc) structure for the LJL potential. This comparison is shown in Fig. 3(b) and in conjunction with Fig. 3(a) confirms that at T = 0 bcc is unstable with respect to fcc and hcp phases across the solid region.
It is instructive to compare the ground state phase behaviour of the LJL model with that of the truncated and shifted LJ potential which has the form
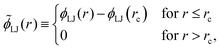 | (5) |
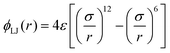 is the full LJ potential, a portion of which is shown in Fig. 1. We have used eqn (5) to calculate the ground state energy as a function of the density for various values of the LJ truncation distance rc. The results, which replicate and extend to higher values of rc similar calculations by Jackson et al.,4 are shown in Fig. 4. This figure also includes the results of calculations for the limiting case of the full LJ potential given by Stillinger18 for which it is important to note there is only a single hcp–fcc transition, which occurs at ρ = 2.1728. On increasing rc, our results for ΔE/N approach the limiting curve, but only for a large truncation distance of rc ≳ 6σ. For smaller cutoffs rc ≲ 5σ, ΔE fluctuates wildly and changes sign at several densities, indicating that in this regime additional hcp–fcc transitions arises which are artifacts in the sense that they are not characteristic of the full LJ potential.
is the full LJ potential, a portion of which is shown in Fig. 1. We have used eqn (5) to calculate the ground state energy as a function of the density for various values of the LJ truncation distance rc. The results, which replicate and extend to higher values of rc similar calculations by Jackson et al.,4 are shown in Fig. 4. This figure also includes the results of calculations for the limiting case of the full LJ potential given by Stillinger18 for which it is important to note there is only a single hcp–fcc transition, which occurs at ρ = 2.1728. On increasing rc, our results for ΔE/N approach the limiting curve, but only for a large truncation distance of rc ≳ 6σ. For smaller cutoffs rc ≲ 5σ, ΔE fluctuates wildly and changes sign at several densities, indicating that in this regime additional hcp–fcc transitions arises which are artifacts in the sense that they are not characteristic of the full LJ potential.
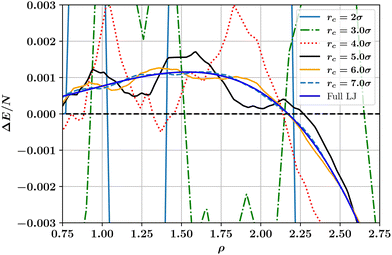 | ||
| Fig. 4 Dependence on number density ρ of the ground state energy difference per particle between hcp and fcc crystalline phases as calculated for the truncated and shifted LJ potential at a selection of cutoff values. Also shown for comparison is the limiting case for the full (untruncated) LJ potential.18 Note how the results for the finite cutoff approach the limiting case for rc ≳ 7.0σ. | ||
We have also considered the changes to the T = 0 phase behaviour of the potential of Wang et al. that result from varying the range parameter rc in eqn (1). The results displayed in Fig. 5 show that the number and location of hcp and fcc phases occurring varies dramatically, similarly to what was found in Fig. 4 for the truncated and shifted LJ potential¶. In order for a single hcp–fcc transition to occur, as in the full LJ potential, one must utilise in eqn (1) a range parameter rc ≳ 7σ. However, as shown in Fig. 1 and discussed below, for this value of the range parameter, the potential of eqn (1) is not at all Lennard-Jones like. The reason for the large sensitivity of ΔE on the range parameter rc and on the density is explained in the next section.
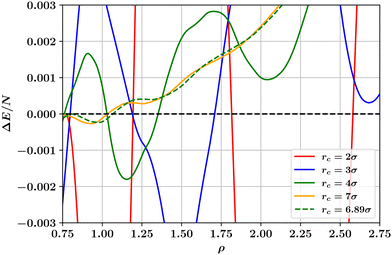 | ||
| Fig. 5 Dependence on number density ρ of the ground state energy difference per particle between hcp and fcc crystalline solid phases as calculated for the LJL potential of eqn (1) at a selection of values of the range parameter rc. For solid like densities (ρ > 0.8), the smallest value of the range parameter for which only a single hcp–fcc transition occurs is rc = 6.89σ. | ||
3 Discussion and conclusions
In this work we have reconsidered the phase diagram of a recently proposed finite-ranged potential, eqn (1), that has been recommended as an alternative to the use of truncated LJ potentials in molecular simulation.1 The advantage of this LJL potential is that while it is similar in shape to the LJ potential, it is defined in such a way as to vanish smoothly at the prescribed value of the range parameter. It thus provides a unique truncation scheme, which contrasts with the multiple approaches in common use for the LJ potential.We have studied the phase diagram of the LJL model both in the liquid–vapor and the crystalline solid regions. While we confirm the original authors' findings for the vapor–liquid binodal, our results in the crystalline phases deviate greatly. Specifically, on increasing the number density starting from the solid branch of the vapor–solid coexistence region, we find a very different hcp–fcc boundary to that reported. Our calculated hcp–fcc boundary (Fig. 2) exhibits relatively weak temperature dependence and intersects the freezing line at a fluid-hcp–fcc triple point. We have traced the discrepancy between our results and those of Wang et al. to an apparently incorrect calculation of the free energy on their part.
We find, moreover, that on increasing the density further within the crystalline region, the LJL potential exhibits not one but multiple reentrant hcp–fcc transitions that extend over a wide range of temperatures down to T = 0. Indeed a previous study by Choi et al.19 of the LJ potential, truncated and shifted at rc = 2.5σ, reported a qualitatively similar phase diagram, displaying reentrant hcp and fcc transitions whose boundaries depend only weakly on temperature, as well as a fluid-hcp–fcc triple point. Importantly, however, such features are absent in the full LJ potential which except for a very small temperature range exhibits only a single hcp–fcc transition line, which is strongly temperature dependent at low T and does not intersect the melting curve.4,5,20,21 Thus the solid phase diagrams of both the LJL potential and the truncated and shifted LJ system can exhibit solid phase behaviour quite different to the full LJ potential.
It is well established that the difference in free energy between hcp and fcc phases for spherically symmetric interparticle potentials can be small across a range of state points.3,4,13,22,23 Previous studies of the ground state (T = 0) energy as a function of number density of the truncated and shifted LJ potential have shown that artifact reentrant transitions arise due to the sensitivity of the sign of the hcp–fcc energy difference ΔE/N to the truncation range.4,5 This is essentially because as one varies the number density, whole shells of neighbouring atoms move in or out of the truncation range.4 The radial distribution functions of the two competing structures being different, the energy difference ΔE can involve non-identical numbers of atoms within the interaction range, leading to a large difference ΔE which can yield re-entrant solid phases. The magnitude of ΔE/N for a truncated potential can be much larger than for the full LJ potential. For instance, when truncating the LJ interaction at some short cutoff, say rc = 2σ, ΔE/N is about 10 times that of the full LJ potential. The size of this energy difference would appear to be responsible for the insensitivity to temperature of the measured hcp–fcc coexistence boundaries, as seen for both the truncated LJ potential19 and the LJL system (Fig. 2), because it dominates over the hcp–fcc entropy difference. It is therefore not surprising that the much smaller value of ΔE associated with the full LJ potential leads to very different crystalline phase diagram.4,20,21 Ground state energy calculations for the truncated and shifted LJ potential performed in the present work (Fig. 4) demonstrate that, at least at T = 0, one requires rc ≳ 6σ in order to eliminate artifact phases. This would therefore seem to represent a lower bound on the truncation length scale necessary to obtain a solid phase diagram in qualitative agreement with that of the full LJ potential.||
For unshifted truncated LJ potentials, a commonly adopted approach is to apply a long-range mean field tail correction24 to account for truncation effects. However, this doesn't solve the problem of the artifact phases highlighted here, because this uniform correction is the same for both phases. By contrast, Jackson et al. have shown that a crystalline phase diagram resembling that of the full LJ potential can be achieved in simulations of a truncated LJ potential with a small range provided one treats the ground state exactly, i.e., one calculates E(ρ) for each phase from the full potential, confining potential truncation effects to the fluctuation spectrum.4,5 This simple correction builds on the fact that the crystalline phase diagram inherits many of its key features from the ground state. It seems to us to provide an economical approach to accurate simulation studies of solid phase behaviour.
In the case of the LJL potential of Wang et al., eqn (1), we find (see Fig. 5) that the number of stable solid phases occurring at T = 0 can be reduced by increasing the range parameter rc, such that for rc ≳ 7σ only a single hcp–fcc transition remains. However, as Fig. 1 shows, for such large values of the range parameter, the potential is no longer similar to the LJ potential. This latter point exposes a significant disadvantage of the LJL potential, eqn (1): whilst for a truncated LJ system one can investigate (and systematically correct for4,5) the effects of the finite potential range when modelling a given physical system, this seems impossible for the LJL potential because the range parameter controls not only the truncation distance but also the entire potential shape. Thus while the LJL potential may be perfectly adequate in situations where one wishes to employ a simple truncated attractive interparticle interaction, it comes with a caveat on its use for crystalline solid phases since it may be unable to represent in a qualitatively correct form the phase behaviour of real atomic systems whose overall features are determined in significant part by long-ranged dispersion interactions.
Author contributions
All authors were involved in conceiving and directing the research. O. M. and V. B. performed the numerical calculations. All authors wrote the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
NBW thanks Francesco Turci for drawing attention to a relevant reference and R. Evans for helpful comments on the manuscript. The computer simulations were carried out using the computational facilities of the Institute UTINAM and of the Mésocentre de calcul de Franche-Comté. This work was partly funded by UBFC within the project I-SITE BFC “STABHYDRA”.Notes and references
- X. Wang, S. Ramírez-Hinestrosa, J. Dobnikar and D. Frenkel, Phys. Chem. Chem. Phys., 2020, 22, 10624–10633 RSC.
- A. D. Bruce, N. B. Wilding and G. J. Ackland, Phys. Rev. Lett., 1997, 79, 3002–3005 CrossRef CAS.
- A. D. Bruce, A. N. Jackson, G. J. Ackland and N. B. Wilding, Phys. Rev. E, 2000, 61, 906–919 CrossRef CAS PubMed.
- A. N. Jackson, A. D. Bruce and G. J. Ackland, Phys. Rev. E, 2002, 65, 036710 CrossRef CAS PubMed.
- A. N. Jackson, PhD Thesis: Structural Phase Behaviour Via Monte Carlo Techniques, Univ. Edinburgh, 2001, Available at https://hdl.handle.net/1842/4850 Search PubMed.
- A. D. Bruce and N. B. Wilding, Adv. Chem. Phys., 2003, 127, 1 CrossRef CAS.
- G. R. Smith and A. D. Bruce, Europhys. Lett., 1996, 34, 91 CrossRef CAS.
- G. C. McNeil-Watson and N. B. Wilding, J. Chem. Phys., 2006, 124, 064504 CrossRef PubMed.
- A. V. Brukhno, J. Grant, T. L. Underwood, K. Stratford, S. C. Parker, J. A. Purton and N. B. Wilding, Mol. Sim., 2021, 47, 131–151 CrossRef CAS.
- A. V. Brukhno and J. Grant and T. L. Underwood, DL_Monte Source Code, v2.07, https://gitlab.com/dl_monte.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comp. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- P. Bauer, B. Hess and E. Lindahl, GROMACS 2022.6 Source code DOI:10.5281/zenodo.6103568.
- D. Frenkel and A. J. C. Ladd, J. Chem. Phys., 1984, 81, 3188–3193 CrossRef CAS.
- J. L. Aragones, C. Valeriani and C. Vega, J. Chem. Phys., 2012, 137, 146101 CrossRef CAS PubMed.
- J. L. Aragones, E. G. Noya, C. Valeriani and C. Vega, J. Chem. Phys., 2013, 139, 034104 CrossRef CAS PubMed.
- C. Vega, E. Sanz, J. L. F. Abascal and E. G. Noya, J. Phys.: Condens. Matter, 2008, 20, 153101 CrossRef.
- D. Frenkel, Eur. Phys. J. Plus, 2013, 128, 10 CrossRef.
- F. H. Stillinger, J. Chem. Phys., 2001, 115, 5208–5212 CrossRef CAS.
- Y. Choi, T. Ree and F. H. Ree, J. Chem. Phys., 1991, 95, 7548–7561 CrossRef CAS.
- A. Travesset, J. Chem. Phys., 2014, 141, 164501 CrossRef PubMed.
- A. J. Schultz and D. A. Kofke, J. Chem. Phys., 2018, 149, 204508 CrossRef PubMed.
- C. H. Loach and G. J. Ackland, Phys. Rev. Lett., 2017, 119, 205701 CrossRef PubMed.
- L. B. Pártay, C. Ortner, A. P. Bartók, C. J. Pickard and G. Csányi, Phys. Chem. Chem. Phys., 2017, 19, 19369–19376 RSC.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford U.P., 1987 Search PubMed.
- H. Adidharma and S. P. Tan, J. Chem. Phys., 2016, 145, 014503 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05474h |
‡ Note that in common with Wang et al., our treatment of the hcp phases fixes the c/a unit cell ratio to its ideal value 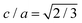 which can potentially create a small bias in the free energy.22 Other close packed structures are possibly stable23 but we do not consider them here. which can potentially create a small bias in the free energy.22 Other close packed structures are possibly stable23 but we do not consider them here. |
| § Note that this is a different choice of integration path to that adopted by Wang et al.1 |
| ¶ We find additionally (results not shown) that bcc is unstable with respect to fcc and hcp for all values of rc shown in Fig. 5. |
| || This cutoff accords with previous comparisons of the r dependence of the radial distribution functions for the fcc and hcp phases.25 |
| This journal is © the Owner Societies 2024 |