Internal conversion induced by external electric and magnetic fields†
R. R.
Valiev
 *a,
R. T.
Nasibullin
b,
B. S.
Merzlikin
b,
K.
Khoroshkin
b,
V. N.
Cherepanov
b and
D.
Sundholm
*a,
R. T.
Nasibullin
b,
B. S.
Merzlikin
b,
K.
Khoroshkin
b,
V. N.
Cherepanov
b and
D.
Sundholm
 a
a
aDepartment of Chemistry, Faculty of Science, P.O. Box 55 (A.I. Virtanens plats 1), FIN-00014 University of Helsinki, Helsinki, Finland. E-mail: valievrashid@gmail.com
bTomsk State University, 36 Lenin Avenue, Tomsk, Russia
First published on 11th January 2024
Abstract
We have developed a new methodology for calculating contributions to the rate constants (kIC) of internal conversion that are induced by external electric (kIC-E) or magnetic (kIC-M) fields. The influence of the external electric and magnetic fields on the kIC was estimated for seven representative molecules. We show that the kIC-E contribution calculated at a field strength of 1011 V m−1 is generally as large as the kIC rate constant in the absence of the external field. For indocyanine green, azaoxa[8]circulene, and pyromitene 567, the kIC-E contribution is as large as kIC already at a field strength of 109 V m−1. Such electric-field strengths occur for example in plasmonic studies and in strong laser-field experiments. The induced effect on the kIC rate constant should be accounted for in calculations of photophysical properties of molecules involved in such experiments. The induced effect of an external magnetic field on kIC can be neglected in experiments on Earth because the magnetic contribution becomes significant only at very strong magnetic fields of 104–105 T that cannot be achieved on Earth. However, the magnetic effect on the rate constant of internal conversion can be important in astrophysical studies, where extremely strong magnetic fields occur near neutron stars and white dwarfs.
1. Introduction
The interaction of electromagnetic fields with matter at the molecular level is one of the main tasks in photophysical studies1–7 since the knowledge of the energies of electronic states and their lifetime are important for understanding molecular luminescence properties.8–10 The energy of excited states can at low molecular concentration be converted to vibrational energy of lower-lying states by nonradiative transitions and to light by radiative intramolecular electronic transitions.11 The intramolecular nonradiative electronic transitions are the internal conversion (IC) and the intersystem crossing (ISC). The IC process is the electronic transition between states with the same electron spin and the ISC transition occurs between states with different spin. The radiative transition between the singlet electronic states is called fluorescence and phosphorescence between state with different spin multiplicity.The expressions for the rate constants can be derived by using first-order perturbation theory.12 The nonadiabatic coupling interaction (NAC) operator is the perturbation operator in case of IC and the spin–orbit coupling (SOC) interaction operator is the perturbation operator of the ISC process. The electric dipole operator is the perturbation operator for fluorescence when adopting the electric dipole approximation. A variety of theoretical models for quantum chemical calculations of rate constants or deactivation-channel probabilities of electronic excited states of isolated molecules have been developed by many research groups.12–19 More deactivation channels are opened when the molecule interacts with an electromagnetic field. For example, when a molecule is located near a plasmonic nanoparticle, the radiative rate constant or fluorescence efficiency can be strongly enhanced or it decreases due to the interaction with the electromagnetic field of the plasmon,7 which also influences the fluorescence quantum yield. In general, it is assumed that the rate constants of IC and ISC are not significantly affected when a molecule is in the vicinity of a plasmonic system or by a strong laser field.20–22 However, this assumption can be questioned. Strek estimated the influence of external electric fields on the internal conversion rate constant (kIC) using a simple model.23 It was shown that an external electric field of 108–109 V m−1 can strongly influence the kIC rate constant. An electric field of that strength is comparable to the strength of the plasmonic field of nanoparticles.7
In this work, we derive expressions for calculating rate constants of internal conversion for molecules that are exposed to strong electric or magnetic fields. The expressions have been adapted for quantum chemical calculations. We use the new theoretical model in calculation of rate constants of internal conversion to estimate the influence of external electric and magnetic fields on the kIC rate constants. The methods are applied to molecules that emit light in the infrared, red, green, blue, and ultraviolet range of the spectrum. The studied molecules are isophlorin (ISO), indocyanine green (ICG), pyromitene (PM567) azaoxa8circulene (4B), 2,2′′-dimethyl-p-terphenyl (BM-Terphenyl), 2-(4-Biphenylyl)-5-(4-t-butylphenyl)-1,3,4-oxadiazol (BPBD-365) and 2-(1-Naphthyl)-5-phenyloxazol (a-NPO).
2. Theory and computations
2.1. Internal conversion in the absence of external fields
In the works of Plotnikov24 and Artyukhov25 as well as in our recent studies,12,15 it was shown that the approximation, where the energy of the first excited singlet state (S1) is converted mainly into the vibrations of the X–H bonds (X = N, O and C), yields kIC values that agree within one order of magnitude with those calculated at more accurate levels of theory. The kIC rate constant between the p and q states is then given by | (1) |
![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) |ψq〉 with
|ψq〉 with  is the matrix element of the nonadiabatic coupling operator (NACME) between Ψp and Ψp, and Epq is energy difference between the p and q states. The Rα coordinate is along the α-th X–H bond. Qpq is a vibrational factor that can be written as
is the matrix element of the nonadiabatic coupling operator (NACME) between Ψp and Ψp, and Epq is energy difference between the p and q states. The Rα coordinate is along the α-th X–H bond. Qpq is a vibrational factor that can be written as| Qpq = NXH × 6.25 × 106 × e−Epq/2.17 | (2) |
Here, NXH is the number of accepting X–H modes, Epq in the expressions (1) and (2) is the energy difference in 103 cm−1. The expression for the square of the NACME can be written as
 | (3) |
 and
and  are Slater determinants and Aiap, Ajbq are configurational interaction coefficients. The a, b are indices denote virtual molecular orbitals (MO) and i, j are indices of the occupied MOs. The NACME in (3) is non-zero when the left and right determinants differ by at most one MO because
are Slater determinants and Aiap, Ajbq are configurational interaction coefficients. The a, b are indices denote virtual molecular orbitals (MO) and i, j are indices of the occupied MOs. The NACME in (3) is non-zero when the left and right determinants differ by at most one MO because ![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) is one electron operator. Expression (3) consists of two terms:
is one electron operator. Expression (3) consists of two terms: | (4) |
The MOs are expanded in the basis functions (χ) located at the X–H bonds yielding the final expression for NACME:
 | (5) |
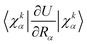 is 0.1 for each X–H bond. More details can be found in ref. 15 and 25. The final expression for kIC can then be written as
is 0.1 for each X–H bond. More details can be found in ref. 15 and 25. The final expression for kIC can then be written askIC = 1.6 × 109·〈ψp|![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) |ψq〉2, |ψq〉2, | (6) |
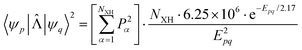 | (7) |
 for each X–H bond. Using this model, it is possible to estimate the individual contributions from each X–H mode to the NACME.
for each X–H bond. Using this model, it is possible to estimate the individual contributions from each X–H mode to the NACME.
2.2. Internal conversion in the presence of electric or magnetic fields
The influence of external field on kIC can be obtained by using second-order perturbation theory,26 where Ô =![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) +
+ ![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) ·
·![[W with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0057_20d1.gif) is the perturbation operator.
is the perturbation operator. ![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) denotes the electric or the magnetic dipole-moment operator and
denotes the electric or the magnetic dipole-moment operator and ![[W with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0057_20d1.gif) is the field strength. The zero order Hamiltonian is then
is the field strength. The zero order Hamiltonian is then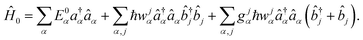 | (8) |
Here 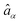 ,
, 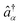 are fermion annihilation and creation operators of the electronic state α and Eα0 is its electronic energy.
are fermion annihilation and creation operators of the electronic state α and Eα0 is its electronic energy. ![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) j and
j and  are the boson annihilation and creation operators of the phonons, wαj is the frequency of the j-th phonon, and gαj= (Mjwjα/2ħ)1/2ΔRjα is dimensionless parameter where ΔRjα corresponds to the displacement from the equilibrium position of the ground state.
are the boson annihilation and creation operators of the phonons, wαj is the frequency of the j-th phonon, and gαj= (Mjwjα/2ħ)1/2ΔRjα is dimensionless parameter where ΔRjα corresponds to the displacement from the equilibrium position of the ground state. ![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) is the perturbation operator that in the absence of external fields gives the first-order contribution to the IC rate constant (kIC). In the presence of external fields, the perturbation operator can either be Ô =
is the perturbation operator that in the absence of external fields gives the first-order contribution to the IC rate constant (kIC). In the presence of external fields, the perturbation operator can either be Ô = ![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) +
+ ![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) ·
·![[W with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0057_20d1.gif) or Ô =
or Ô = ![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) ·
·![[W with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0057_20d1.gif) . In the first case, the non-vanishing contribution to induced radiationless transition appears only at the second order of perturbation theory. When Ô =
. In the first case, the non-vanishing contribution to induced radiationless transition appears only at the second order of perturbation theory. When Ô = ![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) ·
·![[W with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0057_20d1.gif) , the radiative process is the first order and the induced radiationless transition appear at the second order without the
, the radiative process is the first order and the induced radiationless transition appear at the second order without the  operator. Such process must occur in two steps27,28 and has smaller contribution to the induced IC than with Ô =
operator. Such process must occur in two steps27,28 and has smaller contribution to the induced IC than with Ô = ![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) +
+ ![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) ·
·![[W with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0057_20d1.gif) . Therefore, we consider only the case with Ô =
. Therefore, we consider only the case with Ô = ![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) +
+ ![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) ·
·![[W with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0057_20d1.gif) as the perturbation operator.
as the perturbation operator.
The electronic matrix elements of Ô = ![[capital Lambda, Greek, circumflex]](https://www.rsc.org/images/entities/char_e0a8.gif) +
+ ![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) ·
·![[W with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0057_20d1.gif) at the second-order perturbation theory level is
at the second-order perturbation theory level is
 | (9) |
Here, Pspj is electronic factor of the j-th mode between the electronic p and s states. The q and p can be associated with the singlet electronic ground state (S0) and the first excited electronic singlet state (S1), respectively. The intermediate state s is an electronic state that is energetically above S1. Eqn (7) can be simplified to
 | (10) |
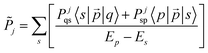 | (11) |
Thus, external fields influence only the electronic factor. Eqn (11) can be inserted into eqn (7) yielding expression (10), which can be used for estimating the rate constants for internal conversion kIC-E and kIC-M in the presence of external electric or magnetic fields, respectively.
 | (12) |
![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) is the electric dipole operator (
is the electric dipole operator (![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) ) in case of an electric field and the magnetic dipole operator (
) in case of an electric field and the magnetic dipole operator (![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) ) when the molecule is exposed to a magnetic field. Expression (10) shows that it is possible to estimate the influence of external fields separately for each vibrational mode via
) when the molecule is exposed to a magnetic field. Expression (10) shows that it is possible to estimate the influence of external fields separately for each vibrational mode via ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) j.
j.
The electric and magnetic transition moments between the electronic states q and s are given by  and
and  , respectively.
, respectively.
The X–H bond approximation of kIC calculations can be used only for molecules having X–H bonds including organometallic compounds.16,29,30
2.3. Computational details
The molecular structure optimizations, calculations of the second derivative of the potential energy surface (hessian) of the S1 state and the electric (dif) and magnetic (mif) transition dipole moment between the Si and Sf states were performed at the density functional theory (DFT) and the time-dependent density functional theory (TDDFT)31,32 levels using the B3LYP33 functional and the 6-31G**34 basis set with the DALTON software.35 We calculated Pj for the 50 lowest electronic states. We assume that the molecule is oriented such that the scalar product of E or B with the electric dipole moment or magnetic dipole moment is largest, which can is obtained when these vectors are collinear. kIC-E and kIC-M denote the contributions to the rate constants of internal conversion that are induced by electric or magnetic external fields, respectively.To verify the role of double excitations, which are not explicitly considered at the TDDFT level, we calculated the 50 lowest electronic singlet states at the complete active space self-consistent (CASSCF) level for molecules with the smallest (ISO), medium (4B) and largest (BM-Terphenyl) excitation energy (S1–S0).36 The active space consisted of 12 electrons in 12 molecular orbitals. The calculations were performed using Firefly.37,38 The calculations show that the double excitations contribute with about less than 10% to the wavefunctions of the 50 excited states suggesting that the results obtained at the TDDFT level are reliable.
3. Result and discussion
Rate constants for internal conversion have been calculated for isophlorin (ISO), indocyanine green (ICG), pyromitene (PM567) azaoxa8circulene (4B), 2,2′′-Dimethyl-p-terphenyl (BM-Terphenyl), 2-(4-Biphenylyl)-5-(4-t-butylphenyl)-1,3,4-oxadiazol (BPBD-365) and 2-(1-Naphthyl)-5-phenyloxazol (a-NPO) at the B3LYP/6-31G** level using the approach described in Section 2. The calculated kIC in the absence of external fields and the strengths of the electric (E) and magnetic (H) fields when induced contributions kIC-E and kIC-M are as large as kIC are given in Table 1.| E pq | k IC | E | B | |
|---|---|---|---|---|
| ISO | 7829 | 3.7 × 1010 | 2.1 × 1011 | 5.0 × 105 |
| ICG | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
4.1 × 108 | 1.0 × 109 | 1.4 × 104 |
| PM567 | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 333 333 |
2.0 × 106 | 7.0 × 109 | 1.9 × 104 |
| 4B | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 637 637 |
6.6 × 106 | 5.7 × 109 | 1.4 × 104 |
| a-NPO | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 180 180 |
3.2 × 106 | 9.0 × 1010 | 1.7 × 104 |
| BPBD-365 | 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 664 664 |
2.1 × 106 | 7.0 × 109 | 1.8 × 105 |
| BM-Terphenyl | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504 504 |
3.4 × 105 | 3.0 × 1010 | 6.0 × 104 |
The electric-field induced contribution to kIC-E become as large as kIC when the external electric field strength is stronger than 1.0 × 109–2.1 × 1011 V m−1. An electric field of 1010–1011 V m−1 is very strong and can be compared to the strength of the internal electric field in molecules caused by its electrons. When molecules are exposed to that strong external electric fields they might dissociate. However, a field strength of 1.0 × 109 V m−1 can be observed in molecules exhibiting plasmonic effects. Indocyanine molecules are widely used in plasmonic enhancement fluorescence measurements.7 The dependence of kIC-E on E is a quadratic. At an electric field strength of 1.0 × 109 V m−1, the kIC-E contribution to kIC of ICG becomes one order of magnitude larger than the kIC rate constant in the absence of the electric field. Thus, at the contribution to kIC due to the electric field can significantly change its molecular photophysical properties implying that the kIC-E contribution must be considered when calculating the fluorescence quantum yield.7 In general, the kIC-E contribution is larger than kIC at a field strength of 1011 V m−1 and kIC-E does not significantly depend on the energy gap between S1 and S0.
The magnetic-field induced effect on IC is almost negligible at the experimental conditions on Earth because it becomes significant at very strong magnetic fields (B) of about 104 T. The kIC-M contribution does not depend on the energy gap between S1 and S0. The magnetic-field induced contribution to kIC for isophlorin becomes as large as kIC for a very strong magnetic field (B) of 105 T, which is one order of magnitude stronger than for the other studied molecules. The kIC-M contribution to the kIC of isophlorin is small because most of its magnetic dipole transition moments between Si and S0 are equal to zero. The kIC-M contribution can be important in atomic spectroscopy39,40 and in astrophysical studies of the interstellar medium,41,42 of white dwarfs,43,44 and of neutron stars at different stages of their existence.45
We also analysed the main acceptors of the electronic excitation energy both in the absence and the presence of an electric or a magnetic field. The acceptors are shown with ellipses in Fig. 1–3. Where one sees that the number of X-H acceptors increases when the molecules are exposed to an external electric field. In case of ISO, all X–H bonds become good acceptors when the molecule is exposed to an electric field. Substitution of the X–H bonds can either increase or decrease kIC because some X–H bonds may be good acceptors in the presence of an external field and others are good acceptors in the absence of the field.
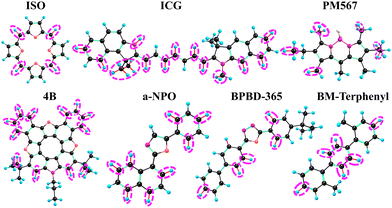 | ||
| Fig. 1 The main acceptors of the energy of the S1 state in the IC process in the absence of the external electric field. | ||
 | ||
| Fig. 2 The main acceptors of the energy of the S1 state in the IC process in the presence of the external electric field. | ||
 | ||
| Fig. 3 The main acceptors of the energy of the S1 state in the IC process in the absence of the external magnetic. | ||
Summary and conclusion
The influence of external electric and magnetic fields on the kIC for seven representative molecules was estimated using the theoretical model developed in this work. We showed that the electric-field contribution to the rate constant of internal conversion kIC-E at strong field strengths of 1011 V m−1 can generally become as large as the rate constant of internal conversion kIC in the absence of the field. The present study showed that kIC-E for ICG, 4B, and PM is as large as kIC at a field strength of about 109 V m−1, which may affect the photophysical properties of ICG derivatives that are widely used in plasmonic enhancement fluorescence7 and of PM derivatives that are used in lasing processes.21 The electric fields of plasmons or the electric field in strong laser-radiation experiments can reach this field strength. The electric-field effect can decrease the fluorescence quantum yield in such applications. The induced effect of an external magnetic field appears at very strong magnetic fields of 104–105 T. The magnetic-field contribution to the rate constant of internal conversion kIC-M can therefore be omitted in experiments on Earth. However, the magnetic-filed contribution may become significant in astrophysical studies of molecules and chemical processes near neutron stars and white dwarfs, whose atmospheres are exposed to extreme magnetic fields.The developed model also gives the opportunity to determine which X–H bonds accept the electronic excitation energy and how the number of acceptors changes due to the presence of an external field. For the studied molecules, the number of X-H acceptors increases when they are exposed to an external electric field. By substituting the X–H bonds, the induced electric-field effect on the internal conversion can either increase or decrease the rate constant because some X–H bonds can be good acceptors in the presence of an external field and others are good acceptors in the absence of the field.
When the external fields are strong, kIC-E and kIC-M that are obtained at the second order in perturbation theory can be compared to kIC, which is obtained at first-order perturbation theory level, without violating the applicability condition of the perturbation theory because we deal with internal conversion processes of different physical nature. Thus, none of them serves as a correction to the other one in the sense of perturbation theory.
The developed model can be applied to organic or organometallic compounds that have X–H bonds. The X–H bond approximation can be applied to lots of molecules because such molecules are common. It cannot be applied to specific molecules without X–H bonds such as fullerenes, cyclocarbons or pure metallic clusters. We considered only 50 excited states in expression (9), which may limit the accuracy of the calculated rate constants because further contributions can occur when including higher electronic intermediate states in the calculation. However, these contributions are not expected to significantly affect the kIC-E and kIC-M contributions to the rate constants because the contribution from the last five (from the 46th to the 50th) electronic states is negligible for kIC-E and kIC-M.
In strong external magnetic fields, the zero-field splitting of triplet states increase. The energy gap between the S1 state and energetically lower triplet states will decrease. Therefore, the influence of the external magnetic field on the intersystem crossing (ISC) process can increase and may appear at a weaker magnetic field than for IC. The acceptors modes of the ISC process are mainly C–C bonds with vibrational energies of ∼1400 cm−1 in the Franck–Condon approximation and the out-of-plane modes with vibrational energies of 400–600 cm−1 in the Herzberg–Teller approximation.14,46 Therefore, the approximation considering only X–H bonds is not expected to work well for ISC processes.
Author contributions
Rashid Valiev suggested the theory and the algorithms. Rashid Valiev and Rinat Nasibullin implemented the algorithms and carried out the quantum chemical calculations. All authors contributed by participating in the discussion of the results and writing the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by Russian Science Foundation (project No. 23-73-10081). We acknowledge computational resource SKIF ‘‘Siberia’’. This work was also supported by the Academy of Finland through projects 340582 (RRV) and 340583 (DS).References
- H. Ren, J.-L. Yang, W.-M. Yang, H.-L. Zhong, J.-S. Lin, P. M. Radjenovic, L. Sun, H. Zhang, J. Xu, Z.-Q. Tian and J.-F. Li, ACS Mater. Lett., 2020, 3, 69–76 CrossRef.
- R. Kumar, S. Y. Janbandhu, G. K. Sukhadeve and R. S. Gedam, J. Mater. Res., 2022, 38, 557–570 CrossRef.
- B. Pramanick, M. Chawla and P. F. Siril, Opt. Mater., 2023, 137, 113553 CrossRef CAS.
- A. Nazir, P. Huo, H. Wang, Z. Weiqiang and Y. Wan, J. Mater. Sci., 2023, 58, 6474–6515 CrossRef CAS PubMed.
- B. Ai, Z. Fan and Z. J. Wong, Microsyst. Nanoeng., 2022, 8, 5 CrossRef CAS.
- M. M. Olaimat, L. Yousefi and O. M. Ramahi, J. Opt. Soc. Am. B, 2021, 38, 638–651 CrossRef.
- N. K. Ibrayev, E. V. Seliverstova, R. R. Valiev, A. E. Kanapina, A. A. Ishchenko, A. V. Kulinich, T. Kurtén and D. Sundholm, Phys. Chem. Chem. Phys., 2023, 25, 22851–22861 RSC.
- D. Blasco, R. T. Nasibullin, R. R. Valiev and D. Sundholm, Chem. Sci., 2023, 14, 3873–3880 RSC.
- L. Tučková, M. Straka, R. R. Valiev and D. Sundholm, Phys. Chem. Chem. Phys., 2022, 24, 18713–18721 RSC.
- I. Soldevilla, A. García-Camacho, R. T. Nasibullin, M. E. Olmos, M. Monge, D. Sundholm, R. R. Valiev, J. M. López-de-Luzuriaga and M. Rodríguez-Castillo, J. Mater. Chem. C, 2022, 10, 4894–4904 RSC.
- E. S. Medvedev and V. I. Osherov, Radiationless transitions in polyatomic molecules, Springer Series in Chemical Physics, Springer, vol. 57, 1995 Search PubMed.
- R. R. Valiev, B. S. Merzlikin, R. T. Nasibullin, A. Kurtzevitch, V. N. Cherepanov, R. R. Ramazanov, D. Sundholm and T. Kurtén, Phys. Chem. Chem. Phys., 2023, 25, 6406–6415 RSC.
- R. R. Valiev, V. N. Cherepanov, G. V. Baryshnikov and D. Sundholm, Phys. Chem. Chem. Phys., 2018, 20, 6121–6133 RSC.
- R. R. Valiev, V. N. Cherepanov, R. T. Nasibullin, D. Sundholm and T. Kurtén, Phys. Chem. Chem. Phys., 2019, 21, 18495–18500 RSC.
- R. R. Valiev, R. T. Nasibullin, V. N. Cherepanov, G. V. Baryshnikov, D. Sundholm, H. Ågren, B. F. Minaev and T. Kurtén, Phys. Chem. Chem. Phys., 2020, 22, 22314–22323 RSC.
- R. R. Valiev, R. T. Nasibullin, V. N. Cherepanov, A. Kurtsevich, D. Sundholm and T. Kurtén, Phys. Chem. Chem. Phys., 2021, 23, 6344–6348 RSC.
- M. Bracker, C. M. Marian and M. Kleinschmidt, J. Chem. Phys., 2021, 155, 014102 CrossRef CAS PubMed.
- Y. Niu, Q. Peng, C. Deng, X. Gao and Z. Shuai, J. Phys. Chem. A, 2010, 114, 7817–7831 CrossRef CAS PubMed.
- Q. Peng, Y. Niu, Q. Shi, X. Gao and Z. Shuai, J. Chem. Theory Comput., 2013, 9, 1132–1143 CrossRef CAS PubMed.
- N. Ibrayev, G. Omarova, E. Seliverstova, A. Ishchenko and N. Nuraje, Eng. Sci., 2020, 14, 69–77 Search PubMed.
- R. R. Valiev, E. N. Telminov, T. A. Solodova, E. N. Ponyavina, R. M. Gadirov, G. V. Mayer and T. N. Kopylova, Chem. Phys. Lett., 2013, 588, 184–187 CrossRef CAS.
- E. Alikhaidarova, D. Afanasyev, N. Ibrayev and N. Nuraje, Polym. Adv. Technol., 2021, 33, 1000–1008 CrossRef.
- W. Strek, Chem. Phys. Lett., 1978, 57, 121–124 CrossRef CAS.
- V. G. Plotnikov, Int. J. Quantum Chem., 1979, 16, 527–541 CrossRef CAS.
- V. Y. Artyukhov, A. I. Galeeva, G. V. Maier and V. V. Ponomarev, Opt. Spectrosc., 1997, 83, 685–690 Search PubMed.
- J. Jortner and A. Ben-Reuven, Chem. Phys. Lett., 1976, 41, 401 CrossRef CAS.
- L. D. Landau and L. M. Lifshitz, Quantum Mechanics Non-Relativistic Theory, Butterworth-Heinemann, 3rd edn, 1981, vol. 3 Search PubMed.
- B. S. Merzlikin, V. N. Cherepanov, K. Khoroshkin and R. R. Valiev, Chem. Phys. Lett., 2024, 836, 141032 CrossRef CAS.
- E. A. Katlenok, D. M. Kryukov, A. E. Kurtsevich, K. M. Degtyarenko, R. R. Valiev, O. V. Levin, V. Y. Kukushkin and A. V. Rozhkov, Inorg. Chem., 2023, 62(28), 11080–11094 CrossRef CAS PubMed.
- E. A. Katlenok, A. V. Rozhkov, R. R. Ramazanov, R. R. Valiev, O. V. Levin, D. O. Goryachiy, I. V. Taydakov, M. L. Kuznetsov and V. Y. Kukushkin, Inorg. Chem., 2022, 61(23), 8670–8684 CrossRef CAS PubMed.
- M. Casida, Recent Advances in Density Functional Methods, World Scientific, Singapore, 1999, pp. 155–192 Search PubMed.
- M. Casida and M. Huix-Rotllant, Annu. Rev. Phys. Chem., 2012, 63, 287–323 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- V. A. Rassolov, J. A. Pople, M. A. Ratner and T. L. Windus, J. Chem. Phys., 1998, 109, 1223–1229 CrossRef CAS.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansik, H. J. Aa. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. Rybkin, P. Salek, C. C. M. Samson, A. Sánchez de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, WIREs Comput. Mol. Sci., 2014, 4, 269–284 CrossRef CAS PubMed.
- B. O. Roos and P. R. Taylor, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- A. A. Granovsky, J. Chem. Phys., 2011, 134, 214113 CrossRef PubMed.
- A. Granovsky, Firefly version 8, https://classic.chem.msu.su/gran/firefly/index.htm.
- C. Iu, G. R. Welch, M. M. Kash, D. Kleppner, D. Delande and J. C. Gay, Phys. Rev. Lett., 1991, 66, 145–148 CrossRef CAS PubMed.
- G. R. Welch, M. M. Kash, C. Iu, L. Hsu and D. Kleppner, Phys. Rev. Lett., 1989, 62, 893–896 CrossRef CAS PubMed.
- L. F. Burlaga, N. F. Ness, D. B. Berdichevsky, L. K. Jian, W. Kurth, J. Park, J. Rankin and A. Szabo, Astrophys. J., 2022, 932, 59–75 CrossRef.
- R. Skalidis and K. Tassis, Astron. Astrophys., 2021, 647, A186 CrossRef CAS.
- R. H. Garstang, Rep. Prog. Phys., 1977, 40, 105–154 CrossRef CAS.
- P. Dufour, J. Liebert, G. Fontaine and N. Behara, Nature, 2007, 450, 522–524 CrossRef CAS PubMed.
- D. Lai, Rev. Mod. Phys., 2001, 73, 629–662 CrossRef CAS.
- C. M. Marian, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(2), 187–203 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05409h |
| This journal is © the Owner Societies 2024 |
