Experimental determination of solvation free energy of protons in non-protic ionic liquids using Raman spectroscopy†
Aurelie
Rensonnet
 and
Cedric
Malherbe
and
Cedric
Malherbe
 *
*
University of Liege, Laboratory of Mass Spectrometry – Vibrational Spectroscopy, Allee du 6 aout 11 (Bat B6B), 4020 Liege, Belgium. E-mail: c.malherbe@uliege.be
First published on 4th January 2024
Abstract
Room temperature imidazolium-based ionic liquids (ILs) often present super-acidity, which can be characterized by the free energy of solvation of protons in ILs, ΔsolvG°(H+)IL. It can be derived from the consensus value of the free energy of solvation of protons in water if the free energy of transfer of protons from water to the ILs, ΔtG°(H+), is determined. However, the experimental determination of the free energy of transfer of protons relies on extra-thermodynamic hypotheses, as protons cannot be transferred from one solvent to another without a counterion. Here we propose to measure the Hammett acidity functions, which relies on the protonation equilibrium of specific pH-reporters, for the first time by Raman spectroscopy directly in acidic solution of 2,6-dichloro-4-nitroaniline in three 1-alkyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ILs. We demonstrated that the ΔtG°(H+) obtained by Raman spectroscopy and UV-visible spectroscopy were identical in the same 1-butyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide. Also, when the butyl substituent is replaced by a longer alkyl chain such as an octyl chain, the acidity in the IL is lowered. The free energies of solvation are calculated in four ILs from Raman spectroscopy data recorded directly in the acidic solutions. These values confirmed that the protons are less solvated in ILs than in water, hence their acidity. Raman spectroscopy also enables determination of the solvation number of the proton in imidazolium-based bis(trifluoromethylsulfonyl)imide ILs. The benefits of implementing Raman spectroscopy to determine the Hammett acidity function in ILs using a non-colored pH-reporter and in colored media are also discussed.
Introduction
Second-generation ionic liquids (ILs) are organic salts that are often molten at room temperature (by definition their fusion temperature must be below 100 °C). ILs are composed of large and asymmetric cations (e.g. disubstituted imidazoliums, Fig. 1A) often coupled with poorly coordinating anions (e.g. the bis(trifluoromethane)sulfonimide anion, NTf2−, Fig. 1A).1–4 Since the 1980s, these imidazolium-based ILs have replaced the first-generation ILs, built with chloroaluminates and that were extensively studied in the 1960s and 1970s. Indeed, the first-generation ILs were water and air sensitive, which is not the case for the second-generation.4 In the last two decades, the latter have been identified as interesting alternative solvents to conventional volatile organic compounds (VOCs, largely used as molecular solvents) due to their very low vapor pressure, low flammability, high electrical conductivity and large electrochemical window.5,6 One of the most interesting characteristics of ILs is that their physico-chemical properties, such as their viscosity or their acidity, can be controlled according to their constitutive ions, in opposition to classic molecular solvents.4,7 ILs have been used in various applications, for instance as electrolytes for batteries, fuel cells and solar cells, or as solvents for catalytic processes and liquid–liquid separation.3 Actually, for many chemical applications, the level of acidity achievable in the ILs, which is much higher than the acidity accessible in water for instance (i.e. negative pH), turns out to be critical in terms of reactivity, and yet difficult to predict.The fundamental level of acidity accessible in ILs is related to the activity of protons, hence to the free energy of solvation of protons in these solvents, ΔsolvG°(H+).8–10 Data of free energy of solvation for the proton in non-aqueous solvents, and especially ILs, are still missing because their experimental evaluation is not straightforward.11 Yet, according to the Hess law shown in Fig. 1B, ΔsolvG°(H+) data for non-aqueous solvents can be derived from the consensus value in water, taken as the solvent of reference, with a free energy of solvation for protons of −1112.5 kJ mol−1 (−265.9 kcal mol−1).10 The key point is estimating the free energy of transfer, ΔtG°(H+), corresponding to the transfer of protons from water to the non-aqueous solvents like ILs. Indeed, ΔtG°(H+) is related to the activity coefficient of transfer, Γt(H+), defined as the ratio of the relative activities of the solvated protons in water, a(H+)W, and in the IL, a(H+)IL (eqn (1)).8 By definition, the cologarithm of Γt(H+) also expresses the shift between the relative acidity (pH) scales in both solvents as shown in Fig. 1C.12
 | (1) |
The difficulty in estimating the energy of transfer of protons, either experimentally or by computation, relies in that the proton carries a positive charge and therefore cannot be transferred from one solvent to another without a counter-anion, which itself is experiencing a change in solvation during the transfer. As a consequence, the experimental estimation of Γt(H+) or ΔtG°(H+) relies on extra-thermodynamic assumptions.8,13,14 Hammett and Deyrupt proposed the Hammett acidity function, H0, defined by eqn (2), based on the protonation equilibrium of a colored pH-reporter, chosen so that the transfer activity coefficients of the basic (R) and the acid forms (HR+) of the pH-reporter are equal.15 The extra-thermodynamic hypothesis proposed by Hammett postulates that both forms are actually experiencing the same change of solvation from water to the non-aqueous solvent. While the method was proposed to measure the acidity of concentrated solutions of sulfuric and perchloric acids in water using nitroanilines by UV-Vis spectroscopy, the approach was extended and has become the reference method to measure the acidity in non-aqueous solvents, including ILs.12,16,17 In eqn (2), (pKA,R)W is the pKA of the pH-reporter couple (HR+/R) determined in water, while the ratio of relative activities of the acidic and basic forms of the pH-reporter are to be experimentally determined in diluted solution in the non-aqueous solvent. Since the acidity constant for an acid–base couple in one solvent is defined by eqn (3), we can demonstrate that the value of the H0 is equivalent to the pH value of the solution in the non-aqueous solvent, expressed in the scale of pH developed in water (Fig. 1C), if we hypothesize that the activity coefficient of transfer of the acidic form of the pH-reporter (HR+) is identical to the activity coefficient of transfer of the basic form of the pH-reporter (R), as shown in eqn (4). The Hammett acidity function extrapolated for a standard solution of H+ in non-aqueous molecular solvents (a(H+)IL = 1) enables estimation of the Γt(H+) (eqn (5)).8,9,15
 | (2) |
 | (3) |
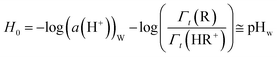 | (4) |
 | (5) |
However, the method initially proposed by Hammett suffers from a few limitations, especially in ILs, mainly due to the choice of colored nitroanilines as pH-reporter. Indeed, the nitroaniline conjugated π-system may induce specific interactions with the aromatic rings of the IL's cations, hence invalidating the extra-thermodynamic hypothesis. Also, different colored pH-reporters followed by UV-Vis spectroscopy led to a shifted value of H0 indicating the presence of ion pairs in ILs and leading to the experimental measurement of an apparent acidity function, as suggested by Bruckenstein.17,18 Complementary techniques to UV-Vis spectroscopy have been proposed to extend the Hammett method to non-colored pH-reporters, such as NMR measurements using mesityl oxide, or IR measurements using pyridine or acetonitrile, but they are often limited to qualitative acidity analyses.19–21
In this paper, we proposed to study the acidity of three imidazolium-based ILs ([BMIm][NTf2], [EMIm][NTf2] and [OMIm][NTf2]) by Raman spectroscopy using the 2,6-dichloro-4-nitroaniline as a pH-reporter in comparison to data obtained by UV-Vis spectroscopy. This approach was never attempted before, even though Raman spectroscopy offers more flexibility to meet the extra-thermodynamic hypotheses than UV-Vis spectroscopy, as we described in this paper. The data obtained enables us to discuss the influence of a longer alkyl chain (octyl) on the imidazolium cations on the acidity experienced in the corresponding IL.
Material and methods
Materials
All chemicals, either purchased or synthesized, were transferred and handled under dry conditions (atmosphere water content below 3 ppm) in an argon-filled glovebox. Bis(trifluoromethanesulfonyl)imide (HNTf2, 99%, TCI Chemicals) and 2,6-dichloro-4-nitroaniline (96%, SigmaAldrich) were purchased and transferred in the glovebox without further purification. N-Methylimidazole (MIm, Sigma Aldrich, 99%) was distilled once under vacuum (10−2 mbar) on KOH (Sigma Aldrich). 1-Bromoethane, 1-bromobutane and 1-bromooctane (TCI Chemicals, ≥99%), ethyl acetate (AE, Fisher Chemical, ≥99.8%), acetonitrile (AN, Fisher Chemical, ≥99.9%) were distilled twice in the open air on P2O5 (VWR Chemicals, ≥82%). The 1-bromooctane was distilled under reduced pressure due to its high boiling temperature. Dichloromethane (DCM, Acros Organics, ≥99.8%) and methanol (MeOH, Fisher Chemical, ≥99.8%) were once distilled at atmospheric pressure. Deionized water was distilled three times on quartz. Commercial 1-butyl-3-methylimidazolium Bis(trifluoromethanesulfonyl)imide ([BMIm][NTf2], 98%, TCI Chemicals) was dried under vacuum (10−2 mbar) at 50 °C for 36 hours before being transferred in the glovebox. Three imidazolium-based ionic liquids were synthesized (as described in the ESI†) to study the influence of the hydrophobicity on the acidity of the medium with the same anion: 1-ethyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide ([EMIm][NTf2]), 1-butyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide ([BMIm][NTf2], to be compared with the commercial product), and 1-methyl-3-octylimidazolium bis(trifluoromethanesulfonyl)imide ([OMIm][NTf2]).Solutions
For each ionic liquid studied in this paper, a series of acidic solution of HNTf2 in the ionic liquid (either [BMIm][NTf2], [EMIm][NTf2] or [OMIm][NTf2]) were prepared by dissolving the right amount of HNTf2 directly in the ionic liquid or in a solution of the pH-reporter in the ionic liquid. The preparation of all solutions studied in this paper is detailed in the ESI.†Methods
Raman spectra were obtained directly in the ionic liquid solutions kept under argon atmosphere using a Labram 300 Raman spectrometer (Horiba) interfaced with a 532 nm DPSS laser (input power on the sample 40 mW) and with a 90° angle objective. The spectra were recorded in the Raman wavelength shift ranging from 200 to 3600 cm−1 with an acquisition time typically of a few seconds. Since the addition of HNTf2 in the solution led to the observation of a fluorescent background, the Raman spectra were baseline corrected using a polynomial of the 4th order in the entire range of Raman wavelength shift. The data processing is further described in the ESI.†Molecular absorption spectra in the ultraviolet-visible (UV-Vis spectroscopy) were obtained using a Lambda 25 UV-Vis spectrophotometer (PerkinElmer) in the wavelength region between 300 and 700 nm. The spectra were obtained using a TrayCell (Hellma Analytics) with a 10× factor mirror.
Determining the Hammett acidity function
It has been proposed that the determination of the Hammett acidity functions can be used to determine the Brønsted acidity of ionic liquids,12 but only a few literature studies report H0 values for ILs. The H0 value of a solution of pH-reporter can be calculated from eqn (2), knowing that the pKa of the 2,6-dichloro-4-nitroaniline in water is −3.329 and by estimating the degree of protonation of uncharged 2,6-dichloro-4-nitroaniline (xR). Indeed, for diluted solutions, the relative activity of a solute equals its molar concentration, in which case the ratio of relative activities in eqn (2) can be estimated from spectroscopic data as described in eqn (6), where xR is the molar fraction of the basic form of the pH-reporter (R), (1 − xR) is the molar fraction of the acidic form of the pH-reporter, I is the intensity measured for the solution, IR is the intensity measured for the solution for which all pH-reporter molecules are in the basic form, and IHR+ is the intensity measured for the solution for which all pH-reporter molecules are in the acidic form. Eqn (2) can therefore be rewritten as eqn (7). | (6) |
 | (7) |
Results and discussion
Raman spectra of [BMIm][NTf2] and solution of 2,6-dichloro-4-nitroaniline
Typical Raman spectra obtained for the pure ionic liquid [BMIm][NTf2] and the solution of the pH-reporter 2,6-dichloro-4-nitroaniline in [BMIm][NTf2] are shown in Fig. 2. In that range of wavelength shifts, the ionic liquid contributes to the spectrum by both its cation (BMIm+) and anion (NTf2−). The main contributions of the imidazolium are located at 1026 cm−1 (attributed to the stretching of the CN and the bending of the CNC from the aromatic ring), 1341 cm−1 (attributed to the in phase stretching of the CN–Calkyls) and 1421 cm−1 (attributed to the asymmetric stretching of the CNC from the aromatic ring and the in phase bending of the CN–Calkyls). The main contributions of the bistriflimide are located at 743 cm−1 (symmetric stretching of the SNS), 1138 cm−1 (attributed to the in plane symmetric stretching of the OSO) and 1244 cm−1 (attributed to the symmetric stretching of the CF3).22 All observed Raman bands associated to the bistriflimide anions are sensitive to the addition of HNTf2, acting as a strong acid in [BMIm][NTf2]. The Raman bands of the bistriflimide experience a shift in position upon protonation as discussed in the next section and shown in Fig. 3A.When the pH reporter 2,6-dichloro-4-nitroaniline is added to the [BMIm][NTf2], additional signals are observed at 1359 cm−1 (attributed to the symmetric stretching of the nitro substituent) and at 851 cm−1 (attributed to the elongation of the CN bonding the nitro substituent to the aromatic carbon) as shown in Fig. 2. Both signals tend to disappear when the pH reporter is protonated. While only the Raman band at 851 cm−1 appears as isolated from any contribution from the solvent, the band at 1359 cm−1 is five times higher in intensity and is readily isolated by decomposing the spectrum with two Voigt profiles (hybrid Gaussian–Lorentzian profiles) between 1320 and 1380 cm−1 (see Fig. 4). That band will be followed to derive the value of the Hammett acidity function by Raman spectroscopy.
Solvation number of protons in [BMIm][NTf2]
As shown in Fig. 3A, upon protonation of the amine of the pH-reporter following the addition of HNTf2 (a strong acid) in the medium, the band at 743 and 1244 cm−1 of the IL are red-shifted to 766 and 1255 cm−1 respectively, and to a lesser extent, the band at 1138 cm−1 is blue-shifted to 1135 cm−1. The molar fraction of free NTf2− anion in regards to the total amount of bistriflimide (either from the ionic liquid or the added HNTf2) can be determined by following the intensities of the Raman band at 743 cm−1 (associated to the deprotonated bistriflimide) and 766 cm−1 (associated to the bistriflimide acid) and knowing that the bistriflimide acid is 1.11 more Raman active than the bistriflimide anion. As shown in Fig. 3B, the molar fraction of free NTf2− decreases linearly when the molar fraction of HNTf2 in the medium increases, with a unitary slope of −0.99 ± 0.02. This behavior is consistent with a solvation number for protons of one. Indeed, when one proton is added to the medium through the dissociation of HNTf2, it only consumes one NTf2−. Would the solvation of proton involve two NTf2−, the slope would be −2 as drawn in Fig. 3B. That result indicates that the ionic liquid as solvent stabilizes the proton to a lower extent than water, in which the proton is coordinated by 6 molecules of water in the first sphere of solvation (although the molecules of water fast rearrange themselves).23 As a consequence, the proton would have a greater ability to react with bases in [BMIm][NTf2] that is less solvating, which is consistent with the super-acidity experienced in ionic liquids.Hammett acidity function in commercial [BMIm][NTf2] by Raman spectroscopy
The Raman spectra recorded for the solutions of 2,6-dichloro-4-nitroaniline (51.17 mM) in the [BMIm][NTf2] when the concentration of HNTf2 is increased are presented in Fig. 4A. The intensity of the Raman band of the basic form of the 2,6-dichloro-4-nitroaniline decreased as the quantity of HNTf2 increased. Indeed, as the strong acid HNTf2 dissolved in the ionic liquid, acidic protons are liberated in the solution, and can react with the basic form of the pH-reporter (R). However, a small amount of these protons will also react with basic impurities present in the ionic liquids. Indeed, imidazolium-based ionic liquids often contain residues of unreacted precursors, such as imidazole or halide (either chloride or bromide), as well as traces of solvent, such as water, all of which act as basic impurities in ionic liquids. Fig. 4B shows the evolution of the ratio of the molar fraction of the acidic form (1 − xR) and basic form (xR) of the pH-reporter as a function of the added concentration of HNTf2 (CHA) in the [BMIm][NTf2]. According to eqn (8), where xR is the molar fraction of the basic form of the pH-reporter, KA,R is the acidity constant for the pH-reporter in the considered solvent, CHA is the concentration of the added strong acid (here HNTf2) and CImp is the concentration of basic impurities in the ionic liquid, a straight line was drawn through the experimental data. The slope of the straight line enables to estimate the acidity constant of the 2,6-dichloro-4-nitroaniline to be 15 ± 1, which corresponds to a pKA value of 1.17 ± 0.03. The intercept enables to estimate the concentration of basic impurities in the concentrated solution of 2,6-dichloro-4-nitroaniline in [BMIm][NTf2] to 15 ± 6 mM. The experimental data corresponding to the solution with a concentration of HNTf2 of 13.8 was discarded (in red in Fig. 4B), since that concentration did not suffice to neutralize all basic impurities. | (8) |
Finally, the values of H0 calculated from the Raman spectra as a function of the cologarithm of the HNTf2 concentration, corrected to take the neutralization of the basic impurities into account, are shown in Fig. 4C. The values follow a linear model, with a unitary slope as proposed by the Hammett acidity function (eqn (7)). The intercept, extrapolated for a standard solution of proton (aH+ = 1, log aH+ = 0), is equal to H00 = −5.2 ± 0.2. The negative value obtained here indicates that, for an identical chemical potential for the proton, the relative activity of the proton in the [BMIm][NTf2] is higher than the relative activity of the proton in water. In other word, for an identical amount of proton in [BMIm][NTf2] or in water, the proportion of reactive proton will be higher in [BMIm][NTf2] than in water. The value of H00 corresponds to a free energy of transfer for protons ΔtG° of 30 ± 1 kJ mol−1, which is positive, demonstrating that the protons are less solvated in the [BMIm][NTf2] than they are in water.
Hammett acidity function in commercial [BMIm][NTf2] by UV-Vis spectroscopy
We confronted the values obtained for the Hammett acidity function derived from Raman data, with data derived from UV-Vis spectroscopy (method of reference). The UV-Vis spectra recorded for the diluted solutions of 2,6-dichloro-4-nitroaniline (531.3 μM) in [BMIm][NTf2] when the concentration of HNTf2 is increased are presented in Fig. 5A. UV-Vis data were obtained for the diluted solutions of pH-reporter to avoid the saturation of the signal of the 2,6-dichloro-4-nitroaniline. The intensity of the absorption band of the basic form of the 2,6-dichloro-4-nitroaniline decreased as the quantity of HNTf2 increased. Fig. 5B shows the evolution of the ratio of the molar fraction of the acidic form (1 − xR) and basic form (xR) of the pH-reporter as a function of the added concentration of HNTf2 (CHA) in the [BMIm][NTf2]. Here again, a straight line was drawn through the experimental data, the concentration of basic impurities in the [BMIm][NTf2] was determined to be 15 ± 2 mM, and the acidity constant of the 2,6-dichloro-4-nitroaniline in the [BMIm][NTf2] was determined to be 12 ± 1, which correspond to a pKA value of 1.08 ± 0.04. The experimental data corresponding to the solution with a concentration of HNTf2 of 6.5 was discarded (in red in Fig. 5B), since that concentration did not suffice to neutralize all basic impurities. The values of H0 calculated from the UV-Vis spectra as a function of the cologarithm of the HNTf2 concentration, again corrected to take the neutralization of the basic impurities into account, are shown in Fig. 5C. The H00 value of −5.3 ± 0.3 was extrapolated for a standard solution of proton (aH+ = 1, log aH+ = 0). This value corresponds to a free energy of transfer for protons ΔtG° of 30 ± 2 kJ mol−1, which is statistically equivalent of the value derived from Raman data. This result demonstrates that the Hammett acidity function can be measured by Raman spectroscopy, directly in the ionic liquid, and even if it requires a 100 time more concentrated solution of the pH-reporter. The concentration of pH-reporter in the range between 0.5 to 50 mM does not significantly impact the estimated value of the activity coefficient of transfer of protons in [BMIm][NTf2]. Actually, even at a concentration of 50 mM, the pH-reporters are surrounded by molecules of solvent that are present in excess (∼70 equivalent) compared to the nitroanilines, preventing π-stacking interactions between the pH-reporters.Hammett acidity function in synthetized [EMIm][NTf2], [BMIm][NTf2] and [OMIm][NTf2] by Raman spectroscopy
The values of the Hammett acidity function, H0, were also calculated from the Raman spectra of acidic solutions of the pH-reporter 2,6-dichloro-4-nitroaniline in the three synthesized ionic liquids: [EMIm][NTf2], [BMIm][NTf2] and [OMIm][NTf2], with a different alkyl substituent on the imidazolium, respectively ethyl, butyl and octyl, but all sharing the same bistriflimide anion coordinating the protons. The H0 values calculated as a function of the cologarithm of the HNTf2 concentration, are shown in Fig. 6. The spectra, the determination of the basic impurities and the individual Hammett plot are shown in ESI.† The derived pKa value for the HR+/R couple, the intercepts, H00 extrapolated for a standard solution of proton, as well as the corresponding free energy of transfer of protons are summarized in Table 1. As shown in Fig. 6, the values obtained for the H0versus the cologarithm of the strong acid concentration follow a linear function with a unitary slope, but different H00 values are obtained for the three ILs. Both [EMIm][NTf2] and [BMIm][NTf2] are characterized with the same statistic value of H00 (−4.65 ± 0.2 in average), while the [OMIm][NTf2] is characterized with a less negative value (−4.4 ± 0.1), indicating that the [OMIm][NTf2] is actually less acidic than the two others ILs. Actually, this indicates that the Hammett acidity function is very sensitive, as a shift of 0.2 of H0 corresponds to a change of free energy of only 0.3 kcal mol−1 (∼1.1 kJ mol−1). Yet, that shift is to be related to a change of solvation in the solvent. Indeed, this shift cannot be associated with the basic behavior of the pH-reporter, as the concentration of the pH-reporter for the solutions in the [OMIm][NTf2] is lower compared to the concentration of pH-reporter for the solutions in either the [BMIm][NTf2] or the [EMIm][NTf2]. Likewise, the shift of H0 cannot be linked to the presence of basic impurities. While the [OMIm][NTf2] is more viscous than the [BMIm][NTf2] or the [EMIm][NTf2], due to the octyl chain that confers an oily texture to the solvent (which may require a longer purification process to remove the non-reacted precursors such as imidazole or water), the concentration of basic impurities was determined to be lower in [OMIm][NTf2] than in the other ILs. Actually, we suggest that the lower acidity measured in the [OMIm][NTf2] is the consequence of the hydrophobic ion pairing24 following the destabilization of the free charged proton, which is therefore more stabilized by ion pairing with the NTf2−. Indeed, the [OMIm][NTf2] is more hydrophobic than the other ILs due to the octyl substituent on the imidazolium. However, in terms of energy, the experimental shifts observed are low and the free energies of transfer for protons from water to these ILs are similar as shown in Table 1. The similarity indicates that the solvation of protons is not prominently sensitive to the molecular structure of the imidazolium cation, even though the presence of a long alkyl chain on the cation decreases slightly the acidity experienced in the medium.| Solvent | Data set | pKa(HR+/R) | H 00 | ΔtG°(H+) (kJ mol−1) | ΔsolvG°(H+) (kJ mol−1) |
|---|---|---|---|---|---|
| [BMIm][NTf2] | Commercial IL, [R]0 = 51.17 mM | 1.17 ± 0.03 | −5.2 ± 0.2 | 30 ± 1 | −1083 |
| [BMIm][NTf2] | Synthetized IL, [R]0 = 74.22 mM | 1.66 ± 0.06 | −4.7 ± 0.2 | 27 ± 1 | −1086 |
| [EMIm][NTf2] | Synthetized, [R]0 = 79.17 mM | 1.64 ± 0.03 | −4.6 ± 0.1 | 26.2 ± 0.6 | −1086 |
| [OMIm][NTf2] | Synthetized, [R]0 = 65.87 mM | 1.76 ± 0.02 | −4.4 ± 0.1 | 25.1 ± 0.6 | −1087 |
Discussion
For the first time, we demonstrated that the Hammett acidity function can be determined in non-protic imidazolium-based ILs by Raman spectroscopy instead of UV-Vis spectroscopy, using the same nitroaniline pH-reporter. This result is particularly interesting as Raman spectroscopy (based on the inelastic scattering of monochromatic light by vibrating molecule) is not limited to the use of colored pH-reporters, therefore extending the range of pH-reporters that might be deployed for estimating the Hammett acidity function in ILs beyond the nitroanilines, as initially proposed by Hammett and Deyrup as pH-reporter. Actually, in aromatic imidazolium-based ILs, π-stacking between the imidazolium and the nitroanilines are likely to occur, which may invalidate the extra-thermodynamic assumption behind the Hammett acidity function (i.e. that both forms of the pH-reporter, R and HR+, are experiencing an identical change of solvation when transferred from water to the ionic liquid). Raman spectroscopy offers the possibility to work with non-aromatic bulky pH-reporter, where the charge will be less accessible to the solvent molecules, better meeting the extra-thermodynamic requirements. Besides, Raman spectroscopy will also enable studying the acidity of colored mediums, which is less straightforward by UV-Vis spectroscopy, hence allowing, for instance, in situ kinetics measurements of the acidity evolution during a chemical process producing or consuming protons.Raman spectroscopy also offers the capability to inform on the coordination of the protons by the anions of the ILs, which is not feasible with UV-Vis spectroscopy. In this study, we measured that the solvent number for the proton in 1-alkyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide ILs is one. As a consequence, the protons in these ILs will demonstrate a greater ability to react with bases than protons in water (solvent number of 6), which translates into the more acidic behavior of these ILs in comparison to most molecular solvents. This also corroborates with the positive values obtained for the pKA,R determined in the four ILs studied here. All pKa values associated to the pH-reporter 2,6-dichloro-4-nitroaniline were higher than the pKA,R value in water (−3.32), indicating that the 2,6-dichloro-4-nitroaniline is less acidic in the ILs than in water, due to the solvent leveling effect and possible ion pairing that have been suggested in ILs.14 However, resolving the contribution of the solvent leveling effect and the ion pairing effect on the pKA,R values is not straightforward and would require to study a series of homologues pH-reporters in various ILs. Also, variation of temperature of a few degrees can lead to a variation of the pKa for a weak acid, such as the 2,6-dichloro-4-nitroanilinium, as a weak acid tends to dissociate more if the thermal vibration energy increases.25
The Hammett acidity functions calculated for the synthetized ILs by Raman spectroscopy are shifted to less negative values compared to the Hammett acidity function calculated for the commercial [BMIm][NTf2], as shown in Fig. 6. Only the solvents (with their intrinsic concentration of basic impurities) are different between these series of data, the pH-reporter and the HNTf2 were identical. Therefore, the shift observed between the synthetized ILs and the commercial [BMIm][NTf2] must be related to the solvent and may have several origins. First, the shift might be due to the presence of a higher amount of basic impurities in the synthesized ILs than in the commercial [BMIm][NTf2], which is not likely as the global concentration of basic impurities was determined to be lower or similar in the synthesized ILs and in the commercial [BMIm][NTf2]. Second, the shift of H0 can also be related to the amount of pH-reporter, which is added in the ILs as the basic form. Indeed, the concentration of pH-reporter are slightly higher in the synthetized ILs than in the commercial [BMIm][NTf2]. However, this is dubious as the amount of pH-reporter did not influence the value of H0 determined in the same commercial [BMIm][NTf2] either by UV-Vis spectroscopy or Raman spectroscopy, even if the pH-reporter concentration was 100 times higher for solutions analyzed by Raman spectroscopy. Also, the amount of pH-indicator in the synthesized [OMIm][NTf2] was lower than the concentration of pH-reporter in the other synthetized ILs. As discussed above, the shift of H0 values observed for the synthesized [OMIm][NTf2] is more likely due to hydrophobic ion pairing. Indeed, the formation of ion pairs between the protons and the basic form of the pH-reporter can induce a positive shift of the H0 values as described by Bruckenstein when several pH-reporters are used in the same medium.18 Actually, ion pairing can be the cause of the experimental shift observed for the commercial and the synthetized [BMIm][NTf2]. The ILs are identical and so is the pH-reporter, but the nature of the basic impurities happened to be different. The commercial [BMIm][NTf2] contained water as the basic impurities, while the basic impurity in our synthesized ILs was residual imidazole (as was shown by NMR). Since the basicity of imidazole is higher than the basicity of water in the IL, by leveling effect, the presence of imidazole in the ILs may induce some ion pairing, leading to an apparent Hammett acidity function. Finally, the Hammett acidity function is sensitive to temperature fluctuation, as the H0 values are equivalent to the pH in the ILs, expressed as the corresponding pH that an aqueous solution would exhibit. Indeed, according to the Henderson Hasselbalch equation, an increase of pH can be caused by an increase of pKa due to thermal fluctuation between measurements.
Despite the slight shift observed for the Hammett acidity functions determined for the commercial and synthetized ILs, the free energy of transfer for the protons, ΔtG°(H+), from water to the ILs was estimated to be in the range between 25 and 30 kJ mol−1 (7 to 8 kcal mol−1), which is higher than the energy of transfer experienced by the protons in protic molecular solvents (e.g. methanol, ethanol) and closer to the free energy of transfer experienced by proton in non-protic molecular solvents (e.g. dimethyl sulfoxide).9,10,26 The values obtained for the activity coefficient of transfer by Raman spectroscopy are in agreement with previous data derived from UV-Vis and electrochemical measurements in [BMIm][NTf2].12,17 From the consensus value of the free energy of solvation for protons in water (−1112.5 kJ mol−1 or −265.9 kcal mol−1), the free energy of solvation for protons in the ILs 1-alkyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide ILs ranges from −1083 to −1087 kJ mol−1 (or from −258.7 to −259.9 kcal mol−1) for the commercial [BMIm][NTf2] and the [OMIm][NTf2] respectively.
Conclusions
In this article, the determination of the Hammett acidity functions and the free energy of solvation of protons in ionic liquids was successfully implemented using, for the first time, Raman spectroscopy. We demonstrated that the data obtained by Raman spectroscopy led to an identical value of free energy of transfer of protons from water to the studied ILs to the value obtained using the UV-Visible spectroscopy, which is the reference method. We demonstrated that the amount of nitroaniline pH-reporter does not influence the value of the free energy of transfer, if present at a concentration below 50 mM in the ILs. We determined that the free energy of solvation of protons in three 1-alkyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imides were very close to each other, between −258.7 to −259.9 kcal mol−1, indicating that the protons are less solvated in ILs than in water by an energy of 6 to 7 kcal mol−1, which is why these ILs are super-acidic media. We also show that the method is very sensitive, and a shift of free energy of transfer as low as 0.6 kcal mol−1 can be measured, enabling us to describe that while the energy of solvation of protons is not prominently sensitive to the molecular structure of the imidazolium cation, the [OMIm][NTf2] was less acidic than its two other counterparts, which is believed to originate from hydrophobic ion pairing between the charged proton and the bistriflimide anion. The successful use of Raman spectroscopy to derive the Hammett acidity function in ILs paves the way to the analysis of new mediums, such as colored solutions, which is not possible in UV-Vis spectroscopy. Raman spectroscopy also enables extension of the range of molecular pH-reporters beyond the nitroanilines, better meeting the extra-thermodynamic requirement, as nitroanilines might develop more specific interactions in the ILs than in molecular solvents. Also, Raman spectroscopy offers the possibility to determine the solvation number of the protons, which is equal to one in these ILs, as described in this paper.Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
AR acknowledges the Fonds de la Recherche Scientifique (FNRS), for the financial support (Grant FNRS-ASP55135).References
- J. P. Hallett and T. Welton, Chem. Rev., 2011, 111(5), 3508–3576 CrossRef CAS PubMed.
- E. W. Castner and J. F. Wishart, J. Chem. Phys., 2010, 132(12), 120901 CrossRef PubMed.
- H. Olivier-Bourbigou, L. Magna and D. Morvan, Appl. Catal., A, 2010, 373(1–2), 1–56 CrossRef CAS.
- T. Welton, Biophys. Rev., 2018, 10(3), 691–706 CrossRef CAS PubMed.
- K. Ghandi, Green Sustainable Chem., 2014, 04(01), 44–53 CrossRef CAS.
- R. Kaur, H. Kumar and M. Singla, J. Ionic Liq., 2022, 2(2), 100036 CrossRef.
- H. F. T. Klare and M. Oestreich, J. Am. Chem. Soc., 2021, 143(38), 15490–15507 CrossRef CAS PubMed.
- O. Popovych and R. P. T. Tomkins, Nonaqueous Solution Chemistry, Wiley, Hoboken, New Jersey, 1981 Search PubMed.
- B. Trémillon, Chemistry in Non-Aqueous Solvents, D. Reidel Publishing Company, Dordrecht, Holland, 1974 Search PubMed.
- E. Rossini and E.-W. Knapp, J. Comput. Chem., 2016, 37(12), 1082–1091 CrossRef CAS PubMed.
- Z. Marković, J. Tošović, D. Milenković and S. Marković, Comput. Theor. Chem., 2016, 1077, 11–17 CrossRef.
- C. Thomazeau, H. Olivier-Bourbigou, L. Magna, S. Luts and B. Gilbert, J. Am. Chem. Soc., 2003, 125(18), 5264–5265 CrossRef CAS PubMed.
- Y. Marcus, Chem. Rev., 2007, 107(9), 3880–3897 CrossRef CAS PubMed.
- B. G. Cox, Acids and Bases: Solvent Effects on Acid-Base Strength, Oxford University Press, Oxford, 2013 Search PubMed.
- L. P. Hammett and A. J. Deyrup, J. Am. Chem. Soc., 1932, 54(7), 2721–2739 CrossRef CAS.
- T. Robert, L. Magna, H. Olivier-Bourbigou and B. Gilbert, J. Electrochem. Soc., 2009, 156(9), F115 CrossRef CAS.
- L. Magna, J. Bildé, H. Olivier-Bourbigou, T. Robert and B. Gilbert, Oil Gas Sci. Technol. – Rev. l’IFP, 2009, 64(6), 669–679 CrossRef CAS.
- S. Bruckenstein, J. Am. Chem. Soc., 1960, 82(2), 307–310 CrossRef CAS.
- S. Zhang, T. Zhang and S. Tang, J. Chem. Eng. Data, 2016, 61(6), 2088–2097 CrossRef CAS.
- J. Gräsvik, J. P. Hallett, T. G. To and T. Welton, Chem. Commun., 2014, 50(55), 7258–7261 RSC.
- A. I. Horowitz, P. Arias and M. J. Panzer, Chem. Commun., 2015, 51(30), 6651–6654 RSC.
- V. H. Paschoal, L. F. O. Faria and M. C. C. Ribeiro, Chem. Rev., 2017, 117(10), 7053–7112 CrossRef CAS PubMed.
- E. S. Stoyanov, I. V. Stoyanova and C. A. Reed, J. Am. Chem. Soc., 2010, 132(5), 1484–1485 CrossRef CAS PubMed.
- K. D. Ristroph and R. K. Prud’homme, Nanoscale Adv., 2019, 1(11), 4207–4237 RSC.
- A. Soames, S. Iglauer, A. Barifcani and R. Gubner, J. Chem. Eng. Data, 2018, 63(8), 2904–2913 CrossRef CAS.
- C. Kalidas, G. Hefter and Y. Marcus, Chem. Rev., 2000, 100(3), 819–852 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1–S3, Tables S1–S6, synthesis of the ionic liquids, preparation of the solutions, Hammett acidity function in the three synthesised ionic liquids. See DOI: https://doi.org/10.1039/d3cp04741e |
| This journal is © the Owner Societies 2024 |




![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:




