Open Access Article
Open Access ArticleMutual neutralization in collisions of Li+ with CN−
Åsa
Larson
 *a and
Ann E.
Orel
b
*a and
Ann E.
Orel
b
aDepartment of Physics, Stockholm University, SE-106 91 Stockholm, Sweden. E-mail: aasal@fysik.su.se
bDepartment of Chemical Engineering, University of California, Davis, California 95616, USA
First published on 13th December 2023
Abstract
The mutual neutralization reaction in collisions of Li+ with CN− is a promising candidate for rigorous multi-dimensional ab initio studies of atom-molecule charge transfer processes. The reaction is driven by the non-adiabatic interaction between the lowest two 1A′ electronic states at large Li–CN distances, resulting in a large cross section for mutual neutralization. As a first step, the relevant adiabatic potential energy surfaces and non-adiabatic interaction are computed ab initio, and the process is studied quantum mechanically using the vibrational sudden approximation, where the vibrational and rotational motions of the CN molecule are assumed to be frozen during the collision.
1 Introduction
Charge transfer between positive and negative ions, the mutual neutralization (MN) process, limits the density of ion–ion plasmas, such as those found in the lower ionospheres1 or interstellar plasmas.2,3 Depending on the electron affinity and the ionization energy of the neutrals involved, the MN reaction can range from endothermic to a large exothermicity that can lead to products in excited states. Due to interactions among electronic excited states that are changing characters between ionic and covalent, large non-adiabatic couplings among these states are generally present at large internuclear distances. For an ab initio description of the reaction, the adiabatic potential energy curves or surfaces of the involved states of the reaction complex must be computed, as well as the corresponding non-adiabatic coupling elements.Except for a preliminary calculation4 on H− + H2+ in reduced dimensionality, ab initio and fully quantum mechanical studies of the mutual neutralization reaction are so far limited to collisions of atomic ions (see for example5–7 and references therein). There have been numerous studies of mutual neutralization reactions where the nuclear motion is described classically, and the transition probabilities are estimated using, e.g., the Landau–Zener model.8,9 In the case of atom–diatom collisions, the H− + H2+ mutual neutralization reaction has been modeled using a multi-state Landau–Zener model.10,11
Modeling of interstellar clouds and planetary atmospheres requires MN rates and product branching ratios for more complex species. There is a need to go beyond collisions of atomic ions. As mentioned, there are some preliminary ab initio calculations4 on H− + H2+. This system is complicated by the high exothermicity, allowing a multitude of product channels, including three-body breakup. We have chosen to study MN in a simpler system involving collisions with CN−. CN and CN− have similar equilibrium bond distances. CN− has been observed in the interstellar media12 and in the atmosphere of Titan,13 making it a molecule of interest. Of most interest would be collision with complex organic positive ions such as CnHm+. As a first step, however, we will consider the MN reaction with Li+, i.e.
| CN−+ Li+ → CN + Li. |
As shown later, in this system, the MN process involves only two electronic states with significant non-adiabatic coupling at large Li–CN distances. This system serves as a prototype system to step beyond atomic anion–cation collisions.
The ground state potential energy surface of the LiCN system has been studied ab initio at a number of levels.14–18 The focus, however, has been on the ground state surface of the system, determining the stationary structures, calculating ro-vibrational states, and studying the isomerization.19,20 The MN calculations require the ground and excited state surfaces as well as the non-adiabatic coupling. This data is used as input to calculate the MN cross section.
In Section 2, the electronic structure calculations are outlined, and we describe how the mutual neutralization cross section can be estimated using a vibrational sudden approximation.21,22 The one-dimensional coupled Schrödinger equation is then solved using a diabatic representation for fixed CN bond length (r) and Jacobi angle (θ). Then, the cross section is averaged over these coordinates. The resulting cross section for mutual neutralization is discussed in Section 3. We investigate the r- and θ-dependencies of the cross section and discuss the limitations of the present model. Throughout the article, atomic units are used.
2 Theoretical description
In ab initio studies of mutual neutralization, the first step is to compute the relevant potential energy surfaces of the system and the non-adiabatic couplings among these states. Since the non-adiabatic interactions between ionic and covalent states occurring at large internuclear distances are most important, the electronic states with asymptotic limits below the ion-pair limit must be computed. In the next step of the calculation, the coupled Schrödinger equation of the nuclear motion is solved to compute the mutual neutralization cross section. We here describe how this is done and the approximation used in the present study.2.1 Electronic structure calculations
The LiCN system has two covalent electronic states with asymptotic energies below the ion-pair state. The ground electronic state dissociates into Li(2S) + CN(X2Σ+). This state has an avoided crossing with the ion-pair state at a Li–CN distance of about Rx = 17.3 bohr (see Table 1 below). The first excited state of LiCN dissociates into Li(2S) + CN(A2Π) at an energy of about 1.15 eV above the ground state fragments. This state also has an asymptotic limit below the ion-pair limit, Li+ + CN−. However, the predicted curve crossing at Rx ≈ 64 bohr will result in an ionic-covalent electronic coupling that can be neglected. Therefore, only two electronic states, the ground and first excited states of LiCN, must be considered to describe the MN reaction.| Basis | Ion-pair (eV) | R x (bohr) |
|---|---|---|
| aug-cc-pVDZ | 1.759 | 15.4 |
| aug-cc-pVTZ | 1.644 | 16.5 |
| aug-cc-pVQZ | 1.610 | 16.9 |
| aug-cc-pV5Z | 1.597 | 17.0 |
| Expt25,26 | 1.572 | 17.3 |
The quantum chemistry calculations are carried out using the MOLPRO program package.23 We compute the lowest two electronic states of the LiCN system using the multi-reference configuration interaction (MRCI) method with the augmented correlation-consistent basis sets of Dunning,24i.e. aug-cc-pVXZ, where X = D, T, Q and 5. When Li is close to CN, the dominant configuration of the ground state is the ion-pair. The adiabatic states change character at large separations, and the first excited state becomes the ion-pair. The molecular orbitals are obtained using state-averaged complete active space self-consistent field (CASSCF) calculations, including the two lowest electronic states of 1A′ symmetry. The three lowest molecular orbitals in a′ symmetry (composed of 1s atomic orbitals on Li, C, and N) are optimized but kept doubly occupied in the CASSCF calculation. The active space includes 10 electrons and 12 molecular orbitals (10a′, 2a′′). The active space is composed of the molecular orbitals arising from 2s and 2p on Li, C, and N, respectively. The MRCI calculations are then carried out with reference configurations obtained using the same active space as in the CASSCF calculation. Single- and double external excitations out of the reference configurations are included in the MRCI calculation. We compute the two lowest states of the LiCN system of 1A′ symmetry.
The calculations are carried out using Jacobian coordinates (r, R, θ) of the nuclei, where r is the CN bond length, R is the radial coordinate from the center of mass of CN to Li, and θ is the angle between r and R axes. Linear LiCN corresponds to θ = 0°.
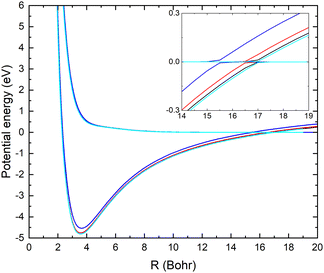
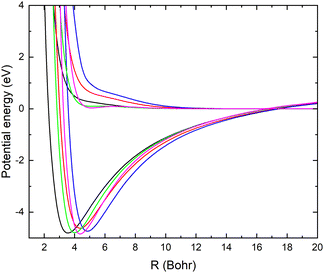
In Fig. 1, the potential energy surfaces of the two lowest 1A′ states of LiCN are displayed for fixed r = 2.22 bohr (corresponding to the equilibrium bond length of CN−) and θ = 90° and using the different basis sets. Calculations with larger basis sets result in potentials with lower energies. In Fig. 1, the potentials are shifted such that E = 0 corresponds to the dissociation limit of the ground state (which has a flat asymptotic potential). We note that improving the basis set causes a shift of the avoided crossing between the ionic and covalent state towards larger internuclear distances. This originates from an improved description of the ion-pair state with the larger basis set. To obtain an accurate asymptotic energy for the ion-pair state, it is necessary to correctly describe both the electron affinity of CN and the ionization potential of Li. Therefore, the larger basis sets provide an improved description of the ion-pair state.
In Table 1, the calculated asymptotic ion-pair energy and the crossing distance between the ionic and covalent state dissociating into ground state fragments (for fixed r = 2.22 bohr and θ = 90°) are compared with experimental values.25,26 As can be seen in Table 1, the larger basis sets yield accurate ion-pair asymptotic energy. The curve crossing moves towards larger distances as the ion-pair state shifts down. Similar behaviors were found in systems such as LiF27 and LiH.28
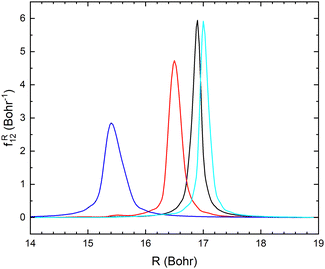
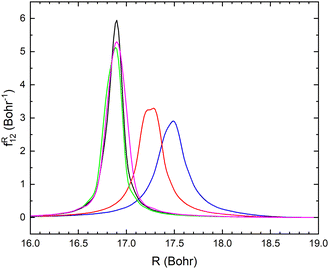
The non-adiabatic coupling element, 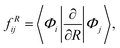 is computed at the MRCI-level between the lowest two states of 1A′ symmetry using a three-point finite difference of the MRCI wave function with dR = 0.01 bohr. The results for fixed r = 2.22 bohr and θ = 90° are shown in Fig. 2 for MRCI calculations with the different basis sets. The non-adiabatic interaction is dominated by a Lorentzian-shaped peak centered at the avoided crossing between the ionic and covalent states. This indicates that the avoided crossing is a pure two-state interaction between the lowest two states of 1A′ symmetry. However, if the non-adiabatic coupling is integrated
is computed at the MRCI-level between the lowest two states of 1A′ symmetry using a three-point finite difference of the MRCI wave function with dR = 0.01 bohr. The results for fixed r = 2.22 bohr and θ = 90° are shown in Fig. 2 for MRCI calculations with the different basis sets. The non-adiabatic interaction is dominated by a Lorentzian-shaped peak centered at the avoided crossing between the ionic and covalent states. This indicates that the avoided crossing is a pure two-state interaction between the lowest two states of 1A′ symmetry. However, if the non-adiabatic coupling is integrated 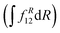 over the range of the avoided crossing, the integral is smaller than π/2. Therefore, contrary to the Li+–F− diatomic system,27 there is not a complete “switch-over” between the diabatic states when moving at fixed (r, θ) across the region of the avoided crossing. This is because LiCN is a polyatomic system with non-zero non-adiabatic coupling elements not only in the R-direction but also in the other vibrational degrees as will be discussed in Section 3.3. As seen in Fig. 2, when the basis set is improved, the avoided crossing moves towards larger R, and the peak of the non-adiabatic coupling becomes more narrow.
over the range of the avoided crossing, the integral is smaller than π/2. Therefore, contrary to the Li+–F− diatomic system,27 there is not a complete “switch-over” between the diabatic states when moving at fixed (r, θ) across the region of the avoided crossing. This is because LiCN is a polyatomic system with non-zero non-adiabatic coupling elements not only in the R-direction but also in the other vibrational degrees as will be discussed in Section 3.3. As seen in Fig. 2, when the basis set is improved, the avoided crossing moves towards larger R, and the peak of the non-adiabatic coupling becomes more narrow.
2.2 Reactive scattering calculations
As a first step to perform ab initio studies of atom–diatom mutual neutralization, the cross section is calculated by applying the vibrational sudden approximation,21,22 where the vibrational- and the rotational motions of the CN system are assumed to be frozen during the collision. For this approximation to be valid, the scattering has to be fast compared to the vibrational- and rotational motions. This approximation is usually valid at higher collision energies. However, in mutual neutralization with a Coulomb attraction between the reactants and high angular momenta contribute, the approximation might also be justified at lower collision energies. We compute the mutual neutralization cross section in the energy range of 0.1–50 eV. The limitations of the approximations are further discussed in Section 3.3 below.We first compute the cross section for mutual neutralization in Li+ + CN− collision at fixed CN bond length r and angle θ. This is done by applying a partial wave decomposition and for fixed angular momenta, solving the radial Schrödinger equation of the nuclear wave function in a diabatic representation, where there is only one active degree of freedom. We follow a strict diabatization method to obtain the diabatic potential matrix. The diabatic potential matrix is obtained from the similarity transformation Vd = TtVadT. The orthogonal adiabatic-to-diabatic transformation matrix is obtained by numerically solving the equation29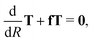 where f is the anti-symmetric non-adiabatic coupling matrix with the elements fij = fRij(1 − δij). Note that here only the component of non-adiabatic coupling in the R degree-of-freedom (reaction coordinate) is included. The transformation martix is computed using the Runge–Kutta Fehlberg method,30 with the boundary condition T = 1 at R = 20 bohr and the integration performed inwards with a grid size of 1010−3 bohr. The two lowest 1A′ electronic states of LiCN are included in the model, and only the non-adiabatic coupling in the R-direction is considered. We perform the diabatization for the adiabatic states calculated with the MRCI method and the aug-cc-pVXZ, X = D, T, Q, 5 basis sets discussed above.
where f is the anti-symmetric non-adiabatic coupling matrix with the elements fij = fRij(1 − δij). Note that here only the component of non-adiabatic coupling in the R degree-of-freedom (reaction coordinate) is included. The transformation martix is computed using the Runge–Kutta Fehlberg method,30 with the boundary condition T = 1 at R = 20 bohr and the integration performed inwards with a grid size of 1010−3 bohr. The two lowest 1A′ electronic states of LiCN are included in the model, and only the non-adiabatic coupling in the R-direction is considered. We perform the diabatization for the adiabatic states calculated with the MRCI method and the aug-cc-pVXZ, X = D, T, Q, 5 basis sets discussed above.
The coupled Schrödinger equation is solved numerically for fixed angular momentum, l, using Johnson's logarithmic derivative method31,32 with a regular wave boundary condition. The scattering matrix, Sij,l, is obtained by matching the logarithmic derivative of the radial wave function to the appropriate asymptotic solutions of the covalent or ionic channels, respectively.33 Here, the R-grid ranges from 1.1 to 20 bohr with a grid size of 5 × 10−3 bohr. The fixed (r, θ) cross section for mutual neutralization is then obtained by summarizing the contributions from all partial waves:
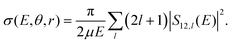 | (1) |
For MN to occur, there must be a non-adiabatic transition during the collision. In a simple picture, the collision partners proceed through the avoided crossing twice. If we consider the probability for a non-adiabatic transition to be P, the MN cross section is proportional to P(1 − P). Therefore, the cross section depends both on the position of the avoided crossing and the magnitude of the coupling.
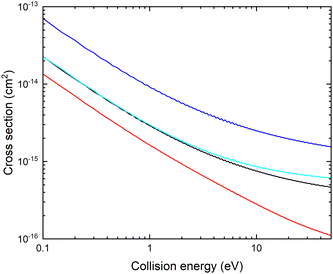
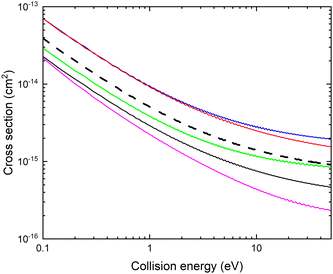
In Fig. 3, we show the fixed (r, θ) = (2.22 bohr, 90°) cross sections for mutual neutralization computed using the adiabatic potential energy surfaces and non-adiabatic coupling elements obtained with the different basis sets.
There is a significant shift in the position of the avoided crossing towards larger internuclear distances as the basis set is improved (see Fig. 1 and 2) and the calculated MN cross sections change significantly. Note that there is not a simple scaling with a magnitude of the non-adiabatic coupling. There is a small difference between the cross sections calculated with the aug-cc-pVQZ and aug-cc-pV5Z basis sets. In the remainder of the article, the calculations are carried out using the aug-cc-pVQZ basis set. At collision energies smaller than 1 eV, the fixed (r, θ) mutual neutralization cross section has the 1/E energy dependence in accordance with the Wigner threshold law for collisions of oppositely charged particles.34
In the vibrational sudden approximation,21 the cross section is weighted with the probability distribution obtained from the vibrational wave function [χv=0(r)] of the CN− molecule according to
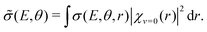 | (2) |
Next, the angle dependence is integrated out, and the averaged mutual neutralization cross section is obtained from
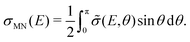 | (3) |
3 Results and discussion
3.1 Dependence on the CN distance
As mentioned above, the potential energy curves of the electronic ground states of CN and CN− have the minimum at similar equilibrium bond lengths. In Fig. 4, the asymptotic potential energy curves Vi(R∞, r, θ = 90°) are displayed together with the square of the vibrational wave function of CN−, |χv=0(r)|2. To investigate the dependence on the CN distance, the adiabatic potentials and non-adiabatic coupling, fR12, are computed for 1.0 bohr ≤ R ≤ 20 bohr using the MRCI method and the aug-cc-pVQZ basis set for θ = 90° and r = 2.1, 2.17, 2.22, 2.25, 2.3 and 2.35 bohr. These r-values cover the range where the vibrational wave function of CN− is non-zero. The resulting adiabatic potentials of the lowest two 1A′ electronic states of Li–CN are displayed in Fig. 5 for r = 2.1, 2.22 and 2.35 bohr. The energy scale in Fig. 5 is shifted such that E = 0 corresponds to the asymptotic energy of the electronic ground state when r = 2.22 bohr and θ = 90°. Note that for both electronic states, the adiabatic potentials calculated with r = 2.22 bohr are lower in energy than the other slices of the potentials. This is because the equilibrium bond lengths of CN− and CN are close, and r = 2.22 bohr is close to the “minimum of the valley” of both adiabatic potentials. The non-adiabatic interaction between the lowest two states, fR12, is shown for r = 2.1, 2.22 and 2.35 bohr in Fig. 6. The position of the avoided crossing is shifted when r is varied, which can be seen by the calculated non-adiabatic coupling element.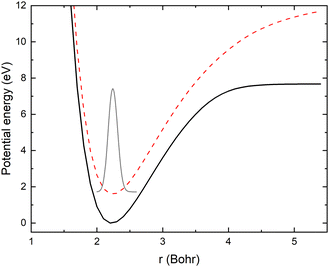 | ||
| Fig. 4 Asymptotic adiabatic potential energy curves of CN (black solid curve) and CN− (red dashed curve) as well as |χv=0(r)|2 of CN− vibrational wave function (grey solid curve). | ||
 | ||
| Fig. 5 The two lowest adiabatic potential energy surfaces of LiCN calculated with the MRCI/aug-cc-pVQZ method for θ = 90° and r = 2.1 bohr (red), 2.22 bohr (black) and 2.35 bohr (blue). | ||
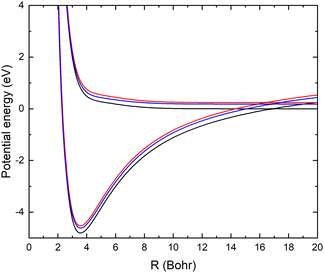
 | ||
| Fig. 6 Non-adiabatic coupling elements fR12 between the lowest two LiCN states of 1A′ symmetry at fixed θ = 90° and r = 2.1 bohr (red), 2.22 bohr (black) and 2.35 bohr (blue). | ||
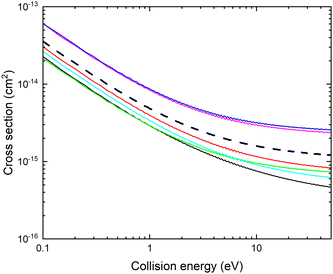
The resulting cross section σ(E, r, θ) is displayed with thin lines in Fig. 7. The cross section increases for r larger than the equilibrium bond length.
The cross section obtained from weighting of σ(E, r, θ) with the vibrational probability distribution according to eqn (2) is approximated with
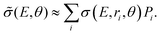 | (4) |
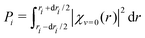 . The cross section
. The cross section ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) (E,θ) is displayed with a thick black dashed line in Fig. 7. Note that the averaged cross section is larger than the cross section calculated at r = 2.22 bohr.
(E,θ) is displayed with a thick black dashed line in Fig. 7. Note that the averaged cross section is larger than the cross section calculated at r = 2.22 bohr.
3.2 Dependence on the angle
The angular dependence of the mutual neutralization cross section is investigated keeping r = 2.22 bohr, corresponding to a distance close to the equilibrium bond lengths of both CN− and CN. The adiabatic potentials and non-adiabatic couplings are displayed for some angles in Fig. 8 and 9. Again the energy scale of the potentials are shifted such that E = 0 corresponds to the asymptotic limit of the ground state when r = 2.22 bohr and θ = 90°. At large distances there are small θ-dependencies of the potentials. However, at small R values, the potentials show strong angular dependencies since the atomic separation in the reaction complex will depend on the Jacobi angle.The resulting fixed (r, θ) cross sections for mutual neutralization, σ(E, r, θ) are displayed in Fig. 10 for r = 2.22 bohr and various values of θ. The non-adiabatic coupling for small angles, θ ≤ 45° occur at larger distances, R and result in a larger MN cross section. The mutual neutralization cross section is approximated with σMN(E) obtained with eqn (3). The cross section obtained by averaging over the angle is shown with a thick black dashed curve in Fig. 9.
It should be noted that this estimated mutual neutralization cross section for collisions of CN− with Li+ is relatively large. At 1 eV, it is about a factor of four smaller than the mutual neutralization cross section for H+ + H−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 and a factor of eight smaller than the cross section for Li+ + D−, measured using single pass merged-beam apparatus.35
5 and a factor of eight smaller than the cross section for Li+ + D−, measured using single pass merged-beam apparatus.35
3.3 Limitations of the model
In the vibrational sudden approximation, the rotational and vibrational motions of the CN− molecule are assumed to be slow compared to the scattering process. In order to test the validity of the approximation, we make rough estimates of the corresponding timescales. The CN− electronic ground state has a rotational constant of B = 56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 133 MHz.36 Within a rigid rotor approximation, the rotational period becomes
133 MHz.36 Within a rigid rotor approximation, the rotational period becomes 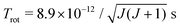 . The vibrational period is estimated using the vibrational frequency of CN−, ωe = 2035 cm−1,25 corresponding to a period of 1.6 × 10−14 s. Finally, the timescale of the scattering process can be estimated from the classical propagation time along the one-dimensional slice of the potentials from the region where the two states start to interact (R ≈ 17a0) moving inwards to the classical turning point and then out again until the system has passed through the region where the two states interact on the way out. The system propagates on effective potentials obtained by adding the centrifugal barrier to the potential of the electronic state. In mutual neutralization, as described in section IIB, high angular momenta contribute and the system is reflected towards the centrifugal barrier at large distances. By using the angular momentum with the largest contribution to the mutual neutralization cross section in eqn (1), at a collision energy of 10 eV, the scattering timescale is estimated to 4.7 × 10−14 s. Thus, the timescale of the scattering is at this energy fast compared to the rotational motion and comparable to the vibrational motion. Above 10 eV, the vibrational sudden approximation becomes more justified.
. The vibrational period is estimated using the vibrational frequency of CN−, ωe = 2035 cm−1,25 corresponding to a period of 1.6 × 10−14 s. Finally, the timescale of the scattering process can be estimated from the classical propagation time along the one-dimensional slice of the potentials from the region where the two states start to interact (R ≈ 17a0) moving inwards to the classical turning point and then out again until the system has passed through the region where the two states interact on the way out. The system propagates on effective potentials obtained by adding the centrifugal barrier to the potential of the electronic state. In mutual neutralization, as described in section IIB, high angular momenta contribute and the system is reflected towards the centrifugal barrier at large distances. By using the angular momentum with the largest contribution to the mutual neutralization cross section in eqn (1), at a collision energy of 10 eV, the scattering timescale is estimated to 4.7 × 10−14 s. Thus, the timescale of the scattering is at this energy fast compared to the rotational motion and comparable to the vibrational motion. Above 10 eV, the vibrational sudden approximation becomes more justified.
In the vibrational sudden approximation, we have only included the R-component of the non-adiabatic coupling. This approximation will be investigated in future studies. In Fig. 11, we show the comparison of the R- and r-components of the non-adiabatic coupling for one slice of the surfaces (r = 2.22 bohr, θ = 90°). In the case of the angle, the non-adiabatic coupling in this degree of freedom is essentially zero. The curve crossing occurs at a large distance, so there is little change as the angle changes. Therefore, the approximation used – averaging over the fixed angle calculations should be accurate.
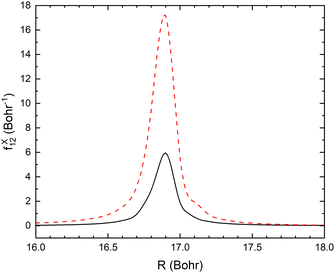 | ||
| Fig. 11 Non-adiabatic coupling elements, fX12, in the r-direction (dashed red line) and R-direction (solid black line) at fixed r = 2.22 bohr and θ = 90°. | ||
However, in the case of the CN distance, the component of the non-adiabatic coupling in this degree of freedom is larger than the component in the active degree of freedom used in the calculation. In the region of the crossing, both the neutral and ion-pair surfaces have a harmonic dependence as the CN distance changes. The surfaces, however, have slightly different shapes, and as a result, there will be a significant non-adiabatic coupling in the CN mode. In the present calculation this dimension is frozen and this coupling is ignored.
In the next step of the calculation, both radial coordinates r and R have to be included in the dynamics. At the same time, the angular motion can be assumed to be frozen during the collision. The two-dimensional scattering problem can be treated using wave-packet propagation on coupled states or a vibronic close coupling scheme. This will be addressed in a future study.
4 Conclusions
We have presented calculations of the potential energy surfaces and non-adiabatic coupling elements relevant for the MN reaction of Li+ and CN−. The process is investigated using a vibrational sudden approximation, where the vibrational and rotational motions of the CN molecule are assumed to be frozen during the collision. The MN cross section for collisions of CN− with Li+ is relatively large and therefore it should be experimentally accessible. Future calculations will study the effect of the CN degree-of-freedom. These calculations should be expanded to other systems. One possibility is the collision of C+ with CN− which is of interest for the atmosphere of Titan.Author contributions
Å. L.: data curation, formal analyses, visualisation, writing – original draft; A. E. O: data curation, formal analyses, writing – review & editing.Conflicts of interest
There are no conflicts to declare.References
- N. S. Shuman, D. E. Hunton and A. A. Viggiano, Chem. Rev., 2015, 115, 4542 CrossRef CAS PubMed.
- D. Smith, Chem. Rev., 1992, 92, 1473 CrossRef CAS.
- D. Smith, N. Adams and M. Church, Planet. Space Sci., 1976, 24, 697–703 CrossRef CAS.
- Å. Larson, P. Hedvall, M. Sahlin, M. Khamesian and A. E. Orel, J. Phys.: Conf. Ser., 2020, 1412, 062004 CrossRef.
- J. Hörnquist, P. Hedvall, A. Larson and A. E. Orel, Phys. Rev. A, 2022, 106, 062821 CrossRef.
- P. Hedvall, M. Odelius and Å. Larson, J. Chem. Phys., 2023, 158, 014305 CrossRef CAS PubMed.
- A. K. Belyaev, P. S. Barklem, A. Spielfiedel, M. Guitou, N. Feautrier, D. S. Rodionov and D. V. Vlasov, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 032704 CrossRef.
- L. Landau, Phys. Soviet Union, 1932, 2, 46 CAS.
- C. Zener, Proc. R. Soc. London, Ser. A, 1932, 137, 696 Search PubMed.
- M. J. J. Eerden, M. C. M. van de Sanden, D. K. Otorbaev and D. C. Schram, Phys. Rev. A: At., Mol., Opt. Phys., 1995, 51, 3362–3365 CrossRef CAS PubMed.
- C. L. Liu, J. G. Wang and R. K. Janev, J. Phys. B: At., Mol. Opt. Phys., 2006, 39, 1223 CrossRef CAS.
- T. J. Millar, C. Walsh and T. A. Field, Chem. Rev., 2017, 117, 1765 CrossRef CAS PubMed.
- V. Vuitton, P. Lavvas, R. V. Yelle, M. Galand, A. Wellbrock, G. R. Lewis, A. J. Coates and J. E. Wahlund, Planet. Space Sci., 2009, 57, 1558 CrossRef CAS.
- E. Clementi, H. Kistenmacher and H. Popkic, J. Chem. Phys., 1973, 58, 2460 CrossRef CAS.
- A. Schmiedekamp, C. W. Bock and P. George, J. Mol. Struct., 1980, 67, 107 CrossRef CAS.
- G. Brocks, J. Tennyson and A. van der Avoird, J. Chem. Phys., 1984, 80, 3223 CrossRef CAS.
- J. Makarewicz and T.-K. Haa, Chem. Phys. Lett., 1995, 232, 497 CrossRef CAS.
- B. S. Jursic, J. Mol. Struct.:THEOCHEM, 1998, 428, 41 CrossRef CAS.
- E. Martin-Fierro, F. Borondo, J. M. G. Llorente and R. M. Benito, J. Chem. Phys., 2002, 116, 10183 CrossRef CAS.
- M. Feldmaier, J. Reiff, R. M. Benito, F. Borondo, J. Main and R. Hernandez, J. Chem. Phys., 2020, 153, 084115 CrossRef CAS PubMed.
- R. T. Skodje, W. R. Gentry and F. Giese, J. Chem. Phys., 1976, 65, 5532 CrossRef CAS.
- E. Rozsályi, L. F. Errea, L. Méndez and I. Rabadán, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 042701 CrossRef.
- H.-J. Werner and P. J. Knowleset al.MOLPRO, version, a package of ab initio programs, see https://www.molpro.net Search PubMed.
- J. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef.
- S. E. Bradforth, E. H. Kim, D. W. Arnold and D. M. Neumark, J. Chem. Phys., 1993, 98, 800 CrossRef CAS.
- R. R. Reddy, Y. N. Ahammad, K. R. Gopal and D. B. Basha, Astrophys. Space Sci., 2003, 286, 419 CrossRef CAS.
- S. M. Nkambule, P. Nurzia and Å. Larson, Chem. Phys., 2015, 462, 23 CrossRef CAS.
- T. Leininger and F. X. Gadéa, Theor. Chem. Acc., 2023, 142, 95 Search PubMed.
- C. A. Mead and D. G. Truhlar, J. Chem. Phys., 1982, 77, 6090 CrossRef CAS.
- W. W. Cheney and D. Kincaid, Numerical Mathematics and Computing, Brooks/Cole Publishing Co., USA, 2nd edn, 1985 Search PubMed.
- B. R. Johnson, J. Comput. Phys., 1973, 13, 445 CrossRef.
- B. R. Johnson, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 32, 1241–1242 CrossRef PubMed.
- M. Stenrup, Å. Larson and N. Elander, Phys. Rev. A, 2009, 79, 012713 CrossRef.
- E. P. Wigner, Phys. Rev., 1948, 73, 1002 CrossRef CAS.
- T. Launoy, J. Loreau, A. Dochain, J. Liévin, N. Vaeck and X. Urbain, Astrophys. J., 2019, 883, 85 CrossRef CAS.
- T. Amano, J. Chem. Phys., 2008, 129, 244305 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2024 |