 Open Access Article
Open Access ArticleReactivity of cationic silver clusters with O2: a probe of interplay between clusters’ geometric and electronic structures†
Jin
Hu
,
Jun
Ma
,
Zhengqian
Jin
,
Wen
Liu
,
Lulu
Huang
,
Xuefeng
Wang
 * and
Xiaopeng
Xing
* and
Xiaopeng
Xing
 *
*
School of Chemical Science and Engineering, Shanghai Key Lab of Chemical Assessment and Sustainability, Tongji University, 1239 Siping Road, Shanghai, 200092, China. E-mail: xfwang@tongji.edu.cn; xingxp@tongji.edu.cn
First published on 30th January 2024
Abstract
We explored the size-dependent reactivity of Agn+ (n = 2–22) with O2 under mild conditions and found that only a few sizes of Agn+, with even values of n = 4, 6, 12, 16, 18, and 22, are reactive. Possible structures of Agn+ (n = 2–22) were determined using a genetic algorithm with incomplete local optimizations at the DFT level, and the calculated bonding strengths of O2 on these structures are consistent with experimental observations. Analyses revealed a close relationship between the reactivity of Agn+ with O2 and its HOMO–LUMO gap: cationic silver clusters with a small HOMO–LUMO gap are reactive, which can be rationalized by the covalent character of chemical bonds between Agn+ and O2 involving their frontier orbitals. The peculiar size-dependent HOMO–LUMO gaps and reactivity with O2 correlate with the subtle interplay between the electronic configurations and geometric structures of these silver cluster cations.
1. Introduction
The geometric and electronic structures of small clusters are fundamental to understanding their properties and exploring their potential applications.1–4 For a bulk system, the geometric and electronic structures are independent, while the electronic properties of nanoparticles or sub-nano clusters are generally correlated with their geometric structures. Like small molecules, the geometric and electronic structures of sub-nano clusters interplay with each other, which can be rationalized using the Jahn–Teller effect.5–9 Metal clusters with good ductility and relatively simple electron configurations are ideal examples to explore this interplay, and the free electron shell model applied in these species needs to take their geometric characteristics into account.10–12Silver clusters serve as valuable model systems for investigating the active sites of silver-based catalysts in various oxidation processes with significant industrial relevance, for example, the partial oxidation of ethylene to ethylene oxide,13,14 partial oxidation of methanol or ethanol to their aldehydes,15 and selective oxidation removal of CO from H2 used in fuel cells.16,17 In addition, the relatively simple electronic configuration and bonding character of the silver element make silver clusters ideal models for understanding many fundamental concepts in the cluster field. By analyzing the mass spectra of Agn+ and Agn formed in the gas phase, previous investigations showed that the enhanced abundances of certain sizes can be rationalized using the free electron model initially observed in the alkali metal clusters.18,19 The electronic properties of Agn− were characterized using photoelectron spectroscopy, and size-dependent electron detachment energies provide evidence for the applicability of the electron shell model in anionic silver systems.20–22 The geometric structures of some Agn− and Agn+ species were explored by combining the fingerprint information from various experiments using photoelectron spectrometry, ion mobility, and trapped ion electron diffraction techniques and theoretical calculations.21–27
Reactions between Agn− and O2 used as supplemental probes for the electronic properties of anionic silver clusters according to a scenario in which one electron transfers from the anionic silver moiety to the adsorbed O2 in formed complexes.28–33 There are drastic changes in the reactivity for sizes of Agn− containing 8 and 20 free electrons, which implies the formation of electron shells like those in an atom.30,31 The interplay between the geometric and electronic structures was discussed in sizes containing 14 and 30 free electrons.30,33 A recent study combining reaction experiments and theoretical calculations showed the remarkable stability of Ag17− due to its closed electronic as well as geometric shells,32 and a single congener doping atom can result in the rearrangement of the geometry of Ag17− and significantly change its electronic properties and reactivity.34
In contrast to the good understanding of the electronic properties of anionic silver clusters and therefore the correlation with the reactivity with O2, there are no efficient techniques to directly characterize the electronic properties of cationic silver clusters. Reactions between Agn+ and O2 species were previously explored in the extension region of the cluster source at low temperatures.35–39 The results showed a general even–odd oscillation of the reactivity in the size range up to one nanometre. It was proposed that Agn+ containing 2, 8, and 20 free electrons form closed electron shells, which endows them enhanced stability, and a slight increase of the temperature (∼105 K) leads to the dissociation of O2 on Agn+ to form the oxide state of silver.35,38,39 A recent experiment using an ion trap running at room temperature showed that the even-odd oscillation in the reactivity of Agn+ ends at n = 10, and all larger sizes are highly reactive.40 In these previous experiments, cluster etching paths and reactive odd sizes of Agn+ are hints that extra energies could be ubiquitous in reaction systems, facilitating the crossing of barriers associated with bond breakages or spin accommodation requirements. The reactivity of clusters under relatively violent conditions could partially mask the effects of their intrinsic geometric or electronic characteristics.
Herein, we explored the reactions of Agn+ (n = 2–22) with O2 under mild conditions, in which clusters and reactant O2 were pre-cooled by a helium buffer gas before entering the reaction cell, it was ensured that reaction systems were canonical ensembles at a defined low temperature.31,41 Under conditions described in the Experimental section, a peculiar discontinuous even–odd oscillation was observed for the of reactivity. In addition to the inertness of odd sizes which was attributed to barriers from the spin accommodation requirement,30 a few even sizes, including Ag4+ and Ag10+ which were expected to have alkali-like electron configurations and high reactivity,36,39 were shown to be inert. Combining these carefully designed experiments and large theoretical calculations, we found that the peculiar discontinuous odd–even oscillation of the reactivity of clusters reflects the size-dependent feasibility of the transition from physisorption to chemisorption of the combined O2. This feasibility closely correlates with the varying HOMO–LUMO gaps of Agn+, which reflect a subtle interplay between their electronic and geometric structures.
2. Experimental and computational methods
The cluster reaction experiments were carried out using an instrument composed of a magnetron sputtering cluster source, a continuous micro tube reactor and a time-of-flight (TOF) mass spectrometer. The device diagram is shown in Fig. S15 (ESI†), and the details of this instrument were described elsewhere.31,42 Briefly, the cluster source has a liquid-nitrogen-cooled aggregation chamber enclosing a magnetron sputter discharge head. A small tube reactor was installed at the exit of the source chamber, which is isolated from the source by a ceramic spacer. The temperature of this tube reactor was adjusted using a controlled heater and was stabilized at 150 K in this work.The clusters formed inside the source chamber were carried by the helium buffer gas and argon discharging gas (110 sccm and 14 sccm, respectively) and flowed into the tube reactor. Only those species near the central axis can enter the reaction region, and most clusters were filtered by multi-layer meshes. The intentional decrease in the concentration of metal species in the reaction region is to stop the cluster growth processes. Another function of the multi-layer meshes is to thermalize the carrier gas to the set temperature of the reactor. The reactant O2 was introduced through two copper tubes extending close to the axial center of the reactor, which were also thermalized to the temperature of the reactor inside the mantle layer. The flow rates were about 0.02–0.2 sccm. The total pressure inside the aggregation chamber of the cluster source and tube reactor was about 0.5 torr, and the partial pressure of the reactant in the reactor was around 10−4 torr. The reaction time was estimated to be several milliseconds. The generated species, including parent clusters and reaction products, went through a skimmer at the end of the flow reactor. The continuous ion beam from the skimmer was directed to and analyzed using a time-of-flight (TOF) mass spectrometer operating at 800 Hz. The mass spectra of species at a series of O2 flow rates were recorded using the TOF mass spectrometer. The intensity of one parent cluster Agn+ at a certain O2 flow rate (I) and that without O2 (I0) were separately integrated.
The adsorption process of clusters and O2 molecules follows the Lindemann reaction mechanism. Taking Agn+ and O2 as an example:
| Agn+ + O2 ⇔ [AgnO2+]* | (1) |
| [AgnO2+]* + He → AgnO2+ + He* | (2) |
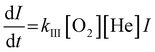 | (3) |
Integrate both sides to get:
 | (4) |
The rate constant kIII is proportional to −ln(I/I0) n since true concentrations of O2 and He (shown as [O2] and [He]) and the reaction time t are constant. Besides, [O2] and [He] are much larger than the partial pressure of metal clusters, so the reaction can be regarded as a quasi-first-order reaction. We plotted the obtained −ln(I/I0) vs. the flow of O2, and the slope of the resulting straight line is proportional to kIII.
The structure search of silver clusters was conducted using our newly encoded genetic algorithm program with an incomplete local optimization strategy,33 in which all optimization processes and energy calculations were carried out using the Gaussian09 program.43 Briefly, we used a module to generate random structures including, a space-free motif, a close packing motif, a simple cubic packing motif, a cage motif, a solid sphere motif, a ring motif and other user-defined motifs. These structures were screened according to their calculated energies and evolved toward low-lying ones through multiple rounds of crossovers, mutations, and competitions. The main feature of this program is that all local optimizations in the structure evolution are terminated in a relatively flat area rather than exact local minimum points on the potential energy surface (PES), and only the structures of the last generation were completely optimized to obtain the global minimum. The efficiency and reliability of methods have been previously shown in searching the structure of Ag30 and other representative clusters.33 The initial structural candidates of AgnO2+ reaction products were generated by randomly putting O2 around all possible adsorption sites of obtained lowest-lying structures of Agn+, and various adsorption patterns including O-atop and O–O doubly connected geometries in their doublet or quartet state were considered. The complete and incomplete optimizations in this study were at the PBE level with the def2-SVP basis set for Ag and def2-TZVP basis sets for O.44–46 After each complete optimization process, the harmonic vibrational frequencies were calculated to confirm that a real minimum point was obtained, and at the same time, the zero-point vibrational energy (ZPVE) was derived. Calculations on the relative energies of various isomers and O2 adsorption energies were based on the electronic energies of related species modified by their ZPVE corrections. The NPA charges and spin populations on O–O in the obtained structures of AgnO2+ were calculated.
3. Results and discussion
3.1 Size-dependent reactivity of Agn+ (n = 2–22) with O2
Fig. 1a shows Agn+ (n = 4–23) species formed in the cluster source and their reaction products with 0.025 sccm and 0.075 sccm O2. The vertical dashed lines indicate Agn+, and circle symbols indicate dominant products, such as AgnO2+. For Agn+ (n < 4), the mass spectra contained cluster complexes with argon from the sputter source and nitrogen or CO molecules possibly from the background. However, the spectra clearly show that there were no oxygen-adsorbed products for Agn+ (n = 1–3) (shown in Fig. S1, ESI†). The relative kinetic rates of Agn+ were obtained as described in the Experimental section, and are summarized in Fig. 1b. The reactivity showed an apparent even-odd oscillation, in which all active sizes contain an even number of atoms, in other words, an odd number of valence electrons. All reactive sizes adsorbed only one O2. Notably, not all even sizes in this range showed detectable activity. Agn+ species with n = 8, 10, 14, and 20 are inert, and the reactivity of n = 4 is very low, which is different from previous experimental observations.36,39,403.2 Theoretical structures and electronic properties of Agn+ (n = 2–22)
To understand the peculiar discontinuous odd–even oscillation of the reactivity, we theoretically explored structural candidates of Agn+ (n = 2–22) using a newly developed genetic algorithm program33 and determined the most likely ones according to their relative energies and comparisons with the results from previous experiments. The low-lying isomers for each size of Agn+ (n = 2–22) are displayed in Fig. S2–S10 (ESI†), and the most likely ones present in experiments are presented in Fig. 2a. The structures of Agn+ (n = 2–13) were recently determined based on a combination of the far-infrared multiple photon dissociation spectra of the complexes of clusters and theoretical calculations.41 The lowest-lying structures of Agn+ (n = 2–5, 8, 10–13) from our calculations (Fig. S2–S6, ESI†) are consistent with this report. The results of Ag6+, Ag7+ and Ag9+ in our calculations (Fig. S2–S4, ESI†) include one or two structures with even lower energies at the present theoretical level, while energy differences are almost negligible. The results of Agn+ (n = 12–15) (Fig. S5–S7, ESI†) are in complete agreement with those in previous theoretical studies.47–50 The minimum structure of optimized Ag19+ (Fig. S9, ESI†) is consistent with the one previously determined using trapped ion electron diffraction experiments and theoretical calculations.27 For n = 16, 17, 18 and 20 (Fig. S7–S9, ESI†), we found one or two new structures with lower energies than those from a previous theoretical report.49 For n = 21 and 22 (Fig. S10, ESI†), our calculation found more than seven isomers which are more stable than the lowest-lying ones reported by previous theoretical studies.49,50 In Fig. 2a, we list the structures of Agn+ (n = 3–13) previously confirmed by the combined experiment and theoretical calculation41 and the lowest-lying ones of Agn+ (n = 14–22) from our calculations. We saw that the shapes of clusters vary with increasing size: the structures undergo a 2D (n = 4) to 3D (n = 5) transition and become near-spherical at n = 8 and 9; the structures of n = 10–14 have elongated prolate shapes and those of n = 15–17 display an oblate sheet formed by two layers of staggered atoms; for sizes with n = 17–19, geometries change into an irregular oblate shape with an embedded silver atom; for those with n = 20–22, all atoms are tightly packed into a quasi-spherical shape and the number of silver atoms trapped inside increases to two or three.We calculated the electronic and energetic features of the most likely structures shown in Fig. 2a, including vertical electron detachment energies (VDE), vertical electron affinities (VEA), the incremental binding energies (IBE), and second-order differences in binding energy (Δ2E), which were defined as follows:
| VDE(Agn+) = E[Agn2+] − E[Agn+] | (5) |
| VEA(Agn+) = E[Agn+] − E[Agn0] | (6) |
| IBE(Agn+) = E[Ag0] + E[Agn−1+] − E[Agn+] | (7) |
| Δ2E(Agn+) = E[Agn+1+] + E[Agn−1+] − 2E[Agn+] | (8) |
As seen in Fig. 2b, there is a general odd–even oscillation in VDE and VEA. For VDE, a high value of odd-sized Agn+ species is due to their lower-energy singlet state formed by an even number of electrons, compared to its even-size neighbors with one unpaired electron. Note that with an increase of n, the variation of VDE gradually becomes smooth, but significantly decreases at Ag22+ (0.58 eV lower than Ag20+ and 0.78 eV lower than Ag21+). VEA is reminiscent of a mirror image of VDE, with a large VDE corresponding to a small VEA. Comparing Fig. 1 and Fig. 2b, we see no evident correlation between the reactivity of Agn+ species with oxygen and their VDEs or VEAs, which is different from the case observed for silver cluster anions.30–32 IBE and Δ2E are depicted in Fig. 2c, both of which show oscillatory trends and do not have a correlation with the reactivity in Fig. 1. HOMO–LUMO gaps in Fig. 2d exhibit a large drop from Ag3+ to Ag22+. Additionally, it was found that there is a threshold of about 0.73 eV that separates reactive clusters from inert ones observed in Fig. 1. Especially, the significantly lower HOMO–LUMO gap and VDE of Ag22+ than those other species correspond to a greater propensity to adsorb one O2 in experiments, whereas Ag20+, with an open-shell size, unexpectedly shows a sizable gap, even larger than its neighbor Ag19+, with a closed 18-electron shell.
3.3 Theoretical exploration of the bonding of O2 on Agn+ (n = 2–22)
We theoretically explored the structures of AgnO2+ (n = 3–12, 20, and 22) and bonding strengths of adsorbed O2. The structure searching started from the structures of Agn+ (n = 3–22) shown in Fig. 2, and one O2 unit was put on each adsorption site in an end-on or side-on manner. Then, all convergent structures were sequenced according to their energies. For all even- and odd-sized clusters, calculations located structures with an end-on O2. There are also some structures for even sizes with a side-on O2, while no such ones for odd sizes. The lowest-lying structures of AgnO2+ (n = 3–12, 20, and 22) with an end-on O2 and those of the AgnO2+ (n = 4, 6, 8, 10, 12, 20, and 22) with a side-on O2 are shown in Fig. 3a and b, respectively. For nearly all structures with either an end-on or a side-on O2, silver moieties remain the original geometries of Agn+. The only exception is the lowest-lying Ag4O2+ in Fig. 3b, in which the frame of Ag4+ changes from a rhomboid to a pyramid after combining with a side-on O2. The binding energy of O2 in each structure and charge and spin populations localized on the O2 unit are shown in Fig. 3c–e. In Fig. 3c, the bonding energies of side-on O2 on Agn+ (n = 4, 6, 12, and 22) are higher than 0.4 eV and those of side-on O2 on Agn+ (n = 8, 10, and 20) are lower than 0.35 eV; the bonding energies of end-on O2 on all even or odd sizes are lower than 0.35 eV. These calculated binding energy values are generally consistent with experimental observations in Fig. 1, since the threshold of the binding energy to resist the entropy decrease accompanying the adsorption was estimated to be around 0.37 eV under similar experimental condition.51 In Fig. 3d, there are very small amounts of negative charge (<0.2 a.u.) populated on end-on O2, while the amounts on side-on O2 in even sizes are apparently larger. In Fig. 3e, the spin populations on side-on O2 are 1.6–2.0 a.u., while those on end-on O2 are 1.0–1.3 a.u. These apparently different charge and spin values imply that end-on and side-on O2 are in different states. To summarize the findings from bonding energies and charge and spin populations, end-on O2 units are physisorbed and side-on O2 units found in even sizes are chemically bonded. The transition paths from the end-on state to the side-on state of O2 in Agn+ (n = 4, 6, 8, 10, and 12) were theoretically explored, and the results are shown in Fig. S11a–e (ESI†). It is interesting to find that the variation of the kinetic barriers of the transitions of these five sizes is consistent with the changes of their HOMO–LUMO gaps, which are summarized in Fig. S11f (ESI†). These trends are also consistent with the observed reactivity variation shown in Fig. 1. Especially, the calculated high binding energy (0.48 eV) of O2 on Ag4+ in Fig. 3c, and the small amounts of reacted Ag4+ in Fig. 1 can be rationalized using the kinetic barrier for the transition from the rhomboid to the pyramid of the silver frame or the presence of a tiny amount of the reactive pyramid isomer. | ||
| Fig. 3 (a) Structures of AgnO2+ (n = 3–12, 20, and 22) containing an end-on O2 and (b) AgnO2+ (n = 4, 6, 8, 10, 12, 20, and 22) containing a side-on O2 formed by Agn+ structures shown in Fig. 2; the calculated properties of above structures including (c) the binding energy of O2, (d) NPA charges on O2, and (e) spin populations on O2. All structures and their properties are from calculations at the PBE level with the def2-SVP basis set for Ag and def2-TZVP basis set for O. | ||
We also explored the structures of AgnO2+ without restrictions that the two oxygen atoms connect together and silver clusters are maintained as one unit. The lowest-lying structures of this kind are shown in Fig. S12 (ESI†). The new structures determined for AgnO2+ (n = 3–7) have higher energies than or energies very close to the ones shown in Fig. 3a. The energies of all even- and odd-sized AgnO2+ (n = 8–12) in Fig. S12 (ESI†) are apparently lower than those of their structures in Fig. 3a, and the energy decreases from separate Agn+ and O2 to these structures are much larger than the estimated threshold (∼0.37 eV) resisting the entropy decrease. The completely different trends of these reaction energies in Fig. S12 (ESI†), and the reactivity shown in Fig. 1 imply that the dissociation of O2 is less likely under present mild conditions. Using the reaction of Ag10+ with O2 as an example, we also considered reaction energies for possible etching reaction channels, which include those reported in previous experiments.35–39 The results shown in Fig. S13 (ESI†) indicate that all etching or dissociation channels are highly endothermic and cannot happen under present mild conditions.
The correlation between the H–L gap of Agn+ clusters and their reactivity to oxygen revealed in this study is in contrast to the reactivity of Agn− highly correlated with the VDE of clusters. The varying reactivity of anionic silver clusters with O2 was generally attributed to two reasons:30–32,42,52 (1) the stable reaction products of odd-sized IB metal cluster anions (singlet) with O2 (triplet) are in a singlet state, and there are always barriers related to the spin accommodation requirement in these reaction systems; (2) even-size IB metal cluster anions with lower electron detachment potentials are generally reactive, because their electronic properties facilitate the directed transfer of the unpaired electron from the metal moiety to bonded O2. In previous studies of the reactions between Agn+ and O2,35–39 observed AgnO2+ complexes were considered to be a combination of Agn2+ and O2− through ionic bonding, where electron transfer similar to that in anionic silver or gold clusters was proposed. Following this assumption, the VDE value of clusters should be qualitatively consistent with their reactivity to O2, as well as the amount of charge transfer from the cluster to the O2 subunit. However, in the present study, there seems to be no apparent correlation between VDE values in Fig. 2b and NPA values in Fig. 3d or HOMO–LOMO gaps in Fig. 2d. The superatomic features in Fig. 4 cannot be associated with VDE values either. Instead, the exclusive dominance of H–L gaps of clusters on the reactivity was revealed, suggesting that the interaction in AgnO2+ involves HOMO and LUMO of Agn+. We show orbital interactions of the silver moiety and O2 molecule using two representative complexes, Ag4O2+ and Ag6O2+, in Fig. S14(a) and (b) (ESI†), respectively. In these two cases, the interaction between Agn+ and O2 can be considered as follows: the single electron on the HOMO of Agn+ was excited to its LUMO, and the combination of this LUMO and one πg of O2 formed the bonding orbital in AgnO2+. In a certain sense, this interaction has a covalent character.
3.4 Interplay between geometries and HOMO–LUMO gaps of Agn+ (n = 2–22)
An unexpected phenomenon in this study is the size-dependence of HOMO–LUMO gaps and therefore the reactivity of even sizes Agn+, which in many points are in marked contrast to the prediction of the free electron shell model.10 For example, even-sized Ag4+ and Ag10+ have one more electron than closed shells composed of 2 and 8 electrons, respectively, and therefore are expected to be like alkali metal atoms with small HOMO–LUMO gaps and high reactivity with O2. This expectation is true for anionic Ag2− (ne = 2 + 1)29,53 and Ag8− (ne = 8 + 1),54 both of which are quite reactive with O2. However, experiments and calculations in this study showed that Ag4+ and Ag10+ have large HOMO–LUMO gaps and have low reactivity or are completely inert. The decrease of HOMO–LUMO gaps and the increase of the reactivity from Ag4+ to Ag6+ and from Ag10+ to Ag12+ are also unexpected. Ag20+ and Ag22+ are expected to have electron configurations like those of alkali metals, because they have one more electron than closed shells composed of 18 and 20 free electrons, respectively. However, Ag20+ is found to have a quite large HOMO–LUMO gap and no reactivity with O2. In Fig. 4, we plot energy levels of three pairs of even-sized species around unexpected turning points (Ag4+ → Ag6+; Ag10+ → Ag12+; Ag20+ → Ag22+). For Ag4+, the lowest-lying rhomboid structure (in Fig. 2) and pyramid structure (an isomer 0.32 eV higher; shown in Fig. S2, ESI†) were considered, since chemisorbed O2 on the rhomboid structure of Ag4+ changed it to the pyramid one (shown in Fig. 3 and Fig. S11, ESI†). The energy levels and orbital shapes of pyramid Ag4+ in Fig. 4a show that its three 1p orbitals are very close, and the electron configuration 1s21p1 leads to a very small HOMO–LUMO gap. The rhomboid Ag4+ (in Fig. 4a) has only two 1p orbitals because of its planar potential field,11 and the energies of these two orbitals are well separated because of the apparent difference between the two diagonals of the rhomboid. The 1p orbital along the longer diagonal is lower in energy and the other along the shorter diagonal is higher. The geometries of Ag6+ (Fig. 4a), Ag10+ and Ag12+ (Fig. 4b) can roughly be viewed as a 3D structure extending longer in one direction (labeled as the z direction using arrows beside structures in Fig. 4) than other two orthogonal ones (x/y). Based on quantum mechanical figures, the orbital extending to the longer direction tends to be lower in energy than others of the same type. In Ag6+ (Fig. 4a), the electron configuration is 1s21pz21px/y1, and the small energy difference between 1px and 1py leads to a small HOMO–LUMO gap. In Ag10+ (Fig. 4b), the electron configuration is 1s21pz21px/y41dz211dxy/yz/…, and the large separation between 1dz2 and other 1dxy/yz/.. orbitals leads to a large HOMO–LUMO gap. In Ag12+ (Fig. 4b), the electron configuration is 1s21pz21px21py21dz221dxy/yz/..,1 and the relatively small energy differences among 1dxy/yz/.. orbitals lead to a small HOMO–LUMO gap. For Ag20+ and Ag22+ (Fig. 4c), the differences among their x/y/z dimensions are insignificant, and the splitting of orbitals of the same type is relatively small. The electron configurations of Ag20+ and Ag22+ are 1s21p61d102s1 and1s21p61d102s21f1, respectively, and their HOMO–LUMO gaps correspond to the large gap between 2s and 1f shells and small gap between two 1f orbitals, respectively.4. Conclusions
We presented a study on reactions of Agn+ (n = 2–22) with O2 by combining experimental measurements and theoretical calculations. Under mild conditions, the reactivity of Agn+ showed a peculiar size dependence, in which only Agn+ species (n = 4, 6, 12, 16, 18, and 22) are reactive. The most likely structures of Agn+ (n = 2–22) are determined using an improved genetic algorithm and a density functional theory method. The bonding strengths of O2 on the determined structures of Agn+ (n = 2–22) are consistent with experimental observations. Analyses of the electronic character of Agn+ (n = 2–22) species indicated that their reactivity with O2 is closely related to their HOMO–LUMO gaps. Theoretical results showed that decreased HOMO–LUMO gaps facilitated the formation of covalent interactions with O2 under thermodynamic and kinetic considerations. The variation of HOMO–LUMO gaps and therefore the reactivity with O2 was further attributed to a subtle interplay between electronic configurations and geometric structures of Agn+.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 22273065, 21673158) and Science & Technology Commission of Shanghai Municipality (14DZ2261100). Theoretical calculations were carried out on the computing resource in National Supercomputing Center in Shenzhen.Notes and references
- S. M. Lang and T. M. Bernhardt, Phys. Chem. Chem. Phys., 2012, 14, 9255–9269 RSC.
- L.-M. Wang and L.-S. Wang, Nanoscale, 2012, 4, 4038–4053 RSC.
- Z. X. Luo, A. W. Castleman and S. N. Khanna, Chem. Rev., 2016, 116, 14456–14492 CrossRef CAS PubMed.
- P. Ferrari, J. Vanbuel, E. Janssens and P. Lievens, Acc. Chem. Res., 2018, 51, 3174–3182 CrossRef CAS PubMed.
- J. L. Martins, J. Buttet and R. Car, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 1804–1816 CrossRef CAS PubMed.
- M. Castro, C. Jamorski and D. R. Salahub, Chem. Phys. Lett., 1997, 271, 133–142 CrossRef CAS.
- W. Satula, J. Dobaczewski and W. Nazarewicz, Phys. Rev. Lett., 1998, 81, 3599–3602 CrossRef CAS.
- M. A. Tofanelli, K. Salorinne, T. W. Ni, S. Malola, B. Newell, B. Phillips, H. Hakkinen and C. J. Ackerson, Chem. Sci., 2016, 7, 1882–1890 RSC.
- Q. Y. Du, X. Wu, P. J. Wang, D. Wu, L. W. Sai, R. B. King, S. J. Park and J. J. Zhao, J. Phys. Chem. C, 2020, 124, 7449–7457 CrossRef CAS.
- W. A. Deheer, Rev. Mod. Phys., 1993, 65, 611–676 CrossRef CAS.
- H. Hakkinen, Adv. Phys.: X, 2016, 1, 467–491 Search PubMed.
- T. Tsukamoto, T. Kambe, T. Imaoka and K. Yamamoto, Nat. Rev. Chem., 2021, 5, 338–347 CrossRef CAS PubMed.
- R. M. Lambert, F. J. Williams, R. L. Cropley and A. Palermo, J. Mol. Catal. A: Chem., 2005, 228, 27–33 CrossRef CAS.
- Y. Lei, F. Mehmood, S. Lee, J. Greeley, B. Lee, S. Seifert, R. E. Winans, J. W. Elam, R. J. Meyer, P. C. Redfern, D. Teschner, R. Schlogl, M. J. Pellin, L. A. Curtiss and S. Vajda, Science, 2010, 328, 224–228 CrossRef CAS PubMed.
- H. I. Mahdi, N. N. Ramlee, D. H. D. Santos, D. A. Giannakoudakis, L. H. de Oliveira, R. Selvasembian, N. I. W. Azelee, A. Bazargan and L. Meili, Mol. Catal., 2023, 537, 112944 CrossRef CAS.
- V. V. Dutov, G. V. Mamontov, V. I. Zaikovskii, L. F. Liotta and O. V. Vodyankina, Appl. Catal., B, 2018, 221, 598–609 CrossRef CAS.
- Z. P. Qu, M. Cheng, C. Shi and X. Bao, J. Mol. Catal. A: Chem., 2005, 239, 22–31 CrossRef CAS.
- I. Katakuse, T. Ichihara, Y. Fujita, T. Matsuo, T. Sakurai and H. Matsuda, Int. J. Mass Spectrom. Ion Processes, 1985, 67, 229–236 CrossRef CAS.
- G. Alameddin, J. Hunter, D. Cameron and M. M. Kappes, Chem. Phys. Lett., 1992, 192, 122–128 CrossRef CAS.
- K. J. Taylor, C. L. Pettiette-Hall, O. Cheshnovsky and R. E. Smalley, J. Chem. Phys., 1992, 96, 3319 CrossRef CAS.
- H. Handschuh, C. Y. Cha, P. S. Bechthold, G. Ganteför and W. Eberhardt, J. Chem. Phys., 1995, 102, 6406–6422 CrossRef CAS.
- K. Majer and B. von Issendorff, Phys. Chem. Chem. Phys., 2012, 14, 9371–9376 RSC.
- P. Weis, T. Bierweiler, S. Gilb and M. M. Kappes, Chem. Phys. Lett., 2002, 355, 355–364 CrossRef CAS.
- H. Hakkinen, M. Moseler, O. Kostko, N. Morgner, M. A. Hoffmann and B. von Issendorff, Phys. Rev. Lett., 2004, 93, 093401 CrossRef PubMed.
- X. P. Xing, R. M. Danell, I. L. Garzon, K. Michaelian, M. N. Blom, M. M. Burns and J. H. Parks, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 081405 CrossRef.
- D. Schooss, M. N. Blom, J. H. Parks, B. von Issendorff, H. Haberland and M. M. Kappes, Nano Lett., 2005, 5, 1972–1977 CrossRef CAS PubMed.
- M. N. Blom, D. Schooss, J. Stairs and M. M. Kappes, J. Chem. Phys., 2006, 124, 244308 CrossRef PubMed.
- T. H. Lee and K. M. Ervin, J. Phys. Chem., 1994, 98, 10023–10031 CrossRef CAS.
- J. Hagen, L. D. Socaciu, J. LeRoux, D. Popolan, T. M. Bernhardt, L. Woste, R. Mitric, H. Noack and V. Bonacic-Koutecky, J. Am. Chem. Soc., 2004, 126, 3442–3443 CrossRef CAS PubMed.
- Z. X. Luo, G. U. Gamboa, J. C. Smith, A. C. Reber, J. U. Reveles, S. N. Khanna and A. W. Castleman, J. Am. Chem. Soc., 2012, 134, 18973–18978 CrossRef CAS PubMed.
- J. Ma, X. Cao, X. Xing, X. Wang and J. H. Parks, Phys. Chem. Chem. Phys., 2016, 18, 743–748 RSC.
- B. Q. Yin, Q. Y. Du, L. J. Geng, H. Y. Zhang, Z. X. Luo, S. Zhou and J. J. Zhao, CCS Chem., 2021, 3, 219–229 CrossRef CAS.
- W. Liu, L. L. Huang, L. Meng, J. Hu and X. P. Xing, Phys. Chem. Chem. Phys., 2023, 25, 14303–14310 RSC.
- Q. Y. Du, L. L. Huang, J. Q. Fu, Y. J. Cao, X. P. Xing and J. J. Zhao, J. Chem. Phys., 2023, 158, 014306 CrossRef CAS PubMed.
- M. Schmidt, P. Cahuzac, C. Brechignac and H. P. Cheng, J. Chem. Phys., 2003, 118, 10956–10962 CrossRef CAS.
- M. Schmidt, A. Masson and C. Bréchignac, Phys. Rev. Lett., 2003, 91, 243401 CrossRef CAS PubMed.
- Y.-N. Wu, M. Schmidt, J. Leygnier, H.-P. Cheng, A. Masson and C. Brechignac, J. Chem. Phys., 2012, 136, 024314 CrossRef PubMed.
- M. Schmidt, A. Masson, H.-P. Cheng and C. Brechignac, ChemPhysChem, 2015, 16, 855–865 CrossRef CAS PubMed.
- M. Schmidt and C. Brechignac, C. R. Phys., 2016, 17, 481–484 CrossRef CAS.
- M. Arakawa, N. Hayashi, K. Minamikawa, T. Nishizato and A. Terasaki, J. Phys. Chem. A, 2022, 126, 6920–6926 CrossRef CAS PubMed.
- J. van der Tol, D. Jia, Y. Li, V. Chernyy, J. M. Bakker, N. Minh Tho, P. Lievens and E. Janssens, Phys. Chem. Chem. Phys., 2017, 19, 19360–19368 RSC.
- T. Wang, J. Ma, B. Yin and X. Xing, J. Phys. Chem. A, 2018, 122, 3346–3352 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria and M. A. Robb, et al., Gaussian 09 Rev. C.01, Wallingford, CT, 2010 Search PubMed.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS PubMed.
- D. Andrae, U. Haussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- H. L. Zhang and D. X. Tian, Comput. Mater. Sci., 2008, 42, 462–469 CrossRef CAS.
- Y. Y. Jin, Y. H. Tian, X. Y. Kuang, C. Z. Zhang, C. Lu, J. J. Wang, J. Lv, L. P. Ding and M. Ju, J. Phys. Chem. A, 2015, 119, 6738–6745 CrossRef CAS PubMed.
- M. L. McKee and A. Samokhvalov, J. Phys. Chem. A, 2017, 121, 5018–5028 CrossRef CAS PubMed.
- S.-Y. Yan, W. Zhang, Z.-X. Zhao, W.-C. Lu and H.-X. Zhang, Theor. Chem. Acc., 2012, 131, 1200 Search PubMed.
- L. Huang, W. Liu, J. Hu and X. Xing, J. Phys. Chem. A, 2021, 125, 9995–10005 CrossRef CAS PubMed.
- B. E. Salisbury, W. T. Wallace and R. L. Whetten, Chem. Phys., 2000, 262, 131–141 CrossRef CAS.
- T. M. Bernhardt, J. Hagen, S. M. Lang, D. M. Popolan, L. D. Socaciu-Siebert and L. Woste, J. Phys. Chem. A, 2009, 113, 2724–2733 CrossRef CAS PubMed.
- Z. Luo, C. Berkdemir, J. C. Smith and A. W. Castleman, Chem. Phys. Lett., 2013, 582, 24–30 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The mass spectra of Agn+ (n = 1–3) with the presence of O2 (Fig. S1; PDF); the calculated low-lying structures of Agn+ (n = 2–22) (Fig. S2–S10; PDF); the reaction paths of the dominant structures of Agn+ (n = 4, 6, 8, 10, 12) with O2, the lowest-lying structures of AgnO2+ (n = 3–12) with O2 inserted into or dissociated on the silver moiety, the relative energies of multiple products of Ag10+ with O2, and the bonding scheme of Ag4O2+ and Ag6O2+ (Fig. S11–S14; PDF); the schematic experimental setup (Fig. S15; PDF). See DOI: https://doi.org/10.1039/d3cp05082c |
| This journal is © the Owner Societies 2024 |



