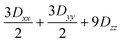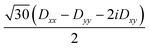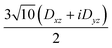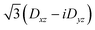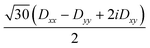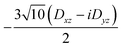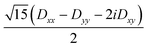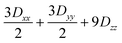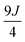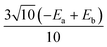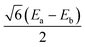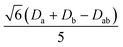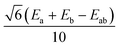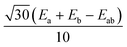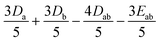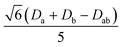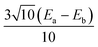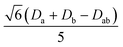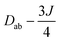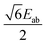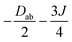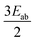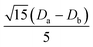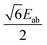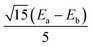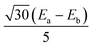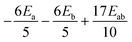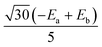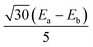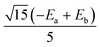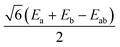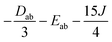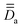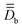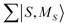Open Access Article
Open Access ArticleThe resolution of the weak-exchange limit made rigorous, simple and general in binuclear complexes†
Dumitru-Claudiu
Sergentu
 abc,
Boris
Le Guennic
abc,
Boris
Le Guennic
 a and
Rémi
Maurice
a and
Rémi
Maurice
 *a
*a
aUniv Rennes, CNRS ISCR (Institut des Sciences Chimiques de Rennes) – UMR 6226, 35000 Rennes, France. E-mail: remi.maurice@univ-rennes.fr
bLaboratorul RA-03 (RECENT AIR), Universitatea Alexandru Ioan Cuza din Iaşi, 700506 Iaşi, Romania
cFacultatea de Chimie, Universitatea Alexandru Ioan Cuza din Iaşi, 700506 Iaşi, Romania
First published on 30th January 2024
Abstract
The correct interpretation of magnetic properties in the weak-exchange regime has remained a challenging task for several decades. In this regime, the effective exchange interaction between local spins is quite weak, of the same order of magnitude or smaller than the various anisotropic terms, which generates a complex set of levels characterized by spin mixing. Although the model multispin Hamiltonian in the absence of local orbital momentum, 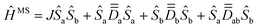 , is considered good enough to map the experimental energies at zero field and in the strong-exchange limit, theoretical works pointed out limitations of this simple model. This work revives the use of ĤMS from a new theoretical perspective, detailing point-by-point a strategy to correctly map the computational energies and wave functions onto ĤMS, thus validating it regardless of the exchange limit. We will distinguish two cases, based on experimentally characterized dicobalt(II) complexes from the literature. If centrosymmetry imposes alignment of the various rank-2 tensors constitutive of ĤMS in the first case, the absence of any symmetry element prevents such alignment in the second case. In such a context, the strategy provided herein becomes a powerful tool to rationalize the experimental magnetic data, since it is capable of fully and rigorously extracting the multispin model without any assumption on the orientation of its constitutive tensors. Furthermore, the strategy allows to question the use of the spin Hamiltonian approach by explicitly controlling the projection norms on the model space, which is showcased in the second complex where local orbital momentum could have occurred (distorted octahedra). Finally, previous theoretical data related to a known dinickel(II) complex is reinterpreted, clarifying initial wanderings regarding the weak exchange limit.
, is considered good enough to map the experimental energies at zero field and in the strong-exchange limit, theoretical works pointed out limitations of this simple model. This work revives the use of ĤMS from a new theoretical perspective, detailing point-by-point a strategy to correctly map the computational energies and wave functions onto ĤMS, thus validating it regardless of the exchange limit. We will distinguish two cases, based on experimentally characterized dicobalt(II) complexes from the literature. If centrosymmetry imposes alignment of the various rank-2 tensors constitutive of ĤMS in the first case, the absence of any symmetry element prevents such alignment in the second case. In such a context, the strategy provided herein becomes a powerful tool to rationalize the experimental magnetic data, since it is capable of fully and rigorously extracting the multispin model without any assumption on the orientation of its constitutive tensors. Furthermore, the strategy allows to question the use of the spin Hamiltonian approach by explicitly controlling the projection norms on the model space, which is showcased in the second complex where local orbital momentum could have occurred (distorted octahedra). Finally, previous theoretical data related to a known dinickel(II) complex is reinterpreted, clarifying initial wanderings regarding the weak exchange limit.
1 Introduction
Recent decades witnessed significant advancements in the engineering of single-molecule magnets (SMMs) with compelling magnetic properties closer and closer to room temperature.1–4 At stake may be the future of storage devices and quantum information systems,5–7 but these SMMs also provide a playground to explore complex electronic structures, and new quantum-mechanical phenomena,8–10 and develop novel strategies for evaluating them.SMMs typically exhibit magnetic anisotropy through the intertwined effect of spin–orbit coupling (SOC) and anisotropic crystal fields (CFs) and retain magnetic bistability with an energy barrier for magnetization reversal below a certain blocking temperature.6 To go beyond the blocking temperatures observed in d-element polynuclear complexes, research shifted to the field of f-element single ion magnets after the discovery of the properties of the bis(phthalocyaninato)terbium anion.11 Although f-element molecules make the current state-of-the-art SMM prototypes,3,4,12–14 with well-known recipes designed to improve their magnetic properties,15,16 potential d- and mixed f/d-element SMMs are also investigated at a pace faster than before.17–20
In the laboratory, information on magnetic anisotropy is commonly evidenced through electron paramagnetic resonance (EPR) and magnetic susceptibility (χ) studies. The outcome is interpreted through the language of model Hamiltonians,21–23 dressed with parameters quantifying the physics of the electronic structure, e.g. magnetic exchange, zero-field splitting (ZFS), Zeeman interaction, etc. Optimal values for these parameters are obtained by fitting measured data,24,25 such as the temperature variation of χT, and concluding on a certain set of uniquely defined values from good grounds may require input from first principles calculations.
With simplistic formulations, model Hamiltonians are appealing in experimental contexts and serve as a bridge between experiments and overly complicated theoretical approaches. In the case of model spin Hamiltonians, only spin operators are at play, with the assumption that the orbital part(s) of the wave function(s) is(are) factored out. In mononuclear complexes, the model Hamiltonian applies to the |S,MS〉 components of the ground spin state. In binuclear complexes and beyond, the model space may include more than one spin state. For instance, it may be constituted of the spin components of all the spin states that are triggered by the Heisenberg-Dirac-van Vleck (HDVV) Hamiltonian.26–28 Yet, these types of models reproduce faithfully magnetic data at low temperatures, in the absence of local orbital degeneracy, as soon as the interaction space encodes the effective physics of the studied system.
In polynuclear systems, two main types of models apply. The giant-spin model, ĤGS, only aims at describing the ZFS of the ground spin state and it is used in a fashion similar to that of mononuclear systems. The multispin model, ĤMS, aims to describe the splitting and mixing of the spin components of the HDVV spectrum. With both model Hamiltonians, the theoretical extraction of relevant parameters is based on an explicit mapping onto an effective Hamiltonian (Ĥeff) that is built on top of the ab initio calculations.29–33 Alternatively, one may skip the explicit projection of the wave functions and work within the pseudospin framework.34 Since ĤGS targets only the ground spin state it is quite clear that it is not fully relevant in the weak-exchange limit.29,35ĤMS is better suited in such cases; it is naturally built up in the |Si,MSi,…〉 basis (the uncoupled basis, the i's denoting the active magnetic centers) and may be further expressed in the |S,MS〉 basis (the coupled one).36
Calculations based on the complete active space self-consistent field (CASSCF) approach37 are appealing in the context of magnetochemistry.38 This approach can describe correctly dn and fn near-degenerate configurations and allows for a systematic improvement of the electron correlation in post-CASSCF multireference treatments. Subsequently, the SOC can be introduced by diagonalization of an electronic energy plus spin–orbit operator matrix, on the basis of the spin components of the previous spin-free CASSCF states, with the electronic energies potentially replaced by dynamically correlated ones. This is the spirit of (dressed) spin–orbit configuration interaction (SOCI).39
Many seminal studies show the use of configuration interaction schemes to calculate magnetic properties.40–47 It is worth noting that density functional theory (DFT) is equally involved in rationalizing magnetic data,48–54 as well as single-reference spin-flip approaches,55–57 and more recently coupled-cluster methods.58–60 In principle, the low-energy ab initio spectrum offers sufficient detail for calculating anisotropy parameters and spin–orbit correction to the exchange interaction if a SOCI is performed,22,33 as well as EPR parameters and χT profiles provided that the Zeeman interaction is treated.46,61–64 This is the starting point of our work.
Extraction of magnetic parameters from ĤMS may be straightforward in centrosymmetric binuclear complexes. In such cases, all rank-2 tensors involved in ĤMS (vide infra) have the same principal axes, or principal axis frames (PAFs). Such a frame, which may be derived from ĤGS if not directly from symmetry arguments,29,30,65 not only simplifies the model construction but also helps in shortcutting the parameter extraction through the effective Hamiltonian theory. In practice, cases were identified in which matrix elements are nil in the model but non-nil in Ĥeff.65 Such inequalities were proposed to arise from the lack of a rank-4, biquadratic anisotropy exchange tensor in ĤMS. The case of low-symmetry binuclear complexes is even more complicated. Although the molecular orientation may correspond to a molecular PAF, derived somehow from ĤGS or from the diagonalization of the EPR g-matrix in the case of pseudospin Hamiltonians,34 this xyz frame may not correspond at all to the local or specific PAFs of all the rank-2 tensors of ĤMS. This must lead to nonzero off-diagonal elements of these tensors if expressed in the molecular frame, which is almost always neglected in experimental studies. Hence, the use of ĤMS in current magnetochemistry applications still appears problematic.
This article aims to revive the utilization of ĤMS for interpreting the low-temperature magnetic properties of binuclear complexes; it forwards a simple, rigorous, and versatile strategy to resolve the model, irrespective of the coordination symmetry or the regime (weak- or strong-exchange). The technique is showcased using dicobalt(II) complexes, a centrosymmetric one, [Co2Cl6]2− (1),66,67 and an unsymmetrical one, [Co2(L)2(acac)2(H2O)]‡ (2).68 The molecular structures are shown in Fig. 1. Dicobalt(II) systems were chosen simply to show that, by using the proposed strategy, full extraction of magnetic parameters can be easily performed even in challenging cases (here, the HDVV matrix being 16 × 16 and the local magnetic centers intrinsically displaying Kramers degeneracies). The article concludes that achieving a strong agreement between the matrix elements of ĤMS and Ĥeff, necessary for the validation and resolution of the former, is possible in any case, and, in practice, easily achievable by
(i) building a first effective Hamiltonian in the coupled basis,
(ii) determining the molecular PAF, which is identified by resolution of the anisotropic model Hamiltonian  effectively at play only in the |S = 3,MS〉 block of the full model space of ĤMS,
effectively at play only in the |S = 3,MS〉 block of the full model space of ĤMS,
(iii) recomputing the effective Hamiltonian in the molecular PAF and consistently revising the ± signs of the cross-blocks matrix elements, coupling MS components belonging to different S-blocks in Ĥeff, and
(iv) expressing all rank-2 tensors of ĤMS in the molecular PAF to finally determine the missing quantities by minimizing the mismatch between ĤMS and Ĥeff.
A recent erratum to ref. 4 also raised the issue of conflicting signs mentioned at point (iii). In order to properly project Ĥeff onto ĤMS, it is essential to use correct prefactors. In fact, the revision of such conflicting signs practically eliminates the need to introduce tensors of rank superior to 2 to achieve agreement between each and every matrix element of ĤMS and Ĥeff, regardless of the coordination symmetry. Thus, the present article concludes that the resolution of ĤMS for [Ni2(en)4Cl2]2+, en = ethylendiamine, was in fact straightforward, and already properly done in the seminal publication.65
The subsequent sections commence with a brief overview of the standard ĤMS and its validation by effective Hamiltonians. This is followed by an outline of the proposed strategy for utilizing these two concepts in deriving magnetic properties for binuclear complexes. The results and discussion extend over two major sections showcasing the resolution of ĤMS, and the subsequent calculation of the χT profile, for the centrosymmetric complex 1 firstly, and for the unsymmetrical complex 2, secondly. The article concludes that, when constructed appropriately, the standard multispin Hamiltonian correctly describes the effective magnetic interactions even in the weak-exchange limit, thus justifying its general relevance in the experimental design of SMMs based on d-elements. Finally, a series of take-home messages will be delivered to the attention of the experimental community involved in molecular magnetism, emphasizing once more the strong need for good, independent, computational input to consistently interpret the data.
2 Theory and computational strategy
2.1 The multispin model Hamiltonian for binuclear complexes
In the absence local orbital momentum, the model multispin Hamiltonian expression reads:33,36,69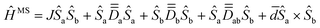 | (1) |
 are rank-2 tensors describing the local anisotropies,
are rank-2 tensors describing the local anisotropies,  is a rank-2 tensor describing the symmetric anisotropic exchange, and
is a rank-2 tensor describing the symmetric anisotropic exchange, and ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) is a pseudovector describing the antisymmetric component of the anisotropic exchange. In centrosymmetric complexes, the latter term of eqn (1), also referred to as the Dzyaloshinskii–Moriya interaction (DMI),70–75 vanishes, and otherwise, may be less important than the other terms unless specific situations are encountered (exotic coordination environment and/or orbital near-degeneracy). In fact, this work does not specifically focus in the DMI, which will be later justified by comparing Ĥeff and ĤMS.
is a pseudovector describing the antisymmetric component of the anisotropic exchange. In centrosymmetric complexes, the latter term of eqn (1), also referred to as the Dzyaloshinskii–Moriya interaction (DMI),70–75 vanishes, and otherwise, may be less important than the other terms unless specific situations are encountered (exotic coordination environment and/or orbital near-degeneracy). In fact, this work does not specifically focus in the DMI, which will be later justified by comparing Ĥeff and ĤMS.
In order to describe interaction with an applied magnetic field, ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) , eqn (1) is completed by the Zeeman Hamiltonian:
, eqn (1) is completed by the Zeeman Hamiltonian:
 | (2) |
 are the local Zeeman splitting tensors. The rank-2 tensors of eqn (1) and (2) are represented as 3 × 3 matrices consisting of up to nine non-zero components in arbitrary xyz frames. The tensors are of course diagonal in their respective PAFs. Though the axial (Da, Db, Dab) and rhombic (Ea, Eb, Eab) local and exchange anisotropic parameters depend only on the diagonal elements of the respective tensors
are the local Zeeman splitting tensors. The rank-2 tensors of eqn (1) and (2) are represented as 3 × 3 matrices consisting of up to nine non-zero components in arbitrary xyz frames. The tensors are of course diagonal in their respective PAFs. Though the axial (Da, Db, Dab) and rhombic (Ea, Eb, Eab) local and exchange anisotropic parameters depend only on the diagonal elements of the respective tensors 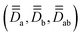 , following D =
, following D = ![[/]](https://www.rsc.org/images/entities/char_e0ee.gif) Dzz and E = ½(Dxx − Dyy),§ it should be noted that the PAFs of
Dzz and E = ½(Dxx − Dyy),§ it should be noted that the PAFs of  may not coincide with each other in the general case, nor with those of
may not coincide with each other in the general case, nor with those of  . Thus, symmetry is key to understanding how to practically deal with so many tensors.
. Thus, symmetry is key to understanding how to practically deal with so many tensors.
If centrosymmetry is present, one may expect that all the tensors of eqn (1) and (2) are diagonal in the same coordinate frame, which effectively corresponds to the molecular PAF. This facilitates the straightforward construction of ĤMS and the extraction of relevant axial and rhombic parameters using the effective Hamiltonian theory. However, if centrosymmetry is not present, two additional challenges arise. Firstly, one must determine the molecular PAF. Secondly, one must express all the rank-2 tensors in this coordinate frame. In this scenario, the rank-2 tensors may no longer be diagonal, although symmetry may still impose some of the off-diagonal elements to be zero in specific situations.
Ĥ
MS and ĤZee are both constructed in the uncoupled spin-basis, |Sa,MSa;Sb,MSb〉, or shortly |MSa,MSb〉. Since we deal with d7 Co(II) centers, Sa = Sb = ![[/]](https://www.rsc.org/images/entities/char_e0ee.gif) and MSa,MSb ∈ {±
and MSa,MSb ∈ {±![[/]](https://www.rsc.org/images/entities/char_e0ee.gif) ,±½}, resulting in a 16 × 16 model space. Thus, the matrices of all terms in eqn (1) and (2) must be expressed in this same 16 × 16 basis. ĤMS is designed here to reproduce the energy levels generated by the coupling of the local spin-quartets, i.e., the septet (S = 3), quintet (S = 2), triplet (S = 1) and singlet (S = 0) coupled-spin states. Translation of ĤMS from the uncoupled-spin basis, |MSa,MSb〉, to the coupled-spin basis, |S,MS〉 (S = 0,1,2,3, MS = +S,…, −S), is achieved via the transformation matrix U based on Clebsch–Gordan (CG) coefficients:36
,±½}, resulting in a 16 × 16 model space. Thus, the matrices of all terms in eqn (1) and (2) must be expressed in this same 16 × 16 basis. ĤMS is designed here to reproduce the energy levels generated by the coupling of the local spin-quartets, i.e., the septet (S = 3), quintet (S = 2), triplet (S = 1) and singlet (S = 0) coupled-spin states. Translation of ĤMS from the uncoupled-spin basis, |MSa,MSb〉, to the coupled-spin basis, |S,MS〉 (S = 0,1,2,3, MS = +S,…, −S), is achieved via the transformation matrix U based on Clebsch–Gordan (CG) coefficients:36
| ĤMS(coupled) = UT·ĤMS(uncoupled)·U | (3) |
2.2 Construction of the effective Hamiltonian
Ĥ eff spans the same model space as ĤMS and it is initially constructed in the coupled-spin basis, in accord with the expressions of the underlying SOCI wavefunctions, by means of the des Cloizeaux formalism:76 | (4) |
2.3 Proposed step-by-step strategy for extracting the multispin Hamiltonian
Step 1. The first step involves determining the molecular PAF. Note that, unlike the energies, the composition of the SOCI wavefunctions varies with the molecular orientation such that their interpretation may become needlessly complex in the event that the cartesian z-axis does not coincide with the one of the molecular PAF. For both the studied complexes (1 and 2), the molecular PAF was determined from the resolution of , describing only the ground S = 3 state. A similar strategy was employed for determining the anisotropy axes of [Ni2(en)4Cl2]2+.65 The procedure consists in:
, describing only the ground S = 3 state. A similar strategy was employed for determining the anisotropy axes of [Ni2(en)4Cl2]2+.65 The procedure consists in:
(i) perform a first reference SOCI calculation with an arbitrary xyz frame, construct the 16 × 16 matrix of Ĥeff according to Section 2.2 and focus only on the S = 3 block. This procedure is in essence different from simply following the giant spin approach: in the case of spin mixing, it ensures that we properly extract the actual PAF of the S = 3 block.
(ii) derive the analytical matrix representation of  in the |S = 3,MS〉 space and extract
in the |S = 3,MS〉 space and extract  by best equating Ĥeff from point (i) to Ĥmod. Since this matrix is uncommon in the transition metal literature (an S = 3 state is impossible to reach within a dn manifold), we provide it in Table 1.
by best equating Ĥeff from point (i) to Ĥmod. Since this matrix is uncommon in the transition metal literature (an S = 3 state is impossible to reach within a dn manifold), we provide it in Table 1.
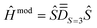 expressed in an arbitrary axis frame in the basis of the |S = 3,MS〉 functions
expressed in an arbitrary axis frame in the basis of the |S = 3,MS〉 functions
(iii) rotate the molecular coordinates from the arbitrary xyz frame to the molecular PAF: xyzMPAFi = V−1·xyzarbi, where xyzarbi are the coordinates of all the i atoms in the arbitrary frame and V is the eigenvector matrix of  (convention may apply for the respective labeling of the x, y and z axes).
(convention may apply for the respective labeling of the x, y and z axes).
With the molecular geometry rotated in the molecular PAF, the SOCI calculations of Step 1 are repeated and the 16 × 16 representative matrix of Ĥeff is re-built. This is the Ĥeff that will be essentially used for the validation and resolution of ĤMS. However, note that the exact same conclusions can be reached by extracting it all in an arbitrary axis frame (in a more tedious way!).
Step 2. SOCI calculations are conducted with two model, monomeric, structures defined by the substitution of a magnetic center with a diamagnetic one. In the present cases, models 1a, 1b and 2a, 2b (Fig. 1) are obtained by replacing one Co with one Zn in the dimeric structures 1 and 2 respectively. The goal here is to extract independently the local anisotropy tensors,  , for the magnetic centers, determine their respective PAFs, and calculate the corresponding axial and rhombic parameters Da, Ea, Db, Eb. For each magnetic center, the eigenvectors of
, for the magnetic centers, determine their respective PAFs, and calculate the corresponding axial and rhombic parameters Da, Ea, Db, Eb. For each magnetic center, the eigenvectors of  , leading to
, leading to 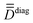 , provide with the V rotation matrix that can be used to express them back in the molecular PAF, through:
, provide with the V rotation matrix that can be used to express them back in the molecular PAF, through:
 | (5) |
Step 3. The 16 × 16 model analytical matrix of ĤMS in the uncoupled-spin basis is derived with the leading terms of it, i.e., the Heisenberg and the local anisotropy terms, by applying simple spin-operator algebra. This matrix is subsequently transformed in the coupled-spin basis using eqn (3).
Afterwards, the quality of the model matrix can be evaluated by expressing it numerically and comparing it to Ĥeff. The less deviation, the better the model. To shortcut the extraction, one may directly use the spin-free J value and the local anisotropy tensors calculated independently at Step 2 (of course, expressed in the molecular PAF for consistency). In principle, this approach should already provide a good representation of Ĥeff since (i) the effect of the SOC on J is usually small30,65 and (ii) the symmetric anisotropy exchange tensor may be of lesser importance than the local ones. Finally, we may also refine the J value and the components of the local anisotropy tensors as well as introduce the symmetric exchange tensor in the model to further improve it. Refinement is carried out through a least-squares fitting of the model parameters, aiming to minimize the root mean square deviation (RMSD) between ĤMS and Ĥeff.
Here, we have deliberately chosen to make use of momoner calculations to (i) validate and provide additional support for this route, which is one of the most commonly employed in current literature when modeling magnetic properties, for instance followed by the POLY_ANISO program,77,78 and (ii) avoid the extraction of too many parameters simultaneously in unsymmetrical cases, such as that of complex 2, thus preventing the occurrence of unnoticed human mistakes by allowing a cross-validation of the extraction procedure based on the much simpler extracted parameters of the monomer calculations. Note that we would be now confident in performing a complete extraction based on a dimer calculation on a new system, or alternatively in performing only monomer calculations if the dimer calculations would prove to be too demanding.
2.4 Computational details
Electronic structure calculations were performed with the ORCA package, v5.0.3.79,80 Scalar relativistic effects were introduced by using the Douglas–Kroll–Hess (DKH) Hamiltonian.81–84 The Co, N, O, and Cl electrons were treated with the all-electron, triple-zeta DKH-def2-TZVP basis sets whereas the C, F, and H electrons were treated with the smaller, double-zeta DKH-def2-SVP ones. These bases were derived from the original def2 variants by recontraction within the DKH framework.85 To speed off the calculation of electron repulsion integrals, the RIJCOSX “chain-of-spheres” density-fitting86 was applied together with large, automatically-generated auxiliary basis sets.87 The geometries of 1 and 2 were extracted from published crystal information data.66,68 Concerning 2, the H coordinates were optimized within the DFT framework, using the Perdew–Burke–Ernzerhof generalized gradient approximation,88 and otherwise the same details as above hold. The xyz coordinates in the initial, arbitrary, coordinate frames are provided in the ESI.†The zero-order wavefunctions were converged within the state-averaged (SA) CASSCF framework, with the active space spanned by the Co(II) d7 shell(s). I.e., CASSCF(14, 10) and CASSCF(7, 5) calculations were performed for the dimeric species 1 and 2 and for the monomeric species 1a, 1b, 2a and 2b, respectively. The production-level SA schemes included 49 states per S = 3, 2, 1 and 0 block for 1, seven S = ![[/]](https://www.rsc.org/images/entities/char_e0ee.gif) states for 1a and 1b, 9 states per S = 3, 2, 1 and 0 block for 2, three S =
states for 1a and 1b, 9 states per S = 3, 2, 1 and 0 block for 2, three S = ![[/]](https://www.rsc.org/images/entities/char_e0ee.gif) states for 2a and 2b. Regarding complex 2 and its monomers, additional SA schemes were explored for validation purposes, which will be discussed in the Results sections. The 49-root per spin-block SA scheme employed for 1 was validated in ref. 67, 49 being the total number of roots generated from the product of the two local (crystal-field split) 4F Co(II) terms. Concerning complex 2, the 9-root per spin-block SA scheme has been validated in this work, 9 corresponding to the number of roots generated from the product of two local 4T1 Co(II) terms.
states for 2a and 2b. Regarding complex 2 and its monomers, additional SA schemes were explored for validation purposes, which will be discussed in the Results sections. The 49-root per spin-block SA scheme employed for 1 was validated in ref. 67, 49 being the total number of roots generated from the product of the two local (crystal-field split) 4F Co(II) terms. Concerning complex 2, the 9-root per spin-block SA scheme has been validated in this work, 9 corresponding to the number of roots generated from the product of two local 4T1 Co(II) terms.
State energies including dynamic correlation effects were calculated with the strongly-contracted, n-electron valence state perturbation theory at second order (NEVPT2).89,90 For 2 in particular, the relative correlated energies for the lowest S = 3, 2, 1 and 0 states were additionally recorrected by difference dedicated CI (DDCI2) and iterative DDCI2 calculations,91,92 with an orbital-energy cutoff between −10 and 1000 Hartree and the Tsel and Tpre thresholds set to 1 × 10−10 and 1 × 10−6, respectively. In this way, a better J value was obtained, or in other words, a better separation of the spin blocks. In the iterative DDCI2 calculation, a limit of ten iterations was employed.
Finally, the production SOCI calculations were performed for all the dimeric and monomeric species. In these calculations, the spin–orbit operator matrix was constructed in the basis of the spin components of the CASSCF states. The SOCI matrix is constituted of off-diagonal elements, triggered by the spin–orbit coupling, and also of diagonal ones, the electronic spin-free energies. The diagonal was dressed with dynamically-correlated energies and the resulting matrix was diagonalized to generate the spin–orbit coupled wavefunctions and energies. Hereafter, SOCI calculations based on NEVPT2 and DDCI2 correlated energies will be referred to as SO-NEVPT2 and SO-DDCI2 respectively. We point out additionally that, in the SO-DDCI2 calculations, only the relative energies of the lowest S = 3, 2, 1, 0 CASSCF states were adjusted by the DDCI2 energy spacings, whereas the NEVPT2 relative energies were retained for the remaining 192 CASSCF states. The intention here was to characterize as best as possible the spin–orbit states that may be populated in the temperature range employed in experimental magnetic susceptibility studies. Since other excited states appear at much higher energies, above 2800 cm−1, they do not contribute much to the observed properties.
Finally, powder-averaged ab initio χT curves were generated for complexes 1 and 2 directly from the outcomes of the SOCI calculations. Note that, in ORCA, χ is calculated by finite differentiation of the partition function by using the (field-corrected) spin–orbit states.46 Furthermore, by using the same approach, we have modeled the χT curves based on the pre-validated ĤMS + ĤZee models, through the usual approximation,
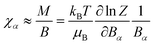 | (6) |
 | (7) |
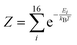 is the partition function, and NA and kB are the Avogadro and Boltzmann constants, respectively. For the present dicobalt(II) cases, eqn (6) and (7) led to practically identical χT = f(T) model curves.
is the partition function, and NA and kB are the Avogadro and Boltzmann constants, respectively. For the present dicobalt(II) cases, eqn (6) and (7) led to practically identical χT = f(T) model curves.
3 Results and discussion
3.1 [Co2Cl6]2−, a centrosymmetric complex
Our first-principles calculations support the previous theoretical data. Namely, complex 1 adopts a spin-singlet GS with a Landé ordering for the triplet, quintet, and septet spin-states with antiferromagnetic J of 7.5 (CASSCF)/11.2 cm−1 (NEVPT2). The J value matches that of ref. 67 within 1 cm−1 at the CASSCF level, but it is three times smaller when the dynamic correlation is included. Although the discrepancy may originate from the choice of the PT2 flavor, here NEVPT2 vs. CASPT2 in ref. 67, both these methods deliver similar accuracy when evaluated against the fitted J value of 23.2 cm−1; i.e. if CASPT2 overestimates it by 11.1 cm−1, NEVPT2 underestimates it by 12 cm−1. In this context, DDCI2 calculations led to J = 21.3 cm−1, within ∼2 cm−1 of the fitted value. Iterative DDCI2 calculations did not converge well on a particular value and delivered J within the ∼18–21.5 cm−1 range in 10 iterations, with the mean J = 20.9 cm−1 still in excellent agreement with the fitted J.
 | ||
Fig. 2 Arbitrarily-chosen coordinate frame and calculated PAFs for complex 1 (from  ) and for the model structure 1a (from ) and for the model structure 1a (from  ). Axes color code: z = red, x = blue, y = green. ). Axes color code: z = red, x = blue, y = green. | ||
Following the strategy presented in Section 2, the first step toward the resolution of ĤMS involves the identification of the molecular PAF. Here, the SOCI wavefunctions of Table S3 (ESI†) already show little spin-mixing due to misalignment of the z-axis with the principal magnetic anisotropy axis of the complex, meaning that the arbitrarily-chosen input frame is not very different from the molecular PAF. The numerical matrix elements of the |S = 3,MS〉 block within Ĥeff are shown in Table 2. Comparison with the analytical  matrix of Table 1 concludes with the perfect one-to-one correspondence of the respective matrix elements showing the validity of the model Hamiltonian. Moreover, it is clear that the matrix elements in Ĥeff that should vanish in the molecular PAF are very close to zero, e.g. 〈3,2|Ĥmod|3,3〉, 〈3,0|Ĥmod|3,1〉, etc., meaning that the arbitrary axis frame is indeed not far from the molecular PAF. Indeed, extraction and diagonalization of
matrix of Table 1 concludes with the perfect one-to-one correspondence of the respective matrix elements showing the validity of the model Hamiltonian. Moreover, it is clear that the matrix elements in Ĥeff that should vanish in the molecular PAF are very close to zero, e.g. 〈3,2|Ĥmod|3,3〉, 〈3,0|Ĥmod|3,1〉, etc., meaning that the arbitrary axis frame is indeed not far from the molecular PAF. Indeed, extraction and diagonalization of 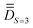 led to the molecular PAF shown in Fig. 2, which essentially differs from the arbitrary frame by axis relabeling, i.e. z → x, x → y and y → z. SOCI performed with complex 1 oriented in the molecular PAF led to the wavefunctions printed in Table S4 (ESI†); these are slightly cleaner than the previous ones and show large spin-mixings between S = 0 and S = 2 spin-components, and between the S = 1 and S = 3 ones.
led to the molecular PAF shown in Fig. 2, which essentially differs from the arbitrary frame by axis relabeling, i.e. z → x, x → y and y → z. SOCI performed with complex 1 oriented in the molecular PAF led to the wavefunctions printed in Table S4 (ESI†); these are slightly cleaner than the previous ones and show large spin-mixings between S = 0 and S = 2 spin-components, and between the S = 1 and S = 3 ones.
| Ĥ mod | |3,3〉 | |3,2〉 | |3,1〉 | |3,0〉 | |3,−1〉 | |3,−2〉 | |3,−3〉 |
|---|---|---|---|---|---|---|---|
| 〈3,3| | 79.0 | 1.0 + 2.0i | −15.0 − 6.0i | 0 | 0 | 0 | 0 |
| 〈3,2| | 1.0 − 2.0i | 87.0 | 1.0 + 1.0i | −21.0 − 9.0i | 0 | 0 | 0 |
| 〈3,1| | −15.0 + 6.0i | 1.0 − 1.0i | 92.0 | 1.0i | −23.0 − 10.0i | 0 | 0 |
| 〈3,0| | 0 | −21.0 + 9.0i | −1.0i | 93.0 | −1.0i | −21.0 − 9.0i | 0 |
| 〈3,−1| | 0 | 0 | −23.0 + 10.0i | 1.0i | 92.0 | −1.0 − 1.0i | −15.0 − 6.0i |
| 〈3,−2| | 0 | 0 | 0 | −21.0 + 9.0i | −1.0 + 1.0i | 87.0 | −1.0 − 2.0i |
| 〈3,−3| | 0 | 0 | 0 | 0 | −15.0 + 6.0i | −1.0 + 2.0i | 79.0 |
 , associated with the two Co centers, and thereof the axial (Da and Db) and rhombic (Ea and Eb) local ZFS parameters (which are here respectively equal by symmetry). To this end, SO-NEVPT2 calculations were performed on the monomeric model structures 1a and 1b shown in Fig. 1, both oriented in the molecular PAF determined above. Because of symmetry, one may here skip the computation of 1b. However, doing it has two advantages, (i) it allows one to validate spreadsheets and (ii) it is generally applicable also in cases with no symmetry. Resolution of the anisotropic Hamiltonians,
, associated with the two Co centers, and thereof the axial (Da and Db) and rhombic (Ea and Eb) local ZFS parameters (which are here respectively equal by symmetry). To this end, SO-NEVPT2 calculations were performed on the monomeric model structures 1a and 1b shown in Fig. 1, both oriented in the molecular PAF determined above. Because of symmetry, one may here skip the computation of 1b. However, doing it has two advantages, (i) it allows one to validate spreadsheets and (ii) it is generally applicable also in cases with no symmetry. Resolution of the anisotropic Hamiltonians,  , was achieved following the effective Hamiltonian workflow for mononuclear complexes.45
, was achieved following the effective Hamiltonian workflow for mononuclear complexes.45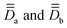 are found identical here, as expected due to the centrosymmetry. Moreover, they are diagonal in the molecular PAF:
are found identical here, as expected due to the centrosymmetry. Moreover, they are diagonal in the molecular PAF: | (8) |
 share the same PAF. The ZFS parameters derived from matrix (8) are Da = Db = 17.4 cm−1 and Ea = Eb = 3.7 cm−1.
share the same PAF. The ZFS parameters derived from matrix (8) are Da = Db = 17.4 cm−1 and Ea = Eb = 3.7 cm−1.
The 16 × 16 analytical matrix of ĤMS was initially derived in the uncoupled-spin basis, |MSa,MSb〉. Subsequently, the matrix was translated into the coupled-spin basis, |S,MS〉, and it is listed in Tables S5–S7 (ESI†). In the molecular PAF, the ĤMS matrix simplifies greatly to that shown in Table 4, where all elements depend only on the axial and rhombic parameters of the local anisotropies, Da and Ea (due to centrosymmetry, Db and Eb can be replaced by Da and Ea respectively), and of the symmetric exchange anisotropy, Dab and Eab. The 16 × 16 Ĥeff matrix derived from the SO-NEVPT2 calculation in the molecular PAF is given in Tables S8 and S9 (ESI†) for the coupled- and uncoupled-spin basis respectively.
In a first approximation, one may assume vanishing symmetric anisotropy, i.e. neglect the contribution of Dab and Eab to Table 4, and use the calculated J = 11.2, Da = 17.4 and Ea = 3.7 cm−1 to evaluate ĤMS. The ĤMS numerical matrix expressed in the coupled- and uncoupled-spin bases is shown in Tables S10 and S11 (ESI†), respectively. Concerning the coupled-spin basis, the correspondence between ĤMS and Ĥeff matrices is outstanding at first glance. A closer look reveals, however, that the 〈0,0|Ĥeff|2,MS〉 and 〈1,MS|Ĥeff|3,MS〉 elements, as well as their complex-conjugates, have opposite sign compared to counterparts in ĤMS. The sign discrepancy reported and clarified in the erratum to ref. 4, occurs since the |S,MS〉 spin functions enter with arbitrary phases in the ab initio spin–orbit eigenvectors, and may show up with random ±1 prefactors between different ab initio runs or runs on different computers. The sign arbitrariness becomes problematic when Ĥeff is translated in the uncoupled-spin basis using tabulated CG coefficients that follow a specific sign convention. The ones used in this work, shown in Table S1 (ESI†), follow the Condon and Shortley convention.94,95 Indeed, comparison between the ĤMS and Ĥeff numerical matrices in the uncoupled-spin basis, S11 vs. S9 (ESI†), is rather poor, generating misleading conclusions. In order to obey sign conventions, one may express the spin-free wavefunctions in a basis of localized orbitals, pick a phase convention, and derive analytically the expressions of the spin–orbit wavefunctions; finally, revise the CG coefficients according to the chosen phase convention. This path has been adopted in ref. 74. Pursuing such a scheme, although rigorous, is tedious and not appealing in general. Instead, one may follow the path taken in ref. 4 and revise the conflicting signs in Ĥeff such that projection onto ĤMS using CG coefficients in the Condon–Shortley convention gives the smallest deviation. In this work, it is realized from the onset that, by construction, the model ĤMS already yields the correct signs that must be adopted in Ĥeff itself. The sign-revised, coupled-spin basis Ĥeff is shown in Table S12 (ESI†) and the uncoupled-spin basis matrix derived thereof is shown in Table S13 (ESI†). Comparison with ĤMS counterparts (Tables S10 and S11, ESI†) reveals outstanding agreement regardless of basis, with maximum deviation not larger than 1 and 1.8 cm−1 for the off-diagonal and diagonal elements respectively (see Tables S14 and S15, ESI†). Three highly important conclusions are here drawn, (i) the local anisotropy parameters calculated independently using monomeric structures 1a and 1b are transferable to calculations on the dimeric complex 1, (ii) the local anisotropies are the main contributors to ĤMS and actually bring the model to very close agreement with Ĥeff, and (iii) the approximate ĤMS, accounting only for the Heisenberg exchange and local anisotropies, is validated through the effective Hamiltonian theory and may be already used in modeling magnetic properties such as the χT curve.
Prior to modeling the χT curve, it may be noted that the comparison between the analytical matrix of ĤMS (Table 4) and the numerical matrix of Ĥeff (Table S12, ESI†) provides with enough equations for a full extraction of all the magnetic parameters at once. Thus, a more precise extraction can be performed on 1 in order to obtain J under the effect of SOC and both the local and the symmetric-exchange anisotropies. Such a full extraction has been performed by least-squares fitting of the ĤMS parameters in order to minimize the RMSD with the Ĥeff matrix elements. The extracted parameters, listed in Table 3, lead to ĤMS matrices (Tables S16 and S17, ESI† for the uncoupled- and coupled-spin basis respectively) that agree with Ĥeff within 1 cm−1 concerning the off-diagonal and diagonal elements (see Tables S18 and S19, ESI†). Furthermore, diagonalization of the model ĤMS matrices leads to highly accurate spin–orbit energies, within 1.2 and 1.8 cm−1 of the ab initio energies (see Table S2, ESI†), further supporting the validity of ĤMS and of our extraction scheme.
| Method | J | D a | E a | D ab | E ab | g |
|---|---|---|---|---|---|---|
| a Obtained from a least-squares fitting procedure minimizing the RMSD between ĤMS and Ĥeff. b Recalculated parameters after relabeling of the axes such that the convention Eab > 0 and |Dab| > 3Eab is fulfilled: x → z, y → x, z → y with SO-NEVPT2 and x ↔ z with SO-DDCI2. c From ref. 66. | ||||||
| SO-NEVPT2 | 10.5 | 17.13 | 3.68 | 0.25a/−0.64b | −0.34a/0.045b | 2.38 |
| SO-DDCI2 | 19.3 | 17.32 | 3.70 | 0.36a/−0.71b | −0.35a/0.004b | n/a |
| Fitc | 23.2 | 29 | — | — | — | 2.25 |
Several aspects may be noted from Table 3: (i) since J only appears on the diagonal of ĤMS in Table 4, switching from NEVPT2 to corrected DDCI2 relative energies affects the J values themselves but leaves mostly unchanged the remaining parameters; the SOC reduces J by 0.7 and 2 cm−1 at the SO-NEVPT2 and SO-DDCI2 levels, respectively, (ii) the re-extracted local anisotropy parameters at the SO-NEVPT2 level, Da = 17.1 and Ea = 3.7 cm−1 are in complete agreement with the counterparts extracted independently with the 1a and 1b monomeric structures, Da = 17.4 and Ea = 3.7 cm−1, reaffirming the transferability of these parameters from monomer to dimer calculations, and (iii) the symmetric exchange anisotropy is indeed minor compared to local anisotropies and thus neglecting it from the construction of ĤMS is not a bad approximation. It is worth noting for specialists that re-labeling the axes describing the PAF of  is necessary in order to respect the conventions Eab > 0 and |Dab| > 3Eab. In particular, the easy axis of magnetization of the symmetric anisotropy, which is collinear with the Co2 internuclear axis, falls perpendicular to the molecular easy axis of local anisotropy, which in turn is almost collinear with the μ-Cl2 internuclear axis.
is necessary in order to respect the conventions Eab > 0 and |Dab| > 3Eab. In particular, the easy axis of magnetization of the symmetric anisotropy, which is collinear with the Co2 internuclear axis, falls perpendicular to the molecular easy axis of local anisotropy, which in turn is almost collinear with the μ-Cl2 internuclear axis.
 for binuclear Co(II) complexes in the molecular PAF expressed in the coupled spin-basis, |S,MS〉
for binuclear Co(II) complexes in the molecular PAF expressed in the coupled spin-basis, |S,MS〉
Finally, the fully extracted ĤMS is used to model the χT curve of complex 1. For this task, one needs to express in matrix form the Zeeman terms of the two magnetic centers,  , and add them to ĤMS. Working in the uncoupled-spin basis, the 16 × 16 analytical matrices of the Zeeman terms are derived in Tables S20 and S21 (ESI†). These matrices are evaluated with
, and add them to ĤMS. Working in the uncoupled-spin basis, the 16 × 16 analytical matrices of the Zeeman terms are derived in Tables S20 and S21 (ESI†). These matrices are evaluated with 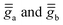 tensors obtained via the effective Hamiltonian theory from SO-NEVPT2 calculations performed on structures 1a and 1b in the molecular PAF:
tensors obtained via the effective Hamiltonian theory from SO-NEVPT2 calculations performed on structures 1a and 1b in the molecular PAF:
 | (9) |
The diagonal form of eqn (9) shows, as expected, that the local PAFs of the  tensors also coincide with the molecular PAF. The isotropic g-factor of 2.38 is very close to the fitted value in ref. 66, g = 2.25.
tensors also coincide with the molecular PAF. The isotropic g-factor of 2.38 is very close to the fitted value in ref. 66, g = 2.25.
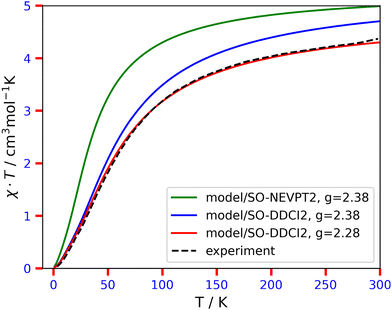
The modeled χT = f(T) curves with magnetic parameters from Table 3, shown in Fig. 3, highlight primarily the role of the magnetic coupling J in achieving agreement with the experiment. Since the J = 10.5 cm−1 extracted from the SO-NEVPT2 calculation is too small, the χT curve increases steadily and diverges from the reference experimental curve. The revised J = 19.3 cm−1 extracted out of the SO-DDCI2 calculation leads to χT in a much closer agreement, especially in the low-temperature range, ∼0–50 K. Furthermore, with a slightly adjusted isotropic g-factor of 2.28, which is even closer to the fitted 2.25 value,66 the modeled χT curve with the SO-DDCI2 parameters fits almost perfectly the experimental curve in the whole temperature range. The present article does not aim to delve into higher-level theoretical approaches that could potentially improve the description of g from the onset. Therefore, we conclude that the successful resolution and utilization of the standard multispin model Hamiltonian for calculating magnetic properties in the centrosymmetric complex 1 have been here neatly demonstrated.
3.2 [Co2(L)2(acac)2(H2O)], an unsymmetrical complex
The ground term of the free-ion Co(II), denoted as 4F, splits in (weak) Oh ligand fields, resulting in a ground 4T1 state and excited 4T2 and 4A2 states. The threefold degeneracy of the orbital-triplet states is then lifted by distortions of the local Oh coordination. According to Table 5, both Co(II) centers exhibit spin-free energy levels with a 4F parentage that are well isolated within specific ranges: approximately 0–1100 cm−1 for 4T1, 8600–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 for 4T2, and above 18
500 cm−1 for 4T2, and above 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 for 4A2. The energy variation of these individual levels on the employed SA scheme is minimal. If the overall degeneracy lift of 4T1 is similar for both Co centers (around 1100 cm−1), the splitting of 4T2 is three times larger in 1a (around 1500 cm−1) than in 1b (around 400 cm−1). Taken together with the fact that the spectral widths of the states listed in Table 5 is about 750 cm−1 higher in 2a compared to 2b, these data reflect the slightly more distorted octahedron around the magnetic center of the former structure. Overall, based on energy gaps alone, one may conclude that the three levels of 4T1 parentage are the primary contributors shaping the local spin–orbit electronic structures. Consequently, performing SOC calculations with a SA/SI scheme involving these three quartets should be sufficient to address the local ZFS parameters.
500 cm−1 for 4A2. The energy variation of these individual levels on the employed SA scheme is minimal. If the overall degeneracy lift of 4T1 is similar for both Co centers (around 1100 cm−1), the splitting of 4T2 is three times larger in 1a (around 1500 cm−1) than in 1b (around 400 cm−1). Taken together with the fact that the spectral widths of the states listed in Table 5 is about 750 cm−1 higher in 2a compared to 2b, these data reflect the slightly more distorted octahedron around the magnetic center of the former structure. Overall, based on energy gaps alone, one may conclude that the three levels of 4T1 parentage are the primary contributors shaping the local spin–orbit electronic structures. Consequently, performing SOC calculations with a SA/SI scheme involving these three quartets should be sufficient to address the local ZFS parameters.
| 2a | 2b | |||||
|---|---|---|---|---|---|---|
| 10Q + 40D | 7Q | 3Q | 10Q + 40D | 7Q | 3Q | |
| a Relative energies and ZFS parameters in cm−1; letters D and Q are used to denote spin-doublet and spin-quartet states; structures 2a and 2b are shown in Fig. 1. b KD in the labeling of the SO states stands for Kramers doublet. | ||||||
| SF | ||||||
| 4T1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 622 | 600 | 610 | 460 | 446 | 468 | |
| 1079 | 1044 | 1059 | 1175 | 1143 | 1154 | |
| 4T2 | 8952 | 8673 | n/a | 9189 | 8895 | n/a |
| 9341 | 9050 | n/a | 9352 | 9059 | n/a | |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 555 555 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 211 211 |
n/a | 9583 | 9280 | n/a | |
| 4A2 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 969 969 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 344 344 |
n/a | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 190 190 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 584 584 |
n/a |
| SOb | ||||||
| KD1 | 0 | 0 | 0 | 0 | 0 | 0 |
| KD2 | 147 | 157 | 178 | 190 | 194 | 205 |
| KD3 | 721 | 708 | 733 | 664 | 659 | 688 |
| Local ZFS parameters and isotropic g-factors | ||||||
|---|---|---|---|---|---|---|
| D a | E a | g a | D b | E b | g b | |
| 86.31 | 11.91 | 2.30 | 93.14 | 25.02 | 2.31 | |
Indeed, we found that the lowest-energy Kramers doublets (KDs) only marginally change when increasing the SA/SI scheme beyond the first three quartet roots. As listed in Table 5, each Co(II) center exhibits one KD below approximately 200 cm−1 and the others above 700 cm−1. Evidently, all these Kramers doublets (KDs) fully arise as admixtures of |S = ![[/]](https://www.rsc.org/images/entities/char_e0ee.gif) ,MS〉 components of the spin-free states correlating with 4T1. Furthermore, the spin-free quartet GS predominantly contributes to the wavefunctions of KD1 (∼75%) and KD2 (∼90%) in both 2a and 2b. The next significant contribution to KD1, approximately 20%, comes from the first excited spin-quartet root. Anyway, one can confidently extract local ZFS parameters from the usual anisotropic spin Hamiltonians
,MS〉 components of the spin-free states correlating with 4T1. Furthermore, the spin-free quartet GS predominantly contributes to the wavefunctions of KD1 (∼75%) and KD2 (∼90%) in both 2a and 2b. The next significant contribution to KD1, approximately 20%, comes from the first excited spin-quartet root. Anyway, one can confidently extract local ZFS parameters from the usual anisotropic spin Hamiltonians 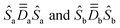 , expressed in the |S =
, expressed in the |S = ![[/]](https://www.rsc.org/images/entities/char_e0ee.gif) ,MS〉 basis of the ground quartet state (the model space thus consisting of the leading contributors to both KD1 and KD2).
,MS〉 basis of the ground quartet state (the model space thus consisting of the leading contributors to both KD1 and KD2).
The extracted axial, Da and Db, and rhombic, Ea and Eb, ZFS parameters are listed at the bottom of Table 5. The PAFs of the local rank-2 tensors,  , shown in Fig. 4, are very distinct this time, with orientations that may not have been guessed without performing those calculations. In comparison with complex 1, the axial parameters Da/b ≃ 90 cm−1 are at least fivefold larger. Furthermore, Eb = 25 cm−1 is twice larger than Ea = 12 cm−1, and both are at least three times larger than the local rhombic parameter in complex 1, 3.7 cm−1. On another hand, the Co centers share similar isotropic g-factor, ga ≃ gb ≃ 2.30, with that of the Co centers in complex 1, ga = gb = 2.35. Here, however, the spans of
, shown in Fig. 4, are very distinct this time, with orientations that may not have been guessed without performing those calculations. In comparison with complex 1, the axial parameters Da/b ≃ 90 cm−1 are at least fivefold larger. Furthermore, Eb = 25 cm−1 is twice larger than Ea = 12 cm−1, and both are at least three times larger than the local rhombic parameter in complex 1, 3.7 cm−1. On another hand, the Co centers share similar isotropic g-factor, ga ≃ gb ≃ 2.30, with that of the Co centers in complex 1, ga = gb = 2.35. Here, however, the spans of  , 1.86–2.66 and 1.81–2.84 respectively, are much larger than the
, 1.86–2.66 and 1.81–2.84 respectively, are much larger than the  -tensor span in complex 2, 2.23–2.40, also highlighting the much larger anisotropy in complex 2 in terms of the local
-tensor span in complex 2, 2.23–2.40, also highlighting the much larger anisotropy in complex 2 in terms of the local  's.
's.
A quick look at Table S23 (ESI†) reveals that the wavefunctions of the 16 lowest-lying spin–orbit levels are plagued by spin-mixing, which may be less important if the molecular PAF is used. We proceeded, therefore, as before to derive the molecular PAF. The matrix elements of the S = 3 block within the 16 × 16 Ĥeff, shown in Table 6, perfectly match the Ĥmod analytical matrix elements listed in Table 1. Unlike in the previous case of complex 1, matrix elements such as 〈3,2|Ĥeff|3,3〉 or 〈3,1|Ĥeff|3,2〉 deviate significantly from zero, whereas they should be zero if the input xyz frame is the molecular PAF. Extraction and diagonalization of 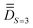 led to the molecular PAF depicted in Fig. 4. This frame is not only distinct from the initial input frame but also distinct from the local PAFs (of
led to the molecular PAF depicted in Fig. 4. This frame is not only distinct from the initial input frame but also distinct from the local PAFs (of  ). The SO-NEVPT2 calculation was repeated in the molecular PAF, leading to much cleaner wavefunctions for the 16 lowest-lying energy levels (see Table S24, ESI†).
). The SO-NEVPT2 calculation was repeated in the molecular PAF, leading to much cleaner wavefunctions for the 16 lowest-lying energy levels (see Table S24, ESI†).
| Ĥ mod | |3,3〉 | |3,2〉 | |3,1〉 | |3,0〉 | |3,−1〉 | |3,−2〉 | |3,−3〉 |
|---|---|---|---|---|---|---|---|
| 〈3,3| | 134.0 | 18.0 + 44.0i | 5.0 + 62.0i | 0 | 0 | 0 | 0i |
| 〈3,2| | 18.0 − 44.0i | 188.0 | 14.0 + 34.0i | 8.0 + 88.0i | 0 | 0 | 0 |
| 〈3,1| | 5.0 − 62.0i | 14.0 − 34.0i | 221.0 | 5.0 + 13.0i | 8.0 + 97.0i | 0 | 0 |
| 〈3,0| | 0 | 8.0 − 88.0i | 5.0 − 13.0i | 232.0 | −5.0 − 13.0i | 8.0 + 88.0i | 0 |
| 〈3,−1| | 0 | 0 | 8.0 − 97.0i | −5.0 + 13.0i | 221.0 | −14.0 − 34.0i | 5.0 + 62.0i |
| 〈3,−2| | 0 | 0 | 0 | 8.0 − 88.0i | −14.0 + 34.0i | 188.0 | −18.0 − 44.0i |
| 〈3,−3| | 0 | 0 | 0 | 0 | 5.0 − 62.0i | −18.0 + 44.0i | 134.0 |
| SO state | ΔE | SO state | ΔE | ||
|---|---|---|---|---|---|
| a SO-NEVPT2 calculations, relative energies in cm−1. Other excited energy levels start at 691 cm−1. b Total contribution from the spin-components of the lowest-energy S = 3, 2, 1 and 0 spin-free states. | |||||
| Ψ 1 | 0 | 0.52 | Ψ 9 | 206.4 | 0.66 |
| Ψ 2 | 1.9 | 0.51 | Ψ 10 | 206.9 | 0.67 |
| Ψ 3 | 3.6 | 0.50 | Ψ 11 | 209.6 | 0.65 |
| Ψ 4 | 7.7 | 0.50 | Ψ 12 | 212.2 | 0.66 |
| Ψ 5 | 177.0 | 0.62 | Ψ 13 | 379.7 | 0.80 |
| Ψ 6 | 177.7 | 0.64 | Ψ 14 | 380.0 | 0.80 |
| Ψ 7 | 180.7 | 0.64 | Ψ 15 | 388.4 | 0.69 |
| Ψ 8 | 182.2 | 0.61 | Ψ 16 | 389.0 | 0.81 |
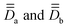 , cannot be diagonal in the molecular PAF. Since our procedure does not require any assumption on the local PAFs, we have re-computed (rotated) them in the molecular PAF prior to assembling ĤMS according to eqn (1):
, cannot be diagonal in the molecular PAF. Since our procedure does not require any assumption on the local PAFs, we have re-computed (rotated) them in the molecular PAF prior to assembling ĤMS according to eqn (1): | (10) |
It should be stressed that no specific relationship appears between the elements of these tensors, in accord with the C1 symmetry point group of complex 2.
We are now in the position to best equate the 16 × 16 matrix of ĤMS with the representative matrix of Ĥeff. We first consider the expressions reported in Tables S5 and S6 (ESI†), meaning that we neglect the symmetric exchange tensor. By using the −2.85 cm−1 spin-free J value and the full  tensors (eqn (10)), the estimated numerical matrix of ĤMS is given in Tables S25 and S26 (ESI†) in the uncoupled |MSa,MSb〉 and coupled |S,MS〉 spin basis, respectively. These are brought in correspondence with the effective Hamiltonians shown in Tables S27 (coupled-spin basis) and S28 (uncoupled-spin basis) (ESI†). As was the case with complex 1, outstanding agreement is obtained from the comparison regardless of the spin basis. Indeed, the difference between Ĥeff and ĤMS is already smaller than 1 and 2.7 cm−1 concerning the off-diagonal and diagonal matrix elements, respectively. It is worth emphasizing once again that the independently calculated local anisotropy tensors,
tensors (eqn (10)), the estimated numerical matrix of ĤMS is given in Tables S25 and S26 (ESI†) in the uncoupled |MSa,MSb〉 and coupled |S,MS〉 spin basis, respectively. These are brought in correspondence with the effective Hamiltonians shown in Tables S27 (coupled-spin basis) and S28 (uncoupled-spin basis) (ESI†). As was the case with complex 1, outstanding agreement is obtained from the comparison regardless of the spin basis. Indeed, the difference between Ĥeff and ĤMS is already smaller than 1 and 2.7 cm−1 concerning the off-diagonal and diagonal matrix elements, respectively. It is worth emphasizing once again that the independently calculated local anisotropy tensors,  , within the framework of the 2a and 2b monomeric structures, can be safely transferred to the dimeric structure 2.
, within the framework of the 2a and 2b monomeric structures, can be safely transferred to the dimeric structure 2.
As with complex 1, we proceeded to extract J under the influence of SOC, as well as the symmetric anisotropy tensor  , without revising the local anisotropies. In other words, we constructed ĤMS as follows:
, without revising the local anisotropies. In other words, we constructed ĤMS as follows:
 | (11) |
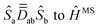 , expressed in an arbitrary axis frame and in the coupled-spin basis, is displayed in Table S7 (ESI†). The contribution of
, expressed in an arbitrary axis frame and in the coupled-spin basis, is displayed in Table S7 (ESI†). The contribution of  in its own PAF is given in Table S31 (ESI†). A careful inspection of all the relevant tables revealed that in fact the previous deviations between the estimated ĤMS and Ĥeff can essentially be explained by Table S31 (ESI†). In other words, the PAF of
in its own PAF is given in Table S31 (ESI†). A careful inspection of all the relevant tables revealed that in fact the previous deviations between the estimated ĤMS and Ĥeff can essentially be explained by Table S31 (ESI†). In other words, the PAF of  practically matches the molecular PAF, and thus we only need to fit the J, Dab, and Eab parameters to refine ĤMS.
practically matches the molecular PAF, and thus we only need to fit the J, Dab, and Eab parameters to refine ĤMS.
Table 8 summarizes all the key magnetic parameters resulting from the resolution of ĤMS for the case of complex 2 (we recall that the  tensors are not diagonal in the molecular PAF). In the coupled-spin basis, the numerical matrix of ĤMS is shown in Table S32 (ESI†). This model is of course in even better agreement with the effective Hamiltonian (Table S27, ESI†). The difference matrix between ĤMS and Ĥeff, displayed in Table S33 (ESI†), now shows that all the elements are generally smaller than 1 cm−1. Furthermore, diagonalization of our model ĤMS yields highly accurate spin–orbit energies, with an average deviation of only 1.2 cm−1 and a maximum deviation of 2.6 cm−1. Consequently, we have successfully applied our new procedure to properly extract all the rank-2 tensors of ĤMS and, ultimately, validated the standard multispin Hamiltonian for any binuclear complex since the key step of unsymmetrical dicobalt(II) complexes is now solved.
tensors are not diagonal in the molecular PAF). In the coupled-spin basis, the numerical matrix of ĤMS is shown in Table S32 (ESI†). This model is of course in even better agreement with the effective Hamiltonian (Table S27, ESI†). The difference matrix between ĤMS and Ĥeff, displayed in Table S33 (ESI†), now shows that all the elements are generally smaller than 1 cm−1. Furthermore, diagonalization of our model ĤMS yields highly accurate spin–orbit energies, with an average deviation of only 1.2 cm−1 and a maximum deviation of 2.6 cm−1. Consequently, we have successfully applied our new procedure to properly extract all the rank-2 tensors of ĤMS and, ultimately, validated the standard multispin Hamiltonian for any binuclear complex since the key step of unsymmetrical dicobalt(II) complexes is now solved.
| J | D ab | E ab | D a | E a | D b | E b |
|---|---|---|---|---|---|---|
| a Generated from a least-squares fitting of the model parameters in order to minimize the RMSD between ĤMS and Ĥeff. b Recalculated parameters after relabeling of the MPAF axes such that the convention Eab > 0 and |Dab| > 3Eab is fulfilled: y → z, z → x, x → y. | ||||||
| −2.28 | −0.07a/0.22b | −0.13a/0.03b | 86.31 | 11.91 | 93.14 | 25.02 |
Finally, we take a step forward and attempt to model the powder-averaged χT profile of complex 2 using the validated ĤMS. For this purpose, we use again the analytical expressions of the Zeeman Hamiltonians, derived in Tables S20 and S21 (ESI†), using the  tensors obtained with the 2a and 2b structural models, based on calculations performed in the molecular PAF:
tensors obtained with the 2a and 2b structural models, based on calculations performed in the molecular PAF:
 | (12) |
 ). Since the off-diagonal elements are smaller than the diagonal ones in eqn (12), one can still consider that
). Since the off-diagonal elements are smaller than the diagonal ones in eqn (12), one can still consider that  are close to being diagonal in the molecular PAF, even if a detailed analysis may reveal an interchange between the respective hard and intermediate axes of magnetization between
are close to being diagonal in the molecular PAF, even if a detailed analysis may reveal an interchange between the respective hard and intermediate axes of magnetization between  .
.
Fig. 5, top panel, demonstrates the excellent agreement between the reference, experimental χT curve68 and the one obtained directly out of the SO-NEVPT2 calculation. Therefore, we can be confident in the quality of our ab initio calculations and now aim at producing good quality model curves, in view of further supporting the validity of both ĤMS and of our procedure to extract the magnetic parameters. The model curve, obtained from ĤMS + ĤZee dressed with quantities from Table 8 and eqn (12), agrees with the reference data in the low-temperature region. As the temperature increases, it deviates more and more, eventually reaching a plateau around 150 K which is quite lower than the experimental curve. The behavior may be caused by (i) the lack of excited states in our model that may be populated at some point and in particular at 300 K and (ii) an underestimation of the isotropic g value for each Co center. Concerning point (i), the sum of the Boltzmann populations of the first 16 energy levels is 94% at 300 K. We hypothesize that the remaining 6% in terms of population are not mandatory to explain the discrepancy between this first model curve and the ab initio one. Furthermore, it appears that the model curve is too low for a much larger temperature range, in particular from 30 to 300 K. At 30 K, it is clear that only the first 16 energy levels are populated, hence the problem may fully lie on the isotropic g values, as was observed in complex 1 (in this case, the isotropic g value had to be tempered to a lower value). By following this hypothesis, we here need to increase the isotropic g value, which leads to a revised model curve that is more satisfactory for the whole 30–300 K problematic range, without compromising the already good 0–30 K range. The fitted g = 2.55 value is not completely random as it may be justified based on the measured room-temperature χT value of 6.03 cm3 mol−1 K, or rather 3.015 cm3 mol−1 K per Co center, according to:
 | (13) |
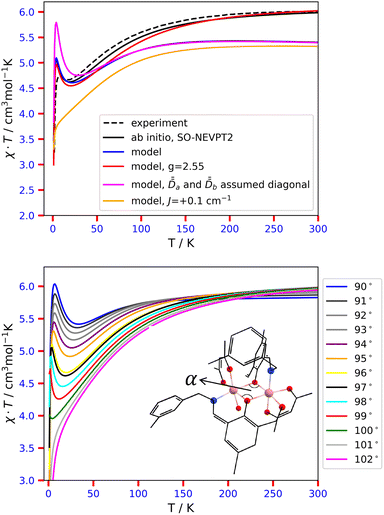 | ||
| Fig. 5 Top: Experimental χT = f(T) curve of complex 2, digitized from ref. 68, and generated from ab initio calculations and multispin Hamiltonian models. Bottom: χT = f(T) curves obtained with SO-NEVPT2 as a function of the angle α° = ∠Co–O–Co. In the crystal structure, α = 97°, and the black curve represents the best approximation of the experimental χT. | ||
This expression leads to g = 2.54 with the Boltzmann constant, kB = 0.695 cm−1 K−1, μB = 0.467, cm−1 T−1, and NA·μB = 0.558 cm3 mol−1 T. Note that since our main point here is to understand the zero-field behavior, we do not aim to delve deeper into explaining the reasons behind this revision of the SO-NEVPT2 g value.
Two additional models are displayed in Fig. 5, top panel, evidencing the shape of χT if one assumes that the local anisotropy tensors are diagonal in the molecular frame and if the axial and rhombic parameters displayed in Table 8 are used, or if J is artificially set to a weakly antiferromagnetic value. The first scenario artificially pushes up the model curve in the low-temperature range, meaning that the maximum is too high. While it is quite intuitive that the mismatch of the actual PAFs of the local anisotropy tensors should lower the model curve, we should stress that if one assumes that the tensors are diagonal in the molecular PAF and if one fits the local ZFS parameter values, as could be done to fit the experimental data, this should lead to too weak ZFS parameters. In other words, it is crucial to account for the mismatch of the local PAFs in the model, otherwise, meaningless parameters would be obtained. This is exactly where experimental extractions of ĤMS parameters should not be performed independently from computational chemistry data.
We now aim to better explain the occurrence of a local maximum of χT at low temperatures. From the previous paragraph, we have learned that the mismatch between the local PAFs works towards lowering this χT maximum. Such maximum does not occur if the antiferromagnetic coupling scenario is retained (see Fig. 5). Thus, one could naively think that J must be maximized to favor the occurrence of such a maximum. In practice, to get a local maximum of χT, we believe that it requires population of a state that is much less magnetic than the ones before and after it. A close inspection of Table S24 (ESI†) reveals that the fourth spin–orbit level is essentially derived from the MS = 0 components of the spin-quintet and spin-singlet states so that this must be the states that are looked for. For this state to occur in between the components of the S = 3 state, one needs to be in the weak-exchange limit (note that this also strengthens the spin-mixing with the singlet state, which also pushes down this state in the model). Additionally, this state must be well separated in energy from the subsequent states, otherwise, a continuous enhancement of χT would be observed. According to Table 7, a gap of about 170 cm−1 occurs in complex 2, which corroborates our interpretation.
To strengthen the conclusion drawn earlier, the bottom panel of Fig. 5 illustrates the variation of χT, obtained directly from SO-NEVPT2 calculations, as a function of the Co–O–Co angles. At the crystal-structure value of 97°, the calculated curve best approximates the reference data. Angles below 97° promote stronger ferromagnetic coupling (without getting rid of the weak exchange regime). Consequently, as the “less magnetic” state shifts toward higher energies, the spike in χT is both enhanced and slightly shifted to higher temperatures. On the other hand, angles above 100° promote antiferromagnetism. As a result, the χT curves no longer exhibit local maxima. The overall structural change, induced when the Co–O–Co angle is changed from 97 to, for instance, 101°, is characterized by an RMSD of 0.08 Å, it is thus negligible. Therefore, one can regard the unfolding of χT in complex 2 as an intermediate between the ferromagnetic and antiferromagnetic regimes. This is due to the fact that even a tiny displacement in the molecular structure promptly alters χT, transitioning between these two regimes.
3.3 Reinterpretation of the [Ni2(en)4Cl2]2+ case, a centrosymmetric dinickel(II) complex in the weak-exchange regime
An accurate determination of magnetic parameters in [Ni(en)4Cl2]Cl2 has been reported more than a decade ago in the context of high-field EPR experiments.96 The complex is weakly ferromagnetic, with J = −9.66, Da = −4.78, and Dab = −0.64 cm−1. Maurice et al. performed an extraction of these parameters from the anisotropic multispin Hamiltonian through the effective Hamiltonian theory.65 The generated parameters, J = −5.415, Da = −9.437, Ea = 2.042, Dab = 0.367 and Eab = −0.052 cm−1, which are in reasonable agreement with the experimental counterparts, allow for the derivation of the ĤMS numerical matrix listed in Table 9. Comparison with the numerical Ĥeff matrix, reproduced from ref. 65 in Table 10, shows outstanding agreement down to only ±prefactors for the elements coupling the S = 2 and S = 0 blocks in Ĥeff. Performing a basis-change to the uncoupled basis using tabulated CG coefficients following the Condon–Shortley convention, these conflicting signs lead to unexpected matrix elements, such as 〈1,−1|Ĥeff|−1,1〉 = 8.6 cm−1, that should be null according to the standard ĤMS.65 As discussed in this article, in ab initio calculations, the conflicting signs arise from arbitrary phases and must be adjusted based on the model matrix. This sign adjustment results in a nearly identical model and effective matrices in both the coupled-spin and uncoupled-spin bases, thereby fully validating the standard multispin Hamiltonian for [Ni(en)4Cl2]Cl2. Consequently, in this context, the introduction of a rank-4, biquadratic exchange tensor, in ĤMS is no longer crucial, unless high accuracy is sought after. Therefore, it is important to stress that the weak-exchange limit was correctly solved in the previous experimental and theoretical works.65,96 However, the experimental extraction was based on the assumption that rhombicity is negligible, which is not supported by the calculations. Therefore, the experimental J = −9.66, Da = −4.78, and Dab = −0.64 cm−1 values may be the subject of small uncertainties due to the neglect of rhombicity, though the important features (weak-exchange limit, local easy-axis anisotropies, |Dab| < |Da|) are now no doubt.| Ĥ MS | |2,2〉 | |2,1〉 | |2,0〉 | |2,−1〉 | |2,−2〉 | |1,1〉 | |1,0〉 | |1,−1〉 | |0,0〉 |
|---|---|---|---|---|---|---|---|---|---|
| a Obtained by evaluating the analytical expressions reported by ref. 65. | |||||||||
| 〈2,2| | 1.67 | 0.00 | 1.62 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 2.39 |
| 〈2,1| | 0.00 | 10.74 | 0.00 | 1.99 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 〈2,0| | 1.62 | 0.00 | 13.76 | 0.00 | 1.62 | 0.00 | 0.00 | 0.00 | −9.07 |
| 〈2,−1| | 0.00 | 1.99 | 0.00 | 10.74 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 〈2,−2| | 0.00 | 0.00 | 1.62 | 0.00 | 1.67 | 0.00 | 0.00 | 0.00 | 2.39 |
| 〈1,1| | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 21.81 | 0.00 | −2.09 | 0.00 |
| 〈1,0| | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 12.01 | 0.00 | 0.00 |
| 〈1,−1| | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −2.09 | 0.00 | 21.81 | 0.00 |
| 〈0,0| | 2.39 | 0.00 | −9.07 | 0.00 | 2.39 | 0.00 | 0.00 | 0.00 | 23.96 |
| Ĥ MS | |2,2〉 | |2,1〉 | |2,0〉 | |2,−1〉 | |2,−2〉 | |1,1〉 | |1,0〉 | |1,−1〉 | |0,0〉 |
|---|---|---|---|---|---|---|---|---|---|
| a Reproduced from ref. 65. | |||||||||
| 〈2,2| | 1.67 | 0.00 | 1.62 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −2.37 + 0.02i |
| 〈2,1| | 0.00 | 10.74 | 0.00 | 1.99 | 0.00 | 0.00 | 0.00 | 0.00 | −0.02 − 0.09i |
| 〈2,0| | 1.62 | 0.00 | 13.79 | 0.00 | 1.62 | 0.00 | 0.00 | 0.00 | 9.06 |
| 〈2,−1| | 0.00 | 1.99 | 0.00 | 10.74 | 0.00 | 0.00 | 0.00 | 0.00 | 0.02 − 0.09i |
| 〈2,−2| | 0.00 | 0.00 | 1.62 | 0.00 | 1.67 | 0.00 | 0.00 | 0.00 | −2.37 − 0.02i |
| 〈1,1| | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 21.81 | 0.02 + 0.07i | −2.10 + 0.03i | 0.00 |
| 〈1,0| | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.02 − 0.07i | 12.02 | −0.02 − 0.07i | 0.00 |
| 〈1,−1| | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | −2.10 − 0.03i | −0.02 + 0.07i | 21.81 | 0.00 |
| 〈0,0| | −2.37 − 0.02i | −0.02 + 0.09i | 9.06 | 0.02 + 0.09i | −2.37 + 0.02i | 0.00 | 0.00 | 0.00 | 24.12 |
4 Conclusion
By studying dicobalt(II) complexes, we have confirmed the validity of the standard ĤMS independent from the weak- or strong-exchange regime. Using ab initio calculations, we have demonstrated that it is possible to extract the full tensors that make up the model, without making any assumptions about their principal axis frames (PAFs). Furthermore, the analysis, based on model χT curves, has revealed that assuming the local anisotropy tensors are diagonal in the molecular PAF should lead to erroneous local anisotropy parameters in the fitting process. Therefore, concerning unsymmetrical or low-symmetry binuclear complexes, a rigorous interpretation of low-temperature magnetic data should retain key inputs from quantum mechanical calculations similar to those used in this work, i.e. multiconfigurational and relativistic wave functions methods. We hope that the present article will trigger new joint theory/experiment studies based on this renewed perspective of explicitly mapping ab initio data onto ĤMS.Author contributions
RM conceived the study. DCS, RM and BLG secured funding. DCS performed all the theoretical calculations and implemented all codes utilized in generating the data reported in this manuscript. All authors were equally involved in the data analysis. DCS wrote the first draft of the manuscript. RM and BLG shaped the final form of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
DCS acknowledges support from the European Unions Horizon 2020 Research and Innovation Program under the Marie Sklodowska-Curie Grant Agreement No. 899546, through the BIENVENÜE COFUND program. DCS also acknowledges the infrastructure support provided through the RECENT AIR grant agreement MySMIS no. 127324.Notes and references
- C. A. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Molecular magnetic hysteresis at 60 kelvin in dysprosocenium, Nature, 2017, 548, 439–442 CrossRef CAS PubMed.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, A Dysprosium Metallocene Single-Molecule Magnet Functioning at the Axial Limit, Angew. Chem., Int. Ed., 2017, 56, 11445–11449 CrossRef CAS PubMed.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet, Science, 2018, 362, 1400–1403 CrossRef CAS PubMed.
- C. A. Gould, K. R. McClain, D. Reta, J. G. C. Kragskow, D. A. Marchiori, E. Lachman, E.-S. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Ultrahard magnetism from mixed-valence dilanthanide complexes with metal-metal bonding, Science, 2022, 375, 198–202 CrossRef CAS PubMed.
- L. Bogani and W. Wernsdorfer, Molecular spintronics using single-molecule magnets, Nat. Mater., 2008, 7, 179–186 CrossRef CAS PubMed.
- E. Coronado, Molecular magnetism: from chemical design to spin control in molecules, materials and devices, Nat. Rev. Mater., 2020, 5, 87–104 CrossRef.
- A. Moneo-Corcuera, D. Nieto-Castro, J. Cirera, V. Gómez, J. Sanjosé-Orduna, C. Casadevall, G. Molnár, A. Bousseksou, T. Parella, J. M. Martínez-Agudo, J. Lloret-Fillol, M. H. Pérez-Temprano, E. Ruiz and J. R. Galán-Mascarós, Molecular memory near room temperature in an iron polyanionic complex, Chem, 2023, 9, 377–393 CAS.
- D. Gatteschi and R. Sessoli, Quantum Tunneling of Magnetization and Related Phenomena in Molecular Materials, Angew. Chem., Int. Ed., 2003, 42, 268–297 CrossRef CAS PubMed.
- W. Wernsdorfer, N. E. Chakov and G. Christou, Quantum Phase Interference and Spin-Parity in Mn12 Single-Molecule Magnets, Phys. Rev. Lett., 2005, 95, 037203 CrossRef CAS PubMed.
- C. Schlegel, J. van Slageren, M. Manoli, E. K. Brechin and M. Dressel, Direct Observation of Quantum Coherence in Single-Molecule Magnets, Phys. Rev. Lett., 2008, 101, 147203 CrossRef CAS PubMed.
- N. Ishikawa, M. Sugita and W. Wernsdorfer, Quantum Tunneling of Magnetization in Lanthanide Single-Molecule Magnets: Bis(phtalocyianato)terbium and Bis(phtalocyianato)dysprosium Anions, Angew. Chem., Int. Ed., 2005, 44, 2931–2935 CrossRef CAS PubMed.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Lanthanide Single-Molecule Magnets, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
- N. Ishikawa, M. Sugita, T. Ishikawa, S.-Y. Koshihara and Y. Kaizu, Lanthanide Double-Decker Complexes Functioning as Magnets at the Single-Molecular Level, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed.
- Z. Zhu, M. Guo, X.-L. Li and J. Tang, Molecular magnetism of lanthanide: Advances and perspectives, Coord. Chem. Rev., 2019, 378, 350–364 CrossRef CAS.
- S. T. Liddle and J. van Slageren, Improving f-element single molecule magnets, Chem. Soc. Rev., 2015, 44, 6655–6669 RSC.
- N. F. Chilton, Design Criteria for High-Temperature Single-Molecule Magnets, Inorg. Chem., 2015, 54, 2097–2099 CrossRef CAS PubMed.
- X.-Y. Wang, C. Avendaño and K. R. Dunbar, Molecular magnetic materials based on 4d and 5d transition metals, Chem. Soc. Rev., 2011, 40, 3213–3238 RSC.
- A. Swain, A. Sen and G. Rajaraman, Are lanthanide-transition metal direct bonds a route to achieving new generation 3d-4f SMMs?, Dalton Trans., 2021, 50, 16099–16109 RSC.
- V. Chandrasekhar, Lanthanide and transition metal complexes as molecular magnets, Dalton Trans., 2022, 51, 4199–4201 RSC.
- M. Magott, M. Brzozowska, S. Baran, V. Vieru and D. Pinkowicz, An intermetallic molecular nanomagnet with the lanthanide coordinated only by transition metals, Nat. Commun., 2022, 13, 2014 CrossRef CAS PubMed.
- R. Boča, Zero-field splitting in metal complexes, Coord. Chem. Rev., 2004, 248, 757–815 CrossRef.
- R. Maurice, R. Broer, N. Guihéry and C. de Graaf, in Zero-Field Splitting in Transition Metal Complexes: Ab Initio Calculations, Effective Hamiltonians, Model Hamiltonians, and Crystal-Field Models, ed. W. Liu, Springer Berlin Heidelberg, Berlin, Heidelberg, 2016, pp. 1–31 Search PubMed.
- I. d P. R. Moreira, N. Suaud, N. Guihéry, J. P. Malrieu, R. Caballol, J. M. Bofill and F. Illas, Derivation of spin Hamiltonians from the exact Hamiltonian: Application to systems with two unpaired electrons per magnetic site, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 134430 CrossRef.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed.
- J. J. Borrás-Almenar, J. M. Clemente-Juan, E. Coronado and B. S. Tsukerblat, MAGPACK A package to calculate the energy levels, bulk magnetic properties, and inelastic neutron scattering spectra of high nuclearity spin clusters, J. Comput. Chem., 2001, 22, 985–991 CrossRef.
- W. Z. Heisenberg, Mehrkörperproblem und Resonanz in der Quantenmechanik, Z. Phys., 1926, 38, 411 CrossRef.
- P. A. M. Dirac, Quantum mechanics of many-electron systems, Proc. R. Soc. London, 1929, 123, 714 CAS.
- J. H. Van Vleck, The theory of electric and magnetic susceptibility, Oxford University Press, United Kingdom, 1932 Search PubMed.
- R. Maurice, C. de Graaf and N. Guihéry, Magnetic anisotropy in binuclear complexes in the weak-exchange limit: From the multispin to the giant-spin Hamiltonian, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 214427 CrossRef.
- R. Maurice, A. M. Pradipto, N. Guihéry, R. Broer and C. de Graaf, Antisymmetric Magnetic Interactions in Oxo-Bridged Copper(II) Bimetallic Systems, J. Chem. Theory Comput., 2010, 6, 3092–3101 CrossRef CAS PubMed.
- R. Maurice, K. Sivalingam, D. Ganyushin, N. Guihéry, C. de Graaf and F. Neese, Theoretical Determination of the Zero-Field Splitting in Copper Acetate Monohydrate, Inorg. Chem., 2011, 50, 6229–6236 CrossRef CAS PubMed.
- F. Gendron, J. Autschbach, J.-P. Malrieu and H. Bolvin, Magnetic Coupling in the Ce(III) Dimer Ce2 (COT)3, Inorg. Chem., 2019, 58, 581–593 CrossRef CAS PubMed.
- R. Maurice, T. Mallah and N. Guihéry, in Magnetism in Binuclear Compounds: Theoretical Insights, ed. P. Kalck, Springer International Publishing, Cham, 2023, pp. 207–233 Search PubMed.
- L. F. Chibotaru and L. Ungur, Ab initio calculation of anisotropic magnetic properties of complexes. I. Unique definition of pseudospin Hamiltonians and their derivation, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS PubMed.
- A. Wilson, J. Lawrence, E.-C. Yang, M. Nakano, D. N. Hendrickson and S. Hill, Magnetization tunneling in high-symmetry single-molecule magnets: Limitations of the giant spin approximation, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 140403 CrossRef.
- R. Boča, Theoretical Foundations of Molecular Magnetism, Elsevier, Amsterdam, 1999, pp. 642–680 Search PubMed.
- B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, A Complete Active Space SCF method (CASSCF) using a density matrix formulated super-CI approach, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- J. P. Malrieu, R. Caballol, C. J. Calzado, C. de Graaf and N. Guihéry, Magnetic Interactions in Molecules and Highly Correlated Materials: Physical Content, Analytical Derivation, and Rigorous Extraction of Magnetic Hamiltonians, Chem. Rev., 2014, 114, 429–492 CrossRef CAS PubMed.
- P.-A. Malmqvist, B. O. Roos and B. Schimmelpfennig, The restricted active space (RAS) state interaction approach with spin–orbit coupling, Chem. Phys. Lett., 2002, 357, 230–240 CrossRef CAS.
- C. J. Calzado, J. Cabrero, J. P. Malrieu and R. Caballol, Analysis of the magnetic coupling in binuclear complexes. I. Physics of the coupling, J. Chem. Phys., 2002, 116, 2728–2747 CrossRef CAS.
- C. J. Calzado, J. Cabrero, J. P. Malrieu and R. Caballol, Analysis of the magnetic coupling in binuclear complexes. II. Derivation of valence effective Hamiltonians from ab initio CI and DFT calculations, J. Chem. Phys., 2002, 116, 3985–4000 CrossRef CAS.
- R. Broer, L. Hozoi and W. C. Nieuwpoort, Non-orthogonal approaches to the study of magnetic interactions, Mol. Phys., 2003, 101, 233–240 CrossRef CAS.
- D. Ganyushin and F. Neese, First-principles calculations of zero-field splitting parameters, J. Chem. Phys., 2006, 125, 024103 CrossRef PubMed.
- C. J. Calzado, C. Angeli, D. Taratiel, R. Caballol and J.-P. Malrieu, Analysis of the magnetic coupling in binuclear systems. III. The role of the ligand to metal charge transfer excitations revisited, J. Chem. Phys., 2009, 131, 044327 CrossRef PubMed.
- R. Maurice, R. Bastardis, C. D. Graaf, N. Suaud, T. Mallah and N. Guihéry, Universal Theoretical Approach to Extract Anisotropic Spin Hamiltonians, J. Chem. Theory Comput., 2009, 5, 2977–2984 CrossRef CAS PubMed.
- M. Atanasov, D. Ganyushin, D. A. Pantazis, K. Sivalingam and F. Neese, Detailed Ab Initio First-Principles Study of the Magnetic Anisotropy in a Family of Trigonal Pyramidal Iron(II) Pyrrolide Complexes, Inorg. Chem., 2011, 50, 7460–7477 CrossRef CAS PubMed.
- F. Neese and D. A. Pantazis, What is not required to make a single molecule magnet, Faraday Discuss., 2011, 148, 229–238 RSC.
- F. Neese, Calculation of the zero-field splitting tensor on the basis of hybrid density functional and Hartree-Fock theory, J. Chem. Phys., 2007, 127, 164112 CrossRef PubMed.
- S. Schmitt, P. Jost and C. van Wüllen, Zero-field splittings from density functional calculations: Analysis and improvement of known methods, J. Chem. Phys., 2011, 134, 194113 CrossRef PubMed.
- L. Belkhiri, B. Le Guennic and A. Boucekkine, DFT Investigations of the Magnetic Properties of Actinide Complexes, Magnetochemistry, 2019, 5, 15 CrossRef CAS.
- Q.-C. Luo and Y.-Z. Zheng, Methods and Models of Theoretical Calculation for Single-Molecule Magnets, Magnetochemistry, 2021, 7, 107 CrossRef CAS.
- G. Duplaix-Rata, B. Le Guennic and G. David, Revisiting magnetic exchange couplings in heterodinuclear complexes through the decomposition method in KS-DFT, Phys. Chem. Chem. Phys., 2023, 25, 14170–14178 RSC.
- G. David, N. Ferré and B. Le Guennic, Consistent Evaluation of Magnetic Exchange Couplings in Multicenter Compounds in KS-DFT: The Recomposition Method, J. Chem. Theory Comput., 2023, 19, 157–173 CrossRef CAS PubMed.
- S. Meskaldji, L. Belkhiri, R. Maurice, K. Costuas, B. Le Guennic, A. Boucekkine and M. Ephritikhine, Electronic Structure and Magneto-Structural Correlations Study of Cu2 UL Trinuclear Schiff Base Complexes: A 3d-5f-3d Case, J. Phys. Chem. A, 2023, 127, 1475–1490 CrossRef CAS PubMed.
- N. J. Mayhall and M. Head-Gordon, Computational quantum chemistry for single Heisenberg spin couplings made simple: Just one spin flip required, J. Chem. Phys., 2014, 141, 134111 CrossRef PubMed.
- N. J. Mayhall and M. Head-Gordon, Computational Quantum Chemistry for Multiple-Site Heisenberg Spin Couplings Made Simple: Still Only One Spin-Flip Required, J. Phys. Chem. Lett., 2015, 6, 1982–1988 CrossRef CAS PubMed.
- N. Orms and A. I. Krylov, Singlet-triplet energy gaps and the degree of diradical character in binuclear copper molecular magnets characterized by spin-flip density functional theory, Phys. Chem. Chem. Phys., 2018, 20, 13127–13144 RSC.
- H. Schurkus, D.-T. Chen, H.-P. Cheng, G. Chan and J. Stanton, Theoretical prediction of magnetic exchange coupling constants from broken-symmetry coupled cluster calculations, J. Chem. Phys., 2020, 152, 234115 CrossRef CAS PubMed.
- P. Pokhilko and A. I. Krylov, Effective Hamiltonians derived from equation-of-motion coupled-cluster wave functions: Theory and application to the Hubbard and Heisenberg Hamiltonians, J. Chem. Phys., 2020, 152, 094108 CrossRef CAS PubMed.
- M. Alessio and A. I. Krylov, Equation-of-Motion Coupled-Cluster Protocol for Calculating Magnetic Properties: Theory and Applications to Single-Molecule Magnets, J. Chem. Theory Comput., 2021, 17, 4225–4241 CrossRef CAS PubMed.
- H. Bolvin, An Alternative Approach to the g-Matrix: Theory and Applications, ChemPhysChem, 2006, 7, 1575–1589 CrossRef CAS PubMed.
- S. Vancoillie, L. Rulíšek and K. Pierloot, Theoretical Description of the Structure and Magnetic Properties of Nitroxide-Cu(II)-Nitroxide Spin Triads by Means of Multiconfigurational Ab Initio Calculations, J. Phys. Chem. A, 2009, 113, 6149–6157 CrossRef CAS PubMed.
- L. Ungur and L. F. Chibotaru, Ab Initio Crystal Field for Lanthanides, Chem. – Eur. J., 2017, 23, 3708–3718 CrossRef CAS PubMed.
- S. Dey, G. Rajaraman and H. Bolvin, Analysis of the Magnetic Coupling in a Mn(II)-U(V)-Mn(II) Single Molecule Magnet, Chem. – Eur. J., 2022, 28, e202201883 CrossRef CAS PubMed.
- R. Maurice, N. Guihéry, R. Bastardis and C. D. Graaf, Rigorous Extraction of the Anisotropic Multispin Hamiltonian in Bimetallic Complexes from the Exact Electronic Hamiltonian, J. Chem. Theory Comput., 2010, 6, 55–65 CrossRef CAS PubMed.
- J.-S. Sun, H. Zhao, X. Ouyang, R. Clérac, J. A. Smith, J. M. Clemente-Juan, C. Gómez-Garcia, E. Coronado and K. R. Dunbar, Structures, Magnetic Properties, and Reactivity Studies of Salts Containing the Dinuclear Anion [M2Cl6]2− (M = Mn, Fe, Co), Inorg. Chem., 1999, 38, 5841–5855 CrossRef CAS.
- C. de Graaf and C. Sousa, Assessing the zero-field splitting in magnetic molecules by wave function-based methods, Int. J. Quantum Chem., 2006, 106, 2470–2478 CrossRef CAS.
- X.-j Song and X.-m Xue, Study on the Magneto-Structural Correlation of a New Dinuclear Cobalt(II) Complex with Double μ-Phenoxo Bridges, ACS Omega, 2020, 5, 8347–8354 CrossRef CAS PubMed.
- O. Kahn, Molecular magnetism, VCH, New York, 1993, pp. 135–143 Search PubMed.
- I. Dzyaloshinskii, Theory of helicoidal structures in antiferromagnets. I. Nonmetals, Sov. Phys. JETP, 1964, 19, 960–971 Search PubMed.
- T. Moriya, Anisotropic Superexchange Interaction and Weak Ferromagnetism, Phys. Rev., 1960, 120, 91–98 CrossRef CAS.
- V. Dmitrienko, E. Ovchinnikova, S. Collins, G. Nisbet, G. Beutier, Y. Kvashnin, V. Mazurenko, A. Lichtenstein and M. Katsnelson, Measuring the Dzyaloshinskii-Moriya interaction in a weak ferromagnet, Nat. Phys., 2014, 10, 202–206 Search PubMed.
- M.-A. Bouammali, N. Suaud, C. Martins, R. Maurice and N. Guihéry, How to create giant Dzyaloshinskii-Moriya interactions? Analytical derivation and ab initio calculations on model dicopper(II) complexes, J. Chem. Phys., 2021, 154, 134301 CrossRef CAS PubMed.
- M.-A. Bouammali, N. Suaud, R. Maurice and N. Guihéry, Extraction of giant Dzyaloshinskii-Moriya interaction from ab initio calculations: First-order spin–orbit coupling model and methodological study, J. Chem. Phys., 2021, 155, 164305 CrossRef CAS PubMed.
- M.-A. Bouammali, N. Suaud, N. Guihéry and R. Maurice, Antisymmetric Exchange in a Real Copper Triangular Complex, Inorg. Chem., 2022, 61, 12138–12148 CrossRef CAS PubMed.
- J. des Cloizeaux, Extension d'une formule de Lagrange à des problèmes de valeurs propres, Nucl. Phys., 1960, 20, 321–346 CrossRef.
- L. Chibotaru, L. Ungur and A. Soncini, The origin of nonmagnetic Kramers doublets in the ground state of dysprosium triangles: evidence for a toroidal magnetic moment, Angew. Chem., Int. Ed., 2008, 47, 4126–4129 CrossRef CAS PubMed.
- L. Ungur, W. Van den Heuvel and L. F. Chibotaru, Ab initio investigation of the non-collinear magnetic structure and the lowest magnetic excitations in dysprosium triangles, New J. Chem., 2009, 33, 1224–1230 RSC.
- F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Software update: The ORCA program system-Version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- M. Douglas and N. M. Kroll, Quantum electrodynamical corrections to the fine structure of helium, Ann. Phys., 1974, 82, 89–155 CAS.
- B. A. Hess, Applicability of the no-pair equation with free-particle projection operators to atomic and molecular structure calculations, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 32, 756–763 CrossRef CAS PubMed.
- B. A. Hess, Relativistic electronic-structure calculations employing a two-component no-pair formalism with external-field projection operators, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3742–3748 CrossRef CAS PubMed.
- A. Wolf, M. Reiher and B. A. Hess, The generalized Douglas-Kroll transformation, J. Chem. Phys., 2002, 117, 9215–9226 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Efficient, approximate and parallel Hartree-Fock and hybrid DFT calculations. A 'chain-of-spheres' algorithm for the Hartree-Fock exchange, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- G. L. Stoychev, A. A. Auer and F. Neese, Automatic Generation of Auxiliary Basis Sets, J. Chem. Theory Comput., 2017, 13, 554–562 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, Introduction of n-electron valence states for multireference perturbation theory, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, N-electron valence state perturbation theory: a fast implementation of the strongly contracted variant, Chem. Phys. Lett., 2001, 350, 297–305 CrossRef CAS.
- J. Miralles, O. Castell, R. Caballol and J.-P. Malrieu, Specific CI calculation of energy differences: Transition energies and bond energies, Chem. Phys., 1993, 172, 33–43 CrossRef CAS.
- V. García, O. Castell, R. Caballol and J. Malrieu, An iterative difference-dedicated configuration interaction. Proposal and test studies, Chem. Phys. Lett., 1995, 238, 222–229 CrossRef.
- K. Andersson, P.-Å. Malmqvist and B. O. Roos, Second-order perturbation theory with a Complete Active Space Self-Consistent Field reference function, J. Chem. Phys., 1992, 96, 1218–1226 CrossRef CAS.
- E. U. Condon, E. U. Condon and G. H. Shortley, The theory of atomic spectra, Cambridge University Press, 1951 Search PubMed.
- K. Alder and A. Winther, Phase conventions for angular momentum eigenfunctions, Phys. Lett. B, 1971, 34, 357–358 CrossRef.
- R. Herchel, R. Boča, J. Krzystek, A. Ozarowski, M. Durán and J. van Slageren, Definitive Determination of Zero-Field Splitting and Exchange Interactions in a Ni(II) Dimer: Investigation of [Ni2(en)4Cl2]Cl2 Using Magnetization and Tunable-Frequency High-Field Electron Paramagnetic Resonance, J. Am. Chem. Soc., 2007, 129, 10306–10307 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Complimentary tables and XYZ coordinates of the two dicobalt(II) complexes under study. See DOI: https://doi.org/10.1039/d3cp04943d |
| ‡ L = (4-methyl-2-formyl-6-(((2-trifluoromethyl)phenyl)methyliminomethyl)phenol). |
| § The standard conventions are applied here: the tensor is traceless, |D| > 3E and E > 0. |
| This journal is © the Owner Societies 2024 |