Releasing a bound molecular spring with light: a visible light-triggered photosalient effect tied to polymorphism

Abstract

Here we present a study on the solid state properties of trans tetra-ortho-bromo azobenzene (4Br-Azo). Two distinct crystal polymorphs were identified: the α-phase and β-phase. Notably, only the β-phase exhibited an extraordinary photosalient effect (jumping/breaking) upon exposure to a wide range of visible light. Powder X-ray diffraction and Raman spectroscopy revealed that the β-phase is metastable and can transition to the α-phase when subjected to specific stimuli like heat and light. Furthermore, single crystal X-ray diffraction and density functional theory calculations highlighted the significance of a highly strained conformer in the β-phase, showing that the metastability of the phase potentially arises from relieving this strain. This metastability leads to a light induced phase transition, which appears to be the cause of the photosalient effect in these crystals. Interestingly the polymorphism at the core of 4Br-Azo's dynamic behavior is based on different arrangements of halogen based intermolecular interactions. It is possible that continued study on combining visible light capturing chromophores with halogen interaction-based polymorphism will lead to the discovery of even more visible light controlled dynamic crystal materials.

---

Introduction

Looking to nature we find a plethora of complex motions that are activated by stimuli such as light and heat which would be attractive to mimic for the design of artificial systems.^1–3 Thus, producing mechanical action with non-invasive stimuli has long been a compelling goal in materials research. Great progress has been made with the development of artificial molecular machines and their integration into materials.^4–6 This has led to the demonstration of motions such as bending or reversible expansion in response to heat,⁷ light,⁸ and electrical stimulation.^9,10 Traditionally much of this research has been focused on polymers and supramolecular complexes. Such materials contain various functional groups that can transfer their molecular movement from external stimulation to bulk motion.^11–14 However, in recent years there has been a renewed interest in small molecule crystals.^15,16 This has resulted in the discovery of many new dynamic crystal materials.^17–19 A significant benefit to molecular crystals is their high ordering, which allows the study and potential tuning of their structure in fine detail. By comparison polymers only allow one to study the effects of an averaged response. Thus, the study of relationships between molecular and crystal structure to macroscopic properties is essential for dynamic crystal research.

Polymorphism of molecular crystals represents an important area for diversification of dynamic crystal responses. This is because both the physicochemical properties of the constituent molecules, and the way they are able react due to their crystal environment contribute to photomechanical responses. For this reason researchers have shown very different photomechanical responses can be achieved in different polymorphs of the same material.^20–22 This makes continuing to study the diverse in bulk photoresponse between polymorphs an important goal for crystal engineering research.

One unique class of motions exhibited by some dynamic crystals are so called salient effects, where crystals jump when stimulated. Salient effects have been reported in response to heat (thermosalient)²³ and light irradiation (photosalient).²⁴ Several underlying molecular mechanisms like bond rearrangement,²⁴ photochemical reaction,^25–28 and polymorphic phase transitions^29,30 have been found to trigger a salient response. Some materials even display salient versus nonsalient polymorphs.²⁰ One thing all these events have in common is they result in a sudden anisotropic shift in the unit cell in those crystals. This is thought to cause significant strain within the crystal that can manifest in a rapid jump or hop motion. Cracking or complete breaking of the crystals is also commonly observed in this process.

Azobenzene derivatives represent one of the most well studied classes of dynamic crystal materials.^15,17,31,32 Owing to the photochromic nature of azobenzene they have been found to exhibit motions such as crawling^33,34 and bending^17,31,35 from light irradiation. Activating these motions often requires UV irradiation to trigger the well-known trans to cis isomerization of azobenzene. Though with the rise in azobenzenes that can be isomerized purely with visible light, researchers have reported photomechanical azobenzene crystals that do not require UV irradiation.^17,36 Purely visible light responsive systems are ideal for the widest range of uses because UV light can cause unwanted chemical reactions and damage biological tissue.³⁷ One of the most popular molecular design strategies for creating visible light responsive azobenzenes is substitution of halogen atoms on the ortho positions of the aromatic rings.^36,38,39 Though this molecular design strategy has been applied to various solution state systems, there are few reports on the solid-state properties of ortho halogenated azobenzenes.^40–42 Thus, further investigation of these materials is expected to be valuable.

Here we present a study on the solid-state properties of tetra-ortho-bromo azobenzene (4Br-Azo, Fig. 1a). The synthesis of this compound has been reported previously,^43,44 but, to the best of our knowledge, this is the first solid-state study of the material. During preliminary experiments two distinct type of crystals were observed. They have since been identified as two crystal polymorphs of trans 4Br-Azo, which will be referred to as α-phase and β-phase from now on. Although most recrystallization conditions yielded mixed crystals of the polymorphs, they were successfully crystallized individually by optimizing the solvent and concentration (see ESI†). Due to their striking differences in colour and shape (Fig. 1b) they immediately drew interest for further study. Upon exposing the α-phase to visible light irradiation (filtered Hg lamp), no change was detected. However, within seconds of exposure to the same irradiation the β-phase crystals showed a photosalient effect (Fig. 1c and Video S1, ESI†). This effect was reproducibly observed using three different wavelengths of visible light. To the best of our knowledge this relative independence on incident wavelength is unique among reported photosalient materials.^{24–28,45–48} Understanding the underlying molecular structure differences between the polymorphs and the reason for the photosalient effect in the β-phase crystals then became an important question. Through characterization with X-ray diffraction (XRD), Raman spectroscopy, and computational chemistry methods we have determined the critical factors to 4Br-Azo's photosalient effect and proposed its molecular mechanism. The findings of this study highlight the fascinating potential in combining halogen interaction-based polymorphism with visible light chromophores.

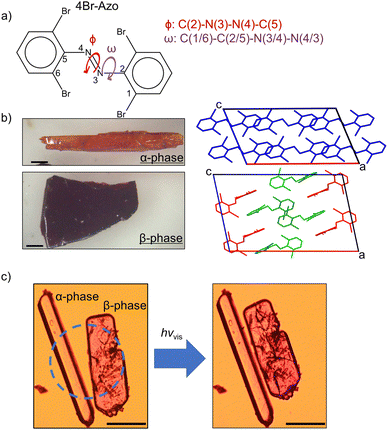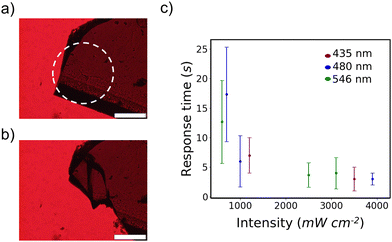
Fig. 1 (a) Molecular structure of 4Br-Azo with discussed dihedral angles labelled. (b) Microscope photographs of the two isolated polymorphs of trans 4Br-Azo (left) alongside their respective unit cells viewed normal to the [010] face (right). Scale bars indicate 1 mm. (c) Representative microscope photos of each polymorph before (left) and after (right) strong visible light irradiation (Video S1, ESI†). Dashed circle indicates the irradiated area. Scale bars indicate 200 μm.

Results and discussion

Photosalient observations

After initially observing the photosalient effect of 4Br-Azo the light irradiation conditions needed to produce the effect were evaluated. It was found that crystals which were too thick (>150 μm) showed a cracking response but no photosalient effect, so crystals with an average thickness of 74.7 ± 10.5 μm showing no clear twinning were studied. No clear dependence on the other dimensions was observed as long as the crystal was large enough to not be completely enveloped by light. Irradiation was always done on a crystal corner as an additional control condition.

The clearest way to discuss the effect of these irradiation conditions is the photosalient response time, which we define as the time after beginning irradiation when at least one piece of the crystal jumped away from its starting position (Fig. 2a, b and Video S2, ESI†). At least one piece typically travelled on the order of millimeters. Within the intensity range of approximately 600–3900 mW cm⁻² it was found that a photosalient response could be reliably produced in less than 30 s and that higher light intensities accelerated the response (Fig. 2c). The deviation in response time also lowers significantly with increased intensity. On the other hand, wavelength supplied appeared to have no clear relationship with the viability or response time of 4Br-Azo's photosalient effect. One possible exception is the measured faster response with green versus blue light at 600 mW cm⁻² and 700 mW cm⁻² respectively. However, between experimental error in the intensity estimations, uncontrollable variations in sample morphology, and the large standard deviation in photosalient response time at these lower intensities, it is not reasonable to conclude that there is a statistically significant difference in the average response time at those two conditions.

Fig. 2 (a) and (b) Representative microscope images of 4Br-Azo before (a) and after (b) a photosalient event. Dashed circle indicates the irradiated area. Scale bars indicate 200 μm. (c) Plot of average photosalient response time versus incident light intensity with three different wavelengths. Error bars represent standard deviation.

This relative independence of visual light response is well rationalized by the wide visual light absorption band measured for the β-phase (Fig. S1, ESI†). It was also noted that irradiation with 200 mW cm⁻² light could induce minor to major cracking of the crystals, suggesting that thinner crystals may exhibit photosalience at these intensities. Only the lowest intensity used (<100 mW cm⁻²) showed no visible change to the crystals. The observed thickness dependence suggests that this photosalient effect is primarily due to a surface reaction on the β-phase which produces strain that becomes explosive when the bulk crystal is not thick enough to absorb it. The intensity dependence should be directly related to the rate of the photoreaction taking place and follows a similar trend to the earliest report of the photosalient effect.²⁴ As previously noted this wide wavelength response is unique though.

Crystal structure analysis

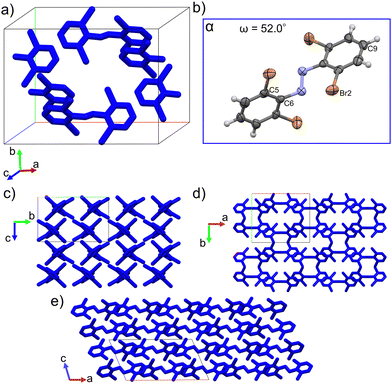
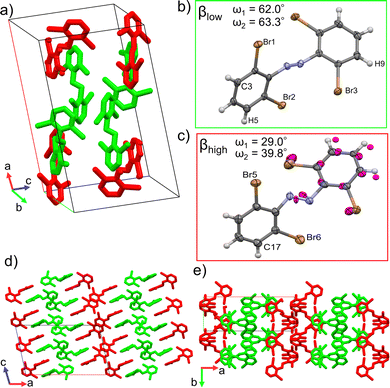
Single crystal structure analyses revealed the molecular structure of both polymorphs and showed that they both contain the trans isomer with different conformations. The α-phase crystalizes in the C2/c (monoclinic) space group and features one molecular conformation in its unit cell (Fig. 3a and b). Only half the molecule is crystallographically unique in this polymorph. The β-phase crystalizes in the P2₁/c (monoclinic) space group and features two unique molecular conformations in its unit cell (Fig. 4a–c). This difference in molecular conformations between the two phases stands out because while the geometry of one of the molecules, β_low, (Fig. 4b) in the β-phase is similar to the one observed in the α-phase, the other, β_high (Fig. 4c), is quite different. Full structure and refinement details for all crystals as determined by single crystal (SC) XRD are included in Table S1 (ESI†). We also note that the cis isomer crystal structure was solved (Table S1, ESI†), but no evidence of solid-state isomerization was found in the current study. Thus, we reserve the discussion for the trans polymorphs.

Fig. 3 (a) Packed unit cell of the α-phase. (b) and (c) Molecular structure of the conformation found in the α-phase with discussed atoms labeled. Thermal ellipsoids drawn at the 50% level. (c)–(e) Supercells (2 × 2 × 2) viewed along the a-axis (c), c-axis (d) and the b-axis (e). Hydrogens omitted for clarity.

Fig. 4 (a) Packed unit cell of the β-phase. (b) and (c) Molecular structures of the two conformations found in the β-phase with discussed atoms labeled. Magenta atoms indicate disorder that has been modeled with 0.45 occupancy of the magenta sites and 0.55 occupancy of their corresponding sites. Thermal ellipsoids drawn at the 50% level. (d) and (e) Supercells (2 × 2 × 2) viewed along the b-axis (d) and the c-axis (e). Hydrogens omitted for clarity.

To discuss the geometry differences in these conformations we will highlight the ring twisting dihedral angles (ω) as detailed in Fig. 1a. The aromatic ring twisting dihedral angles of 52.0° in the α-phase conformation are completely symmetrical and are relatively large compared to the nearly planar conformation of unsubstituted azobenzene.⁴⁹ They are also slightly larger than those reported for tetra-ortho-chloro azobenzene,³⁸ which is a logical trend given the increase in size of the ortho substituent. While the β_low conformation is not completely symmetrical in the same way, the difference in ω values is still small, with ω₁ = 62.0° and ω₂ = 63.2°. Such small asymmetry in the ring twisting is also common in crystals of azobenzene derivatives.^38,40,50

On the other hand, the β_high conformer stands out among previously reported azobenzene crystals and the other 4Br-Azo conformations. Firstly, to properly model the observed disorder of the azo bond and the aromatic ring closest to the β_low conformer, it was necessary to split the involved atoms into two parts (Fig. 4c). Part 1 (colored by element in Fig. 4c) has 0.55 occupancy and part 2 (magenta atoms in Fig. 4c) has 0.45. This treatment of the β_high conformer was found to give good quality refinement statistics for the β-phase structure. The need to describe the β_high conformer in this unique way offers the first indication that it is key to the dynamic behavior of the β-phase, because it may indicate that there is more flexibility of the molecules in these crystal sites compared to the α and β_low sites. Additionally, the twisting angles of the aromatic rings are significantly different from those of the other conformers. When considering part 1 of the β_high conformation the angles are ω₁ = 29.0 and ω₂ = 39.8, with ω₁ = 59.7 and ω₂ = 68.4 using part 2.

In addition to the differences in the molecular conformations present in the two crystal phases there are notable differences in their packing. The α-phase has a tightly ordered structure consisting of end-to-end chains of molecules along the a-axis which have alternating ring stacking orientations (Fig. 3d and e). Sets of these chains align nearly in parallel to create sheets roughly in the (010) plane. Interestingly, these sheets are slightly interdigitated which leads to an alternating two-sheet pattern along the b-axis (Fig. 3c and d). This is significantly different than the β-phase, where the two-fold rotation axis in the [010] direction is lost due to the presence of two conformers. Instead, there is a the two-fold screw axis in the [010] direction, which creates a more complex packing network. Viewed normal to the [010] face (Fig. 4d) this leads to the appearance of sheets made of alternating columns of β_high and β_low conformers but looking to the c-axis projection (Fig. 4e) it is clear that the interdigitation from the screw axis disrupts any clear sheet-like description of the structure. However, while there is not a sheet analogue within the β-phase structure there is still a chain with similar orientation to the one seen in the α-phase. As can be seen most clearly in Fig. 4a, it has a β_high–β_low–β_low–β_high pattern and follows a twisted distortion from the straight chains of molecules seen in the α-phase. Visualizing the differences in these two polymorphs as a collection of linear chains organized into slightly offset sheets (α-phase) versus a collection of twisted chains with alternating twisting direction (β-phase) is helpful for interpreting their relative behaviors. Particularly for the case of a potential polymorphic phase transition as we will discuss in detail later.

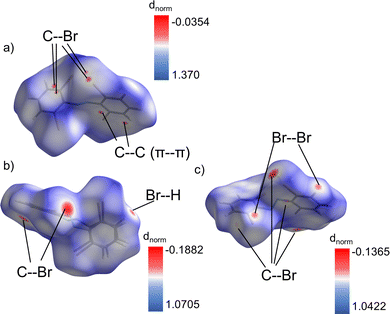
Interestingly the only difference in the types of close contact (<sum of VdW radii-0.01 Å) intermolecular interactions present in the two polymorphs is that Br–Br interactions are present in the β-phase, but not the α-phase (Fig. S13 and S14, ESI†). Otherwise, both contain Br–H, Br–C, and C–C (π–π) interactions with no clear differences in magnitude among them. This makes identifying the most dominating interactions in the coordination of each conformer a point of significant interest. To do this Hirshfeld surface analysis⁵¹ was employed for each conformer. Hirshfeld surfaces of each conformer are shown in Fig. 5a–c, which have been used to identify the dominating intermolecular interactions by mapping the d_norm property⁵² on them. The areas of red coloration on these surfaces highlight the regions of most dominant close contact interactions for each conformer. By filtering the regions of the surface by atom type we can identify which types of atom-to-atom contacts these red regions correspond to. This highlights that the α-phase contains some dominant π–π stacking interactions (C5–C9 (3.340 Å)) along with C–Br interactions (C5–Br2 (3.498 Å), C6–Br2(3.514 Å)). These contacts are all shorter than the sum of the vdW radii of the participating atoms by 0.060, 0.052, and 0.036 respectively (Table S4, ESI†). On the other hand, the β-phase is dominated only by Br based intermolecular interactions (Br2–C3 (3.524 Å), Br6–C17(3.219 Å), Br1–Br2(3.446 Å), Br2–Br2(3.618 Å), Br3–H5(2.954 Å), Br5–H9(3.011 Å)). They are shorter than the vdW radii sums by 0.026, 0.331, 0.254, 0.082, 0.096, and 0.039 respectively (Table S5, ESI†). Effectively this allows one to summarize that the relative effects of π–π stacking versus Br contacts lead to the differences in packing for each polymorph.

Fig. 5 (a)–(c) Hirshfeld surfaces of the α (a), β_high (b), and β_low (c) conformers mapped with the d_norm property. The most dominant interactions for each conformer are revealed by the areas of red coloration. They have been labeled according to their filtered fingerprint plots.

The Br–Br interactions within the β-phase serve as an important case study for its unique behavior. Based on the commonly accepted geometry-based definitions⁵³ the three unique interactions have been classified as type I or type II (Table S5, ESI†). Specifically, the Br2–Br2 contact is type I (dispersion interaction) while the Br1–Br2 interaction is type II (true halogen bond). There is also a second type II interaction, Br3–Br4 (3.64 Å) which is filtered out from the Hirshfeld surface analysis due to its large length. That contact is only 0.060 less than the sum of Br vdW radii, which is much smaller than the 0.254 difference for the Br1–Br2 contact. This indicates a much stronger interaction in the Br1–Br2 case, which is further supported by interaction angles of 89.9° and 174.6°. These are much closer to the ideal 90°/180° pair than 105.5° and 157.6° as seen for the Br3–Br4 contact. All of these interactions are between two different β_low molecules which appears to provide a backbone of β_low molecules in the unit cell of that phase. The stabilization from these strong interhalogen interactions and the coordination of the β_high sites that is further made possible by the Br–H interaction between the β_low and β_high molecules must be key to the relatively high metastability of this phase. Which ultimately leads to its photosalient behavior.

Identifying metastability of the β-phase

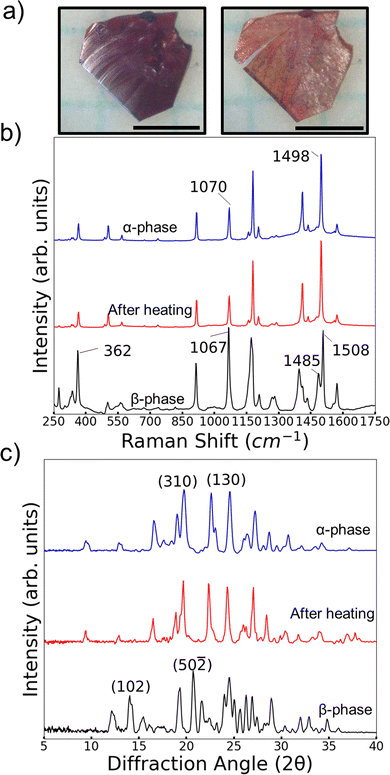
A series of characterization experiments revealed that the β-phase is metastable and can transition to the α-phase. Thermal characterization of α-phase and β crystals was done with differential scanning calorimetry (DSC). Heating of α-phase crystals of 4Br-Azo consistently showed one large endothermic peak corresponding to a melting point of 135–137 °C (Fig. S4a, ESI†). It was also noted that when heating and cooling the α-phase below the melting point no DSC peaks are observed. On the other hand, DSC cycles of the β-phase are more complex. On the first heating a shallow, wide endothermic peak was consistently observed below the melting peak (Fig. S4b, ESI†). The melting point was identical to the α-phase measurement. The second heating then appeared identical to an α-phase heating cycle. This behavior suggests that the small endothermic peak observed on first heating of a β-phase crystal is from a polymorphic transition from β-phase to α-phase. Heating and cooling of a β-phase crystal below the melting point showed only one solid-state transition peak, classifying the transition as monotropic (Fig. S4c and d, ESI†).

The DSC observations were further confirmed to be related to a monotropic β-to-α transition by Raman and powder (P) XRD measurements (Fig. 6b and c). For the Raman measurements, it was found that the molecular conformation differences in the different polymorphs produce a distinct vibrational signature for each phase in the molecular fingerprint region. Most notably are peaks in the region of coupled azo bond and aromatic ring stretching vibrations (∼1100–1600 cm⁻¹).⁵⁴ In the α-phase there is a single strong sharp peak at 1498 cm⁻¹. The corresponding area for the β-phase spectrum features two overlapped peaks centered at 1485 cm⁻¹ and 1508 cm⁻¹. It is likely that this difference arises from the presence of two conformers in the β-phase. Also, there is a clear difference in relative intensity of the peaks near 1100 cm⁻¹ for the two polymorphs. For the α-phase the peak is centered at 1070 cm⁻¹ and is noticably weaker than the 1498 cm⁻¹ peak. Meanwhile the 1067 cm⁻¹ centered peak in the β-phase spectrum has a similiar relative intensity to its pair in the 1500 cm⁻¹ region.

Fig. 6 (a) Representative β-phase crystal before (left) and after(right) being heated to 130 °C for 1 min. Scale bars indicate 1 mm. Raman (b) and PXRD (c) measurements showing the transition of β-phase 4Br-Azo crystals to the α-phase after heating to 130 °C. Key identifying reflection planes are labelled by their Miller indices.

We also note that the largest peak in the region of CCC/CCBr bending (∼200–400 cm⁻¹) has comparable relative intensity to the azo/aromatic stretching region in the β-phase. On the other hand, the α-phase features no peaks there with similar intensity to its higher wavenumber regions. By considering the combination of these features it was simple to quickly identify the change of an originally β-phase crystal to the α-phase after heating to 130 °C for 1 minute (Fig. 6b). This spectral shift was further confirmed to be related to a periodic structure change by looking at the PXRD patterns of the two polymorphs before and after the same heating procedure (Fig. 6c). Though it can be challenging to confidently identify polymorphs by their powder patterns due to potential overlapping of peaks it was possible to identify at least two key peaks for each polymorph. For the β-phase we use the (50–2̄) and (102) peaks. Characteristic peaks for the α-phase were chosen as (310) and (130). These peaks were chosen by comparing the relative intensities of the predicted powder patterns (Fig. 6c and Fig. S9, S10, ESI†) with the measured patterns. Using these characteristic peaks, it is clear to see that the β-phase peaks disappeared, and the α-phase peaks emerged after heating the powder.

Given the fact that polymorphic phase transitions have been reported as a potential driving force of some thermosalient effects in the literature,^30,55 the observation of this transition in 4Br-Azo did raise the question of whether it might exhibit a thermosalient effect too. However, even under a wide variety of heating conditions no displacement of the β-phase crystals was observed by heating. Only a distinct color change and minor morphology change were observed (Fig. 6a).

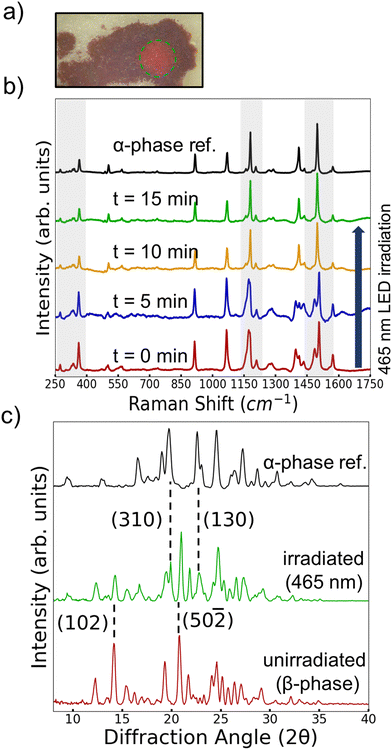
Even though no thermosalient effect was observed for β-phase 4Br-Azo the question of whether the metastability of β-phase was related to the photosalient effect remained open. To test for the possibility of a light induced phase transition a thin layer of β-phase powder was placed between two layers of colorless polyimide film and irradiated with a 465 nm LED. In between 5 min periods of irradiation the Raman spectrum of the irradiated region was measured. After about 10 min of irradiation it was found that the Raman spectrum started to take on distinctly α-phase character (Fig. 7b). No additional changes in the spectrum could be detected after 15 min, so it was considered that the sample was at a steady state. The final sample was also measured with XRD for further characterization (Fig. 7c). The PXRD pattern shows characteristic diffraction peaks from the α-phase as expected, but some characteristic β-phase peaks also remain present. Since the α-phase Raman peaks showed higher intensity, it is reasonable that the mixed powder only showed an α-phase signature at a certain point. It is possible that this light induced phase transition occurs due to radiationless decay through the crystals after excitation, effectively creating regions of “hot” molecules, similiar to Förster's description of class I photoreactions.⁵⁶ This explanation could offer a consistant explanation for both heat and light induced transitions even though the ensemble temperature of the powder did not exceed 45 °C during light irradiation.

Fig. 7 (a) Photograph of β-phase 4Br-Azo powder that was irradiated (465 nm LED, I ∼ 500 mW cm⁻²) in the area marked with a green circle. Surface temperature of the sample was measured at a maximum of 45 °C during irradiation. Scale bar indicates 1 mm. (b) A series of Raman spectra of the area circled in green on (a) measured in between 5-minute periods of irradiation. (c) Powder XRD patterns of the sample pictured in (a) for the unirradiated and irradiated areas. Characteristic α-phase measurements included for reference.

In all, the observation of the light induced β to α transition highlights an important aspect of the metastability of the β-phase and presents the light induced transition as a potential driving force for the photosalient effect. Considering the previously discussed packing of the two polymorphs, the β-to-α transition can basically be described as the twisted chains of the β-phase being “pulled” straight. In the heat induced case this would be relatively concerted, so only observing slight expansion and damage (Fig. 6a) is reasonable. On the other hand, the more scattered and gradual light induced transition could create significant stress within single crystals producing the photosalient effect. Even though one would expect the amount of bulk transition on the seconds timescale needed for the photosalient effect to be small previous studies have shown that relatively little photoproduct is required to produce the photosalient effect.²⁶

Computational investigation

Since it has been well reported to give accurate geometries for substituted azobenzene derivatives,^57,58 the B3LYP-GD3//6-311G(d) level of theory was chosen for geometry optimizations of 4Br-Azo. All single molecule density functional thoery (DFT) calculations were performed with Gaussian 16.⁵⁹ The isolated gas phase geometries given by these calculations offer valuable insight on the effects of the crystal environment. Selected geometry details are given in Table 1. Notably, the calculated trans geometry (trans-opt) features symmetrical ω values of 51.7°, nearly the same as the α-phase. As previously noted the β_low conformer also has nearly symmetrical ring twist dihedrals, though they are about 10° higher than the fully optimized geometry. This also further highlights that the β_high geometry is highly unusual since it is quite distorted from equilibrium while the α-phase and β_low geometries have been minimally constrained by their crystal environments in comparison.

Table 1 Selected geometry details and DFT calculated energies of the discussed molecular conformations of 4Br-Azo

Conformer	ω 1(°)	ω 2(°)	ϕ(°)	E (kJ mol^−1)^a
a Single point calculation with B3LYP-GD3//cc-pvtz (relative to trans-opt). βhigh value is the weighted average of calculations considering both parts. b Geometry from B3LYP-GD3//6-311(d) optimization. c Geometry extracted from structures solved by SCXRD.
trans-opt^b	51.7	51.7	175.4	0
α	52.0	52.0	178.0	18.8
β low	62.0	63.3	176.6	9.02
β high	Part 1:29.0	Part 1:39.8	Part 1:174.6	45.9
	Part 2:59.7	Part 2:68.4	Part 2:174.1

---

While molecular geometries offer direct comparison with XRD measurements, the energy values from DFT calculations offer further insight to the 4Br-Azo crystal systems. Single point energy calculations (B3LYP-GD3//cc-pvtz) were performed for each calculated and measured 4Br-Azo geometry. These energy calculations clearly show the extent of the combined distortions on the β_high molecules. For clarity it is useful to discuss these energies relative to the lowest value, which is trans-opt. The α and β_low geometries have relatively low energies at 18.8 kJ mol⁻¹ and 9.02 kJ mol⁻¹ respectively. In contrast, the β_high geometry's energy is significantly higher at 45.9 kJ mol⁻¹. Between the geometry distortions and the energy difference, one can clearly see that alleviating the strain on the β_high molecule must be the driving force behind the observed metastability of the β-phase. The monotropic behavior of this transition is also well rationalized by the geometry and energy considerations because expecting half the molecules within an α-phase crystal to twist back to the β_high conformation by cooling does not seem reasonable. Instead, the β-phase must only form when distorted molecules get trapped during crystallization to form a metastable solid. This makes quantifying the intermolecular interactions holding the β-phase together a high point of interest. Particularly since one may assume the β-phase to be much less stable than observed if only these single molecule properties are considered. Indeed, one can imagine that this could be a key factor to the photosalient effect in β-phase 4Br-Azo.

To investigate the relative binding energy in the crystal environments of 4Br-Azo, CrystalExplorer21⁶⁰ (CE) was used. This was done using the interaction energies calculated by CE to compute the lattice energy of each phase through the literature method.⁶¹ The calculated lattice energies are −119.563 kJ mol⁻¹ for α-phase and −124.840 kJ mol⁻¹ for β-phase. Firstly, the relatively strong lattice energy of the β-phase is logical given the fact that it is stable until close to the melting point of the compound despite the expected instability of the β_high conformation. Furthermore, transition from the more tightly bound β-phase to the slightly less bound α-phase is consistent with the endothermic nature of the phase transition peak observed by DSC. The magnitude of the difference between calculated lattice energies is also consistent with the DSC peak integration (∼5.3 kJ mol⁻¹vs. ∼1.2 kJ mol⁻¹). Furthermore, this small difference is consistent with commonly observed differences in energy of organic polymorphs.⁶²

Considering these computational results alongside the experimental evidence a clear picture of what could be driving the photosalient effect in β-phase 4Br-Azo emerged. If one were to imagine the strained β_high conformation as analogous to a loaded spring trapped by the strong intermolecular interactions present in that crystal structure, then it is reasonable to expect that releasing this spring-like tension could lead to the observed cracking and jumping behavior. Interestingly this does not manifest in a thermosalient effect, as previously discussed. Instead the mixed phase end point of the light-induced phase transition suggests that inducing a phase mixture in a single crystal might be the key factor to the photosalient effect.

Conclusions

The solid-state study of red-shifted azobenzene derivatives led to the surprising observation of a photosalient effect in one of two isolated polymorphs of trans 4Br-Azo. By characterizing the properties of the two polymorphs it was found that the photosalient β-phase is metastable and has the potential to shift to the light inert α-phase by heat and light stimulation. It appears that strain put on the bulk crystal by the uneven light-induced phase transition leads to the photosalient effect. We do note that the potential role of trans to cis isomerization in this mechanism remains unclear except to say that no cis isomer was detected in any samples after irradiation with the wavelengths of light used in this study. What is clear at this time is that the α-phase of the trans isomer is clearly the equilibrium state that 4Br-Azo settles in upon exposure to various stimuli. Additionally, we would like to highlight the important role of the dynamic Br based intermolecular interactions in the interesting properties of 4Br-Azo. This highlights a potential area of exploration for further design of azobenzene crystal properties. In the future mastering our understanding of these interactions may lead to practical photosalient based devices similar to the recently demonstrated thermosalient analogues.^63,64 We expect that the findings of this study will contribute to the fields of crystal engineering and solid-state chemistry for designing future photofunctional materials.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was supported by JSPS KAKENHI (Grant No. JP21K18860, JP22K14531, and JP23H01702), JST, the establishment of university fellowships towards the creation of science technology innovation, Grant Number JPMJFS2106, and JST-Mirai Program (Grant Number JPMJMI21ED; Japan). K. M. acknowledges financial support from the Suuri Fellowship, University of Tsukuba. The authors thank Dr Hiroyasu Sato at Rigaku Corporation for his valuable assistance with SCXRD data analysis for the β-phase.

References

1. S. Shinkai, Switch-functionalized systems in biomimetic chemistry, Pure Appl. Chem., 1987, 59, 425–430.
2. K. Kinbara and T. Aida, Toward intelligent molecular machines: Directed motions of biological and artificial molecules and assemblies, Chem. Rev., 2005, 105, 1377–1400.
3. S. Erbas-Cakmak, D. A. Leigh, C. T. McTernan and A. L. Nussbaumer, Artificial Molecular Machines, Chem. Rev., 2015, 115, 10081–10206.
4. B. L. Feringa, The Art of Building Small: From Molecular Switches to Motors (Nobel Lecture), Angew. Chem., Int. Ed., 2017, 56, 11060–11078.
5. P. Martins, D. M. Correia, V. Correia and S. Lanceros-Mendez, Polymer-based actuators: back to the future, Phys. Chem. Chem. Phys., 2020, 22, 15163–15182.
6. I. Apsite, S. Salehi and L. Ionov, Materials for Smart Soft Actuator Systems, Chem. Rev., 2022, 122, 1349–1415.
7. A. Buguin, M. H. Li, P. Silberzan, B. Ladoux and P. Keller, Micro-actuators: When artificial muscles made of nematic liquid crystal elastomers meet soft lithography, J. Am. Chem. Soc., 2006, 128, 1088–1089.
8. D. H. Wang, K. Min Lee, Z. Yu, H. Koerner, R. A. Vaia, T. J. White and L. S. Tan, Photomechanical response of glassy azobenzene polyimide networks, Macromolecules, 2011, 44, 3840–3846.
9. R. M. Meira, D. M. Correia, S. Ribeiro, P. Costa, A. C. Gomes, F. M. Gama, S. Lanceros-Méndez and C. Ribeiro, Ionic-Liquid-Based Electroactive Polymer Composites for Muscle Tissue Engineering, ACS Appl. Polym. Mater., 2019, 1, 2649–2658.
10. L. Zhang, D. Wang, P. Hu, J. W. Zha, F. You, S. T. Li and Z. M. Dang, Highly improved electro-actuation of dielectric elastomers by molecular grafting of azobenzenes to silicon rubber, J. Mater. Chem. C, 2015, 3, 4883–4889.
11. J. Wang, Q. Li, S. Yi and X. Chen, Visible-light/temperature dual-responsive hydrogel constructed by α-cyclodextrin and an azobenzene linked surfactant, Soft Matter, 2017, 13, 6490–6498.
12. S. Santer, Remote control of soft nano-objects by light using azobenzene containing surfactants, J. Phys. D. Appl. Phys., 2018, 51, 013002.
13. W. R. Browne and B. L. Feringa, Chiroptical Molecular Switches, Mol. Switch., 2011, 1, 121–179.
14. V. Balzani, M. Clemente-León, A. Credi, B. Ferrer, M. Venturi, A. H. Flood and J. F. Stoddart, Autonomous artificial nanomotor powered by sunlight, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 1178–1183.
15. P. Naumov, D. P. Karothu, E. Ahmed, L. Catalano, P. Commins, J. Mahmoud Halabi, M. B. Al-Handawi and L. Li, The Rise of the Dynamic Crystals, J. Am. Chem. Soc., 2020, 142, 13256–13272.
16. N. K. Nath, M. K. Panda, S. C. Sahoo and P. Naumov, Thermally induced and photoinduced mechanical effects in molecular single crystals - A revival, CrystEngComm, 2014, 16, 1850–1858.
17. O. S. Bushuyev, T. A. Singleton and C. J. Barrett, Fast, reversible, and general photomechanical motion in single crystals of various Azo compounds using visible light, Adv. Mater., 2013, 25, 1796–1800.
18. T. Taniguchi, T. Asahi and H. Koshima, Photomechanical azobenzene crystals, Crystals, 2019, 9, 437.
19. W. M. Awad, D. W. Davies, D. Kitagawa, J. Mahmoud Halabi, M. B. Al-Handawi, I. Tahir, F. Tong, G. Campillo-Alvarado, A. G. Shtukenberg, T. Alkhidir, Y. Hagiwara, M. Almehairbi, L. Lan, S. Hasebe, D. P. Karothu, S. Mohamed, H. Koshima, S. Kobatake, Y. Diao, R. Chandrasekar, H. Zhang, C. C. Sun, C. Bardeen, R. O. Al-Kaysi, B. Kahr and P. Naumov, Mechanical properties and peculiarities of molecular crystals, Chem. Soc. Rev., 2023, 52, 3098–3169.
20. M. K. Mishra, A. Mukherjee, U. Ramamurty and G. R. Desiraju, Crystal chemistry and photomechanical behavior of 3,4-dimethoxycinnamic acid: Correlation between maximum yield in the solid-state topochemical reaction and cooperative molecular motion, IUCrJ, 2015, 2, 653–660.
21. L. Gao, Y. Hao, X. Zhang, X. Huang, T. Wang and H. Hao, Polymorph induced diversity of photomechanical motions of molecular crystals, CrystEngComm, 2020, 22, 3279–3286.
22. S. Hasebe, Y. Hagiwara, K. Takechi, T. Katayama, A. Furube, T. Asahi and H. Koshima, Polymorph-Derived Diversification of Crystal Actuation by Photoisomerization and the Photothermal Effect, Chem. Mater., 2022, 34, 1315–1324.
23. J. Gigg, R. Gigg, S. Payne and R. Conant, J. Chem. Soc., Perkin Trans. 1, 1987, 6–9.
24. P. Naumov, S. C. Sahoo, B. A. Zakharov and E. V. Boldyreva, Dynamic single crystals: Kinematic analysis of photoinduced crystal jumping (the photosalient effect), Angew. Chem., Int. Ed., 2013, 52, 9990–9995.
25. I. Colombier, S. Spagnoli, A. Corval, P. L. Baldeck, M. Giraud, A. Leaustic, P. Yu and M. Irie, Diarylethene microcrystals make directional jumps upon ultraviolet irradiation, J. Chem. Phys., 2007, 126, 2005–2008.
26. R. Medishetty, A. Husain, Z. Bai, T. Runčevski, R. E. Dinnebier, P. Naumov and J. J. Vittal, Single crystals popping under UV light: A photosalient effect triggered by a [2 + 2] cycloaddition reaction, Angew. Chem., Int. Ed., 2014, 53, 5907–5911.
27. E. Hatano, M. Morimoto, K. Hyodo, N. Yasuda, S. Yokojima, S. Nakamura and K. Uchida, Photosalient Effect of a Diarylethene with a Perfluorocyclohexene Ring, Chem. – A Eur. J., 2016, 22, 12680–12683.
28. R. Medishetty, S. C. Sahoo, C. E. Mulijanto, P. Naumov and J. J. Vittal, Photosalient behavior of photoreactive crystals, Chem. Mater., 2015, 27, 1821–1829.
29. H. F. Lieberman, R. J. Davey and D. M. T. Newsham, Br⋯Br and Br⋯H interactions in action: Polymorphism, hopping, and twinning in 1,2,4,5-tetrabromobenzene, Chem. Mater., 2000, 12, 490–494.
30. B. A. Zakharov, A. A. L. Michalchuk, C. A. Morrison and E. V. Boldyreva, Anisotropic lattice softening near the structural phase transition in the thermosalient crystal 1,2,4,5-tetrabromobenzene, Phys. Chem. Chem. Phys., 2018, 20, 8523–8532.
31. M. Horie, S. C. Cheng, C. H. Wang, Y. C. Lin, Y. Tsuchido, Y. Suzaki, Y. Sei and T. S. Kuo, Photoinduced mechanical motions of pseudorotaxane crystals composed of azobenzene and ferrocenyl groups on an axle and a crown ether ring, ACS Appl. Mater. Interfaces, 2022, 12, 50002–50010.
32. M. Koch, M. Saphiannikova, S. Santer and O. Guskova, Photoisomers of Azobenzene Star with a Flat Core: Theoretical Insights into Multiple States from DFT and MD Perspective, J. Phys. Chem. B, 2017, 121, 8854–8867.
33. E. Uchida, R. Azumi and Y. Norikane, Light-induced crawling of crystals on a glass surface, Nat. Commun., 2015, 6, 7310.
34. K. Saito, M. Ohnuma and Y. Norikane, Negative phototactic behaviour of crystals on a glass surface, Chem. Commun., 2019, 55, 9303–9306.
35. O. S. Bushuyev, T. C. Corkery, C. J. Barrett and T. Friščić, Photo-mechanical azobenzene cocrystals and in situ X-ray diffraction monitoring of their optically-induced crystal-to-crystal isomerisation, Chem. Sci., 2014, 5, 3158–3164.
36. A. L. Leistner and Z. L. Pianowski, Smart Photochromic Materials Triggered with Visible Light, Eur. J. Org. Chem., 2022, e202101271.
37. M. Gao, D. Kwaria, Y. Norikane and Y. Yue, Visible-light-switchable azobenzenes: Molecular design, supramolecular systems, and applications, Nat. Sci., 2023, 3, 1–45.
38. D. B. Konrad, G. Savasci, L. Allmendinger, D. Trauner, C. Ochsenfeld and A. M. Ali, Computational Design and Synthesis of a Deeply Red-Shifted and Bistable Azobenzene, J. Am. Chem. Soc., 2020, 142, 6538–6547.
39. C. Knie, M. Utecht, F. Zhao, H. Kulla, S. Kovalenko, A. M. Brouwer, P. Saalfrank, S. Hecht and D. Bléger, Ortho-Fluoroazobenzenes: Visible Light Switches with Very Long-Lived Z Isomers, Chem. – A Eur. J., 2014, 20, 16492–16501.
40. D. Hermann, H. A. Schwartz and U. Ruschewitz, Crystal Structures of Z and E ortho-Tetrafluoroazobenzene, ChemistrySelect, 2017, 2, 11846–11852.
41. O. S. Bushuyev, A. Tomberg, T. Friščić and C. J. Barrett, Shaping crystals with light: Crystal-to-crystal isomerization and photomechanical effect in fluorinated azobenzenes, J. Am. Chem. Soc., 2013, 135, 12556–12559.
42. D. Kwaria, K. McGehee, S. Liu, Y. Kikkawa, S. Ito and Y. Norikane, Visible-Light-Photomeltable Azobenzenes as Solar Thermal Fuels, ACS Appl. Opt. Mater., 2023, 1, 633–639.
43. C. Nallaiah and J. A. Strickson, Oxidation of aromatic amines with chromyl chloride-I. Oxidation of aromatic primary amines, Tetrahedron, 1986, 42, 4083–4087.
44. Q. Liu, X. Luo, S. Wei, Y. Wang, J. Zhu, Y. Liu, F. Quan, M. Zhang and C. Xia, Palladium-catalyzed direct ortho C[sbnd]X bond construction via C[sbnd]H activation of azobenzenes: Synthesis of (E)-1,2-b(2,6-dibromo(chloro)-phenyl)diazene, Tetrahedron Lett., 2019, 60, 1715–1719.
45. T.-Y. Xu, F. Tong, H. Xu, M.-Q. Wang, H. Tian and D.-H. Qu, Engineering Photomechanical Molecular Crystals to Achieve Extraordinary Expansion Based on Solid-State [2 + 2] Photocycloaddition, J. Am. Chem. Soc., 2022, 144, 6278–6290.
46. C. E. Mulijanto, H. S. Quah, G. K. Tan, B. Donnadieu and J. J. Vittal, Curved crystal morphology, photoreactivity and photosalient behaviour of mononuclear Zn(II) complexes, IUCrJ, 2017, 4, 65–71.
47. K. Yadava, G. Gallo, S. Bette, C. E. Mulijanto, D. P. Karothu, I. H. Park, R. Medishetty, P. Naumov, R. E. Dinnebier and J. J. Vittal, Extraordinary anisotropic thermal expansion in photosalient crystals, IUCrJ, 2020, 7, 83–89.
48. B. Dutta, S. Bera, C. Sinha and M. H. Mir, Sunlight-Induced In Situ Isomerization of Both Ligands in a Mixed-Ligand Coordination Polymer: From Photosalient to Photoinert Crystals, Chem. – A Eur. J., 2022, 28, 2–5.
49. C. J. Brown, A refinement of the crystal structure of azobenzene, Acta Crystallogr., 1966, 21, 146–152.
50. Y. Le Page, E. J. Gabe, Y. Wang, L. R. C. Barclay and H. L. Holm, 2,2’,4,4’,6,6’-Hexa-{tert}-butylazobenzene, Acta Crystallogr. Sect. B, 1980, 36, 2846–2848.
51. J. J. McKinnon, D. Jayatilaka and M. A. Spackman, Towards quantitative analysis of intermolecular interactions with Hirshfeld surfaces, Chem. Commun., 2007, 3814–3816.
52. M. A. Spackman and D. Jayatilaka, Hirshfeld surface analysis, CrystEngComm, 2009, 11, 19–32.
53. A. Mukherjee, S. Tothadi and G. R. Desiraju, Halogen bonds in crystal engineering: Like hydrogen bonds yet different, Acc. Chem. Res., 2014, 47, 2514–2524.
54. N. Biswas and S. Umapathy, Density functional calculations of structures, vibrational frequencies, and normal modes of trans- and cis-azobenzene, J. Phys. Chem. A, 1997, 101, 5555–5566.
55. D. P. Karothu and P. Naumov, Thermosalience of 1,2,4,5-Tetrachlorobenzene, Isr. J. Chem., 2021, 61, 557–562.
56. T. Förster, Diabatic and adiabatic processes in photochemistry, Pure Appl. Chem., 1970, 24, 443–450.
57. D. Jacquemin, E. A. Perpète, G. E. Scuseria, I. Ciofini and C. Adamo, Extensive TD-DFT investigation of the first electronic transition in substituted azobenzenes, Chem. Phys. Lett., 2008, 465, 226–229.
58. C. Naim, F. Castet and E. Matito, Impact of van der Waals interactions on the structural and nonlinear optical properties of azobenzene switches, Phys. Chem. Chem. Phys., 2021, 23, 21227–21239.
59. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, 2016, Gaussian 16, Revision C.01, Gaussian, Inc., Wallin.
60. P. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, CrystalExplorer: A program for Hirshfeld surface analysis, visualization and quantitative analysis of molecular crystals, J. Appl. Crystallogr., 2021, 54, 1006–1011.
61. S. P. Thomas, P. R. Spackman, D. Jayatilaka and M. A. Spackman, Accurate Lattice Energies for Molecular Crystals from Experimental Crystal Structures, J. Chem. Theory Comput., 2018, 14, 1614–1623.
62. J. Nyman and G. M. Day, Static and lattice vibrational energy differences between polymorphs, CrystEngComm, 2015, 17, 5154–5165.
63. K. Takazawa, J. Ichi Inoue, K. Mitsuishi, Y. Yoshida, H. Kishida, P. Tinnemans, H. Engelkamp and P. C. M. Christianen, Phase-transition-induced jumping, bending, and wriggling of single crystal nanofibers of coronene, Sci. Rep., 2021, 11, 1–11.
64. K. Takazawa, J. Ichi Inoue and Y. Matsushita, Repeatable Actuations of Organic Single Crystal Fibers Driven by Thermosalient-Phase-Transition-Induced Buckling, Small, 2022, 18, 2204500.

---

Footnote

† Electronic supplementary information (ESI) available: Detailed conditions for experiments/calculations, full crystallographic details, and additional characterization. CCDC 2295252–2295254. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3cp04691e

---