Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Widening of the fundamental gap in cluster GW for metal–molecular interfaces†
Štěpán
Marek
 * and
Richard
Korytár
* and
Richard
Korytár

Department of Condensed Matter Physics, Faculty of Mathematics and Physics, Charles University, Ke Karlovu 5, Praha 2, 121 16, Czech Republic. E-mail: stepan.marek@matfyz.cuni.cz; korytar@karlov.mff.cuni.cz
First published on 13th December 2023
Abstract
The GW approximation is very promising for an accurate first-principles description of charged excitations in single-molecule–metal interfaces. In the cluster approach for electronic transport across molecules, the infinite metal (with an adsorbed molecule) is replaced by a finite cluster whose volume should be incrementally increased to test the approach to the thermodynamic limit. Here we show that in GW, the approach to the thermodynamic limit will be much slower than in Kohn–Sham density-functional theory (DFT) because of the Coulomb interaction. To demonstrate this statement, we investigate spectral gaps in an ensemble of disordered sodium clusters in Kohn–Sham DFT, quasiparticle eigenvalue-self-consistent GW and Hartree–Fock. The fundamental gaps (i.e. difference between the lowest unoccupied and highest occupied level) in GW scale as N−1/3 on average, where N is the number of atoms. We demonstrate that this slow decrease artificially depletes the density of states at the Fermi level when the cluster is used to simulate a semi-infinite electrode. Therefore, the GW method cannot be taken as an out-of-the-box improvement of the DFT in cluster geometries, unless careful convergence checks are performed.
1 Introduction
The state-of-the-art theoretical ab initio description of the electronic transport through single molecules attached to metallic contacts proceeds essentially in two steps.1 First, a density functional theory (DFT) calculation is performed, approximating the infinite system by a finite cluster. Second, the electronic Hamiltonian from the DFT calculation is equipped with self-energies to account for infinite reservoirs.2,3 The latter step facilitates the calculation of transport coefficients.4 Their accuracy depends most critically on the DFT output and it has been suggested that replacing the DFT Kohn–Sham spectrum with GW quasiparticle energies constitutes an improvement over the DFT5–7 (see also discussion in ref. 1). We challenge this view by presenting numerical evidence that an artefact develops in the quasiparticle density of states when calculated in GW in the cluster approach. Since the electronic structure of molecular adsorbates is relevant in broader context, e.g. for on-surface catalysis or photovoltaics, this finding may have implications also for the simulations in these related fields.The first step mentioned above is an approximation that is controlled by the size of the metallic cluster (either with periodic or vacuum boundary conditions). Any observable calculated in this way should be extrapolated with increasing size of the clusters (i.e. thermodynamic limit). For a molecular junction with vacuum boundary conditions, the calculation of transport coefficients involves a pair of metallic clusters that approximate semi-infinite electrodes (see ref. 1 and 8–10 for examples). The computed transport coefficients depend on the cluster sizes and this dependence must be extrapolated (see ref. 10, Methods section, for an example). We illustrate this concept in Fig. 1.
Due to the considerable computational demand, ab initio density-functional theory (DFT)11 provides the best trade-off between precision and scalability for moderately correlated systems. However, the salient Kohn–Sham orbitals are not a good approximation for the electronic excitations. In particular, frontier orbitals of molecular adsorbates tend to be too close to the Fermi level (see ref. 12–16 for examples). It is generally accepted that this problem will be ameliorated when DFT is replaced by the more demanding GW methodology.17 There are studies employing the GW approach for adsorbed molecules,5–7,18 which show more promising results than DFT. However, in these studies, the dependence of the conductance on the electrode volume was not given and therefore, it is not clear that the conductances were converged. In this work we alert that the GW method can not be taken as an automatic improvement over DFT because the energy levels of metallic clusters are depleted around the Fermi level and this depletion does not reflect the metallic density of states in the thermodynamic (continuum) limit.
We investigate the scaling of electronic excitation gaps of small metallic clusters. We employ the quasi-particle eigenvalue self-consistent GW (evGW) which yields a single-particle excitation spectrum, analogous to the Kohn–Sham spectrum of DFT. Of special interest is the evGW LUMO–HOMO gap, i.e. the difference between the highest occupied and lowest unoccupied quasiparticle orbital (here we term these orbitals HOMO and LUMO, as is common in chemistry). This energy formally corresponds to the fundamental gap, since the GW quasiparticle energies are energies of charged excitations. Our analysis reveals that the LUMO–HOMO gap is systematically larger than the energetic differences between adjacent occupied or unoccupied quasiparticle orbitals. In other words, the evGW spectrum is depleted around the HOMO. We investigate systematic trends of the gaps of metallic clusters of various sizes as a function of their volume V in DFT, evGW and the Hartree–Fock approximation. The scaling of the evGW LUMO–HOMO gaps is consistent with a V−1/3 law, while the scaling of adjacent gaps is V−1. We conclude that the spectral depletion in evGW is caused by the Coulomb repulsion. We also investigate the local density of states (LDOS) on the metallic clusters and at adsorbed molecules to establish the influence of these findings on transport problems.
This manuscript is organized as follows. In Methodology we define an ensemble of clusters of different sizes. In Results we present and analyse the scaling of spectral gaps and spectral functions (LDOS). In Discussion we reflect upon the implications for transport calculations in molecular electronics.
2 Methodology
The aim of the calculations is to inspect the scaling of the energetic levels of metallic clusters with volume. For the metal we choose sodium for reasons of computational efficiency. The scaling laws should apply generally to sp-bonded metals, to noble metals (for energies away from the d-band); the condition of applicability is that density of states varies slowly in an energy window around the Fermi level. However, the gap widening should occur in all metallic systems.First we discuss the most convenient choice of cluster geometries that supports our objective. Then we describe the computational approach.
2.1 Cluster selection
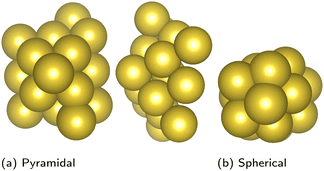
In transport calculations, metallic slabs or pyramidal clusters such as in Fig. 1 and 2a are typically used. In both cases, the structures are (almost) symmetrical, which leads to degeneracies or clustering of levels (see ESI† for illustration). The latter phenomena greatly contaminate the statistical analysis of electronic spectra and effectively slow down the approach to the thermodynamic limit. For our purpose it is more practical to employ disordered structures. We obtain them by a full geometric relaxation of spherical clusters. Relaxation ensures breaking of symmetries and lifting of degeneracies. An example of a relaxed cluster is in Fig. 2b. Several relaxed geometries can be obtained from different initial conditions. Consequently, for a fixed number of atoms, there are several clusters, that constitute an ensemble. From these ensembles, we again discarded the clusters which contained random degeneracies, leaving us only with clusters with approximately homogeneous Kohn–Sham orbital energy spacings (details about cluster choice and relaxation are given in ESI†). In the end, we were left with 2 clusters per specific number of atoms. We perform averages over various spectral variables, such as the LUMO–HOMO gap, within an ensemble.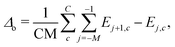 | (1) |
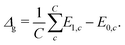 | (2) |
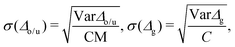 | (3) |
2.2 Electronic structure calculations
The energy spectrum of the clusters was calculated using the TURBOMOLE19 code. The clusters are first geometrically optimized in DFT, using PBE20 functional and def2-SVP basis21 in spin restricted model. Details about convergence with respect to basis size and invariability with functional change are given in ESI.† After the optimization, the DFT spectrum is noted, and both Hartree–Fock and GW calculations are run from the DFT start point.The GW calculation is using the eigenvalue-only self-consistent (evGW) implementation in TURBOMOLE.22,23 Specifically, at each iteration, the energy dependence of the self-energy is linearized in energy and the quasi-particle equation is solved in the linearized regime. The updated spectrum is used in the next iteration to construct updated Green's function, until self-consistency is reached. All states accessible for a given basis size are included in the calculation, Coulomb integrals are solved exactly, i.e. without the RI approximation.24 For the dielectric function, random phase approximation (RPA) is used.22 The choice of the evGW method is a compromise between reduced computational effort and good precision of the results – in previous works,23 evGW method reached spectrum values within 5% of values from quasi-particle fully self-consistent GW.
2.3 Local density of states
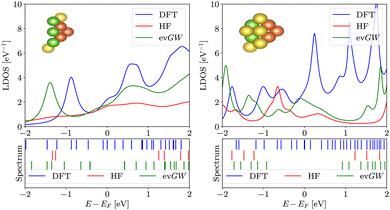
To illustrate the impact of the level scaling on physical observables, we compute a local density of states (LDOS) on the tips of pyramidal clusters with absorbing boundary conditions,2 which simulate an interface with a fermionic continuum, i.e. a semi-infinite electrode. We use pyramids (see Fig. 2a) with either 16 or 20 atoms. Absorbing boundary conditions are enforced by adding complex self-energies, as implemented in the AITRANSS code.2 Specifically, for atoms interfacing the infinite electrode, energy-independent constant self-energy is added to all atomic orbitals. Then, the Green's function is determined in the basis of atomic orbitals as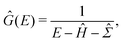 | (4) |
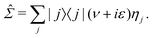 | (5) |
The value of the imaginary part of the self-energy is chosen as ε = 0.1 Ha. This value minimizes the changes in LDOS for small perturbations of the imaginary value and corresponds to the bandwidth of the clusters (see Fig. 5). The chemical potential is determined after the determination of ν by requiring charge neutrality with stricter precision |ΔN/N| < 10−6.
The LDOS itself is determined by projection of density of states onto apex (1st and 2nd layer) molecular orbitals of the pyramidal electrode. Specifically, from Green's function of the system coupled to reservoirs G in the basis of molecular orbitals, the (energy dependent) LDOS ρ(E) is determined as25
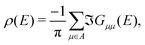 | (6) |
3 Results
3.1 Analytical predictions
For the spectrum of Kohn–Sham levels in DFT within the conduction band, we expect that the average energy level spacing behaves identically to the spacing of free particles in a disordered potential.26 In absence of degeneracies, the average gap between levels in the middle of the band should be proportional to W/N (for sufficiently large clusters), where W is the band-width and N is the number of atoms. When referencing the LUMO–HOMO gap specifically, we call this gap contribution the residual gap. For DFT, this is the only expected contribution to observed LUMO–HOMO gap. Here, we do not consider spin–orbit coupling; spin degeneracy is therefore trivial.For Hartree–Fock systems, there is a distinct difference in energy scaling of the LUMO–HOMO gap, which is caused by the discontinuity of the interaction term for occupied and unoccupied orbitals. Specifically, consider the Hartree–Fock Hamiltonian (in basis of atomic orbitals indexed by i and j)27–29
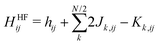 | (7) |
We can estimate the value of the charging gap by considering the electrostatic (Hartree) repulsion of single charge on a sphere
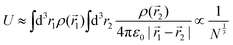 | (8) |
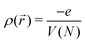 , where volume V is linear function of number of electrons N. See ESI,† for details of this elementary calculation. Therefore, the charging gap scales with the number of atoms with a weaker power than the gaps of the occupied (unoccupied) levels, where 1/N power law is still expected, same as for the residual gap. Hence, as the cluster size increases, the ratio of the charging gap to residual gap increases as N2/3 and the charging gap dominates the overall gap.
, where volume V is linear function of number of electrons N. See ESI,† for details of this elementary calculation. Therefore, the charging gap scales with the number of atoms with a weaker power than the gaps of the occupied (unoccupied) levels, where 1/N power law is still expected, same as for the residual gap. Hence, as the cluster size increases, the ratio of the charging gap to residual gap increases as N2/3 and the charging gap dominates the overall gap.
From this analytical consideration a widening of the fundamental gap in metallic clusters in HF can be expected. This effect can be traced to a known singularity of the exchange energy at the Fermi level of jellium.30 The singularity results from a long-range nature of the unscreened Coulomb interaction. The GW method introduces (partial) screening of the Coulomb interaction. To investigate the widening in the evGW we turn to numerical calculations.
3.2 Numerical results
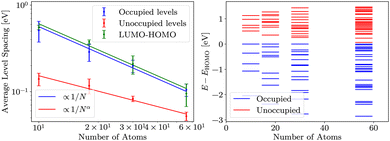
For DFT, HF and evGW, we determined the LUMO–HOMO gap and average spacing of energy levels in valence orbitals of sodium clusters. For cluster containing N atoms, we consider valence levels to be N/2 most energetic occupied levels. This corresponds to the model of sodium with single valence electron. Energy levels below these are significantly offset (about −22 eV), signalising the end of the valence band of sodium. Analogously, we only consider N/2 lowest energy unoccupied states for unoccupied energy level spacing analysis.DFT results are presented in Fig. 3. The occupied levels and LUMO–HOMO gap follow the expected convergence behaviour, while unoccupied levels converge slightly slower. We suspect that this is due to the properties of the basis, specifically due to basis being optimised to represent occupied states well. The error bars in Fig. 3 are determined as described in Methods.
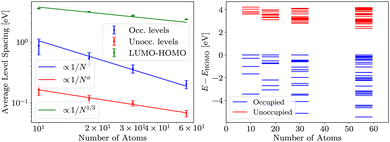
Similar analysis is present for HF in Fig. 4. The average energy spacings in HF remain somewhat similar as in DFT, but the gap is significantly larger and converges slower than in DFT. The convergence of the gap follows the 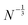 dependence expected from additional repulsion of single electron.
dependence expected from additional repulsion of single electron.
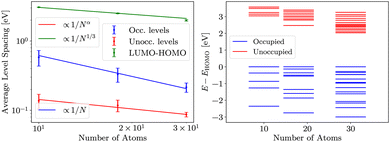
Finally, in evGW, gap follows similar dependence as in HF, but values are smaller than in HF. Results are presented in Fig. 5. The consistency of the evGW LUMO–HOMO gaps with the HF is indicative of the role of the Coulomb repulsion. Namely, the evGW gaps correct for the self-interaction error in PBE.
We also note that the same scaling is present in G0W0 (our results are available in ESI†), albeit with a different (smaller) prefactor.
3.3 Local density of states
To elucidate the impact of the widening of the LUMO–HOMO gap on surface science applications, we now switch to pyramidal clusters (see Fig. 2), which are employed in molecular electronics as electrodes. We calculated the local density of states for the 5 apex atoms of pyramids with 16 and 20 atoms. Results are summarized in Fig. 6. We stress that the LDOS is not a simple convolution of the spectrum; the LDOS follows from the embedding approach (see eqn (6)) The LDOS varies significantly depending on the method used. When the LDOS is averaged in an energy window from −2 eV to 2 eV around EF, both evGW and HF produce lower LDOS than DFT – about 22% lower for evGW and 53% lower for HF for the smaller electrode, as seen in Fig. 6.3.4 Local density of states on methanethiolate adsorbed on sodium
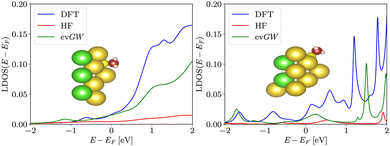
In order to illustrate the effect of the sodium gap widening on a metal-molecular interface, we repeated the pyramidal cluster calculations with an attached methanethiolate molecule, i.e. a methanethiol missing one hydrogen at the sulfur ion. The position of the methanethiolate molecule is optimized with the same parameters as in the case of spherical clusters, the basis used for final calculation is def2-SVP, DFT uses PBE functional. We project the density of states onto the atomic orbitals of the carbon atom. The local density profile, presented in Fig. 7, qualitatively reflects that of the isolated cluster – the depletion of the local density of states around the Fermi energy is adopted by the molecular states at the carbon atom as well.4 Discussion
The widening of the LUMO–HOMO gap seen in the evGW compared to DFT reflects the correction of a self-interaction problem of semi-local density functionals.31 The occupied Kohn–Sham orbital energies are shifted upwards as a result of this error. On the other hand, the observed evGW gap scaling is physical, for it is the correct behaviour of ionization energies. Here we discuss how does the scaling change in presence of a fully-developed screening and what are the implications for computational surface science based on the cluster approximation.4.1 Asymptotic scaling of the fundamental gap
The scaling of the evGW LUMO–HOMO gaps seen in our numerics is consistent with a V−1/3 law for the cluster sizes assumed. It is the scaling of the Coulomb charging energy. However, the larger the cluster the more efficient screening becomes. Therefore, we can not exclude the possibility that the V−1/3 scaling is pre-asymptotic only. Let us assume that the cluster is large enough, so that it is also characterized by a screening length LS. The screening turns the long-range Coulomb potential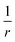 to an effectively short-range,
to an effectively short-range, 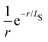 , i.e. the Yukawa potential.30 The scaling of the screened charging energy can be obtained by the dimensional analysis. The charging energy integral is
, i.e. the Yukawa potential.30 The scaling of the screened charging energy can be obtained by the dimensional analysis. The charging energy integral is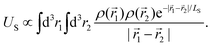 | (9) |
The densities scale as  . The outer integral will scale with cluster volume V, but the inner integral will remain constrained to a constant volume of LS3, due to the exponential. Therefore,
. The outer integral will scale with cluster volume V, but the inner integral will remain constrained to a constant volume of LS3, due to the exponential. Therefore,
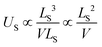 | (10) |
Concluding, when the clusters are large enough so that screening is fully developed, the widening of the fundamental gap will disappear. It is not clear whether this regime can be accessed with contemporary computational resources.
4.2 Implications for studies of surfaces, adsorbates and molecular junctions
Our results have important implications for computational attempts to simulate a semi-infinite metallic electrode in cluster GW, as the charge of the excited states on the finite electrode is not dispersed into infinite reservoir. Suppose that the aim is to investigate the electronic properties of a molecular adsorbate (e.g. conductance, thermopower, level alignment). Since the quasi-continuum density of metallic states is depleted around the Fermi level, consequently, frontier molecular orbitals will not be described correctly. The error in the density of states that we report will affect the width of molecular resonances, and consequently, the computed molecular conductance. This artefact can be avoided only if careful convergence tests with increasing electrode volume are performed.Finally, we remark that our results are also applicable to insulating clusters, as long as the electronic states in question are delocalized. Although the limiting value of the gap scaling is finite, given by the bulk gap, the gaps will approach the bulk gap with the power N−1/3 in evGW.
5 Conclusion
We have investigated the LUMO–HOMO gap and average level spacing of sodium clusters containing 10–56 atoms in the evGW approach. Electron–electron interaction results in widening of the LUMO–HOMO gap, which scales by a factor N2/3 slower on average than the nearby electronic gaps with the number of atoms N. Consequently, when macroscopic surfaces are approximated by clusters for computational studies in surface science, the resulting electronic structure will suffer from artefacts around the Fermi energy. The promising GW method can not be taken as an out-of-the-box method replacing DFT unless careful convergence with cluster volume V is performed. The computed results for an observable O(V) are reliable if the changes of O(V) become negligible with increasing V or in some cases the thermodynamic limit V → ∞ can be reasonably extrapolated from O(V).Author contributions
Štěpán Marek – data curation, formal analysis, software, visualisation, writing – original draft. Richard Korytár – conceptualization, project administration, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the support from the Ministry of Education, Youth and Sports of the Czech Republic through the e-INFRA CZ (ID: 90140) and through the project “e-Infrastruktura CZ” (e-INFRA CZ LM2018140). Financial support for the project was provided by the Charles University through GAUK (ID: 366222) fellowship and the Czech Science foundation (project no. 22-22419S). Discussions with M. Bürkle, J. Wilhelm and F. Evers are acknowledged.Notes and references
- F. Evers, R. Korytár, S. Tewari and J. M. van Ruitenbeek, Rev. Mod. Phys., 2020, 92, 035001 CrossRef CAS.
- A. Arnold, F. Weigend and F. Evers, J. Chem. Phys., 2007, 126, 174101 CrossRef CAS PubMed.
- F. Pauly, J. K. Viljas, U. Huniar, M. Häfner, S. Wohlthat, M. Bürkle, J. C. Cuevas and G. Schön, New J. Phys., 2008, 10, 125019 CrossRef.
- J. C. Cuevas and E. Scheer, Molecular electronics: an introduction to theory and experiment, World Scientific, 2010 Search PubMed.
- J. M. Garcia-Lastra, C. Rostgaard, A. Rubio and K. S. Thygesen, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 245427 CrossRef.
- M. Strange, C. Rostgaard, H. Häkkinen and K. S. Thygesen, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115108 CrossRef.
- C. Jin, M. Strange, T. Markussen, G. C. Solomon and K. S. Thygesen, J. Chem. Phys., 2013, 139, 184307 CrossRef PubMed.
- C. Hsu, W. M. Schosser, P. Zwick, D. Dulić, M. Mayor, F. Pauly and H. S. J. van der Zant, Chem. Sci., 2022, 13, 8017–8024 RSC.
- R. Fukuzumi, M. Buerkle, Y. Li, S. Kaneko, P. Li, S. Kobayashi, S. Fujii, M. Kiguchi, H. Nakamura, K. Tsukagoshi and T. Nishino, Small, 2021, 17, 2008109 CrossRef CAS PubMed.
- T. Yelin, R. Korytár, N. Sukenik, R. Vardimon, B. Kumar, C. Nuckolls, F. Evers and O. Tal, Nat. Mater., 2016, 15, 444–449 CrossRef CAS PubMed.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- T. Kim, P. Darancet, J. R. Widawsky, M. Kotiuga, S. Y. Quek, J. B. Neaton and L. Venkataraman, Nano Lett., 2014, 14, 794–798 CrossRef CAS PubMed.
- D. A. Egger, Z.-F. Liu, J. B. Neaton and L. Kronik, Nano Lett., 2015, 15, 2448–2455 CrossRef CAS PubMed.
- Y. Kim, A. Garcia-Lekue, D. Sysoiev, T. Frederiksen, U. Groth and E. Scheer, Phys. Rev. Lett., 2012, 109, 226801 CrossRef PubMed.
- J. B. Neaton, M. S. Hybertsen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216405 CrossRef CAS PubMed.
- J. P. Perdew, W. Yang, K. Burke, Z. Yang, E. K. Gross, M. Scheffler, G. E. Scuseria, T. M. Henderson, I. Y. Zhang and A. Ruzsinszky, et al. , Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 2801–2806 CrossRef CAS PubMed.
- L. Hedin, Phys. Rev., 1965, 139, A796 CrossRef.
- I. Tamblyn, P. Darancet, S. Y. Quek, S. A. Bonev and J. B. Neaton, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 201402 CrossRef.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding and C. Hättig, et al. , J. Chem. Phys., 2020, 152, 184107 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- M. J. van Setten, F. Weigend and F. Evers, J. Chem. Theory Comput., 2013, 9, 232–246 CrossRef CAS PubMed.
- F. Kaplan, M. E. Harding, C. Seiler, F. Weigend, F. Evers and M. J. van Setten, J. Chem. Theory Comput., 2016, 12, 2528–2541 CrossRef CAS PubMed.
- K. Eichkorn, O. Treutler, H. Öhm, M. Häser and R. Ahlrichs, Chem. Phys. Lett., 1995, 240, 283–290 CrossRef CAS.
- A. Bagrets, J. Chem. Theory Comput., 2013, 9, 2801–2815 CrossRef CAS PubMed.
- C. W. J. Beenakker, Rev. Mod. Phys., 1997, 69, 731–808 CrossRef CAS.
- J. C. Slater, Phys. Rev., 1951, 81, 385–390 CrossRef CAS.
- H. Bruus and K. Flensberg, Many-body quantum theory in condensed matter physics: an introduction, Oxford University Press, Oxford, 2004 Search PubMed.
- J. Kohanoff, Electronic structure calculations for solids and molecules: theory and computational methods, Cambridge University Press, 2006 Search PubMed.
- N. W. Ashcroft and N. D. Mermin, Solid State Physics, Harcourt, 1976 Search PubMed.
- J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz Jr, Phys. Rev. Lett., 1982, 49, 1691–1694 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04082h |
| This journal is © the Owner Societies 2024 |


![[capital G, script]](https://www.rsc.org/images/entities/char_e112.gif) is reliable if the cluster volume
is reliable if the cluster volume