Flagellar motor protein-targeted search for the druggable site of Helicobacter pylori

Abstract

The deleterious impact of Helicobacter pylori (H. pylori) on human health is contingent upon its ability to create and sustain colony structure, which in turn is dictated by the effective performance of flagella – a multi-protein rotary nanodevice. Hence, to design an effective therapeutic strategy against H. pylori, we here conducted a systematic search for an effective druggable site by focusing on the structure–dynamics–energetics–stability landscape of the junction points of three 1 : 1 protein complexes (FliF_C–FliG_N, FliG_M–FliM_M, and FliY_C–FliN_C) that contribute mainly to the rotary motion of the flagella via the transformation of information along the junctions over a wide range of pH values operative in the stomach (from neutral to acidic). We applied a gamut of physiologically relevant perturbations in the form of thermal scanning and mechanical force to sample the entire quasi – and non-equilibrium conformational spaces available for the protein complexes under neutral and acidic pH conditions. Our perturbation-induced magnification of conformational distortion approach identified pH-independent protein sequence-specific evolution of precise thermally labile segments, which dictate the specific thermal unfolding mechanism of each complex and this complex-specific pH-independent structural disruption notion remains consistent under mechanical stress as well. Complementing the above observations with the relative rank-ordering of estimated equilibrium binding free energies between two protein sequences of a specific complex quantifies the extent of structure-stability modulation due to pH alteration, rationalizes the exceptional stability of H. pylori under acidic pH conditions, and identifies the pH-independent complex–sequence–segment–residue diagram for targeted drug design.

---

1 Introduction

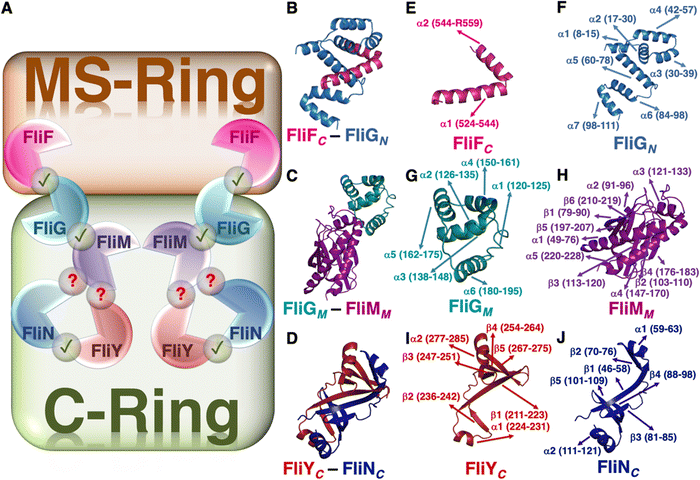
In a myriad of environments, bacterial health is maintained by the rotary nanomachines called bacterial flagella, specifically in the case of colonization in both mammalian and plant cells,^1,2 which particularly demands flagella-driven motility,³ this in turn being controlled by a chemotaxis mechanism that is believed to facilitate the microorganism's dynamical movement in response to signals. Structurally the flagellum can be viewed as a multiprotein complex and can broadly be categorized as a combination of three distinct segments – the filament, the hook, and the basal body. The basal body is essentially an array of rings formed by multimeric proteins that span the entire length between the cytoplasm and the outer membrane and are believed to perform a gamut of important functions – from flagellar biogenesis to torque generation to motor action.^4–6 The motor switch protein complex, known as the cytoplasmic ring (C-ring), is an integral unit of the basal body and it forms the reversible rotary nanodevice by combining itself with three other rings made up of protein oligomers – the L-ring (outer membrane), the P-ring (peptidoglycan layer), and the MS-ring (inner membrane).^7,8 Among these four rings, the MS- and C-rings form the rotor of the flagellar motor.

The MS-ring/C-ring rotor is mainly made up of four proteins – FliG, FliF, FliM, and FliN, and all of them are individually important for the effective formation of the motor⁵ due to their sequence-specific roles.^9–16 Even though there is a consensus on the conserved nature of the structural core of the motor, the similarity in the relative organization of the switch proteins, and the fundamental function of the motor organelle flagella, the diversity among a wide range of microbes originates due to the presence of an additional less abundant protein sequence (FliY).^17–20 One such important bacterial species is Helicobacter pylori (H. pylori).^19,21 Interestingly, the presence of an additional protein does not alter the core structure of the motor¹⁸ and all of them are necessary for the effective performance of the flagella.^19,21 Each of these five proteins can be structurally sub-divided into three parts – the N-terminal, middle, and C-terminal domains (denoted with subscripts N, M, and C, respectively). The interactions between a specific pair of proteins take place in a 1 : 1 stoichiometric ratio, e.g., FliF_C interacts with FliG_N and acts as an anchor for the C-ring;^22–24 FliG_M is extremely crucial for the interaction with FliM_M;²⁵ and FliY_C interacts with both FliM_C and FliN_C.²⁶

We focused on the junction points of the proteins of the MS and C rings of H. pylori (Fig. 1) because – (1) H. pylori is a human pathogenic gut-colonizing bacterium that causes diseases ranging from gastric and peptic ulcer to gastric cancer,^27–29 (2) the unique variability in the composition of the motor switch complex of H. pylori is due to the presence of an otherwise less abundant additional protein sequence,²⁶ and (3) the structural integrity of the junctions practically dictates the effective and smooth propagation of information through the complex multi-protein network for precise motor action.^25,26,30 Additionally, H. pylori generally exists at neutral or near neutral pH in the stomach and since the stomach can produce very low pH conditions, the change in conditions to acidic pH has the potential to shift the conformational landscape and stability pattern of the overall system and consequently the individual protein complexes and this logical intuition drove us to compare the evolution of conformational landscapes of the complexes under both pH conditions.³¹ We used a temperature range with high resolution for thermal scanning-mimic simulations³² to understand the structural, dynamical, and energetic features of the complexes, as it helps us to amplify the thermal malleability of a segment and identify the structurally labile fragments that would otherwise have been hidden or sparsely visible at physiological temperature. Going beyond the limit of thermal fluctuations, we further invested our efforts toward the investigation of the maximum potential of inter-protein interactions by applying AFM-mimic external mechanical force.³³ Importantly, to draw a conclusion on the dominance and extent of inter-protein interactions in a specific complex, we bridged the gap and hence substantiated our quasi-equilibrium (thermal) and non-equilibrium (mechanical) observations with the thermodynamic parameters in terms of binding affinities between a pair of constituting chains of a particular complex by employing enhanced sampling techniques.^34–37 Overall, we cover the entire landscape of the structure-dynamics-energetics-stability-function relationship of the three important complexes that dictate the performance network of the flagellar motor of H. pylori, in turn guiding us to arrive at a specific druggable target site for designing an effective therapeutic strategy against H. pylori, which would be effective in the entire pH range operative in the stomach.

Fig. 1 (A) Schematic representation of the relative organization of the flagellar motor proteins. The green tick signifies the availability of the structure of a specific set of interacting chains of a particular complex (the FliF_C–FliG_N complex, the FliG_M–FliM_M complex, and the FliY_C–FliN_C complex). The question mark denotes the lack of an experimentally determined structure of a specific complex either due to non-existing interaction between a couple of chains (the FliM-FliN complex) or because of the technical bottleneck arising in experiments in assigning structural information (the FliY–FliM complex). Cartoon representations of the three protein complexes with available experimentally determined structures – (B) the FliF_C–FliG_N complex, (C) the FliG_M–FliM_M complex, and (D) the FliY_C–FliN_C complex. Secondary structural information of each of the six chains of the three motor protein complexes in terms of the α-helix and β-strand – (E) the FliF_C sequence, (F) the FliG_N sequence, (G) the FliG_M sequence, (H) the FliM_M sequence, (I) the FliY_C sequence, and (J) the FliN_C complex.

2 Methods

To characterize the conformational landscapes of the molecular motor-forming complexes under various solution conditions and to further estimate the amplitude of binding affinity between a pair of chains of a specific complex, a set of conventional quasi-equilibrium, non-equilibrium, and equilibrium MD simulations with an enhanced sampling approach were performed. The initial configurations of the FliF_C–FliG_N complex, the FliG_M–FliM_M complex, and the FliY_C–FliN_C complex of H. pylori were obtained from the corresponding crystal structures deposited in the protein data bank – 5WUJ,³⁰4FQ0,²⁵ and 5XRW,²⁶ respectively. Importantly, the missing residues were added using PyMOL.³⁸ However, we did not include the FliM–FliN and the FliY–FliM complexes due to the unavailability of their crystal structures. The lack of structure for the FliM–FliN complex has somewhat been justified by an earlier research work, which reports that FliM and FliN do not interact in H. pylori as FliN positions itself at a distant location compared to FliG and FliM.²⁶ However, according to the same report, apparently there should be a structure comprising FliY and FliM as they are supposed to be interacting counterparts,²⁶ but still we could not find any structure reported in that article or otherwise. As these are protein complexes and not individual protein chain systems, we could not opt for a state-of-the-art modeling technique.³⁹

2.1 Conventional quasi-equilibrium MD simulations

Version 5.1.4 of the GROMACS simulation package⁴⁰ was employed for carrying out all the simulations. Protein sequences were modeled using the CHARMM27 atomistic parameter set.⁴¹ Solvent was modeled explicitly using the TIP3P water model.⁴² Each of the three complexes was utilized for a set of ten independent simulations to accommodate all possible combinations of five different temperatures (300 K, 350 K, 400 K, 450 K, and 500 K) and two different pH conditions – one was neutral pH at which the titrable side chains were kept protonated/deprotonated using the default procedure of the software and the other was acidic pH at which all the titrable groups were protonated. We opted for the thermal scanning technique as the enhanced sampling approaches like Replica Exchange Molecular Dynamics (REMD) simulations⁴³ were beyond the scope of usage due to the large size of the complexes to get any form of convergence on simulated observables in a realistic time scale and aggravated technical difficulties associated with constant pH REMD⁴⁴ (acidic pH conditions) due to the approximation and limitation in convergence in electrostatic interactions. So, we effectively sampled states beyond the thermal fluctuation limit without the exchange considered in REMD, i.e., without the Boltzmann weighting. To mimic the acidic pH conditions, we completely protonated the side chains of all the protein sequences considering the extremely low limit of pH as the pH in the human stomach can reach as low as 1.5–2.0⁴⁵ and according to the PROPKA web server⁴⁶ estimation of the initial configurations of the three complexes from their respective PDB structures, the lowest pK_a values appear to be 2.48 for the FliF_C–FliG_N complex, 2.1 for the FliG_M–FliM_M complex, and 2.45 for the FliY_C–FliN_C complex. This justifies the complete protonation of the titrable side chains of the protein sequences of the three complexes. Moreover, defining specific pK_a values based on the native state will not justify the pK_a values in the partially/completely unfolded and exposed states of the proteins and any conformational ensemble in between, which are in dynamic equilibrium and would potentially be sampled by the protein sequences in the near-equilibrium ensemble, as the local environment of any side chain would be changing continuously and this would dynamically modify the pK_a values of the titrable groups as well.

Execution of the above procedure for all three systems gave us a total of thirty systems. Consequently, each one of the thirty systems was put into a rectangular box maintaining a minimum distance of 10 Å between any heavy atom of the system and any edge of the box, which eventually gave us three different box dimensions for the three complexes under investigation – 54.8 × 61.0 × 71.2 ų for the FliF_C–FliG_N complex system, 71.0 × 57.0 × 84.3 ų for the FliG_M–FliM_M complex system, and 66.0 × 59.1 × 67.9 ų for the FliY_C–FliN_C complex system. Then, each system was solvated using the TIP3P water model and electroneutralized using the genion module of GROMACS, where water molecules were replaced randomly by Na⁺ and Cl⁻ ions such that the salt concentration was maintained at 100 mM. Each of the systems was then energy minimized to reduce any existing steric clashes utilizing the steepest descent algorithm. Furthermore, for every system, two sets of equilibrations were performed consecutively where the center of mass of the system was kept fixed at the center of the box by applying a force constant of 1000 kJ mol⁻¹ nm⁻²: 500 ps of NVT equilibration at a constant temperature (mentioned above) employing the modified Berendsen thermostat⁴⁷ and 500 ps of NPT equilibration at a constant temperature (stated above) and at a constant pressure of 1 bar using the modified Berendsen thermostat and Parrinello–Rahman barostat.⁴⁸ Lastly, a production simulation run for 1 μs was performed for each system removing all position restraints at a specific temperature (discussed above) and at 1 bar pressure. Following are the specifications that were implemented during the production run: an integration time step of 2 fs, 20 ps resolution for snapshot storage, 10 step frequency for the nonbonded interactions list update, the LINCS algorithm⁴⁹ having a 30° warning angle to restrain bonds with hydrogen atoms, a relaxation constant of 0.1 ps for temperature coupling, a relaxation constant of 0.1 ps and an isothermal compressibility of 4.5 × 10⁻⁵ bar⁻¹ for pressure coupling, periodic boundary conditions (PBC) with the standard minimum image convention in all three directions, the Particle Mesh Ewald (PME) method⁵⁰ to treat long-range electrostatic interactions with a 10 Å real-space cut-off, and a 10 Å cut-off to consider Lennard-Jones interactions with a Fourier spacing of 1.6 Å. The above protocol produces a total of 30 μs of quasi-equilibrium trajectories of the three systems under ten different solution conditions.

2.2 Steered MD simulations

The crystal structures mentioned in sub-section 2.1 were utilized for steered MD (SMD) simulations³³ of the three complexes. For each complex, a set of two SMD simulations were performed – one under neutral pH and the other under acidic pH conditions. The specific protonation states of the titrable side chains, depending on the target pH, were assigned following the same protocol as described in sub-section 2.1. Each of the complexes was then put in a rectangular box, where the box dimensions were – 196 × 62 × 72 ų for the FliF_C–FliG_N complex system, 72 × 58 × 206 ų for the FliG_M–FliM_M complex system, and 428 × 44 × 46 ų for the FliY_C–FliN_C complex system. Processes of solvation, electro-neutralization, achieving 100 mM salt concentration, and energy minimization to avoid any steric hindrances were mimicked by following the procedures detailed in sub-section 2.1. The above course of action resulted in a set of six systems, i.e., two pH conditions for each of the three complexes. Each of the six systems was then subjected to 500 ps NPT equilibration at 300 K temperature and 1 bar pressure using the Nose–Hoover thermostat^51,52 and Parrinello–Rahman barostat, where the complex, water, and two types of ions were coupled separately. For every system, during NPT equilibration, the initial coordinate of the complex was placed at one of the edges of the box by applying a harmonic force constant of 1000 kJ mol⁻¹ nm⁻². For performing the SMD simulations, for each of the complex systems, the two tethers for pulling simulations were placed on the centers of masses of two chains that constitute a complex. For the FliF_C–FliG_N complex system, the center of mass of the FliG_N chain was kept fixed and that of the FliF_C chain was pulled along the x-axis with a pulling rate of 0.1 Å ps⁻¹ over a time of 900 ps using a harmonic spring having a spring constant of 1000 kJ mol⁻¹ nm⁻². A similar approach was applied for the FliG_M–FliM_M complex system, where the center of mass of the FliM_M chain was kept fixed and the same of the FliG_M chain was pulled along the z-axis. Finally, for the FliY_C–FliN_C complex system, the position of the center of mass of the FliY_C chain was kept fixed and the same of the FliN_C chain was pulled apart along the x-axis. To minimize the uncertainty associated with the non-equilibrium pulling simulations, for each of the six systems, a set of three independent trajectories were generated. The initial and final distances between two chains of a complex were 6.42 ± 0.06 and 87.47 ± 0.59 Å for the FliF_C–FliG_N complex, 30.98 ± 0.78 and 100.43 ± 0.35 Å for the FliG_M–FliM_M complex, and 7.60 ± 0.08 and 91.26 ± 0.83 Å for the FliY_C–FliN_C complex. The rest of the parameters were kept the same as described in sub-section 2.1.

2.3 Umbrella sampling simulations

To generate the potential of mean force (PMF) profiles and subsequently to estimate the extent of binding free energy operative between two constituting chains of a given complex system under two different solution (pH) conditions, we used an enhanced sampling methodology named umbrella sampling simulations,³⁴ where the snapshots obtained from the SMD trajectories, as discussed in sub-section 2.2, were utilized as initial configurations. For each of the six systems, a set of configurations were chosen by using a resolution criterion of 2 Å in the change in the distance between the two separating chains of a complex. We chose the first configuration and all the progressive conformations using the above-mentioned criterion, which eventually gave us a set of 31 umbrella windows for each of the three complexes under two different pH conditions. For each of the six systems, all the umbrella windows were simulated for 100 ns each, resulting in a total of 3.1 μs of trajectories for a specific system and hence, 18.6 μs of trajectories in total. For each of the umbrella windows, a harmonic potential was used having a spring constant of 1000 kJ mol⁻¹ nm⁻². The rest of the parameters for the umbrella simulations were kept the same as detailed in sub-section 2.2. To convert the biased probabilities obtained from the umbrella sampling simulations into Boltzmann distributions, the weighted histogram analysis method (WHAM)^35,37 was employed, which eventually generated the one-dimensional PMF profile as a function of the distance between the centers of masses of two separating chains of a complex. The free energy of binding was estimated by subtracting the lowest value of the profile from the asymptotic limit of the highest value of the profile. The error bar associated with the free energy estimation protocol was obtained by using a standard bootstrap method.³⁶ The magnitudes of the error bars were much lower compared to the calculated binding free energy values, which substantiated the robustness of the estimated equilibrium properties.

3 Results

3.1 Global as well as chain-wise structural and energetic features of the complexes display both predictable and counterintuitive properties

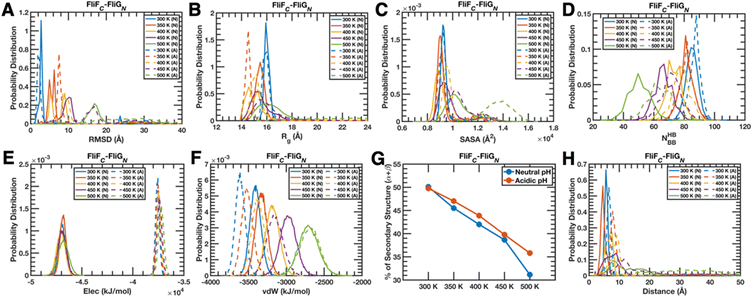
All three complexes and their constituting chains, in general, show that a rise in temperature at any pH and a drop in pH at any temperature individually increase the structural deviation (calculated by estimating the backbone heavy atom-based root mean square deviation (RMSD) with reference to the initial configuration used for simulation) of the whole complex (panel A of Fig. 2 and Fig. S1, S2, ESI†) as well as of the individual chain (panels A and B of Fig. S3–S5, ESI†) and the combined impact of increased temperature/decreased pH is cumulatively structurally destructive. A unique deviation is observed for the FliF_C chain (Fig. S3A, ESI†) only at a lower pH, as it produces less deformed conformations compared to that of the neutral pH at any specific temperature. The similar characteristics of the complexes (panel B of Fig. 2 and Fig. S1, S2, ESI†) and the chains (panels C and D Fig. S3–S5, ESI†) appear even in the compactness analysis (derived by computing the backbone C_α-based radius of gyration (R_g)), where the overall compactness, whether temperature-dependent or pH-dependent, initially increases with the rise in temperature or lowering of pH at lower temperature zones, but gradually decreases at higher temperatures, i.e., there is a sweet spot of ensemble composition. The FliF_C chain mainly follows the above-mentioned trends, only with a slight exception that the compactness remains comparable at lower temperatures and at the neutral pH (Fig. S3C, ESI†). Hence, the FliF_C chain's identity as a trend-breaker sustains. Since the overall solvent exposure of a structure (obtained by calculating the solvent accessible surface area (SASA) of the whole complex/protein) is just the contrasting property of its compactness, the relative trend in the change in exposure for the complexes (panel C of Fig. 2 and Fig. S1, S2, ESI†) as well as for the individual chains (panels E and F of Fig. S3–S5, ESI†) follows the same trend as observed previously, only in an anticorrelated fashion, i.e., an increase in compactness is associated with a decrease in exposure and vice versa (only with a marginal subtle inconsistency for the chains of the FliY_C–FliN_C complex (Fig. S5E and F, ESI†)).

Fig. 2 Evolution of structural and energetic features of the FliF_C–FliG_N complex under thermal scanning and under two different pH conditions. Normalized probability distributions of the intra-complex characteristics – (A) backbone RMSD, (B) backbone C_α-based R_g, (C) global SASA, (D) backbone hydrogen bonds, (E) electrostatic interactions, and (F) van der Waal's forces. (G) Temperature-dependence of the percentage of secondary structural content in terms of the α-helix and β-sheet at two different pH values of the solution. (H) Normalized probability distributions of the inter-chain distance between the centers of masses of two protein chains. Except for panel (G), in all other panels, the solid and dashed lines represent neutral (N) and acidic (A) pH conditions, respectively, and the five different temperatures are denoted by the following color scheme: 300 K (blue), 350 K (red), 400 K (yellow), 450 K (purple), and 500 K (green).

Moving on from the global structural to the energetic features, the impact of higher temperature and lower pH becomes extremely consistent irrespective of the species in terms of intra-chain/complex cohesive forces exerted by backbone hydrogen bonds (N^HB_BB, panel D of Fig. 2 and Fig. S1, S2; panels G and H of Fig. S3–S5, ESI†). Constant-pH and rising temperature or constant-temperature and increasing pH lowers the number of backbone hydrogen bonds, only with a subtle contradicting trend observed for the chains of the FliY_C–FliN_C complex (Fig. S5G and H, ESI†) at acidic pH in a high-temperature range. However, the impact of acidic pH on creating a stronger network remains sustained for both chains at a specific temperature. Interestingly, intra-complex electrostatic interactions (panel E of Fig. 2 and Fig. S1, S2, ESI†) diminish as pH decreases, and the impact of temperature switches from stabilizing to destabilizing as the pH changes from neutral to acidic. The individual chains (panels I and J of Fig. S3–S5, ESI†) experience a more consistent impact of temperature and pH, as lowering either of them destabilizes the interactions. The above observations are less prominent though for the FliF_C–FliG_N complex (Fig. 2E) as well as their constituting chains (Fig. S3I and J, ESI†). Similarly, a rise in temperature and an increment in pH generally reduce the van der Waal's stabilization both for the intra-complex (panel F Fig. 2 and Fig. S1, S2, ESI†) and intra-chain scenario (panels K and L of Fig. S3–S5, ESI†); however, a minute inconsistency appears for the FliG_M–FliM_M complex (Fig. S1F, ESI†) as well as for its constituting chains (Fig. S4K and L, ESI†) at acidic pH and specifically in the lower temperature range.

The intrinsic secondary structural elements of the overall system as well as the individual chains, which were estimated by calculating the probability of specific ϕ–φ dihedral angle combinations evolved during the quasi-equilibrium simulations, that would fall in the α-helix and β-sheet regions according to the Ramachandran plot display a wide range of variations – (1) for the FliF_C–FliG_N complex (Fig. 2G) and its chains (Fig. S3M and N, ESI†), the secondary structural content decreases with increasing temperature, but remains oblivious to the change in pH, though with a tiny exception for the FliG_N chain (Fig. S3N, ESI†) at the highest temperature; (2) for the FliG_M–FliM_M complex (Fig. S1G, ESI†) and its FliM_M chain (Fig. S4M, ESI†), the secondary structural content shows a somewhat consistent decrement at neutral pH with increasing temperature, but a switching point of the trend appears at the acidic pH (prominently for the FliM_M chain (Fig. S4M, ESI†)), and generally, acidic pH increases the overall secondary structural content (observed for the FliG_M chain (Fig. S4N, ESI†) as well). On the contrary, the FliG_M chain (Fig. S4N, ESI†) consistently displays a rise in the secondary structural content with an increment in temperature under both the pH conditions; (3) the FliY_C–FliN_C complex (Fig. S2G, ESI†) and its FliN_C chain (Fig. S5M, ESI†) counterintuitively show an increment in secondary structural content with the rise in temperature and lowering of pH and the FliY_C chain (Fig. S5N, ESI†) behaves in a complete reverse fashion.

Further transitioning from the intra-chain to inter-chain parameters, a few trends evolve from the quasi-equilibrium trajectories of all the three complexes – (1) increasing temperature and decreasing pH generally lead to more separation between two chains (measured by calculating the distance between the centers of masses of two interacting chains) of the three complexes (panel H of Fig. 2 and Fig. S1, S2, ESI†), (2) the electrostatic forces operative between a couple of chains always decrease at the acidic pH compared to the neutral one (panel O of Fig. S3–S5, ESI†), but the trend is not so consistent in terms of the impact of temperature, and (3) the lowering of pH always reduces the magnitude of the inter-chain dispersion interactions (panel P of Fig. S3–S5, ESI†) as well, but as observed previously, it displays a pretty inconsistent trend as a function of temperature.

3.2 Segment-specific structural variability dictates the extent of heterogeneity of the conformational ensembles

As the usage of different popularly used structural reaction coordinates indicates the most possible state of a complex under any given condition with different levels of probability (Fig. 2 and Fig. S1, S2, ESI†), to get rid of the confusion, we chose two intrinsic reaction coordinates of a system – the first two principal components (PCs)⁵³ – to identify the most representative state under a specific condition, as this technique has the unique ability to reduce the dimensionality of an otherwise complex system, while encapsulating the majority of dynamical fluctuations.⁵⁴ Interestingly, the PC-based joint probability distributions substantiate the relative trend of modulation of the conformational ensembles as observed previously for all three complexes. In general, with the rise in temperature, the landscape becomes more diffused leading to increased conformational polymorphism and this observation is robust and independent of the pH of the solution. Additionally, lowering of pH aggravates the diffusive nature of the landscape at any specific temperature producing more heterogeneous configurations. Fig. 3 shows the most representative configurations for each of the complexes under all ten different solution conditions, i.e., by considering only the maximally sampled state in each of the ten situations (shown in the figure) for a complex (two pH conditions and five different temperatures). Comparing the most probable states of a given complex under variable temperature and pH conditions enables us to deconvolute the sequence of events (Fig. S6, ESI†) that would eventually lead to the structural distortion of a complex under thermal and pH-driven environmental perturbations, both individually and as a combination. Interestingly, for any given complex, the unfolding mechanism is consistent under thermal perturbation at any given pH and under acidic pH perturbation at any specific temperature; only the separation, the drastic loss of packing of the chains, and the concomitant loss of secondary structure happen when two perturbations individually reach their maximum limit as the impact is additive. So, the structural transition for a given complex under any specific perturbation, achieved either via thermal or pH-dependent perturbation or by a combination of the two, remains consistent. Following are the complex-specific generic sequence of events that evolve during the unfolding process regardless of the perturbation(s) being applied:

Fig. 3 Comparison of conformational ensembles evolved due to the variability in the temperature and pH of the solution, where the clustering analysis was performed based on the evolution of structures of the three complexes in the phase space of the two most dominant dynamical modes (PC1/PC2) – (top panels) FliF_C–FliG_N complex, (middle panels) FliF_C–FliG_N complex, (bottom panels) FliG_M–FliM_M complex, (left panels) neutral pH, and (right panels) acidic pH. A representative conformation of the most populated state of each of the complexes at any given temperature-pH combination is shown as a cartoon with specific color pairing – FliF_C in sky blue and FliG_N in warm pink (panels A and B); FliG_M in forest green and FliM_M in purple (panels C and D); and FliY_C in fiber brick red and FliN_C in dense blue (panels E and F). The color-coding scheme of the protein sequences was kept the same throughout the manuscript. The neutral pH condition is denoted by (N) in the left panels and the acidic pH condition is denoted by (A) in the right panels. In all the panels, the variable temperature range is depicted by using five different colors – 300 K (blue), 350 K (red), 400 K (yellow), 450 K (purple), and 500 K (green).

For the FliF_C–FliG_N complex (Fig. 3A, B and Fig. S6A and B, ESI†), we arrive at the following general mechanism: the initiation of packing alteration leading to swollen ensembles is caused by the rotation of the C-terminus of the FliG_N chain (α6-α7); this unpacking event gradually unpacks the N-terminus of the FliG_N chain (α1); a combination of the above two events leads to an unfolding of α1 and α7 of the FliG_N chain; consequently, the middle segment of the FliG_N chain starts unpacking while keeping the FliF_C chain almost intact; aggravated unpacking of the mid-part of the FliG_N chain lowers the inter-chain interactions, which allows the FliF_C chain to distance itself slightly from the FliG_N chain; and finally, the chains separate causing substantial unfolding of each of the chains.

For the FliG_M–FliM_M complex (Fig. 3C, D and Fig. S6C and D, ESI†), in general, the variation initially originates due to the change in the orientation of the first half of α1 of the FliM_M chain; consequently, the change in the orientation of α1 propagates to the entire helix, which breaks it into two parts from the middle with a concomitant change in the packing of α2 of the FliM_M chain; and finally, the complete loss of β2 and β4 and a partial loss of β3 of the FliM_M chain materialize. The afore-mentioned process is non-monotonous as in a few instances few of the secondary structural segments gain percentage, even though partially by a small margin. For the FliG_M chain, the diversity originates mainly due to the fluctuating nature of α1.

In the case of the FliY_C–FliN_C complex (Fig. 3E and F and Fig. S6E and F, ESI†), the first point of differentiation originates due to the out-of-register movement of the C-terminal segment of the α2 of the FliN_C chain. The aggravated lack of structural packing between the chains evolves as the mid-part of β1 and N-terminal of β4 of the FliN_C chain lose structural integrity. The FliY_C chain does not contribute to the initial phase of the perturbations and only displays nominal fluctuations. Consequently, the FliN_C chain shows a drastic opening of the N-terminal end of the structure mainly composed of α1, β1, and β2. At this point, the FliY_C chain also joins the unfolding phenomenon by showing the complete unfolding of α2 with a concomitant shift of the segment containing β4 and β5 leading to a lack of packing of the conformation, exhibiting aggravated movement of the β1 away from the rest of the protein and indicating a tendency to higher structural shifts for the rest of the secondary structural elements. Finally, both the FliY_C and FliN_C chains show barely any similarity as further unfolding takes place with residual secondary structural elements.

To further dig deeper into the variability in the evolution of conformational ensembles, we identified the residues belonging to a couple of protein sequences that contribute to the interfacial interactions of a specific complex using PyMOL³⁸ to assess the impact of thermal and pH-driven perturbations (Fig. S7, ESI†). The entire analysis focuses on two major identifiers – the number of residues being involved from each of the protein sequences and the identities of the secondary structural elements that either contribute to or refrain from participating in forming the interface.

In the case of the FliF_C–FliG_N complex under neutral pH conditions (Fig. S7A, ESI†), the contributions from the two chains in terms of the number of residues (FliF_C : FliG_N) change as the temperature increases with the following trend: 28 : 40 (300 K) → 29 : 35 (350 K) → 27 : 40 (400 K) → 24 : 30 (450 K) → 20 : 25 (500 K). The FliF_C chain shows more consistency in keeping the interface intact even at elevated temperatures as the contributions come from both α1 and α2 (α2 is the major contributor) and the impact of temperature is more prominent on the interface residues of the FliG_N chain. On the contrary, α7 of the FliG_N chain never participates in the interface formation (even at 300 K) and as the temperature rises additional secondary structural segments with variable identities pull themselves off from the interface – α1 and α7 at 350 K; α6 at 400 K; α1, α6 and α7 at 450 K; and α1, α5, α6 and α7 at 500 K. The situation is similar under acidic pH conditions (Fig. S7B, ESI†) as well (as expected from the generic unfolding mechanism discussed previously), only with an aggravated scenario. This claim is supplemented by the higher degree of loss of interfacial contacts evidenced by a lower number of residues being involved from each of the chains under acidic pH conditions (FliF_C : FliG_N – 26 : 33 (300 K) → 27 : 35 (350 K) → 23 : 30 (400 K) → 13 : 13 (450 K) → 0 : 0 (500 K)) compared to the neutral pH at a specific temperature. As observed previously for the neutral pH scenario, the FliF_C chain participates with both of its α-helices (α2 being the major one) in all four cases, where the interface exists with variable extents (except at 500 K). The FliG_N chain shows the following trend in terms of (non)contributing secondary structural elements – non-participating α1 and α7 (300 K); without engaging α1, α6, and α7 (350 K); not involving α1, α4, and α6 (400 K); and contributing via α2 and α5 (450 K) – and the element identities are quite similar to what was observed previously under neutral pH conditions.

Mimicking the same technique for the FliG_M–FliM_M complex displays the following pattern for the neutral pH condition (Fig. S7C, ESI†) in terms of the number of residues and the secondary structural elements engaging in the interface formation – 23 (α3, α5, α6) : 25 (α1, α3, α4) at 300 K, 21 (α3, α5, α6) : 20 (α1, α3, α4) at 350 K, 17(α1, α2, α6) : 21 (α1, β1, α4, α5) at 400 K, 9 (α1, α6) : 19 (α1, β1, β5) at 450 K, and 12 (α2, α5) : 15 (α1) at 500 K – where the number ratio represents the number of participating residues from the individual chains (FliG_M : FliM_M) and the secondary structural identities are mentioned within the parentheses. It appears that with the rise in temperature, the number of interacting residues decreases due to the increase in the inter-protein distance and the identities of the secondary structural fragments change due to the concomitant structural distortions. The impact of thermal perturbation is even more drastic under acidic pH conditions (Fig. S7D, ESI†) as both fewer residues and hence fewer secondary structural elements participate at any given temperature and the complex dissociates completely from each other from 400 K onwards, which is exemplified by the following quantitative feature – 25 (α3, α4, α5) : 19 (α4, β4) at 300 K, 8 (α5) : 12 (β2, β3) at 350 K, and no interaction beyond it.

Since the FliY_C–FliN_C complex shows the maximum extent of entanglement between two constituting chains, we preferred to explain the interfacial interactions by mentioning the non-participating secondary structural motifs, when necessary, as those would be fewer in numbers. The situation for the complex (FliY_C : FliN_C) at the neutral pH (Fig. S7E, ESI†) as a function of rising temperature evolves as follows: at 300 K and 350 K, all the secondary structural elements of both the chains participate in the interface formation with number ratios remaining almost constant – 59 : 58 and 57 : 58 respectively; at 400 K, β3 strands of both chains do not belong to the interface anymore displaying a minute reduction of the interacting residue number ratio (54 : 56); at 450 K, the number of residues is reduced by a substantial amount (47 : 48) with a change in the non-participating secondary structural segment identities (α2 for FliY_C and β2 for FliN_C); and the situation at 500 K further reduces the number from the previous case (35 : 34), but it reverts to the identity of the non-participating secondary structural elements as observed at 350 K (β3 strands of both chains) with two additional non-engaging secondary structural motifs of the FliN_C chain (α1 and β5). The above observation proves that the complex can sustain higher perturbations and keep a formidable number of interfacial interactions and the ability is slightly more prominent for the FliY_C chain. Under acidic pH conditions (Fig. S7F, ESI†), interestingly, the events appear as almost similar in terms of identities of participating secondary structural elements only with a higher degree of loss of interfacial interactions at any given temperature – 59 (all) : 56 (except β3) at 300 K, 55 (all) : 55 (except β3) at 350 K, 53 (all) : 48 (except β3) at 400 K, 37 (except α2) : 36 (all) at 450 K, and 21 (α1, β1, β2, β3) : 18 (α1 and β1) at 500 K. The change in identities of the participating secondary structural elements can be attributed to the large extent of structural reorganization with progressively applied thermal perturbations.

3.3 pH-independent protein-specific common distinct labile residues and pH-dependent modulation of long-range crosstalk networks dictate the structural integrity of a complex

To dig deeper into the protein structure, we stretched our information spectrum from the segment-specific (Fig. 3) to the residue-specific domain. Fig. 4 and Fig. S8–S10 (ESI†) respectively show the residue-wise mean fluctuation profiles, obtained by measuring the time-averaged root mean square fluctuations (RMSF) as a function of residue index, and the intra-chain dynamical cross-correlation map (DCCM),⁵⁵ obtained from the covariance matrix of the C_α-based fluctuations.

Fig. 4 Residue-specific thermal fluctuation profiles evolved under thermal and pH-induced perturbations of the six protein chains. Comparison of the RMSF profiles at a specific pH leads to the identification of thermally fluctuating segments (discussed in the text) that eventually initiate the unfolding of individual chains and consequent separation of the complex-forming chains. In all the panels representing RMSF profiles, the solid lines represent neutral (N) pH conditions and dashed lines represent acidic (A) pH conditions. Moreover, in the case of the RMSF profiles, the five different temperatures used in the study were indicated by the following color scheme – 300 K (blue), 350 K (red), 400 K (yellow), 450 K (purple), and 500 K (green) – irrespective of the pH of the solution. The corresponding structural deviations were shown by superimposing the five most probable states obtained at a specific pH and at five different temperatures for all the three complexes and hence six protein sequences as identified in Fig. 3; the superimposition was performed only in a chain-specific manner (shown as cartoon), rather than in a complex-specific manner, and to have parity with the RMSF profiles in terms of demonstration, the chain colors were chosen according to the temperature from which the coordinates were sampled – (A) and (B) FliF_C chain, (C) and (D) FliG_N chain, (E) and (F) FliM_M chain, (G) and (H) FliG_M chain, (I) and (J) FliN_C chain, and (K) and (L) FliY_C chain.

The comparison of the RMSF profiles of the FliF_C chain of the FliF_C–FliG_N complex (Fig. 4A) displays heterogeneous increments of residue-wise thermal fluctuations under two different pH conditions. Estimation of the difference between the profiles under a given pH condition leads to the identification of dominant fluctuating residues under two different pH conditions (Fig. 4B). Interestingly, the identities of the dynamics-dictating residues and/or segments overlap between neutral (I537–K542 and P545–E547) and acidic pH (K536–K542 and P545–A549) conditions and suggest that residues close to either side of the loop connecting α1-α2 dominate the dynamical evolution pattern of the FliF_C chain. The corresponding DCCM analysis (Fig. S8A–J, ESI†) of the FliF_C chain attributes the impact of higher temperatures and lower pH values to the gradual evolution of small, correlated domains throughout the chain compared to the helical-domain-specific correlations and further appearance of strong anti-correlated movements between the two helices, which eventually leads to structural opening. A similar approach applied for the FliG_N chain displays the comparison of the RMSF profiles (Fig. 4C) and identifies the dynamically important residues (Fig. 4D). Under neutral pH conditions, two segments emerge as dynamically dominant regions – one with the N-terminal part of α4 (L41–E48) and the other with the entire α5 and the loop connecting α5 and α6 (Q62–N82). Acidic pH does not alter the number of dominating segments but changes the locations, though with some overlap – one with the loop connecting α4 and α5 and the N-terminal part of α5 (N57–V67) and the other with the C-terminal part of α5 and the loop connecting α5 and α6 (I74–G84). The structural unfolding of the FliG_N chain appears when the DCCM pattern (Fig. S8K–T, ESI†) changes from the appearance of numerous numbers of small correlated and anti-correlated domains to the genesis of marginal longer ones, specifically when the entire segment α1–α4 is highly correlated with itself and extremely anti-correlated with the rest of the chain – mainly from the mid of α4 to the mid of α6.

Interestingly, the comparison of the RMSF profiles of the FliM_M chain of the FliG_M–FliM_M complex (Fig. 4E) and the corresponding identification of the dynamical protagonists (Fig. 4F) show that the number of dominating segments get reduced on going from the neutral (5 segments) to the acidic pH (2 segments). At the neutral pH, the five segments that contribute mainly to the dynamical evolution of the FliM_M conformations are the entire β1 strand (E80–M89), β2 and part of β3 (P101–G116), the loop connecting α3 and α4 and the N-terminal part of α4 (K131–D155), the complete β4 strand (F176–S184), and the C-terminal part of β5 and the N-terminal part of β6 and the loop connecting them (E204–G212). On going from the neutral to the acidic pH, the important segments get focused down to two segments – one with β1, α2, β2, and part of β3 (S77–G116) and the other with the C-terminal part of the α4 and the entire β4 strand (K166–S185). Although it seems like there is a drastic reduction in the number of dominating segments on going from the neutral to the acidic pH, practically this originates due to the merger of segments one and two and the extension of segment four at acidic pH with respect to the neutral one, proving the fact that there is a huge overlap between dominating residues under two different pH conditions. The DCCM profiles (Fig. S9A–J, ESI†) overall state that the unfolding of the FliM_M chain takes place when the segment containing α1–α3 and β1–β3 is extremely correlated and shows strong dynamical anti-correlation with the rest of the chain. For the FliG_M chain (Fig. 4G and H) however things are much simpler as two common dominating segments appear under two different pH conditions, only with slight variations in terms of length – one stretching from the C-terminal part of α2 to the N-terminal half of α3 (F133–I142) and the other constituting the entire α5 (F161–R172); only at acidic pH, an additional region appears, which stretches from the C-terminal part of α3 to the N-terminal half of α4 (L146–A154), and the previously observed two segments are shortened (I135–T141 and I169–L176). Here, the structural unfolding happens when the region stretching from α1–α3 is highly dynamically correlated with itself and shows complete anti-correlation with the regions stretching from α4–α7 (Fig. S9K–T, ESI†).

In the case of the FliY_C–FliN_C complex, the corresponding comparisons of the RMSF profiles and labile dynamically dominating segments are shown in Fig. 4I and J for the FliN_C chain and Fig. 4K and L for the FliY_C chain, respectively. For the FliN_C chain, the major contributing segments overlap nicely even if the solution condition changes from neutral to acidic pH. Overall, three major segments appear as main protagonists – a segment stretching the entire length of the β2 strand and the loop connecting α1 and β2 (E66–I71/F65–P76), a sequence containing the β3 strand and the loop connecting β3 and β4 (V85-G91/D82-I90), and a final segment that stretches from the loop connecting the β4 and β5 strands and the N-terminal segment of the β5 strand (F98-R105/V97–A103) – obviously with nominal fluctuations in terms of their lengths under different solution conditions. Similarly, for the FliY_C chain, the contributing segments toward partial unfolding mainly overlap under different pH conditions. Although it seems that lowering the pH increases the number of thermally malleable segments from three (D232–N244, I249–E260, and D265–Q271 at neutral pH) to four (M231–V236, L242-P246, E248–A257, and V262–N267 at acidic pH), practically it is just a breakage of the continuity of the first labile segment observed at neutral pH into two fluctuating fragments at acidic pH. Broadly, the malleable parts can be classified in terms of their content of secondary structural elements as below: the loop connecting α1 and β2; the β2 strand; the loop joining β2 and β3; the entire segment containing β3 and β4; and finally, the loop connecting β4 and β5 and the N-terminal end of β5. In terms of dynamical communication, the DCCM analysis of the FliN_C chain (Fig. S10A–J, ESI†) shows that the unfolding initiates due to a strongly correlated motion within a continuous stretch of residues consisting of β3, β4, β5, and α1. However, the extensive unfolding appears when the N-terminal segment of the chain containing β1 moves in an anti-correlated fashion with respect to the rest of the chain. The extent of anti-correlation could be higher with the mid-part of the chain containing α1, β2, β3, and β4 or the C-terminal end of the chain consisting of β5 and α2. On the other hand, for the FliY_C chain, a similar cross-correlation analysis (Fig. S10K–T, ESI†) shows that the initiation of the unfolding of the chain develops due to a strongly correlated dynamical segment with β2, β3, and β4 strands. In this case, the extensive unfolding can appear only when there is a strong dynamically correlated domain containing α1, which is highly anti-correlated with the rest of the chain – specifically β2 and a segment containing β4, β5, and α2.

3.4 pH-independent, but complex identity-dependent mechanical unbinding mechanism: sequential unzipping vs. simultaneous separation

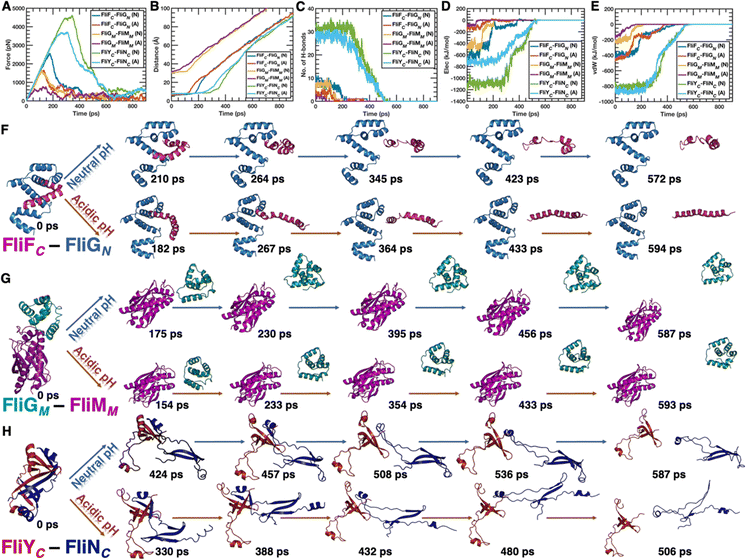
To further enable the complexes to display their ability to withstand different kinds of external perturbations, the mechanical force was chosen as the disruption creator, where one chain of a complex was pulled apart and the other chain was kept fixed. Since the pulling trajectories were non-equilibrium, to achieve the robustness of the simulated observables, a set of three independent trajectories were generated for each system at a given pH and at 300 K (Fig. 5). A few consistent features appear in the mechanical force profiles (Fig. 5A) of all three complexes – (1) for a given complex, the magnitude of the maximum force required to rupture the operative inter-chain cohesive forces always decreases under acidic pH conditions and (2) in a particular complex, the time required to achieve the maximum force also decreases under acidic pH solutions. Additionally, the magnitude of the maximum force value decreases from FliY_C–FliN_C to FliF_C–FliG_N to FliG_M–FliM_M and this observation is consistent throughout the varying pH conditions and could be an indicator not only of the relative order of binding affinity between the complexes but also of the direct impact of pH of the solution. So, the withstanding nature of a complex does not necessarily correlate with the lengths of the constituting chains (FliG_M–FliM_M > FliY_C–FliN_C > FliF_C–FliG_N). Interestingly, the relative order of mechanical stability in terms of withstanding external force between the complexes along with the evident impact of varying pH conditions sustains its signature in the separation distance profiles (Fig. 5B) as well. At any given pH, the separation starts at a longer time scale for the FliY_C–FliN_C complex and the time scale gradually decreases for the FliF_C–FliG_N complex and even more for the FliG_M–FliM_M complex. Moreover, the lowering of the pH of the solution decreases the time required for the initiation of the separation mechanism.

Fig. 5 Mechanical fingerprinting of the three complexes under neutral (N) and acidic (A) pH conditions averaged over three independent non-equilibrium trajectories. (A) Time evolution of the response force curves resulting from the application of external mechanical force to separate the complex-forming chains. (B) The change in the distance between the centers of masses of the two protein sequences that form a complex as a function of time. (C) The gradual loss of the inter-chain hydrogen bond with increasing simulation time. (D) The progressive loss of the electrostatic interactions operative between two chains of a specific complex as a function of time. (E) Time evolution of the van der Waals forces operative between a couple of interacting protein chains that form a complex. The mechanism of the mechanical separation of the three complexes under two contrasting pH conditions depicted via the configurations obtained from one of the three independent pulling simulations for each complex (shown as cartoons) at different time points – (F) the FliF_C–FliG_N complex, (G) the FliG_M–FliM_M complex, and (H) the FliY_C–FliN_C complex.

Similar to the previously observed trends, acidic pH generally breaks the inter-chain hydrogen bond network (Fig. 5C) at a faster rate compared to neutral pH for any given complex. Intriguingly, the relative rank ordering of the absolute values of the inter-chain hydrogen bonds (FliY_C–FliN_C > FliF_C–FliG_N > FliG_M–FliM_M) rationalizes the previously observed rank ordering of both the rupture force values and the separation initiation time scales, as it is directly correlated to each of those parameters. The extent of operative inter-chain non-bonding interactions, whether electrostatic (Fig. 5D) or van der Waals (Fig. 5E), follows the same pattern as observed previously for all the three reaction coordinates (force, distance, and hydrogen bond), i.e., FliY_C–FliN_C > FliF_C–FliG_N > FliG_M–FliM_M irrespective of the pH conditions. Similarly, the impact of pH remains consistent for both the energetic terms, as acidic pH generally reduces the operative forces – be it electrostatic or van der Waals. However, for a given complex, the lowering of pH reduces the inter-chain electrostatic interaction by a much larger factor and that impact is visible in the case of van der Waals forces, but to a much lesser extent. This observation can be attributed to the excessive positive potential of the interacting chains at acidic pH, leading to the generation of electrostatic repulsion between similar types of charges and finally producing less favorable cohesive inter-chain interactions.

The above set of analyses lead to a conclusion that the combined impact of external mechanical force and acidic pH follows an additivity rule as lowering the pH of the solution generally reduces the cohesive interactions and hence the mechanical stability of each of the three complexes. To further decipher the mechanism of the complexes in terms of structural visualization, we chose intermediate conformations from the pulling assays and depicted them as a function of a progressive time scale. Fig. 5F shows the variability in the evolution of the structural features of the FliF_C–FliG_N complex under both solution conditions. The general theme that appears in the mechanical separation process of the FliF_C–FliG_N complex is the retainment of the structural integrity of the FliG_N chain irrespective of the pH conditions. On the contrary, the FliF_C chain shows a loss of compactness of the native fold along with a concomitant loss in secondary structural features and the differentiation of the separation pathways under two different pH conditions mainly arises due to the conformational variability of the FliF_C chain. On the other hand, neither of the two chains of the FliG_M–FliM_M complex shows any hint of loss of global fold as well as loss of secondary structures during the mechanical unfolding process independent of the pH of the solution (Fig. 5G). It seems that during the separation process, the FliG_M and FliM_M chains merely glide past each other and this observation is in accordance with the less amount of cohesive interactions operating between the chains as observed previously. Interestingly, for the FliY_C–FliN_C complex, both chains show a loss of structural integrity in terms of tertiary and secondary structural features irrespective of the pH conditions present (Fig. 5H). Two major important observations evolve in the mechanical separation process of the FliY_C–FliN_C complex – (1) irrespective of the pH conditions, the loss in structural feature is more prevalent in the FliN_C chain and (2) under acidic pH conditions, the FliN_C chain shows an even aggravated loss of secondary structural features. The latter might be attributed to the lowered inter-chain interactions observed for the FliY_C–FliN_C complex under acidic pH conditions.

To add to the categorization of the mechanical unfolding mechanisms, the distance between the constituting chains was computed, however, by deconvoluting them into four possible combinations, where, as a combination, the analysis shows how the two ends of a protein sequence get separated from the other two ends of the complementary complex-forming sequence (Fig. S11, ESI†). For the FliF_C–FliG_N complex, the separation gets initiated by the N-terminus of the FliF_C chain as it starts moving away simultaneously from the N- and C-termini of the FliG_N chain and this is further followed by the second event of separation where the C-terminal end of the FliF_C chain gets separated from the FliG_N chain as well leading to the complete separation of the two proteins (Fig. S11A, ESI†). This suggests that the two proteins of the FliF_C–FliG_N complex undergo mechanical separation via the sequential unzipping mechanism, i.e., the separation of two interacting chains of a specific complex initiates preferentially at one end of the interface and gradually this structural perturbation permeates to the other end of the interface, and interestingly, the mechanism remains consistent under two different pH conditions. In the case of the FliG_M–FliM_M complex, however, the separation event does not show any distinctive bias via any end of the separating strands and hence it can be termed as the simultaneous separation mechanism, which remains sustained irrespective of the pH of the solution (Fig. S11B, ESI†). When it comes to the FliY_C–FliN_C complex, the mechanism slightly changes on going from the neutral to the acidic pH (Fig. S11C, ESI†). At neutral pH, the separation gets initiated by the C-terminus of the FliN_C chain from the C-terminus of the FliY_C chain, which gets further aggravated by the simultaneous separation of the N- and C-termini of the FliN_C chain from the C- and N-termini of the FliY_C chain, respectively, and which finally gets completed by the separation of the two N-termini of the FliY_C and FliN_C chains. Under acidic pH conditions, the initial and final separation events remain similar, and only the middle part of the event where the N- and C-termini of the FliN_C chain get separated from the C- and N-termini of the FliY_C chain varies from the neutral pH conditions as these two events happen sequentially and not simultaneously as observed previously. Overall, the mechanical separation follows a sequential unzipping mechanism in the FliY_C–FliN_C complex irrespective of the solution conditions.

3.5 Protonation drastically lowers the binding affinity of the FliG_M–FliM_M complex compared to the other two complexes

Although the pulling simulation adds additional information about the pH-induced modulation of inter-chain cohesive interactions to the information landscape obtained from quasi-equilibrium thermal scanning, its non-equilibrium nature limits itself to providing any thermodynamic stability pattern required to quantify the impact of intermolecular cohesive forces. Hence, we estimated equilibrium binding affinities by using a combination of umbrella sampling simulations and WHAM, which eventually generated the PMF profiles (Fig. 6). Whether at neutral pH or at acidic pH, the binding affinity between the chains of the FliF_C–FliG_N complex (ΔG_Neutral = 188.11 ± 2.80 kJ mol⁻¹ and ΔG_Acidic = 177.19 ± 6.23 kJ mol⁻¹, Fig. 6A) displays a mid-range value compared to the other two complexes as the binding free energy appears to be minimum between the chains of the FliG_M–FliM_M complex (ΔG_Neutral = 88.62 ± 3.30 kJ mol⁻¹ and ΔG_Acidic = 33.85 ± 2.09 kJ mol⁻¹, Fig. 6B) and maximum between the chains of the FliY_C–FliN_C complex (ΔG_Neutral = 324.68 ± 3.10 kJ mol⁻¹ and ΔG_Acidic = 304.88 ± 4.52 kJ mol⁻¹, Fig. 6C). Interestingly, as the pH of the solution decreases, all three complexes show reduced binding affinities compared to their neutral pH counterparts with the reduction in binding free energy values (ΔΔG) by 10.92 kJ mol⁻¹ for the FliF_C–FliG_N complex, 54.77 kJ mol⁻¹ for the FliG_M–FliM_M complex, and 19.80 kJ mol⁻¹ for the FliY_C–FliN_C complex. Remarkably, these findings are consistent with the non-equilibrium pulling simulation observations in terms of the relative order of stability between the complexes and also the impact of the acidic pH conditions and this could be because a mechanical unfolding pathway was comprehended as an average of multiple sets of non-equilibrium pulling pathways. Interestingly, one common observation that also stems from the comparison of the PMF profiles is that, for any specific complex, the intermediates with similarly distorted constructs signified by the distances between partnering proteins of a complex are achieved at a lower cost of free energy (less stable) when the solution reaches the acidic pH range compared to the neutral pH. The above observation leads to the conclusion that acidic pH facilitates the loss of structural integrity of any complex. Our estimation of the free energy values is robust considering the error bars associated with the measurements and the convergence of the profiles substantiated by the overlap of the individual umbrella distributions for each case (Fig. S12, ESI†).

Fig. 6 PMF profiles (with vertical error bars) obtained for the three complexes under two different pH conditions generated via an enhanced sampling approach. For any specific complex, a pair of PMF profiles signify the destabilizing impact of the acidic pH on the binding affinity of the constituting proteins – (A) FliF_C–FliG_N complex, (B) FliG_M–FliM_M complex, and (C) FliY_C–FliN_C complex.

4 Discussion

The present research aims to identify ways to break the motor protein machinery of H. pylori to find a remedy for its deleterious impact on human lives. The tendency of a complex to dissociate into its constituting protein sequences originates from the inability of the proteins to adapt themselves to dynamically altering environments,⁵⁶ which is achieved by utilizing a gamut of physiologically relevant perturbations, both individually and also as a combination, to identify the extent of comparative sustainability of the three complexes and resultantly to expose their weak spots. Here we connect the dots between the three protein complexes via their generic features and how they portray their complex-specific signatures by the unique characteristics with proper justifications.

Under the thermal and pH-dependent perturbations, the beginning of the structural deformation is exemplified by a subtle gain in backbone compactness with concomitant retainment of the overall solvent exposure of a protein/complex hinting toward the generation of a fluffy state⁵⁷ where labile side chains are loosely packed to the core of the protein and this phenomenon becomes more prominent for α-helix-rich systems. Post-attainment of the fluffy state, the progressive loss of structural integrity comprises an anticipated route with a higher degree of structural unfolding where all the structural order parameters correlatively tell the same story. On the contrary, the energetic features whose balance helps to hold the structural integrity of a protein sequence display an extremely predictable trend of gradual weakening of energetic stabilization, specifically in terms of the backbone hydrogen bond network⁵⁸ and dispersion interactions.⁵⁹ The somewhat counterintuitive trend as observed for the long-range electrostatic interactions under a specific solution condition might be due to the emergence of non-specific interactions within/between protein sequences because of the creation of more exposed conformational ensembles and hence the increased possibility of intra-/inter-chain interactions.⁶⁰ However, the trend also becomes intuitive when two different solution conditions are compared as acidic pH always destabilizes the system electrostatically – be it intra-protein or inter-protein.⁶¹ A similar dual character is displayed by secondary structural content – intuitive (FliF_C–FliG_N system), as aggravated perturbing conditions always reduce it at a specific pH, and counter-intuitive (FliG_M–FliM_M and FliY_C–FliN_C systems), as the earlier trend becomes inconsistent. In the first case, the percentage of secondary structure remains unchanged due to the protonation of side chains (keeping the other conditions unchanged) and this hints that the system loses it tertiary structure at acidic pH, which leads to less packing of the side chains (complementing structural order parameters).⁶² For the latter scenario, the gain in secondary structure with progressively aggravated perturbations under a particular solution condition or due to the lowering of pH without altering the rest of the solution conditions could be attributed to the preferential unfolding of α-helical segments and creating a tendency to generate β-sheet-like structures,⁶³ at least in terms of the ϕ–φ landscape. Additionally, in general, the characteristics of each of these three multi-protein complexes are mainly dictated by its longer protein fragment. Importantly, irrespective of the nature of perturbations being implemented (elevated temperature or low pH), each of the three complexes exhibits a complex-specific generic unfolding mechanism whose sequence of events remains unaltered proving the existence of a complex-and chain-specific maintenance of structural integrity, and this claim is further substantiated by the observed similarity in the modulation of interfacial interactions of a specific complex under thermal/pH-driven perturbations. The combined effect of high temperature and low pH perturbations reduces the withstanding ability of a complex to a much greater extent due to the additive nature of the combined external force acting on the structure.⁶⁴

One of the most important features of the present work is the identification of malleable segments that are prone to extensive fluctuations under thermal and pH-modulated perturbations and hence can act as the potential sites for the initiation of structural disintegration.⁶⁵ Interestingly, the specific segments that appear as labile fragments of a sequence retain their identities in terms of the length and position when solution conditions are changed to the acidic pH, which practically suggests that each protein sequence has multiple generic discrete sites that are vulnerable to any form of cellular perturbations (weak spots) and would start unfolding early. The protein-specific network of dynamical cross-talk percolates these environmental heterogeneity-driven segment-specific perturbations to the entire sequence. The progressive loss of structural integrity of a protein always involves the melting of a large number of smaller dynamical networks to a very few numbers of continuous networks where torque is generated by the out-of-phase dynamical movement of a considerably big part of a chain from the rest of it.⁶⁶

Application of mechanical perturbation in our systems makes sense as the motor proteins experience conversion of electrochemical potential to mechanical force in the process of generating torque.³⁰ Interestingly, the complexes show variability in their mechanical separation processes by projecting two different mechanisms – sequential unzipping and simultaneous separation⁶⁷ – and more importantly, a particular complex does not change its mechanical separation mechanism with varying pH. It is important here to mention that the observed mechanical separation mechanisms of the three individually studied complexes might vary if the entire oligomeric motor protein complex is considered simultaneously where individual complexes are connected as there could be some long-range allosteric impact of one complex on another. Since the conformations evolved in the pulling trajectories are non-equilibrium in nature as well as the thermally perturbed ensembles, a direct comparison between them would not make much sense statistically. Interestingly though, the additivity feature of combined perturbations is found to be valid for mechanical perturbation and acidic pH as well.⁶⁸

The limitation of quasi- to non-equilibrium sampling is overcome by employing enhanced sampling approaches which eventually led us to the equilibrium quantification of binding affinities between two partnering protein sequences of a specific complex. In general, acidic pH lowers the binding affinity between two protein chains of a complex compared to the neutral one and this in turn practically provides robustness to the quasi- and non-equilibrium measurements of structural and energetic variables, which hinted toward the reduction of cohesive forces operative between two partnering proteins of a complex under acidic pH conditions. It is worth emphasizing that the reduction of affinity between a pair of protein chains under acidic pH conditions varies significantly as the affinity gets reduced to a very large extent for the FliG_M–FliM_M complex, but not so much for the other two complexes. Specifically, the FliF_C and FliG_C chains, which form the MS-ring/C-ring junction point, get minimally affected due to the lowering of pH and this might be a testimony of the unperturbed functioning of H. pylori under acidic pH conditions in the stomach.³¹ The extremely lowered affinity between the FliG_M and FliM_M proteins under acidic pH conditions does not show any considerable impact on the flagellar functional activity³¹ and this might be due to the nature of the structure of the FliG_M–FliM_M complex, where the structure-forming proteins are merely held together without any cross-structure entanglements (a larger distance between two partnering proteins), unlike what is observed for the other two complexes (a smaller distance between the structure-forming proteins). The correlation between estimated binding affinities at neutral pH and the extent of entanglement between two partnering protein sequences of a specific complex in their native states is further evidenced by the number of residues involved in the interfacial interactions, which is maximum for the FliY_C–FliN_C complex and minimum for the FliG_M–FliM_M complex.

Although there have been extensive research reports on the H. pylori flagellar motor system, a lack of detail is eminent when it comes to the extremely specific structural and energetic features of the constituting proteins or the junction complexes down to the single molecule level and this presents a hurdle for any simulated observable to be compared and hence to be validated. Still, we found multiple instances where our simulated observables qualitatively/semi-quantitatively match with the existing experimental observations: the highest extent of structural deviation of two helices (α6 and α7) of the FliG_N chain in the FliF_C–FliG_N complex,⁶⁹ which might be due to the fact that those two helices are the loosely bound segments as they form after the complex formation between FliF and FliG;³⁰ acidic pH drives the FliF_C–FliG_N complex more towards the dissociated state;⁷⁰ FliY_C–FliN_C inter-chain interactions are dominated by electrostatic forces;²⁶ both polar and hydrophobic interactions are essential for the FliG_M–FliM_M complex to be in the stable state;²⁵ protonation leads to reduced inter-chain interactions for the FliF_C–FliG_N complex due to lack of polar interactions and residual interactions are contributed by the hydrophobic residues;³⁰ key residues/secondary structural elements contributing to the interfacial interactions of three complexes in their native states corroborate nicely with experimentally determined structural information;^25,26,30 α5 of FliG_N, which is reported to be important for flagellar formation and motility,³⁰ evolves as a malleable segment in our analysis; the loop connecting α5 and α6, which supposedly prevents intramolecular association,³⁰ also appears as a stand out segment in fluctuation profile analysis; cross-species conserved residues²⁵ of both FliG_M (E137, H138 and R172) and FliM_M (R76, D130, L133, R144, S147 and I149) appear to be labile segments in our study as well; and the relative order of binding affinities between FliF_C–FliG_N and FliG_M–FliM_M complexes, as estimated by our simulated approach, matches nicely with the experimentally determined relative trend of dissociation constants of these two complexes.^25,30 All the above comparisons add robustness to our inferences drawn from simulated trajectories.

5 Conclusions

The entire exercise executed in the present research, where we tried to decode the minute detailing of structural and energetic properties of each of the complexes and its constituting chains in various possible solution environments under various perturbing conditions, has helped us to find an effective drug target for H. pylori that would be suitable for the entire pH range of the pancreas. The core idea is to search for the target by funneling down the complex → sequence → segment → residue route. Among the three complexes, the FliG_M–FliM_M complex shows extreme destabilization at acidic pH, yet, in reality, H. pylori performs its functions under acidic pH conditions in the pancreas without any hiccups, proving it not to be the most influential segment of the motor machinery. This leaves us with two other options – the FliF_C–FliG_N complex and the FliY_C–FliN_C complex. The comparatively lower binding affinity (easier to impose destabilization), the least reduction of stability at acidic pH (maximum withstanding ability), and most importantly, the strategic positioning of the FliF_C–FliG_N complex (bridge between the MS-ring and the C-ring, and hence, destabilization would cut-off the most important link in the motor protein complex chain) make it a better choice as a first step for target complex identification compared to the FliY_C–FliN_C complex (extremely stable and hence harder to destabilize). Therefore, the obvious choice for a specific sequence of the FliF_C–FliG_N complex should be the FliF_C sequence, as it shows extreme consistency in displaying common thermally malleable segments in terms of the number of segments, lengths of those segments, and positioning of those segments compared to the FliG_N sequence under two different pH conditions. Consequently, between the two malleable segments of the FliF_C sequence, the smarter choice would be to target the post-kink P545-D546-E547 segment, as it has the shortest length (lower uncertainty), which is a prerequisite for an effective drug target. Finally, to get down to a single residue, the comparatively logical choice would be residue P545 as – (1) it shows maximum elevation of fluctuation under thermal scanning and at acidic pH and hence would be more accessible to the incoming drug molecules,⁷¹ and (2) mutation of P545 would likely remove the kink shape of the FliF_C sequence (proline being a kink generator⁷²), which structurally seems like a necessity for the effective interaction with the complementary FliG_N sequence and hence the integrity of the FliF_C–FliG_N complex and as a result would facilitate the complex dissociation process. Although our current research addresses an extremely important query regarding the therapeutic strategy against H. pylori, there is a limitation associated with the present approach as we have not dealt with the whole flagellar motor, which calls for future research works on the entire motor device.

Author contributions

V. T. and A. D. designed research; V. T., R. A., D. S., and A. D. performed research; V. T., R. A., D. S., and A. D. analyzed data; and V. T. and A. D. wrote the paper. All authors approved the final version of the manuscript.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

V. T. acknowledges the research fellowship from the Council of Scientific and Industrial Research (31/GATE/11(46)/2020-EMR-I). A. D. acknowledges the start-up research grant from CSIR-NCL. The authors acknowledge the computational facilities provided by the CSIR-NCL, the CSIR Fourth Paradigm Institute, and the National Supercomputing Mission (NSM) of “PARAM Brahma” at IISER Pune, which is implemented by C-DAC and supported by the Ministry of Electronics and Information Technology (MeitY) and Department of Science and Technology (DST), Government of India.

References

1. Z. Otwinowski and W. Minor, [20] Processing of X-ray diffraction data collected in oscillation mode, in Methods in Enzymology, Elsevier, 1997, vol. 276, pp. 307–326.
2. C. Josenhans, K. Jung, C. V. Rao and A. J. Wolfe, Mol. Microbiol., 2014, 91, 6–25.
3. K. M. Ottemann and A. C. Lowenthal, Infect. Immun., 2002, 70, 1984–1990.
4. D. J. DeRosier, Cell, 1998, 93, 17–20.
5. T. Minamino, K. Imada and K. Namba, Curr. Opin. Struct. Biol., 2008, 18, 693–701.
6. D. Stock, K. Namba and L. K. Lee, Curr. Opin. Biotechnol, 2012, 23, 545–554.
7. D. R. Thomas, D. G. Morgan and D. J. DeRosier, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 10134–10139.
8. D. R. Thomas, N. R. Francis, C. Xu and D. J. DeRosier, J. Bacteriol., 2006, 188, 7039–7048.
9. S. Kojima and D. F. Blair, Biochemistry, 2004, 43, 26–34.
10. J. Zhou, L. L. Sharp, H. L. Tang, S. A. Lloyd, S. Billings, T. F. Braun and D. F. Blair, J. Bacteriol., 1998, 180, 2729–2735.
11. S. Kojima and D. F. Blair, Biochemistry, 2001, 40, 13041–13050.
12. Y. V. Morimoto, S. Nakamura, N. Kami-ike, K. Namba and T. Minamino, Mol. Microbiol., 2010, 78, 1117–1129.
13. K. Paul, G. Gonzalez-Bonet, A. M. Bilwes, B. R. Crane and D. Blair, EMBO J., 2011, 30, 2962–2971.
14. M. K. Sarkar, K. Paul and D. Blair, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 9370–9375.
15. S.-Y. Lee, H. S. Cho, J. G. Pelton, D. Yan, R. K. Henderson, D. S. King, L.-S. Huang, S. Kustu, E. A. Berry and D. E. Wemmer, Nat. Struct. Mol. Biol., 2001, 8, 52–56.
16. P. N. Brown, M. A. Mathews, L. A. Joss, C. P. Hill and D. F. Blair, J. Bacteriol., 2005, 187, 2890–2902.
17. M. Beeby, D. A. Ribardo, C. A. Brennan, E. G. Ruby, G. J. Jensen and D. R. Hendrixson, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E1917–E1926.
18. S. Chen, M. Beeby, G. E. Murphy, J. R. Leadbetter, D. R. Hendrixson, A. Briegel, Z. Li, J. Shi, E. I. Tocheva and A. Müller, EMBO J., 2011, 30, 2972–2981.
19. A. C. Lowenthal, M. Hill, L. K. Sycuro, K. Mehmood, N. R. Salama and K. M. Ottemann, J. Bacteriol., 2009, 191, 7147–7156.
20. D. S. Bischoff and G. W. Ordal, Mol. Microbiol., 1992, 6, 2715–2723.
21. P. Lertsethtakarn, K. M. Ottemann and D. R. Hendrixson, Annu. Rev. Microbiol., 2011, 65, 389–410.
22. M. Kihara, G. U. Miller and R. M. Macnab, J. Bacteriol., 2000, 182, 3022–3028.
23. B. r Grünenfelder, S. Gehrig and U. Jenal, J. Bacteriol., 2003, 185, 1624–1633.
24. R. Levenson, H. Zhou and F. W. Dahlquist, Biochemistry, 2012, 51, 5052–5060.
25. K. H. Lam, W. W. L. Lam, J. Y. K. Wong, L. C. Chan, M. Kotaka, T. K. W. Ling, D. Y. Jin, K. M. Ottemann and S. W. N. Au, Mol. Microbiol., 2013, 88, 798–812.
26. K. H. Lam, C. Xue, K. Sun, H. Zhang, W. W. L. Lam, Z. Zhu, J. T. Y. Ng, W. E. Sause, P. Lertsethtakarn and K. F. Lau, J. Biol. Chem., 2018, 293, 13961–13973.
27. B. Marshall and J. R. Warren, Lancet, 1984, 323, 1311–1315.
28. J. Parsonnet, G. D. Friedman, D. P. Vandersteen, Y. Chang, J. H. Vogelman, N. Orentreich and R. K. Sibley, N. Engl. J. Med., 1991, 325, 1127–1131.
29. P. Correa and J. Houghton, Gastroenterology, 2007, 133, 659–672.
30. C. Xue, K. H. Lam, H. Zhang, K. Sun, S. H. Lee, X. Chen and S. W. N. Au, J. Biol. Chem., 2018, 293, 2066–2078.
31. S. Ansari and Y. Yamaoka, Helicobacter, 2017, 22, e12386.
32. J. Seelig and H.-J. Schönfeld, Q. Rev. Biophys., 2016, 49, e9.
33. D. Kosztin, S. Izrailev and K. Schulten, Biophys. J., 1999, 76, 188–197.
34. G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199.
35. S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021.
36. J. S. Hub and B. L. de Groot, Biophys. J., 2006, 91, 842–848.
37. J. S. Hub, B. L. De Groot and D. Van Der Spoel, J. Chem. Theory Comput., 2010, 6, 3713–3720.
38. The PyMOL Molecular Graphics System, Version 2.0 Schrödinger, LLC.
39. J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Žídek and A. Potapenko, Nature, 2021, 596, 583–589.
40. S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson and D. Van Der Spoel, Bioinformatics, 2013, 29, 845–854.
41. P. Bjelkmar, P. Larsson, M. A. Cuendet, B. Hess and E. Lindahl, J. Chem. Theory Comput., 2010, 6, 459–466.
42. P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 105, 9954–9960.
43. Y. Sugita and Y. Okamoto, Chem. Phys. Lett., 1999, 314, 141–151.
44. J. M. Swails, D. M. York and A. E. Roitberg, J. Chem. Theory Comput., 2014, 10, 1341–1352.
45. S. Fujimori, World J. Gastroenterol., 2020, 26, 6706.
46. M. H. Olsson, C. R. Søndergaard, M. Rostkowski and J. H. Jensen, J. Chem. Theory Comput., 2011, 7, 525–537.
47. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
48. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
49. B. Hess, J. Chem. Theory Comput., 2008, 4, 116–122.
50. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
51. W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695.
52. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
53. M. Karplus and J. N. Kushick, Macromolecules, 1981, 14, 325–332.
54. C. C. David and D. J. Jacobs, Principal component analysis: a method for determining the essential dynamics of proteins, in Protein dynamics, Springer, 2014, pp. 193–226.
55. S. Swaminathan, W. Harte Jr and D. L. Beveridge, J. Am. Chem. Soc., 1991, 113, 2717–2721.
56. C. T. Veldkamp, F. C. Peterson, A. J. Pelzek and B. F. Volkman, Protein Sci., 2005, 14, 1071–1081.
57. A. Bachmann, D. Wildemann, F. Praetorius, G. Fischer and T. Kiefhaber, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 3952–3957.
58. M. Wang, T. E. Wales and M. C. Fitzgerald, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 2600–2604.
59. S. S. Sung, Protein Sci., 2015, 24, 1383–1388.
60. Ø. Halskau Jr, R. Perez-Jimenez, B. Ibarra-Molero, J. Underhaug, V. Muñoz, A. Martinez and J. M. Sanchez-Ruiz, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 8625–8630.
61. D. Mercadante, L. D. Melton, G. E. Norris, T. S. Loo, M. A. Williams, R. C. Dobson and G. B. Jameson, Biophys. J., 2012, 103, 303–312.
62. L. Konermann and D. Douglas, Biochemistry, 1997, 36, 12296–12302.
63. R. GhoshMoulick, J. Bhattacharya, S. Roy, S. Basak and A. K. Dasgupta, Biochim. Biophys. Acta, Proteins Proteomics, 2007, 1774, 233–242.
64. N. Poklar, J. Lah, M. Salobir, P. Macek and G. Vesnaver, Biochemistry, 1997, 36, 14345–14352.
65. X. Peng, N. R. Cashman and S. S. Plotkin, J. Phys. Chem. B, 2018, 122, 11662–11676.
66. H. Kamberaj and A. van der Vaart, Biophys. J., 2009, 97, 1747–1755.
67. A. Das and D. E. Makarov, J. Phys. Chem. B, 2016, 120, 11665–11673.
68. C.-L. Chyan, F.-C. Lin, H. Peng, J.-M. Yuan, C.-H. Chang, S.-H. Lin and G. Yang, Biophys. J., 2004, 87, 3995–4006.
69. D. Tupiņa, A. Krah, J. K. Marzinek, L. Zuzic, A. A. Moverley, C. Constantinidou and P. J. Bond, Curr. Res. Struct. Biol., 2022, 4, 59–67.
70. M. J. Lynch, R. Levenson, E. A. Kim, R. Sircar, D. F. Blair, F. W. Dahlquist and B. R. Crane, Structure, 2017, 25, 317–328.
71. D. K. Johnson and J. Karanicolas, PLoS Comput. Biol., 2013, 9, e1002951.
72. D. Barlow and J. Thornton, J. Mol. Biol., 1988, 201, 601–619.

---

Footnote

† Electronic supplementary information (ESI) available: Structural and energetic features obtained from the quasi-equilibrium trajectories of two complexes (FliG_M-FliM_M and FliY_C-FliN_C) and six chains (FliF_C, FliG_N, FliG_M, FliM_M, FliY_C, and FliN_C), generic unfolding mechanisms of three complexes under thermal and/or pH-driven perturbations, modulation of interfacial interactions of three complexes as a function of temperature and pH, intra-chain DCCMs of six chains (FliF_C, FliG_N, FliG_M, FliM_M, FliY_C, and FliN_C), terminus-specific inter-chain distance for three systems (FliF_C-FliG_N, FliG_M-FliM_M and FliY_C-FliN_C), and robustness check for umbrella sampling simulations for the three systems (FliF_C-FliG_N, FliG_M-FliM_M and FliY_C-FliN_C). See DOI: https://doi.org/10.1039/d3cp05024f

---