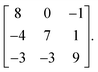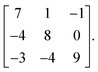Understanding the limits to short-range order suppression in many-component disordered rock salt lithium-ion cathode materials

Abstract

Suppressing unfavourable short-range ordering in disordered rock salt lithium-ion cathode materials is seen as a key research goal on their route to commercialisation. In this study we use cluster-expansion-driven Monte Carlo simulations of a model 3d-transition metal disordered rock salt oxyfluoride system to investigate the effect of many component cation substitution on the suppression of short-range ordering in disordered rock salt cathode materials. We confirm that many-cation substitution is effective in suppressing short-range ordering, but has diminishing returns on increasing the number of component transition metals, or alternatively, increasing the size of the long-range lithium diffusion network as the number of transition metals increases. We particularly emphasize the critical role of lithium excess and fluorine content in the success of the “high-entropy” cation substitution strategy: short-range ordering is strongly influenced by cation–anion bonding preferences, underscoring the need to consider the full composition of the target system when designing high entropy lithium-ion cathode materials.

---

1. Introduction

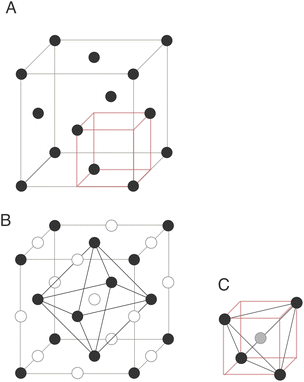
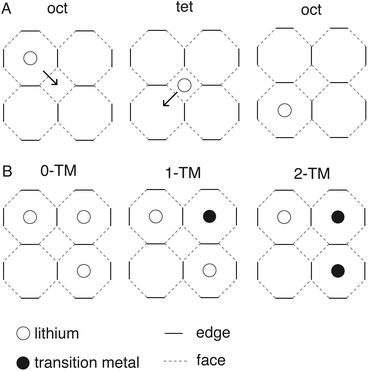
The exploration and optimisation of novel chemistries for lithium-ion cathode materials remains a vast area of research for the materials science community^1–5 owing to the crucial role of electrochemical energy storage in transitioning to a low carbon economy. Disordered rock salt lithium-ion cathodes are an emerging materials class in this area.^6–9 These materials share the close-packed oxygen framework present in most commercial lithium-ion cathode materials such as the layered rock salt cobalt- and nickel-rich structures^10,11 conferring an excellent mass-to-charge ratio and volumetric efficiency. While performant, layered cobalt and nickel rich structures have poor long-term techno-economic prospects.¹² This is in contrast to – for example – manganese and iron which are cheaper and more abundant, but their layered structural analogues are not stable over many intercalation cycles.^13–15

Embracing cation disorder enables the use of novel cathode chemistries that do not need to maintain a layered ordering on cycling.^7,16–23 The performance of any intercalation cathode is limited by the ability of lithium to reversibly intercalate into the host framework which is dependent on atomistic diffusion processes. Fig. 1 illustrates a cubic close-packed oxygen lattice. In both the layered and disordered systems lithium diffusion occurs from an octahedral hole in the O²⁻ framework via an octahedral face, into an interstitial tetrahedron. The diffusing ion then occupies a new octahedral site via another shared octahedral–tetrahedral face (an “oct–tet–oct” hop).⁶ The energy barrier for lithium hopping is then strongly influenced by the stability of lithium in the tetrahedral hole.²⁴ The stability of lithium in this tetrahedral transition state depends on factors such as the identity of the face-sharing cations: too many face-sharing transition metals destabilises the lithium in the tetrahedral transition state increasing the energy barrier for lithium diffusion.^6,25 In disordered rock salt cathodes a percolating network of lithium sites connected by tetrahedral holes with no face-sharing transition metals (referred to as “0-TM” sites) is generally found to be necessary for effective long-range diffusion.^6,8,25 The pathway for single-ion lithium hopping and a range of potential transition state local environments in disordered rock salts are shown as a 2D schematic in Fig. 2.

Fig. 1 (A) Face-centered cubic (FCC) lattice, such as the one exhibited by O²⁻ ions in many lithium-transition metal oxides. (B) Octahedral holes in the FCC lattice (white) that may be filled by cations in a lithium-transition metal oxide. (C) Tetrahedral holes (grey) which form the transition states for lithium diffusion in a disordered rock salt cathode material.

Fig. 2 (A) 2D representation of the oct–tet–oct hop of a lithium ion diffusing in a rock salt structured cathode material. (B) 2D representation of the different face sharing ions for the transition-state tetrahedral site in the oct–tet–oct hop. The energy barrier for the hop will increase as a function of the number of transition metals face-sharing with the tetrahedral site.

In a fully random disordered rocksalt with the general formula Li_1+xM_1−xO₂ – where M is used as a generic symbol for any transition metal – a lithium excess of x ≳ 0.09 is required to ensure a long range percolating 0-TM network.^6,26 It is found the connectivity of the lithium diffusion network is poorer than expected in a totally random system in almost all cases, and substantial lithium excesses are required to give good long-range connectivity of the 0-TM network.²⁵ Minimising the lithium excess is desirable, as the additional lithium substitutes for the redox-active transition metal, reducing the capacity or increasing the anion-redox activity which can cause voltage hysteresis and structural degradation in disordered rock salt cathodes.²⁷

The cause of the reduced lithium percolation in disordered rock salt materials relative to the random limit is understood to be a consequence of the short-range ordering preferences of the cations, which are comprised of contributions from bonding preferences and electrostatics.^8,25,28,29 Thus, finding ways to suppress unfavourable short-range ordering is crucial for improving the capacity and overall performance of disordered rock salt cathode materials. Fluorine substitution allows for the manipulation of short-range ordering preferences on the anion framework by introducing bond-strength considerations between the cations and the anions which will compete with the cation–cation interactions to determine the overall short-range order.³⁰ Transition metals bind more strongly to oxygen, creating locally lithium–fluorine-rich regions and transition-metal–oxygen-rich regions, which alters the short-range ordering. Incorporating enough fluorine can therefore create lithium-rich regions with high numbers of 0-TM sites, and good lithium transport. However, high levels of fluorine incorporation requires energy-intensive mechanochemical synthesis^31–33 and can lead to phase separation.³⁰

An alternative strategy for suppressing unfavourable short-range ordering in disordered rock salt cathode materials is to substitute many different species on the cation sublattice, creating a “high-entropy” material. This approach, first proposed by Lun et al.,³⁴ was inspired by the homogeneous cation distribution observed in high-entropy oxides.^35,36 While not the first work to successfully synthesize high-entropy disordered rock salt lithium-ion cathode materials,³⁷ Lun et al. were the first to link the performance of these materials to short-range order suppression. By increasing the number of species on the cation sublattice, they observed an increase in first-cycle capacity. This was linked a suppression of short-range ordering validated by electron diffraction experiments which showed a reduction in diffuse short-range order scattering as the number of transition metals in the sample was increased. Alternatively, this can be seen as an increase in cation configurational entropy. The short-range order suppression was then linked to an increase in the size of the long-range lithium percolation network by cluster-expansion-driven Monte Carlo simulations.

To extend the current understanding of short range order suppression in many-component disordered rock salt transition metal oxyfluoride cathode materials, we examine the lithium-transition metal ordering in rock-salt-structured 3d-transition-metal lithium oxyfluorides using cluster-expansion-driven Monte Carlo simulations. Such simulations have proved to be an excellent tool in unravelling short range ordering preferences in lithium-ion cathode materials.^25,27,34,38 We examine how the lithium percolation network evolves as a function of the number of transition metals on the cation sublattice and varying lithium excess and fluorine content. In doing so, we identify compositional guidelines for designing effective many-component disordered rock salt lithium-ion cathode materials, showing that any short range order suppression from an increase in cation configurational entropy is highly dependent on the lithium excess and fluorine content.

2. Methodology

A cluster expansion model, trained from density functional theory (DFT) calculations was used to drive Monte Carlo simulations to sample the short-range ordering behaviour of compositionally complex disordered rock salt lithium-ion cathode materials. The cluster expansion basis was taken as a rock salt structure with a = 4.1 Å with Li⁺, Mn²⁺, Mn³⁺, Mn⁴⁺, Ni²⁺, Ti⁴⁺, Fe³⁺, and Cr³⁺ allowed to occupy the cation site, and O²⁻ and F⁻ allowed to occupy the anion site. Ancillary analysis relied on the pymatgen,³⁹ seaborn,⁴⁰ pandas,⁴¹ scipy,⁴² numpy⁴³ and scikit-learn⁴⁴ packages. Visualisation relied on the use of perceptually uniform scientific color maps. Training data and fitted cluster expanions can be found in the associated dataset.^45–47

2.1 Training data generation

All DFT calculations were performed using the plane-wave DFT Vienna Ab initio Simulation Package (VASP).^48–50 Valence electrons were described by a plane-wave basis set with a cutoff of 680 eV. Interactions between core and valence electrons were described using the projector-augmented wave (PAW) method.^51,52 Electronic exchange and correlation were approximated using the Perdew–Burke–Ernzerhof functional, revised for solids and surfaces (PBEsol)⁵³ with rotationally averaged Hubbard U corrections of 3.9 eV, 3.7 eV, 5.3 eV, 6.2 eV and 4.2 eV applied to the Mn, Cr, Fe, Ni and Ti 3d orbitals respectively to approximately correct for the self-interaction error (SIE).^54–56 Reciprocal space was sampled with a discretisation of 0.35 Å⁻¹. All calculations were initialised with transition metal ions in a ferromagnetic configuration.

2.2 Cluster expansion fitting

The final cluster expansion was trained on a total of 7215 unique DFT calculations after filtering out structures which relax to off-lattice configurations, and possess transition metals in oxidation states not included in the model. Oxidation states were assigned using calculated magnetic moments. The variable oxidation state of Mn was assigned using a Bayesian black-box optimization process.^57,58 We employed the icet and trainstation software packages to train the cluster expansion.^44,59,60 The fitting used a pair-cluster cutoff of 7.1 Å and a triplet-cluster cutoff of 4.8 Å (quadruplet clusters were found to make only a very minor contribution to the model performance for increased complexity, so were excluded, as has been noted in other high-component cluster expansion studies of lithium transition metal oxides⁵⁷). The final model has a cross validation score of 9.95 meV. More information on the fitting procedure and training set generation, including a discussion of limitations of the DFT+U methodology used in this paper can be found in the ESI.†

2.3 Monte Carlo simulations

Monte Carlo simulations were performed using the mchammer package.⁵⁹ Simulations of the lithium-excess simulations used a 990 atom expansion of the primitive cell described by the transformation matrix

This structure was selected using an algorithm to determine a cell with optimal cubic character, as implemented in the atomic simulation environment.⁶¹ The simulations of the LiMO₂ system used a 1000 atom cell,

Each Monte Carlo simulation was run at 2000 K. 2000 K falls within the range of empirical simulation temperatures commonly used for Monte Carlo simulations of disordered rock salt structures^27,34,62 and we expect it to capture experimentally relevant trends in the short range order formation. Each simulation ran for at least 5 000 000 trial steps. Values reported from the Monte Carlo simulations are each averaged over five simulations of each composition presented, with 1000 structures extracted from each Monte Carlo simulation, i.e. each value is averaged over 5000 data points. The crystal-torture package was used to extract percolation statistics from the Monte Carlo simulations.⁶³

3. Results and discussion

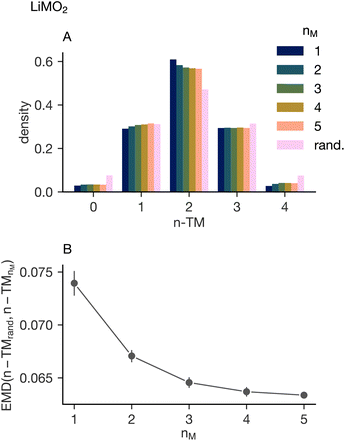
First, we confirm that an increase in configurational entropy of the cation sublattice suppresses the short range ordering. Fig. 3A shows a histogram of the occurrences of the different n-TM sites in LiMO₂ where M represents all equimolar charge-balanced compositions of Mn(III), Cr(III), Fe(III), Ni(II) and Ti(IV). These are then separated into 1, 2, 3, 4, and 5 transition metal simulations. Visual inspection of the histogram indicates that higher-component systems result in an n-TM probability mass function more similar to a random one. However, even when mixing five transition metals, the difference between the simulated and random distribution appears significant. Fig. 3B shows the Earth Mover's Distance (EMD) between the random and simulated distributions. The EMD is a measure of dissimilarity between two probability distributions with a smaller EMD value indicating a closer match.⁶⁴

Fig. 3 (A) Histogram showing the occurrence of the different possible n-TM sites in Monte Carlo simulated LiMO₂, where M is all equimolar charge-balanced combinations of Mn(III), Cr(III), Fe(III), Ni(II) and Ti(IV). (B) The Earth Mover's Distance (EMD) between the Monte Carlo sampled distributions of n-TM sites, and the fully random distribution. The error bars show the 95% confidence interval in the EMD.

The EMD taken between the random and simulated systems supports the observations that can be made from the histogram. The distribution of n-TM sites becomes increasingly similar to a random distribution as a function of the number of transition metals in the simulation and supports the hypothesis that increasing cation configurational entropy leads to a more homogeneous distribution of cations in lithium transition metal oxide disordered rock salts. However, there is a decrease in the rate at which the EMD value decreases as the number of transition metals increases, indicating that the distribution becomes more similar to a random distribution at a slower rate. “Diminishing returns” are observed in the short-range order suppression with respect to the number of transition metals. This indicates that increased cation configurational entropy can improve mixing to an extent, but is unlikely to fully overcome the electrostatic and elastic effects that drive cation short-range ordering in lithium transition metal oxides.^8,25 This implies that moderate entropy systems will see most of the short-range order suppression benefit of the many-transition-metal systems.

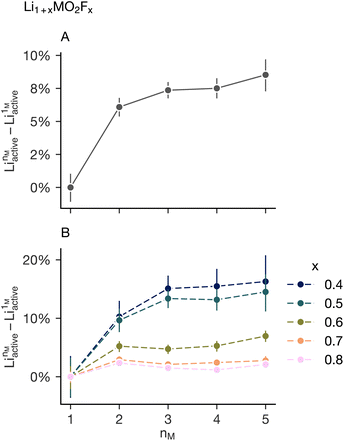
To explore the relationship between the number of transition metals in the simulation and short-range order suppression in a more experimentally relevant compositional space we run additional Monte Carlo simulations on fluorinated lithium-excess disordered rock salt materials. We simulate all equimolar charged balanced compositions maintaining an average transition metal oxidation state of 3+ in the compositional range Li_1+xMO₂F_x, where x ∈ {0.4, 0.5, 0.6, 0.7, 0.8}. The transition metals included remain Mn(III), Cr(III), Fe(III), Ni(II) and Ti(IV). The lithium that is expected to be diffusive, and therefore contribute the capacity, is that which is connected via a percolating network of 0-TM sites,^6,8,25 we label this Li_active. Fig. 4A shows the calculated change in Li_active from the Monte Carlo simulation as the number of transition metals increases, averaged over all values of x. Increasing the number of transition metals on the cation sublattice generally results in an increase in Li_active. However, the increase in the size of the lithium diffusion network levels off as the number of transition metals increases mirroring the short-range order suppression behavior highlighted in Fig. 3. This suggests that the observation of “diminishing returns” of short-range order suppression noted for the LiMO₂ system is extensible to the lithium-excess oxyfluorides.

Fig. 4 (A) The mean change in active lithium in a Li_1+xMO₂F_x as a function of the number of transition metals in the Monte Carlo simulation, relative to the average percolating lithium in single transition metal systems decomposed by the lithium excess and fluorine content. The error bars show the 95% confidence interval in the active lithium fraction. (B) Showing the same data, but decomposed per value of x.

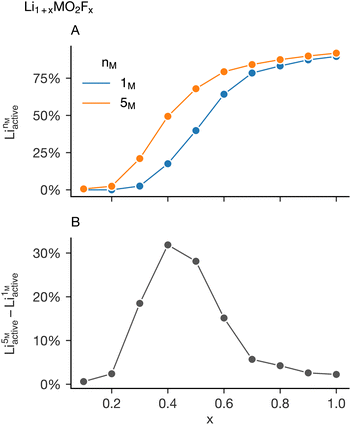
Examining only the mean behaviour in the change in activate lithium as a function of n_M disguises the strongly different responses for each value of x. Fig. 4B shows the average value decomposed into the individual values of x: lower values of x have a much stronger increase in the percolating lithium fraction as a function of the number of transition metals in the simulation cell. This suggests any short-range order suppression observed in “high-entropy” disordered rock salt cathode will be highly dependent on the lithium and fluorine content and warrants further investigation. This dependence is highlighted in Fig. 5 which shows analysis of simulations on the system Li_1+xMO₂F_x over a wider value of x (x ∈ {0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1}). This is done for M = Mn (n_M = 1) and M = Mn_0.2Cr_0.2Fe_0.2Ni_0.2Ti_0.2 (n_M = 5). The increase in Li_active as a function of x for the two systems is shown in Fig. 5A, with the difference between these two series highlighted in Fig. 5B. Low values of x (x < 0.3) and high values of x (x > 0.6) see very little change in the amount of active lithium on increasing the number of transition metals, compatible with the observations made from Fig. 4.

Fig. 5 (A) The change in the mean active lithium percentage as a function of x in Li_1+xMnO₂F_x and Li_1+xMn_0.2Cr_0.2Fe_0.2Ni_0.2Ti_0.2O₂F_x as a function of x. (B) The difference between the two trends shown in plot (A).

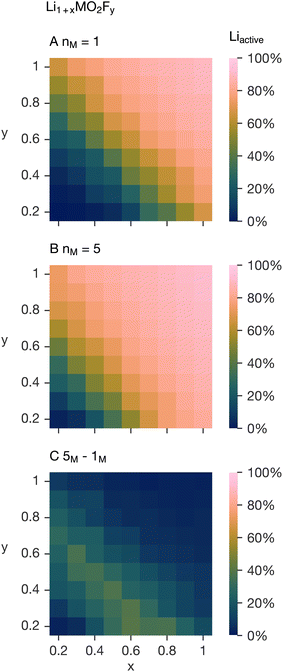
To explain these observations we note the lithium excess and fluorine substitution level are not necessarily coupled and extend the previous Monte Carlo simulations on the system Li_1+xMO₂F_y, i.e. the lithium excess, x, and fluorine content, y, are now varied independently between 0.2 and 1 in the n_M = 1 and n_M = 5 systems examined previously. Fig. 6A and B confirm that the active lithium fraction in the 5-TM system for the equivalent x and y is generally higher. The difference between Fig. 6A and B, shown in Fig. 6C, highlights that the increase in active lithium fraction from the 1-TM system to the 5-TM system is non-uniform as x and y are varied. The increase is minimal at high x and y, and shows a coupled dependence on lithium and fluorine contents at intermediate compositions. Increasing the fluorine content (increasing y) decreases the value of x for which the change between the 1-TM and 5-TM systems is at a maximum.

Fig. 6 (A) Active lithium fraction in Li_1+xMnO₂F_y as a function of x and y (B) active lithium fraction in Li_1+xMn_0.2Cr_0.2Fe_0.2Ni_0.2Ti_0.2O₂F_y as a function of x and y, (C) difference map between plots (A) and (B). Off-diagonal compositions on these plots are not strictly charge balanced, however we expect these fixed-composition simulations to capture local bonding preferences which determine the short range order.

This strong dependence on short-range order suppression by increased cation substitution on the lithium-excess and fluorine content can be understood by considering the cation–anion bonding preferences. The orbital overlap between transition metal d-states and oxygen 2p states will be much stronger than any interaction between the transition metal ions and the fluorine. This general chemical insight is reflected in the cation-coordination preferences observed in multiple previous Monte Carlo studies of transition metal oxyfluoride disordered rock salt cathode materials, with lithium having an above-average number of fluorine nearest neighbors, and transition metals coordinating to a higher number of oxide ions.^27,30,62

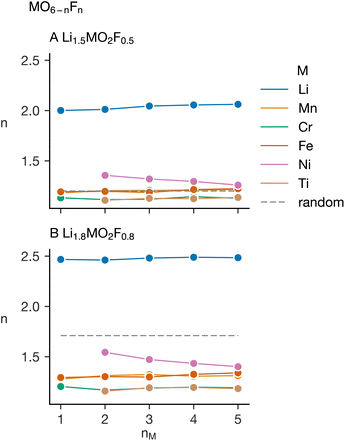
Fig. 7 shows the average coordination number of lithium and the transition metals with fluorine, for two cases: a Li–F poor case, Li_1.5MO₂F_0.5, and a Li–F rich case, Li_1.8MO₂F_0.8. The coordination numbers are displayed as a function of the number of transition metals in the simulation, n_M. As anticipated, lithium coordinates much more strongly to fluorine than the transition metals do. Among the transition metals, Ti(IV) and Cr(III) most strongly favour O²⁻ coordination. This preference, due to the high charge of Ti(IV) and the d³ electron configuration of Cr(III),³⁴ results in O-rich coordination environments. Ni(II), with its comparatively low charge, exhibits the highest average fluorine coordination among the transition metals. In the Li–F poor case, Ni(II) takes on higher-than-random F-coordination, influenced by the other transition metals stronger O²⁻ preferences, driving Ni(II) to coordinate with more fluorine, despite its inherent inclination towards oxygen. In the Li–F rich case, the heightened Li–F content serves to bring down the Ni–F-coordination below that expected in a random distribution. The nickel–fluorine average coordination decreases with increased n_M in these simulations; for charge conservation, there is always an equal Ti(IV) content. Introducing Mn(III) and Fe(III), with a weaker preference for O²⁻ coordination than Ti(IV) and Cr(III), enables Ni(II) to occupy cation sites with comparatively high oxygen coordination. Importantly, these plots underscore that multi-component cation substitution may somewhat mitigate short-range ordering preferences in these materials, but the strong preferences for transition-metal–oxygen bond formation persist.

Fig. 7 (A) A plot of metal–fluorine coordination numbers in Li_1.5MO₂F_0.5 as a function of the number of transition metals included in the simulation. (B) A plot of metal–fluorine coordination numbers in Li_1.8MO₂F_0.8 as a function of the number of transition metals included in the simulation. In both cases the grey dashed line shows the average metal–fluorine coordination number in the fully random system.

Bringing together the observations made in this study, we are able to suggest some guidelines for designing compositionally complex disordered rock salt cathode materials. Our simulations support that substituting many transition metals on the cation sublattice is a route to suppressing short-range order in lithium transition metal oxides, but diminishing returns are observed for short-range order suppression as the number of transition metals in the simulation is increased. This is likely due to extensive transition metal substitution not being able to fully counteract electrostatic and elastic interactions between the transition metals and the lithium which drive short-range order formation in disordered rock salt cathodes. This suggests that most of the benefit of short-range order suppression observed in many component systems should be observed in more “moderate entropy” disordered rock salts.

In addition, the relationship between short-range order suppression and the number of constituent cations is strongly influenced by the lithium-excess and fluorine content. While cation mixing is able to strongly increase the active lithium fraction in systems with comparatively low lithium–fluorine content, when the lithium excess is high and the fluorine content increases, the short range ordering formation is dominated by transition-metal–oxygen and lithium–fluorine bonding preferences as opposed to any improved cation mixing from many-transition-metal substitution.

It is worth noting that there may be beneficial effects in high-entropy disordered rock salt cathode materials with respect to lithium mobility. A “more disordered” system will likely see a wider range of site energies within the lithium transport network improving the conductivity as has been observed in a range of solid electrolyte materials;^65–68 these concepts are clearly extensible to intercalation cathodes.^69,70 However, we postulate that any increase in mobility will also be minimal at high fluorine and lithium contents as the formation of Li–F rich regions will minimise the impact of any local distortions that influence the site energies in the lithium diffusion pathway from introducing more transition metals.

The optimization of disordered rock salt cathode materials is a delicate balance between optimising the capacity of the material and the size of the percolating lithium network, while also considering the cycling stability and the synthesis methods. High lithium and fluorine content can lead to a large capacity from a large lithium-percolation network^30,71 (and redox participation from oxygen⁷) but poor cycling stability²⁷ and high energy intensive synthesis methods.^7,32 In addition, in rock salt structured transition metal oxides, electronic conductivity is mediated by small polaron hopping between adjacent redox-active transition metal sites.^72–75 While understudied in comparison to lithium ion percolation in disordered rock salt cathodes, the electronic carriers must also be able to percolate. As such, reducing the redox-active transition metal content via increasing the lithium content (and d⁰ spectator ion content) may significantly reduce the electronic conductivity of the cathode,⁷⁶ reducing, for example, the rate performance of the battery. These issues could be alleviated by utilising many-component cation mixing as an additional variable in the compositional design of disordered rock salt cathode materials, keeping lithium excesses and fluorine contents low while maintaining a large percolating lithium network. However, our results show that bonding interactions between cations and anions in many-component disordered rock salt cathode materials must be taken into account for optimal short-range order suppression.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Faraday Institution grant number FIRG017 and used the Michael Supercomputer (FIRG030). Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by the UK Engineering and Physical Sciences Research Council (EPSRC; EP/L000202, EP/R029431, EP/T022213), this work used ARCHER2 UK National Supercomputing Services. This work also used the the Myriad (Myriad@UCL) and Kathleen (Kathleen@UCL) supercomputers. We are also grateful to the UK Materials and Molecular Modelling Hub for computational resources, which is partially funded by EPSRC (EP/T022213/1, EP/W032260/1 and EP/P020194/1)

References

1. K. T. Lai, I. Antonyshyn, Y. Prots and M. Valldor, Anti-Perovskite Li-Battery Cathode Materials, J. Am. Chem. Soc., 2017, 139, 9645.
2. J. Cen, B. Zhu and D. O. Scanlon, Exploring battery cathode materials in the Li-Ni-O phase diagrams using structure prediction, ChemRxiv, 2022, preprint,  DOI:10.26434/chemrxiv-2022-gdmdh-v2.
3. B. Zhu and D. O. Scanlon, Predicting lithium iron oxysulfides for battery cathodes, ACS Appl. Energy Mater., 2022, 5, 575.
4. X. Hua, A. S. Eggeman, E. Castillo-Martínez, R. Robert, H. S. Geddes, Z. Lu, C. J. Pickard, W. Meng, K. M. Wiaderek, N. Pereira, G. G. Amatucci, P. A. Midgley, K. W. Chapman, U. Steiner, A. L. Goodwin and C. P. Grey, Revisiting metal fluorides as lithium-ion battery cathodes, Nat. Mater., 2021, 20, 841.
5. B. Zhu, Z. Lu, C. J. Pickard and D. O. Scanlon, Accelerating cathode material discovery through ab initio random structure searching, APL Mater., 2021, 9, 121111.
6. J. Lee, A. Urban, X. Li, D. Su, G. Hautier and G. Ceder, Unlocking the potential of cation-disordered oxides for rechargeable lithium batteries, Science, 2014, 343, 519.
7. R. A. House, L. Jin, U. Maitra, K. Tsuruta, J. W. Somerville, D. P. Förstermann, F. Massel, L. Duda, M. R. Roberts and P. G. Bruce, Lithium manganese oxyfluoride as a new cathode material exhibiting oxygen redox, Energy Environ. Sci., 2018, 11, 926.
8. R. J. Clément, Z. Lun and G. Ceder, Cation-disordered rocksalt transition metal oxides and oxyfluorides for high energy lithium-ion cathodes, Energy Environ. Sci., 2020, 13, 345.
9. H. Ji, J. Wu, Z. Cai, J. Liu, D.-H. Kwon, H. Kim, A. Urban, J. K. Papp, E. Foley, Y. Tian, M. Balasubramanian, H. Kim, R. J. Clément, B. D. McCloskey, W. Yang and G. Ceder, Ultrahigh power and energy density in partially ordered lithium-ion cathode materials, Nat. Energy, 2020, 5, 213.
10. A. Manthiram and J. B. Goodenough, Layered lithium cobalt oxide cathodes, Nat. Energy, 2021, 6, 323.
11. M. M. Thackeray and K. Amine, Layered Li–Ni–Mn–Co oxide cathodes, Nat. Energy, 2021, 6, 933.
12. B. E. Murdock, K. E. Toghill and N. Tapia-Ruiz, A perspective on the sustainability of cathode materials used in lithium-ion batteries, Adv. Energy Mater., 2021, 2102028.
13. Y. Lyu, L. Ben, Y. Sun, D. Tang, K. Xu, L. Gu, R. Xiao, H. Li, L. Chen and X. Huang, Atomic insight into electrochemical inactivity of lithium chromate (LiCrO₂): irreversible migration of chromium into lithium layers in surface regions, J. Power Sources, 2015, 273, 1218.
14. A. R. Armstrong and P. G. Bruce, Synthesis of layered LiMnO₂ as an electrode for rechargeable lithium batteries, Nature, 1996, 381, 499.
15. M. Hirayama, H. Tomita, K. Kubota and R. Kanno, Structure and electrode reactions of layered rocksalt LiFeO₂ nanoparticles for lithium battery cathode, J. Power Sources, 2011, 196, 6809.
16. I. Konuma, D. Goonetilleke, N. Sharma, T. Miyuki, S. Hiroi, K. Ohara, Y. Yamakawa, Y. Morino, H. B. Rajendra, T. Ishigaki and N. Yabuuchi, A near dimensionally invariable high-capacity positive electrode material, Nat. Mater., 2023, 22, 225–234.
17. X. Zhao, Y. Tian, Z. Lun, Z. Cai, T. Chen, B. Ouyang and G. Ceder, Design principles for zero-strain Li-ion cathodes, Joule, 2022, 6, 1654.
18. M. Nakajima and N. Yabuuchi, Lithium-Excess Cation-Disordered Rocksalt-Type oxide with nanoscale phase segregation: Li_1.25Nb_0.25V_0.5O₂, Chem. Mater., 2017, 29, 6927.
19. T. Matsuhara, Y. Tsuchiya, K. Yamanaka, K. Mitsuhara, T. Ohta and N. Yabuuchi, Synthesis and electrode performance of Li₄MoO₅-LiFeO₂ binary system as positive electrode materials for rechargeable lithium batteries, Electrochemistry, 2016, 84, 797.
20. N. Yabuuchi, M. Nakayama, M. Takeuchi, S. Komaba, Y. Hashimoto, T. Mukai, H. Shiiba, K. Sato, Y. Kobayashi, A. Nakao, M. Yonemura, K. Yamanaka, K. Mitsuhara and T. Ohta, Origin of stabilization and destabilization in solid-state redox reaction of oxide ions for lithium-ion batteries, Nat. Commun., 2016, 7, 13814.
21. N. Yabuuchi, M. Takeuchi, M. Nakayama, H. Shiiba, M. Ogawa, K. Nakayama, T. Ohta, D. Endo, T. Ozaki, T. Inamasu, K. Sato and S. Komaba, High-capacity electrode materials for rechargeable lithium batteries: Li₃NbO₄-based system with cation-disordered rocksalt structure, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7650.
22. S. Ren, R. Chen, E. Maawad, O. Dolotko, A. A. Guda, V. Shapovalov, D. Wang, H. Hahn and M. Fichtner, Improved voltage and cycling for Li⁺ intercalation in high-capacity disordered oxyfluoride cathodes, Adv. Sci., 2015, 2, 1500128.
23. X. Xu, L. Pi, J. J. Marie, G. J. Rees, C. Gong, S. Pu, R. A. House, A. W. Robertson and P. G. Bruce, Li₂NiO₂F a new oxyfluoride disordered rocksalt cathode material, J. Electrochem. Soc., 2021, 168, 080521.
24. A. Van der Ven, J. Bhattacharya and A. A. Belak, Understanding Li diffusion in Li-intercalation compounds, Acc. Chem. Res., 2013, 46, 1216.
25. H. Ji, A. Urban, D. A. Kitchaev, D.-H. Kwon, N. Artrith, C. Ophus, W. Huang, Z. Cai, T. Shi, J. C. Kim, H. Kim and G. Ceder, Hidden structural and chemical order controls lithium transport in cation-disordered oxides for rechargeable batteries, Nat. Commun., 2019, 10, 592.
26. A. Urban, J. Lee and G. Ceder, The configurational space of rocksalt-type oxides for high-capacity lithium battery electrodes, Adv. Energy Mater., 2014, 4, 1400478.
27. K. McColl, R. A. House, G. J. Rees, A. G. Squires, S. W. Coles, P. G. Bruce, B. J. Morgan and M. S. Islam, Transition metal migration and O₂ formation underpin voltage hysteresis in oxygen-redox disordered rocksalt cathodes, Nat. Commun., 2022, 13, 5275.
28. A. Urban, I. Matts, A. Abdellahi and G. Ceder, Computational design and preparation of cation-disordered oxides for high-energy-density Li-ion batteries, Adv. Energy Mater., 2016, 6, 1600488.
29. Y. Wang, S. Huang, B. Raji-Adefila, A. Outka, J.-H. Wang and D. Chen, Unraveling the nature and role of layered cation ordering in cation-disordered rock-salt cathodes, J. Am. Chem. Soc., 2022, 144, 19838.
30. B. Ouyang, N. Artrith, Z. Lun, Z. Jadidi, D. A. Kitchaev, H. Ji, A. Urban and G. Ceder, Effect of fluorination on lithium transport and short-range order in disordered-rocksalt-type lithium-ion battery cathodes, Adv. Energy Mater., 2020, 10, 1903240.
31. R. Schlem, C. F. Burmeister, P. Michalowski, S. Ohno, G. F. Dewald, A. Kwade and W. G. Zeier, Energy storage materials for solid-state batteries: design by mechanochemistry, Adv. Energy Mater., 2021, 11, 2101022.
32. N. J. Szymanski, Y. Zeng, T. Bennett, S. Patil, J. K. Keum, E. C. Self, J. Bai, Z. Cai, R. Giovine, B. Ouyang, F. Wang, C. J. Bartel, R. J. Clément, W. Tong, J. Nanda and G. Ceder, Understanding the fluorination of disordered rocksalt cathodes through rational exploration of synthesis pathways, Chem. Mater., 2022, 34, 7015.
33. V. C. Wu, H. A. Evans, R. Giovine, M. B. Preefer, J. Ong, E. Yoshida, P.-E. Cabelguen and R. J. Clément, Rapid and energy-efficient synthesis of disordered rocksalt cathodes, Adv. Energy Mater., 2023, 2203860.
34. Z. Lun, B. Ouyang, D.-H. Kwon, Y. Ha, E. E. Foley, T.-Y. Huang, Z. Cai, H. Kim, M. Balasubramanian, Y. Sun, J. Huang, Y. Tian, H. Kim, B. D. McCloskey, W. Yang, R. J. Clément, H. Ji and G. Ceder, Cation-disordered rocksalt-type high-entropy cathodes for Li-ion batteries, Nat. Mater., 2021, 20, 214.
35. C. M. Rost, E. Sachet, T. Borman, A. Moballegh, E. C. Dickey, D. Hou, J. L. Jones, S. Curtarolo and J.-P. Maria, Entropy-stabilized oxides, Nat. Commun., 2015, 6, 8485.
36. T. J. Harrington, J. Gild, P. Sarker, C. Toher, C. M. Rost, O. F. Dippo, C. McElfresh, K. Kaufmann, E. Marin, L. Borowski, P. E. Hopkins, J. Luo, S. Curtarolo, D. W. Brenner and K. S. Vecchio, Phase stability and mechanical properties of novel high entropy transition metal carbides, Acta Mater., 2019, 166, 271.
37. Q. Wang, A. Sarkar, D. Wang, L. Velasco, R. Azmi, S. S. Bhattacharya, T. Bergfeldt, A. Düvel, P. Heitjans, T. Brezesinski, H. Hahn and B. Breitung, Multi-anionic and -cationic compounds: new high entropy materials for advanced li-ion batteries, Energy Environ. Sci., 2019, 12, 2433.
38. S. W. Coles, V. Falkowski, H. S. Geddes, G. E. Pérez, S. G. Booth, A. G. Squires, C. O’Rourke, K. McColl, A. L. Goodwin, S. A. Cussen, S. J. Clarke, M. Saiful Islam and B. J. Morgan, Anion-polarisation-directed short-range-order in antiperovskite Li₂FeSO, J. Mater. Chem. A, 2023 10.1039/D2TA10037A.
39. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python materials genomics (pymatgen): a robust, open-source python library for materials analysis, Comput. Mater. Sci., 2013, 68, 314.
40. M. L. Waskom, Seaborn: statistical data visualization, J. Open Source Softw., 2021, 6, 3021.
41. Data structures for statistical computing in python, McKinney, 2010, 445.
42. P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt and SciPy 1.0 Contributors, SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python, Nat. Methods, 2020, 17, 261.
43. C. R. Harris, K. J. Millman, S. J. van der Walt, R. Gommers, P. Virtanen, D. Cournapeau, E. Wieser, J. Taylor, S. Berg, N. J. Smith, R. Kern, M. Picus, S. Hoyer, M. H. van Kerkwijk, M. Brett, A. Haldane, J. F. del Río, M. Wiebe, P. Peterson, P. Gérard-Marchant, K. Sheppard, T. Reddy, W. Weckesser, H. Abbasi, C. Gohlke and T. E. Oliphant, Array programming with NumPy, Nature, 2020, 585, 357.
44. F. Pedregosa, Scikit-learn: machine learning in python, J. Mach. Learn. Res., 2011, 12, 2825.
45. F. Crameri, G. E. Shephard and P. J. Heron, The misuse of colour in science communication, Nat Commun, 2020, 11, 5444.
46. F. Crameri, G. E. Shephard and P. J. Heron, The misuse of colour in science communication, Nat. Commun., 2020, 11, 5444.
47. A. G. Squires and D. O. Scanlon, Dataset and Model for “Understanding the limits to short-range order suppression in many-component disordered rock salt lithium-ion cathode materials”, Zenodo, 2023 DOI:10.5281/zenodo.8005679.
48. G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
49. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
50. G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15.
51. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
52. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
53. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Restoring the density-gradient expansion for exchange in solids and surfaces, Phys. Rev. Lett., 2008, 100, 136406.
54. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: an LSDA+U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505.
55. L. Wang, T. Maxisch and G. Ceder, Oxidation energies of transition metal oxides within the GGA+U framework, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107.
56. B. J. Morgan and G. W. Watson, Polaronic trapping of electrons and holes by native defects in anatase TiO₂, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 233102.
57. J. H. Yang, T. Chen, L. Barroso-Luque, Z. Jadidi and G. Ceder, Approaches for handling high-dimensional cluster expansions of ionic systems, npj Comput. Mater., 2022, 8, 1.
58. L. Barroso-Luque, P. Zhong, J. H. Yang, F. Xie, T. Chen, B. Ouyang and G. Ceder, Cluster expansions of multicomponent ionic materials: formalism and methodology, Phys. Rev. B, 2022, 106, 144202.
59. M. Ångqvist, W. A. Muñoz, J. M. Rahm, E. Fransson, C. Durniak, P. Rozyczko, T. H. Rod and P. Erhart, ICET – a python library for constructing and sampling alloy cluster expansions, Adv. Theory Simul., 2019, 2, 1900015.
60. E. Fransson, F. Eriksson and P. Erhart, Efficient construction of linear models in materials modeling and applications to force constant expansions, npj Comput. Mater., 2020, 6, 1.
61. P. Erhart, B. Sadigh, A. Schleife and D. Åberg, First-principles study of codoping in lanthanum bromide, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 165206.
62. P. Zhong, Z. Cai, Y. Zhang, R. Giovine, B. Ouyang, G. Zeng, Y. Chen, R. Clément, Z. Lun and G. Ceder, Increasing capacity in disordered rocksalt cathodes by Mg doping, Chem. Mater., 2020, 32, 10728.
63. C. O'Rourke and B. Morgan, Crystal-torture: a crystal tortuosity module, J. Open Source Softw., 2019, 4, 1306.
64. L. V. Kantorovich, Mathematical methods of organizing and planning production, Manag. Sci., 1960, 6, 366.
65. Y. Zeng, B. Ouyang, J. Liu, Y.-W. Byeon, Z. Cai, L. J. Miara, Y. Wang and G. Ceder, High-entropy mechanism to boost ionic conductivity, Science, 2022, 378, 1320.
66. J. Lin, G. Cherkashinin, M. Schäfer, G. Melinte, S. Indris, A. Kondrakov, J. Janek, T. Brezesinski and F. Strauss, A high-entropy multicationic substituted lithium argyrodite superionic solid electrolyte, ACS Mater. Lett., 2022, 4, 2187.
67. F. Strauss, J. Lin, M. Duffiet, K. Wang, T. Zinkevich, A.-L. Hansen, S. Indris and T. Brezesinski, High-entropy polyanionic lithium superionic conductors, ACS Mater. Lett., 2022, 4, 418.
68. S. Wang, Y. Liu and Y. Mo, Frustration in super-ionic conductors unraveled by the density of atomistic states, Angew. Chem., Int. Ed., 2023, 62, e2022155.
69. Z. Rong, R. Malik, P. Canepa, G. Sai Gautam, M. Liu, A. Jain, K. Persson and G. Ceder, Materials design rules for multivalent ion mobility in intercalation structures, Chem. Mater., 2015, 27, 6016.
70. M. Liu, Z. Rong, R. Malik, P. Canepa, A. Jain, G. Ceder and K. A. Persson, Spinel compounds as multivalent battery cathodes: a systematic evaluation based on ab initio calculations, Energy Environ. Sci., 2015, 8, 964.
71. Z. Lun, B. Ouyang, Z. Cai, R. J. Clément, D.-H. Kwon, J. Huang, J. K. Papp, M. Balasubramanian, Y. Tian, B. D. McCloskey, H. Ji, H. Kim, D. A. Kitchaev and G. Ceder, Design principles for high-capacity Mn-based cation-disordered rocksalt cathodes, Chem, 2020, 6, 153.
72. K. Hoang and M. D. Johannes, Defect chemistry in layered transition-metal oxides from screened hybrid density functional calculations, J. Mater. Chem. A, 2014, 2, 5224.
73. K. Hoang, Understanding the electronic and ionic conduction and lithium over-stoichiometry in LiMn₂O₄ spinel, J. Mater. Chem. A, 2014, 2, 18271.
74. K. Hoang, Defect physics, delithiation mechanism, and electronic and ionic conduction in layered lithium manganese oxide cathode materials, Phys. Rev. Appl., 2015, 3, 024013.
75. A. Bhargava, R. Eppstein, J. Sun, M. A. Smeaton, H. Paik, L. F. Kourkoutis, D. G. Schlom, M. Caspary Toroker and R. D. Robinson, Breakdown of the Small-Polaron Hopping Model in Higher-Order Spinels, Adv. Mater., 2020, 32, e2004490.
76. H. Li, R. Fong, M. Woo, H. Ahmed, D.-H. Seo, R. Malik and J. Lee, Toward high-energy Mn-based disordered-rocksalt Li-ion cathodes, Joule, 2022, 6, 53.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta02088f

---