Bandgap engineering of MXene compounds for water splitting

Abstract

MXene compounds, a recently discovered family of 2D materials, have been found to become semiconductors and photoactive when their pristine surfaces are functionalized with an electronegative termination. MXenes may present different compositions and structures, depending on the transition metal (M), the X-element (C or N), the stacking, and the termination position. The present work uses density functional theory calculations to engineer the bandgap of a wide range of MXenes by their structure, composition, and surface termination with oxygen, in order to find suitable materials for water splitting photocatalysis. Results show that pristine MXenes present metallic character in all cases, while adding the O-termination increases their chance of becoming a semiconductor. Group III and IV MXenes turn out to be the most promising bandgap systems for photocatalysis. Concerning the X element, C-MXenes exhibit more cases with a bandgap than N-MXenes, and, generally, with larger values. Factors such as the specific O-termination hollow site and stacking may affect the bandgap under certain circumstances, but such influences are found to be subtle and irregular. Finally, for all the cases presenting a bandgap larger than 1.23 eV, the minimum demanded for the water splitting process, the band alignment with respect to the water splitting half-reaction potentials was studied, obtaining Zr₂CO₂ as a promising photocatalyst for this process.

---

1. Introduction

With the growing awareness of global warming and environmental pollution, the interest in green fuel manufacturing and the sustainable use of renewable sources of energy has increased. Hydrogen (H₂), a clean-burning fuel, is considered to be one of the most promising power source candidates for accomplishing these goals. There are several methods for hydrogen production, but one of the most sustainable ones is by overall water splitting, where water (H₂O), an affordable and renewable resource, is broken down into hydrogen and oxygen (O₂). However, this is a highly endothermic and energy demanding process —ΔH° = 2.96 eV. As a result, the search for novel materials that serve as catalysts for this reaction is essential for green H₂ generation. A particularly appealing alternative is the use of solar light as a renewable and sustainable source of energy for carrying out such a reaction, and, therefore, photocatalysts have proved to be the leading option. On the other hand, since experiments are costly and time-consuming, the process of identifying suitable photocatalysts may now be accelerated thanks to the vast advancements in computational methodologies, such as density functional theory (DFT) screening.

This is tackled here with light shed upon MXene compounds as potential photoactive materials for water splitting. MXenes are one of the largest two-dimensional (2D) materials family firstly isolated by Naguib et al.¹ These materials are few-layered transition metal carbides and nitrides with chemical formula M_n+1X_n, where n = 1–3, M is commonly an early transition metal from groups III to VI, i.e. Sc, Y, Ti, Zr, Hf, V, Nb, Ta, Cr, Mo or W, and X can be carbon or nitrogen. These 2D compounds originate from the selective removal of A elements from their precursor MAX phases, where A is usually a group XIII–XVI element.² The removal of A is generally carried out by selective etching with acidic solutions such as hydrofluoric acid (HF),³ although other methods including delamination⁴ and vapour deposition⁵ have also been found to be useful in the synthesis of MXenes.

During the last decade, MXenes have been revolutionizing research providing a broad range of applications.^6–8 For instance, MXenes have been found to be convenient materials for storing energy in lithium-based ion batteries,^9,10 and as supercapacitor materials,¹¹ or even for use in cancer therapy.¹² In addition, they have been proposed as methane storage materials,¹³ while computational simulations, mostly DFT-based, showed them to be viable materials for sensors,^14,15 carbon dioxide (CO₂) capture and use,^16,17 hydrogen storage materials,¹⁸ and materials for nanoscale superconductivity.¹⁹ As far as photocatalytic water splitting is concerned, MXenes have also been suggested to be suitable photocatalytic materials for CO₂ photoreduction²⁰ and H₂ generation from water.^21,22 MXenes are appealing materials since their few-layered 2D structures feature high surface area, allowing for large-scale chemical conversions. Besides, even though they are, a priori, metastable compounds —since they can convert into 3D bulk metal carbides and nitrides— they can be stable up to 1000 K, as found for Ti₃C₂T_x,²³ due to their strong chemical bonds. In addition, MXene composition and structure can be easily modified, and this versatility can be used to tune their physicochemical properties at will, ultimately targeting a desired goal.

Aside from the M, X, and n composition of all possible pristine MXenes, these compounds can easily have their surfaces functionalized with various chemical groups, and so are often referred to as M_n+1X_nT_x, with T_x being the termination group. Apart from the regular O, F, OH, and H terminations resulting from HF-based synthesis,²⁴ other terminations have been reported,²⁵ including S, Se, Te, NH, Cl, and Br. On top of that, MXenes do not necessarily have to follow the regular ABC stacking inherited from the precursor MAX phases, and some pristine and O-terminated MXenes, with T_x = O₂, have been shown to prefer to adopt an ABA stacking,²⁶ which influences their electronic properties.²⁷ Thus, in the interest of determining which MXenes are good candidates for possible photocatalytic applications, e.g. water splitting, the bandgap and band structure of these compounds must be inspected as a function of composition, stacking, and termination.

Since the above can be experimentally an expensive, time-consuming process, sometimes inhibited by difficulties in the synthesis of certain MXene compounds, the initial computational assessment is one of the most effective and efficient strategies to quickly screen over large sets of samples. Here, DFT is systematically employed in suited MXene surface slab models to evaluate a wide range of factors affecting the bandgap and band structure in the M₂X and M₂XO₂ subset MXene family, weighting the influence of the M metal and X (C or N) components, the stability of the different possible ABC and ABA stackings, and how the O-termination, which has shown the most promising results so far,^7,28 modifies the electronic properties. There are previous theoretical investigations related to the use of MXenes as photoactive materials for water splitting, but, while most of them focus on a few specific cases^21,29 or MXene nanocomposites,³⁰ the present study particularly offers an unprecedented comprehensive computational study over a wide range of MXenes, including those that have not been extensively investigated before, as group V and VI C-MXenes, and all N-MXenes, also considering all possible structures, including the two possible stackings of the MXene and all the feasible O sites on the surface, which are neglected in most studies. For those MXenes with semiconductor properties, their adequacy to be a candidate to photocatalyze the water splitting process is also evaluated by looking at whether the valence and conduction band edges of the bandgap exceed the potentials of the water splitting half-reactions, and how certain surface properties such as the surface dipole moment are key in the sought band limit placements. Note that the bandgap size and the frontier bands placement are necessary conditions for the photocatalytic water splitting, but not the sole conditions,³¹ and other aspects, such as optical absorption,³² exciton formation, carrier mobility,³³ and the actual reaction energy profile and kinetics in the excited state^34,35 can bias the full process, and should be regarded in future studies after the present screening.

The photocatalytic performance in water splitting for semiconductor materials with the right bandgap size and band alignment has been experimentally proven on textbook semiconductor materials, such as rutile and anatase TiO₂ and ZnO,^36–38 the former being explicitly computationally evaluated on a rutile TiO₂ (110) surface.³⁵ Such studies validate the presently used assessment approach to propose candidate MXenes as educated guesses. Moreover, note that the present information is not only useful for the photocatalytic water splitting, but potentially useful for other light-triggered and/or photoactivated processes.

2. Computational details and models

The present DFT results^39,40 were obtained using the Vienna ab initio simulation package (VASP).⁴¹ The core electrons and their interaction with the valence electrons were represented using projector augmented wave (PAW) pseudopotentials,⁴² while the valence electrons were described using a plane wave basis set with an optimal kinetic energy cutoff of 415 eV, as previously tested and validated.^16,17,26,27 Spin-polarized calculations were carried out using the Perdew–Burke–Ernzerhof (PBE)⁴³ exchange–correlation functional within the generalized gradient approximation (GGA),⁴⁴ with additional calculations applying the PBE0 hybrid functional for a more reliable bandgap estimation.⁴⁵ The convergence criteria for the optimizations were set at 10⁻⁶ eV for the self-consistent field steps in all cases, and optimizations were considered converged when forces acting on atoms were less than 0.01 eV Å⁻¹. During the optimizations, all atomic positions and lattice parameters were allowed to relax.

For all the studied cases, p(1 × 1) hexagonal unit cells were used for modelling the structures, and optimal Γ-centred 7 × 7 × 1 Monkhorst–Pack⁴⁶k-point grids were employed for the Brillouin zone integration, except for band structure calculations, explored along the Γ → K → M path. To represent the slab models, 10 Å of vacuum was always added perpendicular to the MXene 2D surface, since previous studies and present tests revealed it to be enough to avoid possible interactions between adjacent slabs.^17,26 In order to obtain more precision in the band alignment and vacuum energy calculations, a wider vacuum of 30 Å was added to the slab in these single-point calculations.

Since test calculations on Hf₂CO₂ fully relaxed with PBE0 revealed that the band structure and density of states (DOS) results were very similar to the ones obtained from PBE-optimized geometries, and, given the higher computational cost of PBE0 structure optimizations, PBE0 single points were computed on PBE geometries. Nonetheless, PBE0 band structure calculations using plane waves still require a large amount of computational resources, and, therefore, these calculations were carried out using the Fritz-Haber Institute ab initio molecular simulations (FHI-AIMS)⁴⁷ program which uses numerical atomic orbitals (NAOs) as a basis set, and explicitly includes all core electrons in the electronic structure calculations. Despite being an all-electron program, the number of NAOs basis functions needed is smaller than using plane waves, thus outperforming the calculations based on plane waves when applying hybrid functionals. The self-consistent field and optimization criteria for FHI-AIMS are set to be equivalent to the ones used in VASP, to maintain the same computational ground, and, hence, the same 7 × 7 × 1 k-point grid and Γ → K → M path were maintained for the band structure calculations. As a basis set, a light tier-1 level was used, with a quality similar to the Dunning Gaussian type orbitals (GTO) aug-cc-pVDZ basis set, and energy converged to the order of meV.⁴⁸ The effect of dispersion van der Waals interactions on the band gap and relative stability energies have been evaluated in some test systems by including Grimme's D3 correction.⁴⁹ These effects were found to be negligible as can be derived from results shown in Tables S1 and S2 of the ESI.†

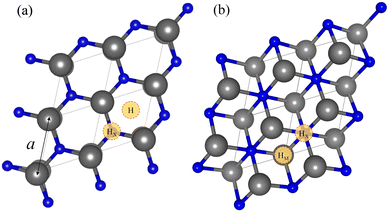
As per the models, we focused on n = 1 MXenes, with chemical formula M₂X when pristine and M₂XO₂ when O-terminated. They were studied for M early transition metals from groups III to VI, i.e. Sc, Y, Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, or W, while X is either carbon (C) or nitrogen (N). Pristine MXene structures consist of an X atom close-packed layer sandwiched in between two M close-packed sheets. Two possible stacking configurations arise for these three layers, ABA stacking, see Fig. 1a, with the M layers in the same relative position along the vacuum direction, or ABC stacking, see Fig. 1b, with the M layers in two different relative positions. The initial lattice parameters and layer width employed are in line with previous studies optimizing such systems also at the PBE level.^26,50,51 The O-terminated MXenes are initially built by adding the O atoms to the optimized pristine MXene structures, sampling different surface hollow sites. Hence, various configurations have been explored: (i) the metal hollow in ABC stacking, H_M, located above an underlying metal atom, (ii) the simple hollow in ABA stacking, H, placed with no atoms underneath, (iii) the carbon or nitrogen hollows, H_X, with an underlying X atom for both stackings, and (iv) a mixture of H_M (H) and H_X on opposite MXene surfaces for ABC (ABA) stacking, H_MX. By combining stacking and hollow sites, each O-terminated MXene has six possible structures, shown in Fig. 2. This notation will be used in the following discussion.

Fig. 1 Top view of the pristine MXene structures with (a) ABA and (b) ABC stacking. The yellow circles mark high symmetry sites where a termination could be placed —H stands for hollow, H_M for metal hollow and H_X for carbon/nitrogen hollow. The transition metal (M) and C or N (X) are represented by grey and blue spheres, respectively. The p(1 × 1) unit cell is indicated by grey lines, and the cell parameter, a, by a black arrow.

Fig. 2 Side views of the six possible configurations for an O-terminated MXene. (a)–(c) represent the H_M, H_MX, and H_X configurations for the ABC stacking, while (d)–(f) represent the H, H_MX, and H_X structures for ABA stacking, respectively. O atoms are shown as red spheres. The rest of the colour coding is as in Fig. 1. The lattice parameter, a, width, d, and M–O interplanar distance, h_MO, are represented by black arrows.

3. Results and discussion

3.1. Pristine MXenes—M₂X

First, a geometry optimization at the PBE level was carried out for the studied pristine MXenes. The relaxed lattice parameters, a, and MXene widths, d, as represented in Fig. 1 and 2, are gathered in Table S3 of the ESI.†Fig. 3 shows the a and d trends along the M series and groups, revealing that the optimized geometry of the MXene is mainly controlled by atom repulsions, as shown in Fig. 3a since, as the M radius increases,⁵² so does the cell parameter a, following similar trends. With respect to the X component, N-MXenes show, overall, lower a values compared to C-MXenes, by ∼0.08 Å on average, mostly due to the smaller size of N compared to C, and the larger electron affinity of N, which translates into shorter M–N bonds. As far as the stacking is concerned, ABC generally shows somewhat larger cell parameters, by ∼0.10 Å on average, but thinner widths, d, by ∼0.32 Å on average, than those found for ABA (see Fig. 3b). This can be easily explained in terms of steric and/or coulombic repulsions between the two M layers (see Fig. 3c). In the ABA stacking the metals are on top of each other, and as a result the repulsion in the vacuum direction is maximized, leading to higher d values. On the other hand, in ABC the M atoms are shifted, interacting more laterally, and resulting in larger cell parameters and lower widths. The outliers of such a trend are Mo₂N and W₂N, displaying d values for ABC larger than for ABA, implying a comparable repulsion in between M layers regardless of the stacking, and also succinctly implying that such repulsion is not screened by the N inner layer.

Fig. 3 (a) Evolution of the cell parameter a, along the M element in the studied M₂X MXenes for ABC (left) and ABA (right) stackings, with a values on the left axis, while red circles indicate M radii,⁵²r, listed on the right axis. (b) Evolution of the MXene width, d, for the studied cases, with dashed and straight lines indicating ABA and ABC stackings, respectively. Filled and blank black circles indicate C- and N-MXenes, respectively. All values are given in Å. (c) Schematic representation of the M–M repulsion in the MXenes unit cell for both stackings.

The stability of the two possible ABC and ABA stackings is also assessed. The relative stacking stabilities are shown in Fig. 4, where ΔE_stack is the difference between ABA and ABC total energies, i.e. ΔE_stack = E_ABA − E_ABC, so the more negative the ΔE_stack is, the more preference there is towards ABA, and vice versa. For most pristine MXenes, ABC stacking is more stable than ABA, with the exception of most group VI M cases, Mo₂X, W₂X, and Cr₂N, plus the group V Ta₂N system, which show an energetic preference for ABA stacking, in accordance with the literature.²⁶ In general terms, having N favours a lower, even negative ΔE_stack, reduced by 0.37 eV on average —with the sole exceptions of W₂X and Y₂X, where the order is reversed, to the point of favouring ABA for Ta₂N and Cr₂N. Down the groups, the relative stacking stability remains roughly constant, except for group III N-MXenes and group IV C-MXenes, which seem to strengthen their ABC preference. Note that in most cases the energy difference is large, i.e. ΔE_stack > 0.5 eV, like for group III and IV metals. Therefore, a clear preference for ABC stacking can be safely claimed. However, for groups V and VI, the ΔE_stack is smaller, to the point of ABC and ABA being nearly degenerate, like in Nb₂N (0.06 eV) or Cr₂C (0.02 eV), which could mean that some MXenes may interconvert between stackings or have co-existing domains with different stackings.

Fig. 4 Relative structural stabilities for ABA and ABC stackings represented by their difference in energy, ΔE_stack, in eV. Negative values indicate preference for ABA stacking.

The electronic properties of pristine M₂X MXenes were studied by means of band structure and DOS calculations, and are shown in Fig. S1 of the ESI.† Given the strong metallic character of the transition metal, all the studied pristine MXenes happen to feature metallic band structures, with no bandgap, and the Fermi level, E_F, is highly populated, in agreement with previous studies.⁷ Specifically, the Fermi level lies mainly in the transition metal d-band, while the presence of the X p-orbitals is mostly in the lower, bonding energy levels, normally separated by a gap from the d-band. Since all considered pristine MXenes were found to be metallic, no further calculations using PBE0 were necessary to estimate the proper bandgap sizes, and the rest of the study focused on O-terminated MXenes.

3.2. O-Terminated MXenes—M₂XO₂

After adding oxygen to the pristine MXene surfaces, the lattice and atomic positions were fully optimized again. The O-terminated MXene structures follow similar patterns to their pristine MXene counterparts, and for that reason we will review the general trends on the same grounds, while the obtained lattice parameters a and widths d are gathered in Table S4 of the ESI.† The trends, available in Fig. S2 and S3 of the ESI,† reveal that the N-MXenes show shorter a values compared to C-MXenes. H_MX and H_X sites present similar a values in both ABC and ABA stackings, with average deviations of ca. 0.03 Å, except for group III H_MX C-MXenes, with differences of 0.16 Å on average. In contrast, H_M in ABC and H in ABA show variations of the order of 0.08 Å on average. This highlights the fact that H_MX and H_X are similar for both stackings, while H_M and H, with different relative positions, are not. Moreover, leaving aside group III C-MXenes, the following trend for the cell parameter is found: a(H_M/H) > a(H_MX) > a(H_X).

In terms of the MXene width, d, ABA stacking presents larger values than ABC, similar to pristine MXenes, and again with singularities in the observed trend for Mo₂NO₂ and W₂NO₂ as earlier seen for pristine MXenes. Validating such geometric data is complicated, since the available experimental data to compare with on fully pristine or O-terminated MXenes is scarce, mostly due to the fact that the synthesis of MXenes from their MAX precursor phases generally leads to functionalized MXenes with different terminations, e.g. having simultaneously F, O, and OH.¹ Nonetheless, some information has been reported, such as the cell parameters of 3.01 Å for Ti₂CO₂ (ref. 25) and 2.86 Å for Mo₂CT_x,⁵³ which essentially match the computed values in the most stable ABC H_M configuration for Ti₂CO₂ of 3.01 Å and ABA H_X configuration for Mo₂CO₂ of 2.87 Å. Furthermore, such cell parameter values are closest to the ones predicted for the most stable configuration, which reinforces the predictive character of the present DFT simulations.

The relative stabilities of the different configurations, ΔE, have been calculated relative to the corresponding ABC H_M structure (see Table S5 of the ESI†). By inspecting trends, as shown in Fig. 5, one sees that ABC stacking is generally preferred except for group VI M₂XO₂ and V₂NO₂ on H_X sites. In the rest of the cases the ABC stacking with the O on the H_M sites is the most stable structure, except for group V Nb₂NO₂ and Ta₂NO₂ where the H_X sites are more favourable, and group III M₂CO₂ which prefers the H_MX sites. As shown before on pristine MXenes, O-terminated N-MXenes feature more cases where the ABA stacking is energetically more favourable than ABC, leading to the conclusion that having X = N favours this arrangement. Last but not least, notice that both C- and N-MXenes follow a similar pattern when increasing the number of d electrons of the metals, i.e. going right on the d series. For groups III and IV, the relative energy difference, ΔE, tends to increase, but then the values reduce for group V, while ΔE < 0 for group VI.

Fig. 5 Relative energy differences, ΔE, in eV, for each O-functionalized MXene, with respect to the ABC H_M case, considering ABC/ABA stacking and different hollow positions. The left (right) panel represents the C-MXenes (N-MXenes).

As previously stated, adding a termination to the MXene surface can greatly change its electronic structure, influencing its band structure and DOS. Even though O-terminated MXenes have an energetically preferred structure from the six configurations explored before, it is important to assess how the stacking and hollow position may affect the MXene electronic properties. The added O atoms generate new bands below the Fermi level and the X p-bands, resulting from the hybridization of O p orbitals with the d orbitals of the M atoms. These new bands withdraw M d-electron density, while shifting the Fermi level to lower energies, to the point that, for some MXenes, E_F lies in the energy gap between the X p- and M d-bands, as seen for Hf₂CO₂ in Fig. 6a. Nevertheless, many MXenes have the X p- and M d-bands overlapped, or the E_F shift is not large enough, and, therefore, no bandgap is generated, exemplified in Hf₂NO₂ in Fig. 6b, ending in a metallic electronic structure.

Fig. 6 Total and projected DOS calculated at the PBE0 level for (a) Hf₂CO₂ and (b) Hf₂NO₂ in their most stable structure, ABC stacking and oxygens in H_M, referenced to the VBM and E_F levels, respectively.

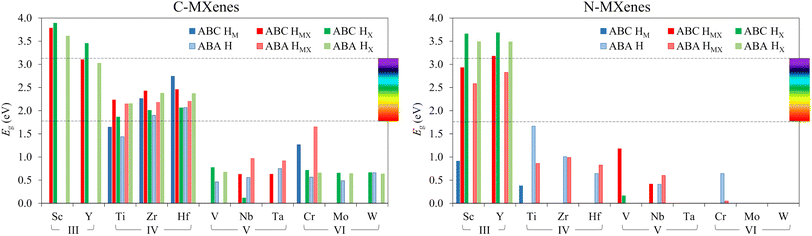
The results of the PBE0 computed bandgaps, E_g, for the studied MXenes are displayed in Fig. 7, while their values, accounting also for PBE results, are reported in Table S6 of the ESI, while Fig. S4 of the ESI† displays the DOS for all such systems. Since the PBE0 bandgap values are, in principle, more accurate and reliable, these will be the ones used in the following discussion. As can be seen in Fig. 7, the candidates with the largest bandgap appear to be group III and IV MXenes —i.e. when M = Sc, Y, Ti, Zr, and Hf. In most of these cases, they present bandgaps that land within the visible spectrum range —from 1.8 to 3.1 eV— or even higher, like in many Sc- and Y-based systems. In contrast, groups V and VI feature fewer semiconducting cases, and when they do, the bandgaps are smaller than those of groups III and IV. In terms of the band structure, almost all semiconducting MXenes present an indirect bandgap —regular values in Table S6 of the ESI†— with the exception of some C-MXenes in their H_X or H_MX structure, specially from group III, having a direct bandgap —bold values in Table S6 of the ESI.†

Fig. 7 Calculated bandgap, E_g, in eV, with the PBE0 functional, for the studied O-terminated MXenes in the six different O-terminated configurations. On the left (right) are represented the C-MXenes (N-MXenes). In each plot the range of the visible spectrum is displayed, from 1.8 to 3.1 eV.

Another observed trend is that C-MXenes feature more cases with a bandgap than N-MXenes, and that most of the C-MXenes with a finite bandgap diminish their values or even present no bandgap when X = N, see for instance the cases of group IV, although this latter trend is not followed, or even reversed, for group III MXenes. Within each group, different tendencies are found. For group III C-MXenes, the bandgap decreases going down the group, i.e. Y₂CO₂ has lower E_g than Sc₂CO₂, though the trend is reversed in group IV C-MXenes. However, such trends for groups III and IV are reversed when inspecting N-MXenes.

Since the metals in each group have similar electronic properties, the resulting bandgap values and band structures are similar, as seen exemplified in group IV C-MXenes in their most stable configuration (see Fig. 8). The comparison of the possible positions of the O-termination shows that H_X is the structure that results in larger bandgaps for group III MXenes and group IV C-MXenes with ABA stacking, leading to the conclusion that the closer the O is to the X atom, the larger the bandgap will become. On the other hand, depending on the M element and the O atom hollow position, the stacking itself may also influence the bandgap. Generally, the changes in E_g due to the stacking are subtle and irregular, except for some particular cases, such as V₂NO₂ and Sc₂CO₂, which have E_g values of 1.17 and 3.79 eV, respectively, with ABC stacking and H_MX O positions, but no bandgap in their analogous structures in ABA stacking. For group III C- and N-MXenes, ABC stacking shows slightly larger E_g than ABA. For group IV C-MXenes, the same trend follows for H_M and H_MX structures, while ABA shows higher E_g for H_X configurations. Instead, when X = N, group IV MXenes only show a bandgap with ABA H and H_MX structures. Group V and VI MXenes normally present lower bandgaps or fewer cases than groups III and IV, so no general trends have been gathered, although group V and VI C-MXenes show more bandgap cases with the ABA stacking.

Fig. 8 PBE0 band structure for (a) Ti₂CO₂, (b) Zr₂CO₂, and (c) Hf₂CO₂ in their most stable structure, ABC H_M. The blue-dotted line indicates the bandgap from the VBM to the CBM. The red-dashed line indicates the Fermi level, E_F, made to coincide with the VBM, to which all energies have been referenced.

Let us now deepen the study of Sc₂CO₂ and Y₂CO₂ systems, which seem interesting considering that their most stable structure is H_MX, instead of the most common H_M. Sc and Y, being group III transition metals, have less electrons in the d valence shell that could be donated to the O termination or the inner C layer. Therefore, in H_M configuration with ABC stacking, since O may not receive sufficient electron density, it could well move to the H_X site, as there would be less coulombic repulsion from the inner C layer, thus explaining the energetic preference of group III C-MXenes for the H_MX and H_X configurations over H_M. Analysing the DOS of the most stable Sc₂CO₂ H_MX structure, see Fig. 9, one can see that, as mentioned above, adding the O layers generates new O–M hybrid bands that shift E_F to lower energies. In the H_M structure, the two Sc atoms are equivalent and show only one band; however, for the H_MX hole, the band splits in two, one for each Sc, since each surface has a different local configuration, and actually could be regarded as Janus materials, i.e. materials with two different surface terminations. Moreover, the broad band where E_F lays on in H_M dissipates in the H_MX position. As Khazaei et al. suggested,²⁸ this could be due to the stronger interaction of the p_z orbitals between C and O being closer in the H_MX structure, splitting the broad non-bonding band into bonding–antibonding counterparts, giving rise to a bandgap.

Fig. 9 Total and projected DOS comparison of (a) Sc₂C (PBE) and Sc₂CO₂ (PBE0) with (b) H_M or (c) H_MX structures, all with ABC stacking. The energy levels are displayed with respect to the E_F level except for Sc₂CO₂ H_MX, referenced to the VBM.

3.3. Water splitting photocatalysis

To address the particular utility of the studied MXenes for water splitting catalysis, one should first recall that, for a semiconducting material to be an efficient solar-light harvesting photocatalyst, it must present a bandgap within the visible spectrum range. Besides, the band edges, this is, the valence band maximum (VBM) and the conduction band minimum (CBM), must also exceed the potentials of the redox half-reactions. For the case of the photocatalytic water splitting, the reduction (H⁺/H₂) and oxidation (H₂O/O₂) potentials are −4.44 eV and −5.67 eV, respectively,⁵⁴ with a difference between them of 1.23 eV. The VBM and CBM are calculated from the E_F and E_g, but need to be corrected with the vacuum potential, V_v, which indicates the electrostatic potential in the vacuum region of the slab model, extracted from the local potential plot along the vacuum direction perpendicular to the MXene surface (see Fig. S5 in the ESI†). The calculated V_v has also been used to estimate the material's work function, ϕ, defined as the energy required to extract an electron from the E_F and place it in the vacuum region, listed in Table 1.

Table 1 Work function, ϕ, values, in eV, for the MXene structures studied for water splitting photocatalysis. The values for H_MX represent the mean between both surfaces

X	M	ABC			ABA
		HM	HMX	HX	H	HMX	HX
C	Sc	—	5.58	6.22	—	—	5.58
	Y	—	4.74	5.55	—	—	4.94
	Ti	6.60	7.81	8.09	5.72	6.98	7.66
	Zr	6.18	7.24	7.74	5.14	6.32	7.22
	Hf	5.06	7.16	7.74	5.10	6.15	7.05
	Cr	8.35	—	—	—	8.65	—
N	Sc	7.92	8.11	8.52	—	7.52	8.19
	Y	—	7.50	8.00	—	6.99	7.62
	Ti	—	—	—	6.40	—	—

---

To determine whether the MXene bandgaps confine the water splitting half-reaction potentials, the VBM and CBM band alignment of promising MXenes showing a bandgap larger than 1.23 eV —the redox potential of the water splitting reaction— has been carried out and is shown in Fig. 10. Since many configurations are considered, different cases show a good band alignment for water splitting photocatalysis. From group IV C-MXenes these include Ti₂CO₂ with ABA stacking and oxygen on the H hollow sites, Zr₂CO₂ ABC H_M and ABA H_MX, and Hf₂CO₂ ABA H_MX. For group III MXenes, when X = C the VBM appears at higher energies and only one configuration has an adequate band alignment, Sc₂CO₂ in its ABC H_X configuration, although other structures such as ABC H_MX and ABA H_X and Y₂CO₂ ABC H_X present the VBM almost aligned with the oxidation process.

Fig. 10 VBM and CBM alignments with respect to H⁺/H₂ and H₂O/O₂ potential energy levels for group IV C-MXenes (left) and group III, Cr₂CO₂, and Ti₂NO₂ MXenes (right). The blue and orange bars indicate the VB and CB, respectively, and darker and lighter colours represent C- and N-MXenes, respectively.

When X = N the group III MXene band edges show much lower energies than their respective C-MXenes, and, in fact, Sc₂NO₂ does not feature any adequate band alignment. In contrast, all four Y₂NO₂ semiconducting configurations display appropriate band edges. As stated in the previous section, MXenes have an energetically preferred structure from the six possible ones. Thus, the ideal case from the studied configurations would be the one that has the most suitable band alignment and is the most stable structure of the corresponding MXene. These conditions hold only for Zr₂CO₂ ABC H_M with a bandgap of 2.26 eV, presenting it as the best applicable O-terminated MXene for photocatalytic water splitting.

Furthermore, in the search for adequate photocatalysts, one aspect to consider is the separation of charge density between the VBM and CBM, and if they are separated enough, localized in different layers for example, the photoexcited electron–hole pair can be efficiently separated, leading to a low electron–hole recombination rate and thus having the electron spending more time in the excited state. As shown in Fig. 11, the studied Zr₂CO₂ MXene presents a clear separation between the charge density of the VBM, which is located in the p orbitals of the C, and the CBM, localized in the d orbitals of the Zr, thus confirming Zr₂CO₂ possesses the features to be an adequate and efficient photocatalyst for the water splitting process.

Fig. 11 Charge density of the VBM (left, indicated with a blue surface) and CBM (right, indicated with an orange surface) of the Zr₂CO₂ MXene with ABC stacking and H_M structure, computed at the PBE0 level. Both surfaces have an isovalue of 0.015 e Å⁻³. The upper images represent the top views, while the lower ones represent the side views of the MXene.

Given that group IV C-MXenes show a bandgap in all six O-terminated structures, a deeper assessment of the band alignment is carried out. As seen in Fig. 10 (left), the same trend is repeated along the different oxygen hollow positions of each metal. In each stacking the H_X hollow site has the lowest VBM and CBM while H_M (ABC) or H (ABA) presents the highest values, leading to a recurrent staircase-like plot. The trend is repeated for all three group IV metals, since they present similar electronic properties, but also seems to hold for the VBM in group III MXenes. This pattern is related to the work function, ϕ, of the studied MXenes, since, as defined here, ϕ = −E_VBM. As seen in Table 1, the H_X configuration shows the highest ϕ in each stacking. The work function also depends on the local dipole moment on the surface of the material, which makes the electron extraction go along or against the dipole direction, easing or handicapping the process. In the studied MXenes, the electronegative O-terminations gather electron density from the transition metal layers, acquiring a negative partial charge (δ⁻), while the metal obtains a positive partial charge (δ⁺), leading to a local dipole moment from the O to the M atoms, thus hindering the electron removal.

Since the work function may be affected by the surface dipole moment, the former can thus be determining in the proper VBM and CBM level alignments. Considering that the dipole moment is related to the distance between the partial charges, one possible explanation for these ϕ and band alignment patterns can be related to the MXene width, d. As mentioned in the structural determination of O-terminated MXenes, the H_X structures generally show higher d and M–O distances than the other hollow sites, mainly due to the larger and direct repulsion between the closer O and X atoms, which translates into larger magnitudes of the dipole moment, and therefore higher ϕ values and lower VBM. The opposite applies, e.g. for H (H_M) sites in ABA (ABC) stacking, and so the surface dipole moment poses as an additional determining factor in the application of MXenes in photocatalysis, together with the extent of the E_g, and can be regarded as a way of tuning the MXenes' photocatalytic activity for desired purposes, e.g. adsorbing on their surfaces certain cations/anions to increase/decrease the work function, or even combining different elements in the surface T_x termination, e.g. mixing S and O atoms.⁵⁵

To provide a more quantitative interpretation of the mentioned trends between the MXene work function and its surface dipole moment, the Bader charges of the surface M and O in the MXene, q_M and q_O, were computed. The corresponding surface dipole moment, P, was calculated with an averaged charge q = (q_O − q_M)/2, times the distance between the M and O layers in the vacuum direction, h_MO, as indicated in Fig. 2, i.e. P = q × h_MO. For the H_MX adsorption sites, given their asymmetry, the layer distance or charges may be different for each surface and thus, the dipoles and work functions were considered as a mean of both surfaces. The results for the group III and IV C-MXene cases are shown in Fig. 12, while the remaining nitrogen ones are presented in Fig. S6 of the ESI.† In general, the trends show that there exists a linear relation—with regression coefficients, R, above 0.94 in almost all cases—between the work function and the surface dipole moment for each studied MXene among its configurations, and, so, the larger the surface dipole moment is, the larger is the work function, and thus the lower is the VBM energy (vide supra). This trend is persistent for N-MXenes. Within the same group, the first series metals, Sc and Ti, show lower surface dipole values than higher period metals, such as Y and Hf.

Fig. 12 Relation between the work function, ϕ, and the absolute surface dipole moment, P, for the group III and IV C-MXenes. On the right are present the colour coded linear regression equations.

3.4. PBE vs. PBE0 functionals

Finally, one has to keep in mind that, in the study of semiconductor materials, the applied computational approach is crucial in order to get a proper description of the systems.⁵⁶ In the present work, a GGA functional, the PBE, and a hybrid functional, PBE0, have been employed for calculating the DOS and band structures of the inspected MXenes. The GGA approach greatly underestimates the bandgap of semiconductor materials due to the undue delocalization of the electron density, resulting from the self-interaction energy error between electron densities, which can be counteracted when back-localizing the electron density using a percentage of Hartree–Fock exact exchange. Thus, for each found semiconducting MXene, the bandgap value as computed with PBE can be regarded as being underestimated, and PBE0 values are posed to deliver considerably larger and better-suited estimates. Still, PBE0 bandgaps can linearly correlate with PBE estimates, as observed for optical gaps on TiO₂ nanoparticles.⁵⁷ This is found here as well for E_g, although with different linear correlations for C- and N-MXenes, yet both with regression coefficients, R, larger than 0.95 (see Fig. 13). These correlations can be useful as they can be used to estimate, in a rapid fashion, the PBE0 bandgaps, which may be, otherwise, rather computationally consuming. Besides, the correlations show that for the same PBE estimate, N-MXenes have larger PBE0 E_g values. Moreover, even when the application of PBE0 increases the size of the bandgap, it does not seem to affect the fundamental DOS shapes and band structure dispersions. As can be seen in Fig. S7 of the ESI,† for Sc₂CO₂ and Y₂CO₂, the use of PBE0 mainly shifts up the virtual bands, keeping the shape, dispersion, and indirect or direct bandgap nature of the electronic excitation.

Fig. 13 Linear correlations between PBE0 and PBE E_g values, alongside the linear equation E_g (PBE0) = a × E_g (PBE) + b, and the regression coefficient, R. Green and blue dots denote C-MXene and N-MXene values, respectively.

4. Conclusions

In the present work, the bandgap of O-terminated MXenes (M = Sc, Y, Ti, Zr, Hf, V, Nb, Ta, Cr, Mo, and W, and X = C and N) was inspected and engineered by tuning their composition, stacking, and termination position using DFT estimates. The structural stability of the different configurations was assessed, revealing ABC to be the most favourable stacking for all cases except group VI MXenes, and finding H_M and H as the most preferable hollow positions in ABC and ABA stackings for group IV and V (III and IV) C-MXenes (N-MXenes), respectively, while H_MX is preferred for Sc₂CO₂ and Y₂CO₂ and H_X for group V N-MXenes and group VI MXenes. For the electronic properties, adding an O termination to the pristine MXene has proven to greatly increase the chance for the MXenes to become semiconductors with a sizeable bandgap. In fact, several O-terminated MXenes have been found to present a bandgap in the visible spectrum, in particular those with metals from group III and IV MXenes. Moreover, C-MXenes have shown more cases with a bandgap and with higher values than N-MXenes. Depending on the transition metal group and the nature of the X atom, the M atom seems to have an effect on the bandgap for group III and VI MXenes: group III (IV) C-MXenes exhibit lower (higher) bandgap values going down the group, while the trend is reversed for N-MXenes. Factors like hollow position and stacking may affect the bandgap under certain circumstances, but such influences are subtle and irregular.

Finally, after inspecting the cases that presented bandgaps over 1.23 eV, we found that Zr₂CO₂ meets the desirable conditions for photocatalysing the water splitting process, while also presenting a significant charge density separation between the VBM and CBM. Other group III and IV MXene configurations have also shown adequate band alignment but are not the most energetically stable structures. Within the band alignment it was gathered that for each stacking, group IV H_X C-MXenes display the lowest VBM and CBM, while H_M (ABC) and H (ABA) present the highest values, which is related to the work function, ϕ, and the local dipole moment present on the MXene surface.

In the present work, we underlined the photoactive properties of O-terminated MXene compounds and their structures in the generation of green H₂ from the water splitting process. Since O-terminated MXenes have presented promising results, it opens the door to study these compounds in different scenarios, such as varying the number of layers, changing the termination, or even combining various termination groups, also affecting the surface dipole moment to better place the VBM and CBM energy limits.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge financial support from the Spanish Ministerio de Ciencia e Innovación through grants PID2021-126076NB-I00 and TED2021-129506B-C22, the unit of excellence María de Maeztu CEX2021-001202-M granted to the IQTCUB, the COST Action CA18234, and the Generalitat de Catalunya 2021SGR00079 grant. F. V. is thankful for the ICREA Academia Award 2023 Ref. Ac2216561.

References

1. M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253.
2. M. Alhabeb, K. Maleski, T. S. Mathis, A. Sarycheva, C. B. Hatter, S. Uzun, A. Levitt and Y. Gogotsi, Angew. Chem., Int. Ed., 2018, 57, 5444–5448.
3. M. Naguib, O. Mashtalir, J. Carle, V. Presser, J. Lu, L. Hultman, Y. Gogotsi and M. W. Barsoum, ACS Nano, 2012, 6, 1322–1331.
4. M. Alhabeb, K. Maleski, B. Anasori, P. Lelyukh, L. Clark, S. Sin and Y. Gogotsi, Chem. Mater., 2017, 29, 7633–7644.
5. D. Geng, X. Zhao and K. Loh, 2D Mater., 2017, 4, 011012.
6. X. Li, F. Ran, F. Yang, J. Long and L. Shao, Trans. Tianjin Univ., 2021, 27, 217–247.
7. A. Champagne and J. C. Charlier, J. Phys. Mater., 2020, 3, 032006.
8. M. Khazaei, A. Ranjbar, M. Arai, T. Sasaki and S. Yunoki, J. Mater. Chem. C, 2017, 5, 2488–2503.
9. M. Naguib, J. Halim, J. Lu, K. M. Cook, L. Hultman, Y. Gogotsi and M. W. Barsoum, J. Am. Chem. Soc., 2013, 135, 15966–15969.
10. X. Tang, X. Guo, W. Wu and G. Wang, Adv. Energy Mater., 2018, 8, 1801897.
11. M. R. Lukatskaya, O. Mashtalir and Y. Gogotsi, Science, 2013, 341, 1502–1505.
12. H. Lin, X. Wang, L. Yu, Y. Chen and J. Shi, Nano Lett., 2017, 17, 384–391.
13. F. Liu, A. Zhou and Q. Hu, Adsorption, 2016, 22, 915–922.
14. X. Yu, Y. Li and B. Xiao, ACS Appl. Mater. Interfaces, 2015, 7, 13707–13713.
15. Y. Li, Z. Peng, N. J. Holl, M. R. Hassan, J. M. Pappas, C. Wei, O. H. Izadi, Y. Wang, X. Dong, C. Wang, Y.-W. Huang, D. Kim and C. Wu, ACS Omega, 2021, 6, 6643–6653.
16. Á. Morales-García, A. Fernández-Fernández, F. Viñes and F. Illas, J. Mater. Chem. A, 2018, 6, 3381–3385.
17. R. Morales-Salvador, J. D. Gouveia, Á. Morales-García, F. Viñes, J. R. B. Gomes and F. Illas, ACS Catal., 2021, 11, 11248–11255.
18. Q. Hu, D. Sun and J. He, J. Phys. Chem., 2013, 117, 14253–14260.
19. J. Zhang and S. Dong, J. Chem. Phys., 2017, 146, 034705.
20. J. Low, L. Zhang, T. Tong, B. Shen and J. Yu, J. Catal., 2018, 361, 255–266.
21. Z. Guo, J. Zhou, L. Zhu and Z. Sun, J. Mater. Chem. A, 2016, 4, 11446–11452.
22. G. Gao, A. P. O'Mullane and A. Du, ACS Catal., 2017, 7, 494–500.
23. Z. Li, L. Wang, D. Sun, Y. Zhang, B. Liu, Q. Hu and A. Zhou, Mater. Sci. Eng., B, 2015, 191, 33–40.
24. M. A. Hope, A. C. Forse, K. J. Griffith, M. R. Lukatskaya, M. Ghidiu, Y. Gogotsi and C. P. Grey, Phys. Chem. Chem. Phys., 2016, 18, 5099–5102.
25. V. Kamysbayev, A. S. Filatov, H. Hu, X. Rui, F. Lagunas, D. Wang, R. F. Klie and D. Talapin, Science, 2020, 369, 979–983.
26. J. D. Gouveia, F. Viñes, F. Illas and J. R. B. Gomes, Phys. Rev. Mater., 2020, 4, 054003.
27. A. Jurado, Á. Morales-García, F. Viñes and F. Illas, J. Phys. Chem. C, 2021, 125(48), 26808–26813.
28. M. Khazaei, M. Arai, T. Sasaki, C.-Y. Chung, N. S. Venkataramanan, M. Estili, Y. Sakka and Y. Kawazoe, Adv. Funct. Mater., 2013, 23, 2185–2192.
29. I. Ibrahim, S. Abdel-Azeim, A. El-Nahas, O. Kühn, C. Chung, A. El-Zatahry and M. Shibl, J. Phys. Chem. C, 2022, 126, 14886–14896.
30. Y. Sun, D. Jin, Y. Sun, X. Meng, Y. Gao, Y. Dall'Agnese, G. Cheng and X. Wang, J. Mater. Chem. A, 2018, 6, 9124–9131.
31. Á. Morales-García, F. Viñes, C. Sousa and F. Illas, J. Phys. Chem. Lett., 2023, 14, 3712–3720.
32. F. Viñes, M. Berneches, G. Konstantatos and F. Illas, Phys. Rev. B, 2016, 94, 235203.
33. A. Iglesias-Juez, F. Viñes, O. Lamiel-García, M. Fernández-García and F. Illas, J. Mater. Chem. A, 2015, 3, 8782–8792.
34. A. Migani and L. Blancafort, J. Am. Chem. Soc., 2016, 138, 16165–16173.
35. A. Migani and L. Blancafort, J. Am. Chem. Soc., 2017, 139, 11845–11856.
36. Z. Guo, F. Ambrosio and A. Pasquarello, ACS Catal., 2020, 10, 13186–13195.
37. A. Wolcott, W. Smith, T. Kuykendall, Y. Zhao and J. Zhang, Adv. Funct. Mater., 2009, 19, 1849–1856.
38. A. Fujishima and K. Honda, Nature, 1972, 238, 37–38.
39. P. Hohenberg and W. Kohn, Phys. Rev. B: Condens. Matter Mater. Phys., 1964, 136, 864–871.
40. W. Kohn and L. J. Sham, Phys. Rev. A: At., Mol., Opt. Phys., 1965, 140, 1133–1138.
41. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 47, 558–561.
42. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
43. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
44. J. P. Perdew and W. Yue, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8800–8802.
45. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
46. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
47. V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196.
48. F. Viñes and F. Illas, J. Comput. Chem., 2017, 38, 523–529.
49. S. Grimme, J. Antony, S. Ehrlich and S. Krieg, J. Chem. Phys., 2010, 132, 154104.
50. N. Zhang, Y. Hong, S. Yazdanparast and M. A. Zaeem, 2D Mater., 2018, 5, 045004.
51. B. Akgenc, Solid State Commun., 2019, 303, 113739.
52. J. C. Slater, J. Chem. Phys., 1964, 41, 3199–3204.
53. E. B. Deeva, A. Kurlov, P. M. Abdala, D. Lebedev, S. M. Kim, C. P. Gordon, A. Tsoukalou, A. Fedorov and C. R. Müller, Chem. Mater., 2019, 31, 4505–4513.
54. S. Trasatti, Pure Appl. Chem., 1986, 58, 955–966.
55. C. Ougherb, T. Ouahrani, M. Badawi and Á. Morales-García, Phys. Chem. Chem. Phys., 2022, 24, 7243–7252.
56. X. Hai, J. Tahir-Kheli and W. A. Goddard, J. Phys. Chem. Lett., 2011, 2, 212–217.
57. Á. Morales-García, R. Valero and F. Illas, Phys. Chem. Chem. Phys., 2018, 20, 18907–18911.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta01933k

---