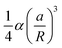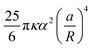DOI:
10.1039/D3SM00851G
(Paper)
Soft Matter, 2023,
19, 6157-6167
Many-body interactions between curvature-inducing membrane inclusions with arbitrary cross-sections
Received
28th June 2023
, Accepted 31st July 2023
First published on 31st July 2023
Abstract
By means of a multipolar expansion, we study analytically and numerically the interaction, in tensionless membranes, between multiple identical curvature-inducing membrane inclusions having arbitrary cross sections but uniform small detachment angles. In particular, for N circular inclusions forming regular polygons, we obtain analytical expressions for the total asymptotic interaction, up to N = 6, and we numerically compute the different multi-body contributions at arbitrary separations. We find that the latter are comparable to the sum of the two-body contributions. For N = 5 inclusions, the analytical asymptotic interaction scales as the inverse sixth power of the nearest neighbors distance d, weaker than the d−4 power for N ≠ 5. The analytical interactions are always repulsive and in good agreement with the numerical results. In the case of noncircular cross sections, we consider the case of two identical inclusions having a given number of equally shaped lobes. Depending on the number of lobes and their amplitude, we find that the interaction is asymptotically either repulsive as d−4 or attractive as d−2, and always repulsive at short distances. We also characterize how the interaction depends on the inclusion rotation angles in the membrane plane.
1. Introduction
Biological membranes consist of two layers of lipid molecules arranged in a tail-to-tail fashion, forming the structural barrier of our cells.1 These membranes have a central hydrophobic core, and two outer hydrophilic layers, made by the lipid heads, which come into contact with the surrounding aqueous solvent. Some proteins are specifically designed to either fit inside the membrane or adhere to its surface. These include the so-called curvature-inducing proteins, which have the ability to bend the membrane so that it can accommodate their conical shape.2
The elastic energy of membranes is controlled by both lateral tension and bending rigidity, as described by Helfrich.3 Since curvature-inducing proteins deform membranes on a large scale, they experience long-range interactions mediated by the energy required for membrane deformation.4 The disk with detachment angle (DDA) model, introduced by Goulian et al.,4–6 was developed to investigate these effects. To describe the deformation caused by a protein, the section of the protein embedded in the hydrophobic membrane core is modeled as a disk of radius a, while the membrane, modeled as a surface, detaches from the disk at a constant angle α. Multipolar expansion methods were used to obtain the leading-order asymptotic interaction between two inclusions.4 In a membrane with bending rigidity κ and negligible tension, two identical curvature-inducing inclusions separated by a distance d were found to repel each other with an asymptotic pairwise interaction energy given by ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) ⋍ 8πκα2(a/d)4. This interaction, obtained from a linearized calculation, is valid in the small detachment angle limit. Using effective field theory, Yolcu et al.7,8 calculated this interaction, for disks of different radii and detachment angles, up to order (1/d)6. Using the original multipolar expansion method, we derived the interaction up to order (1/d)14, making it possible to study how the series converges.9
⋍ 8πκα2(a/d)4. This interaction, obtained from a linearized calculation, is valid in the small detachment angle limit. Using effective field theory, Yolcu et al.7,8 calculated this interaction, for disks of different radii and detachment angles, up to order (1/d)6. Using the original multipolar expansion method, we derived the interaction up to order (1/d)14, making it possible to study how the series converges.9
Note that numerical studies, using triangulated surfaces energy minimization, have been used to explore the regime of large detachment angles, of inclusions with noncircular footprint, and of strongly curved membrane background.10–13 It was shown in particular that DDA-like inclusions with large detachment angle can attract each other when adsorbed on the outer side of strongly curved vesicles13 and that inclusions with crescent-like shapes experience strong attractions.12
Understanding the collective interactions of proteins in biological membranes at room temperature is crucial due to their abundance.1 However, this poses three challenges: the weakness of the interactions at moderate distances, their multibody nature, and the noncircular shape of protein cross-sections (the non-uniformity of the detachment angle will not be addressed here). Let us discuss these points sequentially. Membrane typically have bending rigidities κ ⋍ 30kBT,1 and curvature-inducing proteins can have detachment angles ranging from α ⋍ 10° to 35°. Indeed, while a ⋍ 5 nm, spontaneous curvatures of c ⋍ (25nm)−1 where measured for the KvaP channels2 and c ⋍ (7nm)−1 for BmrA in the ATP-blocked configuration.14 At a distance d ⋍ 6a, where the spacing between the inclusions is large enough to hope that asymptotic expressions are reliable, the interaction energy is only ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) ⋍ 0.1 kBT. Therefore, relying on the first terms of the asymptotic expansion is not sufficient to investigate interactions that are significantly larger than kBT. The range of applicability of the expansion to order (1/d)14 is also uncertain. Therefore, in this paper, we conduct a numerical investigation of the interaction up to the point of contact. Specifically, we include up to 400 multipoles to obtain accurate results.
⋍ 0.1 kBT. Therefore, relying on the first terms of the asymptotic expansion is not sufficient to investigate interactions that are significantly larger than kBT. The range of applicability of the expansion to order (1/d)14 is also uncertain. Therefore, in this paper, we conduct a numerical investigation of the interaction up to the point of contact. Specifically, we include up to 400 multipoles to obtain accurate results.
Using an approximate method based on the energy required to insert a protein into a curved background, Kim et al.15 have argued that multibody interactions are as significant as pairwise interactions. As shown by Yolcu et al., this method correctly captures pairwise and triplet interactions, but neglects higher order multibody interactions.8 Therefore, little is known with certainty about membrane-mediated multibody interactions. In this paper, we use multipolar expansions to derive exact analytical expressions for the asymptotic many-body energy of clusters of up to six inclusions forming regular polygons. Our analysis highlights the relative amplitude of multibody terms. In particular, we show that pentagonal clusters have a small but nonzero many-body energy.15 Furthermore, we numerically calculate the many-body interaction energy of these clusters at very small separations between the inclusions.
Finally, the DDA model assumes the cross-section of the inclusion to be perfectly circular. Real proteins have an irregular shape, so it is important to know whether or not this changes the interaction, especially at short distances where this irregularity is significant. For example, as shown in ref. 8 and 9, the sixth order of the pairwise interaction between two identical perfectly circular disks vanishes. In this paper, we show that this is no longer the case if a shape modulation is present. We give general numerical results concerning the interaction between two curvature-inducing proteins with a noncircular cross-section in a tensionless membrane, discussing in particular the dependence of their interaction on their relative orientation.
Our paper is organized as follows. In Section 2 we review the multipolar method of Goulian et al.4 and we generalize it to inclusions of arbitrary contours. In Section 3 we apply this method to numerically compute the interaction between two identical circular inclusions and we compare the accurate numerical solution to the asymptotic analytical results. In Section 4 we obtain the leading asymptotic term of the interaction energy for N = 3–6 circular inclusions placed on a regular polygon. We compare this analytical results with numerical computations, and we extract from the latter the various multi-body contributions. In Section 5, we study numerically the interaction between two identical noncircular inclusions having a variable number ν = 1–4 of identical lobes. Finally, in Section 6, we summarize and discuss our results.
2. Interaction between arbitrarily shaped inclusions with a fixed detachment angle
We consider a bilayer lipidic membrane with no tension and zero spontaneous curvature, modeled as a geometric surface. We characterize the membrane shape in the Monge gauge by means of its height z = h(x,y) above the reference plane (x,y). For small deformations, the bending free energy of the membrane is given by3| |  | (1) |
where κ is the bending energy, typically of the order of a few tens of the thermal energy kBT, and the integral runs on the reference plane. Note that, in general, an extra contribution to the free energy, proportional to the integral of the Gaussian curvature, should be considered. However, this term only depends on the global topology of the membrane and on the integral of the geodesic curvature along the membrane contours. Therefore, for fixed membrane topologies and fixed membrane contours imposing local fixed detachment angles, the Gaussian free energy is a constant contribution that can be discarded. This is the case for our problem.
Minimizing the free energy F with respect to arbitrary deformations of the membrane height yields that the equilibrium membrane shape is solution of the biharmonic equation
We suppose that
N curvature-inducing inclusions,
e.g. conical integral proteins or adhering colloids, are attached to the membrane. Generalizing the model of Goulian
et al.4 to inclusions of non circular contours, we model each inclusion
k as a planar contour of arbitrary shape from which the membrane detaches with a given fixed angle
αk (see
Fig. 1). We associate to each inclusion
k a reference point
Ok of coordinates
x =
xk0,
y =
yk0, and
z =
zk0, lying in the plane of its contour, of normal

. For each inclusion, we define a local coordinate system (
xk,
yk) in the reference plane, centered on the point (
xk0,
yk0) and possibly rotated with respect to the reference frame (
x,
y), depending on the symmetry of the problem.
 |
| | Fig. 1 Shape of a lipidic membrane around three identical curvature-inducing proteins with noncircular contours and uniform detachment angles. The coordinates used for describing the membrane geometry are shown (see Section 2). | |
The orientation  of each inclusion is given by two angles βk and γk. For small inclinations with respect to the reference plane, we set
of each inclusion is given by two angles βk and γk. For small inclinations with respect to the reference plane, we set
| | 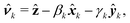 | (3) |
where
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) k
k,
ŷk, and
ẑ are unit vectors in the direction of the corresponding axes. Note that, to first order in the angles
βk and
γk, the projected shapes of the contours on the reference plane coincide with their actual shapes.
With the first order approximation (3), the equation of the k contour's plane is −βkxk − γkyk + z − zk0 = 0. Therefore, the condition that the inclusions are attached to the membrane gives, to first order in the inclinations, the boundary conditions
| | | h(xk,yk) − βkxk − γkyk|Ck = zk0, | (4) |
where |
Ck indicates that the quantity on its left is evaluated along the projection of contour
k on the reference plane. In the following, we will parametrize the latter contours as
in terms of local polar coordinates (
rk,
ϕk) on the reference plane, associated to the Cartesian coordinates (
xk,
yk).
The detachment condition implies that the membrane height, measured from the plane of contour k, has derivative in the direction normal to the contour equal to tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αk. Then, at first order in the inclinations βk and γk and the detachment angles αk, we have the boundary conditions
αk. Then, at first order in the inclinations βk and γk and the detachment angles αk, we have the boundary conditions
| |  | (6) |
where ∂/∂
nk indicates the derivative in the direction

of the outward normal to the contour
rk =
rk(
ϕk):
| |  | (7) |
Note that the equilibrium free energy
(1) can be expressed, by using two integrations by parts and the equilibrium condition
(2), as the sum of line integrals along the contours
Ck of the inclusions:
| |  | (8) |
where d
sk is the elementary arc length
| |  | (9) |
Finally, the interaction energy
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif)
between the inclusions is the difference between the free energy
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif)
and the sum of the free energies of each isolated inclusion.
2.1 Multipolar expansion
Even for two inclusions with circular contours, the boundary problem (2), (4), (6) cannot be exactly solved analytically. Goulian et al., by means of a multipolar expansion, first obtained4–6 an asymptotic expression for the interaction free energy of two identical circular inclusions of radii a, valid to fourth order in the ratio between a and their distance d.
The next to leading, sixth order, asymptotic term for two different circular inclusions was derived by Yolcu et al. using effective field theory.7,8 Higher-order terms, up to fourteen order, were successively obtained by us,9 using the original multipolar technique.
To solve our boundary problem for N inclusions, similarly to ref. 4, 9 and 16 we look for a solution of the biharmonic equation (2) in the form of the multipolar expansion:
| | 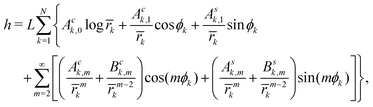 | (10) |
where
L is some characteristic length of the problem, that we use for dimensionalization purposes, and
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) k
k =
rk/
L. The constant coefficients
Ack,m and
Ask,m (resp.
Bck,m and
Bsk,m) multiply elementary solutions of the biharmonic
eqn (2) having vanishing (resp. non vanishing) Laplacian. Up to a constant term,
eqn (10) is the sum of all the elementary separated solutions in polar coordinates of the biharmonic
eqn (2) that are singular only at the centers
rk = 0 of the inclusions and that tend to a flat shape parallel to the reference plane at infinity. Note that not including in
eqn (10) the elementary solutions of the biharmonic equation that have divergent curvatures at infinity implies that, on each inclusion, the force normal to the reference plane and the torques parallel to the latter identically vanish (see Appendix A).
The unknown expansion coefficients in eqn (10) are uniquely determined by the boundary eqn (4) and (6). Indeed, truncating the expansion (10) to a maximum order m = M, yields, for M ≥ 2, N(4M − 1) unknowns. Expanding eqn (4) and (6), for each inclusion k, as Fourier series relative to the angle ϕk, truncated to the same maximum harmonic M, gives 4M + 2 equations for each inclusion. However, the boundary conditions contain, for each inclusion, the three extra unknowns βk, γk (the inclusion tilts) and zk (the inclusion height). Thus, we have a total number of unknowns N(4M + 2) that equals the number of boundary conditions. In practice, it is simpler to disregard the zeroth harmonics of eqn (4) from the boundary equations, along with the corresponding unknowns heights zk. Then, we are left with only N(4M + 1) equations and the same number of unknowns. The remaining unknown heights zk can be determined, once the full solution h is computed, by evaluating the zeroth harmonics of the left-hand side of eqn (4).
3. Numerical solution for two circular inclusions
We start by considering two identical circular inclusions of radius a separated by a center-to-center distance d. We put the projection on the reference plane of the center of inclusion 1 (resp. 2) at x = −d/2, y = 0 (resp. x = d/2, y = 0) and we define the local Cartesian coordinates| | 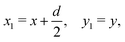 | (11) |
| |  | (12) |
such that the frame (x2, y2) is obtained from (x1, y1) by means of a rotation of angle π around the midpoint of the segment joining the centers of the two inclusions. Then, the polar coordinates associated to the two Cartesian frames are related by the transformations| |  | (13) |
| | ϕ2 = arctan(r1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ1 − d, r1 ϕ1 − d, r1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ1) −π, ϕ1) −π, | (14) |
where arctan(x, y) is the polar angle of the point (x, y). The inverse transformations are obtained by the exchanges r1 ↔ r2, ϕ1 ↔ ϕ2.
By symmetry, Ac1,m = Ac2,m, Bc1,m = Bc2,m, and β1 = β2, while, for k = 1, 2, all the Ask,m and Bsk,m coefficients vanish, as well as the tilt angles γk. We determine numerically all the remaining independent coefficients up to the maximum order m = M by means of a Fast Fourier Transform (FFT) of the boundary conditions (4) and (6) on one of the two inclusions. To avoid aliasing effects, the FFT is computed up to a sufficiently high harmonic P ≫ M and we impose the boundary conditions only on the 1,2, …, M cosine harmonics of eqn (4) and the 0, 1, 2, …, M cosine harmonics of eqn (6) on one of the two boundaries. We then solve numerically the resulting system of 2M + 1 linear equations for the 2M + 1 independent unknowns Ac1,0, Ac1,1, Ac1,2, Bc1,2, …, Ac1,M, Bc1,M, β1. Once the latter are determined, we compute the membrane free energy (8) by taking the zeroth harmonic of the integrand with respect to ϕ1 of eqn (8) and (9). By increasing the maximum order M (together with P), we check for the convergence of the free energy interaction.
In Fig. 2 we show the normalized interaction energy  as a function of the normalized distance
as a function of the normalized distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = d/a between the centers of the inclusions (upper red curve). Note that the free energy of an isolated circular inclusion is zero: therefore the interaction energy
= d/a between the centers of the inclusions (upper red curve). Note that the free energy of an isolated circular inclusion is zero: therefore the interaction energy ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) coincides with
coincides with ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) . To obtain a relative error of the order of 10−3 at contact (
. To obtain a relative error of the order of 10−3 at contact (![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = 2) we set M = 200 and P = 210. Note that, for
= 2) we set M = 200 and P = 210. Note that, for ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) > 2, the relative error rapidly decreases. On the same curve, we show also the analytical asymptotic expansions at order n = 4, 8, 10, 12, 14 obtained in ref. 9. For
> 2, the relative error rapidly decreases. On the same curve, we show also the analytical asymptotic expansions at order n = 4, 8, 10, 12, 14 obtained in ref. 9. For ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) > 2.5, the n = 14 approximation is excellent, while at smaller separation higher-order corrections are needed. For
> 2.5, the n = 14 approximation is excellent, while at smaller separation higher-order corrections are needed. For ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) > 3, the lowest order approximation n = 4 is sufficient. However, as we will see, when multiple or noncircular inclusions are present, the asymptotic interaction does not, in general, faithfully represent the actual interaction at such short separations.
> 3, the lowest order approximation n = 4 is sufficient. However, as we will see, when multiple or noncircular inclusions are present, the asymptotic interaction does not, in general, faithfully represent the actual interaction at such short separations.
 |
| | Fig. 2 Normalized interaction energy  as a function of the normalized center-to-center distance as a function of the normalized center-to-center distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = d/a for two identical circular inclusions. The upper thicker red curve is the exact interaction computed numerically up to the maximum multipolar order M = 200. The thinner black curves are the analytical asymptotic expansions up to order n, with n = 4 (dotted line), 8,10,12,14 from bottom to top. The inset shows a magnification close to the contact = d/a for two identical circular inclusions. The upper thicker red curve is the exact interaction computed numerically up to the maximum multipolar order M = 200. The thinner black curves are the analytical asymptotic expansions up to order n, with n = 4 (dotted line), 8,10,12,14 from bottom to top. The inset shows a magnification close to the contact ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = 2. = 2. | |
4.
N circular inclusions on a regular polygon
To study the importance of multibody interactions, we consider N > 2 identical inclusions with circular cross sections of radius a and centers arranged on a regular polygon:| | 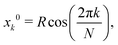 | (15) |
| |  | (16) |
where R is the radius of the circle circumscribed to the regular polygon and k = 0, 1, …, N − 1. As for two identical inclusions, we rotate the local coordinate system centered on inclusion k by the angle 2πk/N, in such a way that the xk direction coincides with the direction joining the center of the polygon to the center of inclusion k, as shown in Fig. 1 for noncircular inclusions. Then, by symmetry, for any k and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , Ack,m = Ac
, Ack,m = Ac![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ,m, Bck,m = Bc
,m, Bck,m = Bc![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ,m, βk = β
,m, βk = β![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , while all the Ask,m and Bsk,m coefficients vanish, as well as the tilt angles γk.
, while all the Ask,m and Bsk,m coefficients vanish, as well as the tilt angles γk.
Following ref. 9, for each inclusion k, we introduce the normalized complex coordinate on the reference plane
| | zk = ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) k k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(iϕk), exp(iϕk), | (17) |
where
i is the imaginary unit and we normalize the lengths with respect to
R. Then, the transformations of coordinates between the local coordinates centered on the inclusions are, in complex notation,
| | 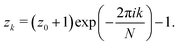 | (18) |
With the given symmetry and the complex coordinates, the multipolar expansion
(10) can be written as the real part of the complex function
| |  | (19) |
where

denotes the complex conjugate of
zk.
By symmetry, it is enough to impose the boundary conditions (4) and (6) on the reference inclusion 0. This can be done analytically by injecting the transformations (18) in the complex function (19), truncating the multipoles to a maximum order m = M, and expanding in Taylor series around z0 = 0 the terms of the function η with k = 1, 2, …, N − 1, regarded as analytical functions of z0 for fixed 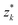 . Taking the real part of η and going back to the polar coordinates
. Taking the real part of η and going back to the polar coordinates ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 and ϕ0, we obtain an expansion of h in the form of a Fourier series in cos(mϕ0), where each Fourier coefficient depends on the coordinate
0 and ϕ0, we obtain an expansion of h in the form of a Fourier series in cos(mϕ0), where each Fourier coefficient depends on the coordinate ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 and the amplitudes Am′ and Bm′, with m′ = 0, 1, …, M. The boundary conditions (4) and (6) on the reference inclusion 0 (
0 and the amplitudes Am′ and Bm′, with m′ = 0, 1, …, M. The boundary conditions (4) and (6) on the reference inclusion 0 (![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = a/R) give then a linear system of 2M equations in the 2M unknowns A0, A1, A2, B2, …, AM, BM, that we solve to the lowest order in a/R giving a nonzero interaction energy. For N = 2,3,4,5,6 we find A0 = αa/R, while the next nonzero multipolar coefficients at lowest order, B2 and B3, are given in Table 1, along with the corresponding interaction energies. The latter, since the inclusions are circular, coincide with the free energy (8)–(9). Note that, generalizing our numerical solution to the case of N identical circular inclusions, we recover numerically the same asymptotic behavior. As one can see, except for N = 5, the next leading nonzero coefficient after A0 is B2 ∝ (a/R)3, giving an interaction free energy ∝ (a/R)4. For N = 5, the next leading coefficient is B3 ∝ (a/R)5 and the corresponding interaction free energy is only ∝ (a/R)6. Note that, contrary to Kim et al.,15 we find that the interaction energy of five identical circular inclusion in a regular pentagonal arrangement is nonzero. Actually, this result is not in contradiction with ref. 15 since, as pointed out by ref. 8, the result of ref. 15, takes into account only pairwise and triplet interactions up to terms scaling with the distance as (a/R)4. Our result, on the other hand, takes into account all the multibody interactions and captures in a controlled way the leading contribution to the interaction in powers of a/R. In agreement with ref. 15 and 8, we can then conclude that, asymptotically, multibody interactions are as significant as the pairwise ones: indeed, for N = 5 the sum of the pairwise interactions scales as (a/R)4, and, for instance, for N = 3, as can be easily checked, the sum of the pairwise interactions is the double of the total many-body interaction.
0 = a/R) give then a linear system of 2M equations in the 2M unknowns A0, A1, A2, B2, …, AM, BM, that we solve to the lowest order in a/R giving a nonzero interaction energy. For N = 2,3,4,5,6 we find A0 = αa/R, while the next nonzero multipolar coefficients at lowest order, B2 and B3, are given in Table 1, along with the corresponding interaction energies. The latter, since the inclusions are circular, coincide with the free energy (8)–(9). Note that, generalizing our numerical solution to the case of N identical circular inclusions, we recover numerically the same asymptotic behavior. As one can see, except for N = 5, the next leading nonzero coefficient after A0 is B2 ∝ (a/R)3, giving an interaction free energy ∝ (a/R)4. For N = 5, the next leading coefficient is B3 ∝ (a/R)5 and the corresponding interaction free energy is only ∝ (a/R)6. Note that, contrary to Kim et al.,15 we find that the interaction energy of five identical circular inclusion in a regular pentagonal arrangement is nonzero. Actually, this result is not in contradiction with ref. 15 since, as pointed out by ref. 8, the result of ref. 15, takes into account only pairwise and triplet interactions up to terms scaling with the distance as (a/R)4. Our result, on the other hand, takes into account all the multibody interactions and captures in a controlled way the leading contribution to the interaction in powers of a/R. In agreement with ref. 15 and 8, we can then conclude that, asymptotically, multibody interactions are as significant as the pairwise ones: indeed, for N = 5 the sum of the pairwise interactions scales as (a/R)4, and, for instance, for N = 3, as can be easily checked, the sum of the pairwise interactions is the double of the total many-body interaction.
Table 1 Multipolar coefficients B2 and B3 and interaction energy ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) at lowest order in a/R as a function of the number N of equal inclusions on a regular polygon. Note that the distance d between the centers of the nearest-neighbor inclusions is
at lowest order in a/R as a function of the number N of equal inclusions on a regular polygon. Note that the distance d between the centers of the nearest-neighbor inclusions is 
|
N
|
B
2
|
B
3
|
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) |
| 2 |

|
0 |

|
| 3 |

|
0 |

|
| 4 |
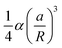
|
0 |

|
| 5 |
0 |

|

|
| 6 |

|
0 |
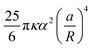
|
4.1 Multibody interactions
To assess the relevance of multibody interactions at any separation, we determine numerically the full many-body interaction ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) of N identical circular inclusions on a regular polygon, along with the p-body contributions
of N identical circular inclusions on a regular polygon, along with the p-body contributions ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) p, with p = 2, 3, …, N. For p inclusions 1, 2, …, p chosen between the N,
p, with p = 2, 3, …, N. For p inclusions 1, 2, …, p chosen between the N, ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) p is defined recursively as
p is defined recursively as| |  | (20) |
where ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (1, 2, …, p) is the full many-body interaction between the p inclusions 1,2,…,p and the innermost sum at the right-hand side of eqn (20) runs over all the different way of choosing 2 ≤ k < p inclusions c1, c2, …, ck between the p inclusions. For instance, for three inclusions, the three-body interaction between the three inclusions is the full many-body interaction of the three inclusions minus the sum of the three two-body interactions between the three different pairs of inclusions. Similarly, for four inclusions, the four-body interaction between the four inclusions is the full many-body interaction of the four inclusions, minus the sum of the four three-body interactions between the four different triplets of inclusions, minus the sum of the six two-body interactions between the six different pairs of inclusions.
(1, 2, …, p) is the full many-body interaction between the p inclusions 1,2,…,p and the innermost sum at the right-hand side of eqn (20) runs over all the different way of choosing 2 ≤ k < p inclusions c1, c2, …, ck between the p inclusions. For instance, for three inclusions, the three-body interaction between the three inclusions is the full many-body interaction of the three inclusions minus the sum of the three two-body interactions between the three different pairs of inclusions. Similarly, for four inclusions, the four-body interaction between the four inclusions is the full many-body interaction of the four inclusions, minus the sum of the four three-body interactions between the four different triplets of inclusions, minus the sum of the six two-body interactions between the six different pairs of inclusions.
Finally, we define the total p-body contribution ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (p) to the interaction energy as the sum of all the p-body contributions over all the possible ways of choosing p inclusions between the N:
(p) to the interaction energy as the sum of all the p-body contributions over all the possible ways of choosing p inclusions between the N:
| |  | (21) |
Then, according to
eqn (20), the full many-body interaction is equal to the sum of the total
p-body contributions:
| |  | (22) |
Fig. (3)–(6) show, for N = 3–6 identical inclusions on a regular polygon, the full many-body normalized interaction  together with the various total multi-body contributions
together with the various total multi-body contributions  for the interaction index p = 2, …, N. The three and higher multi-body contributions are attractive and considerably reduce the two-body repulsion (except, possibly, for some contributions very close to contact). This confirms the result of Kim et al.15 that nonpairwise multi-body interactions are comparable to the pairwise ones, even though their magnitude decreases with their index p, except very close to contact. The black dotted curves in Fig. (3)–(6) are the analytical asymptotic full many-body interactions given in Table 1. As it is apparent, for N = 3 and N = 5 these approximations are actually quite good even rather close to the contact, while for N = 4 and N = 6 (and, to a certain degree, for N = 2, see Fig. 2) the approximation holds only asymptotically (
for the interaction index p = 2, …, N. The three and higher multi-body contributions are attractive and considerably reduce the two-body repulsion (except, possibly, for some contributions very close to contact). This confirms the result of Kim et al.15 that nonpairwise multi-body interactions are comparable to the pairwise ones, even though their magnitude decreases with their index p, except very close to contact. The black dotted curves in Fig. (3)–(6) are the analytical asymptotic full many-body interactions given in Table 1. As it is apparent, for N = 3 and N = 5 these approximations are actually quite good even rather close to the contact, while for N = 4 and N = 6 (and, to a certain degree, for N = 2, see Fig. 2) the approximation holds only asymptotically (![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) > 10). Thus, the leading asymptotic term captures the relevant nonpairwise interactions and is more accurate than the total two-body (pairwise) interaction, even though it is not always quite reliable at distances comparable to the sizes of the inclusions.
> 10). Thus, the leading asymptotic term captures the relevant nonpairwise interactions and is more accurate than the total two-body (pairwise) interaction, even though it is not always quite reliable at distances comparable to the sizes of the inclusions.
 |
| | Fig. 3 Normalized total many-body interaction  (black solid line), along with the total normalized two-body interaction energy (black solid line), along with the total normalized two-body interaction energy 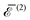 (red dashed line) and the total normalized three-body interaction (red dashed line) and the total normalized three-body interaction  (blue long dashed-dotted line) for three inclusions on a regular polygon as a function of the normalized distance (blue long dashed-dotted line) for three inclusions on a regular polygon as a function of the normalized distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = d/a between the centers of two neighbor inclusions. The black dotted curve is the analytical asymptotic expression = d/a between the centers of two neighbor inclusions. The black dotted curve is the analytical asymptotic expression  (see Table 1). The interaction energies are normalized with respect to κα2. Note that, by definition, (see Table 1). The interaction energies are normalized with respect to κα2. Note that, by definition,  . . | |
 |
| | Fig. 4 Same as Fig. 3 but for four inclusions on a regular polygon. The total normalized four-body interaction is  (green long-dashed line). The analytical asymptotic expression (black dotted curve) is (green long-dashed line). The analytical asymptotic expression (black dotted curve) is  (see Table 1). Note that, as in Fig. 3 and in the following two figures, (see Table 1). Note that, as in Fig. 3 and in the following two figures,  . . | |
 |
| | Fig. 5 Same as Fig. 4 but for five inclusions on a regular polygon. The total normalized five-body interaction is  (pink short dashed-dotted line). The analytical asymptotic expression (black dotted curve) is (pink short dashed-dotted line). The analytical asymptotic expression (black dotted curve) is  (see Table 1). (see Table 1). | |
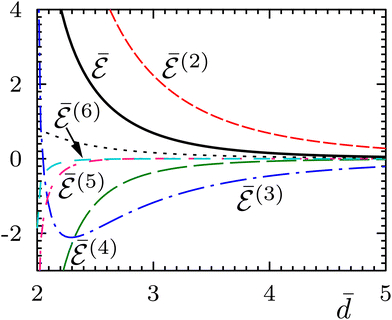 |
| | Fig. 6 Same as Fig. 5 but for six inclusions on a regular polygon. The total normalized six-body interaction is  (turquoise dashed-spaced line). The analytical asymptotic expression (black dotted curve) is (turquoise dashed-spaced line). The analytical asymptotic expression (black dotted curve) is  (see Table 1). (see Table 1). | |
5. Interaction between two identical noncircular inclusions
Since real proteins have irregular shapes, it is important to know how the interaction energy is affected by modifications to the circular contour case. As discussed in Section 2, for the sake of simplicity, we assume that the detachment angle is constant along the contour of the inclusions. We consider two identical inclusions, the contours of which we model by the parametric shapes:| | ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) k(ϕk) = 1 + ε k(ϕk) = 1 + ε![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos[ν(ϕk − ψk)], cos[ν(ϕk − ψk)], | (23) |
where k = 1 (k = 2) for the left (right) inclusion. Here, ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) k and ϕk are polar coordinates centered on inclusion k, with the radial coordinates
k and ϕk are polar coordinates centered on inclusion k, with the radial coordinates ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) k normalized with respect to the average radius a of the inclusions and the angles ϕk counted counterclockwise starting from the segment joining the centers of the two inclusions (see Fig. 7), 0 < ε < 1 is the amplitude of the modulation from a circular shape, ν = 1, 2, … is an integer that counts the number of lobes of the shape, and −π/ν ≤ ψk ≤ π/ν gives the orientation of inclusion k. Note that for ν = 1, although at lowest order in ε ≪ 1 the shape (23) corresponds to a simple translation of a circular contour, for a finite moderate ε the contour is flattened around ϕk = ψk + π.
k normalized with respect to the average radius a of the inclusions and the angles ϕk counted counterclockwise starting from the segment joining the centers of the two inclusions (see Fig. 7), 0 < ε < 1 is the amplitude of the modulation from a circular shape, ν = 1, 2, … is an integer that counts the number of lobes of the shape, and −π/ν ≤ ψk ≤ π/ν gives the orientation of inclusion k. Note that for ν = 1, although at lowest order in ε ≪ 1 the shape (23) corresponds to a simple translation of a circular contour, for a finite moderate ε the contour is flattened around ϕk = ψk + π.
 |
| | Fig. 7 Local coordinates used to describe the geometry of two noncircular inclusions. The angular coordinate ϕ1 (resp. ϕ2) is counted counterclockwise from the x1 (resp. x2) axis. | |
To study the interaction between the two inclusions, we analyze, for a fixed distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) between the centers of the two inclusions, the behavior of the interaction energy
between the centers of the two inclusions, the behavior of the interaction energy 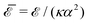 as a function of the two orientation angles ψ1 and ψ2. Note that, rotating by π the system in the reference plane about the midpoint between the two inclusions corresponds to the interchange ψ1 ↔ ψ2, implying the symmetry
as a function of the two orientation angles ψ1 and ψ2. Note that, rotating by π the system in the reference plane about the midpoint between the two inclusions corresponds to the interchange ψ1 ↔ ψ2, implying the symmetry  . Furthermore, turning the membrane upside-down with respect to the direction normal to the reference plane corresponds to the transformation ψk ↔ −ψk, α ↔ −α. Since the energy is invariant with respect to the sign of α, this implies the symmetry
. Furthermore, turning the membrane upside-down with respect to the direction normal to the reference plane corresponds to the transformation ψk ↔ −ψk, α ↔ −α. Since the energy is invariant with respect to the sign of α, this implies the symmetry  . Taking into account these symmetries and the polar angle periodicity 2π/ν of the shapes (23), we represent all the non equivalent angular configurations of the two inclusions by the combinations
. Taking into account these symmetries and the polar angle periodicity 2π/ν of the shapes (23), we represent all the non equivalent angular configurations of the two inclusions by the combinations  and
and  , with 0 ≤ σ, δ ≤ π/ν and σ + δ ≤ π/ν. Note that the points (σ = π/ν, δ = 0) and (σ = 0, δ = π/ν) are the only two points that actually correspond to the same configuration.
, with 0 ≤ σ, δ ≤ π/ν and σ + δ ≤ π/ν. Note that the points (σ = π/ν, δ = 0) and (σ = 0, δ = π/ν) are the only two points that actually correspond to the same configuration.
5.1 One lobe
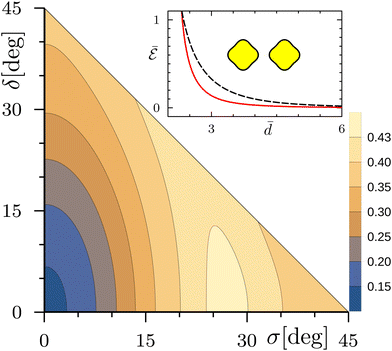
We start by considering the slightly flattened shapes (23) for ν = 1 and ε = 0.4. Fig. 8 shows the contour plot of the interaction energy  as a function of the angles σ and δ for the normalized distance
as a function of the angles σ and δ for the normalized distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = 4. Here and in the following Fig. 9–12, we set the maximum multipolar order M to 40, such that the numerical errors are negligible with respect to the used scales. The energy landscape presents two relative minima on the axes σ = 0 and δ = 0, with the first one corresponding to the absolute minimum. The configurations of the two inclusions at the two minima are shown in the figure. As the inclusions move farther apart, the two minima remain on the axes σ = 0 and δ = 0, continuously shifting towards the positions δ = π/2 and σ = π/2, respectively. For closer distances, the positions of the minima remain on the same axes and tend to δ = π and σ = π, reaching the limiting values at a finite short distance
= 4. Here and in the following Fig. 9–12, we set the maximum multipolar order M to 40, such that the numerical errors are negligible with respect to the used scales. The energy landscape presents two relative minima on the axes σ = 0 and δ = 0, with the first one corresponding to the absolute minimum. The configurations of the two inclusions at the two minima are shown in the figure. As the inclusions move farther apart, the two minima remain on the axes σ = 0 and δ = 0, continuously shifting towards the positions δ = π/2 and σ = π/2, respectively. For closer distances, the positions of the minima remain on the same axes and tend to δ = π and σ = π, reaching the limiting values at a finite short distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ⋍ 2.1. These two corner points of the contour plot, as we pointed out before, actually correspond to the same configuration, having the flattened sides of the inclusions facing each other. Note that, in this configuration, the normalized contact distance is
⋍ 2.1. These two corner points of the contour plot, as we pointed out before, actually correspond to the same configuration, having the flattened sides of the inclusions facing each other. Note that, in this configuration, the normalized contact distance is ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = 2(1 − ε), corresponding to
= 2(1 − ε), corresponding to ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = 1.2 in Fig. 8.
= 1.2 in Fig. 8.
 |
| | Fig. 8 Contour plot of the normalized interaction energy  of two noncircular inclusions, for ν = 1, ε = 0.4 and of two noncircular inclusions, for ν = 1, ε = 0.4 and ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = 4, as a function of the rotation angles = 4, as a function of the rotation angles  and and  . The inset shows the rotation angle δ minimizing the interaction energy as a function of the normalized distance . The inset shows the rotation angle δ minimizing the interaction energy as a function of the normalized distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) (black solid line and left vertical scale), along with the corresponding normalized interaction energy (black solid line and left vertical scale), along with the corresponding normalized interaction energy  (red dashed line and right vertical scale). The shapes and orientations of the two inclusions at the absolute (resp. relative) minimum for (red dashed line and right vertical scale). The shapes and orientations of the two inclusions at the absolute (resp. relative) minimum for ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = 4 are shown in yellow (resp. gray). The orientations ψi (i = 1, 2) of the inclusions are indicated by arrows centered on the inclusions. = 4 are shown in yellow (resp. gray). The orientations ψi (i = 1, 2) of the inclusions are indicated by arrows centered on the inclusions. | |
 |
| | Fig. 9 Contour plot of the normalized interaction energy  of two noncircular inclusions, for ν = 2, ε = 0.2 and of two noncircular inclusions, for ν = 2, ε = 0.2 and ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = 3, as a function of the rotation angles = 3, as a function of the rotation angles  and and  . The red continuous line in the inset shows the normalized interaction energy . The red continuous line in the inset shows the normalized interaction energy  as a function of the normalized distance as a function of the normalized distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) for the orientation ψ1 = ψ2 = 0 corresponding to the minimum interaction energy. The latter orientation is shown inside the inset. The black dashed line in the inset is the normalized interaction energy for two circular inclusions with the same average radius (ε = 0). for the orientation ψ1 = ψ2 = 0 corresponding to the minimum interaction energy. The latter orientation is shown inside the inset. The black dashed line in the inset is the normalized interaction energy for two circular inclusions with the same average radius (ε = 0). | |
 |
| | Fig. 10 Same as Fig. 9 but for ν = 3. | |
 |
| | Fig. 11 Same as Fig. 9 but for ν = 4, ε = 0.1 and M = 40. | |
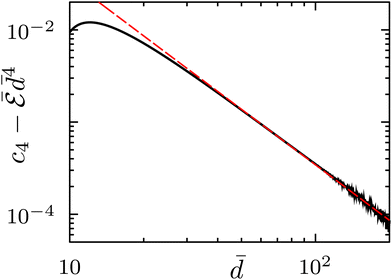 |
| | Fig. 12 Asymptotic interaction energy for ν = 4 and ε = 0.1 as a function of the normalized distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) . Black solid line: . Black solid line:  with c4= 6.819842. Red dashed line: −c6 with c4= 6.819842. Red dashed line: −c6![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) 2, with c6 = −3.44. The 2, with c6 = −3.44. The ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) −2 asymptotic behavior of −2 asymptotic behavior of  shows that shows that  for large for large ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) . . | |
The inset of Fig. 8 shows the angle δ of the absolute minimum as a function of the distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) and the corresponding interaction energy
and the corresponding interaction energy  . At large distances, the interaction is weakly attractive and decays as 1/d2, as we checked numerically. This asymptotic attractive behavior holds for any value of ε. As ε → 0, the position of the energy minimum shifts toward
. At large distances, the interaction is weakly attractive and decays as 1/d2, as we checked numerically. This asymptotic attractive behavior holds for any value of ε. As ε → 0, the position of the energy minimum shifts toward ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) → ∞ and, correspondingly, its depth tends to zero. At short separations, the interaction becomes repulsive.
→ ∞ and, correspondingly, its depth tends to zero. At short separations, the interaction becomes repulsive.
5.2 Two lobes
For ν = 2 and moderate values of ε, the shapes (23) are elongated as a capsule in the two opposite directions ϕk = ψk and ϕk = ψk + π (see inset of Fig. 9). Taking ε = 0.2, we find that at all distances there is only a single minimum at σ = δ = 0 (see Fig. 9), corresponding to the configuration in which the tips of the two inclusions face each other. Again, at large distances the interaction is asymptotically attractive as d−2, behaving similarly for ε → 0, and it becomes repulsive at short separations.
5.3 Three lobes
For ν = 3 and the same value ε = 0.2, we find again that the configuration minimizing the free energy corresponds to the tips of the inclusions facing each other (see Fig. 10). The interaction energy as a function of the distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) and of the modulation amplitude ε has the same qualitative behavior as for ν = 2.
and of the modulation amplitude ε has the same qualitative behavior as for ν = 2.
5.4 Four lobes
A qualitatively different behavior appears for ν = 4 and small ε deformations. Indeed, as shown in Fig. (11) for ε = 0.1, while the configuration minimizing the free energy still corresponds to the tips of the inclusions facing each other, the interaction is now always repulsive. We check that the interaction  decays at large distances as d−4, as for circular contours, by verifying numerically that
decays at large distances as d−4, as for circular contours, by verifying numerically that 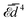 tends to a constant value c4 for large
tends to a constant value c4 for large ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) . Then, to find the next to leading asymptotic contribution to the free energy, we plot in log–log scale the difference
. Then, to find the next to leading asymptotic contribution to the free energy, we plot in log–log scale the difference 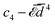 as a function of the distance
as a function of the distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) . As shown in Fig. 12, the latter difference scales as
. As shown in Fig. 12, the latter difference scales as ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) −2, showing that
−2, showing that  . Thus, at variance with perfect circular inclusions,7,9 a non-zero
. Thus, at variance with perfect circular inclusions,7,9 a non-zero ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) −6 asymptotic contribution is now present. Increasing ε, at ε ⋍ 0.15 an inflection point in the
−6 asymptotic contribution is now present. Increasing ε, at ε ⋍ 0.15 an inflection point in the 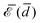 graph appears at
graph appears at ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ⋍ 5, that splits, as ε further increases, into a pair of relative extrema: a minimum followed at a larger distance by a maximum. At even larger values of ε, the maximum disappears, leaving an asymptotic attractive behavior separated from a short distance repulsion by a minimum, as for ν ≤ 3.
⋍ 5, that splits, as ε further increases, into a pair of relative extrema: a minimum followed at a larger distance by a maximum. At even larger values of ε, the maximum disappears, leaving an asymptotic attractive behavior separated from a short distance repulsion by a minimum, as for ν ≤ 3.
5.5 Convergence of the numerical algorithm
As we discussed in Sec. 3, we throughout check the convergence of our numerical algorithm by increasing the maximum order M of the multipoles (along with the maximum order P of the Fourier harmonics). Usually, as we increase M, the interaction energy first tends to stabilize toward a plateau, allowing to estimate the numerical error. By further increasing M (above a few hundreds for two circular inclusions), the numerical error tends to increase again for numerical stability reasons, as is usually the case.
However, for a given number of lobes ν, we find that when increasing the amplitude ε, the algorithm does not converge anymore: as we increase M, the absolute value of the interaction energy  continuously increases. The maximum amplitude εmax for which the algorithm converges decreases as ν increases and also slightly decreases as the distance
continuously increases. The maximum amplitude εmax for which the algorithm converges decreases as ν increases and also slightly decreases as the distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) decreases. For instance, close to contact, εmax ⋍ 0.25 for ν = 2, while εmax ⋍ 0.1 for ν = 6. Indeed, when the inclusions shape presents pronounced lobes, more multipolar expansions inside each inclusions might be necessary to match the boundary conditions on the corrugated contour.
decreases. For instance, close to contact, εmax ⋍ 0.25 for ν = 2, while εmax ⋍ 0.1 for ν = 6. Indeed, when the inclusions shape presents pronounced lobes, more multipolar expansions inside each inclusions might be necessary to match the boundary conditions on the corrugated contour.
6. Conclusions
In this article, using the disk with detachment angle model of curvature-inducing proteins and the multipolar expansion method originally introduced by Goulian et al.,4 valid in the limit of small detachment angles, we have studied the interaction between multiple proteins of arbitrary contours and fixed detachment angle in a tensionless membrane. For two identical proteins with circular contour, we have shown numerically, by taking a very large number of multipoles, that the analytical asymptotic interaction of Goulian et al.4,6 reproduces quite well the exact result up to center-to-center distances of the order of 2.5 times the contour radius, and differs by up to a factor of order 3 at contact.
For N = 3–6 proteins with circular contours arranged at the vertices of a regular polygon, we have obtained analytical asymptotic interaction energies. For all values of N but N = 5, we have found that the interaction decays as the inverse fourth power of the distance d between nearest neighbor inclusions, as originally found by Goulian et al.4 for two inclusions. For N = 5 proteins, instead, we found that the asymptotic interaction decays as d−6. This result is at variance with the null result of ref. 15, but it is compatible with the findings of Yolcu et al.8 that the approximation of ref. 15 only takes into account two and three bodies interactions up to the order d−4. We checked numerically these results, using the multipolar technique truncated at an arbitrary high number of contributions up to convergence.
We also computed numerically the different multi-body contributions to the total interaction energy, verifying that the nonpairwise multi-body interactions are indeed generally comparable to the pairwise ones. Apart possibly very close to contact, the multi-body contributions are all attractive, thus reducing the contribution coming from the sum of the two-body terms.
Finally, in the case of two identical proteins, we have numerically studied the effect of a departure of the contour from the circular shape. For the sake of simplicity, we have considered contour shapes that contain a single Fourier harmonic ν = 1, 2, … of relative amplitude ε in their polar coordinate equation, thus consisting of ν identical lobes. For a small number of lobes (ν = 1–3), we found that, whatever the amplitude of the modulation, the interaction becomes asymptotically attractive, decaying as d−2. This is in agreement with previous models of conical transmembrane proteins with effective non-circular sections,17 or effective nonuniform detachment angles.18,19 Note that for distances comparable to the size of the contours, the interaction remains repulsive. Therefore, contrary to the case of two circular inclusions, for such inclusions the asymptotic interaction does not hold at intermediate distances.
For a larger number of lobes ν ≥ 4 and a small modulation amplitude ε, we recovered, on the other hand, the asymptotic repulsive d−4 character of the interaction. Above a threshold value of ε (⋍0.16 for ν = 4), the large distance behavior becomes attractive, with, as for ν < 4, a repulsion for short distances.
For all but the ν = 1 case, we found that the interaction, at fixed distance, is minimized when the lobes of the two inclusions are facing each other. In the ν = 1 case, on the other hand, the minimum configuration remains symmetric with respect to the mid-plane, but the orientation angle depends on the distance. Up to a given distance close to contact, the facing sides of the inclusions are the flattest parts. Then, on increasing the distance, a second-order orientation transition occurs, with the orientation angles of the two lobes with respect to the line joining the two inclusions centers continuously decreasing from π to π/2 (see Fig. 8). These results are not incompatible with the cases ν ≠ 1, since for ν = 1 the protein contour has a maximum curvature not on the tip of the lobe, but on two symmetric points close to the flat side. Therefore, it seems that the configurations that are favored correspond to having the contours maximum curvatures close to each other. This could also explain why, for ν = 1, an antisymmetric metastable configuration, having an interaction energy only slightly larger than the absolute minimum, is present.
Finally, note that the next to leading order of the asymptotic interaction for two perfectly circular inclusions scales as d−8, the d−6 contribution being exactly zero. Numerically, we found that this anomaly is due to the perfect rotational symmetry of the inclusions and is lost when the rotational symmetry is broken.
Conflicts of interest
There are no conflicts to declare.
A Appendix
The variation δ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) of the free energy (1) with respect to arbitrary infinitesimal variations δh of the height of the membrane that respect the boundary conditions on the inclusions is
of the free energy (1) with respect to arbitrary infinitesimal variations δh of the height of the membrane that respect the boundary conditions on the inclusions is| | 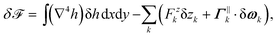 | (24) |
with| | 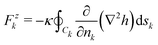 | (25) |
and| |  | (26) |
Here rx = xk![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) k + ykŷk is the vector that locates the points of the reference plane with respect to the local coordinate frame associated to inclusion k and δωk is the infinitesimal rotation, parallel to the reference plane, of inclusion k.
k + ykŷk is the vector that locates the points of the reference plane with respect to the local coordinate frame associated to inclusion k and δωk is the infinitesimal rotation, parallel to the reference plane, of inclusion k.
By the principle of virtual works, Fzk (resp. Γ‖k) is the force (resp. torque) normal (resp. parallel) to the reference plane acting on inclusion k. At equilibrium (δ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) = 0), the forces Fzk and the torques Γ‖k must vanish.
= 0), the forces Fzk and the torques Γ‖k must vanish.
Let us first consider the force (25). We decompose the total height field h in two terms: the contribution hk coming from the multipoles centered on the same inclusion k and the contribution ĥk that is the sum of the multipoles centered on all the other inclusions. Then Fzk = ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) zk +
zk + ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) zk, with
zk, with
| | 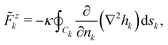 | (27) |
| |  | (28) |
Now, given a membrane height field
h satisfying the equilibrium condition
(2) and an arbitrary contour
C on the reference plane, having outward normal
![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif)
and enclosing a surface
S within which
h is regular, using the Green theorem, we have
| |  | (29) |
reflecting the fact that the stress tensor is divergenceless.
20 If the contour
C encloses singularities of the height field
h, the line integral at the left-hand side of
eqn (29) will be in general different from zero. However,
eqn (29) implies that, if such a contour is continuously deformed without crossing any singularity, the value of the line integral will not change. Therefore, if we take as the contour in
eqn (27) a circle of any radius
r and center on the center of the inclusion, we have
| |  | (30) |
where (
r,
ϕ) are polar coordinates centered on the inclusion. Now, according to the multipolar expansion
(10),
| |  | (31) |
and, therefore, the integral in the right-hand side of
eqn (30) identically vanishes. Finally, since
ĥk is regular inside inclusion
k, according to
eqn (29)![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) zk
zk = 0.
To conclude, whatever the constant coefficients Ack,m, Ask,m, Bck,m and Bsk,m, the membrane profile (10) does not exerce on the inclusions any force normal to the reference plane.
Let us now consider the torque (26). The vector in curly braces in eqn (26) is proportional to
| |  | (32) |
| |  | (33) |
where
x(1) =
x,
x(2) =
y,
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) (1)
(1) =
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif)
,
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) (2)
(2) =
ŷ, and the contour
C coincides with the contour
Ck of inclusion
k. Let us now show that, similarly to
eqn (29), the line integrals
(33) are zero if the height field
h satisfies the equilibrium condition
(2) and is regular inside
C. To this aim, let us first note that
| |  | (34) |
Then, using the identity,
| |  | (35) |
and the Green theorem, to convert the line integral along
C of the first term on the right-hand side of
eqn (35) to a surface integral over the enclosing surface
S, we get
| |  | (36) |
We note that
| | | ∇·∇(x(i)∇2h) = ∇2x(i)∇2h + 2∇x(i)·∇(∇2h) + x(i)∇4h. | (37) |
Since ∇
2x(i) = 0,
∇x(i) =
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) (i)
(i), ∇
4h = 0, and, being
∇·
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) (i)
(i) = 0,
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) (i)
(i)·
∇(∇
2h) =
∇·(
x(i)∇
2h), using the Green theorem we then obtain
| |  | (38) |
Inserting this latter equation in the first term on the right-hand side of
eqn (36), finally proves that the torque
(26) is zero for any height field
h satisfying the equilibrium condition
(2) and regular inside the contour
Ck. Using now the same decomposition as in
eqn (27) and (28) and the same steps, one can readily see that, whatever the constant coefficients
Ack,m,
Ask,m,
Bck,m and
Bsk,m, the membrane profile
(10) does not either exerce on the inclusions any torque parallel to the reference plane.
Notes and references
-
H. Lodish
et al.
, Molecular Cell Biology, W. H. Freeman & Co, New York, 7th edn, 2012 Search PubMed.
- S. Aimon, A. Callan-Jones, A. Berthaud, M. Pinot, G. E. S. Toombes and P. Bassereau, Dev. Cell, 2014, 28, 212–218 CrossRef CAS PubMed.
- W. Helfrich, Z. Naturforsch. C, 1973, 28, 693 CrossRef CAS PubMed.
- M. Goulian, R. Bruinsma and P. Pincus, EPL, 1993, 22, 145 CrossRef CAS.
- M. Goulian, R. Bruinsma and P. Pincus, EPL, 1993, 22, 155 CrossRef.
- J.-B. Fournier and P. G. Dommersnes, EPL, 1997, 39, 681 CrossRef CAS.
- C. Yolcu, I. Z. Rothstein and M. Deserno, Phys. Rev. E, 2012, 85, 011140 CrossRef PubMed.
- C. Yolcu, R. C. Haussman and M. Deserno, Adv. Colloid Interface Sci., 2014, 208, 89–109 CrossRef CAS PubMed.
- J.-B. Fournier and P. Galatola, Eur. Phys. J. E: Soft Matter Biol. Phys., 2015, 38, 86 CrossRef PubMed.
- B. Reynwar, G. Illya, V. Harmandaris, M. Muller, K. Kremer and M. Deserno, Nature, 2007, 447, 461 CrossRef CAS PubMed.
- B. J. Reynwar and M. Deserno, Soft Matter, 2011, 7, 8567–8575 RSC.
- Y. Schweitzer and M. Kozlov, PLoS Comput. Biol., 2015, 11, e1004054 CrossRef PubMed.
- A. H. Bahrami and T. R. Weikl, Nano Lett., 2018, 18, 1259–1263 CrossRef CAS PubMed.
-
P. Bassereau, Private communication.
- K. S. Kim, J. Neu and G. Oster, Biophys. J., 1998, 75, 2274 CrossRef CAS PubMed.
- T. R. Weikl, M. M. Kozlov and W. Helfrich, Phys. Rev. E, 1998, 57, 6988–6995 CrossRef CAS.
- Jeong-Man Park and T. C. Lubensky, J. Phys. I France, 1996, 6, 1217–1235 CrossRef CAS.
- P. G. Dommersnes and J.-B. Fournier, Eur. Phys. J. B, 1999, 12, 9–12 CrossRef CAS.
- J. A. Kwiecinski, A. Goriely and S. J. Chapman, SIAM J. Appl. Math., 2020, 80, 2448–2471 CrossRef.
- J.-B. Fournier, Soft Matter, 2007, 3, 883–888 RSC.
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a and
J.-B.
Fournier
*a and
J.-B.
Fournier
 b
b
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) ⋍ 8πκα2(a/d)4. This interaction, obtained from a linearized calculation, is valid in the small detachment angle limit. Using effective field theory, Yolcu et al.7,8 calculated this interaction, for disks of different radii and detachment angles, up to order (1/d)6. Using the original multipolar expansion method, we derived the interaction up to order (1/d)14, making it possible to study how the series converges.9
⋍ 8πκα2(a/d)4. This interaction, obtained from a linearized calculation, is valid in the small detachment angle limit. Using effective field theory, Yolcu et al.7,8 calculated this interaction, for disks of different radii and detachment angles, up to order (1/d)6. Using the original multipolar expansion method, we derived the interaction up to order (1/d)14, making it possible to study how the series converges.9![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) ⋍ 0.1 kBT. Therefore, relying on the first terms of the asymptotic expansion is not sufficient to investigate interactions that are significantly larger than kBT. The range of applicability of the expansion to order (1/d)14 is also uncertain. Therefore, in this paper, we conduct a numerical investigation of the interaction up to the point of contact. Specifically, we include up to 400 multipoles to obtain accurate results.
⋍ 0.1 kBT. Therefore, relying on the first terms of the asymptotic expansion is not sufficient to investigate interactions that are significantly larger than kBT. The range of applicability of the expansion to order (1/d)14 is also uncertain. Therefore, in this paper, we conduct a numerical investigation of the interaction up to the point of contact. Specifically, we include up to 400 multipoles to obtain accurate results.
 . For each inclusion, we define a local coordinate system (xk, yk) in the reference plane, centered on the point (xk0, yk0) and possibly rotated with respect to the reference frame (x, y), depending on the symmetry of the problem.
. For each inclusion, we define a local coordinate system (xk, yk) in the reference plane, centered on the point (xk0, yk0) and possibly rotated with respect to the reference frame (x, y), depending on the symmetry of the problem.
 of each inclusion is given by two angles βk and γk. For small inclinations with respect to the reference plane, we set
of each inclusion is given by two angles βk and γk. For small inclinations with respect to the reference plane, we set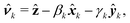
![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) k, ŷk, and ẑ are unit vectors in the direction of the corresponding axes. Note that, to first order in the angles βk and γk, the projected shapes of the contours on the reference plane coincide with their actual shapes.
k, ŷk, and ẑ are unit vectors in the direction of the corresponding axes. Note that, to first order in the angles βk and γk, the projected shapes of the contours on the reference plane coincide with their actual shapes.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αk. Then, at first order in the inclinations βk and γk and the detachment angles αk, we have the boundary conditions
αk. Then, at first order in the inclinations βk and γk and the detachment angles αk, we have the boundary conditions
 of the outward normal to the contour rk = rk(ϕk):
of the outward normal to the contour rk = rk(ϕk):


![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) between the inclusions is the difference between the free energy
between the inclusions is the difference between the free energy ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) and the sum of the free energies of each isolated inclusion.
and the sum of the free energies of each isolated inclusion.
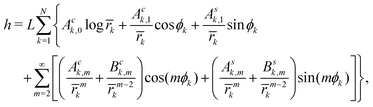
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) k = rk/L. The constant coefficients Ack,m and Ask,m (resp. Bck,m and Bsk,m) multiply elementary solutions of the biharmonic eqn (2) having vanishing (resp. non vanishing) Laplacian. Up to a constant term, eqn (10) is the sum of all the elementary separated solutions in polar coordinates of the biharmonic eqn (2) that are singular only at the centers rk = 0 of the inclusions and that tend to a flat shape parallel to the reference plane at infinity. Note that not including in eqn (10) the elementary solutions of the biharmonic equation that have divergent curvatures at infinity implies that, on each inclusion, the force normal to the reference plane and the torques parallel to the latter identically vanish (see Appendix A).
k = rk/L. The constant coefficients Ack,m and Ask,m (resp. Bck,m and Bsk,m) multiply elementary solutions of the biharmonic eqn (2) having vanishing (resp. non vanishing) Laplacian. Up to a constant term, eqn (10) is the sum of all the elementary separated solutions in polar coordinates of the biharmonic eqn (2) that are singular only at the centers rk = 0 of the inclusions and that tend to a flat shape parallel to the reference plane at infinity. Note that not including in eqn (10) the elementary solutions of the biharmonic equation that have divergent curvatures at infinity implies that, on each inclusion, the force normal to the reference plane and the torques parallel to the latter identically vanish (see Appendix A).
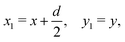


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ1 − d, r1
ϕ1 − d, r1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ1) −π,
ϕ1) −π, as a function of the normalized distance
as a function of the normalized distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = d/a between the centers of the inclusions (upper red curve). Note that the free energy of an isolated circular inclusion is zero: therefore the interaction energy
= d/a between the centers of the inclusions (upper red curve). Note that the free energy of an isolated circular inclusion is zero: therefore the interaction energy ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) coincides with
coincides with ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) . To obtain a relative error of the order of 10−3 at contact (
. To obtain a relative error of the order of 10−3 at contact (![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = 2) we set M = 200 and P = 210. Note that, for
= 2) we set M = 200 and P = 210. Note that, for ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) > 2, the relative error rapidly decreases. On the same curve, we show also the analytical asymptotic expansions at order n = 4, 8, 10, 12, 14 obtained in ref. 9. For
> 2, the relative error rapidly decreases. On the same curve, we show also the analytical asymptotic expansions at order n = 4, 8, 10, 12, 14 obtained in ref. 9. For ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) > 2.5, the n = 14 approximation is excellent, while at smaller separation higher-order corrections are needed. For
> 2.5, the n = 14 approximation is excellent, while at smaller separation higher-order corrections are needed. For ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) > 3, the lowest order approximation n = 4 is sufficient. However, as we will see, when multiple or noncircular inclusions are present, the asymptotic interaction does not, in general, faithfully represent the actual interaction at such short separations.
> 3, the lowest order approximation n = 4 is sufficient. However, as we will see, when multiple or noncircular inclusions are present, the asymptotic interaction does not, in general, faithfully represent the actual interaction at such short separations.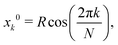

![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , Ack,m = Ac
, Ack,m = Ac![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ,m, Bck,m = Bc
,m, Bck,m = Bc![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ,m, βk = β
,m, βk = β![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) , while all the Ask,m and Bsk,m coefficients vanish, as well as the tilt angles γk.
, while all the Ask,m and Bsk,m coefficients vanish, as well as the tilt angles γk.
![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) k
k![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(iϕk),
exp(iϕk),

 denotes the complex conjugate of zk.
denotes the complex conjugate of zk.
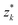 . Taking the real part of η and going back to the polar coordinates
. Taking the real part of η and going back to the polar coordinates ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 and ϕ0, we obtain an expansion of h in the form of a Fourier series in cos(mϕ0), where each Fourier coefficient depends on the coordinate
0 and ϕ0, we obtain an expansion of h in the form of a Fourier series in cos(mϕ0), where each Fourier coefficient depends on the coordinate ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 and the amplitudes Am′ and Bm′, with m′ = 0, 1, …, M. The boundary conditions (4) and (6) on the reference inclusion 0 (
0 and the amplitudes Am′ and Bm′, with m′ = 0, 1, …, M. The boundary conditions (4) and (6) on the reference inclusion 0 (![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 0 = a/R) give then a linear system of 2M equations in the 2M unknowns A0, A1, A2, B2, …, AM, BM, that we solve to the lowest order in a/R giving a nonzero interaction energy. For N = 2,3,4,5,6 we find A0 = αa/R, while the next nonzero multipolar coefficients at lowest order, B2 and B3, are given in Table 1, along with the corresponding interaction energies. The latter, since the inclusions are circular, coincide with the free energy (8)–(9). Note that, generalizing our numerical solution to the case of N identical circular inclusions, we recover numerically the same asymptotic behavior. As one can see, except for N = 5, the next leading nonzero coefficient after A0 is B2 ∝ (a/R)3, giving an interaction free energy ∝ (a/R)4. For N = 5, the next leading coefficient is B3 ∝ (a/R)5 and the corresponding interaction free energy is only ∝ (a/R)6. Note that, contrary to Kim et al.,15 we find that the interaction energy of five identical circular inclusion in a regular pentagonal arrangement is nonzero. Actually, this result is not in contradiction with ref. 15 since, as pointed out by ref. 8, the result of ref. 15, takes into account only pairwise and triplet interactions up to terms scaling with the distance as (a/R)4. Our result, on the other hand, takes into account all the multibody interactions and captures in a controlled way the leading contribution to the interaction in powers of a/R. In agreement with ref. 15 and 8, we can then conclude that, asymptotically, multibody interactions are as significant as the pairwise ones: indeed, for N = 5 the sum of the pairwise interactions scales as (a/R)4, and, for instance, for N = 3, as can be easily checked, the sum of the pairwise interactions is the double of the total many-body interaction.
0 = a/R) give then a linear system of 2M equations in the 2M unknowns A0, A1, A2, B2, …, AM, BM, that we solve to the lowest order in a/R giving a nonzero interaction energy. For N = 2,3,4,5,6 we find A0 = αa/R, while the next nonzero multipolar coefficients at lowest order, B2 and B3, are given in Table 1, along with the corresponding interaction energies. The latter, since the inclusions are circular, coincide with the free energy (8)–(9). Note that, generalizing our numerical solution to the case of N identical circular inclusions, we recover numerically the same asymptotic behavior. As one can see, except for N = 5, the next leading nonzero coefficient after A0 is B2 ∝ (a/R)3, giving an interaction free energy ∝ (a/R)4. For N = 5, the next leading coefficient is B3 ∝ (a/R)5 and the corresponding interaction free energy is only ∝ (a/R)6. Note that, contrary to Kim et al.,15 we find that the interaction energy of five identical circular inclusion in a regular pentagonal arrangement is nonzero. Actually, this result is not in contradiction with ref. 15 since, as pointed out by ref. 8, the result of ref. 15, takes into account only pairwise and triplet interactions up to terms scaling with the distance as (a/R)4. Our result, on the other hand, takes into account all the multibody interactions and captures in a controlled way the leading contribution to the interaction in powers of a/R. In agreement with ref. 15 and 8, we can then conclude that, asymptotically, multibody interactions are as significant as the pairwise ones: indeed, for N = 5 the sum of the pairwise interactions scales as (a/R)4, and, for instance, for N = 3, as can be easily checked, the sum of the pairwise interactions is the double of the total many-body interaction.![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) at lowest order in a/R as a function of the number N of equal inclusions on a regular polygon. Note that the distance d between the centers of the nearest-neighbor inclusions is
at lowest order in a/R as a function of the number N of equal inclusions on a regular polygon. Note that the distance d between the centers of the nearest-neighbor inclusions is 
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) of N identical circular inclusions on a regular polygon, along with the p-body contributions
of N identical circular inclusions on a regular polygon, along with the p-body contributions ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) p, with p = 2, 3, …, N. For p inclusions 1, 2, …, p chosen between the N,
p, with p = 2, 3, …, N. For p inclusions 1, 2, …, p chosen between the N, ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) p is defined recursively as
p is defined recursively as
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (1, 2, …, p) is the full many-body interaction between the p inclusions 1,2,…,p and the innermost sum at the right-hand side of eqn (20) runs over all the different way of choosing 2 ≤ k < p inclusions c1, c2, …, ck between the p inclusions. For instance, for three inclusions, the three-body interaction between the three inclusions is the full many-body interaction of the three inclusions minus the sum of the three two-body interactions between the three different pairs of inclusions. Similarly, for four inclusions, the four-body interaction between the four inclusions is the full many-body interaction of the four inclusions, minus the sum of the four three-body interactions between the four different triplets of inclusions, minus the sum of the six two-body interactions between the six different pairs of inclusions.
(1, 2, …, p) is the full many-body interaction between the p inclusions 1,2,…,p and the innermost sum at the right-hand side of eqn (20) runs over all the different way of choosing 2 ≤ k < p inclusions c1, c2, …, ck between the p inclusions. For instance, for three inclusions, the three-body interaction between the three inclusions is the full many-body interaction of the three inclusions minus the sum of the three two-body interactions between the three different pairs of inclusions. Similarly, for four inclusions, the four-body interaction between the four inclusions is the full many-body interaction of the four inclusions, minus the sum of the four three-body interactions between the four different triplets of inclusions, minus the sum of the six two-body interactions between the six different pairs of inclusions.
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) (p) to the interaction energy as the sum of all the p-body contributions over all the possible ways of choosing p inclusions between the N:
(p) to the interaction energy as the sum of all the p-body contributions over all the possible ways of choosing p inclusions between the N:

 together with the various total multi-body contributions
together with the various total multi-body contributions  for the interaction index p = 2, …, N. The three and higher multi-body contributions are attractive and considerably reduce the two-body repulsion (except, possibly, for some contributions very close to contact). This confirms the result of Kim et al.15 that nonpairwise multi-body interactions are comparable to the pairwise ones, even though their magnitude decreases with their index p, except very close to contact. The black dotted curves in Fig. (3)–(6) are the analytical asymptotic full many-body interactions given in Table 1. As it is apparent, for N = 3 and N = 5 these approximations are actually quite good even rather close to the contact, while for N = 4 and N = 6 (and, to a certain degree, for N = 2, see Fig. 2) the approximation holds only asymptotically (
for the interaction index p = 2, …, N. The three and higher multi-body contributions are attractive and considerably reduce the two-body repulsion (except, possibly, for some contributions very close to contact). This confirms the result of Kim et al.15 that nonpairwise multi-body interactions are comparable to the pairwise ones, even though their magnitude decreases with their index p, except very close to contact. The black dotted curves in Fig. (3)–(6) are the analytical asymptotic full many-body interactions given in Table 1. As it is apparent, for N = 3 and N = 5 these approximations are actually quite good even rather close to the contact, while for N = 4 and N = 6 (and, to a certain degree, for N = 2, see Fig. 2) the approximation holds only asymptotically (![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) > 10). Thus, the leading asymptotic term captures the relevant nonpairwise interactions and is more accurate than the total two-body (pairwise) interaction, even though it is not always quite reliable at distances comparable to the sizes of the inclusions.
> 10). Thus, the leading asymptotic term captures the relevant nonpairwise interactions and is more accurate than the total two-body (pairwise) interaction, even though it is not always quite reliable at distances comparable to the sizes of the inclusions.
 (black solid line), along with the total normalized two-body interaction energy
(black solid line), along with the total normalized two-body interaction energy 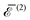 (red dashed line) and the total normalized three-body interaction
(red dashed line) and the total normalized three-body interaction  (blue long dashed-dotted line) for three inclusions on a regular polygon as a function of the normalized distance
(blue long dashed-dotted line) for three inclusions on a regular polygon as a function of the normalized distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = d/a between the centers of two neighbor inclusions. The black dotted curve is the analytical asymptotic expression
= d/a between the centers of two neighbor inclusions. The black dotted curve is the analytical asymptotic expression  (see Table 1). The interaction energies are normalized with respect to κα2. Note that, by definition,
(see Table 1). The interaction energies are normalized with respect to κα2. Note that, by definition,  .
.
 (green long-dashed line). The analytical asymptotic expression (black dotted curve) is
(green long-dashed line). The analytical asymptotic expression (black dotted curve) is  (see Table 1). Note that, as in Fig. 3 and in the following two figures,
(see Table 1). Note that, as in Fig. 3 and in the following two figures,  .
.
 (pink short dashed-dotted line). The analytical asymptotic expression (black dotted curve) is
(pink short dashed-dotted line). The analytical asymptotic expression (black dotted curve) is  (see Table 1).
(see Table 1).
 (turquoise dashed-spaced line). The analytical asymptotic expression (black dotted curve) is
(turquoise dashed-spaced line). The analytical asymptotic expression (black dotted curve) is  (see Table 1).
(see Table 1).![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) k(ϕk) = 1 + ε
k(ϕk) = 1 + ε![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos[ν(ϕk − ψk)],
cos[ν(ϕk − ψk)],![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) k and ϕk are polar coordinates centered on inclusion k, with the radial coordinates
k and ϕk are polar coordinates centered on inclusion k, with the radial coordinates ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) k normalized with respect to the average radius a of the inclusions and the angles ϕk counted counterclockwise starting from the segment joining the centers of the two inclusions (see Fig. 7), 0 < ε < 1 is the amplitude of the modulation from a circular shape, ν = 1, 2, … is an integer that counts the number of lobes of the shape, and −π/ν ≤ ψk ≤ π/ν gives the orientation of inclusion k. Note that for ν = 1, although at lowest order in ε ≪ 1 the shape (23) corresponds to a simple translation of a circular contour, for a finite moderate ε the contour is flattened around ϕk = ψk + π.
k normalized with respect to the average radius a of the inclusions and the angles ϕk counted counterclockwise starting from the segment joining the centers of the two inclusions (see Fig. 7), 0 < ε < 1 is the amplitude of the modulation from a circular shape, ν = 1, 2, … is an integer that counts the number of lobes of the shape, and −π/ν ≤ ψk ≤ π/ν gives the orientation of inclusion k. Note that for ν = 1, although at lowest order in ε ≪ 1 the shape (23) corresponds to a simple translation of a circular contour, for a finite moderate ε the contour is flattened around ϕk = ψk + π.

![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) between the centers of the two inclusions, the behavior of the interaction energy
between the centers of the two inclusions, the behavior of the interaction energy 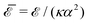 as a function of the two orientation angles ψ1 and ψ2. Note that, rotating by π the system in the reference plane about the midpoint between the two inclusions corresponds to the interchange ψ1 ↔ ψ2, implying the symmetry
as a function of the two orientation angles ψ1 and ψ2. Note that, rotating by π the system in the reference plane about the midpoint between the two inclusions corresponds to the interchange ψ1 ↔ ψ2, implying the symmetry  . Furthermore, turning the membrane upside-down with respect to the direction normal to the reference plane corresponds to the transformation ψk ↔ −ψk, α ↔ −α. Since the energy is invariant with respect to the sign of α, this implies the symmetry
. Furthermore, turning the membrane upside-down with respect to the direction normal to the reference plane corresponds to the transformation ψk ↔ −ψk, α ↔ −α. Since the energy is invariant with respect to the sign of α, this implies the symmetry  . Taking into account these symmetries and the polar angle periodicity 2π/ν of the shapes (23), we represent all the non equivalent angular configurations of the two inclusions by the combinations
. Taking into account these symmetries and the polar angle periodicity 2π/ν of the shapes (23), we represent all the non equivalent angular configurations of the two inclusions by the combinations  and
and  , with 0 ≤ σ, δ ≤ π/ν and σ + δ ≤ π/ν. Note that the points (σ = π/ν, δ = 0) and (σ = 0, δ = π/ν) are the only two points that actually correspond to the same configuration.
, with 0 ≤ σ, δ ≤ π/ν and σ + δ ≤ π/ν. Note that the points (σ = π/ν, δ = 0) and (σ = 0, δ = π/ν) are the only two points that actually correspond to the same configuration. as a function of the angles σ and δ for the normalized distance
as a function of the angles σ and δ for the normalized distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = 4. Here and in the following Fig. 9–12, we set the maximum multipolar order M to 40, such that the numerical errors are negligible with respect to the used scales. The energy landscape presents two relative minima on the axes σ = 0 and δ = 0, with the first one corresponding to the absolute minimum. The configurations of the two inclusions at the two minima are shown in the figure. As the inclusions move farther apart, the two minima remain on the axes σ = 0 and δ = 0, continuously shifting towards the positions δ = π/2 and σ = π/2, respectively. For closer distances, the positions of the minima remain on the same axes and tend to δ = π and σ = π, reaching the limiting values at a finite short distance
= 4. Here and in the following Fig. 9–12, we set the maximum multipolar order M to 40, such that the numerical errors are negligible with respect to the used scales. The energy landscape presents two relative minima on the axes σ = 0 and δ = 0, with the first one corresponding to the absolute minimum. The configurations of the two inclusions at the two minima are shown in the figure. As the inclusions move farther apart, the two minima remain on the axes σ = 0 and δ = 0, continuously shifting towards the positions δ = π/2 and σ = π/2, respectively. For closer distances, the positions of the minima remain on the same axes and tend to δ = π and σ = π, reaching the limiting values at a finite short distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ⋍ 2.1. These two corner points of the contour plot, as we pointed out before, actually correspond to the same configuration, having the flattened sides of the inclusions facing each other. Note that, in this configuration, the normalized contact distance is
⋍ 2.1. These two corner points of the contour plot, as we pointed out before, actually correspond to the same configuration, having the flattened sides of the inclusions facing each other. Note that, in this configuration, the normalized contact distance is ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = 2(1 − ε), corresponding to
= 2(1 − ε), corresponding to ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = 1.2 in Fig. 8.
= 1.2 in Fig. 8.


![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) and the corresponding interaction energy
and the corresponding interaction energy  . At large distances, the interaction is weakly attractive and decays as 1/d2, as we checked numerically. This asymptotic attractive behavior holds for any value of ε. As ε → 0, the position of the energy minimum shifts toward
. At large distances, the interaction is weakly attractive and decays as 1/d2, as we checked numerically. This asymptotic attractive behavior holds for any value of ε. As ε → 0, the position of the energy minimum shifts toward ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) → ∞ and, correspondingly, its depth tends to zero. At short separations, the interaction becomes repulsive.
→ ∞ and, correspondingly, its depth tends to zero. At short separations, the interaction becomes repulsive.![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) and of the modulation amplitude ε has the same qualitative behavior as for ν = 2.
and of the modulation amplitude ε has the same qualitative behavior as for ν = 2.
 decays at large distances as d−4, as for circular contours, by verifying numerically that
decays at large distances as d−4, as for circular contours, by verifying numerically that 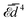 tends to a constant value c4 for large
tends to a constant value c4 for large ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) . Then, to find the next to leading asymptotic contribution to the free energy, we plot in log–log scale the difference
. Then, to find the next to leading asymptotic contribution to the free energy, we plot in log–log scale the difference 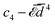 as a function of the distance
as a function of the distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) . As shown in Fig. 12, the latter difference scales as
. As shown in Fig. 12, the latter difference scales as ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) −2, showing that
−2, showing that  . Thus, at variance with perfect circular inclusions,7,9 a non-zero
. Thus, at variance with perfect circular inclusions,7,9 a non-zero ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) −6 asymptotic contribution is now present. Increasing ε, at ε ⋍ 0.15 an inflection point in the
−6 asymptotic contribution is now present. Increasing ε, at ε ⋍ 0.15 an inflection point in the 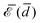 graph appears at
graph appears at ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ⋍ 5, that splits, as ε further increases, into a pair of relative extrema: a minimum followed at a larger distance by a maximum. At even larger values of ε, the maximum disappears, leaving an asymptotic attractive behavior separated from a short distance repulsion by a minimum, as for ν ≤ 3.
⋍ 5, that splits, as ε further increases, into a pair of relative extrema: a minimum followed at a larger distance by a maximum. At even larger values of ε, the maximum disappears, leaving an asymptotic attractive behavior separated from a short distance repulsion by a minimum, as for ν ≤ 3.
 continuously increases. The maximum amplitude εmax for which the algorithm converges decreases as ν increases and also slightly decreases as the distance
continuously increases. The maximum amplitude εmax for which the algorithm converges decreases as ν increases and also slightly decreases as the distance ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) decreases. For instance, close to contact, εmax ⋍ 0.25 for ν = 2, while εmax ⋍ 0.1 for ν = 6. Indeed, when the inclusions shape presents pronounced lobes, more multipolar expansions inside each inclusions might be necessary to match the boundary conditions on the corrugated contour.
decreases. For instance, close to contact, εmax ⋍ 0.25 for ν = 2, while εmax ⋍ 0.1 for ν = 6. Indeed, when the inclusions shape presents pronounced lobes, more multipolar expansions inside each inclusions might be necessary to match the boundary conditions on the corrugated contour.![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) of the free energy (1) with respect to arbitrary infinitesimal variations δh of the height of the membrane that respect the boundary conditions on the inclusions is
of the free energy (1) with respect to arbitrary infinitesimal variations δh of the height of the membrane that respect the boundary conditions on the inclusions is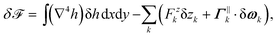
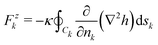

![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) k + ykŷk is the vector that locates the points of the reference plane with respect to the local coordinate frame associated to inclusion k and δωk is the infinitesimal rotation, parallel to the reference plane, of inclusion k.
k + ykŷk is the vector that locates the points of the reference plane with respect to the local coordinate frame associated to inclusion k and δωk is the infinitesimal rotation, parallel to the reference plane, of inclusion k.
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) = 0), the forces Fzk and the torques Γ‖k must vanish.
= 0), the forces Fzk and the torques Γ‖k must vanish.![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) zk +
zk + ![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) zk, with
zk, with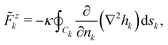

![[n with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_006e_0302.gif) and enclosing a surface S within which h is regular, using the Green theorem, we have
and enclosing a surface S within which h is regular, using the Green theorem, we have


![[F with combining circumflex]](https://www.rsc.org/images/entities/i_char_0046_0302.gif) zk = 0.
zk = 0.


![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) (1) =
(1) = ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) ,
, ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) (2) = ŷ, and the contour C coincides with the contour Ck of inclusion k. Let us now show that, similarly to eqn (29), the line integrals (33) are zero if the height field h satisfies the equilibrium condition (2) and is regular inside C. To this aim, let us first note that
(2) = ŷ, and the contour C coincides with the contour Ck of inclusion k. Let us now show that, similarly to eqn (29), the line integrals (33) are zero if the height field h satisfies the equilibrium condition (2) and is regular inside C. To this aim, let us first note that


![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) (i), ∇4h = 0, and, being ∇·
(i), ∇4h = 0, and, being ∇·![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) (i) = 0,
(i) = 0, ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0078_0302.gif) (i)·∇(∇2h) = ∇·(x(i)∇2h), using the Green theorem we then obtain
(i)·∇(∇2h) = ∇·(x(i)∇2h), using the Green theorem we then obtain