 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Comparative study of the self-assembly behaviour of 3-chloro-4-hydroxy-phenylazo dyes†
Wenke
Müller
 *a,
Ralf
Schweins
*a,
Ralf
Schweins
 a,
Bernd
Nöcker
b,
Hans
Egold
c and
Klaus
Huber
a,
Bernd
Nöcker
b,
Hans
Egold
c and
Klaus
Huber
 c
c
aInstitut Laue-Langevin, DS/LSS, 71 Avenue des Martyrs, 38000 Grenoble, France. E-mail: we-mue@gmx.net
bKAO Germany GmbH, Pfungstädter Straße 98-100, 64297 Darmstadt, Germany
cUniversität Paderborn, Warburger Straße 100, 33098 Paderborn, Germany
First published on 9th June 2023
Abstract
The complexity of intermolecular interactions and the difficulty to predict assembly behaviour solely based on chemical constitution was demonstrated by studying the self-assembly of three one-fold negatively charged 3-chloro-4-hydroxy-phenylazo dyes (Yellow, Blue and Red). Dye self-assembly was investigated using UV/vis- and NMR-spectroscopy, light- and small-angle neutron scattering. Significant differences between the three dyes were observed. While Yellow does not self-assemble, Red assembles into higher-order aggregates and Blue forms well-defined H-aggregate dimers with a dimerization constant of KD = (728 ± 8) L mol−1. Differences between dyes were suggested to emerge from variations in the propensity to form π–π-interactions due to electrostatic repulsion, sterical constraints and hydrogen-bonding interactions.
Introduction
Dye molecules have been subject to scientific investigations for decades in order to respond to the needs from industries in the field of textile- or paper dyeing. The replacement of natural dyes by synthetic dyes permitted the fine–tuning of dye properties by variation of chemical functionalities.1–3 Apart from traditional dye research, the use of dyes as functional materials, e.g. in dye-sensitized solar cells or organic light-emitting diodes (OLEDs), has received increasing attention over the past 20 years.4–6 Contrary to traditional dye research, where it often sufficed to consider molecular structure – molecular property relationships, the design of functional materials requires understanding dye–dye intermolecular interactions, which impacts properties such as absorption, solid-state fluorescence and electron transport in the solid state material.4,7A possibility to reduce the complexity of a system whilst getting valuable insight into intermolecular interactions affecting the solid-state system is to consider the self-assembly of dye molecules in solution, as they constitute an intermediate between the monomeric dye and the solid-state material.4,7 Furthermore, the investigation of dye self-assembly in solution may be helpful to understand and mimic biological systems within which dye molecules assemble to fulfil specific tasks like the assembly of chlorophylls in photosynthetic organisms.4,8–11
π–π-interactions are considered as one of the major driving forces for dye self-aggregation in solution.12 Depending on chemical constitution of the dye and geometrical constraints, other intermolecular interactions such as Coulomb forces, hydrophobic effect and dispersion forces or hydrogen bonding may additionally influence self-assembly.13 Owing to the amount and complexity of possible intermolecular interactions, the prediction of dye self-assembly structure was reported to be difficult if no distinct dominant contribution exists.12
Herein we report investigations confirming the difficulty to predict dye self-assembly structure solely based on the chemical constitution of the dye. For this purpose, the self-assembly behaviour of three azo dyes with one congruent structural sub-unit (Fig. 1) is investigated by means of UV/vis-spectroscopy, scattering methods and NMR-spectroscopy. Self-assembly structures are elucidated and analogies and differences discussed.
 | ||
| Fig. 1 Chemical structure of three azo dyes with their common structural sub-unit marked in blue. At alkaline pH such as pH = 10.5, the phenolate group is deprotonated in all cases. | ||
Experimental
Chemicals and sample preparation
Three azo dyes Yellow (HC Yellow 16, ≥99%), Blue (HC Blue 18, ≥99.8%) and Red (HC Red 18, ≥99%) were provided by KAO GmbH, Germany. The buffer salts sodium carbonate Na2CO3 (≥99.8%) and sodium bicarbonate NaHCO3 (≥99.7%) were obtained from Sigma Aldrich Chemie GmbH, Germany. MilliQ water was used to prepare the NaHCO3/Na2CO3 buffer solutions (pH = 10.5, ionic strength I ≈ 0.25 M) for UV/vis-spectroscopy and light scattering samples. D2O was used to prepare the NaHCO3/Na2CO3 buffer solutions (pD = 10.7, ionic strength I ≈ 0.25 M) for NMR and small-angle neutron scattering samples. D2O (99.90% D) was obtained from Eurisotop, France. Chemicals were used without further purification. Samples were prepared from stock solutions, followed by a minimum equilibration time of 20 h at room temperature prior to analysis.UV/vis spectroscopy
UV/vis spectra were recorded using a V-630 spectrometer from Jasco. Hellma quartz glass cuvettes with optical path lengths ranging from 0.01 cm to 1 cm were used for this purpose. The spectrometer was equipped with a thermostat to guarantee a constant measurement temperature of 25 °C.Small-angle neutron scattering
Samples for small-angle neutron scattering (SANS) measurements were obtained by dissolving the respective dye in a NaHCO3/Na2CO3 buffer in D2O (pD = 10.7, ionic strength I ≈ 0.25 M). The solution was subsequently filtered (MACHEREY-NAGEL, CHROMAFIL Xtra H-PTFE syringe filters, pore size 0.2 μm) into a dust-free sample vial and equilibrated for a minimum of 20 h at room temperature.SANS was performed at the small-angle neutron scattering instrument D11 at the Institut Laue-Langevin (Grenoble, France). Different setups were used: (1) samples containing the dye Blue were measured at three sample-to-detector distances (28 m collimation 28 m), (8 m collimation 8 m), (1.7 m collimation 4.0 m) at a neutron wavelength of 6 Å to cover a q-range of 0.002 Å−1 to 0.5 Å−1. A circular neutron beam with a diameter of 15 mm was used. (2) The sample containing [Red]tot = 10 mM was measured at three sample-to-detector distances (38.0 m collimation 40.5 m), (10.5 m collimation 10.5 m), (1.7 m collimation 2.5 m) at a neutron wavelength of 6 Å to cover a q-range of 0.0014 Å−1 to 0.5 Å−1. A circular neutron beam with a diameter of 14 mm was used. (3) The sample containing [Red]tot ≈ 5 mM was measured at three sample-to-detector distances (38.0 m collimation 40.5 m), (10.5 m collimation 10.5 m), (2.5 m collimation 2.5 m) at a neutron wavelength of 6 Å to cover a q-range of 0.0014 Å−1 to 0.5 Å−1. A circular neutron beam with a diameter of 14 mm was used.
Neutrons were detected with a 3He-detector (Reuter-Stokes multi-tube detector consisting of 256 tubes with a tube diameter of 8 mm and a pixel size of 8 mm × 4 mm), detector images azimuthally averaged, corrected to the transmission of the direct beam and scaled to absolute intensity using the Mantid software.14,15 Solvent scattering and incoherent background were subtracted from the scattering curves.16 SANS data were collected at a sample temperature of 25 °C.
NMR-spectroscopy
Samples for NMR-spectroscopy were obtained by dissolving the respective dye in a NaHCO3/Na2CO3 buffer in D2O (pD = 10.7, ionic strength I ≈ 0.25 M). The solution was subsequently filtered (MACHEREY-NAGEL, CHROMAFIL Xtra H-PTFE syringe filters, pore size 0.2 μm) into the NMR-tube. 1H-NMR- and 2-dimensional rotating frame nuclear Overhauser effect spectroscopy- (EASY ROESY) spectra were recorded with a NMR Ascent 700 spectrometer (700 MHz) equipped with a cryogenic probe with z-gradient at 298 K. The ROESY field strength was 5000 Hz. The magnetization was locked at an angle of 45° off the z-axis which ensures suppression of TOCSY artefacts. Chemical shifts were referenced to residual HDO.17Discussion
In the aqueous NaHCO3/Na2CO3 buffer (pH = 10.5, ionic strength I ≈ 0.25 M), which was used as a solvent, the three azo dyes shown in Fig. 1 are present in their phenolate form in all cases, as the phenolic hydroxyl group common to all dyes is deprotonated. Fig. 2 compares the absorption spectra of all three dyes at a concentration of 5 mM. In the following, a brief overview of UV/vis spectroscopic observations will be given for all three dyes, followed by a detailed discussion of some specifically interesting features.First insights into dye solubility and self-aggregation can be obtained from UV/vis spectroscopy: in case the dye is soluble on a molecular level and does not self-aggregate, Beer–Lambert law (eqn (1)) is fulfilled at each wavelength of the absorption spectrum.
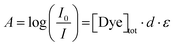 | (1) |
 | (2) |
Self-assembly of Blue
Concentration-induced changes in the absorption spectrum of Blue were attributed to dimer formation: Fig. 3 shows UV/vis absorption spectra of solutions containing different concentrations of Blue.Increasing [Blue]tot leads to a shift of the absorption maximum to lower wavelengths and a decrease in the maximum molar extinction coefficient εmax. In addition to that, an isosbestic point at λisosbestic = (655 ± 2) nm and εisosbestic = (4350 ± 110) L mol−1 cm−1 is observed. This is characteristic of only two species contributing to the total sample absorption.12,20 Even though absorption spectra do not directly provide information on aggregation number, it is reasonable to assume an equilibrium between a monomeric dye molecule M and a dimer D.
 | (3) |
| Ad(λ) = [M]·εM(λ) + [D] εD(λ) | (4) |
| [Blue]tot = [M] + 2·[D] | (5) |
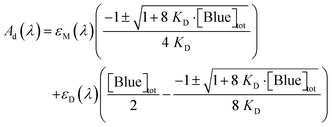 | (6) |
The dimer spectrum in Fig. 3 shows two clearly discernible peaks with absorption maxima at energies higher and lower than that of the monomer. This can be explained by exciton theory where the first excited energy state of the monomer splits into two due to dipole–dipole interaction in case the transition dipole moments of the two monomers are aligned in a face-to-face mode (H-aggregation).24 The transition with the higher energy is based on an in-phase oscillation of the two transition dipole moments and the transition with the lower energy is attributed to an out-of-phase oscillation of the two transition dipole moments.24 In this context, the change in dye absorption spectrum permits insight into dimer geometry.19,25 Quantitative analysis of the Blue dimer spectrum was performed and geometrical parameters of the dimer calculated. This calculation and the model are discussed in detail in the ESI.† It was found, that the transition dipole moments of two interacting molecules are twisted by an angle of α = 42°. The two transition dipole moments show no inclination, meaning that the centres of two molecules are stacked on top of each other. The interplanar spacing R between those centres was determined to be R = 5.2 Å in the model of non-parallel transition dipoles.
SANS was carried out on two solutions of Blue (Fig. 4). The sample containing [Blue]tot = 5 mM shows a lower scattering intensity Is than the sample with [Blue]tot = 10 mM. Furthermore, the scattering intensity declines at higher values of the modulus of the scattering vector q for [Blue]tot = 5 mM. These observations point towards a lower mass and smaller size of assemblies in the sample with [Blue]tot = 5 mM.
Guinier analysis was performed to obtain forward scattering intensities I0 and the average radius of gyration of the scatterers Rg according to eqn (7).26
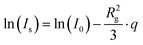 | (7) |
R
g obtained for both samples are summarized in Table 1. Linearized Guinier plots can be found in the ESI† (Fig. SI8). From I0 the coherent forward scattering intensity I0,coherent is obtained by subtracting the incoherent background BGin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) coherent. The value for the incoherent background was determined by averaging Is in the high-q range of the scattering curve which is displayed as dashed line in Fig. 4. The weight-averaged molar mass of the scatterers Mw can then be determined from I0,coherent with eqn (8).16
coherent. The value for the incoherent background was determined by averaging Is in the high-q range of the scattering curve which is displayed as dashed line in Fig. 4. The weight-averaged molar mass of the scatterers Mw can then be determined from I0,coherent with eqn (8).16
I0,coherent = I0 − BGin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) coherent = c·K·Mw coherent = c·K·Mw | (8) |
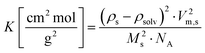 | (9) |
| Parameter | [Blue]tot = 5 mM | [Blue]tot = 10 mM |
|---|---|---|
| c [10−3 g cm−3] | 1.85 ± 0.02 | 3.70 ± 0.03 |
| ρ s [cm−2] | 3.004 × 1010 | |
| ρ solv [cm−2] | 6.376 × 1010 | |
| V m,s [cm3 mol−1] | 246.31 | |
| M s [g mol−1] | 368.82 | |
| SANS | [Blue]tot = 5 mM | [Blue]tot = 10 mM |
| I 0,coherent [10−3 cm−1] | 0.6 ± 0.1 | 1.6 ± 0.1 |
| M w [g mol−1] | 362 ± 97 | 502 ± 47 |
| R g [Å] | 1.6 ± 0.1 | 3.1 ± 0.1 |
| K D = (728) L mol−1 | [Blue]tot = 5 mM | [Blue]tot = 10 mM |
| [M] [mM] | 1.54 ± 0.02 | 2.30 ± 0.02 |
| [D] [mM] | 1.73 ± 0.01 | 3.85 ± 0.01 |
| M w (KD) [g mol−1] | 624 ± 1 | 653 ± 1 |
The weight average molar mass of the scatterer is furthermore compared to the theoretical weight average molar mass of a mixture of Blue monomers and dimers according to the dimerization equilibrium described by eqn (3) with the calculated dimerization constant of KD = (728 ± 8) L mol−1. Knowing the total molar dye concentration, the molar concentrations of Blue monomer [M] and Blue dimer [D] are obtained by combining eqn (3) and (5). Mw(KD) is then obtained from:
 | (10) |
From Table 1, several observations are made: (1) according to Guinier analysis, Mw and Rg of scatterers in the sample containing [Blue]tot = 10 mM are higher than Mw and Rg of scatterers in the sample containing [Blue]tot = 5 mM. This is consistent with the assumption of concentration-induced aggregation. (2) Due to the extremely low scattering intensities from the dye solutions and concomitant poor statistics, errors in Mw from SANS are high in this case. (3) Mw from SANS does not directly compare to Mw(KD) from the experiments presented here. This could be due to the high error in Mw, low values of Mw and uncertainty in scattering contrast.27 It should, however, be noted that Mw from SANS is smaller than Mw(KD) in both cases, rendering the possibility of aggregates of more than two monomers unlikely. (4) The radius of gyration of the scatterers at either concentration is very small. Considering the model of a homogeneous cylinder, Rg = 4 Å was estimated for the dimer considering its chemical structure and results from exciton analysis. The calculation is outlined in the ESI.†Rg = 4 Å is not significantly higher than the experimentally determined Rg from SANS for the sample with [Blue]tot = 10 mM. A direct comparison of this theoretical value to the experimental ones is difficult, as each solution contains a mixture of monomer and dimer and the homogeneous cylinder model is only an approximation. Nevertheless it shows that the interplanar spacing R = 5.2 Å obtained by exciton theory is within an acceptable size range.
Information on the cause for dimer formation in solutions of Blue may be obtained by elucidating how Blue molecules assemble within the dimeric aggregate. For this purpose, ROESY (rotating frame nuclear Overhauser effect spectroscopy) has been used to evaluate correlations through space. This type of NOE (nuclear Overhauser effect) spectroscopy permits to study the spatial proximity of protons up to a distance of about 5 Å.28 In contrast to the more frequently performed NOESY (nuclear Overhauser effect spectroscopy), ROESY cross peak signals are always positive and do not vanish if the molecule or assembly exhibits a medium tumbling rate.29,30Fig. 5 displays the ROESY spectrum of a solution containing [Blue]tot = 10 mM. Cross peaks for signals a′–b′ and d′–e′ are expected due to the chemical structure of Blue. However, cross peaks are also observed between signals a′–e′, b′–f′ and c′–f′. They exhibit much weaker intensities than the cross peaks mentioned before, which is likely caused by a greater distance between corresponding protons. These cross peaks are therefore related to the proximity of protons of two different molecules.
Fig. 6(B) displays the structure of the Blue dimer, which explains cross peaks that were observed in the ROESY spectrum and is chemically meaningful. For readability, observed intermolecular NOE couplings are marked on two aligned but displaced chemical structures of Blue in Fig. 6(A). In terms of intermolecular interactions, three major driving forces leading to the observed self-assembly are expected: (1) electrostatic repulsion between negatively charged phenolate groups, (2) π–π stacking of aromatic moieties and (3) hydrogen bonding interactions between the phenolate oxygen atom and hydrogen atoms from the sulphonamide groups.
 | ||
| Fig. 6 Fig. 6 (A) Chemical structure of two molecules of Blue aligned as expected in the dimeric assembly but displaced for visibility. Protons are labelled according to the peak assignment in the ROESY spectrum (Fig. 5). Observed intermolecular NOE coupling is indicated by red dotted lines. (B) Structure of the Blue dimer. Grey, dotted lines indicate potential hydrogen bonding interactions. | ||
The formation of assemblies with higher aggregation numbers may be hindered by steric requirements of the sulphonamide group and resulting packing constraints as well as electrostatic repulsion between nearby phenolate groups, which supports the assumption of dimer formation.
The dimer structure shown in Fig. 6(B) is relatively symmetrical, indicating that protons from both molecules participating in dimer formation experience similar chemical environments, which leads to narrow 1H-NMR signals.28 Furthermore, the proposed structure complies with results from preceding analysis of UV/vis spectra according to exciton theory: within the model of non-planar transition dipoles a tilt angle α = 42° between two molecular planes was found, which agrees with the proposed structure as these planes are not given a direction and α < 90°.19 Furthermore, an interplanar spacing of R = 5.2 Å does not rule out the occurrence of a NOE between interacting Blue molecules.
To conclude this section, the self-assembly of Blue in an aqueous NaHCO3/Na2CO3 buffer with pH = 10.5 and I ≈ 0.25 M was elucidated using UV/vis-spectroscopy, SANS and NMR-spectroscopy. Concentration-dependent UV/vis spectra pointed towards dimer formation and H-aggregation of Blue molecules with a dimerization constant of KD = (728 ± 8) L mol−1. SANS confirmed concentration-induced aggregation while proving higher-than-dimer aggregation unlikely. Dimer geometry was elucidated with the help of NMR-spectroscopy and the quantitative analysis of UV/vis spectra according to exciton theory, suggesting π–π- and hydrogen bonding interactions as the most relevant attractive forces. Conversely, electrostatic repulsion between phenolate groups and steric requirements of the sulphonamide group potentially inhibit the formation of higher-order aggregates.
Self-assembly of Red
The absorption spectra of the dye Red are affected by concentration induced self-aggregation (Fig. 7). An increase in concentration leads to a shift of the absorption maximum to lower wavelengths. However, no well-defined isosbestic point exists, suggesting more than two absorbing species contributing to the overall spectrum. Therefore, we abstained from an attempt to decompose the spectra into contributions from components.SANS was performed on solutions of Red (Fig. 8), one solution containing [Red]tot = 10 mM and the other one containing Red at an approximate concentration of [Red]tot ≈ 5 mM. The concentration of Red in the latter sample was obtained by comparing forward scattering intensities of both SANS curves, as the sample with [Red]tot ≈ 5 mM was intended to contain a higher concentration of Red, but was filtered too soon after its preparation when the dye was not yet completely dissolved, resulting into a loss of material. Details can be found in the ESI† (Fig. S10). For both curves, two Guinier shoulders are discernible at q < 0.003 Å−1 and q > 0.05 Å−1. This likely results from scattering of at least two morphological features: A small structure, showing a Guinier-plateau in the high-q region at q > 0.05 Å−1 and a large structure, causing the scattering intensity in the mid- and low-q region to rise.
 | ||
| Fig. 8 SANS data of two solutions of Red in buffer and at 25°. The form factor fit corresponding to the contribution of a Guinier fit (Rg = 8.5 Å) with a fractal structure (Df = 2.66 ± 0.03, Lcorr = (437 ± 10) Å, Rblock = (9 ± 1) Å) is shown as a red line.31 Both displayed fits only differ by scaling factors. χ2([Red]tot = 10 mM) = 1.52, χ2([Red]tot ≈ 5 mM) = 3.31. | ||
The radius of gyration of the species contributing to the scattering signal in the high-q region was determined to 8.5 Å by model-independent Guinier analysis for both curves. Furthermore, the SANS curves were described using the sum of a fractal form factor and a Guinier fit.31 The fractal model describes the mid- and low-q region and is characterized by the radius of spherical building blocks, Rblock, its scattering length density ρblock, the fractal dimension Df and the cluster correlation length Lcorr, which represents the total fractal cluster size. Rblock = (9 ± 1) Å was found to be similar to Rg = 8.5 Å obtained for the small species. The sum of a fractal model and a Guinier fit describes both SANS curves sufficiently well. Both curves can be described using identical geometrical parameters and fractal dimension when permitting the scaling of the fractal and the Guinier contribution to be different. Size parameters are given in the caption of Fig. 8 and are summarized in the ESI† (Table S2).
Aside from reproducing the scattering pattern of true fractals, the fractal form factor model can often be used for hierarchically structured aggregates, which cannot be further specified in terms of a more specific form factor model such as sphere, ellipsoid or cylinder without introducing a large number of fitting parameters, e.g. concerning polydispersity.32–34 The fractal model has been successfully applied for instance in asphaltene research, where asphaltene molecules in a nonpolar solvent are assumed to aggregate in a three-step hierarchy from core aggregates due to π–π-stacking of molecules, over medium aggregates, which are secondary aggregates of core aggregates, to fractal aggregates.35
Concerning the dye Red, the assumption of π–π-stacking interactions leads to cylinders as the first choice to describe SANS curves of corresponding solutions.4 However, an apparent scaling of Is ∝ q−2.66 instead of Is ∝ q−1 in the low- to mid-q region contradicts the presence of simple, non-interacting cylinders.36 Furthermore, the Kratky plot of corresponding SANS curves (Fig. S11, ESI†) shows an initial maximum and in the Holtzer plot (Fig. S12, ESI†) a minimum is visible before reaching a plateau in the high-q region. Both observations point towards a structure, which is more compact than a random coil polymer chain.36 However, these observations do not rule out the existence of cylinders as a structural feature, particularly because a Is ∝ q−1 dependency is observed in the mid- to high-q region. A possible explanation could be branching of these cylinders.37,38 A more in-depth discussion is given in the ESI.† The presence of at least two structural levels is therefore likely to occur and visualized in Fig. 9. Herein, the formation of cylinder-like aggregates induced by π–π-stacking of Red is the onset of the aggregation. These π-stacks may elongate to cylindrical aggregates, which could show branching. Alternatively, further assembly of short cylinder segments may lead to fractal aggregates. The cluster correlation length in the fractal model would correspond to the overall size of the branched cylinder aggregate and the thickness (or size) of the building units in the fractal model would reproduce the cylinder cross section in the branched cylinder picture.
 | ||
| Fig. 9 Potential hierarchy in the aggregation of Red. The image and theory were adapted from considerations regarding the aggregation of asphaltenes in n-heptane according to Tanaka et al.35 | ||
Fig. 10 shows the 1H-NMR spectrum of a 10 mM solution of Red. In addition to that, it was attempted to obtain an idea about spatial proximity of protons belonging to different Red molecules using ROESY (Fig. S15, ESI†). However, no cross peaks were observed in the ROESY spectrum. As not even the a–b cross peak expected from chemical structure of the Red molecule was visible, the absence of observable spatial correlations in the ROESY spectrum was attributed to the extreme peak broadening of signals b and c. Peak broadening is often a sign of aggregation arising from increased spin–spin relaxation rates due to slower molecular motion in aggregates.39,40 This is a rather frequently observed phenomenon for systems exhibiting π–π-stacking, like dye molecules in solution.30,41,42 Nevertheless it is remarkable, that signals a and d are not as strongly line broadened as signals b and c, which could result from corresponding protons experiencing a smaller variety of chemical environments and protons of type d potentially tumbling faster leading to the observation of an average chemical shift.43 Following these observations, protons b and c are likely located closer to the structural sub-unit leading to intermolecular aggregation of Red, which results in a greater variety of chemical environments and rigidity, whereas protons of type a and d are located further away from that part of the molecule. Considering that π–π-stacking interactions between 1,2,4-oxadiazole moieties were shown of great relevance for the aggregation of molecules containing such a heterocycle, it is likely that the aggregation of Red molecules results from π–π-stacking interactions between the similar 1,2,4-thiadiazole heterocyclic moieties.44 This aligns well with the assumption of electrostatic repulsion between phenolate groups, as these are free to point towards opposite directions when π–π-stacking occurs on the 1,2,4-thiadiazole aromatic sub-unit.
 | ||
| Fig. 10 1H-NMR spectrum of a solution containing Red at [Red]tot = 10 mM in a NaHCO3/Na2CO3 buffer (pD = 10.7, I ≈ 0.25 M) prepared in D2O. | ||
To conclude, the self-assembly of Red in an aqueous NaHCO3/Na2CO3 buffer with pH = 10.5 and I ≈ 0.25 M commences with a cylindrical arrangement of Red monomers. NMR spectroscopic investigations suggest π–π-stacking between the 1,2,4-thiadiazole sub-units of different Red molecules to be the main reason for this arrangement. The cylinders probably elongate and eventually branch. The SANS curves of the resulting aggregates can be reproduced by a simplified fractal model.
Conclusions
Three 3-chloro-4-hydroxy-phenylazo dyes, each of them carrying a negative charge due to deprotonation of the phenolic hydroxyl group at alkaline pH, were shown to significantly differ in their self-assembly behaviour. This confirms the complexity of intermolecular interactions and the difficulty to predict assembly behaviour of molecules just from their chemical structure.Unlike to Blue and Red, the dye Yellow does not self-assemble. In addition to that, Yellow shows a solubility limit of 11 mM in the aqueous buffer used as a solvent, which was not observed for the other dyes. The lack of Yellow self-aggregation can be attributed to the impossibility to form intermolecular π–π-stacking interactions. π–π-stacking between phenolate groups is likely hindered by electrostatic repulsion between the deprotonated hydroxyl groups. Furthermore, π–π-stacking between pyrazole sub-units might be hindered by steric constraints due to the substitution of one nitrogen atom with a methyl group.
The self-assembly of Blue and Red can be followed using UV/vis spectroscopy. Blue was observed to form dimers with a dimerization constant of KD = (728 ± 8) L mol−1. With the calculated dimer spectrum, H-aggregation of Blue molecules is revealed. Their aggregation geometry calculated with exciton theory, yields a twist angle of transition dipole moments of α = 42° and an interplanar spacing of 5.2 Å in the model of non-parallel transition dipoles. Driving forces for self-aggregation include π–π-stacking, electrostatic repulsion between phenolate groups and likely hydrogen bonding between the phenolate oxygen and hydrogen atoms of the sulphonamide group. Steric effects due to spatial requirements of the sulphonamide group and electrostatic repulsion between phenolate groups pointing towards the same direction could hinder the formation of larger aggregates.
The self-aggregation of Red is more complex than that of Blue. The absence of an isosbestic point in concentration-dependent UV/vis spectra suggests the presence of multiple aggregate species. SANS revealed an average aggregate size of at least 400 Å. Self-aggregation of Red likely occurs due to π–π-stacking of the 1,2,4-thiadiazole sub-unit, leading to cylindrical building blocks which are able to form larger aggregate structures, most likely via branching.
Following these investigations, it becomes evident, that assembly properties cannot easily be predicted based on structural similarities. Rather, assembly morphology is directed by a subtle balance of intermolecular interactions and steric effects, which can be influenced dramatically by minor constitutional changes. Therefore, care has to be taken when expecting similar behaviour from molecules with similar chemical functionalities.
Author contributions
Conceptualization: WM, RS, BN, KH, experimental: WM, RS, HE, analysis: WM with contributions from RS, HE, KH, BN, writing: WM, editing: WM, RS, BN, KH, HE, funding acquisition: RS, BN, KH.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Institut Laue-Langevin for the provision of internal beamtime (https://doi.ill.fr/10.5291/ILL-DATA.INTER-557). The authors gratefully acknowledge the use of the Partnership for Soft Condensed Matter (PSCM) facilities. W. M. acknowledges funding for a PhD scholarship from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 847439 within the InnovaXN framework (Project number XN2019-ILL23).Notes and references
- T. Bechtold, A. Mahmud-Ali and R. Mussak, Dyes Pigm., 2007, 75, 287–293 CrossRef CAS.
- N. ElGuesmi, A. Farghaly, A. Y. Khormi, M. R. Shaaban, K. P. Katin and S. Kaya, J. Mol. Struct., 2023, 1271, 134002 CrossRef CAS.
- H. Jiang, L. Zhang, J. Cai, J. Ren, Z. Cui and W. Chen, Dyes Pigm., 2018, 151, 363–371 CrossRef CAS.
- D. Bialas, E. Kirchner, M. I. S. Röhr and F. Würthner, J. Am. Chem. Soc., 2021, 143, 4500–4518 CrossRef CAS PubMed.
- A. Hagfeldt, G. Boschloo, L. Sun, L. Kloo and H. Pettersson, Chem. Rev., 2010, 110, 6595–6663 CrossRef CAS PubMed.
- P.-T. Chou and Y. Chi, Chem. – Eur. J., 2007, 13, 380–395 CrossRef CAS PubMed.
- F. Würthner, C. R. Saha-Möller, B. Fimmel, S. Ogi, P. Leowanawat and D. Schmidt, Chem. Rev., 2016, 116, 962–1052 CrossRef PubMed.
- X. Hu, T. Ritz, A. Damjanović, F. Autenrieth and K. Schulten, Q. Rev. Biophys., 2002, 35, 1–62 CrossRef CAS PubMed.
- X. Hu, A. Damjanović, T. Ritz and K. Schulten, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 5935–5941 CrossRef CAS PubMed.
- H. Tamiaki, Coord. Chem. Rev., 1996, 148, 183–197 CrossRef CAS.
- T. S. Balaban, H. Tamiaki and A. R. Holzwarth, in Supermolecular Dye Chemistry, ed. F. Würthner, Springer, Berlin, Heidelberg, 2005, pp. 1–38 Search PubMed.
- Z. Chen, A. Lohr, C. R. Saha-Möller and F. Würthner, Chem. Soc. Rev., 2009, 38, 564–584 RSC.
- C. F. J. Faul and M. Antonietti, Adv. Mater., 2003, 15, 673–683 CrossRef CAS.
- Mantid Project, Mantid (2013): Manipulation and Analysis Toolkit for Instrument Data DOI:10.5286/SOFTWARE/MANTID.
- O. Arnold, J. C. Bilheux, J. M. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. Ferraz Leal, M. A. Gigg, V. E. Lynch, A. Markvardsen, D. J. Mikkelson, R. L. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. G. Perring, P. F. Peterson, S. Ren, M. A. Reuter, A. T. Savici, J. W. Taylor, R. J. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166 CrossRef CAS.
- Neutrons, X-rays, and light: scattering methods applied to soft condensed matter, ed. P. Lindner and T. Zemb, Elsevier, Amsterdam, Boston, 1st edn, 2002 Search PubMed.
- H. E. Gottlieb, V. Kotlyar and A. Nudelman, J. Org. Chem., 1997, 62, 7512–7515 CrossRef CAS PubMed.
- F. Cuétara-Guadarrama, M. Vonlanthen, K. Sorroza-Martínez, I. González-Méndez and E. Rivera, Dyes Pigm., 2021, 194, 109551 CrossRef.
- M. Kasha, H. R. Rawls and M. A. El-Bayoumi, Pure Appl. Chem., 1965, 11, 371–392 CAS.
- B. Neumann, K. Huber and P. Pollmann, Phys. Chem. Chem. Phys., 2000, 2, 3687–3695 RSC.
- M.-L. Horng and E. L. Quitevis, J. Chem. Educ., 2000, 77, 637 CrossRef CAS.
- R. Sabaté, M. Gallardo, A. de la Maza and J. Estelrich, Langmuir, 2001, 17, 6433–6437 CrossRef.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa and P. Van Mulbregt, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- M. Kasha, Radiat. Res., 1963, 20, 55–70 CrossRef CAS PubMed.
- K. K. Rohatgi, J. Mol. Spectrosc., 1968, 27, 545–548 CrossRef CAS.
- W. Schärtl, Light Scattering from Polymer Solutions and Nanoparticle Dispersions, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007 Search PubMed.
- K. A. Rubinson, C. Stanley and S. Krueger, J. Appl. Crystallogr., 2008, 41, 456–465 CrossRef CAS.
- J. B. Lambert, Spektroskopie: Strukturaufklärung in der Organischen Chemie, Pearson, 2012 Search PubMed.
- T. D. W. Claridge, High-Resolution NMR Techniques in Organic Chemistry, Elsevier, 2nd edn, 2009, vol. 27, pp. 247–302 Search PubMed.
- M. P. Renshaw and I. J. Day, J. Phys. Chem. B, 2010, 114, 10032–10038 CrossRef CAS PubMed.
- J. Teixeira, J. Appl. Crystallogr., 1988, 21, 781–785 CrossRef.
- M. P. Hoepfner, C. Vilas Bôas Fávero, N. Haji-Akbari and H. S. Fogler, Langmuir, 2013, 29, 8799–8808 CrossRef CAS PubMed.
- J. Eyssautier, P. Levitz, D. Espinat, J. Jestin, J. Gummel, I. Grillo and L. Barré, J. Phys. Chem. B, 2011, 115, 6827–6837 CrossRef CAS PubMed.
- K. L. Gawrys, G. A. Blankenship and P. K. Kilpatrick, Langmuir, 2006, 22, 4487–4497 CrossRef CAS PubMed.
- R. Tanaka, E. Sato, J. E. Hunt, R. E. Winans, S. Sato and T. Takanohashi, Energy Fuels, 2004, 18, 1118–1125 CrossRef CAS.
- J. S. Pedersen, Adv. Colloid Interface Sci., 1997, 70, 171–210 CrossRef CAS.
- K. Huber and W. Burchard, Macromolecules, 1989, 22, 3332–3336 CrossRef CAS.
- K. Huber, W. Burchard, S. Bantle and L. J. Fetters, Polymer, 1987, 28, 1997–2003 CrossRef CAS.
- D. J. Edwards, J. W. Jones, O. Lozman, A. P. Ormerod, M. Sintyureva and G. J. T. Tiddy, J. Phys. Chem. B, 2008, 112, 14628–14636 CrossRef CAS PubMed.
- C. Shao, M. Grüne, M. Stolte and F. Würthner, Chem. – Eur. J., 2012, 18, 13665–13677 CrossRef CAS PubMed.
- M. J. Ahrens, L. E. Sinks, B. Rybtchinski, W. Liu, B. A. Jones, J. M. Giaimo, A. V. Gusev, A. J. Goshe, D. M. Tiede and M. R. Wasielewski, J. Am. Chem. Soc., 2004, 126, 8284–8294 CrossRef CAS PubMed.
- M. J. Ahrens, R. F. Kelley, Z. E. X. Dance and M. R. Wasielewski, Phys. Chem. Chem. Phys., 2007, 9, 1469–1478 RSC.
- I. Furó, J. Mol. Liq., 2005, 117, 117–137 CrossRef.
- S. V. Baykov, A. S. Mikherdov, A. S. Novikov, K. K. Geyl, M. V. Tarasenko, M. A. Gureev and V. P. Boyarskiy, Molecules, 2021, 26, 5672 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sm00500c |
| This journal is © The Royal Society of Chemistry 2023 |





