Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Curvature and confinement effects on chiral liquid crystal morphologies
Viviana
Palacio-Betancur
 a,
Julio C.
Armas-Pérez
a,
Julio C.
Armas-Pérez
 b,
Juan P.
Hernández-Ortiz
b,
Juan P.
Hernández-Ortiz
 *acd and
Juan J.
de Pablo
*acd and
Juan J.
de Pablo
 *ae
*ae
aPritzker School of Molecular Engineering, University of Chicago, Chicago, IL 60637, USA. E-mail: depablo@uchicago.edu
bDivisión de Ciencias e Ingenierías, Campus León, Universidad de Guanajuato, Loma del Bosque 103, León (Gto.) 37150, Mexico
cDepartamento de Materiales y Minerales, Universidad Nacional de Colombia—Sede Medellín, Medellín, Colombia. E-mail: jphernandezo@unal.edu.co
dColombia/Wisconsin One-Health Consortium, Universidad Nacional de Colombia Sede Medellín, Medellín, Colombia
eMaterials Science Division, Argonne National Laboratory, Lemont, IL 60439, USA
First published on 8th June 2023
Abstract
Chiral liquid crystals (ChLCs) exhibit an inherent twist that originates at the molecular scale and can extend over multiple length scales when unconstrained. Under confinement, the twist is thwarted, leading to formation of defects in the molecular order that offer distinct optical responses and opportunities for colloidal driven assembly. Past studies have explored spheroidal confinement down to the nanoscopic regime, where curved boundaries produce surface defects to accommodate topological constraints and restrict the propagation of cuboidal defect networks. Similarly, strict confinement in channels and shells has been shown to give rise to escaped configurations and skyrmions. However, little is known about the role of extrinsic curvature in the development of cholesteric textures and Blue Phases (BP). In this paper, we examine the palette of morphologies that arises when ChLCs are confined in toroidal and cylindrical cavities. The equilibrium morphologies are obtained following an annealing strategy of a Landau-de Gennes free energy functional. Three dimensionless groups are identified to build phase diagrams: the natural twist, the ratio of elastic energies, and the circumscription of a BP cell. Curvature is shown to introduce helical features that are first observed as a Double Twist, and progress to Chiral Ribbons and, ultimately, Helical BP and BP. Chiral ribbons are examined as useful candidates for driven assembly given their tunability and robustness.
1 Introduction
The role of curvature on the ordering and assembly of building blocks is fundamental to the understanding of flexible bilayer membranes,1,2 viral capsids,3–5 spherical crystallography,6 quasi-2D materials,7,8 and active matter.9,10 From a 2D perspective, curvature provides subtle changes to the local order, leading to bistability and a means to manipulate the preferred alignment through the confining geometry.8,11,12 In three dimensions, confinement provides an additional parameter with which to balance bulk elasticity and surface curvature for design of responsive materials.13–18 In the context of liquid crystals, orientational order becomes frustrated and defects, regions of low order, emerge as a result of topological constraints.15,19–22Past studies have produced stable LC morphologies through geometrical confinement, particularly for chiral liquid crystals (ChLCs) where elongated molecules collectively break rotational symmetry and organize along a main helical path, thereby favoring twist over splay or bending deformations. In spherical cavities, ChLCs' inherent twist conforms to the surface curvature and generate frustrated concentric structures such as the Twisted Bipolar and the Radial Spherical Structure.21–27 Highly chiral ChLCs contain disclination lines in the bulk, and curvature can mold them into hybrid structures.27–30 For shells, the inner anchoring conditions generate escaped configurations, and the shell homogeneity and thickness become important parameters to control morphology.31–38 More intricate geometries, such as droplets with handles, have been found to guide disclination lines into knots and other non-trivial textures.39–42
Toroidal and cylindrical confinement offer ample grounds for discovery of new phases, as demonstrated in experiments where the ground state of a non-chiral LC is the double twisted morphology,39,43–46 in contrast to the uniform orientation along the main axis of a cylindrical cavity.47–49 Under homeotropic confinement, LCs have been shown to exhibit spontaneous twist resulting in escaped radial configurations induced by the curved boundaries.50,51 From a computational standpoint, traditional numerical methods are generally limited by the need to formulate an ansatz (or “initial guess”) corresponding to each geometry,45,52 and by the scale of the discretization needed to capture a morphology's nuances.53
ChLCs offer several characteristics of interest for photonic and electro-optical devices. They exhibit fast response times and rich optical behaviors. The characteristic length scale of the helical trajectory, or molecular pitch, determine the equilibrium morphology of the system. For long pitches, the material exhibits a cholesteric phase, where molecules can twist uniformly without forming defects. For a sufficiently short pitch, defect lines form spontaneously and self-organize into space filling lattices with cubic symmetry, leading to the so-called Blues Phases (BPs).54
However versatile, BPs are only stable over a narrow range of temperature. Furthermore, in the bulk they form polycrystalline domains, posing challenges to applications.55,56 External stimuli can help enhance and stabilize morphologies of interest. Lithographic patterns, for example, have been successful in achieving monocrystalline domains of BPII and BPI, where the substrate chemistry is tailored to guide the orientation of the BP unit cells.57,58 Polymerization has also been used to enhance the thermal stability of BPs, by setting the underlying defect network into a permanent scaffold.59–62
More recently, Negro et al. reported a detailed analysis of the patterns that appear on the surface of chiral LC shells. These authors relied on lattice Boltzmann simulations to identify the equilibrium morphologies of highly chiral LCs as they transition into an ordered phase from an isotropic state.63 Building on that work, in this study we examine how geometrical frustration in toroidal and cylindrical cavities can be manipulated to preserve key characteristics of chiral nematics while introducing new geometrical features that do not arise when in bulk. Specifically, curvature is used to engineer new mesophases of ChLCs – curvature couples to defects by screening their topological charge. Recent theoretical reports indicate that strict planar confinement of 2D ChLCs hinders the development of double twist, leading to the formation of a novel chiral structure.64
In Section 2 we outline the details of the phenomenological model adopted here, as well as the numerical methods used to find equilibrium configurations. Section 3 introduces our results and discussion by presenting the underlying free energy surface as a function of chirality and cavity size. We continue by presenting phase diagrams at different temperatures, and a more detailed analysis of the surface patterns corresponding to each system. In Section 4 we provide a short summary of our findings and several remarks about future applications of this work.
2 Models and methods
The free energy functional includes a short-range Landau polynomial expansion in Q(x) to model the isotropic-nematic transition, a long-range functional that accounts for elastic distortions, and a surface contribution that imposes a preferred orientation at the boundaries.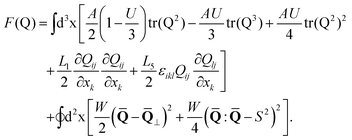 | (1) |
The model parameters include the Landau coefficient A that sets the energy density scale, the dimensionless parameter U that determines the IN transition (inverse temperature); L1 and L5 are the elastic constants and W represents the strength of the surface anchoring. Additionally, the preferred orientation at the boundaries is tangential and is determined by the planar projection of Q as ![[Q with combining macron]](https://www.rsc.org/images/entities/b_char_0051_0304.gif) ⊥ = p·
⊥ = p·![[Q with combining macron]](https://www.rsc.org/images/entities/b_char_0051_0304.gif) ·p with
·p with ![[Q with combining macron]](https://www.rsc.org/images/entities/b_char_0051_0304.gif) = Q + Sδ/3 and p = δ − νν. Details of the free energy densities in eqn (1) can be found in our previous works.27,65–67
= Q + Sδ/3 and p = δ − νν. Details of the free energy densities in eqn (1) can be found in our previous works.27,65–67
Two characteristic length scales arise naturally from the free energy functional: the nematic coherence length 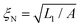 , and the surface extrapolation length ξS = L1/W. The elastic constants Li are related to the different elastic moduli and chirality. For a uniaxial LC under a one-elastic constant approximation, they can be estimated through L1 = k11/2S2 and L5 = 2q0k22/S2. L5 quantifies the chirality of the LC with inverse pitch, q0 = 1/p0.
, and the surface extrapolation length ξS = L1/W. The elastic constants Li are related to the different elastic moduli and chirality. For a uniaxial LC under a one-elastic constant approximation, they can be estimated through L1 = k11/2S2 and L5 = 2q0k22/S2. L5 quantifies the chirality of the LC with inverse pitch, q0 = 1/p0.
For efficient exploration of configuration space, we adopt a theoretically-informed Monte Carlo relaxation introduced in our previous works.27,65–67 This approach is particularly effective for discovery of unknown morphologies, particularly in systems with a rough free energy surface. The minimization is achieved by performing random changes to the Q tensor according to a Metropolis algorithm to sample different morphologies of the free energy functional outlined above. The uniform sampling over the five independent components of Q is ensured by mapping the tensor onto an orthonormal basis introduced by Hess et al.68 This replaces all tensor operations by faster, scalar ones.
Trial moves are accepted with probability Pacc(o → n) = min[1, exp(−βΔF)], where β−1 = kB![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) , kB is the Boltzmann constant,
, kB is the Boltzmann constant, ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is an artificial temperature and ΔF is the change in the free energy due to changes in Q. The domains are discretized into quadratic tetrahedral elements in Cubit (ver 14.1)69 and optimized with the libMesh library.70 The numerical integration to calculate the free energy is implemented with a Gauss–Legendre quadrature over the elements. The finite element-based meshing allows us to capture fine details of the geometry while providing a robust framework for non-linear behavior,26,27,30,71 and is able to find equilibrium configurations consistent with those obtained by more traditional minimization techniques.65–67
is an artificial temperature and ΔF is the change in the free energy due to changes in Q. The domains are discretized into quadratic tetrahedral elements in Cubit (ver 14.1)69 and optimized with the libMesh library.70 The numerical integration to calculate the free energy is implemented with a Gauss–Legendre quadrature over the elements. The finite element-based meshing allows us to capture fine details of the geometry while providing a robust framework for non-linear behavior,26,27,30,71 and is able to find equilibrium configurations consistent with those obtained by more traditional minimization techniques.65–67
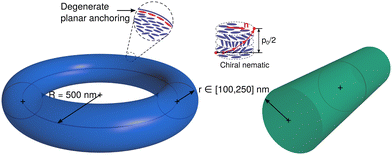
The toroidal and cylindrical cavities shown in Fig. 1 (R = 500 nm and r0 ∈ [100, 250] nm) impose planar degenerate alignment with moderate (W = 1 × 10−4 J m−2) to weak (W = 1 × 10−6 J m−2) anchoring strength onto a chiral liquid crystal with pitch po ∈ [100, 1000] nm. The nematic parameter is close to the IN transition, between U = 2.7 and U = 2.9, the regime in which BPs are stable in the bulk. The parameters for 4′-pentyl-4-cyanobiphenyl (5CB) are used as the model system with A = 1 × 105 J m−3, L1 = 5.11 pN, and ξN = 7.15 nm. The free energy minimization requires approximately 4 × 105 Monte Carlo cycles. The system was quenched over five stages through ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) . The meshes for these simulations vary in size according to the confinement size r0; on average, they are comprised of 3 × 105 nodes and 2 × 105 elements for r0 = 100 nm, and up to 9.5 × 105 nodes and 7 × 105 elements for r0 = 250 nm.
. The meshes for these simulations vary in size according to the confinement size r0; on average, they are comprised of 3 × 105 nodes and 2 × 105 elements for r0 = 100 nm, and up to 9.5 × 105 nodes and 7 × 105 elements for r0 = 250 nm.
3 Results
We begin our discussion by exploring the free energy contributions as a function of chirality and confinement, shown in Fig. 2a. For convenience, we use the dimensionless group 2q0r0, analog to the chirality, which characterizes the natural twist in the confined system and allows us to collapse our results onto master curves shown in gray.At low chirality, in the cholesteric (Chol) regime, all components of the free energy are close to zero, meaning that at equilibrium the resulting configuration is uniform and without defects, and the orientation of the LC at the boundary follows its curvature. For higher chirality, the material adopts a double twist configuration that results in a cuboidal defect network (Blue Phases, BP). Their emergence increases the Landau-de Gennes free energy, and the confluence of double twist domains creates regions of high splay, as reflected by the corresponding elastic contribution. At the boundary, the curvature interrupts the cubic symmetry of the defect network and produces a fingerprint pattern, a collection of half-skyrmions that will be described later in our analysis.
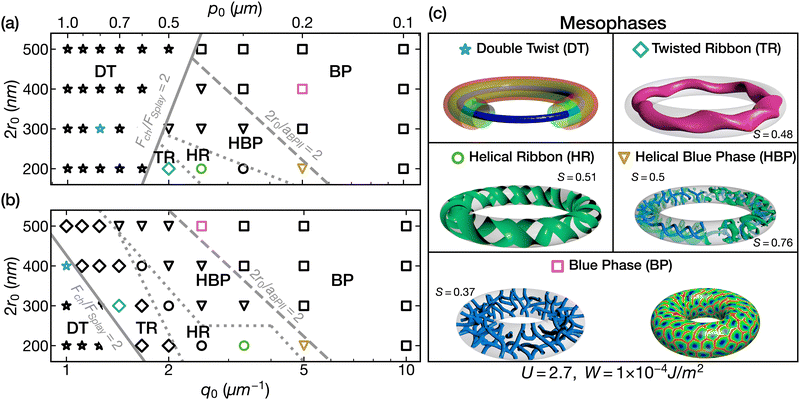
The ratio between chiral and splay elastic contributions serves as a proxy for the family of morphologies that arise in these systems, illustrated in Fig. 2b as a function of natural twist. Two lines serve to delineate the characteristics of the morphologies at equilibrium. The first is |FCh|/FSplay = 2, and refers to the limiting energy for disclination lines to interweave the bulk of the system. The second line is defined by the balance between the cavity size (2r0) and the Blue Phase unit cell aBP, and plays a crucial role in systems with high chirality. For 2r0/aBP < 2, confinement frustrates a fully developed BP cell, and the disclination lines adopt helical features conforming to the geometry. In this case, since U = 2.7, the unit cell is that of the Blue Phase II calculated as aBPII = p0/1.72. The inset in Fig. 2b shows the ratio 2r0/aBPII as a function of inverse pitch q0, where a horizontal line delimits the systems in which helical morphologies are favored over fully developed Blue Phases.
The free energy analysis is consistent with the phase diagrams generated in terms of q0 = 1/p0 and 2r0, shown in Fig. 3 for (a) U = 2.7 and (b) U = 2.9 in a toroidal cavity. Highlighted markers in the phase diagram correspond to the morphologies illustrated in Fig. 3c. The first three morphologies occur at low chirality: Double Twist (DT), Twisted Ribbon (TR), and Helical Ribbon (HR). They are best described by the alignment of the director with respect to the major (toroidal) axis. First, the DT is a cholesteric morphology and exhibits a continuous twist in the radial direction. At the core of the cavity, the director is aligned with the toroidal axis such that the midline is straight. At the boundary, the director is tangential to the surface and is tilted with respect to the toroidal axis. The illustration in Fig. 3c shows three concentric tubes, each corresponding to regions in which the director tilt with respect to the midline is 0° (blue), 20° (green) and 45° (red).
As chirality increases, a smooth double twist within the torus can no longer be sustained, and each concentric layer of the DT buckles to form a twisted ribbon (TR). Each ribbon retains a straight midline while isosurfaces of the order parameter exhibit saddle-like curvature, as illustrated by the magenta ribbon with S = 0.48 in Fig. 3c. Additional twisting of the order field requires widening of the ribbon, which is not attainable due to the confining surface. Instead, the ribbon twists on itself forming two Helical Ribbons (HR), in which the midline draws a helix in space and the saddle-like curvature of the ribbon transitions to isosurfaces with zero mean curvature. The HR can also be described as two interlocking torus knot with invariant T(1,q) where q is related to the ratio of the molecular pitch and the major radius of the tori. Previous works on chiral nematic colloids have characterized these type of knots as linkers for colloidal lattices.72
Lastly, we examine the region of systems with 2q0r0 >1 and |FCh|/FSplay > 2, populated with Blue Phase-like defects. In this regime, one can appreciate the pronounced effects of geometrical frustration on the Helical Blue Phase (HBP). For conditions where confinement is smaller than the unit cell of a BP, disclination lines are interwoven with lingering features of the HR morphology. The defects are evenly spaced but do not always grow radially; instead they follow the helical midline, resulting in sections where the defects form a double helix (drawn in blue), and are encased by two helical ribbons (drawn in green).
Under less severe confinement (2r0/aBPII > 2), a BP unit cell is fully circumscribed by the torus, and replicated throughout the toroidal axis. In such a way, the resulting BP morphologies adopt varying crystallographic orientations, thereby affecting the intensity of the Bragg reflections. In this sense, curvature hinders monocrystallinity but leads to new surface features. For both HBP and BP, the defects are truncated by the curved surface, resulting in a collection of −1/2 defects, spaced by double twist cylinders with +1 topological charge. These structures are most commonly known as half-skyrmions, or merons, and have been observed as dark spots in microscope images. Half-skyrmions are stable and tend to pack in hexagonal lattices; the −1/2 defects form vertices while the +1 defects become the faces of the polygon.
The sequence of transitions, critical values of |FCh|/FSplay and 2q0r0, and the characteristics of each mesophase are identical to those for cylindrical confinement. This indicates that the role of extrinsic curvature is more nuanced and its effect is not localized. On the other hand, the role of temperature, mediated by the thermal parameter U, reduces the stability region of the DT structure. This becomes apparent when comparing the phase diagrams in Fig. 3a and b, where the slope of |FCh|/FSplay = 2 changes. At lower temperatures, it is more favorable for defects to nucleate, requiring a lower chirality for the double twist to transform into a chiral ribbon structure.
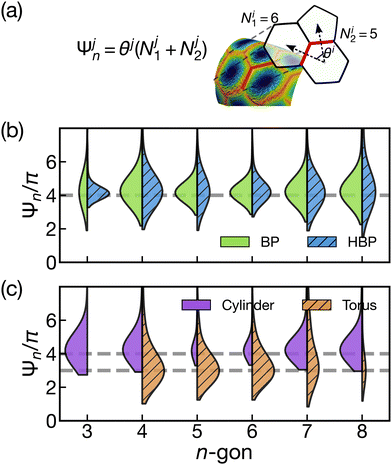
When packed on the surface of a droplet, “scars” are formed in the lattice and pairs of 5–7 polygons arise. However, the effect of extrinsic curvature on the packing of half-skyrmions is unclear. We seek to quantify the regularity of the half-skyrmion network with the phenomenological surface parameter Ψn, illustrated in Fig. 4a. For each pair of neighboring edges j that belong to an n-gon, Ψjn = θj(![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) j1 +
j1 + ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) j2), where
j2), where ![[scr N, script letter N]](https://www.rsc.org/images/entities/char_e52d.gif) ji are the number of sides of each neighboring polygon. It follows that, for a regular hexagonal network, only Ψ6 exists, and its probability distribution function is a Dirac delta centered at 4π. The procedure to calculate Ψn is as follows. First, the locations where n·ν ≈ 1 are extracted and grouped by clusters using the k-means algorithm. The clusters are then compared to the original surface to confirm that the correct polygon centroids have been identified. Using Voronoi and Delaunay triangulation, we successfully identify the edges of each polygon. Additionally, we compute the total topological charge to ensure morphologies are in equilibrium according to the Poincaré–Hopf theorem. We then proceed to calculate Ψn for each n-gon found, and we estimate the normalized probability function. This systematic procedure allows us to characterize the differences between BP and HBP morphologies, as well as the role of confinement.
ji are the number of sides of each neighboring polygon. It follows that, for a regular hexagonal network, only Ψ6 exists, and its probability distribution function is a Dirac delta centered at 4π. The procedure to calculate Ψn is as follows. First, the locations where n·ν ≈ 1 are extracted and grouped by clusters using the k-means algorithm. The clusters are then compared to the original surface to confirm that the correct polygon centroids have been identified. Using Voronoi and Delaunay triangulation, we successfully identify the edges of each polygon. Additionally, we compute the total topological charge to ensure morphologies are in equilibrium according to the Poincaré–Hopf theorem. We then proceed to calculate Ψn for each n-gon found, and we estimate the normalized probability function. This systematic procedure allows us to characterize the differences between BP and HBP morphologies, as well as the role of confinement.
From the violin plot in Fig. 4b, cylindrical confinement broadens the family of polygons expressed on the surface of both BP and HBP. Spherical confinement of a BPII disrupts the regular hexagonal lattice and 5–7 polygon pairs are formed to relieve the stress created by the closed surface. The strict confinement of a cylindrical cavity makes it such that 4–8 pairs of polygons also arise. The probability for Ψn in both morphologies is centered around 4π, indicating that all merons are concave polygons. Additionally, the distributions for HBP have a higher variance compared to those of the BP, meaning that the polygons are more irregular in shape. This is a consequence of the helical ribbons interrupting the growth of the defects, and results in the detection of triangular polygons where sections of a ribbon separate merons.
In Fig. 4c, we investigate the effect of extrinsic curvature by comparing BP morphologies in cylindrical and toroidal cavities. As a result of the secondary curvature, the polygon lattice experiences additional strain and the average value of Ψn shifts to 3π. This implies that besides the polygons being irregular, each polygon has neighbors with different numbers of sides, leading to an amorphous lattice. Recent experimental and computational work has revealed that these are also characteristics of the Blue Phase III, where the authors suggest it is a fluid composed of skyrmions.73
We finish our discussion by exploring the stability of the Helical Ribbon morphology. As explained above, the HR is stable for systems with low natural twist (2q0r0 < 1) and higher thermal parameter (U = 2.9). Furthermore, the chiral elastic energy surpasses the limit of purely cholesteric morphologies (|FCh|/FSplay > 2), with a non-negligible Landau contribution. This indicates that at the center of each ribbon lies a defect core that follows the same helical path. This can be harnessed to drive the assembly of particles into arrays with supramolecular order, since the core of each ribbon will attract particles in order to relieve elastic distortions. Additionally, the helical pattern is imprinted on the surface with tangential orientation of the director, providing an alternative platform for driven assembly of nano or micro particles. Furthermore, the optical properties of LCs and the precise control over the ribbon pitch can be harnessed to engineer optical guides with spiral paths74–79
To further consider potential applications of HR, we also explored how the pitch of the HR (pHR) is connected related to the molecular pitch (p0)? We performed additional simulations within the stable HR region for cylindrical cavities (2r0 = 200 nm and 2r0 = 300 nm) under moderate anchoring conditions (W = 1 × 10−4 J m−2) and U = 2.9. Fig. 5 shows the HR pitch as a function of molecular pitch, including two illustrative HR structures. The pitch was measured from sections throughout the length of each cylinder, and the error bars are represented in the shaded region. There is a linear correlation between both pitches, and the HR pitch is offset by an average of 50 nm from the molecular pitch. The two illustrations represent the helical defect core with pHR = 377 nm, as well as the surface helical pattern with pHR = 614 nm.
4 Conclusions
A theoretical study of chiral liquid crystals confined in cylindrical and toroidal cavities has revealed the existence of new, previously unknown morphologies that arise from the interplay between confining curvature and the inherent twist of the material. These morphologies were generated by relying on a stochastic sampling technique expressed in terms of the five independent components of the order tensor Q, which was mapped onto an orthonormal basis set. These morphologies can be classified in terms of three ratios: (i) the natural twist, 2q0r0, which captures the two characteristic dimensions of the system and collapses the free energy onto master curves; (ii) the elastic ratio |FCh|/FSplay = 2, which demarcates the limit above which defects emerge in order to minimize the free energy; (iii) the competition between confinement and the BP cell size 2r0/aBP = 2, which determines whether a BP cell can develop or instead adopt helical features. Following a progression of chirality, five morphologies are observed in the underlying phase diagrams when expressed in terms of such ratios: Double Twist, Twisted Ribbon, Helical Ribbon, Helical Blue Phase, and Blue Phase.An in-depth analysis of the patterns that arise on the surface of the cavities for HBP and BP reveals polygonal lattices, in which −1/2 defects form the vertices and +1 regions form the faces. Our analysis indicates that the HBP is amorphous, mostly due to sections of chiral ribbons that intersect the lattice. In the case of BP, the defects resemble those of BPII, but the geometry interrupts the cubic symmetry that leads to optical activity in narrow ranges. Finally, we discussed how chiral ribbons, and Helical Ribbons, specifically, can serve as a platform for directed assembly. The nature of the helical defect cores makes them a strong candidate for attracting particles, which alleviate elastic stresses, both in the bulk and adsorbed on the surface. The pitch of the ribbon is tunable and it follows a linear relationship with the cavity size and molecular pitch.
Author contributions
J. C. A. P. and V. P. B. performed simulations and calculations. V. P. B., J. C. A. P., and J. P. H. O conducted the analysis of results. V. P. B and J. J. dP wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors wish to thank Chuqiao (Elise) Chen and Dr Pablo Zubieta Rico for valuable discussions. V. P. B. thanks the Fulbright commission in Colombia and Colciencias for support through the PhD student scholarship. This work was supported by the Department of Energy, Basic Energy Sciences, Materials Sciences and Engineering Division, DESC0019762.References
- T. Kohyama, D. M. Kroll and G. Gompper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 061905 CrossRef CAS PubMed.
- H. Noguchi, C. Tozzi and M. Arroyo, Soft Matter, 2022, 18(17), 3384–3394 RSC.
- J. Lidmar, L. Mirny and D. R. Nelson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 051910 CrossRef PubMed.
- R. Zandi, D. Reguera, R. F. Bruinsma, W. M. Gelbart and J. Rudnick, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 15556–15560 CrossRef CAS.
- S. Dharmavaram, F. Xie, W. Klug, J. Rudnick and R. Bruinsma, Phys. Rev. E, 2017, 062402, 1–19 Search PubMed.
- A. R. Bausch, M. J. Bowick, A. Cacciuto, A. D. Dinsmore, M. F. Hsu, D. R. Nelson, M. G. Nikolaides, A. Travesset and D. A. Weitz, Science, 2003, 299, 1716–1718 CrossRef CAS PubMed.
- N. Stoop and J. Dunkel, Soft Matter, 2018, 14, 2329–2338 RSC.
- G. Napoli and L. Vergori, Phys. Rev. E, 2018, 97, 52705 CrossRef PubMed.
- P. W. Ellis, D. J. Pearce, Y. W. Chang, G. Goldsztein, L. Giomi and A. Fernandez-Nieves, Nat. Phys., 2017, 14(1), 85–90 Search PubMed.
- R. Zhang, Y. Zhou, M. Rahimi and J. J. de Pablo, Nat. Commun., 2016, 7, 13483 Search PubMed.
- M. J. Bowick and L. Giomi, Adv. Phys., 2009, 58, 139 CrossRef.
- D. J. Pearce, Soft Matter, 2022, 18, 5082–5088 RSC.
- R. J. Ondris-Crawford, G. P. Crawford, S. Žumer and J. W. Doane, Phys. Rev. Lett., 1993, 70, 194–198 CrossRef CAS PubMed.
- S. I. Hernández, J. A. Moreno-Razo, A. Ramírez-Hernández, E. Díaz-Herrera, J. P. Hernández-Ortiz and J. J. de Pablo, Soft Matter, 2012, 8, 1443–1450 RSC.
- I. H. Lin, D. S. Miller, P. J. Bertics, C. J. Murphy, J. J. de Pablo and N. L. Abbott, Science, 2011, 332, 1297–1300 CrossRef CAS PubMed.
- D. Miller, X. Wang and N. Abbott, Chem. Mater., 2013, 26, 496–506 CrossRef PubMed.
- X. Wang, Y. Zhou, V. Palacio-Betancur, Y.-K. Kim, L. Delalande, M. Tsuei, Y. Yang, J. D. Pablo and N. Abbott, Langmuir, 2019, 35, 16312–16323 CrossRef CAS PubMed.
- K. Peddireddy, S. Čopar, K. V. Le, I. Muševič, C. Bahr and V. S. Jampani, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2011174118 CrossRef CAS.
- J. W. Milnor and D. W. Weaver, Topology from the Differentiable Viewpoint, Univ of Virginia Press, 1965 Search PubMed.
- P. W. Oakes, J. Viamontes and J. X. Tang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 1–11 CrossRef.
- D. Seč, T. Porenta, M. Ravnik and S. Žumer, Soft Matter, 2012, 8, 11982 RSC.
- Y. Zhou, E. Bukusoglu, J. A. Martinez-Gonzalez, M. Rahimi, T. F. Roberts, R. Zhang, X. Wang, N. L. Abbott and J. J. de Pablo, ACS Nano, 2016, 10(7), 6484–6490 CrossRef CAS PubMed.
- H. Yoshida, Y. Tanaka, K. Kawamoto, H. Kubo, T. Tsuda, A. Fujii, S. Kuwabata, H. Kikuchi and M. Ozaki, Appl. Phys. Express, 2009, 2, 121501 CrossRef.
- Y. Geng, D. Seč, P. L. Almeida, O. D. Lavrentovich, S. Žumer and M. H. Godinho, Soft Matter, 2013, 9, 7928–7933 RSC.
- E. Bukusoglu, X. Wang, Y. Zhou, J. A. Martinez-Gonzalez, M. Rahimi, Q. Wang, J. J. de Pablo and N. L. Abbott, Soft Matter, 2016, 8781–8789 RSC.
- Y. Li, J. J. Yan Suen, E. Prince, E. M. Larin, A. Klinkova, H. Thérien-Aubin, S. Zhu, B. Yang, O. D. Lavrentovich and E. Kumacheva, Nat. Commun., 2016, 7, 12520 CrossRef CAS.
- V. Palacio-Betancur, J. C. Armas-Pérez, S. Villada-Gil, N. L. Abbott, J. P. Hernández-Ortiz and J. J. de Pablo, Soft Matter, 2020, 16, 870–880 RSC.
- J. A. Martínez-González, Y. Zhou, M. Rahimi, E. Bukusoglu, N. L. Abbott and J. J. de Pablo, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 13195–13200 CrossRef.
- M. Sadati, J. A. Martinez-Gonzalez, Y. Zhou, N. T. Qazvini, K. Kurtenbach, X. Li, E. Bukusoglu, R. Zhang, N. L. Abbott, J. P. Hernandez-Ortiz and J. J. de Pablo, Sci. Adv., 2020, 6, eaba6728 CrossRef CAS.
- Y. Yang, V. Palacio-Betancur, X. Wang, J. J. Pablo and N. L. Abbott, Small, 2022, 18, 2105835 CrossRef CAS PubMed.
- V. Vitelli, J. B. Lucks and D. R. Nelson, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12323–12328 CrossRef CAS PubMed.
- T. Lopez-Leon, M. A. Bates and A. Fernandez-Nieves, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 1–4 CrossRef.
- V. Koning, T. Lopez-Leon, A. Fernandez-Nieves and V. Vitelli, Soft Matter, 2013, 9, 4993 RSC.
- A. Darmon, M. Benzaquen, D. Seč, S. Čopar, O. Dauchot and T. Lopez-Leon, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 9469–9474 CrossRef CAS PubMed.
- M. Sadati, Y. Zhou, D. Melchert, A. Guo, J. A. Martinez-Gonzalez, T. F. Roberts, R. Zhang and J. J. D. Pablo, Soft Matter, 2017, 13, 7465–7472 RSC.
- A. Javadi, J. Eun and J. Jeong, Soft Matter, 2018, 14, 9005–9011 RSC.
- G. Napoli, O. V. Pylypovskyi, D. D. Sheka and L. Vergori, Soft Matter, 2021, 17, 10322–10333 RSC.
- S. Norouzi, A. Tavera-Vazquez, J. R.-D. Arellano, D. S. Kim, T. Lopez-Leon, J. J. D. Pablo, J. A. Martinez-Gonzalez and M. Sadati, ACS Nano, 2022, 16, 15894–15906 CrossRef CAS.
- E. Pairam, J. Vallamkondu, V. Koning, B. C. van Zuiden, P. W. Ellis, M. A. Bates, V. Vitelli and A. Fernandez-Nieves, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9295–9300 CrossRef CAS PubMed.
- M. Tasinkevych, M. G. Campbell and I. I. Smalyukh, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 16268–16273 CrossRef CAS.
- D. Jesenek, S. Kralj, R. Rosso and E. G. Virga, Soft Matter, 2015, 11, 2434–2444 RSC.
- L. N. Carenza, G. Gonnella, D. Marenduzzo, G. Negro and E. Orlandini, Phys. Rev. Lett., 2022, 128, 027801 CrossRef CAS PubMed.
- I. M. Kulić, D. Andrienko and M. Deserno, Europhys. Lett., 2004, 67, 418–424 CrossRef.
- J. S. Evans, P. J. Ackerman, D. J. Broer, J. van de Lagemaat and I. I. Smalyukh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 032503 CrossRef.
- V. Koning, B. C. van Zuiden, R. D. Kamien and V. Vitelli, Soft Matter, 2014, 10, 4192 RSC.
- Y. H. Kim, M.-J. Gim, H.-T. Jung and D. K. Yoon, RSC Adv., 2015, 5, 19279–19283 RSC.
- R. D. Kamien and T. R. Powers, Liq. Cryst., 1997, 23, 213–216 CrossRef CAS.
- J. Jeong, L. Kang, Z. S. Davidson, P. J. Collings, T. C. Lubensky and A. G. Yodh, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E1837–E1884 CAS.
- K. Nayani, R. Chang, J. Fu, P. W. Ellis, A. Fernandez-Nieves, J. O. Park and M. Srinivasarao, Nat. Commun., 2015, 6(1), 1–7 Search PubMed.
- P. W. Ellis, K. Nayani, J. P. McInerney, D. Z. Rocklin, J. O. Park, M. Srinivasarao, E. A. Matsumoto and A. Fernandez-Nieves, Phys. Rev. Lett., 2018, 121, 247803 CrossRef CAS PubMed.
- J. P. McInerney, P. W. Ellis, D. Z. Rocklin, A. Fernandez-Nieves and E. A. Matsumoto, Soft Matter, 2019, 15, 1210–1214 RSC.
- A. Pedrini and E. G. Virga, Liq. Cryst., 2018, 45, 2054–2064 CrossRef CAS.
- C. R. Wand and M. A. Bates, Phys. Rev. E, 2019, 100(5), 052702 CrossRef CAS PubMed.
- E. Dubois-Violette and B. Pansu, Frustration and Related Topology of Blue Phases, 1988 Search PubMed.
- F. Castles, S. M. Morris, E. M. Terentjev and H. J. Coles, Phys. Rev. Lett., 2010, 104, 157801 CrossRef CAS PubMed.
- I. Dierking, W. Blenkhorn, E. Credland, W. Drake, R. Kociuruba, B. Kayser and T. Michael, Soft Matter, 2012, 8, 4355 RSC.
- X. Li, J. A. Martínez-González, K. Park, C. Yu, Y. Zhou, J. J. de Pablo and P. F. Nealey, ACS Appl. Mater. Interfaces, 2019, 11, 9487–9495 CrossRef CAS PubMed.
- X. Li, J. A. Martínez-González, O. Guzmán, X. Ma, K. Park, C. Zhou, Y. Kambe, H. M. Jin, J. A. Dolan, P. F. Nealey and J. J. D. Pablo, Sci. Adv., 2019, 5, 9112–9141 CrossRef PubMed.
- H. Kikuchi, M. Yokota, Y. Hisakado, H. Yang and T. Kajiyama, Nat. Mater., 2002, 1, 64–68 CrossRef CAS PubMed.
- E. Kemiklioglu and L. Chy Chien, Appl. Phys. Express, 2014, 7, 091701 CrossRef CAS.
- I. Gvozdovskyy, Liq. Cryst., 2015, 42, 1391–1404 CrossRef CAS.
- M. Sadati, J. A. Martinez-Gonzalez, A. Cohen, S. Norouzi, O. Guzmán and J. J. de Pablo, ACS Nano, 2021, 15, 15972–15981 CrossRef CAS PubMed.
- G. Negro, L. N. Carenza, G. Gonnella, D. Marenduzzo and E. Orlandini, Soft Matter, 2023, 19, 1987–2000 RSC.
- C. Long and J. V. Selinger, Soft Matter, 2022, 19, 519–529 RSC.
- A. Londoño-Hurtado, J. C. Armas-Pérez, J. P. Hernández-Ortiz and J. J. de Pablo, Soft Matter, 2015, 11, 5067–5076 RSC.
- J. C. Armas-Pérez, A. Londoño-Hurtado, O. Guzmán, J. P. Hernández-Ortiz and J. J. D. Pablo, J. Chem. Phys., 2015, 143, 044107 CrossRef PubMed.
- J. C. Armas-Pérez, J. P. Hernández-Ortiz and J. J. de Pablo, J. Chem. Phys., 2015, 143, 243157 CrossRef PubMed.
- P. Kaiser, W. Wiese and S. Hess, J. Non-Equilib. Thermodyn., 1992, 17, 153–170 CAS.
- Sandia National Laboratories, CUBIT Geometry and Meshing Toolkit, 2014, https://cubit.sandia.gov/public/14.1/Cubit-14.1-announcement.html.
- B. S. Kirk, J. W. Peterson, R. H. Stogner and G. F. Carey, Eng. Comput., 2006, 22, 237–254 CrossRef.
- M. Sadati, A. I. Apik, J. C. Armas-Pérez, J. A. Martínez-González, J. P. Hernández-Ortiz, N. L. Abbott and J. J. de Pablo, Adv. Funct. Mater., 2015, 25, 6050–6060 CrossRef CAS.
- U. Tkalec, M. Ravnik, S. Čopar, S. Žumer and I. Muševič, Science, 2011, 333, 62–65 Search PubMed.
- J. Pišljar, S. Ghosh, S. Turlapati, N. Rao, M. Škarabot, A. Mertelj, A. Petelin, A. Nych, M. Marinčič, A. Pusovnik, M. Ravnik and I. Muševič, Phys. Rev. X, 2022, 12(1), 011003 Search PubMed.
- S. Slussarenko, A. Alberucci, C. P. Jisha, B. Piccirillo, E. Santamato, G. Assanto and L. Marrucci, Nat. Photonics, 2016, 10(9), 571–575 CrossRef CAS.
- M. Ravnik and J. Pišljar, Opt. Express, 2018, 26(20), 26327–26338 CrossRef PubMed.
- G. Poy, A. J. Hess, A. J. Seracuse, M. Paul, S. Žumer and I. I. Smalyukh, Nat. Photonics, 2022, 16, 454–461 CrossRef CAS.
- M. G. Clerc, G. González-Cortés and S. Echeverría-Alar, Phys. Rev. Res., 2022, 4, L022021 CrossRef CAS.
- H. Abbaszadeh, M. Fruchart, W. van Saarloos and V. Vitelli, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2020525118 CrossRef CAS.
- S. Echeverría-Alar, M. G. Clerc and I. Bordeu, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2221000120 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2023 |