Effect of connectivity on the elasticity of athermal network materials

Abstract

Network materials with stochastic structure are ubiquitous in biology and engineering, which drives the current interest in establishing relations between their structure and mechanical behavior. In this work we focus on the effect of connectivity defined by the number of fibers emerging from a crosslink, z, and compare networks with identical (z-homogeneous) and distinct (z-heterogeneous) z at the crosslinks. We observe that the functional form of strain stiffening is z-independent, and that the central z-dependent parameter is the small strain stiffness, E₀. We confirm previous results indicating that the functional form of E₀(z) is a power function with 3 regimes and observe that this applies to a broad range of z. However, the scaling exponents are different in the z-homogeneous and z-heterogeneous cases. We confirm that increasing z across the Maxwell's central force isostatic point leads to a transition from bending to axial energy storage. However, we observe that this does not necessarily imply that deformation becomes affine in the large z limit. In fact, networks of fibers with low bending stiffness retain a relaxation mode based on the rotational degree of freedom of the crosslinks which allows E₀ in the large z limit to be smaller than the affine model prediction. We also conclude that in the z-heterogeneous case, the mean connectivity z̄ is sufficient to evaluate the effect of connectivity on E₀ and that higher moments of the distribution of z are less important.

---

1. Introduction

The mechanical behavior of stochastic fiber networks was studied intensely over the last decades^1–5 since such structures are proxies for a wide range of material systems known generically as network materials. Their behavior is defined by a network of filaments with non-vanishing bending stiffness. Examples include biological structures such as the cellular cytoskeleton,^6,7 connective tissue and the extracellular matrix,^8,9 and man-made materials such as paper,^10,11 cellulose products and non-wovens.¹² Other network materials exist, including elastomers and various entangled polymeric melts, but in these cases the bending stiffness of the corresponding molecules is negligible compared to the axial stiffness. This distinction between axially-dominated networks and the networks of filaments stiff in bending is important, as it was shown that the second class exhibits a much richer physics.^2,4,5,13,14

The small strain modulus, E₀, of network materials composed from fibers with non-zero bending and axial stiffness is controlled by the fiber density, ρ (total length of fiber per unit volume), the relative importance of the bending and axial stiffnesses, characterized by parameter 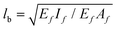(E_fI_f and E_fA_f are the bending and axial rigidities of fibers), and the connectivity index, z, which represents the number of filament segments emerging from a crosslink. It has been shown that low density networks of floppy filaments (small l_b) deform non-affinely and store most of the strain energy in the bending mode of the fibers, while dense and densely crosslinked networks, with filaments rigid in bending, deform almost affinely and store the strain energy in the axial mode of fibers.^4,15,16 This non-affine-to-affine transition reported for network with low z may be characterized using the structural parameter w = log₁₀ρ^x−1l²_b, large values of w corresponding to the affine deformation regime. The exponent x takes the value of 2 for cellular networks like the open cell foams and Voronoi structures,¹⁷ 3 for fibrous networks in 3D¹⁸ and collagen networks,^19,20 and takes larger values in 2D.^21,22

Fiber networks may be unstable (vanishing stiffness) at small strains in certain conditions. Maxwell determined that a central force network is unstable (floppy) when the number of constraints the structure is subjected to is smaller than the number of degrees of freedom.²³ This may be written in terms of the connectivity index as z < z_c = 2d, where z_c represents the connectivity at the central force isostaticity point (CFIP) and d is the dimensionality of the embedding space (we note that for a finite size model, the Maxwell counting argument leads to z_c = 2d − 6(d − 1)/N_x, where N_x is the number of crosslinks in the model; the models used here have N_x > 20 000 and hence z_c is closely approximated by 2d). Virtually all engineering and biological networks have connectivity much smaller than z_c = 6; in fibrous networks a crosslink is formed by two fibers in contact and hence z = 4, cellular networks of Voronoi type in 3D have z = 4, and crosslinks in collagen-based connective tissue are formed by the separation of fiber bundles into (typically two) sub-bundles and hence z = 3. Such networks have finite small strain stiffness due to the stabilizing effect of the fiber bending stiffness and/or the presence of pre-stress,^24–27 as captured by the updated stability criterion of Calladine.²⁸ Therefore, if filaments have finite bending stiffness and the crosslinks transmit forces and bending moments, the network has non-vanishing stiffness when z ≤ z_c.

Interestingly, it has been shown that in networks with non-zero axial and bending stiffness, CFIP remains a critical point associated with diverging strain amplitude fluctuations and associated correlation length.^24,29,30 Specifically, while the emergence of non-zero stiffness as the network density increases takes place at the stiffness percolation threshold, which corresponds to z_p ≈ 2.6 for these networks,^13,27,31 the non-affinity measure diverges at z_c. In the hypostatic range z_p < z < z_c the behavior is of the type described in the preceding paragraph, i.e., it is bending dominated and non-affine when w is small and becomes axially dominated and approximately affine as w increases. In the hyperstatic regime z > z_c, the axial deformation mode becomes energetically dominant.^24,30

Most studies investigating the effect of connectivity on network behavior were performed with lattice-based models in which struts were removed with specified probability to adjust the mean z of the network.^24,29,30 This procedure modifies ρ at the same time and renders z spatially non-uniform. While in such networks the connectivity parameter is described by a distribution, it is generally conjectured that all above arguments hold provided the mean connectivity, z̄, is used as parameter in place of z.

In this work we revisit the effect of z on the small strain stiffness of networks by comparing structures in which all crosslinks have the same z, which we denote as z-homogeneous, with z-heterogeneous networks constructed by modifying a fraction of the crosslinks of an initially z-homogeneous network with z = 4 to z = 8. This fraction is varied to adjust z̄. Here and in the following, z and z̄ always refer to z-homogeneous and z-heterogeneous cases respectively. In both cases we investigate hypo- and hyperstatic cases and seek the relation between E₀, w and z (or z̄ in z-heterogeneous networks). We recover the behavior previously reported for z-heterogeneous networks^24,29,30 and confirm that z̄ is indeed a sufficient descriptor for such structures. However, we observe that the scaling exponents relating z (or z̄) to E₀ are strongly dependent on the type of structure considered. Further, we determine that the effects of z and w on the degree of deformation non-affinity are not equivalent. A network of large w is essentially insensitive to increasing z since its deformation is already approximately affine. However, a network of small w is not rendered affine by increasing z. To demonstrate this, we introduce a measure of the rotational non-affinity of the crosslinks and use it along with the commonly used measure of translational non-affinity. We determine that in the small w range, increasing z (or z̄) into the hyperstatic range decreases the translational non-affinity, but the rotational non-affinity remains large. This indicates that hyperstatic networks relax relative to the perfect affine deformation and hence their stiffness is smaller than the stiffness of the purely affine regime reached at large w. We also investigate the large deformation response of networks with low w for both hypo- and hyperstatic conditions and confirm that the functional form of strain stiffening is independent of z,^24,29 but high z structures, which have much larger E₀ than the low z structures of same w, undergo a structural instability before the onset of the non-linear, stiffening regime.

The types of networks and models considered are presented in Section 2, the relation between stiffness and network parameters is discussed in Section 3.1, followed by an evaluation of the degree of non-affinity and energy partition (Section 3.2) and of the large deformation response (Section 3.3).

2. Models and structural parameters

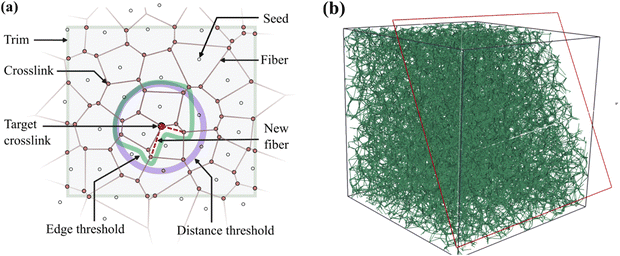
The networks used in this study are derived from Voronoi networks with z = 4. These are generated by tessellation of uniformly distributed seed points in 3D which are defined in a cube of edge length 4L, where L is the size of the network model to be obtained. The initially generated tessellation is then trimmed to a 2L cube to remove boundary effects and the edges of the tessellation are retained as fibers. The fiber lengths in the initial network are exponentially distributed with mean l_c. Short edges (l < l_c/25) and dangling ends are removed.

To generate z-homogeneous networks with z > 4, fibers are added to the initial network by fulfilling two constraints: (i) the crosslinks connected by an added fiber are separated in the graph space of the original network by no more than 3 edges, and (ii) the length of added fibers should be smaller than 2.5l_c in real space. Further, fibers are added to connect nearest neighbor crosslinks first. These conditions ensure that the mean segment length of the resulting network is within 6% to that of the original network, l_c. This method prevents the creation of very long fibers which may trigger non-local effects and allows separating the effect of connectivity from that of non-local interactions. Fibers are added iteratively to reach the target coordination number, after which the modified network is trimmed to the intended size, L, such to ensure that the boundary regions have density comparable to the interior. This procedure leads to z-homogeneous networks in which at least 90% of the crosslinks have exactly the desired z for all target connectivity values considered (z = 4…10). The interior crosslinks (not located along the boundary of the model) have mean connectivity marginally different from the target. For example, with target z = 6, the network we generate has z = 5.97 for the interior crosslinks. Fig. 1a shows a 2D schematic of the procedure used to select crosslinks to be connected by additional fibers and Fig. 1b shows a sectioned 3D network with z = 7 produced by this procedure.

Fig. 1 (a) Schematic of the network generation process. The newly connected crosslinks are required to be within prespecified distance in both graph and real spaces to reduce the effect of non-local interactions. (b) Example of a hyperstatic (z = 7) network used in this study.

The same procedure is applied to generate z-heterogeneous networks. z is increased to a value of 8 at a target fraction, f, of spatially uncorrelated crosslinks selected through uniform random sampling. f varies from 0.05 to 0.90. Hence, z-heterogeneous networks have f fraction of crosslinks with z = 8 and 1 − f fraction of crosslinks with z < 8. This creates heterogeneity within the network which is described by a characteristic length scale equal to the mean distance between crosslinks with z = 8, approximated by 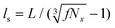, where N_x is the total number of crosslinks in a model of edge length L. To avoid size effects, models with L\l_s ≈ 35 are used for z-heterogeneous networks with f > 0.10 which translates to 40 < L/l_c < 85 for these models. For all homogeneous networks considered, L/l_c ≈ 35.

Fibers are considered athermal and are represented as beams. The crosslinks transmit both forces and moments and are rigid welds (the angle between fibers is not allowed to change during deformation). The model is discretized using beam finite elements³² (Timoshenko beam element, B32 in Abaqus) and the commercial package Abaqus Standard (2022)³³ is used to obtain the solution.

The boundary conditions represent uniaxial tension. Displacements are prescribed for one face of the cubic model in the direction normal to that face (loading direction), while zero normal displacements are prescribed to the nodes on the opposite face. The other degrees of freedom of the loaded faces are left free. The lateral model faces are kept planar. To this end, the nodes on each of the lateral faces are kinematically coupled and remain coplanar, although the respective plane is free to move in its normal direction such that tractions on these faces vanish, in average, and the model is free to contract in the direction transverse to loading. The rotational degrees of freedom of the nodes on the lateral faces are left free.

For the results presented in this study, approximately 600 realizations are used, with 6 samples for each homogeneous and 3 for each heterogeneous network specification (given z and l_b). The homogeneous network models have between 50 000 and 122 000 fibers, function of the average connectivity. The total number of degrees of freedom per model ranges from 500 000 to 1 000 000. For reasons outlined in the previous paragraphs, z-heterogeneous networks of average connectivity z̄ are much larger than z-homogeneous networks with z = z̄. The nominal stress is used in all calculations and only one component of this tensor (normal stress in the loading direction, S) is non-zero.

3. Results and discussion

3.1. Dependence of stiffness on network parameters

The dependence of the small strain stiffness on structural parameters is typically represented in the form of a master plot showing the normalized stiffness, E* = E₀/ρE_fA_f, vs. parameter w.¹⁶ The normalization factor, ρE_fA_f, is, up to a constant, the modulus predicted by the affine model. For 3D Voronoi structures, w = log₁₀ρl²_b. In the hypostatic case, z < z_c, such plot shows two regimes: a plateau for w > −1, which indicates that E₀ ∼ ρE_fA_f (denoted here as the affine regime III), and a regime at smaller w, of slope 1, and for which E₀ ∼ ρ²E_fI_f (denoted here as the non-affine, hypostatic regime I).¹⁶ In these regimes, deformation is approximately affine and non-affine, respectively. The fact that E₀ ∼ E_fA_f and E₀ ∼ E_fI_f in the two regimes indicates the primary energy storage mode as axial and bending, respectively. Such master plot, which was previously discussed in the literature,^15,22,34 does not consider the effect of z on E₀.

Fig. 2a shows the master plot for z-homogeneous networks with z ranging from 4 to 10. Hypostatic networks exhibit the two regimes I and III described in the previous paragraph. The curves corresponding to networks of increasing z shift gradually to the left in the z < z_c = 6 range.

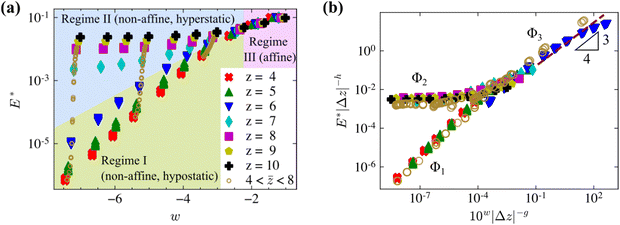Fig. 2 (a) Normalized stiffness, E* = E₀/ρE_fA_fvs. the structural parameter w for z-homogenous (filled symbols) and z-heterogeneous (open circles) networks. (b) Collapse of the data in panel (a) based on eqn (1). The legend in (a) applies to both panels. The three regimes are highlighted in (a) by color shades and labeled as defined in text.

Networks with z > z_c behave differently in the low w range: the stiffness is z-dependent, but essentially w-independent (regime II). As z increases above z_c, E₀ exhibits a large jump from regime I to II. The asymptote of E₀ at constant w as z increases is lower than the affine limit of the stiffness reached for w > −1, in regime III. This implies that, if w is sufficiently small, the network retains a relaxation mechanism which is inactive in regime III; this is discussed further in Section 3.2. It is instructive to recall the expectation for E₀ in the affine limit of regime III: E₀ ∼ ρE_fA_f. This relation results by observing that fibers are loaded axially, and deformation is approximately affine. The stiffness depends on the total fiber length per unit volume and not on how fibers are connected. This justifies the z-independence of the curves in regime III.

The data in Fig. 2a is collapsed using the relation:^24,29

E*|Δz|^−h = Φ_i(ρl_b²|Δz|^−g) = Φ_i(10^w|Δz|^−g), (1)

where Δz = z − z_c and function Φ has 3 branches (i= 1,2,3) corresponding approximately to the 3 regimes in Fig. 2a. The two branches at small values of the argument x = 10^w|Δz|^−g are Φ₁(x) ∼ x and Φ₂(x) = const. The slope of the branch Φ₃(x) at larger values of the argument is defined by the observation that, as Δz → 0, E₀ is neither zero nor infinity and the behavior must be independent of Δz. The slope in this regime results equal to h/g.^24,29 The data collapse is shown in Fig. 2b, where the three regimes are visible. The data corresponding to all z-homogeneous networks collapses with h = 1.5 and g = 2.5.

Three sets of z-heterogeneous networks are constructed as described in Section 2. Each set has specific l_b and w values and the mean connectivity z̄ varies within each set from close to 4 to close to 8 as the fraction f of crosslinks with z = 8 increases from 0.05 to 0.9. Results for these systems are shown in Fig. 2 with open circles. Data for given set does not align perfectly along a vertical line in Fig. 2a due to the minor variation of the density with increasing fraction f. No jump is observed in this case as z̄ increases past z_c = 6. The data collapse based on eqn (1) leads to exponents h = 3 and g = 4, which are different from those obtained for the z-homogeneous networks. The collapse of such data for z-heterogeneous networks was reported in the previous literature^24,29,30 and the present results are in agreement with the respective reports, although the values of h and g are different. This points to the dependence of these exponents on the structure and possibly the size of the networks considered.

3.2. Non-affinity and energy partition

The behavior discussed in Section 3.1 can be explained, in part, by evaluating the non-affinity and the energy partition of networks in different regimes. Fig. 3 shows the fraction of the total strain energy stored in the axial deformation mode of fibers for networks with 4 different w values function of z. The filled and open symbols correspond to z-homogeneous and z-heterogeneous cases, respectively. The reminder of the strain energy is stored primarily in the bending mode, with only a small fraction (below 10%) stored in the shear and torsion deformation modes of fibers. It is observed that networks with low w which deform primarily in the bending mode in the hypostatic regime, z < z_c, exhibit a transition to the axial deformation mode as z shifts to the hyperstatic regime. Networks with w in the transition regime deform by a combination of the axial and bending modes and are much less sensitive to the variation of z, which indicates that the effect of the fiber diameter is much stronger than that of connectivity. It is also observed that the energy partition of z-homogeneous and z-heterogeneous network of same w is identical provided z = z̄.

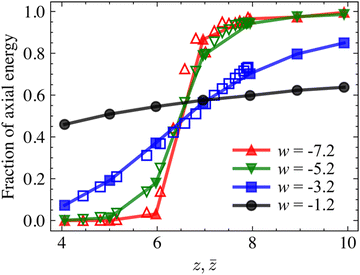Fig. 3 Fraction of axial energy in z-homogeneous (filled symbols) and z-heterogeneous (open symbols) networks of selected w subjected to small deformations.

This z-controlled energy storage transition was observed before, and it was interpreted as an indication that deformation becomes affine with increasing connectivity.⁴ This interpretation emerges by analogy with the similar bending-to-axial transition controlled by w which, indeed, is associated with a gradual reduction of the degree of non-affinity. However, this analogy does not apply to the z-controlled transition. A suggestion that this might be the case is provided by the observation made in Section 3.1 in relation to Fig. 2a, that the asymptotic values of E₀ in the low w regime as z increases (regime II) is lower than the asymptotic value obtained in regime III as w increases. To clarify the nature of the relaxation mode leading to this effect, two non-affinity measures are evaluated here characterizing translational and rotational degrees of freedom of the crosslinks. The translational non-affinity is evaluated as:

Γ_t = 〈|u−u_a|〉/l_c, (2)

where u and u_a are the actual and affine crosslink displacements, the average is performed over all crosslinks and the measure is normalized for convenience with the mean segment length of the network. u_a is computed based on the global deformation gradient defined by the imposed network stretch and the transverse stretch measured during the uniaxial deformation. A measure based on comparing nodal displacements with the affine model prediction, similar to that of eqn (2), is typically used to evaluate the degree of non-affinity of stochastic networks.^24,29,35

The second measure introduced here quantifies the magnitude of the crosslink rotation and is evaluated as:

Γ_r = 〈θⁱ〉_i, (3)

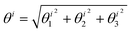where is the magnitude of the rotation of crosslink i (i = 1…N_x), and θⁱ_j is the angle of rotation of crosslink i about axis j (see also Fig. 4c for a 2D schematic). Parameter Γ_r is computed by averaging θⁱ over all crosslinks in the model. Note that the relative angular position of fibers forming a crosslink is fixed, but the crosslink may rotate rigidly. Since nodal translations and rotations are independent degrees of freedom, the two non-affinity measures of eqn (2) and (3) are nominally independent. However, they are coupled through the overall network kinematics.

Fig. 4 Non-affinity measures for (a) translational, Γ_t, and (b) rotational, Γ_r, degrees of freedom in z-homogeneous networks for various z-values. The data points represent the average of 6 replicas for each set of parameters (z, w). The legend in (a) applies to both panels. The bars represent standard error. (c) 2D schematic of the kinematics of a generic fiber MN with crosslinks that translate by uⁱ and rotate by θⁱ. MN and MN′ are the undeformed and deformed states of the fiber and the deformed configuration is shifted such to overlap the end M.

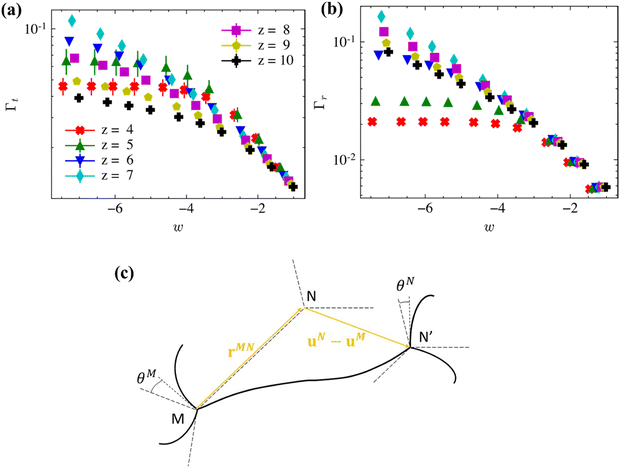
Fig. 4 shows the variation of Γ_t and Γ_r with w and z in the small deformation range for all homogeneous networks considered. Γ_t exhibits features previously reported:^36,37 (i) in the hypostatic range, the non-affinity increases as w decreases and the rate of increase is smaller in the low w range, (ii) Γ_t exhibits a peak at z ≈ z_c in the low w range, and (iii) Γ_t is independent of z in the large w range. This correlates well with the shift from the bending to the axial deformation mode controlled either by w or by z (at low w). We note that in the previous literature,^5,13,24 a peak of Γ_t for non-affine networks is reported to occur exactly at the CFIP threshold, while in the present data the peak is shifted to slightly larger values. This apparent discrepancy emerges since here we report z as the network internal connectivity, ignoring surfaces. Accounting for the low connectivity of surface crosslinks would reduce slightly the effective z but would also render the z of z-homogeneous networks a fractional number, which is not representative for the present networks.

Γ _r leads to additional conclusions: (i) Γ_r increases as w decreases, (ii) Γ_r increases as z increases across the transition defined by z_c and remains large in the hyperstatic regime, and (iii) Γ_r is independent of z in the large w range. Therefore, in the hyperstatic, low w regime II of Fig. 2a the network relaxes by crosslink rotation even though the translational non-affinity is inhibited by the high connectivity. Interestingly, this relaxation mode which necessarily involves fiber bending, does not lead to bending energy dominance. Rotational non-affinity is sufficient to allow the reduction of E₀ relative to the prediction of the affine model, but it is not large enough to change the energy storage mode of the network.

To gain further insight into the mechanics underlying the rotational non-affinity measure of eqn (3), refer to Fig. 4c. This 2D schematic shows a generic fiber of crosslinks M and N in the undeformed (dashed lines) and deformed states (continuous lines). The deformed configuration is shifted such to remove the translation of crosslink M and hence, the displacement of N is u^N − u^M. Let us assume that the deformation is translationally affine, i.e.u^N − u^M = (F − I)r^MN, where F is the deformation gradient of the respective macroscale deformation and r^MN is the position vector of N relative to M. Two possibilities exist: (i) the deformation is affine only at (and above) the scale of the crosslinks while the points along fiber MN may take any position, which is not constrained by F, and (ii) the deformation is strictly affine at all scales, which implies that all points of MN move as defined by F and MN remains straight. In case (i), the strain energy of the network subjected to affine crosslink displacements may be reduced by fiber bending and crosslink rotation. The softer the bending mode (lower w), the more pronounced this relaxation is. This explains the observation that rotational non-affinity is pronounced in the low w range of hyperstatic networks in which the high z values force a reduction of the translational non-affinity. In case (ii), crosslink rotation is entirely defined by the affine displacements (Fig. 4c) and hence in the large w regime, where the bending mode is inhibited, the rotational and translational non-affinity measures vary in proportion.

Further insight into the effect of the connectivity on energy partition and the associated stiffening may be obtained by examining the z-heterogeneous networks. As described in section 2, these structures are generated by starting with a Voronoi network with z = 4 at all crosslinks and transforming a fraction f of the total number of crosslinks to z = 8 via enriching the local neighborhood of these crosslinks with additional fibers. In the dilute limit, e.g., for f = 0.05, the crosslinks with z = 8 are isolated within the network with z ≈ 4, i.e., almost all fibers emerging from a z = 8 crosslink have z = 5 crosslink at the other end. Fig. 5a shows the average energy partition for the neighborhood of crosslinks with z = 8 and with z = 4 in networks with various f and z̄, and with w ≈ −7.5. Interestingly, all fibers deform in the bending mode in the dilute limit, up to f ≈ 0.2, regardless of the connectivity at the crosslinks. For 0.2 < f < 0.4, fibers associated with z = 8 crosslinks deform strongly in the axial mode, while those bounded at least at one end by crosslinks with z = 4 deform in the softer bending mode. As f increases (f > 0.4), the probability for a fiber emerging from a z = 8 crosslink to have another z ⪢ 4 crosslink at the other end increases. At the same time, the energy partition of the neighborhood of crosslinks with z = 8 (considering only the fibers emerging from such node) shifts to axial. Two reasons can be identified for this behavior in relation to Fig. 5b. First, fibers with higher connectivity nodes tend to be axially dominated. Secondly, the rapid change near f ≈ 0.30 for all fibers suggests that stiffening in the broader neighborhood (mean field) has also an effect. This is suggested by the data in Fig. 5b which shows that the energy partition of a fiber with given z at the two crosslinks shifts to axial as f increases, i.e., it depends on the broader neighborhood and not just on its own connectivity.

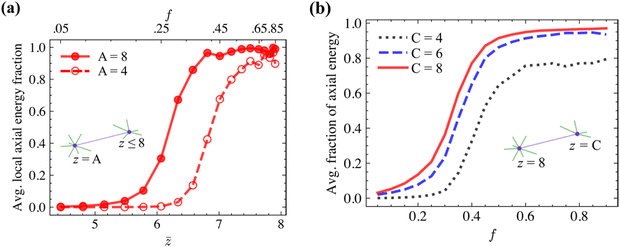Fig. 5 (a) Average fraction of axial energy of the neighborhood of crosslinks with z = 8 and z = 4. (b) Variation of the fraction of axial energy with f for fibers with specified z at the two ends.

3.3. Non-linear behavior

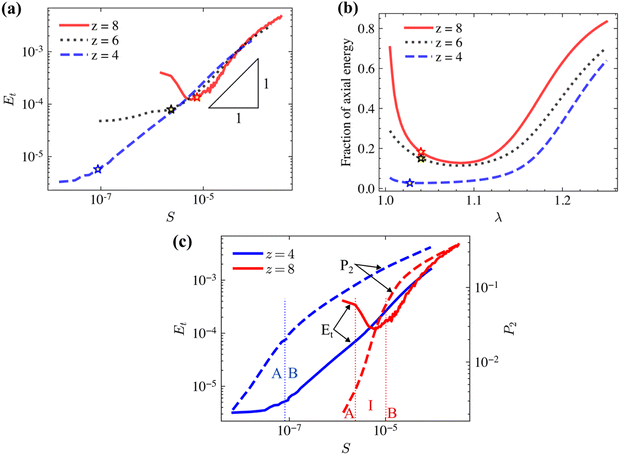
z-Homogeneous networks with w ≈ −5.25 and z = 4, 6 and 8 are subjected to large uniaxial deformations. The tangent stiffness versus stress curves for these three types of networks are shown in Fig. 6a. The tangent stiffness is computed based on the nominal stress as E_t = dS/dλ. The curves exhibit the linear and first non-linear regimes (denoted here as A and B, respectively) of the non-linear network deformation discussed in the literature⁴ and the stars mark the transition between these two regimes. The hypostatic networks have constant stiffness E₀ in regime A and exhibit exponential stiffening (E_t ∼ S) in regime B. The hyperstatic network with z = 8 undergoes an instability in regime A, after which it exhibits exponential stiffening in regime B. The instability is necessary in order to unlock the initial structure and allow for structural reorganization, which makes possible the emergence of the exponential stiffening regime B. It is interesting to observe that the stiffness-stress curves for networks with different z overlap in regime B. This indicates not only that the functional form of stiffening is independent of z, but also that the only z-dependent parameter is the small strain stiffness, E₀. A similar observation was made before regarding the structural parameter w: networks with given z and different w lead to E_t(S) curves that overlap in regime B and the relevant w-dependent parameter is E₀.²⁰ The present data indicate that the effect of z and w on the large deformation behavior is similar. The novel observation here is the presence of the instability that separates the small and large strain regimes A and B in the case of hyperstatic networks. Although the analysis of this phenomenon falls outside the scope of the present discussion, we present in Fig. 6c the fiber orientation parameter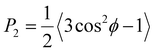 versus the stress, along with the tangent stiffness-stress curves from Fig. 6a, for z = 8 and z = 4. Here ϕ is the angle made by the end-to-end vector of a fiber with the stretch direction and the average is performed over all fibers. P₂ = 0 if fibers are randomly oriented and P₂ = 1 when fibers are perfectly oriented in the loading direction. In the linear regime A, P₂ has small values and increases approximately in proportion to the nominal stress for both z values. For z = 4, there is no softening (reduction of E_t) observed at the end of regime A and the network enters regime B directly. The rate of alignment (increase of P₂) decreases in the exponential stiffening regime B. However, for z = 8, a rapid increase of alignment is observed during the softening regime that separates regimes A from B (marked by I in Fig. 6c). The P₂ curves for the two z values become parallel in regime B.

Fig. 6 (a) The tangent stiffness vs. nominal stress under large deformations for networks with z = 4, 6 and 8 and with w ≈ −5.35 and (b) their energy partition. The approximate transition point to the exponential stiffening regime B is marked by star symbols. (c) Data in (a) replotted along with fiber orientation data (P₂vs. S) for networks with z = 4 and 8. Regimes A, B, which are separated in the z = 8 case by an instability (denoted by I) are marked by vertical dotted lines.

Fig. 6b shows the evolution of energy partition during large deformations for the networks in Fig. 6a. In the small strain limit (λ → 1) the fraction of energy stored in the axial mode increases as z increases from the hypo- to the hyperstatic regime, in agreement with the data in Fig. 3. The hyperstatic network shifts from the axial to the bending mode as it goes through the intermediate state labeled by I in Fig. 6c. This variation of the energy partition supports the suggestion made above that large structural re-organization/alignment takes place as the network moves from regime A to regime B. Both hypo- and hyperstatic networks deform in the bending mode up to a stretch of ≈1.15, after which the axial fraction increases. The increase of the axial fraction at stretches above 1.2 is due to the emergence of stress paths, as typically observed in hypostatic networks.^38,39 Interestingly, the hyperstatic networks gain sufficient kinematic freedom upon the instability to undergo the structural re-organization required to produce stress paths.

Conclusions

The mechanical behavior of z-homogeneous and z-heterogeneous networks of hypo- and hyperstatic types is compared in the linear and non-linear range. It is concluded that the functional form of strain stiffening is exponential and z-independent. The central z-dependent parameter is the small strain stiffness, E₀. The dependence of E₀ on the connectivity, z, exhibits 3 regimes and is described by power functions with regime-specific exponent. The exponent is sensitive to the type of network (z-homogeneous vs. z-heterogeneous). As z shifts from the hypo- to the hyperstatic regime, the axial mode becomes the preferred energy storage mode, but the deformation does not become affine. For low w and in the limit of large z the network retains a relaxation mechanism associated with the rotation of the crosslinks which allows E₀ to be smaller than the affine model prediction. In the case of z-heterogeneous networks, the mean connectivity z̄ appears to be sufficient to characterize the network behavior as it plays a role similar to that of z of z-homogeneous structures.

Conflicts of interest

The authors have no conflicts of interest to declare.

Acknowledgements

This work was supported by the National Institutes of Health (NIH) through Grant No. U01 AT010326-06 and by the National Science Foundation through grant CMMI-2007909.

References

1. M. Alava and K. Niskanen, Rep. Prog. Phys., 2006, 69, 669–723.
2. C. P. Broedersz and F. C. MacKintosh, Rev. Mod. Phys., 2014, 86, 995–1036.
3. B. Erman and J. E. Mark, Structures and Properties of Rubberlike Networks, Oxford University Press, 1997.
4. C. R. Picu, Network Materials: Structure and Properties, Cambridge University Press, 1st edn, 2022.
5. A. J. Licup, A. Sharma and F. C. Mackintosh, Phys. Rev. E, 2016, 93, 1–12.
6. Cytoskeletal Mechanics: Models and Measurements in Cell Mechanics, ed. M. R. K. Mofrad and R. D. Kamm, Cambridge University Press, 1st edn, 2001.
7. D. Boal, Mechanics of the Cell, Cambridge University Press, Cambridge, 2nd edn, 2012.
8. S. C. Cowin and S. B. Doty, Tissue Mechanics, Springer Science & Business Media, 2006.
9. I. K. Piechocka, A. S. G. van Oosten, R. G. M. Breuls and G. H. Koenderink, Biomacromolecules, 2011, 12, 2797–2805.
10. K. Niskanen, Mechanics of Paper Products, Walter de Gruyter, 2011.
11. J. A. Bristow and P. Kolseth, Paper Structure and Properties, Taylor & Francis, 1986.
12. S. J. Russell, Handbook of Nonwovens, Woodhead Publishing, 2022.
13. C. P. Broedersz, M. Sheinman and F. C. MacKintosh, Phys. Rev. Lett., 2012, 108, 078102.
14. K. Baumgarten and B. P. Tighe, Soft Matter, 2021, 17, 10286–10293.
15. J. Wilhelm and E. Frey, Phys. Rev. Lett., 2003, 91, 108103.
16. A. Shahsavari and R. C. Picu, Phys. Rev. E, 2012, 86, 1–5.
17. L. J. Gibson and M. F. Ashby, Cellular Solids: Structure and Properties, Cambridge University Press, Cambridge, 2nd edn, 1997.
18. M. R. Islam and R. C. Picu, J. Appl. Mech., 2018, 85, 1–8.
19. D. Vader, A. Kabla, D. Weitz and L. Mahadevan, PLoS One, 2009, 4, e5902.
20. A. J. Licup, S. Münster, A. Sharma, M. Sheinman, L. M. Jawerth, B. Fabry, D. A. Weitz and F. C. MacKintosh, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 9573–9578.
21. A. S. Shahsavari and R. C. Picu, Int. J. Solids Struct., 2013, 50, 3332–3338.
22. D. A. Head, A. J. Levine and F. C. MacKintosh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 1–15.
23. J. C. Maxwell, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1864, vol. 27, pp. 294–299.
24. C. P. Broedersz, X. Mao, T. C. Lubensky and F. C. MacKintosh, Nat. Phys., 2011, 7, 983–988.
25. A. Sharma, A. J. Licup, K. A. Jansen, R. Rens, M. Sheinman, G. H. Koenderink and F. C. MacKintosh, Nat. Phys., 2016, 12, 584–587.
26. S. Arzash, J. L. Shivers, A. J. Licup, A. Sharma and F. C. MacKintosh, Phys. Rev. E, 2019, 99, 042412.
27. E. M. Huisman and T. C. Lubensky, Phys. Rev. Lett., 2011, 106, 088301.
28. C. R. Calladine, Int. J. Solids Struct., 1978, 14, 161–172.
29. R. Rens and E. Lerner, Eur. Phys. J. E: Soft Matter Biol. Phys., 2019, 42, 114.
30. J. Feng, H. Levine, X. Mao and L. M. Sander, Soft Matter, 2016, 12, 1419–1424.
31. E. M. Huisman, T. van Dillen, P. R. Onck and E. Van der Giessen, Phys. Rev. Lett., 2007, 99, 208103.
32. T. J. R. Hughes, The Finite Element Method: Linear Static and Dynamic Finite Element Analysis, Courier Corporation, 2012.
33. M. Smith, ABAQUS/Standard User's Manual, Version 6.9, Dassault Systèmes Simulia Corp, 2009.
34. S. Deogekar and R. C. Picu, J. Mech. Phys. Solids, 2018, 116, 1–16.
35. P. R. Onck, T. Koeman, T. van Dillen and E. van der Giessen, Phys. Rev. Lett., 2005, 95, 178102.
36. D. A. Head, A. J. Levine and F. C. MacKintosh, Phys. Rev. Lett., 2003, 91, 108102.
37. H. Hatami-Marbini and R. C. Picu, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 062103.
38. G. Žagar, P. R. Onck and E. Van Der Giessen, Macromolecules, 2011, 44, 7026–7033.
39. T. Kim, W. Hwang, H. Lee and R. D. Kamm, PLoS Comput. Biol., 2009, 5, e1000439.

---