Effect of the polar group content on the glass transition temperature of ROMP copolymers

Abstract

Polar groups have long been recognized to greatly influence the glass transition temperature (T_g) of polymers, but understanding the underlying physical mechanism remains a challenge. Here, we study the glass formation of ring-opening metathesis polymerization (ROMP) copolymers containing polar groups by employing all-atom molecular dynamics simulations. We show that although the number of hydrogen bonds (N_HB) and the cohesive energy density increase linearly as the content of polar groups (f_pol) increases, the T_g of ROMP copolymers increases with the increase of f_pol in a nonlinear fashion, and tends to plateau for sufficiently high f_pol. Importantly, we find that the increase rate of Gibbs free energy for HB breaking gradually slows down with the increase of f_pol, indicating that the HB is gradually stabilized. Therefore, T_g is jointly determined by N_HB and the strength of HBs in the system, while the latter dominates. Although N_HB increases linearly with increasing f_pol, the HB strength increases slowly with increasing f_pol, which leads to a decreasing rate of increase in T_g.

---

Introduction

Glass transition temperature (T_g) of polymers is an important intrinsic quantity that is closely related to their applications.¹ This quantity can be strongly influenced by many factors such as chain length,^2,3 chain flexibility,^4–9 and intermolecular interactions.^10–13 Among them, modifying the monomer with polar groups can dramatically change the intermolecular interactions and thus the T_g of the polymer.^14,15 In particular, T_g can be adjusted by changing the type and content of polar groups (f_pol). However, how non-covalent interactions, such as hydrogen bonds (HBs), between polar groups affect the T_g of polymers is not well understood.

Pan et al.¹⁶ found that Raman spectroscopy can be used to monitor in situ ring-opening metathesis polymerization (ROMP) of cyclic olefins, enabling real-time monitoring of the incorporation rate of individual monomers into polymers to obtain the desired chain compositions. Thus, the number of polar groups available for HB in the polymer can be precisely controlled. Norbornene (NB) with a bicyclic structure and modified with polar functional groups are important monomers for ROMP^17,18 to obtain cyclic olefin polymers (COPs).¹⁹ The COPs possess the properties of excellent transparency and low birefringence, while at the same time these materials can be processed into thin films for display fabrication due to their high T_g.^20,21 Experimentally, Dennis et al.²² synthesized homopolymers and copolymers of 5-ethylidene-2-norbornene (ENB) and 5-methanol-2-norbornene (NBCH₂OH) using ROMP. They systematically varied the NBCH₂OH content and found that the increasing trend of T_g with the NBCH₂OH content was in good agreement with the prediction of the Kwei^23–25 model. Their results indicate that there are strong HBs in the system. However, this work does not reveal how the HB interaction strength affects the variation trend of T_g, and why T_g gradually increases with the increase of the NBCH₂OH content, but the increase rate gradually slows down. In order to explain this phenomenon at the molecular scale, we use molecular dynamics (MD) simulations to study the influence of the type and f_pol of polar groups on T_g from the perspective of HBs.

Inspired by experimental calorimetry and dilatometry, linear temperature quenching is traditionally used in MD simulations to estimate T_g based on the temperature at which the temperature dependence of the system's energy or volume undergoes a change in the slope from liquid to glassy states.^26–28 Although this method is simple and easy to implement, the linear cooling method keeps the cooling rate constant throughout the process, resulting in the system being simulated for times that exceed that required to reach equilibrium and therefore low computational efficiency at high temperatures. In contrast, the structure is highly unrelaxed at low temperatures since the simulation time is much less than the relaxation time of the system. Simmons and coworkers²⁹ developed a so-called Predictive Stepwise Quenching (PreSQ) algorithm, which provides both easy access to supercooled states and high-throughput simulations of supercooled liquid dynamics. The method employs a designed quench process to obtain configurations within a range of temperatures, performs an isothermal annealing step on each of these configurations to obtain a well-defined equilibrium state, and then calculates relaxation times at different temperatures. This method can predictively find the appropriate equilibrium time at each temperature, so that each conformation is sufficiently relaxed, and avoids a simulation time exceeding the required equilibrium time. Because the annealing at different temperatures is completely parallel, this strategy also makes better use of modern computer hardware, greatly improving the simulation efficiency. For these reasons, this is the most advanced method for modern simulations to study supercooled state dynamics and the glass transition process.²⁹

In this study, we first predict T_g of cyclic olefin copolymers (COC) composed of ethylene, NB and its derivatives by all-atom molecular dynamics simulation to verify the effectiveness of the PreSQ approach and the chosen force field. The simulation results are in good agreement with the reported experimental results. Subsequently, we investigate the effect of polar groups on the T_g of COPs from the ROMP reaction by focusing on systems with two different polar groups, namely NBCH₂OH (labelled as COP1) and NBCOOH (COP2). We find that the T_g of COP2 is higher than that of COP1 at the same f_pol. After systematically varying the content of the two polar groups in COP, it is found that the T_g increases with the increase of f_pol, and tends to plateau for high f_pol, which is consistent with the previous experimental results.²² The observed variation trend in T_g can be described reasonably by the Kwei^23–25 model, but the classic Fox²³ equation significantly underestimates T_g. The deviation between the Fox equation and predicted T_g can be attributed to the existence of strong hydrogen bonding (HB) interactions in the system. Therefore, we analyze the cohesive energy density (Π_CED) and HB interactions in the system. We find that Π_CED increases linearly with f_pol, and the increase rate of the COP2 system is larger than that of the COP1 system, resulting in a higher T_g in the COP2 system. The increase rate of T_g gradually slows down with the increase of Π_CED, which is similar to the variation trend with f_pol. In addition, the number of HBs (N_HB) also increases linearly with f_pol, as does Π_CED, and has a linear relationship with Π_CED. Consequently, the variation trend of T_g with N_HB is similar to that with Π_CED. To further understand the intrinsic factors from HB interactions, we calculate the Gibbs free energy (ΔG) for HB breaking. Importantly, we find that the variation trend of ΔG with f_pol also gradually slows down, indicating that the HB strength is gradually stable. Therefore, even if N_HB increases linearly, their strength gradually stabilizes, resulting in a nonlinear increase of T_g with the increase of the polar groups.

Simulation methods

All-atomic force field

The all-atom optimized potentials for the liquid simulations (OPLS-AA)^30,31 force field is considered to be the best comprehensive force field for describing liquid organic molecules due to its ability to reproduce the thermodynamic properties of the liquid phase. However, simulations for n-alkanes with the original OPLS-AA force-field show an overestimation of the intermolecular attractive force and therefore result in a higher heat of vaporization than the experiment.³² To solve the above problem, Siu et al.³³ developed an optimized version called L-OPLS, where partial charges and the coefficients defining the potential function of several dihedral angles are modified. In ref. 34, Zangi found that simulations with the original OPLS-AA force-field will lead to unphysical spontaneous crystallization of 1-octanol, 1-nonanol, and 1-decanol at temperatures which are about 35–55 K higher than the experimental melting temperatures, while using a mixed version (adopts L-OPLS parameters for the hydrocarbon tail of the alcohols, while using the original OPLS-AA force-field parameter for the hydroxyl head group) can avoid the crystallization of long-chain alcohols above the experimental melting temperature. Inspired by their work, we also use a combination of the original OPLS-AA and L-OPLS force fields for norbornene with polar groups. We use the L-OPLS force field for the alkane part, and the original OPLS-AA for the polar groups, and this combinational usage of the original OPLS and L-OPLS is labeled as mix-OPLS in the following text.

Simulated systems and preparation of the initial configuration

As mentioned above, benchmark simulations are performed for COC polymers based on ethylene (Eth) and NB (labelled as COC1), Eth and NBCH₂OH (labelled as COC2), and the results of T_g are compared with the available experimental values. Thereafter the effect of polar groups is studied in COP polymers of NB and NBCH₂OH (labelled as COP1), and that of NB and NBCOOH (COP2). Note that COC1 with different chain lengths are studied. Details of these systems are listed in Table 1. For the initial configuration, firstly a self-avoiding walk chain configuration is constructed, which is subsequently duplicated several times according to the system size, and thereafter these chains are packed into the simulation box using the PACKMOL program³⁵ at a low density of 0.02 g cm⁻³ and subjected to an energy minimization process. Subsequently, we equilibrate the system at 1000 K for a long time under the NPT ensemble to eliminate local stresses and to attain an equilibrated density, and the equilibration times t_eq of different systems are shown in the Table 1. When the polymer chains are appropriately equilibrated, bond vectors that are far apart along the chain are uncorrelated. This feature can be characterized by the Flory's characteristic ratio (C_n).³⁶where n is the number of backbone bonds, and θ_ij is the angle between the bond vector r_i and r_j. As an example, the results for the COC1 polymer with a chain length of 240 are shown in Fig. 1, where a fast convergence is shown, demonstrating the appropriate equilibration of the chain conformation.

Table 1 Chain length, number of chains, and the initial equilibration times at 1000 K for the simulated COC and COP polymers containing ethylene (Eth), NB and its derivatives

Systems	Chain length	Number of chains	t eq (ns)
COC1 (Eth/NB)	60	20	300
	240	20	770
	500	8	1000
	1000	4	1690
COC2 (Eth/NB/NBCH2OH)	130	20	360
COP1 (NB/NBCH2OH)	40	20	100
COP2 (NB/NBCOOH)	40	20	100

---

Fig. 1 Flory's characteristic ratio C_n saturates at C_∞ for the Eth/NB system with a chain length of 240. The x-axis is the number of backbone bonds.

Relaxation time calculations

We calculate the incoherent intermediate scattering function F_s(q,t)^37–45 to quantify the segmental relaxation time from the simulation. This function is computed aswhere q is a wavevector, r_j(t) is the position of atom j at time t, the summation is over all N atoms in the system, and the brackets denote an ensemble average. We chose the wavenumber q* corresponding to the first peak in the static structure factor. We define the relaxation time as the time at which F_s(q,t) relaxes to 0.2.^40,46–48 Note that we use a consistent value of q* throughout our calculation for all the systems, unless otherwise noted.

Upon cooling, segmental dynamics of polymers often exhibit a super-Arrhenius behavior, especially at low temperatures approaching T_g, where relaxation times become highly sensitive to temperature. As discussed in ref. 49, the temperature dependence of segmental dynamics of polymer systems can be well captured by the Vogel–Fulcher–Tammann (VFT) equation,^50–52

where τ_α(T) is the segmental relaxation time at temperature T, τ₀ is an extrapolated high-temperature relaxation time, T₀ is the characteristic temperature at which τ_α is extrapolated to diverge, and D is a thermal breadth parameter. Due to this highly sensitive super-Arrhenius temperature dependence of segmental dynamics at low temperatures, supercooled liquid dynamics approaching T_g are therefore not feasible in conventional linear quench simulations, since the method is simulated for times that exceed those needed to reach equilibrium at high temperatures while the simulation at low temperatures is far from enough for the equilibrium.

Simulation strategy and details of the PreSQ algorithm

We used the PreSQ algorithm²⁹ to simulate the T_g of polymers, the basic idea of this approach is to progressively increase the simulation time at lower temperatures during a cooling process. In practice, this algorithm divides relaxation time τ_α(T) space into different windows (τ₁ = 10⁰–10¹ ps, τ₂ = 10¹–10^1.5 ps, τ₃ = 10^1.5–10² ps,…) located sequentially at successive temperature ranges. A priori choice of appropriate equilibration simulation times in these temperature ranges is the major challenge, which is solved by an iterative process in the PreSQ algorithm. Here are the detailed steps we adopt in our simulation:

(i) The first step is to take the equilibrated configuration from the NPT simulation at 1000 K as the initial configuration for the first relaxation time window. We preset the temperature range for the 1^st window from 980 K to 900 K. The equilibration time (τ_e) is set to 10 times the segmental relaxation time at 1000 K, we calculate the segmental relaxation time (τ_α) at each temperature point in this range and compare it with the equilibration time, if τ_e < 10τ_α, we prolong the simulation at this point until τ_e > 10τ_α. The segmental relaxation time at the last temperature point is recorded as .

(ii) After the simulations at these temperature points are finished, the segmental relaxation time (τ_α) data in this window are fitted with the VFT equation. Thereafter we extend this VFT relationship to estimate the next temperature range where the last temperature point in this range satisfies the condition 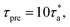where τ_pre is the predicted segmental relaxation time at this last temperature point from the VFT equation.

(iii) The above two steps are iteratively performed along the temperature axes until the segmental relaxation time reaches the order of 10⁴ ps. We find that the predicted T_g value can have a reasonable convergence on this simulation timescale. A detailed discussion can be found in Fig. S1 (ESI†).

(iv) We fit all the obtained structural relaxation time data at different temperatures from the above procedure with the VFT equation and thereafter extrapolate the relaxation time data to a timescale of 100 s for the experimental glass transition, from which the T_g of the system is obtained.

Note that during the above process, the temperature is cooled down step-wise with a step size of ΔT = −20 K. At each temperature, a 3 ns NPT MD simulation is performed. When the system reaches an equilibrium density, the last frame of the conformation is annealed under NVT conditions for sampling. The Berendsen thermostat with a coupling time of 0.5 ps and Berendsen barostat with a coupling time of 5.0 ps are used to control the temperature and pressure, respectively. A cutoff of 1.0 nm is used for the calculation of the van der Waals interactions and the particle-mesh Ewald method is used to treat the electrostatic interactions. The energy and pressure calculations are corrected by the long-range dispersion. The leap-frog algorithm is used to integrate the Newton's equations of motion with a time step of 1 fs for all the simulations. All all-atom MD simulations are performed using the GROMACS 2018 molecular dynamics package.⁵³

Results

Verification of the validity of the chosen force-field and the PreSQ algorithm

In this section, we simulate a copolymer system of ethylene and norbornene, namely COC1 in Table 1 with different chain lengths, and compare the simulated T_g value with the available experimental data.⁵⁴ In particular, we simulate alternating copolymers with various molecular weights (M_n = 3660 g mol⁻¹, 14 640 g mol⁻¹, 30 500 g mol⁻¹, 61 000 g mol⁻¹), where the ratio of ethylene and norbornene in the block copolymer chain is 0.5/0.5 (Scheme 1). Considering the computational efficiency, the number of chains in the simulated systems with different chain lengths is different, and is set to 20, 20, 8, and 4, respectively.

Scheme 1 Ethylene and norbornene copolymerization.

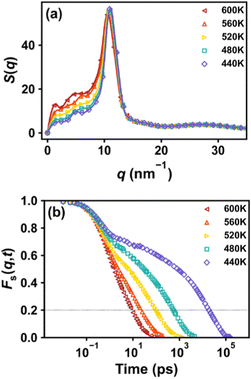
As described above, an incoherent intermediate scattering function F_s(q,t) is calculated to analyze the alpha relaxation behavior. ‘q’ is taken from the first peak of the static structure factor, S(q), as shown in Fig. 2a for an example with a molecular weight of M_n = 3660 g mol⁻¹ at 480 K. Fig. 2b shows the results of F_s(q,t) at different temperatures. These scattering functions show characteristic temperature dependence and a two-step relaxation behavior at lower temperatures typical for glass formers. From these curves, the time at which F_s(q,t) relaxes to 0.2 is recorded as the segmental relaxation time, τ_α(T).

Fig. 2 (a) Static structure factor S(q) at 480 K, and (b) incoherent intermediate scattering function F_s(q,t) at different temperatures, for the system with a molecular weight of M_n = 3660 g mol⁻¹. The dotted line in (b) indicates the definition of the structural relaxation time.

The results of τ_α(T) are plotted in Fig. 3a, and T_g is obtained by extrapolating the functional form of the VFT equation to the experimental 100-second time scale. The predicted T_g values for systems with different chain lengths are listed in Table 2. For comparison, we additionally use the original OPLS-AA force field to simulate the system with a molecular weight of 30 500 g mol⁻¹. All the data points and experimental values from ref. 54 are plotted in Fig. 3b. We see that the T_g of different chain lengths obtained by the L-OPLS force field are quite consistent with the experimental value, and follow the Fox–Flory relationship,⁵⁵T_g = T^∞_g − K/M_n. However, the T_g value predicted from the original OPLS-AA force field is much higher due to the excessive intermolecular attraction. Therefore, the use of the L-OPLS force field and PreSQ algorithm is suitable for the purpose of this study.

Table 2 Glass transition temperature for alternating COC1 polymers of ethylene and NB with different molecular weights using original OPLSAA and L-OPLSAA force fields

M n × 10^−3 (g mol^−1)	3.66	14.64	30.50	61.00
Sim. Tg (K) (L-OPLS)	390	401	406	410
Sim. Tg (K) (OPLS-AA)			428

---

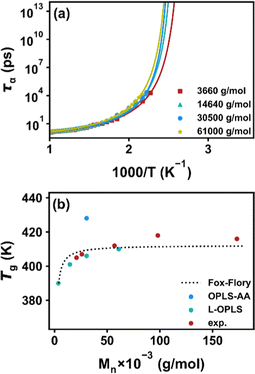Fig. 3 (a) Temperature dependence of segmental relaxation time for COC1 polymers with different molecular weights, lines represent the least-squares fitting with the VFT equation. (b) Comparison of the simulated data using L-OPLS and the original OPLS force-field, and that of the experimental data from ref. 54. The dotted line represents the Fox–Flory relationship between molecular weight and T_g of the copolymers.

Glass transition temperature of polar group functionalized COC

Before studying the effect of polar groups on the T_g for the COP system, a comparison with available experimental data is performed to verify the validity of the method and the force field for predicting the T_g of systems with polar groups. We simulate a block copolymer (COC2 listed in Table 1) composed of three monomers: Eth/NB/NBCH₂OH (Scheme 2), where Eth is the ethylene unit. We setup the simulation according to the experimental system details in ref. 56, i.e., the ratio of Eth : NB : NBCH₂OH is 80% : 10% : 10%, the ratio of NBCH₂OH(endo) and NBCH₂OH(exo) is 5 : 8, and the molecular weight is 5758 g mol⁻¹. To be consistent with the experiment, the copolymer chain in our simulation has a degree of polymerization of N = 130, and each chain contains 13 NB, 13 NBCH₂OH (5 endo conformation, 8 exo conformation), and 104 Eth units. To control the stereoisomerism of the NBCH₂OH group, we set the improper dihedral angle in the topology file to control its stereoisomerism. For simplicity, Eth and NB (or NBCH₂OH) units are evenly arranged in one chain as much as possible in our simulation. Twenty block copolymer chains are placed in a simulation box. For comparison, the original OPLS-AA force field and the mix-OPLS force field are used for comparison. Fig. 4 shows the segmental relaxation time data for simulations with both force fields and corresponding fitting with the VFT equation. The T_g obtained by using the original OPLS-AA force field is 351 K, and the T_g obtained from the mix-OPLS force field is 321 K, which are both higher than T_g = 316 K measured experimentally by DSC. Since our method for predicting the T_g is based on the kinetic properties of the system, it is comparable to the experimental DMTA results. The T_g measured by DMTA is usually higher than that of DSC. Therefore, the results obtained using mix-OPLS are in reasonable agreement with the experiment.

Scheme 2 Ethylene, norbornene and 5-methanol-2-norbornene copolymer.

Fig. 4 Temperature dependence of relaxation time for the Eth/NB/NBCH₂OH copolymer using both the original OPLSAA and mix-OPLS force fields. Lines represent the least-squares fitting with the VFT equation.

Influence of the polar group content on the glass transition temperature of COP polymers

As discussed in the introduction, the T_g of the polymer will increase with the increase of f_pol, but the increasing rate is gradually slowed down. The HBs caused by the introduction of polar groups must play an important role, but the underlying mechanism remains unknown. The influence of polar groups on the T_g is significant, and there is no doubt that both type and f_pol are important influencing factors determining the value of T_g. Therefore, in this section, we will use the above-validated method and force field to study the effect of polar groups on the T_g, and to determine the variation trend of T_g with f_pol from the perspective of HB interactions. The systems we simulated are ROMP^22,57–59 COP of norbornene partially functionalized with polar groups of CH₂OH or COOH, as demonstrated in Scheme 3. The content of 5-methanol-2-norbornene (NBCH₂OH) or 5-carboxylic-2-norbornene (NBCOOH) is varied systematically. Each system contains 20 monomers, and there are 20 chains in total.

Scheme 3 Ring Opening Metathesis Polymerization of norbornene and its derivative functionalized with CH₂OH or COOH.

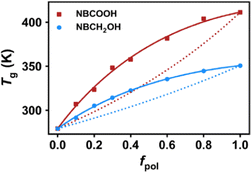
Fig. 5 shows the glass transition temperature as a function of f_pol. From the simulated results, the T_g obtained for the COP2 system containing the NBCOOH group is higher than that of the COP1 containing NBCH₂OH group, indicating that the COOH polar group has a greater influence on T_g than the CH₂OH polar group. And the two prediction models, Fox equation eqn (4)²³ and Kwei eqn (5)^23–25 models are used to fit with the variation trend of T_g,

The classic Fox equation eqn (4), which assumes a simple mixing rule for the two components where w_i and T_g,I are the weight fraction and T_g of the constituent components. We find that fitting with the Fox equation fails for both systems and there are obvious underestimations of T_g, suggesting that the system must involve strong specific interactions that are not taken into account by the Fox equation.⁶⁰ In contrast, the Kwei eqn (5) model can accurately predict the variation trend of the T_g with f_pol over the whole range. The parameter k is the unequal contribution to T_g from the individual components. The parameter p counts the contribution from HBs in the system.^{23–25,61,62} The p value obtained from the fitting of the Kwei equation is positive, indicating strong intermolecular HB interactions in the system. The p value in the COP1 and COP2 systems are 16 and 28, respectively, indicating that the HB strength between COOH groups in the COP2 system is greater than that between CH₂OH groups in the COP1 system.

Fig. 5 Simulated glass transition temperature for COP1 and COP2 systems with different content of NBCH₂OH or NBCOOH groups, respectively. The x-axis is the polar group content. Solid lines represent least-squares fitting with the Kwei model, while dotted lines are for the Fox equation.

A direct consequence of raising the content of HB interaction agent, polar groups, in the system will be an increase in cohesive energy density (Π_CED), which is an important parameter determining the T_g of polymers.¹³ We estimate Π_CED in our simulation as,^63,64

where Ψ_inter is the total intermolecular potential energy and V is the volume of the simulation box. The results for both COP1 and COP2 systems with different f_pol at a fixed temperature of 480 K are plotted in Fig. 6a. This shows that Π_CED increases with increasing f_pol in a linear fashion for both COP1 and COP2 systems. As expected, the COP2 system has a much higher slope than the COP1 system due to stronger HB interactions in the former. In Fig. 6b, we plot the increase of the glass transition temperature (ΔT_g) as a function of that of the cohesive energy density (ΔΠ_CED) for both systems. We find that ΔT_g increases in a sub-linear manner with ΔΠ_CED. Two empirical models are used to fit the data. The first model we used was proposed early by Tsutsui and Tanaka,⁶⁵ ΔT_g = K (ΔΠ_CED)^1/2, the variation trend is nicely captured by this model, as demonstrated by the dotted lines in the figure. The fitting parameter K = 9 and 11 for the COP1 and COP2 systems, respectively. A larger value for the COP2 system indicates a stronger dependence. Another equation we used is the one proposed by Xu et al.^7,8 based on the generalized entropy theory, ΔT_g = (b + cΔΠ_CED)/(1 + dΔΠ_CED), we see that this model works much better, as indicated by solid lines in the figure. In their original model, an interaction strength parameter is used. Here we directly used ΔΠ_CED in the equation since both parameters have a linear relationship with each other according to their calculations.^7,8 Note that this relationship was originally used by Broadhurst^66,67 to describe the dependence of the melting temperature T_m of the alkane polymers on their molecular weight. We speculate that the direct consequence of the variation in molecular weight will be the variation in Π_CED, therefore our usage of this equation on the correlation between ΔT_g ∼ ΔΠ_CED is reasonable.

Fig. 6 (a) The cohesive energy density plotted as a function of polar group content in both COP1 and COP2 systems at 480 K. (b) The increase of glass transition temperature (ΔT_g) plotted as a function of the increase of cohesive energy density (ΔΠ_CED) at 480 K. Dotted lines represent least-squares fitting with the model of Tsutsui and Tanaka,⁶⁵ while solid lines represent the model of Xu et al.^7,8

Hydrogen bonding interaction in both COP systems

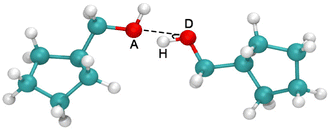
The results in Fig. 6b demonstrate that the variations in T_g are directly determined by the change in cohesive energy density, Π_CED. However, the Π_CED of polymers with polar groups is the sum of the contributions from various interactions, such as van der Waals interactions, Coulombic interactions, and HB interactions etc. For the current systems, HB interactions have a major contribution. In order to analyze the HBs interactions quantitatively, we define two criteria for the HB formation in our calculation, (i) the distance between the acceptor A and the donor D, r ≤ 0.35 nm, and (ii) the angle between the hydrogen, the donor D, and the acceptor A, α ≤ 30° (Fig. 7). Once both conditions are met, it is counted as a formed HB pair.

Fig. 7 Schematic illustration of the geometrical criterion for the HB formation.

By the above criteria, we calculate the number of HBs (N_HB) formed between NBCH₂OH groups in COP1 and between NBCOOH groups in the COP2 system respectively. The results are denoted as N_HB as shown in Fig. 8a, where these data are calculated at a fixed temperature of 480 K. The N_HB increases linearly with polar groups. At a fixed f_pol, the N_HB of NBCOOH is higher than that of NBCH₂OH, resulting in higher Π_CED and hence higher T_g in the COP2 system than in the COP1 system. Since COOH contains two different kinds of oxygen atoms, HBs formed by these two different oxygen atoms are plotted in Fig. 8b. It can be seen that the HBs are dominated by those formed by carbonyl oxygen, while the HBs formed by hydroxyl oxygen are negligible. In Fig. 8c, we plot the correlation between Π_CED and N_HB, where a linear relationship is found as expected. Not surprisingly, T_g increases with the N_HB in a sub-linear manner (Fig. 8d) and this trend is consistent with the variation trend of T_g with Π_CED as shown in Fig. 6b. Again, we show that Xu's equation^7,8 performs much better fitting with the data than that of Tsutsui and Tanaka.⁶⁵ In addition, it shows that N_HB increases with f_pol, resulting in an increase in Π_CED and therefore an increase in T_g. The above results indicate that the hydrogen bonding interaction plays a dominant role in determining Π_CED and consequently the T_g of the system. By analyzing the variation trend of T_g with Π_CED and N_HB, it shows that there must be a factor in the system that slows down the rate of T_g rise.

Fig. 8 (a) The number of HBs formed in COP1 and COP2 systems with different polar group contents at 480 K. (b) HBs formed by carbonyl and hydroxyl oxygen atoms in the COP2 system. (c) The cohesive energy density as a function of the number of HBs for both systems at 480 K. (d) The increase of glass transition temperature (ΔT_g) plotted as a function of the increase of the number of HBs (ΔN_HB) at 480 K. Dotted lines represent least-squares fitting with the model of Tsutsui and Tanaka,⁶⁵ while solid lines represent the model of Xu et al.^7,8

In order to further understand the underlying mechanism for the influence of HBs on T_g, we adopt the model proposed by Schroeder and Cooper,^68,69 where the fraction of HBs (X_HB) can be related to the Gibbs free energy (ΔG) for HB breaking. The equilibrium for the hydrogen bonding can be expressed as

(OH⋯OH)_bonded ⇋ 2(OH)_free (7)

The associated equilibrium constant K is given by,The Gibbs free energy can be written as,where R is the gas constant. According to the above equations, a higher value of ΔG indicates a higher stability of HB pair. X_HB is the hydrogen bond fraction, which is the number of hydrogen bonds divided by the number of polar groups, as shown in Fig. 9a. By calculating X_HB, ΔG at each temperature can be obtained using eqn (9). For the COP2 system containing NBCOOH, the HBs formed by the carbonyl oxygen dominates, therefore we calculate the ΔG for HB breaking formed by the carbonyl oxygen. We also plot the ΔG for systems with different f_pol at temperatures of 480 K (Fig. 9b). The ΔG of the COP2 system is higher than that of the COP1 system containing the NBCH₂OH group, which is direct evidence that the hydrogen bond strength in the COP2 system is stronger than that of the COP1 system. Importantly, ΔG in both systems increase in a sub-linear manner with f_pol with the increase rate gradually slowing down, indicating that hydrogen bond stability increases in a sub-linear manner. Therefore, even though the N_HB and the Π_CED both increase linearly with f_pol, the T_g does increase nonlinearly, with a gradually decreasing rate of increase. Not surprisingly, we find that T_g increases with ΔG in a linear fashion for both COP1 and COP2 systems (Fig. 9c). From the aspect of the slope of T_g with ΔG, the COP2 system is larger than the COP1 system. This is because T_g is determined collectively by the number and strength of HBs. The number of HBs in the COP2 system is more than that in the COP1 system. Therefore, when the change in ΔG is the same, the change of T_g of the COP2 system is greater than that of the COP1 system.

Fig. 9 (a) The fraction of HBs formed in COP1 and COP2 systems with different polar group contents at 480 K. (b) The Gibbs free energy of HB breaking plotted at different polar group contents for both COP1 and COP2 systems at temperatures of 480. (c) Glass transition temperature plotted as a function of the Gibbs free energy of HB breaking.

Conclusions

Atomistic molecular dynamics simulations are carried out for ROMP COP containing NB, a non-polar aliphatic monomer, NBCH₂OH or NBCOOH, polar monomers capable of forming HBs. Our aim is to elucidate the effects of the types and contents of polar functional groups on the T_g of ROMP polymers. First, we successfully establish a T_g prediction model by using the PreSQ algorithm. T_g values of cyclic olefin copolymers composed of ethylene, NB and its derivatives are successfully predicted, and the obtained results are highly consistent with the experiments. Based on the above results, we investigate the effect of two kinds of polar groups (CH₂OH and COOH) on the T_g of COP polymers. It is found that enhancement in T_g introduced by including the COOH group is much higher than that of the CH₂OH group. However, the rate of increase in T_g decreases gradually with the content of both groups. In order to explain this phenomenon, we analyze the cohesive energy density Π_CED and hydrogen bond interactions in both systems. We find that both Π_CED and the number of N_HB increase linearly with f_pol. Not surprisingly, they have a linear relationship, since the increase in Π_CED is mainly caused by N_HB. As expected, T_g does not increase linearly with Π_CED and N_HB, and the growth rate gradually slows down. In order to further figure out the factor that slows down the growth rate of T_g, we calculate the free energy ΔG for hydrogen bond breaking at 480K. We find that the ΔG in the COP2 system containing the COOH group is larger than that in the COP1 system containing CH₂OH, indicating that the COP2 system has stronger HBs and hence a higher T_g at a given fraction of polar groups. Importantly, we find that the increase rate of ΔG gradually slows down with the increase of f_pol, and T_g increases with ΔG in a linear fashion. Therefore, even though N_HB increases linearly with f_pol, the increasing rate in its strength gradually slows down, which in turn leads to T_g increasing sub-linearly. Our results demonstrate that the HB interaction has a strong effect on T_g, while the HB strength plays a dominant role. Overall, our work successfully predicts the T_g of ROMP COP polymers and provides a new understanding of the effect of polar groups on polymer T_g.

Author contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (21873040, 22133002 and 21833008). H.-J. Q. and Z.-Y. L. also acknowledge the support from the Program for JLU Science and Technology Innovative Research Team. We are also grateful for the financial support from ExxonMobil Asia Pacific Research & Development Co., Ltd. The authors acknowledge the high performance computing center of Jilin University.

Notes and references

1. S.-W. Kuo, W.-P. Liu and F.-C. Chang, Macromolecules, 2003, 36, 5165–5173.
2. A. R. Baljon, G. Mendoza, N. Balabaev and A. Lyulin, Polym. Sci., Ser. A, 2021, 63, 356–362.
3. S.-J. Xie, H.-J. Qian and Z.-Y. Lu, J. Chem. Phys., 2014, 140, 044901.
4. H. A. Schneider, J. Appl. Polym. Sci., 2003, 88, 1590–1599.
5. S. Della Sciucca, G. Spagnoli, M. Penco, S. Battiato, F. Samperi and R. Mendichi, J. Polym. Sci., Part B: Polym. Phys., 2009, 47, 596–607.
6. P. Carbone, A. Rapallo, M. Ragazzi, I. Tritto and D. R. Ferro, Macromol. Theory Simul., 2006, 15, 457–468.
7. X. Xu, J. F. Douglas and W.-S. Xu, Macromolecules, 2021, 54, 6327–6341.
8. W.-S. Xu, J. F. Douglas and X. Xu, Macromolecules, 2020, 53, 9678–9697.
9. W.-S. Xu, J. F. Douglas and X. Xu, Macromolecules, 2020, 53, 4796–4809.
10. A. Askadskii, T. Matseevich and V. Markov, Polym. Sci., Ser. A, 2016, 58, 506–516.
11. J. Konieczkowska, H. Janeczek, J. G. Malecki and E. Schab-Balcerzak, Eur. Polym. J., 2018, 109, 489–498.
12. S. Pawlus, A. Grzybowski, S. Kołodziej, M. Wikarek, M. Dzida, P. Góralski, S. Bair and M. Paluch, Sci. Rep., 2020, 10, 1–8.
13. Z. Yang, X. Xu and W.-S. Xu, Macromolecules, 2021, 54, 9587–9601.
14. F. Krohn, C. Neuber, E. A. Rössler and H.-W. Schmidt, J. Phys. Chem. B, 2019, 123, 10286–10293.
15. K. Li, L. Zhou, S. Wu, Q. Yu and L. Yang, High Perform. Polym., 2020, 32, 316–323.
16. Y. Pan, T. Li, Y. Zhou and L. Li, Polymer, 2022, 242, 124613.
17. M. Abubekerov, S. M. Shepard and P. L. Diaconescu, Eur. J. Inorg. Chem., 2016, 2016, 2634–2640.
18. B. Liu, Y. Li, B. G. Shin, D. Y. Yoon, I. Kim, L. Zhang and W. Yan, J. Polym. Sci., Part A: Polym. Chem., 2007, 45, 3391–3399.
19. J. Mol, J. Mol. Catal. A: Chem., 2004, 213, 39–45.
20. S. H. Moon, K. L. Park, J. W. Baek, H. J. Lee, J. H. Choi, Y. Lee and B. Y. Lee, J. Polym. Sci., 2020, 58, 1253–1261.
21. M. Rosenberger, S. Kefer, M. Girschikofsky, G.-L. Roth, S. Hessler, S. Belle, B. Schmauss and R. Hellmann, Opt. Lett., 2018, 43, 3321–3324.
22. J. M. Dennis, T. R. Long, A. Krishnamurthy, N. T. Tran, B. A. Patterson, C. E. Busch, K. A. Masser, J. L. Lenhart and D. B. Knorr Jr, ACS Appl. Polym. Mater., 2020, 2, 2414–2425.
23. L. Weng, R. Vijayaraghavan, D. R. MacFarlane and G. D. Elliott, Cryobiology, 2014, 68, 155–158.
24. A. A. Lin, T. Kwei and A. Reiser, Macromolecules, 1989, 22, 4112–4119.
25. X. Lu and R. Weiss, Macromolecules, 1992, 25, 3242–3246.
26. A. Cavagna, Phys. Rep.-Rev. Sec. Phys. Lett., 2009, 476, 51–124.
27. P. G. Debenedetti and F. H. Stillinger, Nature, 2001, 410, 259–267.
28. M. Ediger and P. Harrowell, J. Chem. Phys., 2012, 137, 080901.
29. J.-H. Hung, T. K. Patra, V. Meenakshisundaram, J. H. Mangalara and D. S. Simmons, Soft Matter, 2019, 15, 1223–1242.
30. M. L. Price, D. Ostrovsky and W. L. Jorgensen, J. Comput. Chem., 2001, 22, 1340–1352.
31. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Ceram. Soc., 1996, 118, 11225–11236.
32. L. L. Thomas, T. J. Christakis and W. L. Jorgensen, J. Phys. Chem. B, 2006, 110, 21198–21204.
33. S. W. Siu, K. Pluhackova and R. A. Böckmann, J. Chem. Theory Comput., 2012, 8, 1459–1470.
34. R. Zangi, ACS Omega, 2018, 3, 18089–18099.
35. L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164.
36. M. Vacatello and P. Flory, Macromolecules, 1986, 19, 405–415.
37. F. W. Starr, F. Sciortino and H. E. Stanley, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1999, 60, 6757.
38. B. A. P. Betancourt, P. Z. Hanakata, F. W. Starr and J. F. Douglas, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2966–2971.
39. Y. Cheng, J. Yang, J.-H. Hung, T. K. Patra and D. S. Simmons, Macromolecules, 2018, 51, 6630–6644.
40. R. J. Lang and D. S. Simmons, Macromolecules, 2013, 46, 9818–9825.
41. J. Baschnagel and F. Varnik, J. Phys.: Condes. Matter, 2005, 17, R851.
42. F. W. Starr, J. F. Douglas and S. Sastry, J. Chem. Phys., 2013, 138, 12A541.
43. D. S. Simmons and J. F. Douglas, Soft Matter, 2011, 7, 11010–11020.
44. D. D. Hsu, W. Xia, J. Song and S. Keten, ACS Macro Lett., 2016, 5, 481–486.
45. A. Shavit and R. A. Riggleman, Macromolecules, 2013, 46, 5044–5052.
46. P. Z. Hanakata, J. F. Douglas and F. W. Starr, J. Chem. Phys., 2012, 137, 244901.
47. J.-H. Hung, J. H. Mangalara and D. S. Simmons, Macromolecules, 2018, 51, 2887–2898.
48. J. H. Mangalara and D. S. Simmons, ACS Macro Lett., 2015, 4, 1134–1138.
49. B. Schmidtke, M. Hofmann, A. Lichtinger and E. Rössler, Macromolecules, 2015, 48, 3005–3013.
50. G. S. Fulcher, J. Am. Ceram. Soc., 1925, 8, 339–355.
51. G. Tammann and W. Hesse, Z. Anorg. Allg. Chem., 1926, 156, 245–257.
52. C. Rodríguez-Tinoco, J. Ràfols-Ribé, M. González-Silveira and J. Rodríguez-Viejo, Sci. Rep., 2016, 6, 1–8.
53. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25.
54. N. Ekizoglou, K. Thorshaug, M. L. Cerrada, R. Benavente, E. Pérez and J. M. Pereña, J. Appl. Polym. Sci., 2003, 89, 3358–3363.
55. T. G. Fox Jr and P. J. Flory, J. Appl. Phys., 1950, 21, 581–591.
56. R. A. Wendt and G. Fink, Macromol. Chem. Phys., 2000, 201, 1365–1373.
57. K. Szwaczko, I. Czeluśniak and K. Grela, J. Organomet. Chem., 2017, 847, 146–153.
58. K. Nomura, S. Takahashi and Y. Imanishi, Polymer, 2000, 41, 4345–4350.
59. S. I. Subnaik and C. E. Hobbs, Polym. Chem., 2019, 10, 4524–4528.
60. J. Prinos and C. Panayiotou, Polymer, 1995, 36, 1223–1227.
61. S. W. Kuo, H. Xu, C. F. Huang and F. C. Chang, J. Polym. Sci., Part. B: Polym. Phys., 2002, 40, 2313–2323.
62. S. W. Kuo and F. C. Chang, Macromolecules, 2001, 34, 5224–5228.
63. W.-S. Xu, J. F. Douglas and K. F. Freed, Macromolecules, 2016, 49, 8341–8354.
64. J. K. Maranas, M. Mondello, G. S. Grest, S. K. Kumar, P. G. Debenedetti and W. W. Graessley, Macromolecules, 1998, 31, 6991–6997.
65. T. Tsutsui and T. Tanaka, Polymer, 1977, 18, 817–821.
66. M. G. Broadhurst, J. Chem. Phys., 1962, 36, 2578–2582.
67. M. G. Broadhurst, J. Res. Natl. Bur. Stand., Sect. A, 1966, 70, 481.
68. L. Schroeder and S. L. Cooper, J. Appl. Phys., 1976, 47, 4310–4317.
69. H. A. Karimi-Varzaneh, P. Carbone and F. Müller-Plathe, Macromolecules, 2008, 41, 7211–7218.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01229d

‡ Current address: South China Advanced Institute for Soft Matter Science and Technology, School of Emergent Soft Matter, South China University of Technology, Guangzhou 510640, China.

---