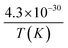Multiscale modelling potentialities for solid oxide fuel cell performance and degradation analysis

Abstract

Solid oxide fuel cells are electrochemical devices that are able to directly convert the chemical energy of fed fuels to electricity as well as to provide heat through exhausted gases allowing a higher energy efficiency compared to tradition thermal engines. However, the state-of-the-art materials show a drastic performance drop after too few working hours because of irreversible microstructural changes. Here the main issue consists of improving cell durability by optimising its structure and operative conditions. Modelling can significantly support this target, permitting a better understanding of different phenomena and providing information that are difficult to directly measure. However, degradation simulation is a quite challenging task due to the complexity of the studied systems, where different phenomena overlap, as well as due to the numerous data requested on both electrochemical and microstructural features. Depending on the available cell information and the analysis detail level, a multiscale modelling approach is a promising solution for providing effective results with reduced computational efforts. Based on a macroscale characterization, for example, semi-empirical degradation functions can be directly derived from electrochemical impedance spectra and area-specific resistance variations without knowing anything on the microstructure in order to estimate global cell performance and durability through a lumped-parameter model. Whereas, when aiming at the identification of an aged element specific behaviour, detailed formulations have to be introduced for each mechanism following a microscale approach. In such cases, a local-level modelling is fundamental in view of uneven distributions of properties on the cell plane which influence locally the degradation process development and resulting performance.

---

1. Introduction

Solid Oxide Fuel Cells (SOFCs) are electrochemical devices commonly applied in gas to power applications.¹ The electrochemical exothermic oxidation of hydrogen permits direct electricity generation with minimum environmental issues realizing water as the primary product. Modularity, performance independence from the system scale, reduced noise and absence of mobile parts are other significant advantages compared to conventional power generators.² Different from other available fuel cell designs, high working temperatures favour the use of SOFCs as co-generation units, which are mainly applied at the residential level providing ∼0.75–1.5 kW_el and ∼1 kW as the maximum thermal power.³ There have been also some attempts of use in the mobile sector as auxiliary power units or for vehicle propulsion combined with batteries.^4–6 Despite promising results in terms of nominal performance, SOFCs are still characterised by an insufficient lifetime reaching 40 000–45 000 h as the best still rare durability in stationary applications.⁷ Whereas the commercial target requires a double value at least to be competitive with other solutions.⁸ This limit derives from significant microstructural variations which involve electrodes as well as interconnects and, to a lesser extent, the electrolyte.⁹ Indeed, the state-of-the-art anode consists of a Ni–YSZ (Yttria Stabilized Zirconia) cermet, where the hydrogen reacts at the Triple Phase Boundary (TPB) sites, namely the active zones characterised by the contemporaneous presence of an electron conductor (i.e., the metal), an ionic conductor (i.e., the ceramic) and the gas phase to favour reactant transport. Ni permits the achievement of excellent performance due to its good catalytic activity and electron conductivity, on the other hand this metal becomes unstable under long-lasting operation with observed agglomeration and migration.¹⁰ Indeed, high working temperatures favour the particle growth reducing the active area and thus provoking a significant performance reduction (∼18–41% of the total losses).¹¹ Under a stressful fuel utilization, Ni can be oxidised by the produced steam and then reduced again when the nominal operation is restored, which provokes crack formation because of the volume changes between these two states.¹² Moreover, Ni migrates away from the electrolyte interface further varying the effective active area.¹³ At the cathode, perovskites are commonly applied as a pure layer or mixed with high ionic conductor materials in order to increase their performance by extending TPB sites and enhancing ion migration. LSCF–CGO (Lanthanum Strontium Cobalt Ferrite–Cerium Gadolinium Oxide) or LSM–YSZ (Lanthanum Strontium Manganite–Yttria Stabilized Zirconia) are the main available solutions at the industrial level.¹⁴ However, both these electrodes easily react with other cell components forming high resistive phases,¹⁵ without the introduction of barrier layers. For instance, LSCF demixing consists of a heavy accumulation of strontium and cobalt, in less amount, near the electrolyte interface creating insulating zirconate deposits.¹⁶ Moreover, secondary phase formation also derives from the interactions with ferritic stainless-steel based interconnects, which release Cr volatile species covering the catalytically active sites.¹⁷ In addition to the release of Cr, interconnects provoke fracture development and electrical resistance increase due to the thickening of the oxide scale used to prevent steel corrosion.^18,19 Less frequently, YSZ electrolyte can progressively change its lattice from the initial cubic phase to the tetragonal one reducing ion conductivity.²⁰

In view of these several degradation mechanisms, further experimental and theoretical studies are still required in order to have a better insight of long-lasting cell operation and to project effective mitigation strategies.

As underlined in several experimental tests, cell degradation is strictly correlated to applied working conditions and the initial material structure. Temperature has been pointed out as one of the main sources, since an increase of ∼100° can result in an acceleration of 1.5–2 times.²¹ Gas composition, and above all, the humidity level significantly influence cell durability, with an observed increase of anodic Ni instability at high steam content.²² System performance has also a relevant dependence on the initial material structure. For instance, the presence of protective layers among electrodes, electrolyte and the interconnect reduces the risk of secondary phase formation.²¹ Moreover, larger Ni particles in the anodic cermet are more prone to agglomeration resulting in a lower catalytic activity.²³ Due to the degradation variability being a function of specific test features, quite different results have been presented in the literature for long-lasting cell operations. For instance, in ref. 24, the Ni–YSZ/YSZ/LSM–YSZ system was tested for 6000 h at 1123 K and 0.3 A cm⁻² reporting a degradation rate of 1.4 V% kh⁻¹. After 5000 h at 1023 K and 0.2 A cm⁻², a lower degradation rate was reported resulting in 0.75 V% kh⁻¹.²⁵ Whereas the Ni–YSZ/YSZ/LSCF–CGO system showed a more stable performance with an overall value of 0.5 V% kh⁻¹ after 100 000 h of operation working at 973 K and 0.5 A cm⁻².²⁶

Referring to modelling activity, a multiscale analysis well fits the challenge to study SOFCs at nominal and aged states. However, significant computation efforts have to be made in order to merge different simulation levels. For the nominal cell behaviour, some studies have been recently published in the literature, where a multiscale approach has been followed starting from atomic level models of specific transport phenomena and reaction paths to heat and material transport macro models, as well as from 3D material reconstruction to cell voltage prediction.^27–30 Looking at degradation analysis, different modelling approaches have been proposed which include both formulations of single mechanisms and general expressions for voltage time evolution. Referring to a specific phenomenon, the easiest alternative consists of determining semi-empirical correlations which represent the time changes of cell-specific features or microstructural variables. For instance, the Ni particle size increase or directly the resulting TPB density reduction were modelled through a power-law formulation to represent agglomeration mechanisms.^11,31 The decrease of electrolyte conductivity due to phase changes was forecast by introducing an empirical temperature-dependent corrective coefficient.³² Otherwise, theoretical studies have formulated physically based kinetics to predict degradation mechanisms. In ref. 33, the oxide scale growth on the interconnects was computed considering the oxidation reaction at the metal interface as well as the oxygen diffusion through the formed oxide. In ref. 34 the anodic Ni reduction and oxidation kinetics were evaluated in the cell working temperature range to understand if they are characterised by a reaction or a diffusion controlled path. In view of the fundamental role of microstructural features in the electrode catalytic activity, geometrical models have been developed to predict the specific surface area and TPB density for composite electrodes, such as Ni–YSZ and LSCF–CGO.^35,36 These were considered as a random distribution of interconnected spheres evolving during cell operation to reach lower energy-level states. Considering the simulation of global cell degradation, some empirical correlations have been formulated which express the total resistance variation measured through electrochemical impedance spectra as a further polarization loss.³⁷ In addition, the time evolution of different resistances has been determined by applying a proper equivalent circuit model which suggests the needed corrective terms in the kinetic formulation.³⁸ However, multiscale simulation codes that are able to merge all aspects, from the single mechanisms to global cell degradation, and involving simultaneously empirical correlations as well as microstructure-dependent kinetic formulations to be applied depending on the available experimental observations, are still rare in the literature.^39–41

In such a scenario, the authors propose SIMFC (SIMulation of Fuel Cells) as an effective multiscale simulation code which combines the different levels of analysis in a single tool for predicting cell performance and durability. SIMFC is an in-home Fortran code for high-temperature cell operation including MCFCs (Molten Carbonate Fuel Cells) and SOFCs.^42,43 Based on the conservation equation resolution for anodic and cathodic sides, it permits global performance prediction by a lumped-parameter modelling approach for a preliminary analysis of the system. Solving the same formulae for each sub-element discretizing the cell plane in a local-level modelling approach, the global cell behaviour is evaluated as a function of local physicochemical parameter distributions.⁴⁴ Focusing on SOFC durability, specific degradation functions derived empirically for a macroscale approach and dependent on the local microstructure for a microscale approach were introduced into the kinetic formulations. In addition to being one of the rare comprehensive tools for solid oxide cell modelling, it is also characterised by a high computational velocity reaching convergency usually under one minute. This is a significant improvement compared to reference multiscale models, mainly based on computational fluid dynamic software.³⁹ All potentialities of SIMFC as a simulation tool are described in the following chapters, also reporting the results of two specific case studies as examples.

2. Nominal performance modelling

SIMFC is a physically based model which evaluates the cell behaviour solving conservation equations in terms of material, energy and momentum balances as described in authors' previous studies.^43,45 Its core consists of ad hoc electrochemical kinetics to compute the cell voltage derived from Nernst, Ohm and Butler–Volmer equations (eqn (1)), described in detail elsewhere.^44–46

Considering overpotential formulations reported in Table 1, the main kinetic parameters are derived semi-empirically for a macroscale analysis, whereas in a microscale study they are expressed as a function of material features following the percolation theory to estimate available catalytic sites, conductivities and gas diffusion paths. In such a model, the electrodes are assumed as a random packing of ideal spheres consisting of electronic and ionic conductive phases.⁴⁷ Here the ohmic term (i.e., charge migration resistance) results in the combination of different layer contributions, where the effective conductivity is computed knowing the pure material value, particle radius and phase fraction. However, according to this formulation the pure ionic–electronic transport resistances are just evaluated, neglecting the effects due to cell setup and contact resistances. The activation overpotential depends on the availability of catalytically active sites or, in other terms, the triple phase boundary density. Finally, the diffusion overpotential for gas mass transport considers the diffusion coefficients and transport paths in view of the particle distribution. Table 1 summarises the proposed multiscale formulation for overpotential terms applied to different cell layers referring to the nominal behaviour; introduced degradation functions are discussed in detail in the following sections.

Table 1 SIMFC kinetic multiscale formulation^a44,46,48

Term	Macroscale formulation	Microscale formulation	Material properties
a Nomenclature for electrochemical kinetics. d: thickness (an: anode, cat: cathode), D^eff: effective diffusion coefficient (ac: active layer, sup: support), D^K: Knudsen diffusion coefficient, D^M: molecular diffusion coefficient according to Chapman–Enskog theory, Eact: activation energy, E^0: reversible voltage, Eeq: open circuit voltage, F: Faraday constant, J: current density, J0: exchange current density, lTPB: triple phase boundary density, M: molecular weight in g mol^−1, P: percolation network probability, p: gas partial pressure, R: ideal gas constant, red: electron conductive particle radius, rel: ion conductive particle radius, rp: pore radius, Rohm: ohmic resistance, T: temperature, y: molar fraction, VSOFC: cell voltage under load, Z: coordination number, z: charge number, α: kinetic order, β: contact angle, γ: kinetic constant, η: overpotential, ϑ: combination of cathodic diffusion coefficients, ξ: tortuosity, σ: conductivity, σ0: pure material conductivity, φ: porosity, Ψ: phase fraction (ed: electronic conductive, el: ionic conductive), and Ψ^t: threshold phase fraction.
Ohmic overpotential	η ohm = RohmJ
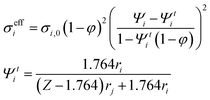
Activation overpotential		γ = γ′lTPBPelPed
Diffusion overpotential

---

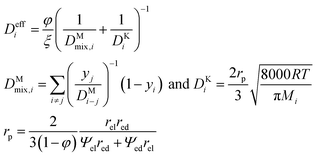
As results, SIMFC computes the voltage dependence on working conditions as the global cell behaviour index and maps of main physicochemical parameters on the cell plane as local results. SOFC performance is estimated referring to the electric efficiency ε_SOFC (i.e., the ratio between the produced power P_SOFC and the power corresponding to the fed hydrogen flow rate N_H2 in terms of its Lower Heating Value LHV_H2) and the Degradation Rate DR_SOFC (i.e., the voltage or resistance/overpotential variation over time t normalised to its initial value), as shown in eqn (2) and (3), respectively.

where A is the cell active area. Here, eqn (2) represents the energy conversion efficiency from fuel chemical energy to electricity through the electrochemical process, whereas eqn (3) provides a preliminary quantification of performance degradation assuming a linear variation of voltage or resistance/overpotential resulting in a negative value for the first case (i.e., voltage reduction) and a positive one for the second (i.e., resistance/overpotential increase).

3. Macro-level cell degradation modelling

3.1 Methodology

At a macroscale level without knowing the cell microstructure, the performance degradation can be modelled through the introduction of further time-dependent overpotential terms η_deg distinguishing between the increase of ohmic and polarization contributions (eqn (4)). These degradation functions are determined based only on electrochemical characterization measurements, such as electrochemical impedance spectra and characteristic curves (Fig. 1). Here the attending voltage drop can be predicted during cell operation; nevertheless, these equations are quite specific for just the studied system.

Fig. 1 Macroscale evaluation of SOFC voltage degradation based on electrochemical characterization under operation.

In detail, the ohmic evolution derives from the time profile of internal resistance (i.e., the first intercept of the real axis in electrochemical impedance spectra) independently from measured conditions, at the open circuit voltage or under load, in view of the direct proportionality between the ohmic resistance and the current density. Whereas the degradation function of the polarization term requires the J–V curve profile knowledge because of its more complex dependences summing activation and diffusion overpotentials (Table 1). Knowing the ohmic resistance every time, η_deg,pol can be obtained by the punctual variation of the differential resistance R_d, defined as the derivative of the voltage with respect to the current density.⁴⁹ Indeed, the voltage reduction means an R_d increase under fuel cell operation. Note the R_d profile is usually distinguished in three domains as a function of applied loads. The initial rapid decrease at low current densities represents the region where the activation loss dominates, the second with a plateau is due to charge transport resistances which are constant terms independent of load according to Ohm’s law, and the last one shows gas diffusion limitations resulting in a drastic increase at high current densities.

3.2 Case study

This approach was validated based on reference data of an anode supported cell tested for 9000 hours (∼375 days) in fuel cell mode under 0.5 A cm⁻² to avoid the fuel starvation (H₂ utilization equal to 60%).⁵⁰ The 9 cm² cell consisted of a Ni–YSZ anode (∼260 μm), a YSZ electrolyte (∼8 μm), a CGO barrier layer (∼5 μm) and an LSCF–CGO cathode (∼50 μm). Electrochemical characterization included continuous voltage monitoring during the operation, electrochemical impedance spectra and characteristic curves at regular time steps after the first 4000 testing hours, allowing for the determination of the discussed empirical degradation functions. Assuming an isothermal behaviour, 0D-level SIMFC was applied as a simulation tool in view of the small-scale cell and missing microstructural data. Table 2 reports the tested working conditions of the cell, the kinetic parameters with reference ranges and the derived empirical degradation functions for ohmic and polarization contributions dependent on current density, J, in A cm⁻² and time, t, in hours. Note the ohmic term follows the linear proportionality consistent with Ohm’s law. Whereas the polarization overpotential degradation was computed punctually assuming 0.05 A cm⁻² as the current density step ΔJ in differential resistance calculation.

Table 2 Operating conditions, kinetic parameters and degradation functions for a 9000-hour working Ni–YSZ/YSZ/LSCF–CGO cell

Working condition	Anode	Cathode
T [K]	1023	1023
p [atm]	1	1
Flow rate [Nl h^−1]	3.16	22.6
Feed composition	Pure hydrogen	Dry air

---

Kinetic parameter	Anode	Cathode
E act [kJ mol^−1]	100	110
	100–120 as ref. 51	110–160 as ref. 51
Kinetic order α [—]	0.1 for H2 0.1–2 as ref. 52	0.20 for O2 ref. 53
	0.44 for H2O −0.5–1 as ref. 52
γ [A cm^−2]	6 × 10^4	1 × 10^6
	5.5 × 10^4–5.5 × 10^6 as ref. 54	7 × 10^4–7 × 10^6 as ref. 54

---

Degradation function
η deg,ohm [V]	(10^−9t^2 + 2 × 10^−5)J
η deg,pol [V]	(2J^2 + 3J + 1) × 10^−5tΔJ

---

The obtained good match between simulated and experimental voltages validated the proposed approach, suitable as a preliminary study of the cell durability without performing detailed microstructural analysis but only based on common measurements carried out during operation. Both voltage time evolution and characteristic curves show an averaged relative error lower than 2% (Fig. 2). A bit lower accuracy with a still acceptable relative error of 3% characterises OCV conditions (∼1.2 V) which might be due to leakage issues reducing the experimental value. The voltage had a degradation rate of −0.7 V% kh⁻¹, reducing from 0.813 V to 0.763 V. This trend showed a more significant reduction in the first 2000 hours (DR_SOFC higher than −1 V% kh⁻¹), followed by a quite stable operation and then a gradual continuous decrease in the final testing hours. Looking at different kinetic terms, at the nominal state the ohmic loss had the main weight among different overpotentials representing 57% vs. 42% of the activation loss and only 1% of the diffusion loss. Under operation the cell underwent a drastic increase of ohmic contribution, which had a difference of ∼37 mV after 5000 and of ∼49 mV after 9000 h at the reference working condition of 0.5 A cm⁻², representing the 66% of the total losses at the test end. Polarization contribution varied only about some millivolts. This cell aging caused an efficiency reduction of 8% after 9000 h, starting from an initial value of 38% in view of imposed quite low hydrogen utilization.

Fig. 2 Comparison between experimental and simulated voltages looking at the durability test (A) and J–V curve measurements at different operation hours (B) for a 9000-h working Ni–YSZ/YSZ/LSCF–CGO cell.

4. Micro-level cell degradation modelling

4.1 Methodology

Knowing microstructural parameter variations, a more detailed analysis can be performed trying to distinguish the role of different degradation mechanisms in the global cell performance worsening. In this framework, a local-level model is fundamental to evaluate the specific structure changes as a function of local working conditions, such as temperature and gas composition, which have a significant influence on the system behaviour.⁴⁸ Here, starting from the time evolution profiles of microstructural features, the simulation can estimate the overpotential changes and the resulting cell voltage decrease as schematized in Fig. 3. Referring to the most severe degradation processes, a local-level simulation was carried to evaluate the performance failure of an anode supported cell due to anodic Ni agglomeration and Cr poisoning at cathodic active sites in the case of poorly working interconnect barrier layers.⁹ Following both experimental and theoretical observations,^23,55 the agglomeration of the Ni–YSZ electrode was modelled using a power law type formulation (eqn (5)).

r_Niⁿ(t) − r_Niⁿ(t₀) = k(T) × (1 − exp^−λt) (5)

where r_Ni is the Ni radius within the cermet, t is the observation time, and n, k and λ are the empirical parameters (k depends on the temperature).

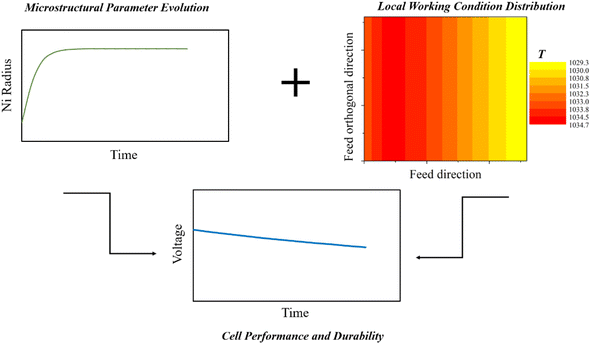Fig. 3 Microscale evaluation of SOFC voltage degradation based on microstructural parameter time evolution and local working condition maps.

Knowing Ni radius time evolution, the consequences on cell behaviour can be evaluated by applying the microscale kinetics formulation presented in Table 1, which expresses the exchange current density J₀, the material conductivity σ and gas diffusion coefficients D^eff as functions of the particle size. As observed in reference studies,^{23,35,40,56,57} the radius increase causes the reduction of the particle surface area, which means a lower contact section between both metal–ceramic particles (i.e., lower catalytic activity and TPB density) and metal–metal, ceramic–ceramic particles (i.e., lower electron and ion conductivity, respectively). Moreover, larger particles influence material porosity also by increasing the pore dimension.

Referring to cathodic degradation processes, LSM–YSZ poisoning is mainly due to electrochemical reactions of gaseous chromium-based compounds which deposit on the active sites. Considering CrO₂(OH)₂ as the vapour phase species with the highest partial pressure in equilibrium with the formed Cr₂O₃ solid phase, p_CrO2(OH)2 was computed according to an empirical correlation showing an Arrhenius-type dependence on the temperature (eqn (6)). Assuming Cr oxidation as a single electrochemically driven process, the current density J_Cr required for this reaction was evaluated by applying the Butler–Volmer equation and it allowed to determine the time evolution profile of cathodic TPB density (eqn (7)), as presented in ref. 58. Since the charge transfer associated with Cr deposition is significantly smaller than the oxygen evolution value, J_Cr can be neglected in the global overpotential calculation.

where K and K′ are constants dependent on Cr₂O₃ physical properties. If Ni agglomeration can also occur without applying a load, Cr deposition is driven by the local cathodic overpotential. Moreover, in this second process the electrode conductivity is less influenced by not varying the particle size and thereby the contact area between them. Nevertheless, the points where LSM and YSZ should interact with the gas mixture are covered preventing oxygen diffusion into the catalytic surface and thereby blocking its electrochemical reduction. In other terms, TPB density decrease occurs as pointed out in ref. [^32,59–61].

4.2 Case study

Advantages of following a microscale approach were underlined in a devoted case study, analysing a commercial size anode supported cell with 80 cm² active area. A current density of 0.4 A cm⁻² was imposed resulting in 70% hydrogen utilization and 16% oxygen utilization. Considering a cell composed of a Ni/YSZ anode (∼250 μm), a YSZ electrolyte (∼8 μm) and an LSM–YSZ oxygen electrode (∼50 μm), Ni particle agglomeration and Cr poisoning were modelled following the methodology proposed in the previous section. Working conditions, electrode microstructure, kinetics parameters and degradation coefficients are reported in Table 3 (note that anodic kinetic values are equal to previous case study values using the same electrocatalytic material). In view of a larger size, the cell was not assumed isothermal; the temperature local gradient was computed on the cell plane to underline the influence on degradation through a sensitivity analysis in a common working range. Note that modelled results referred to an ideal case where only Ni-agglomeration and Cr deposition were considered, here these values could not be validated on reference experimental tests where other mechanisms are also observed, such as interconnect oxidation, electrolyte phase transition, secondary phase formation, crack development and layer delamination.^9,20,62 However, their addition went beyond the aim of this work which wanted to show the relevance of the variable local control in having an effective prediction of commercial-scale cells as well as of the simulation being a support for experimental activities where the isolation of single processes is quite difficult when a full cell is tested.

Table 3 Operating conditions, kinetic and microstructural parameters and degradation model coefficients for 1000-h working Ni–YSZ/YSZ/LSM–YSZ cell simulation

Working condition	Anode	Cathode
T [K]	973–1123	973–1123
p [atm]	1	1
Flow rate [Nl h^−1]	20	200
Feed composition	96/4% vol H2/H2O fed mixture	Air with 0.1% vol of steam

---

Kinetic parameter	Anode	Cathode
E act [kJ mol^−1]	100	120
	100–120 as ref. 51	110–160 as ref. 51
α [—]	0.10 for H2 0.1–2 as ref. 52	0.20 for O2 ref. 53
	0.44 for H2O −0.5–1 as ref: 52
γ′ [mA]	0.26	0.9

---

Microstructural parameter	Anode	Cathode
r [μm]	Ni: 0.4 – YSZ: 0.3	LSM: 0.6 – YSZ: 0.4
	Ref. 63	Ref. 58
Ψ [—]	Ni: 0.53 – YSZ: 0.47	LSM: 0.52 – YSZ: 0.48
	Ref. 63	Ref. 58
φ [—]	0.15 (active layer) – 0.3 (support)	0.3
	Ref. 63	Ref. 58
ξ [-]	4	3
	Ref. 64	Ref. 64

---

Degradation model coefficient
n [—]	5 as ref. 55
k(T) [m^5]	ref. 56
λ [h^−1]	0.001 ref. 56
[h^−1]	70 ref. 58

---

Assuming a 1000-h working cell with a gas inlet temperature of 1023 K at both sides, the simulation allowed the estimation of performance worsening as a function of the Ni particle and Cr deposition increase. In such conditions, the voltage decreased from 0.832 V as the nominal performance value to 0.824 V as the aged status. At both electrodes the main effects were detected looking at the activation overpotential (Fig. 4). Indeed, the particle agglomeration caused ∼7% increase of Ni size, which meant a reduction of catalytic sites (i.e., anodic TPB density decrease of ∼10%) and a resulting ∼10% increase of anodic activation loss. Whereas the consequences on anode conductivity and gas diffusion were less evident. The growth of particles reduced the contact area among them,⁴⁷ increasing the ohmic resistance of ∼18%; however its value was quite low with respect to electrolyte contribution still guaranteeing an effective continuous network for the charge migration within the anode. Ni agglomeration also influenced the pore size and here the gas transport, yet the effects on diffusion overpotential in the studied time interval were negligible. Looking at the cathodic side, Cr poisoning provoked a TPB density decrease of ∼11% resulting in ∼6% increase of cathodic activation overpotential. In the proposed modelling no specific functions were introduced to evaluate the Cr deposition effect on other cathodic losses, however, these resulted quite negligible compared to the activation one looking at previous experimental observations.⁵⁸ In more detail, according to SIMFC local analysis a higher anodic TPB density decrease characterized the inlet section where the temperature was higher due to the faster reaction rate, resulting in more significant Ni particle sizes. Whereas the cathodic term showed an opposite trend since the worst performance occurred at the outlet due to lower temperatures.

Fig. 4 Voltage and activation overpotential variations during 1000 h of working of the Ni–YSZ/YSZ/LSM–YSZ cell at 1023 K as the gas inlet temperature.

The proposed local approach provided not only additional information useful for the local control of cell operation, but also more effective results of global performance for industrial scale systems. Neglecting the temperature gradient on the cell plane underestimated the activation overpotential degradation rates as shown in Fig. 5, where main differences between an isothermal and a non-isothermal cell behaviour are reported for 1023 K and 1123 K anodic and cathodic gas inlet temperatures as examples. According to experimental observations,⁹ the temperature is one of the main degradation source as confirmed by model results where ∼10–15° increase on the cell plane due to the exothermic reaction was sufficient to have a non-negligible higher performance worsening. For instance, on feeding gas at 1123 K, DR_ηact changed from 25 V% kh⁻¹ to 29 V% kh⁻¹ for the anodic side and from 9 V% kh⁻¹ to 10 V% kh⁻¹ for the cathodic side, comparing isothermal and non-isothermal results. At each temperature, more significant anodic variations confirmed the Ni agglomeration process to be more sensitive to temperature than Cr deposition, as discussed in more detail below.

Fig. 5 Degradation rate of activation overpotential because of anodic and cathodic TPB density reduction assuming an isothermal and a non-isothermal Ni–YSZ/YSZ/LSM–YSZ cell working for 1000 h.

In view of the significant role of temperature in degradation processes, a devoted analysis was performed to underline the changes of the Ni–YSZ/YSZ/LSM–YSZ cell behaviour in the common working range. As Table 4 reports, better nominal voltages occurred at high gas inlet temperatures due to lower polarization losses; indeed both catalytic activity and charge migration are thermoactivated mechanisms. Global voltage DR_VSOFC after 1000 h of operation was also slower (remember a negative value means voltage decrease): it was halved varying from 973 K to 1123 K because of better initial performances.

Table 4 Ni–YSZ/YSZ/LSM–YSZ cell performance and the voltage degradation rate after 1000 h of working at variable gas inlet temperatures

Gas inlet temperature [K]	Voltage @ 0 h [V]	DRVSOFC @ 1000 h [V% kh^−1]
973	0.794	−1.07
998	0.815	−1.02
1023	0.832	−0.95
1048	0.845	−0.86
1073	0.854	−0.75
1098	0.860	−0.62
1123	0.861	−0.50

---

Looking at the local performance time evolution, further information was obtained. Fig. 6 shows the maps of the fuel cell produced power P_SOFC, the electric efficiency ε_SOFC and the voltage degradation rate DR_VSOFC computed every 100 h operation. As observed, increasing the inlet temperature allowed for a bit higher electricity production in terms of some watts due to lower overpotentials every time. During operation the degradation caused a gradual power decrease, showing a more evident variation at 973 K compared to 1123 K: ∼271 mW vs. ∼137 mW (Fig. 6A). This lower value derived from the major weight of cathodic overpotential compared to the anodic one using LSM–YSZ as the electrocatalyst. Indeed, the oxygen reduction is limited at the TPB sites showing a higher resistance compared to the Ni–YSZ cermet, different from LSCF and LSCF–CGO where oxygen reduction can also occur directly on the perovskite surface without contacts with the ionic conductor.^14,65 If on one hand a higher temperature favoured Ni agglomeration in view of a thermally activated surface diffusion as the driving mechanism,⁵⁵ on the other hand it slowed down Cr poisoning since the applied cathodic overpotential decrease disadvantages its deposition reaction.⁶⁶ Here, a lower global degradation rate and higher power were observed at 1123 K.

Fig. 6 Ni–YSZ/YSZ/LSM–YSZ cell performance time evolution in terms of the produced power (A), the electric efficiency (B) and the voltage degradation rate (C) at variable inlet gas temperatures assuming 1000 h operation.

According to this trend, the electric efficiency reached its maximum at the 1123 K inlet temperature (i.e., ∼47% at the nominal state) and, however, a quite negligible variation was reported during 1000 h ageing (Fig. 6B), requiring more hours before a visible change of the efficiency.⁷ Also at lower temperatures, ε_SOFC never dropped below ∼42.5% which is a still accepted performance.

Finally, considering the DR_VSOFC time evolution (Fig. 6C), a decreasing trend of absolute values occurred at each temperature condition. After the first 100 h operation the lowest value of −1.28 V% kh⁻¹ was obtained at 973 K, whereas it changed until −0.93 V% kh⁻¹ in the final 100 hours. This trend was observed also at higher temperatures (−1.12 V% kh⁻¹vs. −0.70 V% kh⁻¹ and −0.76 V% kh⁻¹vs. −0.35 V% kh⁻¹ at gas inlet temperatures of 1048 K and 1123 K, respectively). The slowdown was correlated to the asymptotic growth of the Ni particle size which was characterized by a rapid increase within the first working hours and then stabilized to an asymptotic value due to the inhibiting effect of the YSZ backbone, since the YSZ percentage was sufficiently high to guarantee a good percolated network.⁶⁷ This stabilization for long-term operation was also observed for Ni–YSZ based cells in ref. 68. Moreover, the degradation rate value reduction was faster at higher working temperatures: ∼54% at 1123 K vs. ∼31% at 998 K. As observed, the anodic agglomeration had a major influence at higher temperatures due to the slowdown of the Cr deposition mechanism.

Looking now at the specific electrode performance to better understand previously discussed results on the global cell behaviour, both Ni agglomeration and Cr poisoning provoked TPB density decrease: in the first case for the reduction of the contact area between anodic particles, in the second for Cr deposition on the cathodic active sites. Nevertheless, different dependences on temperature and time evolution were underlined (Fig. 7). Indeed, the Ni particle size growth is a strongly thermoactivated process driven by vacancy diffusion from larger into smaller particles: here an increase of just ∼4% was computed after 1000 h at 973 K, whereas it reached ∼17% at 1123 K. This caused a more significant l_TPB decrease at higher temperatures, changing from the reference structure of 3.11 μm⁻² to 2.4 μm⁻² at 1123 K compared to 2.9 μm⁻² at 973 K (Fig. 7A). Similar trends were reported for the active layer of anode supported cells in ref. 23, where TPB density reduction differed more than 1.5 μm⁻² from 1023 K to 1123 K in performed durability tests. Consequently, the anodic activation overpotential variation was more highlighted by increasing working temperatures overcoming already ∼20% after 500 h and ∼29% after 1000 h. Whereas it never exceeded the 10% in the range between 973 K and 1023 K (Fig. 8A). In view of Ni asymptotic growth as previously discussed (eqn (5)), the degradation was faster in the initial working hours, whereas it slowed down after 600–700 h. Looking at the cathode behaviour, the opposite trend is visible: TPB density reduction occurred mainly at low temperatures decreasing of ∼0.16 μm⁻² at 973 K vs. ∼0.08 μm⁻² at 1123 K (Fig. 7B). In theory, Cr volatilization is favoured at temperature rise resulting in higher CrO₂(OH)₂ partial pressures (eqn (6)), for instance 7.4 × 10⁻⁹ atm at 998 K vs. 1.6 × 10⁻⁸ atm at 1123 K. Devoted tests on stainless steel interconnects confirmed a higher evaporated Cr amount at 1123 K with respect to 923 K.⁶⁹ Nevertheless, simultaneously a higher temperature increases the exchange current density (Table 1) and here the local cathodic activation loss decreases (eqn (7)), becoming the predominant contribution for Cr deposition process, as confirmed in previous references for the LSM–YSZ electrode.^60,66 Looking at the cathodic activation overpotential variation (Fig. 8B), a more homogeneous map was obtained due to a lower discussed thermal dependence. Moreover, a quite proportional increase is visible along 1000 h operation with higher variations in the final hours in agreement with trends observed experimentally.^70,71

Fig. 7 Ni–YSZ/YSZ/LSM–YSZ electrode performance time evolution in terms of TPB density for anodic (A) and cathodic (B) sides at variable gas inlet temperatures assuming 1000 h operation.

Fig. 8 Ni–YSZ/YSZ/LSM–YSZ electrode performance time evolution in terms of activation overpotential variation for anodic (A) and cathodic (B) sides at variable gas inlet temperatures assuming 1000 h operation.

5. Conclusions

A multiscale approach results in an effective solution to study solid oxide fuel cell performance and durability for both experimental and, above all, simulation activities. Indeed, it allows the choice of the most proper model dimension as a function of the investigation goal as well as of the system scale, moving from few centimetres in laboratory tests to the industrial size. Moreover, depending on the cell characterization available information, different levels of study can be applied into electrochemical kinetics formulation and degradation functions.

In this framework, in-home built SIMFC (SIMulation of Fuel Cells) was proposed as an effective tool resulting in one of the few available models comprehensive of all discussed features. Its potentialities were presented with reference to devoted case studies providing clear examples of its possible uses. For a preliminary analysis of cell durability, empirical correlations as a function of the applied load and time were derived by looking at the electrochemical impedance spectrum and J–V curve variations. Here, the weight of different overpotentials was evaluated by identifying the main sources of the global performance drop, as shown in the proposed case study on a 9000-h working anode supported cell. Whereas, knowing microstructural features, models specific for each degradation mechanism were applied and then correlated to kinetic parameters such as TPB density, conductivity and diffusivity coefficient. This more detailed approach is needful for industrial scale applications in view of working-condition-significant local gradients which have a relevant influence on degradation development. Considering temperature-dependent processes such as Ni agglomeration and Cr deposition reducing TPB density above all, neglecting local gradients predicted wrong activation losses of aged samples. This was more evident for the anodic contribution (error of ∼4% after 1000 h operation) since a high temperature promotes the particle growth. Whereas Cr deposition is less sensitive to temperature changes, achieving an activation overpotential variation of ∼5–7% at most.

Note that, after a proper tuning of the specific studied system, the proposed macroscale model approach is already ready to simulate the global cell behaviour and durability. Whereas in the microscale model approach two of the main degradation causes (i.e., Ni agglomeration and Cr deposition) were only considered as examples. Following steps could focus on including further degradation mechanisms, after specific ex situ experimental campaigns where the behaviour of single layers is underlined. Indeed, in view of model robustness the computational time would not vary. A more challenging task consists of formulating degradation functions to predict domino effects, namely the correlations among different processes that can enhance or inhibit each other. Since the literature is quite scarce, an ad hoc design of the experiment would be projected, including both electrochemical and microstructural characterization of the cell to have appropriate information for modelling activities.

Author contributions

Bosio: conceptualization, methodology, software, and writing – review & editing; Bianchi: conceptualization, methodology, software, validation, visualization, writing – original draft, and writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research has received funding from the Fuel Cells and Hydrogen 2 Joint Undertaking (now Clean Hydrogen Partnership) under Grant Agreement no. 825027 (AD ASTRA project). This Joint Undertaking received support from the European Union's Horizon 2020 Research and Innovation program and Hydrogen Europe and Hydrogen Europe Research. The authors thank Daria Vladikova and her group for providing data on the 9000 h durability test used in the macroscale approach discussion.

Notes and references

1. Solid Oxide Fuel Cells: materials properties and performance, ed. J. Fergus, R. Hui, X. Li, D. P. Wilkinson and J. Zhang, CRC Press, 2019, ISBN: 978-0-367-38643-6.
2. Fuel Cell Handbook, ed. EG&G Technical Services, Inc, U.S. Department of Energy, Office of Fossil Energy, National Energy Technology Laboratory, Seventh Edition, 2004, ISBN: 9781365101137.
3. S. J. McPhail, J. Kiviaho, B. Conti, The yellow pages of SOFC technology, International Status of SOFC deployment, VTT Tech Res Cent Finl, 2017, p. 34.
4. J. Rechberger, A. Kaupert, J. Hagerskans and L. Blum, Demonstration of the First European SOFC APU on a Heavy Duty Truck, Transp. Res. Proc., 2016, 14, 3676–3685.
5. Sunfire, 50 kW SOFC for ship-integrated fuel cell project in Germany, Fuel Cells Bull., 2015, 2015(11), 3–4,  DOI:10.1016/S1464-2859(15)30337-0.
6. e-Bio Fuel Cell, cited 2022 Jun 7, available from: https://www.nissan-global.com/EN/INNOVATION/TECHNOLOGY/ARCHIVE/E_BIO_FUEL_CELL/.
7. F. R. Bianchi and B. Bosio, Operating Principles, Performance and Technology Readiness Level of Reversible Solid Oxide Cells, Sustainability, 2021, 13(9), 4777,  DOI:10.3390/su13094777.
8. Fuel cells: data, facts and figures, ed. Stolten D, Samsun RC and Garland N, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2016, p. 391.
9. S. J. McPhail, S. Frangini, J. Laurencin, E. Effori, A. Abaza and A. K. Padinjarethil, et al., Addressing planar solid oxide cell degradation mechanisms: A critical review of selected components, Electrochem. Sci. Adv., 2021, 2(5), e2100024,  DOI:10.1002/elsa.202100024.
10. Y. Liu, Z. Shao, T. Mori and S. P. Jiang, Development of nickel based cermet anode materials in solid oxide fuel cells – Now and future, MRE, 2021, 1(1), 100003,  DOI:10.1016/j.matre.2020.11.002.
11. M. Z. Khan, M. T. Mehran, R. H. Song, J. W. Lee, S. B. Lee and T. H. Lim, A simplified approach to predict performance degradation of a solid oxide fuel cell anode, J. Power Sources, 2018, 391, 94–105,  DOI:10.1016/j.jpowsour.2018.04.080.
12. A. Faes, A. Hessler-Wyser, A. Zryd and J. Van herle, A Review of RedOx Cycling of Solid Oxide Fuel Cells Anode, Membranes, 2012, 2(3), 585–664,  DOI:10.3390/membranes2030585.
13. M. B. Mogensen, M. Chen, H. L. Frandsen, C. Graves, A. Hauch and P. V. Hendriksen, et al., Ni migration in solid oxide cell electrodes: Review and revised hypothesis, Fuel Cells, 2021, 202100072,  DOI:10.1002/fuce.202100072.
14. J. Laurencin, M. Hubert, K. Couturier, T. L. Bihan, P. Cloetens and F. Lefebvre-Joud, et al., Reactive Mechanisms of LSCF Single-Phase and LSCF–CGO Composite Electrodes Operated in Anodic and Cathodic Polarisations, Electrochim. Acta, 2015, 174, 1299–1316,  DOI:10.1016/j.electacta.2015.06.080.
15. T. Matsui, S. Li, Y. Inoue, N. Yoshida, H. Muroyama and K. Eguchi, Degradation Analysis of Solid Oxide Fuel Cells with (La,Sr)(Co,Fe)O_3−δ Cathode/Gd₂O₃–CeO₂ Interlayer/Y₂O₃–ZrO₂ Electrolyte System: The Influences of Microstructural Change and Solid Solution Formation, J. Electrochem. Soc., 2019, 166(4), F295–F300,  DOI:10.1149/2.0841904jes.
16. F. Monaco, D. Ferreira-Sanchez, M. Hubert, B. Morel, D. Montinaro and D. Grolimund, et al., Oxygen electrode degradation in solid oxide cells operating in electrolysis and fuel cell modes: LSCF destabilization and interdiffusion at the electrode/electrolyte interface, Int. J. Hydrogen Energy, 2021, 46(62), 31533–31549,  DOI:10.1016/j.ijhydene.2021.07.054.
17. Y. Chen, S. Yoo, X. Li, D. Ding, K. Pei and D. Chen, et al., An effective strategy to enhancing tolerance to contaminants poisoning of solid oxide fuel cell cathodes, Nano Energy, 2018, 47, 474–480,  DOI:10.1016/j.nanoen.2018.03.043.
18. G. Ghiara, P. Piccardo, V. Bongiorno, C. Geipel and R. Spotorno, Characterization of Metallic Interconnects Extracted from Solid Oxide Fuel Cell Stacks Operated up to 20,000 h in Real Life Conditions: The Air Side, Energies, 2020, 13(24), 6487,  DOI:10.3390/en13246487.
19. R. Spotorno, F. R. Bianchi, D. Paravidino, B. Bosio and P. Piccardo, Test and Modelling of Solid Oxide Fuel Cell Durability: A Focus on Interconnect Role on Global Degradation, Energies, 2022, 15(8), 2762,  DOI:10.3390/en15082762.
20. L. Barelli, E. Barluzzi and G. Bidini, Diagnosis methodology and technique for solid oxide fuel cells: A review, Int. J. Hydrogen Energy, 2013, 38(12), 5060–5074,  DOI:10.1016/j.ijhydene.2013.02.024.
21. L. Blum, Q. Fang, S. M. Groß-Barsnick, L. G. J. (Bert) de Haart, J. Malzbender, N. H. Menzler and W. J. Quadakkers, Long-term operation of solid oxide fuel cells and preliminary findings on accelerated testing, Int. J. Hydrogen Energy, 2020, 45(15), 8955–8964,  DOI:10.1016/j.ijhydene.2020.01.074.
22. L. Holzer, B. Iwanschitz, T. Hocker, B. Münch, M. Prestat, D. Wiedenmann, U. Vogt, P. Holtappels, J. Sfeir, A. Mai and T. Graule, Microstructure degradation of cermet anodes for solid oxide fuel cells: Quantification of nickel grain growth in dry and in humid atmospheres, J. Power Sources, 2011, 196(3), 1279–1294,  DOI:10.1016/j.jpowsour.2010.08.017.
23. F. Monaco, M. Hubert, J. Vulliet, J. P. Ouweltjes, D. Montinaro, P. Cloetens, P. Piccardo, F. Lefebvre-Joud and J. Laurencin, Degradation of Ni–YSZ Electrodes in Solid Oxide Cells: Impact of Polarization and Initial Microstructure on the Ni Evolution, J. Electrochem. Soc., 2019, 166(15), F1229–F1242,  DOI:10.1149/2.126195jes.
24. Y. S. Chou, J. W. Stevenson and J. P. Choi, Long-term evaluation of solid oxide fuel cell candidate materials in a 3-cell generic short stack fixture, part I: Test fixture, sealing, and electrochemical performance, J. Power Sources, 2014, 255, 1–8,  DOI:10.1016/j.jpowsour.2013.12.067.
25. A. Ido, K. Asano, H. Morita, T. Yamamoto and Y. Mugikura, Degradation Analysis of SOFC Performance (1) — Severe Operation with High Fuel Utilization, ECS Trans., 2019, 91(1), 801–808,  DOI:10.1149/09101.0801ecst.
26. N. H. Menzler, D. Sebold, Y. J. Sohn and S. Zischke, Post-test characterization of a solid oxide fuel cell after more than 10 years of stack testing, J. Power Sources, 2020, 478, 228770,  DOI:10.1016/j.jpowsour.2020.228770.
27. P. Priya and N. R. Aluru, A multiscale framework to predict electrochemical characteristics of yttrium doped Barium Zirconate based solid oxide cells, J. Power Sources, 2021, 481, 228969,  DOI:10.1016/j.jpowsour.2020.228969.
28. D. Chen, H. Wang, S. Zhang, M. O. Tade, Z. Shao and H. Chen, Multiscale model for solid oxide fuel cell with electrode containing mixed conducting material, AIChE J., 2015, 61(11), 3786–3803,  DOI:10.1002/aic.14881.
29. M. Mozdzierz, K. Berent, S. Kimijima, J. S. Szmyd and G. Brus, A Multiscale Approach to the Numerical Simulation of the Solid Oxide Fuel Cell, Catalysts, 2019, 9(3), 253,  DOI:10.3390/catal9030253.
30. E. Da Rosa Silva, M. Hubert, B. Morel, H. Moussaoui, J. Debayle and J. Laurencin, A Dynamic Multi-Scale Model for Solid Oxide Cells Validated on Local Current Measurements: Impact of Global Cell Operation on the Electrodes Reaction Mechanisms, ECS Trans., 2021, 103(1), 893–907,  DOI:10.1149/10301.0893ecst.
31. M. Hubert, J. Laurencin, P. Cloetens, B. Morel, D. Montinaro and F. Lefebvre-Joud, Impact of Nickel agglomeration on Solid Oxide Cell operated in fuel cell and electrolysis modes, J. Power Sources, 2018, 397, 240–251,  DOI:10.1016/j.jpowsour.2018.06.097.
32. A. Nakajo, P. Tanasini, S. Diethelm, J. Van herle and D. Favrat, Electrochemical Model of Solid Oxide Fuel Cell for Simulation at the Stack Scale II: Implementation of Degradation Processes, J. Electrochem. Soc., 2011, 158(9), B1102,  DOI:10.1149/1.3596435.
33. D. Monceau and B. Pieraggi, Determination of Parabolic Rate Constants from a Local Analysis of Mass-Gain Curves, Oxid. Met., 1998, 50(5/6), 477–493,  DOI:10.1023/A:1018860909826.
34. N. M. Tikekar, T. J. Armstrong and A. V. Virkar, Reduction and Reoxidation Kinetics of Nickel-Based SOFC Anodes, J. Electrochem. Soc., 2006, 153(4), A654,  DOI:10.1149/1.2167949.
35. H. Moussaoui, R. K. Sharma, J. Debayle, Y. Gavet, G. Delette and J. Laurencin, Microstructural correlations for specific surface area and triple phase boundary length for composite electrodes of solid oxide cells, J. Power Sources, 2019, 412, 736–748,  DOI:10.1016/j.jpowsour.2018.11.095.
36. H. Moussaoui, A. Nakajo, G. Rinaldi, M. Hubert, J. Laurencin and J. Van Herle, Modeling Nickel Microstructural Evolution in Ni–YSZ Electrodes Using a Mathematical Morphology Approach, ECS Trans., 2021, 103(1), 997–1009,  DOI:10.1149/10301.0997ecst.
37. M. Gallo, P. Polverino, J. Mougin, B. Morel and C. Pianese, Coupling electrochemical impedance spectroscopy and model-based aging estimation for solid oxide fuel cell stacks lifetime prediction, Appl. Energy, 2020, 279, 115718,  DOI:10.1016/j.apenergy.2020.115718.
38. A. Staffolani, A. Baldinelli, L. Barelli, G. Bidini and F. Nobili, Early-Stage Detection of Solid Oxide Cells Anode Degradation by Operando Impedance Analysis, Processes, 2021, 9(5), 848,  DOI:10.3390/pr9050848.
39. Z. Li, H. Zhang, H. Xu and J. Xuan, Advancing the multiscale understanding on solid oxide electrolysis cells via modelling approaches: A review, Renewable Sustainable Energy Rev., 2021, 141, 110863,  DOI:10.1016/j.rser.2021.110863.
40. P. Polverino, M. Gallo and C. Pianese, Development of mathematical transfer functions correlating Solid Oxide Fuel Cell degradation to operating conditions for Accelerated Stress Test protocols design, J. Power Sources, 2021, 491, 229521,  DOI:10.1016/j.jpowsour.2021.229521.
41. O. Babaie Rizvandi, X. Y. Miao and H. L. Frandsen, Multiscale modeling of degradation of full solid oxide fuel cell stacks, Int. J. Hydrogen Energy, 2021, 46(54), 27709–27730,  DOI:10.1016/j.ijhydene.2021.05.204.
42. E. Audasso, B. Bosio and S. Nam, Extension of an effective MCFC kinetic model to a wider range of operating conditions, Int. J. Hydrogen Energy, 2016, 41(12), 5571–5581,  DOI:10.1016/j.ijhydene.2015.10.152.
43. B. Conti, B. Bosio, S. J. McPhail, F. Santoni, D. Pumiglia and E. Arato, A 2-D model for Intermediate Temperature Solid Oxide Fuel Cells Preliminarily Validated on Local Values, Catalysts, 2019, 9(1), 36,  DOI:10.3390/catal9010036.
44. F. R. Bianchi, A. Baldinelli, L. Barelli, G. Cinti, E. Audasso and B. Bosio, Multiscale Modeling for Reversible Solid Oxide Cell Operation, Energies, 2020, 13(19), 5058,  DOI:10.3390/en13195058.
45. A. K. Padinjarethil, F. R. Bianchi, B. Bosio and A. Hagen, Electrochemical Characterization and Modelling of Anode and Electrolyte Supported Solid Oxide Fuel Cells, Front. Energy Res., 2021, 9, 668964,  DOI:10.3389/fenrg.2021.668964.
46. F. R. Bianchi, B. Bosio, A. Baldinelli and L. Barelli, Optimization of a Reference Kinetic Model for Solid Oxide Fuel Cells, Catalysts, 2020, 10(1), 104,  DOI:10.3390/catal10010104.
47. D. Chen, W. Bi, W. Kong and Z. Lin, Combined micro-scale and macro-scale modeling of the composite electrode of a solid oxide fuel cell, J. Power Sources, 2010, 195(19), 6598–6610,  DOI:10.1016/j.jpowsour.2010.04.065.
48. F. R. Bianchi, R. Spotorno, P. Piccardo and B. Bosio, Solid Oxide Fuel Cell Performance Analysis through Local Modelling, Catalysts, 2020, 10(5), 519,  DOI:10.3390/catal10050519.
49. Z. B. Stoynov, D. E. Vladikova, B. G. Burdin, J. Laurencin, D. Montinaro, A. Nakajo, P. Piccardo, A. Thorel, M. Hubert, R. Spotorno and A. Chesnaud, Differential Resistance Analysis – a New Tool for Evaluation of Solid Oxide Fuel Cells Degradation, MRS Adv., 2017, 2(64), 3991–4003,  DOI:10.1557/adv.2017.592.
50. Z. Stoynov, D. Vladikova, B. Burdin, J. Laurencin, D. Montinaro, G. Raikova, G. Schiller and P. Szabo, Differential analysis of SOFC current-voltage characteristics, Appl. Energy, 2018, 228, 1584–1590,  DOI:10.1016/j.apenergy.2018.06.138.
51. F. Zabihian and A. S. Fung, Macro-level modeling of solid oxide fuel cells, approaches, and assumptions revisited, J. Renewable Sustainable Energy, 2017, 9(5), 054301,  DOI:10.1063/1.5006909.
52. T. Yonekura, Y. Tachikawa, T. Yoshizumi, Y. Shiratori, K. Ito and K. Sasaki, Exchange Current Density of Solid Oxide Fuel Cell Electrodes, ECS Trans., 2019, 35(1), 1007–1014,  DOI:10.1149/1.3570081.
53. H. Okamoto, G. Kawamura and T. Kudo, Study of oxygen adsorption on platinum through observation of exchange current in a solid electrolyte concentration cell, Electrochim. Acta, 1983, 28(3), 379–382,  DOI:10.1016/0013-4686(83)85137-8.
54. A. Leonide, Y. Apel and E. Ivers-Tiffee, SOFC Modeling and Parameter Identification by Means of Impedance Spectroscopy, ECS Trans., 2009, 19(20), 81–109,  DOI:10.1149/1.3247567.
55. S. Gao, J. Li and Z. Lin, Theoretical model for surface diffusion driven Ni-particle agglomeration in anode of solid oxide fuel cell, J. Power Sources, 2014, 255, 144–150,  DOI:10.1016/j.jpowsour.2014.01.033.
56. J. Zhu and Z. Lin, Degradations of the electrochemical performance of solid oxide fuel cell induced by material microstructure evolutions, Appl. Energy, 2018, 231, 22–28,  DOI:10.1016/j.apenergy.2018.09.127.
57. A. Faes, A. Hessler-Wyser, D. Presvytes, C. G. Vayenas and J. Van herle, Nickel-Zirconia Anode Degradation and Triple Phase Boundary Quantification from Microstructural Analysis, Fuel Cells, 2010, 10(2), 325,  DOI:10.1002/fuce.200800147.
58. K. Miyoshi, H. Iwai, M. Kishimoto, M. Saito and H. Yoshida, Chromium poisoning in (La,Sr)MnO₃ cathode: Three-dimensional simulation of a solid oxide fuel cell, J. Power Sources, 2016, 326, 331–340,  DOI:10.1016/j.jpowsour.2016.06.110.
59. T. Horita, D. H. Cho, F. Wang, T. Shimonosono, H. Kishimoto, K. Yamaji, M. E. Brito and H. Yokokawa, Correlation between degradation of cathode performance and chromium concentration in (La,Sr)MnO₃ cathode, Solid State Ionics, 2012, 225, 151–156,  DOI:10.1016/j.ssi.2012.02.048.
60. J. J. Bentzen, J. V. T. HÃgh, R. Barfod and A. Hagen, Chromium Poisoning of LSM/YSZ and LSCF/CGO Composite Cathodes, Fuel Cells, 2009, 9(6), 823–832,  DOI:10.1002/fuce.200800143.
61. E. Konysheva, J. Mertens, H. Penkalla, L. Singheiser and K. Hilpert, Chromium Poisoning of the Porous Composite Cathode, J. Electrochem. Soc., 2007, 154(12), B1252,  DOI:10.1149/1.2784197.
62. P. Moçoteguy and A. Brisse, A review and comprehensive analysis of degradation mechanisms of solid oxide electrolysis cells, Int. J. Hydrogen Energy, 2013, 38(36), 15887–15902,  DOI:10.1016/j.ijhydene.2013.09.045.
63. A. K. Padinjarethil, F. R. Bianchi, B. Bosio and A. Hagen, Degradation of Ni–YSZ and Ni–GDC fuel cells after 1000 h operation: Analysis of different overpotential contributions according to electrochemical and microstructural characterization, E3S Web Conf., 2022, 334, 04011,  DOI:10.1051/e3sconf/202233404011.
64. K. J. Yoon, S. Gopalan and U. B. Pal, Analysis of Electrochemical Performance of SOFCs Using Polarization Modeling and Impedance Measurements, J. Electrochem. Soc., 2009, 156(3), B311,  DOI:10.1149/1.3046158.
65. E. Effori, J. Laurencin, E. D. R. Silva, M. Hubert, T. David, M. Petitjean, G. Geneste, L. Dessemond and E. Siebert, An Elementary Kinetic Model for the LSCF and LSCF–CGO Electrodes of Solid Oxide Cells: Impact of Operating Conditions and Degradation on the Electrode Response, J. Electrochem. Soc., 2021, 168(4), 044520,  DOI:10.1149/1945-7111/abf40a.
66. S. Taniguchi, M. Kadowaki, H. Kawamura, T. Yasuo, Y. Akiyama, Y. Miyake and T. Saitoh, Degradation phenomena in the cathode of a solid oxide fuel cell with an alloy separator, J. Power Sources, 1995, 55(1), 73–79,  DOI:10.1016/0378-7753(94)02172-Y.
67. D. Chen, Z. Lin, H. Zhu and R. J. Kee, Percolation theory to predict effective properties of solid oxide fuel-cell composite electrodes, J. Power Sources, 2009, 191(2), 240–252,  DOI:10.1016/j.jpowsour.2009.02.051.
68. F. Monaco, M. Hubert, J. Vulliet, D. Montinaro, J. P. Ouweltjes, P. Cloetens, F. Lefebvre-Joud and J. Laurencin, Impact of Microstructure and Polarization on the Degradation of Ni–YSZ Electrode: An Experimental and Modeling Approach, ECS Trans., 2019, 91(1), 653–664,  DOI:10.1149/09101.0653ecst.
69. R. Spotorno, D. Paravidino, S. Delsante and P. Piccardo, Volatilization of chromium from AISI 441 stainless steel: Time and temperature dependence, Surf. Coat. Technol., 2022, 433, 128125,  DOI:10.1016/j.surfcoat.2022.128125.
70. X. Chen, Y. Zhen, J. Li and S. P. Jiang, Chromium deposition and poisoning in dry and humidified air at (La_0.8Sr_0.2)_0.9MnO₃+ cathodes of solid oxide fuel cells, Int. J. Hydrogen Energy, 2010, 35(6), 2477–2485,  DOI:10.1016/j.ijhydene.2009.12.185.
71. Y. Matsuzaki and I. Yasuda, Dependence of SOFC Cathode Degradation by Chromium-Containing Alloy on Compositions of Electrodes and Electrolytes, J. Electrochem. Soc., 2001, 148(2), A126,  DOI:10.1149/1.1339869.

---