Triplet quenching pathway control with molecular dyads enables the identification of a highly oxidizing annihilator class

Abstract

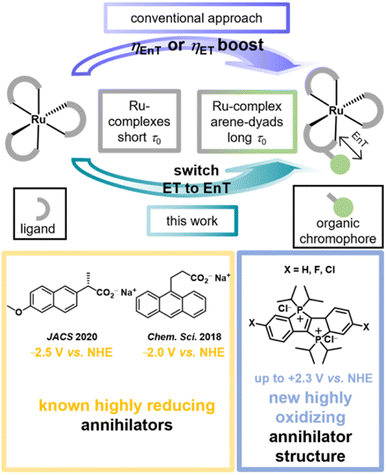
Metal complex – arene dyads typically act as more potent triplet energy donors compared to their parent metal complexes, which is frequently exploited for increasing the efficiencies of energy transfer applications. Using unexplored dicationic phosphonium-bridged ladder stilbenes (P–X²⁺) as quenchers, we exclusively observed photoinduced electron transfer photochemistry with commercial organic photosensitizers and photoactive metal complexes. In contrast, the corresponding pyrene dyads of the tested ruthenium complexes with the very same metal complex units efficiently sensitize the P–X²⁺ triplets. The long-lived and comparatively redox-inert pyrene donor triplet in the dyads thus provides an efficient access to acceptor triplet states that are otherwise very tricky to obtain. This dyad-enabled control over the quenching pathway allowed us to explore the P–X²⁺ photochemistry in detail using laser flash photolysis. The P–X²⁺ triplet undergoes annihilation producing the corresponding excited singlet, which is an extremely strong oxidant (+2.3 V vs. NHE) as demonstrated by halide quenching experiments. This behavior was observed for three P²⁺ derivatives allowing us to add a novel basic structure to the very limited number of annihilators for sensitized triplet–triplet annihilation in neat water.

---

Introduction

The excitation energies and (excited-)state redox properties of photoactive metal complexes can be tuned over wide windows by ligand modifications.^1–10 This modularity allows the preparation of tailor-made photocatalysts or photosensitizers for a given light-driven application. It seems natural to assume that even more pronounced changes in photoreactivity are within reach when so-called molecular dyads or bichromophores are employed, in which metal complexes are covalently linked with organic chromophores.^11–14 In such dyads the beneficial properties of both inorganic and organic photoactive compounds are frequently combined, e.g. visible-light absorptivity and quantitative intersystem crossing of the former and long-lived triplet states of the latter.^15–18 Furthermore, the organic chromophores (OC) can possess completely different redox properties than the metal complexes (MC)¹⁹ such that dyads with lowest excited states that are OC-centered offer more pronounced variations of the photoredox properties than those obtained by conventional ligand modification. This extended photoredox and triplet reactivity control for selective photoreactions with molecular dyads is underexplored, presumably because most studies have focused on inherent photophysical dyad properties.

Most MC-OC dyads known to date are based on ruthenium complexes with covalently connected aromatic hydrocarbons (arenes),^15,16,20 but there are also many examples with other 4d/5d (ref. 21–23) and even some dyads with non-precious 3d (ref. 24–26) metals. Dyads of the type MC-OC have been successfully employed for increasing the energy transfer (EnT)^20,27 or electron transfer (ET)^28–32 reactivity compared to conventional metal complexes (see Fig. 1). The long-lived triplet states of these monometallic dyads have been successfully exploited for sensing³³ and imaging³⁴ applications, photodynamic therapy,³⁵ photon upconversion^36–40 and, in some cases, for photocatalytic key reaction steps.^{27,28,31,32,41} Despite the popularity of these compounds it seems that relatively easily accessible dyads have a hidden application potential in controlling the quenching pathway and the bimolecular photoreactivity. The above-mentioned triplet lifetime increase that is accessible in well-designed dyads is of particular importance for systems in which the energy or electron acceptor concentration is inherently low. This holds true for annihilators in aqueous photon upconversion (UC) systems. The first bimolecular photoreaction in a sensitized triplet–triplet annihilation upconversion pair is an EnT between the excited sensitizer (usually in a triplet state)⁴² and the annihilator molecule in its ground state. Only a few annihilator structures for UC in neat water have been identified so far.^27,43–46 In addition to solubility, aggregation or excimer formation issues, one main reason for this situation is that highly polar water as the solvent favors ET over EnT reactions owing to the stabilization of (radical) ions.^43,45

As we will show using laser flash photolysis (LFP) as key method, the reduced redox reactivity of arene-localized triplets produced in a water-soluble Ru-containing dyad previously developed in one of our groups enables selective EnT quenching, whereas the parent Ru complexes exclusively operate via ET under otherwise identical conditions (Fig. 1). This dyad-induced quenching pathway switch allowed us to identify a novel annihilator class − the recently discovered dicationic phosphonium-bridged ladder stilbenes (P–X²⁺)⁴⁷ − with unmatched properties for aqueous upconversion. This compound class with previously unknown triplet photochemistry is not only sufficiently water-soluble but it has also very high emission quantum yields. These properties are highly beneficial for (aqueous) photon upconversion systems^48–52 and we speculate that the bulky iso-propyl groups prevent the formation of undesired excimers⁵³ during the triplet–triplet annihilation (TTA) step. Two dyads, three reference complexes and three P–X²⁺ derivatives are analyzed in detail to establish the reactivity switch approach and the novel annihilator class with some generality. While the previously known aqueous annihilators are strong photoreductants (lower part of Fig. 1),^44,45 initial photoreactivity studies of the singlet-excited P–X²⁺ annihilators show that they are strong photooxidants with excited-state reduction potentials of up to +2.3 V vs. NHE and sufficiently long lifetimes for bimolecular reactions. This unique combination could result in novel photooxidation applications in water.

Fig. 1 Triplet lifetime elongation in molecular dyads with covalently connected organic chromophores is well established to increase the efficiency of energy or electron transfer (η_EnT or η_ET) reactions. In this work, switching of the quenching mechanism when comparing dyad and parent ruthenium complex was observed and exploited for the identification of the first highly oxidizing annihilator in water.

Results and discussion

The annihilators P–X²⁺ (X = H, Cl, F) were synthesized as described in Fig. 2. Employing appropriately substituted 2,2′-dibromotolanes as starting materials, the corresponding dilithiated intermediates were generated in situ via bromine–lithium exchange, which proceeds smoothly upon treatment with n-BuLi at −20 °C. The resulting intermediates were quenched with chloro di(iso-propyl)phosphine at −40 °C to afford the required diphosphinotolane precursors (prec-P–X). For the unsubstituted derivative (X = H), prec-X–H and the target compound P–H²⁺ have been reported previously,⁴⁷ but a significantly more complicated synthesis of P–H²⁺ (starting from prec-X–H) has been employed originally. In our first report,⁴⁷ P–H²⁺ was prepared using a three-step approach via (i) twofold cyclization of prec-P–H followed by (ii) a one-electron oxidation step to afford a radical cation and (iii) a second one-electron oxidation step. Here, it is shown that these three steps can be combined to a one-pot procedure using hexachloroethane (C₂Cl₆) as an oxidant (see Fig. 2). Only tetrachloroethylene (C₂Cl₄) is generated as by-product, while the products (P–X²⁺) precipitate from the reaction mixture. All three derivatives were characterized comprehensively (see ESI for details, Sections S2 and S4†), not only NMR spectroscopically in D₂O solution, but also via single crystal X-ray diffraction in the solid state. The dicationic core in P–X²⁺ (X = H, Cl, F) is basically isostructural in all three compounds, although a different stacking pattern (see ESI† for additional ORTEP plots) is observed in P–F²⁺ (brick layer stacking) in comparison to P–H²⁺ and P–Cl²⁺ (herringbone stacking), which may be related to the nature of the co-crystallized solvent (P–F²⁺: MeOH, P–H²⁺ and P–Cl²⁺: H₂O). Hence, all compounds were finely ground and rigorously dried (i.e. the co-crystallized solvents were removed) prior to the photochemical studies.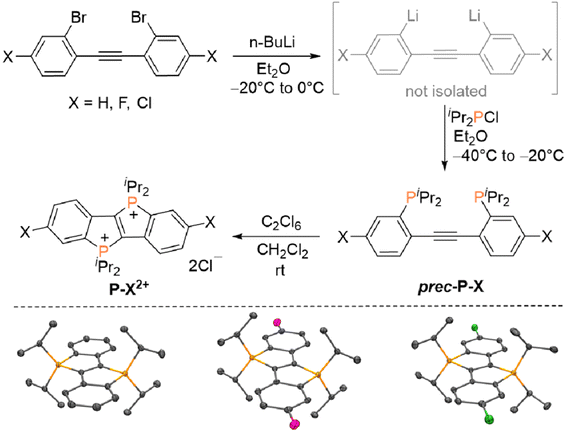

Fig. 2 Top: Synthesis of annihilators P–H²⁺, P–F²⁺ and P–Cl²⁺ (X = H, Cl, F). Bottom: ORTEP plots of the dications in P–H²⁺, P–F²⁺ and P–Cl²⁺ (hydrogen atoms, Cl⁻ counter ions and co-crystallized solvents omitted for clarity, see ESI† for details).

Initial UV/vis absorption studies in neutral air-saturated water indicated the decomposition of all P–X²⁺ derivatives on a timescale of several hours. However, as we found, P–X²⁺ solutions that are acidified with H₂SO₄ (50 mM) are bench-stable allowing us to reliably investigate their photophysical and photochemical properties. Calibrated UV/vis absorption and normalized emission spectra of the annihilators in this medium are summarized in Fig. 3 (right part). All derivatives have an intense long-wavelength absorption band in the violet/blue spectral region, while they show greenish emission with lifetimes on the order of 15 ns in argon-saturated solution. The energy of the first excited singlet is lower for the halogen-substituted derivatives by 0.10 eV to 0.15 eV compared to the parent compound (P–H²⁺). All derivatives are excellent emitters with fluorescence quantum yields approaching 90%, making them an ideal candidate for a potential annihilator chromophore. Control experiments with freshly prepared solutions in neat MilliQ water at pH ∼ 7 established that H₂SO₄ does not affect the photophysical properties. In welcome contrast, the kinetic salt effect resulting from the H₂SO₄ dissociation products is regarded to accelerate the bimolecular photoreactions between the cationic species in the sTTA mechanism.

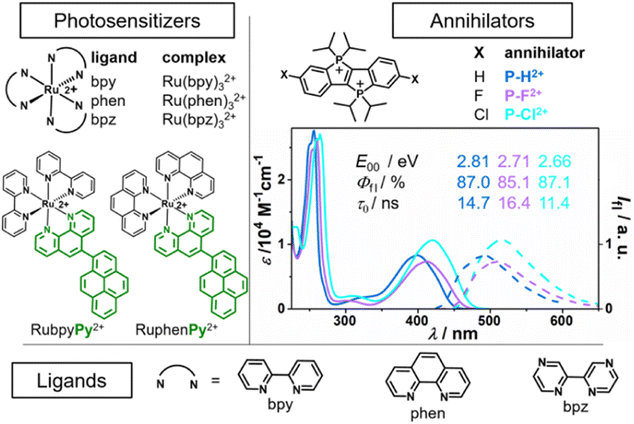Fig. 3 Left and bottom: Ruthenium complexes and dyads with the respective ligands used as photosensitizers (PS), for more details see ref. 4, 19 and 27. Right: Novel annihilator structure (P–H²⁺)⁴⁷ and derivatives (P–F²⁺, P–Cl²⁺), their calibrated UV/vis absorption and emission spectra and basic photophysical characteristics in Ar-saturated 50 mM H₂SO₄ (see ESI† for details).

The fluorescence quantum yields (Fig. 3, Φ_fl) close to unity imply highly inefficient intersystem crossing ISC, and indeed we did not detect any long-lived species with our transient absorption setup (see ESI for details, Section S8.5†) upon direct excitation of P–X²⁺ with 355 nm pulses of ∼10 ns duration. Previous DFT calculations on the basic structure P–H²⁺ (ref. 47) and additional calculations (see ESI, Section S5†) with a computational method that has been quite useful for the accurate prediction of triplet energies for organic chromophores^54–57 allowed us to conclude that the P–X²⁺ triplet energy levels are in the range from 1.50 eV to 1.75 eV. With the aim in mind to sensitize the P–X²⁺ triplets with low-energy photons, we selected tris(diimine)ruthenium(II)-based chromophores as they provide a sufficiently high triplet energy and they can be selectively excited with a frequency-doubled Nd:YAG laser (532 nm) in the presence of ground-state P–X²⁺. The commercially available ruthenium complexes Ru(bpy)₃²⁺, Ru(phen)₃²⁺ and Ru(bpz)₃²⁺ as well as the recently prepared dyads²⁷ RubpyPy²⁺ and RuphenPy²⁺ were used in this study (see left part of Fig. 3 for the structures).

Comparative Stern–Volmer studies with Ru(bpy)₃²⁺ and the corresponding dyad RubpyPy²⁺ using P–H²⁺ as the quencher gave linear lifetime-based plots as displayed in Fig. 4 (left part). The Stern–Volmer constant with the latter was higher by a factor of 36, which can be traced to the much longer unquenched triplet lifetime of the dyad (see Table 1 for details). Transient absorption (TA) spectra recorded right after complete quenching of the respective sensitizer triplet are shown in the right part of Fig. 4. These spectra look completely different with a pronounced bleach below 500 nm and a TA maximum at ∼570 nm (Ru(bpy)₃²⁺), or with two maxima at ∼470 and ∼630 nm (RubpyPy²⁺). The characteristic negative band in the former (emission-corrected) spectrum has to be due to a redox reaction of Ru(bpy)₃²⁺ as both the oxidized and reduced species of this metal complex show negative difference spectra in this region,^58–60 and the ground state of the quencher P–H²⁺ does not absorb between 500 and 460 nm (see Fig. 3). Owing to (i) the facile reduction of P–H²⁺ in organic solvents,⁴⁷ which is certainly feasible when conventional photoexcited ruthenium complexes such as Ru(bpy)₃²⁺ or Ru(phen)₃²⁺ are used, (ii) the characteristic bleach below 500 nm that has also been observed upon chemical oxidation of Ru(bpy)₃²⁺ (see ESI, Fig. S21†) and (iii) the fact that the remaining absorption features in the visible region are in line with the bands predicted by DFT calculations for P–H˙⁺ (ESI†), we conclude that P–H˙⁺ and Ru(bpy)₃³⁺ are the only primary quenching products. Furthermore, an absorption spectrum of the chemically prepared P–H˙⁺ in MeOH (where it is sufficiently stable) is in very good agreement with the spectrum of the photoinduced ET product above 500 nm (ESI, Fig. S22†), where the ruthenium complexes do not show clear absorption bands. In contrast, the red spectrum that was recorded right after ³RubpyPy²⁺ quenching with P–H²⁺ does not show negative signals and both absorption bands decay with wavelength-independent and almost pure first-order kinetics on a timescale of a few hundreds of microseconds. We assigned this spectrum to the triplet of P–H²⁺, which is further substantiated by DFT calculations (ESI†) and delayed emission measurements (see below). Time-resolved measurements at selected wavelengths (Fig. 4, central part) clearly demonstrated that both photoproducts are directly formed from the different triplet-excited sensitizers. For the kinetic trace showing the ³P–H²⁺ formation, a spectral separation had to be carried out because the sensitizer triplet (which has a triplet pyrene signature)²⁷ absorbs more strongly that ³P–H²⁺ throughout the TA spectrum. Qualitatively identical results have been observed with the phenanthroline-containing dyad and the purely inorganic counterpart Ru(phen)₃²⁺, i.e. P–H²⁺ triplet formation with the dyad and oxidative quenching with the conventional metal complex (ESI†). Second-order rate constants and inherent sensitizer properties under our conditions are summarized in Table 1. The results presented in this paragraph unambiguously establish that a photoexcited dyad can enable a completely different quenching mechanism compared to that observed for the parent metal complex. Clearly, the pyrene-localized triplets in the dyads are less reducing than the MLCT triplet states of the corresponding metal complexes, laying the grounds for the observed effects.

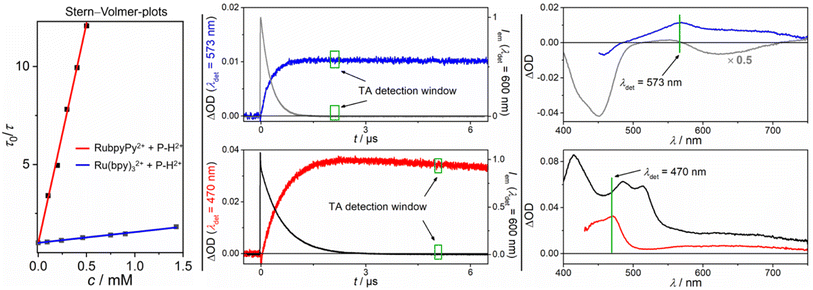Fig. 4 Left panel: Stern–Volmer plots for the triplet quenching with P–H²⁺ using ³RubpyPy²⁺ (red fit) and ³Ru(bpy)₃²⁺ (blue fit) as photosensitizers; Central panel: Kinetic sensitizer emission traces (upper for ³Ru(bpy)₃²⁺ in gray, concentration 30 μM λ_exc = 532 nm, 42 mJ and lower for ³RubpyPy²⁺ in black, concentration 31 μM, λ_exc = 532 nm, 42 mJ) with P–H²⁺ (2.0 mM with Ru(bpy)₃²⁺, 0.5 mM with RubpyPy²⁺), together with the formation kinetics of the quenching products (blue trace corresponds to the one electron reduced P–H˙⁺ after ET, red trace corresponds to the ³P–H²⁺ after EnT); Right panel: TA spectra of the triplet excited photosensitizer (upper, gray spectrum ³Ru(bpy)₃²⁺, and lower, black spectrum ³RubpyPy²⁺) and ³P–H²⁺ (red, lower graph) after EnT or P–H˙⁺ and Ru(bpy)₃³⁺ (blue, upper graph) after ET. All measurements were carried out in 50 mM H₂SO₄. Further explanations are given in the text and ESI.†

Table 1 Key reactivity properties for all ruthenium photosensitizers with the quencher P–H²⁺ in 50 mM H₂SO₄. For more detail, see text and ESI

PS	RuphenPy^2+	RubpyPy^2+	Ru(bpz)3^2+	Ru(phen)3^2+	Ru(bpy)3^2+
a Estimated to be slightly lower than for ^3pyrene.^19,27 b Taken from ref. 1. c Estimated relative error below 5%. d In neat water due to protonation of the PS. e EnT. f ET. g Estimated rate constant in 50 mM H2SO4, 0.25 × 10^9 M^−1 s^−1. h Recalculated vs. NHE from values in V vs. SCE^4,19 see ESI for details.
E T/eV	∼2.0^a	∼2.0^a	2.16^b	2.19^b	2.12^b
τ 0/μs	43.1^c	15.0^c	0.55^c^,^d	1.09^c	0.59^c
k q/10^9 M^−1 s^−1	1.44 ± 0.01^e	1.50 ± 0.09^e	0.09 ± 0.02^d^,^e^,^g	1.39 ± 0.05^f	1.05 ± 0.10^f
E([PS]^3+/^3[PS]^2+) V vs. NHE	>−0.5	>−0.5	−0.06^h	−0.69^h	−0.59^h

---

Further evidence for our spectral assignment is provided by experiments with Ru(bpz)₃²⁺. This metal complex is known to be less reducing in its excited state (compare, excited-state oxidation potentials in Table 1), while maintaining a high triplet energy. We clearly observed ³P–H²⁺ (ESI, Fig. S29†) but a very high concentration of the tailor-made annihilator had to be used owing to the short ³Ru(bpz)₃²⁺ lifetime (see also the efficiency discussion in the next paragraph). Moreover, we tested several additional photosensitizers that should have the potential to produce ³P–H²⁺, based on their triplet energies, absorption properties at our laser wavelength (532 nm) and solubility properties. Electron transfer quenching was clearly demonstrated (see ESI for details, Section S7.8†) with four commercially available photosensitizers (two metal complexes and two organic dyes) and a tailor-made ruthenium complex–anthracene dyad. We, therefore, speculate that the P–H²⁺ triplet and its annihilator properties would have been overlooked without the ruthenium complex–pyrene dyads, highlighting their unique energy transfer capability. The second-order rate constants for the EnT reactions are comparable for both dyads (∼1.5 × 10⁹ M⁻¹ s⁻¹). For Ru(bpz)₃²⁺, however, that reaction is about six times slower even after salt effect corrections (H₂SO₄ could not be used owing to Ru(bpz)₃²⁺ protonation,^61,62 see ESI† for details). More pronounced coulombic repulsion between the cationic energy donor Ru(bpz)₃²⁺ and P–H²⁺ might explain these observations.⁴⁴ ET quenching with Ru(bpy)₃²⁺ and Ru(phen)₃²⁺ occurs with diffusion-controlled rates taking coulombic interactions into account.

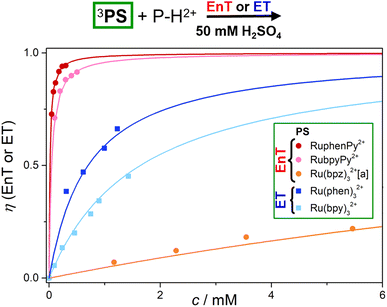
The efficiencies of the photoreactions employing P–H²⁺ as quencher and the corresponding mechanisms are visualized in Fig. 5. Using our Stern–Volmer quenching data sets (ESI, Section S7†) and the well-known photokinetic equations,⁶³ we simulated the P–H²⁺ concentration-dependent quenching efficiencies. Owing to the long unquenched triplet lifetimes of the dyads, the P–H²⁺ concentrations required for >90% quenching are below 400 μM. In contrast, the EnT efficiency with Ru(bpz)₃²⁺ is slightly below 25% at the highest experimental P–H²⁺ concentration employed (about 5.5 mM, see Fig. 5). Efficient EnT quenching (>90%) with Ru(bpz)₃²⁺ would require unreasonably high P–H²⁺ concentrations exceeding 0.2 M, which would correspond to P–H²⁺ amounts of almost 100 mg per mL of the chloride salt. The quenching efficiencies with ³Ru(bpy)₃²⁺ and ³Ru(phen)₃²⁺, which transfer a single electron to P–H²⁺ rather than the triplet energy, are in-between the extreme kinetic scenarios of highly efficient and highly inefficient quenching.

Fig. 5 Comparative quenching efficiency analysis for EnT (color-coded bullets) or ET (color-coded squares) between the excited photosensitizers at a constant concentration of 50 mM H₂SO₄ ([a] in H₂O due to sensitizer protonation in acidic solution).

Fig. 6 focuses on the triplet of P–H²⁺ and its decay via annihilation. Time-gated emission measurements upon 532 nm laser excitation were carried out with RuphenPy²⁺ in the presence of P–H²⁺ (left part of Fig. 6). With an integration window of 150 μs duration starting shortly after the excitation pulse, we clearly detected some unquenched ³RuphenPy²⁺ emission peaking at ∼605 nm. In addition, we observed an emission band with a maximum at ∼495 nm. This band resembles that of singlet-excited P–H²⁺ in strongly diluted solution taking filter effects into account (see also ESI, Fig. S41†), and it shows the non-linear power dependence being typical for the UC mechanism under study (ESI, Fig. S38†). A time-gated emission measurement with a longer delay between green laser pulse and detection window allowed us to (blue spectrum in Fig. 6) detect the greenish emission in isolation, whereas a control experiment in the absence of the sensitizer did not yield any delayed emission. The fact that a pure annihilator emission spectrum could be obtained without contaminations by the emissive ruthenium complex indicates that back energy transfer from ³P–H²⁺ to the sensitizer ground state does not take place. This observation implies a pronounced triplet energy difference of at least 0.2 eV, allowing us to set an upper limit for the P–H²⁺ triplet energy of 1.8 eV (in line with the DFT calculations mentioned above). More evidence for sensitized TTA was obtained from kinetic absorption and emission measurements monitoring the sensitizer triplet, ³P–H²⁺ and the annihilation product ¹P–H²⁺* under identical conditions (right part of Fig. 6). Both annihilator-derived species reach their maximum intensities at about 4 μs after the green laser pulse. As a result of the bimolecular nature of the annihilation process, the rise and fall of the singlet emission intensity (blue) are in a quadratic relation to concentration-dependent signals of the precursor ³P–H²⁺ (red), resulting in the characteristic behavior displayed in Fig. 6.^55,64 All these results unambiguously establish that ³P–H²⁺ acts as annihilator in neat water.

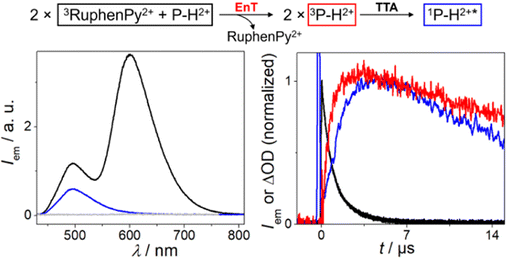Fig. 6 Reaction scheme (top) of sTTA with RuphenPy²⁺ as PS (30 μM) and P–H²⁺ (0.5 mM) as annihilator. Left: Time-gated emission spectra (excitation at λ = 532 nm) of ³RuphenPy²⁺ and ¹P–H²⁺* (black, time delay 300 ns integrated over 150 μs), the isolated ¹P–H²⁺* spectrum after sTTA (blue, time delay 15 μs integrated over 150 μs) and a P–H²⁺ solution without the photosensitizer (gray) as control measurement (time delay 500 ns integrated over 150 μs). Right: Normalized kinetic traces (excitation at λ = 532 nm) of ³RuphenPy²⁺ emission with P–H²⁺ (black, λ_det = 600 nm), formation of ³P–H²⁺ absorption (red, λ_det = 475 nm, corrected kinetic trace, for details see ESI†) and the formation and decay of ¹P–H²⁺* emission after sTTA (blue, λ_det = 500 nm).

To test whether the dyad quenching pathway control holds also true for the two halogen-substituted annihilators P–X²⁺ (X = Cl, F), comparative experiments with Ru(phen)₃²⁺ and ³RuphenPy²⁺ were carried out (see ESI, Sections S7.5 and S8.4†). In the presence of the conventional metal complex, we clearly observed the signatures of the radical cations P–X˙⁺ in the TA spectra (intense band at ∼590 nm) along with the Ru(phen)₃²⁺ bleach below 500 nm. Employing the dyads as sensitizers, however, a positive TA band could be observed below 500 nm, which we ascribe to ³P–X²⁺. That assignment is again substantiated by delayed annihilator emission for both derivatives ¹P–X²⁺*, which was only detectable in the presence of the dyad. Based on these findings, dicationic phosphonium-bridged ladder stilbenes can be regarded as a new annihilator class. Furthermore, these experiments imply that the quenching pathway control with molecular dyads might well be developed into a versatile method for the generation of triplets and/or radical ions that cannot be formed with well-established sensitizers.

Having established that ¹P–X²⁺* is accessible via sTTA with two low-energy photons, we next turned to the photochemical reactivity of this species. The ET quenching observations with the commercial ruthenium complexes with their well-known redox properties indicate that P–X²⁺ is reduced at a potential between −0.6 and −0.1 vs. NHE in water (compare, Table 1). In consequence, the annihilators must be highly oxidizing in their singlet-excited states, taking their S₁ energies of ∼2.7 eV into account (see Fig. 3). Owing to the observed instability of the chemically prepared P–X˙⁺ in water and the inherent difficulties associated with (reductive) cyclic voltammetry in aqueous solvents,⁶⁵ the P–X²⁺ reduction potentials could not be measured directly. Alternatively, we estimated the P–X²⁺ reduction potentials both in the ground states and in the first excited singlet states with several reference reactions and chromophores possessing well-defined potentials in water. The previously identified aqueous annihilators MAMA⁺ (a cationic anthracene derivative) and 1,5-naphthalenedisulfonate are relatively strong oxidants in their excited singlet states with excited-state reduction potentials of +1.6 and +1.9 V vs. NHE, respectively (see Table 2 for details). As test reactions, we selected the chloride/bromide oxidation to the respective halogen atom.⁶⁶ To study the quenching kinetics in a direct manner without potentially disturbing effects on triplet decay rates or annihilation rate constants, we directly produced the emissive singlet states of the annihilator molecules (i.e. without sensitizers, see ESI† for details). Averaging several potentials from the literature estimated or determined for aqueous solution,⁶⁷ we took a reference potential of +2.4 V vs. NHE for the chloride oxidation and +1.8 V vs. NHE for bromide (the latter value was also used in a recent study addressing the Br⁻ oxidation in water).⁶⁸ As another test system, we investigated the weakly oxidizing ³Ru(bpy)₃²⁺, which, as we found, does not react with both halide ions under our conditions (Table 2). During the emission quenching studies presented below, high salt or H₂SO₄ concentrations were added to minimize kinetic salt effects on one hand and coulombic effects on the diffusion on the other.

Table 2 Reactivity studies via halide quenching with the new annihilators as well as known annihilator structures and Ru(bpy)₃²⁺ as reference compounds. All quenching rate constants k_q were measured at identical ionic strength (aqueous 50 mM H₂SO₄), except for 1,5-NDS^2−a

	Ru(bpy)3^2+	MAMA^+	1,5-NDS^2−	P–Cl^2+	P–F^2+	P–H^2+
a In 50 mM NaOH (in H2O). b Taken from ref. 70. c Taken from ref. 44. d Estimated from 9-methyl-anthracene.^19 e Taken from ref. 45 and 71. f Estimated from quenching studies, see text for details. Reference values: E(Cl˙^/−) = 2.4 V vs. NHE^67 and E(Br˙^/−) = 1.8 V vs. NHE.^67,68
k q(Cl^−)/10^8 M^−1 s^−1	No quenching	<0.1	No quenching^a	0.60 ± 0.01	0.45 ± 0.02	5.10 ± 0.18
k q(Br^−)/10^8 M^−1 s^−1	No quenching	4.05 ± 0.09	8.06 ± 0.17 (6.68 ± 0.17)^a	102 ± 2	104 ± 1	122 ± 1
E 00/eV	2.12^b	3.18^c	3.87^e	2.66	2.71	2.81
E(PC/PC˙^−) V vs. NHE	−1.3^b	−1.7^d	−1.97^e	∼−0.5^f	∼−0.5^f	∼−0.5^f
E(*PC/PC˙^−) V vs. NHE	0.8^b	1.6	1.9	∼2.2^f	∼2.2^f	∼2.3^f

---

Interestingly, P–H²⁺ is the only compound being able to oxidize chloride in its excited state rapidly with a quenching rate constant of ∼5 × 10⁸ M⁻¹ s⁻¹ (Fig. 7). The other excited P–X²⁺ derivatives quench slower by one order of magnitude and the seemingly less oxidizing 1,5-NDS²⁻, whose generation requires one UVB photon or two blue photons,⁴⁵ is not quenched by chloride at all. The less challenging bromide oxidation is diffusion controlled (∼10¹⁰ M⁻¹ s⁻¹) for all excited P–X²⁺ derivatives, while quenching with the reference compounds occurs with about 20 times slower rate constants. The observed trends are in perfect accordance with halide oxidation and other potential quenching pathways are thus seen to be unimportant. The well-established relation between the second-order rate constants and the Gibbs energy of photoinduced electron transfer^69,70 allows us to estimate the excited state reduction potentials of the novel photoactive compounds E(*PC/PC˙⁻). E(*PC/PC˙⁻) has to be higher than 2 V due to the rapid bromide and detectable chloride oxidation, and we estimate 2.3 V vs. NHE for the most highly oxidizing ¹P–H²⁺* (see Table 2 for all potentials). The very high potential for ¹P–H²⁺* is further corroborated by kinetic experiments with 1,5-NDS²⁻ acting as quencher. The oxidation of the latter requires 2.03 V vs. NHE⁷¹ and we observed diffusion-controlled quenching (ESI, page S40†), which is in perfect accordance with the annihilator's redox potential estimated via halide quenching. This outstanding reactivity for photochemical oxidations is comparable with that observed for the famous acridinium photocatalysts.^72–75

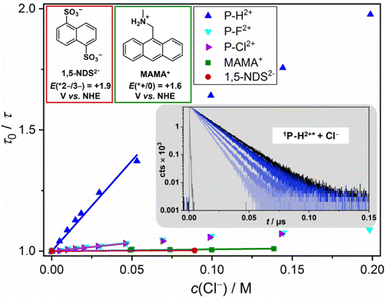Fig. 7 Main: Color-coded Stern–Volmer (SV) plots for the singlet-state chloride quenching of the new annihilators and two literature-known aqueous annihilators (1,5-NDS²⁻ (ref. 45) and MAMA⁺ (ref. 44), together with the structures and excited-state potentials); inset (gray): selected kinetic traces for ¹P–H²⁺* quenching with increasing concentrations of Cl⁻ (added to the solutions as NaCl, see ESI† for all data sets). The downward curvature of the SV plots at higher quencher concentrations is due to the kinetic salt effect. The linear regions have been used for the kinetic analysis.

Initial LFP experiments employing RuphenPy²⁺ as sensitizer and P–H²⁺ as annihilator indicate that green-light driven chloride oxidation is indeed feasible via sTTA in water (see ESI for details, Section S9.4†). These results demonstrate that the new annihilator class has the potential to be integrated in upconversion schemes for challenging oxidative bond activation reactions, even in aqueous solution. This is an important finding considering that most known upconversion-driven photoreactions have to rely on a reductive substrate activation step,^63,76–78 and the lack of highly oxidizing annihilator molecules likely contributed to this situation.

Conclusions

As has emerged from this work, molecular dyads that are easily accessible can be exploited for the efficient generation of quencher-derived triplets, while the parent metal complexes and widely used organic photosensitizers exclusively generate electron transfer products. This quenching pathway manipulation (thermodynamics), in combination with the very long triplet lifetimes (kinetics) of the dyads, paved the way for the identification of a novel annihilator class in water with unmatched photoredox properties. We believe that this extended dyad-induced reactivity switching will find further useful applications in the broad photochemistry field, especially (i) with regard to triplet properties of highly redox-active or charged chromophores, and (ii) for controlling the reaction pathways in photocatalysis. The latter idea would be most promising with metal complexes possessing even higher triplet energies and excited-state oxidation as well as reduction potentials accordingly. Owing to the rather low triplet energy of the dicationic phosphonium-bridged ladder stilbenes (about 1.6 eV), sensitization with lower-energy photons approaching the biological window seems to be within reach. We are currently working on identifying such systems which would have potential applications in red-light driven photocatalysis in water or biochemical applications.

Data availability

All experimental and computational data have been provided in the main text and the ESI.† The data sets shown in the main paper and DFT output files can be found under http://doi.org/10.25358/openscience-9298.

Author contributions

M.-S. B. and K. H. designed photochemical studies, carried out spectroscopic experiments and analyzed data. M.-S. B. carried out the DFT calculations. K. H. prepared the dyads. The synthetic and the crystallographic work was carried out by J.-M. M. and J. B. C. K. conceived the project, provided guidance and wrote the initial draft of the manuscript with input from J. B. and M.-S. B. All authors contributed to the writing and editing of the manuscript and the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge generous financial support from the JGU Mainz, SusInnoScience and the German Research Foundation (DFG, grant numbers KE 2313/3-1 and KE 2313/7-1). C. K. is grateful to the Chemical Industry Funds for a Liebig fellowship. J.-M. M. and J. B. thank the Vector foundation for financial support. We thank Arne C. Sell for assistance with the dyad synthesis.

References

1. A. A. Vlcek, E. S. Dodsworth, W. J. Pietro and A. B. P. Lever, Inorg. Chem., 1995, 34, 1906–1913.
2. L. Schmid, C. Kerzig, A. Prescimone and O. S. Wenger, JACS Au, 2021, 1, 819–832.
3. D. M. Arias-Rotondo and J. K. McCusker, Chem. Soc. Rev., 2016, 45, 5803–5820.
4. K. Teegardin, J. I. Day, J. Chan and J. Weaver, Org. Process Res. Dev., 2016, 20, 1156–1163.
5. C. Sandoval-Pauker, G. Molina-Aguirre and B. Pinter, Polyhedron, 2021, 199, 115105.
6. Y. Wu, D. Kim and T. S. Teets, Synlett, 2022, 33, 1154–1179.
7. T. Koike and M. Akita, Inorg. Chem. Front., 2014, 1, 562–576.
8. W. R. Kitzmann and K. Heinze, Angew. Chem., Int. Ed., 2023, 62, e202213207.
9. C. B. Larsen and O. S. Wenger, Chem.–Eur. J., 2018, 24, 2039–2058.
10. Z. Mahmood, J. He, S. Cai, Z. Yuan, H. Liang, Q. Chen, Y. Huo, B. König and S. Ji, Chem.–Eur. J., 2023, 29, e202202677.
11. E. A. Medlycott and G. S. Hanan, Chem. Soc. Rev., 2005, 34, 133–142.
12. G. J. Wilson, A. Launikonis, W. H. F. Sasse and A. W.-H. Mau, J. Phys. Chem. A, 1997, 101, 4860–4866.
13. W. E. Ford and M. A. J. Rodgers, J. Phys. Chem., 1992, 96, 2917–2920.
14. V. Balzani, P. Ceroni, A. Credi and M. Venturi, Coord. Chem. Rev., 2021, 433, 213758.
15. A. J. Howarth, M. B. Majewski and M. O. Wolf, Coord. Chem. Rev., 2015, 282–283, 139–149.
16. F. N. Castellano, Acc. Chem. Res., 2015, 48, 828–839.
17. S. A. Denisov, S. Yu, J.-L. Pozzo, G. Jonusauskas and N. D. McClenaghan, ChemPhysChem, 2016, 17, 1794–1804.
18. J. A. Roque III, H. D. Cole, P. C. Barrett, L. M. Lifshits, R. O. Hodges, S. Kim, G. Deep, A. Francés-Monerris, M. E. Alberto, C. G. Cameron and S. A. McFarland, J. Am. Chem. Soc., 2022, 144, 8317–8336.
19. M. Montalti, A. Credi, L. Prodi and M. T. Gandolfi, Handbook of photochemistry, CRC/Taylor & Francis, Boca Raton, 3rd edn, 2006.
20. M. Schmid, J. Brückmann, J. Bösking, D. Nauroozi, M. Karnahl, S. Rau and S. Tschierlei, Chem.–Eur. J., 2022, 28, e202103609.
21. X. Guo, Y. Liu, Q. Chen, D. Zhao and Y. Ma, Adv. Opt. Mater., 2018, 6, 1700981.
22. J. Brückmann, C. Müller, I. Friedländer, A. K. Mengele, K. Peneva, B. Dietzek-Ivanšić and S. Rau, Chem.–Eur. J., 2022, 28, e202201931.
23. Y. Sasaki, N. Yanai and N. Kimizuka, Inorg. Chem., 2022, 61, 5982–5990.
24. C. Wegeberg, D. Häussinger and O. S. Wenger, J. Am. Chem. Soc., 2021, 143, 15800–15811.
25. P. Dierks, A. Päpcke, O. S. Bokareva, B. Altenburger, T. Reuter, K. Heinze, O. Kühn, S. Lochbrunner and M. Bauer, Inorg. Chem., 2020, 59, 14746–14761.
26. M. Sandroni, Y. Pellegrin and F. Odobel, C. R. Chim., 2016, 19, 79–93.
27. A. C. Sell, J. C. Wetzel, M. Schmitz, A. W. Maijenburg, G. Woltersdorf, R. Naumann and C. Kerzig, Dalton Trans., 2022, 51, 10799–10808.
28. S. Neumann, O. S. Wenger and C. Kerzig, Chem.–Eur. J., 2021, 27, 4115–4123.
29. G. J. Wilson, A. Launikonis, W. H. F. Sasse and A. W.-H. Mau, J. Phys. Chem. A, 1998, 102, 5150–5156.
30. C. Weinheimer, Y. Choi, T. Caldwell, P. Gresham and J. Olmsted, J. Photochem. Photobiol., A, 1994, 78, 119–126.
31. L. Ma, P. Wang, J.-Z. Wang, S. Guo, Z.-M. Zhang, X.-S. Zeng and T.-B. Lu, Dyes Pigm., 2021, 196, 109811.
32. S. Guo, K.-K. Chen, R. Dong, Z.-M. Zhang, J. Zhao and T.-B. Lu, ACS Catal., 2018, 8, 8659–8670.
33. D. Hara, H. Komatsu, A. Son, S. Nishimoto and K. Tanabe, Bioconjugate Chem., 2015, 26, 645–649.
34. H. Komatsu, K. Yoshihara, H. Yamada, Y. Kimura, A. Son, S. Nishimoto and K. Tanabe, Chem.–Eur. J., 2013, 19, 1971–1977.
35. M. Stephenson, C. Reichardt, M. Pinto, M. Wächtler, T. Sainuddin, G. Shi, H. Yin, S. Monro, E. Sampson, B. Dietzek and S. A. McFarland, J. Phys. Chem. A, 2014, 118, 10507–10521.
36. F. Deng, M. S. Lazorski and F. N. Castellano, Philos. Trans. R. Soc., A, 2015, 373, 20140322.
37. K. Chen, M. Hussain, S. S. Razi, Y. Hou, E. A. Yildiz, J. Zhao, H. G. Yaglioglu and M. D. Donato, Inorg. Chem., 2020, 59, 14731–14745.
38. S. Ji, H. Guo, W. Wu, W. Wu and J. Zhao, Angew. Chem., Int. Ed., 2011, 50, 8283–8286.
39. Y. Wei, Y. Li, M. Zheng, X. Zhou, Y. Zou and C. Yang, Adv. Opt. Mater., 2020, 8, 1902157.
40. Y. Lu, J. Wang, N. McGoldrick, X. Cui, J. Zhao, C. Caverly, B. Twamley, G. M. Ó Máille, B. Irwin, R. Conway-Kenny and S. M. Draper, Angew. Chem., Int. Ed., 2016, 55, 14688–14692.
41. P. Wang, S. Guo, H.-J. Wang, K.-K. Chen, N. Zhang, Z.-M. Zhang and T.-B. Lu, Nat. Commun., 2019, 10, 3155.
42. C. Wang, F. Reichenauer, W. R. Kitzmann, C. Kerzig, K. Heinze and U. Resch-Genger, Angew. Chem., Int. Ed., 2022, 61, e202202238.
43. K. A. El Roz and F. N. Castellano, Chem. Commun., 2017, 53, 11705–11708.
44. C. Kerzig and O. S. Wenger, Chem. Sci., 2018, 9, 6670–6678.
45. B. Pfund, D. M. Steffen, M. R. Schreier, M.-S. Bertrams, C. Ye, K. Börjesson, O. S. Wenger and C. Kerzig, J. Am. Chem. Soc., 2020, 142, 10468–10476.
46. Y. Nakadai, S. Tsuchiya, M. Uehara, S. Umezawa, R. Motoki, H. Umezawa, T. Ikoma and T. Yui, J. Phys. Chem. B, 2022, 126, 8245–8250.
47. P. Federmann, H. K. Wagner, P. W. Antoni, J.-M. Mörsdorf, J. L. Pérez Lustres, H. Wadepohl, M. Motzkus and J. Ballmann, Org. Lett., 2019, 21, 2033–2038.
48. T. N. Singh-Rachford and F. N. Castellano, Coord. Chem. Rev., 2010, 254, 2560–2573.
49. L. Zeng, L. Huang, J. Han and G. Han, Acc. Chem. Res., 2022, 55, 2604–2615.
50. J. Pedrini and A. Monguzzi, J. Photonics Energy, 2017, 8, 022005.
51. V. Gray, K. Moth-Poulsen, B. Albinsson and M. Abrahamsson, Coord. Chem. Rev., 2018, 362, 54–71.
52. J. Zhao, S. Ji and H. Guo, RSC Adv., 2011, 1, 937–950.
53. C. Ye, V. Gray, J. Mårtensson and K. Börjesson, J. Am. Chem. Soc., 2019, 141, 9578–9584.
54. M.-S. Bertrams and C. Kerzig, Chem. Commun., 2021, 57, 6752–6755.
55. T. J. B. Zähringer, J. A. Moghtader, M. Bertrams, B. Roy, M. Uji, N. Yanai and C. Kerzig, Angew. Chem., Int. Ed., 2023, 62, e202215340.
56. T. R. Blum, Z. D. Miller, D. M. Bates, I. A. Guzei and T. P. Yoon, Science, 2016, 354, 1391–1395.
57. V. Gray, A. Dreos, P. Erhart, B. Albinsson, K. Moth-Poulsen and M. Abrahamsson, Phys. Chem. Chem. Phys., 2017, 19, 10931–10939.
58. M. Goez, D. von Ramin-Marro, M. H. Othman Musa and M. Schiewek, J. Phys. Chem. A, 2004, 108, 1090–1100.
59. T.-T. Tran, M.-H. Ha-Thi, T. Pino, A. Quaranta, C. Lefumeux, W. Leibl and A. Aukauloo, J. Phys. Chem. Lett., 2018, 9, 1086–1091.
60. B. Shan and R. Schmehl, J. Phys. Chem. A, 2014, 118, 10400–10406.
61. O. S. Wenger, Coord. Chem. Rev., 2015, 282–283, 150–158.
62. R. J. Crutchley, N. Kress and A. B. P. Lever, J. Am. Chem. Soc., 1983, 105, 1170–1178.
63. F. Glaser, C. Kerzig and O. S. Wenger, Angew. Chem., Int. Ed., 2020, 59, 10266–10284.
64. Y. Murakami and K. Kamada, Phys. Chem. Chem. Phys., 2021, 23, 18268–18282.
65. N. Elgrishi, K. J. Rountree, B. D. McCarthy, E. S. Rountree, T. T. Eisenhart and J. L. Dempsey, J. Chem. Educ., 2018, 95, 197–206.
66. L. Troian-Gautier, M. D. Turlington, S. A. M. Wehlin, A. B. Maurer, M. D. Brady, W. B. Swords and G. J. Meyer, Chem. Rev., 2019, 119, 4628–4683.
67. P. Wardman, J. Phys. Chem. Ref. Data, 1989, 18, 1637–1755.
68. A. M. Deetz, L. Troian-Gautier, S. A. M. Wehlin, E. J. Piechota and G. J. Meyer, J. Phys. Chem. A, 2021, 125, 9355–9367.
69. A. Rosspeintner, G. Angulo and E. Vauthey, J. Am. Chem. Soc., 2014, 136, 2026–2032.
70. R. Naumann and M. Goez, Green Chem., 2019, 21, 4470–4474.
71. C. Kerzig and M. Goez, Phys. Chem. Chem. Phys., 2014, 16, 25342–25349.
72. S. Fukuzumi and K. Ohkubo, Chem. Sci., 2013, 4, 561–574.
73. C. Fischer, C. Kerzig, B. Zilate, O. S. Wenger and C. Sparr, ACS Catal., 2020, 10, 210–215.
74. V. A. Pistritto, S. Liu and D. A. Nicewicz, J. Am. Chem. Soc., 2022, 144, 15118–15131.
75. Y.-M. Lee, W. Nam and S. Fukuzumi, Chem. Sci., 2023, 14, 4205–4218.
76. L. Zeng, L. Huang, W. Lin, L.-H. Jiang and G. Han, Nat. Commun., 2023, 14, 1102.
77. R. Pérez-Ruiz, Top. Curr. Chem., 2022, 380, 23.
78. B. D. Ravetz, A. B. Pun, E. M. Churchill, D. N. Congreve, T. Rovis and L. M. Campos, Nature, 2019, 565, 343–346.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental details, synthetic protocols and characterization data, additional spectroscopic results as well as raw data sets, and quantum-mechanical calculations. CCDC 2224633 and 2224634. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3sc01725g

---