Open Access Article
Open Access ArticleAn efficient multiparameter method for the collection of chemical reaction data via ‘one-pot’ transient flow†
Linden
Schrecker
 a,
Joachim
Dickhaut
b,
Christian
Holtze
b,
Philipp
Staehle
b,
Andy
Wieja
b,
Klaus
Hellgardt
c and
King Kuok (Mimi)
Hii
a,
Joachim
Dickhaut
b,
Christian
Holtze
b,
Philipp
Staehle
b,
Andy
Wieja
b,
Klaus
Hellgardt
c and
King Kuok (Mimi)
Hii
 *a
*a
aDepartment of Chemistry, Imperial College London, Molecular Sciences Research Hub, 82 Wood Lane, London W12 0BZ, UK. E-mail: mimi.hii@imperial.ac.uk
bBASF SE, 8 Carl-Bosch-Straße, 67056, Ludwigshafen, Rhein, Germany
cDepartment of Chemical Engineering, Imperial College London, Exhibition Road, South Kensington, London SW7 2AZ, UK
First published on 1st September 2023
Abstract
The advent of transient flow methods has increased the efficiency and diversity of reaction data collected through the collection of data series in a wider reaction space, beyond traditionally temporal series. Thus far, these methods have been limited to studying continuous reaction parameters. In this work, transient flow is combined with “one-pot” chemistry (OP-TF) to efficiently collect diverse reaction data on a continuous-discrete multiparameter space, exemplified with the aromatic Claisen rearrangement. Six independent substrates were studied simultaneously, producing data on temperature and substituent effects in a single experiment, extending into the supercritical phase. This data allowed us to extract thermodynamic information and predict kinetic parameters for other substrates accurately, thus allowing synthetic feasibility of a substrate to be assessed a priori.
Introduction
The availability of high-quality and reliable reaction data covering a diverse range of the chemical space is critical for the development of the chemical sciences in the modern digital era.1 However, the collection of continuous series data on multiple discrete reactions simultaneously remains a considerable challenge. With recent advances in high throughput experimentation and analytical techniques, reaction data can be collected across diverse discrete variables, including different substrates and catalysts.2 For example, by using multi-well plates, a large number of different reactions can be run in parallel, however, this usually only collects reaction data at a single time point. Furthermore, as all the reactions are performed on a single plate, only one particular set of reaction conditions can be evaluated at any one time.Transient flow is an emergent tool for the collection of reaction data. As demonstrated by us3 and others,4–8 this method can accurately and efficiently collect temporal kinetic data, and also extend to other continuous reaction parameters such as temperature,4,9–12 initial reactant stoichiometry,3 and additive concentration.4,7 However, transient flow is currently limited in its ability to rapidly analyse certain discrete parameters, such as different reactants.
In the present work, multiple substrates are combined with transient flow in a single experiment (‘one-pot’) – a strategy that has been shown to be effective for generating discrete parameter series data for Hammett plots,13–18 but had never been demonstrated in flow. The aim of this work is to utilize this method to study continuous and discrete parameter effects, greatly increasing the efficiency of diverse data collection (Fig. 1).
The method is exemplified by using the aromatic Claisen rearrangement as a case study (Scheme 1). As the first example of a [3,3]-sigmatropic rearrangement reported by Ludwig Claisen in 1912,19 the reaction has been deployed in the synthesis of numerous biologically active molecules.20 In comparison, kinetic studies of the thermal rearrangement are limited to a handful of publications between 1958–1962,21–26 with only two studies on para-substituted phenyl allyl ethers.21,22 Much of this early work focussed on establishing the Hammett relationships, from which it was concluded that the reactions are likely to proceed through polar transition states. The activation energies (Ea) for the thermal rearrangement for para-substituted phenyl allyl ethers were found to be between 124–146 kJ mol−1 in high boiling solvents carbitol22 and diphenyl ether,21 from measurements recorded from two or three temperature points.
In 2013, Noël and Hessel exploited the wider process window afforded by flow reactors to perform Claisen rearrangements in alcoholic solvents at temperatures up to 300 °C.27 While the effects of changing different reaction parameters (residence time, temperature, alcoholic solvent, pressure) were studied, the effect of substituents was not investigated.
Herein, we will describe the design and utilisation of a flow reactor system that can efficiently investigate substituent rate dependencies whilst varying other parameters simultaneously. Data collection is facilitated by automated on-line HPLC analysis,4,28–34 further enhanced by combining transient flow and one-pot multi-substrate experiments in a novel method (OP-TF, Fig. 1c). The data was used to determine the fundamental kinetic parameters and their dependencies on temperature and substituent effects. A model was also produced to support reaction prediction and the accuracy of computational calculations.
Results and discussion
A previously described flow reactor system3 was modified for this work (Fig. S1†), by integrating a (GC) oven to implement precise temperature ramps, and an on-line HPLC system to monitor and quantify multiple reaction species in an accessible manner. The unimolecular Claisen rearrangement reaction can be performed at high dilution (ca. 2 mM) and is amenable to direct HPLC sampling and analysis, while also suppressing any intermolecular interactions. Bimolecular competition reactions could be performed at higher concentrations would require in-line dilution prior to on-line HPLC analysis. Ethanol has previously been reported as a good alcoholic solvent for the reaction,27 but also transpires to be a green, benign, and UV-inactive solvent appropriate for the study.Eight para-substituted phenyl allyl ether substrates 1a–h containing electron-donating and withdrawing substituents across a range of σ+ parameters35,36 – previously shown to provide a good linear Hammett correlation21,22 – were selected for this work and synthesized. The substrates were separated into a ‘training set’ of six substrates: Z = OMe (a), Me (b), F (c), H (d), C(O)CH3 (e), CN (f), and a ‘testing set’ of two: Z = NHAc (g), Br (h).
Individual substrate transient flow (IS-TF, Fig. 1b) experiments
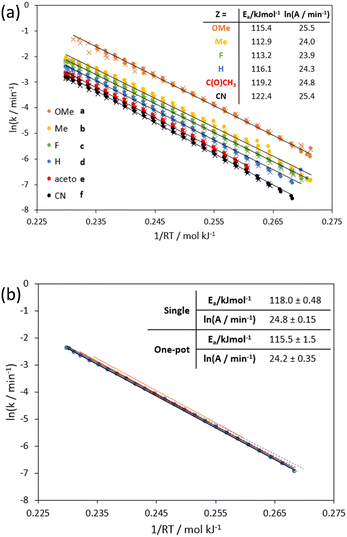
The flow system was validated for this reaction by performing two different transient flow methods with the unsubstituted substrate 1d (Z = H):(i) Residence time ramps, produced via a step change of the cumulative flow rate, allow access to time series data in the desired residence time range.4–7 Temporal data was collected at 200, 220, and 240 °C, maintaining a high back pressure (95–105 bar) to avoid pressure dependent fluctuations in the near critical region.37 Under these conditions, the transformation of allylphenylether (1d) proceeded with first order kinetics (Fig. S4†) to produce solely the ortho-allyl substituted phenol (2d). As previously reported,27 residence time correction was needed due to solvent expansion at super-ambient temperatures and pressures via the Tait equation38 (see discussion in ESI,† S3.5). The resultant Arrhenius plot yielded an activation energy that is comparable with previously reported results in ethanol (118 kJ mol−1, cf. 116 kJ mol−1).27
(ii) Temperature ramps,4,9–12 allowing access to a continuous range of pseudo-steady state reactions across different temperatures, to expeditiously generate an Arrhenius or Eyring plot from a single experiment at a given flow rate. Although temperature ramps have been demonstrated in batch,39 the temperature range accessible in a pressurized flow setup is much broader.4 By fixing the flow rate at 0.2 mL min−1 (ca. 16 min residence time) and changing the temperature of the reactor between 170–250 °C at a rate of 0.5 °C min−1, almost ideal linear Arrhenius and Eyring plots for allylphenylether (1d) can be obtained (Fig. 2).
The robustness of the result was tested by performing repeat experiments and different temperature ramp ranges, with excellent reproducibility, furnishing an activation energy (Ea) of 118 ± 0.48 kJ mol−1 and enthalpy of activation (ΔH‡) of 114 ± 0.47 kJ mol−1 (R2 > 0.99). Bi-directional temperature ramps were also performed within the same experimental run, to confirm the absence of hysteresis in the system. Interestingly, the plots appear to retain linearity even when temperature was ramped above the supercritical point of ethanol (241 °C, 63 bar40) whilst maintaining a pressure of 100 bar. This suggests that the rearrangement is insensitive to the change in solvent polarity associated with the phase change under these conditions.37
One-pot transient flow (OP-TF, Fig. 1c) experiments
Although transient flow chemistry allows rapid screening of continuous reaction parameters, it is usually more challenging to intensify the collection of discrete reaction parameters, such as different substituents. Traditionally, these are studied individually in flow32,41 or by parallel batch methods.2 In this work, we decided to combine substrate screening with continuous parameter screening, with in situ measurements.To test whether it was possible to kinetically assess all six training set substrates (1a–f) simultaneously, a short (6 min) HPLC method was developed to resolve a mixture of the substrates and their products quantitatively (Table S3†), and a Python script was written to efficiently extract the chromatographic data in a tabulated form. By including an internal standard in the reaction mixture, quantitative concentration data was collected to confirm good mass balance for all reactions (Fig. S5†). This would allow any peak overlap with known or unknown reaction species, such as potential side products, to be observed.
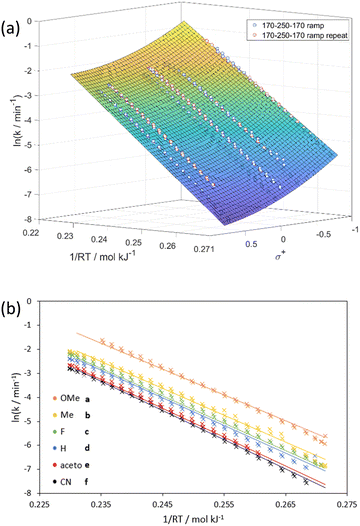
Using a solution containing an equimolar mixture of 1a–f, residence time step changes were repeated at 190, 210 and 230 °C (temperatures were lowered to avoid full conversions of the more reactive substrates) confirming first order kinetics for all six substrates. By performing a bi-directional temperature ramp (170–250–170 °C), we could generate six Arrhenius plots in a single experiment (Fig. 3a) with Ea values between 112.9–122.4 kJ mol−1. A comparison of the Arrhenius plots for allylphenylether (1d) obtained from the individual substrate (IS-TF) and one-pot (OP-TF) experiments showed good agreement (Fig. 3b); suggesting negligible interaction effects between substrates, thus validating the one-pot method.
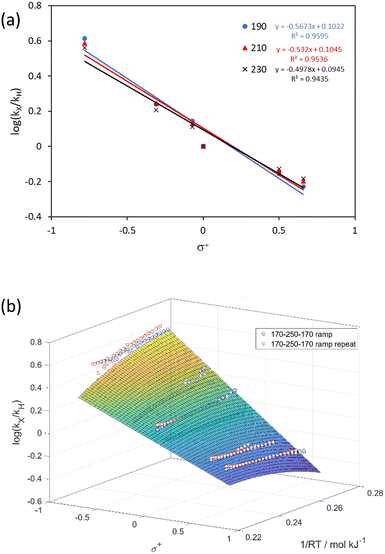
By plotting the base 10 logarithm of the relative rates (log(kX/kH)) of a substituted substrate (kX) and the unsubstituted substrate (kH) against different Hammett parameters (σp, σm, σ+, σ−), we can confirm the previously reports that σ+ best represents the substituent effect of the thermal aromatic Claisen rearrangement (Fig. S6†).21,22 Generally, the reaction rate is reduced by greater σ+ value, commensurate with the involvement of a polar transition state, which is destabilized by electron withdrawing groups.
The data gathered from the OP-TF experiments can be used to generate individual Hammett plots at each temperature (Fig. 4a). In this case, the gradient of the Hammett plot (ρ) decreases in magnitude (from −0.57 to −0.50) as the temperature increases from 190 to 230 °C,42i.e. the effect of the substituent is less prominent at higher temperatures. The data can also be visualized as a temperature-dependent Hammett plot, allowing a more rigorous evaluation of the assumed Hammett dependency (Fig. 4b).
Thermodynamic dependencies and predictive model
The data generated by this method on the example reaction were used to derive fundamental thermodynamic understanding and predict conditions for other substrates for this reaction.Previously it was hypothesized that the change in ρ of a linear Hammett plot should be proportional to 1/RT.42 We found when plotted against 1/RT, this data was best fitted by a first order dependence in σ+ and a second order dependence in 1/RT (Fig. 4b, R2 = 0.9489). When differentiated with respect to σ+ this afforded the relationship: ρ = 1.035 − 6.31(1/RT), which is different from the previously hypothesized form of ρ = m(1/RT); where m is a constant hypothetically dependent on the dielectric constant of the solvent and distance of the substituent from the reaction site.42
Mathematically, this dependency can be derived by combining the Hammett equation (1) with the Eyring equation (2). The final expression (3) shows the intercept and gradient to be related to changes in reaction entropy (dΔS‡/dσ+) and enthalpy (dΔH‡/dσ+), respectively, with changing substituent (see S4.1† for derivation). Ensuing calculations revealed values of dΔS‡/dσ+ = 20.9 J mol−1 K−1 and dΔH‡/dσ+ = 14.9 kJ mol−1, representing an interplay between the entropic and enthalpic contributions to the aromatic Claisen rearrangement reaction, and an isokinetic temperature of 715 K (ρ = 0).
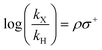 | (1) |
 | (2) |
 | (3) |
Beyond fundamental dependencies, this data allows the generation of a predictive “Arrhenius–Hammett model”, σ+vs. 1/RT vs. ln(k), for predicting rate constants for a given substrate and temperature (Fig. 5a).‡ The data used to fit this model was collected in two bi-directional temperature ramps (170–250–170 °C) on all six training substrates simultaneously. The model was fitted as first order in 1/RT (an Arrhenius relationship) and second order in σ+ for the best empirical fit to be obtained for ln(k).
The model was validated by predicting ln(k), Ea and ln(A) values for the training set of phenyl allyl ethers 1a–1f. Gratifyingly, predictions of ln(k) values yielded good results with mean absolute error (MAE) between 0.060 and 0.114, compared with the experimental data for the training substrates over the wide temperature range (Table 1 and Fig. 5b). Due to the Arrhenius dependency built into the model, Ea and ln(A) values were also generally predicted well, despite the model not being trained to produce these values accurately. With the exception of 1a, predictions of Ea values were within circa 1 kJ mol−1 of observed values. The worse prediction of substrate 1a (under-estimated by 8 kJ mol−1) is attributed to the σ+ value lying at the upper extreme of the model.
| 1×/2× | Z | MAEa of ln(k/min−1) predictions | E a/kJ mol−1 | ln(A/min−1) | ||
|---|---|---|---|---|---|---|
| Exp. | Pred. | Exp. | Pred. | |||
| a Mean absolute error (MAE) is a measure of prediction accuracy. | ||||||
| a | MeO | 0.086 | 115.4 | 107.5 | 25.5 | 23.5 |
| b | Me | 0.114 | 112.9 | 112.0 | 24.0 | 23.8 |
| c | F | 0.110 | 113.2 | 114.3 | 23.9 | 24.1 |
| d | H | 0.101 | 116.1 | 115.0 | 24.3 | 24.2 |
| e | C(O)CH3 | 0.064 | 119.2 | 119.8 | 24.8 | 24.9 |
| f | CN | 0.060 | 122.4 | 121.3 | 25.4 | 25.2 |
| g | NHAc | 0.205 | 106.9 | 109.3 | 22.9 | 23.6 |
| h | Br | 0.086 | 117.9 | 116.4 | 24.8 | 24.3 |
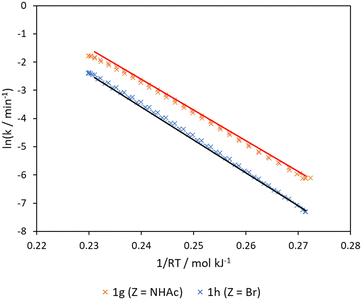
The predictability of the “Arrhenius–Hammett model” was finally tested by using it to generate the rate constants of the Claisen rearrangement of two other para-substituted phenyl allyl ether substrates 1g (Z = NHAc, σ+ = −0.60) and 1h (Z = Br, σ+ = 0.15) across the wide temperature range. The result was compared with the Arrhenius plots collected for these substrates using a bi-directional temperature ramp between 170–250 °C (Fig. 6). Pleasingly, a close match between the predicted and experimental Arrhenius plots can be obtained, despite the observation of competitive de-brominated side product for 1h (Z = Br) (Fig. S7†). Activation energy and pre-exponential factor are also adequately predicted (Table 1). These out-of-sample predictions confirm the validity of the model to interpolate to other substrates over the temperature range.
Conclusions
Through the novel combination of one-pot and transient flow (OP-TF) methodology, we have shown great improvements in the diversity, quality and efficiency of the collection of reaction data, compared to traditional methods. Data was collected on continuous parameter series (time and temperature) with simultaneous collection of discrete parameter series (substrate substituent).Reaction data for six Claisen rearrangement substates over an 80 °C temperature range can be obtained in just 6 h, including repeats. From this data challenging fundamental kinetic parameters can be obtained and a predictive multivariate polynomial model can be constructed to predict rate constants for different temperatures and substrates, thus assessing synthetic feasibility of this rearrangement. As σ+ values are widely available43 or calculable44 for such substrates, this should prove a valuable tool to those wishing to implement an aromatic Claisen rearrangement. The parameter space used includes liquid and supercritical ethanol over which a solvent polarity change occurs; interestingly, no change in activation energy was observed, implying minimal solvent polarity effect on the reaction.
We believe that the novel method described in this work is readily transferable to other unimolecular reactions, including not only pericyclic rearrangements but also other sigmatropic and isomerization reactions – many of which occur in a similar challenging thermal reaction space. Although exemplified on a unimolecular reaction, our method could be applied as generally as previous ‘one-pot’ and related competition experiment methods.13,17,45–47 These have been utilised on a range of uni- and bimolecular reactions to examine substituent effects, limited only by the deconvolutional power of the chosen analytical method. The applicability of our method to bimolecular reactions is currently underway and will be reported in due course.
Finally, other spectroscopic tools could also be utilised but would impose more specific analytical limitations to our method.14,45,48 However, deployment of an on-line HPLC in our work improved our method as it can offer accurate quantification of each reaction component, which cannot be achieved easily by on-line spectroscopic techniques. We envisage that the applicability of the method can be further expanded by recent advances in newer techniques for the analysis of complex mixtures, including ultra-performance (UPLC), ultra-fast (UFLC) and Rapid Resolution (RRLC) liquid chromatography, along with the availability of ever more sophisticated detectors.49
Author contributions
LS conducted the experimental work, collected and analysed the data. All other authors offered advice during the work and mentorship to LS. LS and KKH wrote the original draft and subsequent revisions of the manuscript, which were reviewed by all the other authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to BASF SE for financial support. This project was supported by access to instrumentation and expertise at the Centre for Rapid Online Analysis of Reactions (ROAR) at Imperial College London [EPSRC, EP/R008825/1 and EP/V029037/1]. We are grateful to Imperial College Advanced Hackspace for their help in constructing the Peltier cooling device.Notes and references
- N. A. of E. and I. of M. National Academy of Sciences, Ensuring Integrity, Access. Steward. Res. Data Digit. Age, 2009, DOI:10.17226/12615.
- S. M. Mennen, C. Alhambra, C. L. Allen, M. Barberis, S. Berritt, T. A. Brandt, A. D. Campbell, J. Castañón, A. H. Cherney, M. Christensen, D. B. Damon, J. Eugenio De Diego, S. García-Cerrada, P. García-Losada, R. Haro, J. Janey, D. C. Leitch, L. Li, F. Liu, P. C. Lobben, D. W. C. Macmillan, J. Magano, E. McInturff, S. Monfette, R. J. Post, D. Schultz, B. J. Sitter, J. M. Stevens, I. I. Strambeanu, J. Twilton, K. Wang and M. A. Zajac, Org. Process Res. Dev., 2019, 23, 1213–1242 CrossRef CAS.
- L. Schrecker, J. Dickhaut, C. Holtze, P. Staehle, M. Vranceanu, K. Hellgardt and K. K. Hii, React. Chem. Eng., 2022, 8, 41–46 RSC.
- F. Florit, A. M. K. Nambiar, C. P. Breen, T. F. Jamison and K. F. Jensen, React. Chem. Eng., 2021, 6, 2306–2314 RSC.
- S. Mozharov, A. Nordon, D. Littlejohn, C. Wiles, P. Watts, P. Dallin and J. M. Girkin, J. Am. Chem. Soc., 2011, 133, 3601–3608 CrossRef CAS PubMed.
- J. S. Moore and K. F. Jensen, Angew. Chem., Int. Ed., 2014, 53, 470–473 CrossRef CAS PubMed.
- B. M. Wyvratt, J. P. McMullen and S. T. Grosser, React. Chem. Eng., 2019, 4, 1637–1645 RSC.
- C. J. Taylor, M. Booth, J. A. Manson, M. J. Willis, G. Clemens, B. A. Taylor, T. W. Chamberlain and R. A. Bourne, Chem. Eng. J., 2021, 413, 127017 CrossRef CAS.
- M. V. Gomez, A. M. Rodriguez, A. De La Hoz, F. Jimenez-Marquez, R. M. Fratila, P. A. Barneveld and A. H. Velders, Anal. Chem., 2015, 87, 10547–10555 CrossRef CAS PubMed.
- P. Sagmeister, J. Poms, J. D. Williams and C. O. Kappe, React. Chem. Eng., 2020, 5, 677–684 RSC.
- J. S. Moore, C. D. Smith and K. F. Jensen, React. Chem. Eng., 2016, 1, 272–279 RSC.
- K. C. Aroh and K. F. Jensen, React. Chem. Eng., 2018, 3, 94–101 RSC.
- H. M. Yau, A. K. Croft and J. B. Harper, Chem. Commun., 2012, 48, 8937–8939 RSC.
- H. M. Yau, R. S. Haines and J. B. Harper, J. Chem. Educ., 2015, 92, 538–542 CrossRef CAS.
- K. W. Fiori and J. Du Bois, J. Am. Chem. Soc., 2007, 129, 562–568 CrossRef CAS PubMed.
- J. B. C. Mack, T. A. Bedell, R. J. Deluca, G. A. B. Hone, J. L. Roizen, C. T. Cox, E. J. Sorensen and J. Du Bois, J. Chem. Educ., 2018, 95, 2243–2248 CrossRef CAS.
- R. J. Mullins, A. Vedernikov and R. Viswanathan, J. Chem. Educ., 2004, 81, 1357–1361 CrossRef CAS.
- J. Lu, I. Paci and D. C. Leitch, Chem. Sci., 2022, 13, 12681–12695 RSC.
- L. Claisen, Ber. Dtsch. Chem. Ges., 1912, 45, 3157–3166 CrossRef CAS.
- A. M. M. Castro, Chem. Rev., 2004, 104, 2939–3002 CrossRef CAS PubMed.
- H. L. Goering and R. R. Jacobson, J. Am. Chem. Soc., 1958, 80, 3277–3285 CrossRef CAS.
- W. N. White, D. Gwynn, R. Schlitt, C. Girard and W. Fife, J. Am. Chem. Soc., 1958, 80, 3271–3277 CrossRef CAS.
- W. N. White and W. K. Fife, J. Am. Chem. Soc., 1961, 83, 3846–3853 CrossRef CAS.
- W. N. White and C. D. Slater, J. Org. Chem., 1961, 26, 3631–3638 CrossRef CAS.
- W. N. White and C. D. Slater, J. Org. Chem., 1962, 27, 2908–2914 CrossRef CAS.
- W. N. White and E. F. Wolfarth, J. Org. Chem., 1961, 26, 3509–3510 CrossRef CAS.
- H. Kobayashi, B. Driessen, D. J. G. P. Van Osch, A. Talla, S. Ookawara, T. Noël and V. Hessel, Tetrahedron, 2013, 69, 2885–2890 CrossRef CAS.
- M. Christensen, F. Adedeji, S. Grosser, K. Zawatzky, Y. Ji, J. Liu, J. A. Jurica, J. R. Naber and J. E. Hein, React. Chem. Eng., 2019, 4, 1555–1558 RSC.
- C. Waldron, A. Pankajakshan, M. Quaglio, E. Cao, F. Galvanin and A. Gavriilidis, React. Chem. Eng., 2019, 4, 1623–1636 RSC.
- C. A. Hone, N. Holmes, G. R. Akien, R. A. Bourne and F. L. Muller, React. Chem. Eng., 2017, 2, 103–108 RSC.
- D. Cortés-Borda, E. Wimmer, B. Gouilleux, E. Barré, N. Oger, L. Goulamaly, L. Peault, B. Charrier, C. Truchet, P. Giraudeau, M. Rodriguez-Zubiri, E. Le Grognec and F. X. Felpin, J. Org. Chem., 2018, 83, 14286–14289 CrossRef PubMed.
- D. Perera, J. W. Tucker, S. Brahmbhatt, C. J. Helal, A. Chong, W. Farrell, P. Richardson and N. W. Sach, Science, 2018, 359, 429–434 CrossRef CAS PubMed.
- B. J. Reizman and K. F. Jensen, Org. Process Res. Dev., 2012, 16, 1770–1782 CrossRef CAS.
- P. Sagmeister, R. Lebl, I. Castillo, J. Rehrl, J. Kruisz, M. Sipek, M. Horn, S. Sacher, D. Cantillo, J. D. Williams and C. O. Kappe, Angew. Chem., 2021, 60, 8139–8148 CrossRef CAS PubMed.
- H. C. Brown and Y. Okamoto, J. Am. Chem. Soc., 1958, 80, 4979–4987 CrossRef CAS.
- D. H. McDaniel and H. C. Brown, J. Org. Chem., 1958, 23, 420–427 CrossRef CAS.
- J. Lu, E. C. Boughner, C. L. Liotta and C. A. Eckert, Fluid Phase Equilib., 2002, 198, 37–49 CrossRef CAS.
- J. H. Dymond and R. Malhotra, Int. J. Thermophys., 1988, 9, 941–951 CrossRef.
- O. P. Schmidt and D. G. Blackmond, ACS Catal., 2020, 10, 8926–8932 CrossRef CAS.
- A. R. Bazaev, I. M. Abdulagatov, E. A. Bazaev and A. Abdurashidova, Int. J. Thermophys., 2007, 28, 194–219 CrossRef CAS.
- L. M. Baumgartner, J. M. Dennis, N. A. White, S. L. Buchwald and K. F. Jensen, Org. Process Res. Dev., 2019, 23, 1594–1601 CrossRef CAS.
- H. Jaffé, Chem. Rev., 1953, 53, 191–261 CrossRef.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef CAS.
- M. Bragato, G. F. Von Rudorff and O. A. Von Lilienfeld, Chem. Sci., 2020, 11, 11859–11868 RSC.
- M. Ballard, M. Bown, S. James and Q. Yang, Energy Procedia, 2011, 4, 291–298 CrossRef CAS.
- N. D. Bartolo and K. A. Woerpel, J. Org. Chem., 2018, 83, 10197–10206 CrossRef CAS PubMed.
- T. Holm, J. Org. Chem., 2000, 65, 1188–1192 CrossRef CAS PubMed.
- M. V. Gomez and A. de la Hoz, Beilstein J. Org. Chem., 2017, 13, 285–300 CrossRef CAS PubMed.
- C. Bhati, N. Minocha, D. Purohit, S. Kumar, M. Makhija, S. Saini, D. Kaushik and P. Pandey, Biomed. Pharmacol. J., 2022, 15, 729–746 CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3re00439b |
| ‡ ln(k) is a more useful term to predict than log(kX/kH) as it is an absolute measure of rate instead of a relative term. |
| This journal is © The Royal Society of Chemistry 2023 |