Open Access Article
Open Access ArticleKinetic analysis of silicon–lithium alloying reaction in silicon single crystal using soft X-ray absorption spectroscopy†
Nur Chamidah a,
Akito Suzukia,
Takeshi Shimizua,
Chengchao Zhonga,
Keiji Shimoda
a,
Akito Suzukia,
Takeshi Shimizua,
Chengchao Zhonga,
Keiji Shimoda a,
Ken-ichi Okazakia,
Toyonari Yajib,
Koji Nakanishic,
Motoaki Nishijimad,
Hajime Kinoshitad and
Yuki Orikasa
a,
Ken-ichi Okazakia,
Toyonari Yajib,
Koji Nakanishic,
Motoaki Nishijimad,
Hajime Kinoshitad and
Yuki Orikasa *a
*a
aDepartment of Applied Chemistry, Graduate School of Life Sciences, Ritsumeikan University, 1-1-1 Nojihigashi, Kusatsu, Shiga 525-8577, Japan. E-mail: orikasa@fc.ritsumei.ac.jp
bResearch Organization of Science and Engineering, Ritsumeikan University, 1-1-1 Nojihigashi, Kusatsu, Shiga 525-8577, Japan
cLaboratory of Advanced Science and Technology for Industry, University of Hyogo, 3-1-2 Koto, Ako-gun, Kamigori-cho, Hyogo 678-1205, Japan
dKRI Inc, 134 Chudojiminami-machi, Shimogyo-ku, Kyoto 600-8813, Japan
First published on 7th June 2023
Abstract
Silicon has been considered to be one of the most promising anode active materials for next-generation lithium-ion batteries due to its large theoretical capacity (4200 mA h g−1, Li22Si5). However, silicon anodes suffer from degradation due to large volume expansion and contraction. To control the ideal particle morphology, an experimental method is required to analyze anisotropic diffusion and surface reaction phenomena. This study investigates the anisotropy of the silicon–lithium alloying reaction using electrochemical measurements and Si K-edge X-ray absorption spectroscopy on silicon single crystals. During the electrochemical reduction process in lithium-ion battery systems, the continuous formation of solid electrolyte interphase (SEI) films prevents the achievement of steady-state conditions. Instead, the physical contact between silicon single crystals and lithium metals can prevent the effect of SEI formation. The apparent diffusion coefficient and the surface reaction coefficient are determined from the progress of the alloying reaction analyzed by X-ray absorption spectroscopy. While the apparent diffusion coefficients show no clear anisotropy, the apparent surface reaction coefficient of Si (100) is more significant than that of Si (111). This finding indicates that the surface reaction of silicon governs the anisotropy of practical lithium alloying reaction for silicon anodes.
1. Introduction
Lithium-ion batteries have become ubiquitous in our daily lives, powering everything from smartphones to electric vehicles. However, they suffer from low energy density, cost, and safety issues, which hinder their widespread adoption in some applications.1 The quest to face this challenge has led many researchers to explore the potential of silicon as an anode material for lithium-ion batteries. Its extraordinarily high theoretical specific capacity of up to 4200 mA h g−1 for alloyed silicon Li22Si5 is approximately eleven times higher than ∼372 mA h g−1 of graphite, which is currently used as anodes.2,3 In addition, the abundant resources of silicon and its high safety indicate the potential of silicon to revolutionize the energy storage industry.4–6 However, many have known that typical silicon anodes suffer from huge volume expansion during the lithiation process (up to 400%), leading to capacity fade due to mechanical and electrical integrity failures.6–9 Furthermore, the slow kinetics caused by the lower diffusion coefficient value of Li in silicon provides an extra challenge for achieving high-performance lithium-ion batteries.8,10 Therefore, the fundamental understanding of silicon-lithium (Si–Li) alloying reaction mechanism is essential to develop a silicon anode with less capacity degradation during the electrochemical reaction.One of the origins of capacity degradation is the cracking of silicon particles, which accelerates the further electrolyte decomposition, causing the irreversible charge reaction.11,12 The cracks are caused by anisotropic lithium diffusion, where inhomogeneous volume expansion and silicon compression cause enormous strain in the particles.13–16 The scanning electron microscopic studies of electrochemical lithiation into silicon nanowires indicated that the Si–Li alloying reaction exhibits anisotropy properties based on the crystal plane.13,17–22 Nevertheless, the effect of the anisotropy of the lithiation with silicon of different orientations remains unclear.
Many findings have reported energetically favourable Li–Si alloying reactions in the [110] direction of the Si crystal plane since it experiences less structural degradation and minimizes the amount of capacity lost during electrochemical cycling.14,18,20,23–25 Meanwhile, even though stresses are concentrated in the Si (100) crystal plane due to the tensile and compressive forces,23,26,27 recent findings also indicate that Si (100) has better cycle reversibility and faster Li diffusion compared to Si (111) and (110) due to its better interfacial reaction with lithium.26,28–30 The simulation study by the finite element method has also successfully demonstrated the crack formation in the (100) direction,23 which leads to more exposure of the silicon surface to lithium.26 To suppress degradation caused by anisotropy, morphology control such as nanowires and leaf shapes have been proposed.14,31–33 Moreover, Lau et al. reported that the effect of highly doped n-type silicon single crystal seems to reduce surface fragmentation during initial lithiation.30 Uncovering the anisotropy of the Si–Li alloy reaction will be valuable insight for improving the cycle properties of Si. In this work, we present an approach to observe the lithium alloying mechanism using a straightforward model by employing Sb-doped Si (100) and Si (111) single crystals as the electrode material in the electrochemical system.
Electrochemical of Si–Li alloying reaction consists of the following four processes: (1) desolvation of Li ions, (2) anisotropic lithium ion intercalation to the Si surface, (3) anisotropic diffusion of lithium ions into the Si crystal, (4) phase transformation to the Si–Li alloy phase.15,21,26 Furthermore, solid electrolyte interphase (SEI) exists in electrochemical reactions using organic electrolytes and forms a complex electrode/electrolyte interface.34,35
Theoretical studies have been carried out to analyze the anisotropy of alloying reactions, especially at the atomic level.14 Similarly, the anisotropy of diffusion phenomena with surface reactions has also been analyzed.36 Nonetheless, to the best of the authors' knowledge, experimental attempts to quantify the anisotropy of diffusion phenomena have not been successful. Many attempts have been made to calculate the apparent diffusion coefficient by electrochemical measurements, such as galvanostatic intermittent titration technique (GITT) and impedance spectroscopy.37–39 It appears that anisotropy phenomena can be analyzed by the electrochemistry of single crystals. However, some results were reported for GITT using thin films, where the apparent diffusion coefficient highly depends on the electrolyte.34 In addition, excessive expansion and compression of silicon cause irreversible changes in the SEI, which in this case, is excluded from the application of electrochemical determination of chemical diffusion coefficient.
In this study, we propose the method of attaching Li to Si single crystals for the Si–Li alloy reaction without SEI formation. That is, the Si–Li alloying reaction can be analyzed by the adhesion of Si and Li with the simple interface of Si|Si–Li|Li. The contact time dependence of the progress of the Si–Li alloying reaction is analyzed for single crystals with Si (100) and (111) planes by Si K-edge X-ray absorption spectroscopy (XAS) measurements. Using the diffusion solution obtained by solving the diffusion equation, the apparent diffusion coefficient inside the silicon single crystal and the surface reaction coefficient on the silicon single crystal can be separated, and their parameters are discussed.
2. Experimental
2.1 Materials
Sb-doped Si single crystals (length: 10 mm, width: 10 mm, thickness: 0.525 mm) were purchased from Crystal Base Co., Ltd. The resistances of Si single crystals (100) and (111) were 0.0018–0.02 and 0.01–0.02 Ω cm, respectively. Si single crystals were immersed in piranha solution (a mixture of H2SO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O2 = 2
H2O2 = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in volume ratio) for 30 min and then washed with ultrapure water. In order to remove the surface oxide film, Si single crystals were immersed in 5 wt% of HF for 5 min. Each pretreatment process was always followed by a thorough rinsing using ultrapure water. These samples were enclosed in a laminated bag in a glove box filled with Ar atmosphere to be characterized with X-ray photoelectron spectroscopy (XPS) (PHI5000 Versa Probe 2, ULVAC-PHI, Inc.).
1 in volume ratio) for 30 min and then washed with ultrapure water. In order to remove the surface oxide film, Si single crystals were immersed in 5 wt% of HF for 5 min. Each pretreatment process was always followed by a thorough rinsing using ultrapure water. These samples were enclosed in a laminated bag in a glove box filled with Ar atmosphere to be characterized with X-ray photoelectron spectroscopy (XPS) (PHI5000 Versa Probe 2, ULVAC-PHI, Inc.).
2.2 Electrochemistry
Three-electrodes electrochemical cells (Fig. S1†) were fabricated in an Ar-filled glove box. Pretreated Si single crystals were used as working electrodes, and lithium metal foils (99.9%, thickness: 200 μm, Honjo Metal Co., Ltd.) were used as the counter and reference electrodes. 1 mol dm−3 LiPF6 in ethylene carbonate and ethyl methyl carbonate (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 in volume ratio, Kishida Chemical Co., Ltd) was used as an electrolyte. After keeping the initial voltage for 1 hour, cyclic voltammogram (CV) measurements were carried out using potentiostat (HZ-7000, Hokuto Denko) at the scan rate of 1 mV s−1 between 0.01 V–2.40 V (vs. Li/Li+). Electrochemical impedance spectroscopy (EIS) measurements (voltage amplitude: 10 mV, frequency: 0.1 Hz–1 MHz, VersaSTAT4, AMETEK) were carried out at 25 °C in the thermostat (SU-221, ESPEC) after the voltage was set to 0.01 V (vs. Li/Li+). Time dependence was investigated every 1 hour in the same frequency and voltage amplitude mentioned above.
7 in volume ratio, Kishida Chemical Co., Ltd) was used as an electrolyte. After keeping the initial voltage for 1 hour, cyclic voltammogram (CV) measurements were carried out using potentiostat (HZ-7000, Hokuto Denko) at the scan rate of 1 mV s−1 between 0.01 V–2.40 V (vs. Li/Li+). Electrochemical impedance spectroscopy (EIS) measurements (voltage amplitude: 10 mV, frequency: 0.1 Hz–1 MHz, VersaSTAT4, AMETEK) were carried out at 25 °C in the thermostat (SU-221, ESPEC) after the voltage was set to 0.01 V (vs. Li/Li+). Time dependence was investigated every 1 hour in the same frequency and voltage amplitude mentioned above.
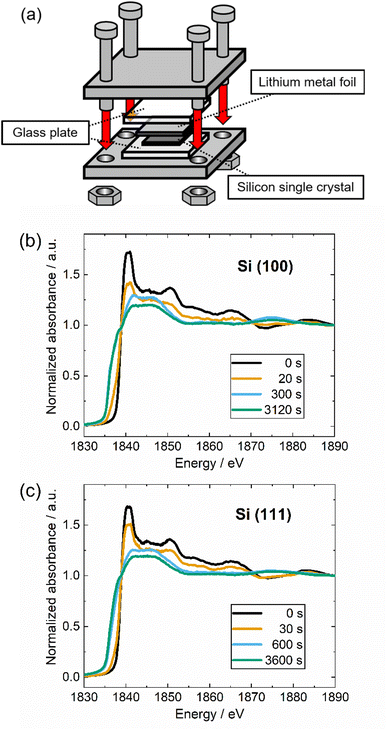
2.3 Contact between Si single crystal and Li
Si single crystals were contacted with Li metal foil at various times using homemade jigs. The jigs were disassembled, and Li metal was removed from Si single crystals. The Si single crystals were put into the transfer vessel for the XAS measurements. These procedures were carried out in an Ar-filled glove box. Si K-edge XAS measurements were performed at the soft X-ray double crystal beamline, BL-10, in the SR Center Ritsumeikan University. Si single crystals were put into a vacuum chamber without air exposure. X-ray was monochromized by InSb (111) double-crystal and XAS was measured in a fluorescence yield mode.3. Results and discussion
Silicon surface condition is crucial for understanding the initiation of alloying reactions. Si crystals were pretreated with piranha solution and hydrofluoric acid to remove the organic contamination and oxide layer at the surface before assembling into the electrochemical cell. We then examined the chemical state changes of the Si (100) and (111) crystal surface before and after the pretreatment process by XPS (Fig. S2†). O 1s XPS spectra (Fig. S2(a) and (c)†) describe the peak intensity at binding energy 532 eV, which reduces to less than 10% after the pretreatment. This reduction corresponds to the removal of oxide film by HF solution, resulting in a decrease of oxygen atoms ratio in the total spectrum. In addition, Si 2p XPS spectra (Fig. S2(b) and (d)†) show two peaks at 103 eV and 99 eV for pristine silicon single crystal before pretreatment. The peak at the binding energy of 103 eV, which corresponds to SiOx peak, is no longer traced after the pretreatment. Considering these results, the pretreatment process of silicon crystals before assembling them to the cell is considered essential since the surface reaction in the silicon will determine the Si–Li alloying reaction.The analysis of lithium alloying reaction by electrochemical measurement was examined. CV measurements were performed to study the electrochemical behaviour of silicon single crystal in different crystal planes. Fig. 1 shows the cyclic voltammograms of Si (100) and Si (111). A sharp reduction peak is confirmed at 0.1 V, suggesting that a large reduction current is induced by Si–Li alloying reaction.40,41 Oxidation peaks are observed around 0.31 and 0.51 V, corresponding to lithium dealloying from the silicon crystal structure.29,41 The pattern of the CV profile is consistent with previously reported CVs of silicon single crystal (100) or (111) crystal planes; the cathodic peak below 0.1 V originates from the formation of the Li15Si4 alloying phase with amorphization, and the two peaks in the anodic process originate from the dealloying from the Li15Si4 alloying phase to crystalline Si with Li4.2Si.30,42–44 To our knowledge, there have been no reports comparing (100) and (111) CVs of silicon single crystals. The coulomb charge during the first cathodic scan is 4.58 × 10−6 mA h cm−2 for Si (100) and 2.25 × 10−6 mA h cm−2 for Si (111). The current density of the reduction and oxidation current of Si (100) is about two times larger than the Si (111) during the first cycle. This phenomenon can be attributed to the lithium insertion behaviour, which exhibits a higher tendency to diffuse along Si (100) than in Si (111).26 After the second cycle, cathodic currents begin to be observed at higher potentials. This result is consistent with reports of higher lithium alloying potentials after the second cycle as an effect of amorphization.28,30,45 The cycle-by-cycle current value change indicates that the kinetics varies continuously due to morphological changes on the silicon surface. Therefore, it is difficult to calculate the chemical diffusion coefficient of silicon through CV analysis.
 | ||
| Fig. 1 Cyclic voltammograms of (a) Si (100) and (b) Si (111) single crystal, respectively. The scan rate was set at 1.0 mV s−1, and the scan range was 0.01–2.40 V (vs. Li/Li+) for 5 cycles. | ||
The electrochemical process of Si–Li alloying reaction involves the formation of SEI. The time dependence of SEI formation at low potentials is analyzed by EIS. The potential was set to 0.01 V through chronoamperometry measurements. EIS measurements were performed at each hour for a total of 5 hours. The results are plotted in the Nyquist plot shown in Fig. 2, showing an increase in the size of semicircle. In the case of single crystal measurements, the alloying reaction is concentrated on the surface of single crystal at a depth of a few micrometers.41 The semicircle of the EIS in this measurement corresponds to the reaction at the electrode/electrolyte at the interface. Once the steady state of lithium alloying reaction is reached, increasing the time of the alloying reaction by holding the potential at 0.01 V should not significantly change the size of the semicircle. Therefore, the enlargement of the semicircle over time is likely attributed to the electrolyte decomposition at low potential, leading to the formation of SEI. Consequently, this alteration in the SEI layer influences the impedance behavior. Further analysis was conducted by XAS measurement to investigate the apparent diffusion of lithium in silicon, which could not be evaluated using electrochemical measurement. The silicon single crystals were examined by scanning the potential down to 0.01 V using LSV method and maintained for 5 hours (Fig. S3(a)†). X-ray absorption near-edge structure (XANES) region of Si K-edge XAS spectra shows an energy shift in the initial and alloyed silicon single crystals (100) (Fig. S3(b)†), but the shift is relatively small. The impedance results indicate that holding the potential to the silicon at 0.01 V leads to an increase in Si expansion associated with lithium alloying, further promoting SEI formation and slowing the electrochemical lithium alloying reaction. These results suggest that the continuous formation of SEI occurs at the electrode–electrolyte interface, especially at low potentials. Therefore, the determination of chemical diffusion coefficients by EIS or GITT methods is not applicable.
The formation of SEI on the surface of silicon single crystals during electrochemical reactions involves complex phenomena that pose challenges to conducting quantitative analysis using XANES. As a strategy to eliminate the SEI formation, the silicon single crystal samples were contacted directly to the lithium metal into a jig, as shown in Fig. 3(a). The overall alloying mechanism of Si–Li alloying reaction may differ between the direct contact and alloying process with the presence of electrolyte. Nevertheless, the underlying principles and reaction phenomena related remain consistent in terms of its chemical potential. The alloying of Li to Si in our direct contact system is derived by the reducibility of lithium which occur at 0 V vs. Li/Li+. Meanwhile, the electrochemical potential for Li-alloying reaction for Si anode is approximately 0.1 V vs. Li/Li+.10 By taking this into account, our direct contact method enables a straightforward analysis of the fundamental aspects of the alloying reaction between Si and Li independently from the complex reaction involving the SEI formation. Si K-edge XANES results of Si (100) and Si (111) for various contacted times are shown in Fig. 3(b) and (c), respectively. Compared to Si (111), the peak intensity of Si (100) significantly reduces after 20 seconds of contact with lithium, and the low energy side of the absorption edge is significantly broadened. This result qualitatively indicates that the alloying reaction of Si (100) with lithium takes a shorter time. The peak intensity around 1840 eV reduces, and with the longer contacting time, the entire spectrum shifts to a lower energy level. The significant change of electron density caused by the lithium insertion into silicon is assumed to be responsible for this shift.15,46 Furthermore, an isosbestic point is observed around 1838 eV for both types of silicon crystal due to the fact that the observed Si–Li alloying reaction is an apparent two-phase reaction system.19,45,47 From this trend, by decomposing the XANES spectra into the initial Si and lithiated phase components, quantitative information can be obtained on the progress of the alloying reaction.
The calculated progression of the lithium alloying reaction versus reaction time from the two-component XANES analysis of Si(100) and (111) are shown in Fig. 4(a) and (b), respectively. For Si (100), the alloying reaction is sufficiently well completed within approximately 100 s after the contact starts, whereas for Si (111) takes approximately 500 s. The apparent lithium alloying reaction can be divided into a lithium insertion process at the silicon surface and lithium diffusion into the silicon subsurface, followed by phase transformation. In this study, the former reaction is regarded as the surface reaction process and the latter as the apparent diffusion process. The surface reaction coefficient and the diffusion coefficient are calculated by fitting the data shown in Fig. 4(a) and (b).
 | ||
| Fig. 4 Relationship between the contacting time and the state of alloying reaction in (a) Si (100) and (b) Si (111) single crystals. These plots were fitted to diffusion solution equation proposed by Crank.48 | ||
The thickness of the silicon is 0.525 mm, which is thicker than that of a general electrode active material. Therefore, we assumed that the diffusion length was sufficient for the semi-infinite diffusion approximation.48 The one-dimensional diffusion equation is given by eqn (1) according to Fick's second law:48
 | (1) |
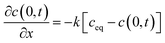 | (2) |
 | (3) |
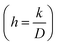 | (4) |
 | (5) |
The graph plotting eqn (3) is shown in Fig. S4.†
Furthermore, to calculate the reaction ratio at the reaction time t (0 ≤ t ≤ T, T is the equilibrium time of Si–Li alloying reaction) using the eqn (3), we defined Mτ is the amount of molar of Si–Li alloy (mol) at the reaction time τ (s) and Meq which is the amount of molar of Si–Li alloy (mol) at T, and Mτ/Meq as reaction ratio. In this work, we assumed that L, which is the depth of Si–Li alloy (cm) at the time of T is equal to the detection depth of fluorescence XAS λf (cm) in the eqn (6) because the diffusion length of lithium in Si single crystals can be only detected up to λf as follows:49
 | (6) |
The amount of substance of Si–Li alloy present up to the depth L at the time τ is determined by the integral value up to the depth L. In addition, Meq was calculated as CeqL because C(x,t) reached Ceq at the time of T. Therefore, the reaction ratio of Mτ/Meq at the time of τ as follows:
 | (7) |
| L=l1 + l2 | (8) |
 | (9) |
In this work, we calculated the apparent diffusion coefficients and surface reaction coefficients using eqn (9) for fitting.
The calculated apparent diffusion coefficients (D) of Si (100) and Si (111) are 6.6 × 10−10 and 3.2 × 10−10 cm2 s−1, respectively. In this experiment, lithium in single crystal can diffuse easily to various crystal planes, indicating that the diffusion is not one-dimensional. Hence, even if there is anisotropy of the diffusion coefficient, the apparent diffusion coefficient obtained in this experiment would not differ significantly. On the other hand, the calculated surface reaction coefficients (k) of Si (100) and Si (111) are 5.0 × 10−5 and 4.0 × 10−6 cm s−1, respectively. The surface reaction coefficient at [100] is more than one order of magnitude higher because the surface reaction occurs at a two-dimensional interface.
The calculated surface reaction coefficients for Si (100) and (111) in this study show the opposite trend to the energy barrier for surface layer lithiation, as obtained by density functional theory (DFT).18,26,50 This is likely because the energy barrier calculated by DFT is based on the assumption that the crystal structure remains intact, whereas in actual lithium alloying, the crystal structure is amorphized as lithium penetrates from the surface to the first Si layer.41 In the actual alloying reaction, amorphization occurs by displacing silicon atoms on the surface. Wang et al. calculated the degree of amorphization progression at each crystal plane by molecular dynamics and found that the crystals are more likely to collapse in the order of (100), (111), and (110).23 Once amorphized, the cage-like silicon structure which hindered the insertion of lithium is destroyed. As a result, Si (100) reacts more with lithium and accelerates the reaction, leading to a higher surface area.
In order to gain more comprehensive understanding of the structural properties and electric states of the LiSi alloy, future studies can explore the integration of soft X-ray emission spectroscopy (SXES) with synchrotron radiation light source such as XAS.51 Aoki et al. have demonstrated the applicability of SXES with XRD and SEM in characterizing the structure, composition, and electronic states of similar LiSi alloy systems.41 Incorporating SXES and XAS would further enhance the structural analysis capabilities for future investigations of LiSi alloy.
4. Conclusion
We have examined the anisotropy of the lithium alloying reaction of Si (100) and (111) single crystal anodes. The electrochemical reaction causes the continuous formation of SEI, which disturbs the steady state for electrochemical analysis for EIS and GITT. The physical contact between lithium metal and silicon crystals allows the alloying reaction without the effect of SEI. Si K-edge XAS provides the state of the alloying reaction. The time dependence of the alloying state provides the apparent diffusion coefficient and the surface reaction coefficient. The apparent diffusion coefficients in Si (100) and Si (111) are not significantly different because practical lithium diffusion in bulk Si is three-dimensional. Nevertheless, the surface reaction coefficient of Si (100) is one order higher than that of Si (111), indicating that the anisotropy of the Li alloying reaction in Si is dominated by the surface reaction.Author contributions
Nur Chamidah: data curation, investigation, writing – original draft. Akito Suzuki: methodology, formal analysis, writing – original draft. Takeshi Shimizu: visualization. Chengchao Zhong: writing – review & editing. Keiji Shimoda: writing – review & editing. Ken-ichi Okazaki: writing – review & editing. Toyonari Yaji: data curation, investigation. Koji Nakanishi: methodology. Motoaki Nishijima: conceptualization. Hajime Kinoshita: conceptualization. Yuki Orikasa: conceptualization, supervision, project administration, funding acquisition, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The part of this work was supported by JSPS KAKENHI Grant Number 19H02694, Ritsumeikan Global Innovation Research Organization, Ritsumeikan Advanced Research Academy, and The Science Research Promotion Fund in Promotion and Mutual Aid Corporation for Private Schools of Japan.References
- J.-M. Tarascon and M. Armand, Nature, 2001, 414, 359–367 CrossRef CAS PubMed.
- M. Gu, Y. He, J. Zheng and C. Wang, Nano Energy, 2015, 17, 366–383 CrossRef CAS.
- L. Sun, Y. Liu, R. Shao, J. Wu, R. Jiang and Z. Jin, Energy Storage Mater., 2022, 46, 482–502 CrossRef.
- M. Li, J. Lu, Z. Chen and K. Amine, Adv. Mater., 2018, 30, 1–24 Search PubMed.
- K. Feng, M. Li, W. Liu, A. G. Kashkooli, X. Xiao, M. Cai and Z. Chen, Small, 2018, 14, 1702737 CrossRef PubMed.
- Y. X. Yin, L. J. Wan and Y. G. Guo, Chin. Sci. Bull., 2012, 57, 4104–4110 CrossRef CAS.
- W. J. Zhang, J. Power Sources, 2011, 196, 13–24 CrossRef CAS.
- K. Mala, Y. Jadhav, W. Malik, D. Late, S. I. Patil and S. M. Jejurikar, Surf. Interfaces, 2020, 19, 100476 CrossRef CAS.
- D. M. Piper, T. A. Yersak and S.-H. Lee, J. Electrochem. Soc., 2013, 160, A77–A81 CrossRef CAS.
- G. Zhu, Y. Wang, S. Yang, Q. Qu and H. Zheng, J. Mater., 2019, 5, 164–175 Search PubMed.
- S. H. Kim, K. Dong, H. Zhao, A. A. El-Zoka, X. Zhou, E. V. Woods, F. Giuliani, I. Manke, D. Raabe and B. Gault, J. Phys. Chem. Lett., 2022, 13, 8416–8421 CrossRef CAS PubMed.
- J. S. Corsi, S. S. Welborn, E. A. Stach and E. Detsi, ACS Energy Lett., 2021, 6, 1749–1756 CrossRef CAS.
- C. K. Chan, H. Peng, G. Liu, K. McIlwrath, X. F. Zhang, R. A. Huggins and Y. Cui, Nat. Nanotechnol., 2008, 3, 31–35 CrossRef CAS PubMed.
- Y. Li, K. Zhang, Y. Pan and F. Yang, J. Energy Storage, 2023, 57, 106271 CrossRef.
- Y. Domi, H. Usui, A. Ando, K. Nishikawa and H. Sakaguchi, ACS Appl. Energy Mater., 2020, 3, 8619–8626 CrossRef CAS.
- J. L. Goldman, B. R. Long, A. A. Gewirth and R. G. Nuzzo, Adv. Funct. Mater., 2011, 21, 2412–2422 CrossRef CAS.
- T. L. Chan and J. R. Chelikowsky, Nano Lett., 2010, 10, 821–825 CrossRef CAS PubMed.
- Q. Zhang, W. Zhang, W. Wan, Y. Cui and E. Wang, Nano Lett., 2010, 10, 3243–3249 CrossRef CAS PubMed.
- S. Huang and T. Zhu, J. Power Sources, 2011, 196, 3664–3668 CrossRef CAS.
- S. C. Jung, J. W. Choi and Y. K. Han, Nano Lett., 2012, 12, 5342–5347 CrossRef CAS PubMed.
- S. C. Jung and Y. K. Han, Electrochim. Acta, 2012, 62, 73–76 CrossRef CAS.
- J. L. Goldman, B. R. Long, A. A. Gewirth and R. G. Nuzzo, Adv. Funct. Mater., 2011, 21, 2412–2422 CrossRef CAS.
- H. Wang, X. Ji, C. Chen, K. Xu and L. Miao, AIP Adv., 2013, 3, 112102 CrossRef.
- C. Wang, J. Wen, F. Luo, B. Quan, H. Li, Y. Wei, C. Gu and J. Li, J. Mater. Chem. A, 2019, 7, 15113–15122 RSC.
- M. K. Y. Chan, C. Wolverton and J. P. Greeley, J. Am. Chem. Soc., 2012, 134, 14362–14374 CrossRef CAS PubMed.
- S. C. Jung and Y. K. Han, Phys. Chem. Chem. Phys., 2011, 13, 21282–21287 RSC.
- F. Shi, Z. Song, P. N. Ross, G. A. Somorjai, R. O. Ritchie and K. Komvopoulos, Nat. Commun., 2016, 7, 1–8 Search PubMed.
- D. Martín-Yerga, M. Bahri, M. E. Curd, X. Xu, W. Li, T. L. Burnett, P. J. Withers, B. Layla Mehdi, N. D. Browning, P. R. Unwin, C. J. Philip Withers, H. Royce Institute and N. Sci, Nat. Sci., 2023, 3, e20210607 CrossRef.
- B. R. Long, M. K. Y. Chan, J. P. Greeley and A. A. Gewirth, J. Phys. Chem. C, 2011, 115, 18916–18921 CrossRef CAS.
- D. Lau, C. A. Hall, S. Lim, J. A. Yuwono, P. A. Burr, N. Song and A. Lennon, ACS Appl. Energy Mater., 2020, 3, 1730–1741 CrossRef CAS.
- H. Wu, G. Chan, J. W. Choi, I. Ryu, Y. Yao, M. T. Mcdowell, S. W. Lee, A. Jackson, Y. Yang, L. Hu and Y. Cui, Nat. Nanotechnol., 2012, 7, 310–315 CrossRef CAS PubMed.
- M. Saito, T. Yamada, C. Yodoya, A. Kamei, M. Hirota, T. Takenaka, A. Tasaka and M. Inaba, Solid State Ionics, 2012, 225, 506–509 CrossRef CAS.
- M. Inaba, M. Haruta, M. Saito and T. Doi, Electrochemistry, 2017, 85, 623–629 CrossRef CAS.
- B. Wu, C. Chen, D. L. Danilov, M. Jiang, L. H. J. Raijmakers, R. A. Eichel and P. H. L. Notten, ACS Omega, 2022, 7, 32740–32748 CrossRef CAS PubMed.
- U. S. Vogl, S. F. Lux, E. J. Crumlin, Z. Liu, L. Terborg, M. Winter and R. Kostecki, J. Electrochem. Soc., 2015, 162, A603–A607 CrossRef CAS.
- A. Suzuki, M. Nishijima, H. Kinoshita, Y. Yaji, M. Yoshimura, K. Nakanishi, T. Ohta and Y. Orikasa, Mem. SR Cent. Ritsumeikan Univ., 2019, 20, 17–21 Search PubMed.
- N. Ding, J. Xu, Y. X. Yao, G. Wegner, X. Fang, C. H. Chen and I. Lieberwirth, Solid State Ionics, 2009, 180, 222–225 CrossRef CAS.
- F. Di, Z. Wang, C. Ge, L. Li, X. Geng, C. Sun, H. Yang, W. Zhou, D. Ju, B. An and F. Li, J. Mater. Sci. Technol., 2023, 157, 1–10 CrossRef.
- D. Uxa, E. Hüger and H. Schmidt, J. Phys. Chem. C, 2020, 124, 27894–27899 CrossRef CAS.
- J. J. Wu and W. R. Bennett, 2012, IEEE Energytech, 2012, 217739, pp. 1–5 Search PubMed.
- N. Aoki, A. Omachi, K. Uosaki and T. Kondo, ChemElectroChem, 2016, 3, 959–965 CrossRef CAS.
- E. Pollak, G. Salitra, V. Baranchugov and D. Aurbach, J. Phys. Chem. C, 2007, 111, 11437–11444 CrossRef CAS.
- B. Jerliu, E. Hüger, L. Dörrer, B. K. Seidlhofer, R. Steitz, M. Horisberger and H. Schmidt, Phys. Chem. Chem. Phys., 2018, 20, 23480–23491 RSC.
- M. N. Obrovac and L. Christensen, Electrochem. Solid-State Lett., 2004, 7, 3–7 CrossRef.
- D. Ma, Z. Cao and A. Hu, Nano-Micro Lett., 2014, 6, 347–358 CrossRef PubMed.
- M. Ogawa, S. Ohmori, T. Azami, T. Yaji and T. Ohta, JFE Tech. Rep., 2022, 27, 16–20 Search PubMed.
- K. J. Zhao, Y. G. Li and L. Brassart, Acta Mech. Sin./Lixue Xuebao, 2013, 29, 379–387 CrossRef CAS.
- J. Crank, Mathematics of Diffusion, Oxford University Press, London, 2005 Search PubMed.
- L. Tröger, D. Arvanitis, K. Baberschke, H. Michaelis, U. Grimm and E. Zschech, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 3283 CrossRef PubMed.
- M. K. Y. Chan, C. Wolverton and J. P. Greeley, J. Am. Chem. Soc., 2012, 134, 14362–14374 CrossRef CAS PubMed.
- X. Zhou, S. Qiao, N. Yue, W. Zhang and W. Zheng, Mater. Res. Lett., 2023, 11, 239–249 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra02554c |
| This journal is © The Royal Society of Chemistry 2023 |