New ab initio potential energy surface of NaFH (1A′) system and quantum dynamics studies for the Na + HF (v, j) → NaF + H reaction

Abstract

A global potential energy surface (PES) for the electronic ground state of the Na + HF reactive system is constructed by three-dimensional cubic spline interpolation of 37 000 ab initio points obtained using the multireference configuration interaction method including the Davidson's correction (MRCI + Q) with auc-cc-pV5Z basis set. The endoergicity, well depth and properties of the separated diatomic molecules are in good agreement with experimental estimations. Quantum dynamics calculations have been performed and compared with those of the previous MRCI PES as well as experimental values. The better agreement between theory and experiment indicates the accuracy of the new PES.

---

1. Introduction

The reactions between alkali metals and hydrogen halides have been of fundamental importance in the understanding of elementary chemical kinetics. The Na + HF reaction is a typical metal-halide harpooning reaction¹ which implies the involvement of electronic rearrangement during the course of the reaction. Such reactions have been the subject of many theoretical and experimental studies.^2–30

Many experiments had been done to gain insights into the characteristics of Na + HF reaction.^2–9 They found that the ground state reaction, namely Na(3S) + HF, was endoergic by about 0.87–0.93 eV ^5,7 and no reaction took place with low vibrational state of HF (v < 2).^2,4–6 However, the reactivity was highly enhanced with the vibrational excitations of HF (v ≥ 2) and the rate constants increased linearly with v, which is a typical characteristic of the late-barrier reaction.² Meanwhile, the influences of HF(j) initial rotational excitations had also been measured and the reaction rates showed initially decreasing then increasing dependence on j.³ In addition, from the rainbow structures of the nonreactive differential cross sections, the existence of van der Waals wells were predicted to locate in the entrance channel of both ground and first excited potential energy surfaces (PESs) and the estimations for the well depths were also given.^5,6,8

As for theoretical studies, the PES is crucial in reaction dynamic calculations. For the Na + HF reaction system, the PESs of the ground as well as excited electronic states were constructed using semiempirical¹⁰ or ab initio^8,9,11–17 methods. The ground state PESs and relevant dynamics studies had successfully reproduced some of the experimental results, such as the existence of van der Waals well and late barrier, the large endoergicity and the effect of initial vibrational excitation.^{13–15,17,23–29} The research on excited electronic states had been carried out by Sevin¹² and Truhlar et al.^15–17 using different methods. They confirmed the involvement of harpooning process during the reactions whether the reaction started in the ground or the excited electronic state. They also confirmed the experimental prediction of the existence of a deep well in the first excited state. Therefore, a metastable complex could be formed and dissociated to ground state via harpooning process.

We had also done some dynamics studies both in the adiabatic and nonadiabatic representations^31,32 based on the 2 × 2 diabatic PES¹⁷ (denoted as TTCPP-B). In our previous work, for the Na(3P) + HF reaction, the agreement between the nonadiabatic results and the experiment implied that the interstate coupling term of the employed PES was quite accurate. For the Na(3S) + HF reaction, the probabilities obtained in the two representations were almost indistinguishable, which indicated the negligibly small nonadiabatic effect. So, if we focused on the dynamic characteristics of the ground state, the adiabatic PES was sufficient. The theoretical results were in good agreement with experimental ones as a whole. However, theory–experiment disparity still existed. The reaction rate for the v = 2 state was much smaller than the experimental data and the effects of the initial rotational excitations were only in qualitative agreement with the experiment, which implied that the PES probably overestimated the true barrier height. Further refinement of the ground state PES was needed to close the theoretical and experimental gap.

Following our previous work, in this paper, we construct a new PES for the ground electronic state of NaFH system. The MRCI + Q level of theory is used with aug-cc-pV5Z basis set. The global PES was obtained by fitting a larger number of ab initio points (37 000 points) which cover not only the interaction region but also the asymptotic regions of Na + HF and NaF + H channels. Quantum wave packet calculations are performed based on the new PES and compared with the experimental data to examine its accuracy. The new PES has a lower barrier than TTCPP-B PES and the dynamic results show better agreement with the experiment.

This letter is organized as follows. In Section 2, the relevant theoretical and numerical methods are briefly described. In Section 3, the new developed PES and corresponding dynamic results are displayed and discussed. Final conclusions are made in the last section.

2. Theoretical and computational methods

2.1 NaFH potential energy surface

The electronic energies of the electronic ground state of NaFH system were performed using Molpro 2012 package.³³ The internally contracted multi-reference configuration interaction method with the Davidson correction (icMRCI + Q)^34–36 was employed with the augmented correlation-consistent polarized valence quintuple zeta (aug-cc-pV5Z) basis set,³⁷ which generated a total of 530 Gaussian-type orbitals. All calculations were performed within Cs symmetry.

The reference configuration state functions for the MRCI calculations were taken from state-averaged complete active space self-consistent field (CASSCF)^38,39 calculations for equally weighted 1²A′ and 2²A′ states. In the CASSCF calculations, the active space consists of seven electrons distributed in eight valence orbitals, including the 3s and 3p orbitals of Na, the 2p orbitals of F and the 1s orbital of H. The inner orbitals were constrained to be doubly occupied but fully optimized. The total number of contracted configurations in the MRCI calculations was about 2.0 × 10⁶ corresponding to about 6.6 × 10⁷ uncontracted configurations.

A nonuniform and truncated direct product grid was used in the internal coordinates (R_HF, R_NaF, θ_NaFH), where R_AB stands for the distance between A and B atoms and θ_NaFH stands for the bond angle enclosed by Na–F and H–F bonds. We chose 50 grids in the R_HF coordinate ranging from 1.0 to 20.0 Bohr, 37 grids in the R_NaF coordinate ranging from 2.2 to 25.0 Bohr and 20 grids in the θ_NaFH coordinate within 0°–180°, which gives rise to a total of 37 000 grids. The ab initio energies computed on these grids were then used to generate the PES by fast three-dimensional cubic spline interpolation method.⁴⁰

2.2 Quantum wave packet calculation

We employ the Chebyshev real wave packet propagation scheme to study the Na(3S) + HF reaction. The method is detailed in the ESI† and previous works.^41–51 Hence, we give a brief outline here. The real initial wave packet which is designed to represent the specific rovibrational state is propagated using the modified Chebyshev recursion relation,

|ψ₁〉 = DĤ_scaled|ψ₀〉,

|ψ_k+1〉 = D(2Ĥ_scaled|ψ_k〉 − D|ψ_k−1〉), k ≥ 1

where the Hamiltonian is properly scaled (Ĥ_scaled = aĤ + b) to make its spectrum varies between −1 and +1 just as the Chebyshev polynomial require.⁴² The damping function D is applied at the edges of grids to enforce the outgoing boundary condition.^46,47 The initial wave packet is launched from the asymptotic region of the reactant and propagated until the wave packet remaining in the interaction region is negligibly small. Then, the total reaction probability can be calculated by computing flux at a sufficiently elongated reactant diatomic distance.^52,53 When the reaction probabilities for various total angular momentums (J) have been calculated, the integral cross section (ICS) and rate constant can be obtained by the standard procedure.

The Hamiltonian and wave packet are expressed in the reactant Jacobi coordinates and discretized in terms of a mixed DVR/FBR (discrete variable representation/finite basis representation) scheme.⁵⁴ The equidistant Fourier grid representation is utilized for the two radial degrees of freedom and the actions of the radial kinetic energy operators onto the wave packet are evaluated using the fast sine Fourier transform. For the angular degrees of freedom, the associated Legendre function and the Wigner rotation matrix are used. In this FBR, the rotational kinetic energy operators can be expressed as a diagonal or a tridiagonal matrix, so actions of them onto the wave packet can be evaluated in a straightforward manner. In order to calculate the action of the PES operator, the wave packet is transformed to a grid representation through a pseudospectral transformation^55,56 so that the operator is diagonal in this case.

3. Results and discussion

3.1 Potential energy surface

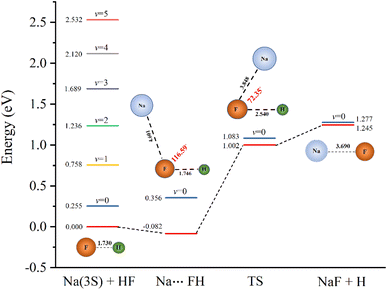
The geometries and energies of stationary points obtained from this ab initio calculation are listed in Table 1 and compared with those from the TTCPP-B PES¹⁷ and experimental values.⁵⁷

Table 1 The geometries and energies of stationary points obtained from this study and comparisons with experimental data as well as TTCPP-B PES. The bond lengths and bond angles are given in Bohr and degree, respectively. All the energies are given in eV. D₀ stands for the dissociation energy taking zero point energy into account

Feature	Property	This work	TTCPP-B^17	Exp^57
a The separated atom and diatomic molecule were set to 60 a.u. apart when performing the geometry optimization. The calculated results did not change with the further increase of this distance, indicating that there was no interaction between them, as was the case at infinity.
Reactant (Na + HF):
	RHF	1.73	1.73	1.73
	RNaF	60.00^a	∞	∞
	D0 (HF)	6.00	5.66	5.90
van der Waals well (Na⋯FH):
	RHF	1.75	1.74	—
	RNaF	4.60	4.68	—
	θNaFH	116.59°	118.0°	—
Transition state:
	RHF	2.54	3.49	—
	RNaF	3.85	3.66	—
	θNaFH	72.35°	90.8°	—
Product (NaF + H):
	RHF	60.00^a	∞	∞
	RNaF	3.69	3.64	3.64
	D0 (NaF)	4.98	4.58	5.0 ± 0.1

---

As can be seen, the equilibrium geometries as well as the dissociation energies of HF and NaF molecules are in excellent agreement with the experimental data. The endoergicity, defined as ΔE = D₀(HF) − D₀(NaF), which is a key factor of the reaction, is 1.02 eV in this PES. Some uncertainty exists in the experimental value of D₀ for NaF molecule. So, the experimental suggestions of endoergicity are about 0.87–0.93 eV.^5,7 The location of the van der Waals well in the new PES is similar with TTCPP-B PES,¹⁷ but the well depth of the former is a little deeper than of the latter (−0.082 eV vs. −0.074 eV, with respect to the energy minimum of the Na(3S) + HF asymptote). The geometries of the transition state in the two PESs are quite different. The saddle point in the new PES has shorter F–H distance and less bent structure, although the Na–F distance is similar. Whereas, our value of θ_NaFH is in good agreement with that obtained by Laganà et al. (75°),¹⁴ and similar with Shapiro and Zeiri's result (60°).¹⁰ As we mentioned in our previous work,³¹ the noticeable difference between theory and experiment shown on the rates for Na + HF (v = 2) may due to the overestimated barrier height of the PES. The barrier height resulting from our ab initio calculation is 1.002 eV relative to the Na(3S) + HF asymptote which is lower than that on the TTCPP-B (1.270 eV)¹⁷ or semiempirical (1.266 eV) PES¹⁰ but close to Laganà's result (0.811 eV) in which some artificial corrections to the original ab initio energies are made.¹⁴ The lower barrier may have a significant effect on the reactivity and we will discuss this in detail in the next section.

To further characterize the reactive properties of the reaction, the schematic one-dimensional minimum energy path is displayed in Fig. 1. The eigen-energies of several vibrational states of the reactant and the ZPEs of the stationary points are also given to help illustrate the results of dynamic calculations. The detailed rovibrational eigen-energies of the HF/NaF (v = 0–5, j = 0–7) molecules which are obtained by solving the one-dimensional Schrödinger equation are listed in the ESI.† As the figure shows, the v ≤ 1 states of HF energetically lie below while the higher vibrational states above the saddle point. It is worth noticing that the v = 2 state energetically lies above the saddle point, but below the ground state of product by about 0.041 eV. Even though the barrier height is lower than TTCPP-B PES, the reaction probability of v = 2 state still has threshold energy which will be illustrated in detail below.

Fig. 1 Schematic diagram for the ground state potential energy surface. The eigen-energies of the v = 0–5 vibrational states of the reactant, and the zero point energies at the van der Waals well, transition state (TS) and asymptotic product region are depicted. The configurations of the saddle points are also displayed.

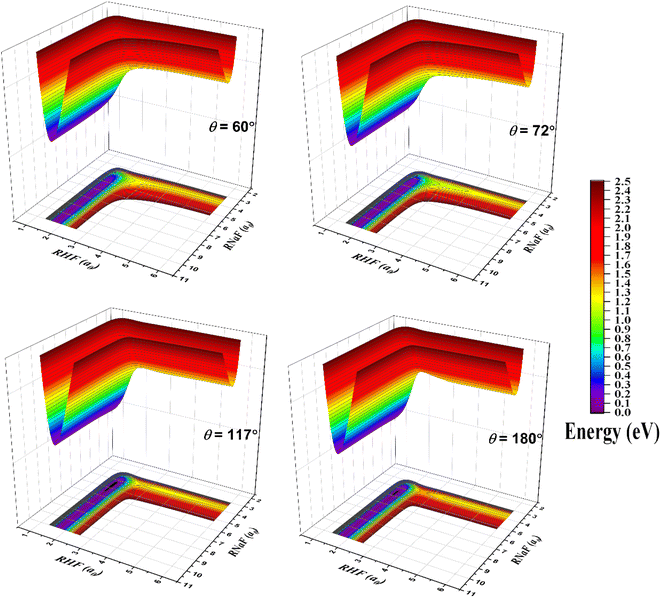
The fitted PES is exhibited by three-dimensional surfaces as a function of the R_NaF and R_HF bond coordinates in Fig. 2 and the corresponding two-dimensional contour plots are displayed in the ESI.† The bond angles (θ_NaFH) are equal to 60°, 72°, 117° and 180°, respectively. Among them, the surfaces for 72° and 117° outline the topography near the transition state and van der Waals well, respectively. As the figure shows, the PES is smooth all through the configuration space from the asymptotic to interaction regions. The well is visible in the surface for 117° in the entrance channel. The PES flattens so the saddle point is very inconspicuous which parallels the observation made by Sevin et al. at MRCI level¹² and by Truhlar et al. at MBPT(2) level.¹⁵

Fig. 2 The three-dimensional potential energy surfaces in terms of Na–F bond length and H–F bond length for several fixed bond angles, θ_NaFH = 60°, 72°, 117°, 180°. Isoenergetic contours are drawn every 0.1 eV from 0 to 2.5 eV with respect to the energy of the global minimum of the PES.

3.2 Reaction dynamics

We have performed quantum wave packet calculations based on the newly developed PES. According to the results of previous studies, the reaction hardly takes place at low initial vibrational states (v < 2). Therefore, we only study the reaction dynamics for high initial vibrational states (v = 2, 3, 4, 5). Convergence tests have been done for all the initial vibrational states with J = 0. The optimized numerical parameters used in the dynamic calculations are summarized in Table 2.

Table 2 The numerical parameters used in the Na(3S) + HF (v = 2, 3, 4, 5) dynamics calculations (in atomic units unless otherwise specified)

Parameters	Na(3S) + HF (v, j = 0)
Grids/basis	NR = 445, R ∈ [0.5, 22]
	Nr = 115, r ∈ [0.5, 12]
	Nθ = 45, θ ∈ [0°, 180°]
	j = 0, 1, 2, … , 44
Damping; exp(−dx(x − xd)^2), x = R or r	Rd = 18.0, dR = 0.005; rd = 8.0, dr = 0.005
Initial wave packet; exp(−(R − R0)^2/2δ^2) × cos(k0R)	E0 = ℏ^2k0^2/2μR = 0.2 eV; δ = 0.15, R0 = 16.0
Dividing surface	rf = 7.9
Propagation steps	40 000
Jmax	130 (v = 2); 170 (v = 3); 180 (v = 4); 220 (v = 5)

---

The Coriolis coupling effect is fully considered in the J > 0 partial waves. In our calculation, the body-fixed z axis is chosen to coincide with the R⃑ vector which joins the Na atom and the center of mass of HF. Because the H atom is relatively light, we can assume that the z axis nearly coincides with the principal axis of inertia of the system. The Coriolis term should be rather small in this case. Therefore, we truncate the maximum helicity quantum number (Ω) to save computational costs. We set Ω_max = min(3, J) for J < 100 and Ω_max = 5 for J > 100 and it can provide indistinguishable results from the ones with Ω_max = J. In order to let the ICSs converge to more than 0.7 eV and the rate constants up to more than 1000 K, a large number of J partial waves contributions should be calculated. We calculated explicitly at intervals of ΔJ = 5 and 20 for J ∈ [0, 20] and [20, J_max] respectively. The probabilities of uncalculated partial waves were obtained by means of interpolation over the J space. The accuracy of this method has been proven in previous work.^50,58,59

In the previous studies, the disparity between experimental and theoretical results mainly exists in the v = 2 state.³¹ Therefore, we focus on the reactivity of this state first. The reaction probabilities for three different partial waves, J = 0, 40, 100, for the v = 2 state are displayed in Fig. 3 and compared with the results obtained on the TTCPP-B PES. Although the new PES has a lower barrier which energetically lies below the eigen-energy of v = 2 state, a threshold still appears at about 0.04 eV due to the endothermic nature of the reaction and the reaction probabilities show monotonically increasing energy dependence. On the other hand, in the TTCPP-B PES, the effective barrier height for the v = 2 state is 0.08 eV which is in good correlation with its threshold energy. The sources of the threshold energies are different with the two PESs. The better agreement between theory and experiment of the relative rate constants (which shown below in Fig. 6) indicates that the new developed PES is more accurate. From this point of view, the threshold energy of this work is more accurate. Because of the lower barrier and endothermicity, the probability obtained using the new PES is larger than the old one obviously for every partial wave. The threshold energy of each newly calculated partial wave probability is smaller than the corresponding value based on TTCPP-B PES and the difference between the corresponding two thresholds increases with J. Otherwise, all the reaction probability curves show oscillatory energy dependence and the oscillation is more pronounced in the probability curves obtained with the new PES, which is probably due to the deeper well in the reactant valley.

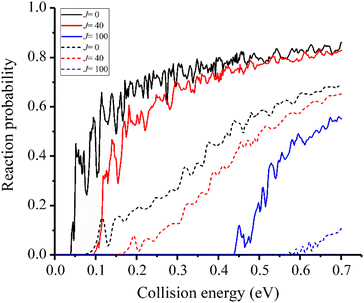Fig. 3 Initial state specified HF (v = 2, j = 0) total reaction probabilities for several selected J_s with two different PESs (solid lines for the new PES and dash lines for TTCPP-B PES³¹).

For the v ≥ 3 states, whose eigen-energies are greater than the endoergicity, the reaction probabilities are threshold-less and remain large throughout the energy range as shown in Fig. 4. Due to the deeper well, the oscillatory structures are much more pronounced in the probability curves calculated with the new PES similar to the v = 2 case and the probabilities of J = 0 obtained with the new PES are smaller than those obtained with TTCPP-B PES. The probabilities shift towards higher energies as J increases due to the additional centrifugal barrier. As the figure shows, the threshold energies increase more slowly with J in the results obtained with the new PES, leading to lower threshold energies for J > 0 probabilities compared to the results obtained with TTCPP-B PES. It may due to the relatively long R (3.81 vs. 3.67 a.u.) of the transition state in the new PES which is called “corner cutting” for reactions of heavy–light-heavy systems.^60,61 So, we need more J partial waves to make the ICSs converge using the new PES.

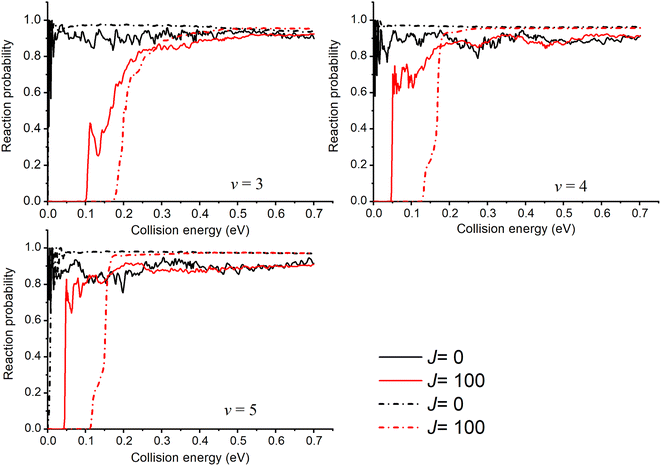Fig. 4 Initial state specified HF (v = 3, 4, 5, j = 0) total reaction probabilities for several selected J_s with two different PESs (solid lines for the new PES and dash lines for TTCPP-B PES³¹).

In Fig. 5, the initial state specified ICSs are displayed and compared with the previous values. At a first glance, the initial vibrational excitation is effective in promoting the reactivity for this late-barrier reaction. Although the new PES has a lower barrier height, the calculated ICSs show similar characteristic to the previous results. The ICS for v = 2 state increases monotonically from the threshold energy while those for v ≥ 3 states are threshold-less and decrease sharply from very large values. However, differences still exist between the two sets of data. The new obtained ICSs for a given vibrational state are greater than the corresponding one obtained with TTCPP-B PES, especially in the low energy region. This enhancement of reactivity may be due to the increase of the cone of acceptance. In addition, the resonance structures are not fully canceled out by partial wave summation at low collision energies and the locations of the peaks are consistent with each other for different initial vibrational states which presumably suggests the same origin of them. On the other hand, the differences between the two PESs seem to have slight effects on the reactivity of the threshold-less reactions at high collision energies and their ICSs nearly the same at the collision energies greater than 0.4 eV.

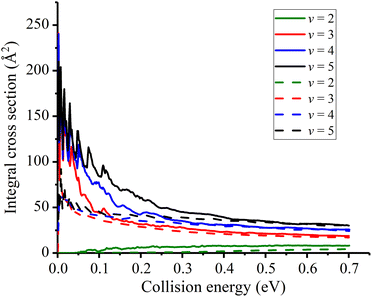Fig. 5 Initial state specified HF (v = 2, 3, 4, 5, j = 0) integral cross sections for the Na(3S) + HF reaction (Solid lines for the new PES and dash lines for TTCPP-B PES³¹).

To test the accuracy of the newly constructed PES, in Fig. 6, the initial state specified rate constants are computed and compared with the experimental data² as well as our previous results using TTCPP-B PES.³¹ The data shown in the figure is relative rate constants with respect to k_v=3 (i.e. k_v/k_v=3) at T = 940 K to mimic the experimental conditions. As displayed in the figure, the newly calculated rate constants for v > 3 states are in excellent agreement with the experimental results. The k_v=4/k_v=3 ratio is exactly equal to the average experimental value and the k_v=5/k_v=3 ratio is exactly equal to one of the experimental values which is closest to the average value. Unfortunately, the new PES still underestimates the k_v=2/k_v=3 ratio. In our previous work, we had artificially modified the TTCPP-B PES to reduce the barrier height and found it could narrow down the theory–experiment disparity effectively.³¹ In this work, the barrier height of the new PES is lower than that of the TTCPP-B PES by 0.268 eV. However, the k_v=2/k_v=3 ratio increases only by a factor of 6.36 (0.089 vs. 0.014) and is still much smaller than the experimental value (k_v=2/k_v=3 = 0.65–0.96), partly because of the non-zero threshold energy of v = 2 state. Another possible reason for the disparity is the role of initial rotational excitation. The experimental measurement is carried out at T = 940 K at which the maximally populated rotational state is j = 4. In order to clarify the effect of rotational excitation, we perform additional dynamics calculations for other four initial rotational states (j = 2, 4, 6, 7) of the v = 2 manifold. The eigen-energies of these state are 1.250, 1.284, 1.336 and 1.369 eV, respectively. The eigen-energy of j = 2 state is still smaller than that of the product. The calculated ratios for these states also displayed in Fig. 6. As the figure shows, the initial rotational excitations promote the reactivity as the ratios increase with j and up to 0.24 at j = 7. However, the ratios are still smaller than the experimental result. In the experimental side, the possibility of error in the measurement cannot be completely excluded. If we accept the experimental result, the theory–experiment disparity shown for v = 2 state calls for further study.

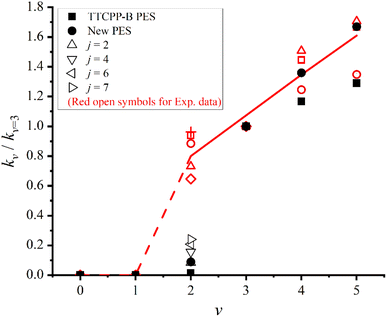Fig. 6 Initial state specified relative rate constants (k_v/k_v=3) of the Na(3S) + HF (v = 2–5) → NaF + H reaction with respect to the v = 3 state (k_v=3) at T = 940 K. + and red open symbols denote the experimental values measured at different conditions, and the solid and dashed lines denote the average experimental values.² The theoretical results calculated on the new and TTCPP-B³¹ PESs are denoted as solid circles and solid squares, respectively. Black hollow triangles denote the values of different initial rotational states (j) of v = 2 state on the new PES.

4. Conclusions

In this work, we report a new global PES for the electronic ground state of the NaFH system. By employing a high-level ab initio method (MRCI + Q/aug-cc-pV5Z), the PES is fitted using the fast three-dimensional cubic spline interpolation algorithm with a larger number of ab initio points. The newly constructed PES has a lower barrier than that of the earlier MRCI PES as expected and a slightly deeper van der Waals well in the Na + HF asymptotic region. The endoergicity, well depth and properties of the separated atoms and diatomic molecules are in good agreement with experimental estimations.

Quantum dynamics studies are carried out using Chebyshev wave packet method to verify the accuracy of the new PES. The initial vibrational excitations enhance the reactivity significantly in line with the experimental observations. The oscillation is more pronounced in the newly calculated probabilities of every initial state due to the deeper well. The centrifugal barriers of J partial waves increase more slowly using the new PES due to the “corner cutting” for reactions of heavy–light-heavy systems. For v ≥ 3 states, the reactions are threshold-less and the newly calculated ICSs are obviously greater than the old ones in low energy area then tend to be the same in the high collision energy region. The difference in the details of the PESs seems to have no effect on the ICSs of the threshold-less reaction at high collision energy. The better agreement between the relative reaction rates and the experimental values for v > 3 states indicates that the new PES is more accurate. We pay more attention to the v = 2 state because of the theory-experiment disparity shown in the previous work. Although the new PES has a lower barrier, the probability of v = 2 state still has threshold because v = 2 state energetically lies below the product. For v = 2 state, the new PES gives enhanced reactivity compared to the TTCPP-B PES. However, the relative reaction rate is still much smaller than the experimental value. The consideration of rotational state excitation, which improves the agreement though, is not enough to remove the theory-experiment disparity. The reason for this theory–experiment disparity is still unclear and calls for further studies.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant No. 21073109 and 11274202) and the Doctoral Research Fund of Shandong Jianzhu University (Grant No. X20073Z).

References

1. D. R. Herschbach, Adv. Chem. Phys., 1966, 10, 319–393.
2. F. E. Bartoszek, B. A. Blackwell, J. C. Polanyi and J. J. Sloan, J. Chem. Phys., 1981, 74, 3400–3410.
3. B. A. Blackwell, J. C. Polanyi and J. J. Sloan, Chem. Phys., 1978, 30, 299–306.
4. P. S. Weiss, J. M. Mestdagh, M. H. Covinsky, B. A. Balko and Y. T. Lee, Chem. Phys., 1988, 126, 93–109.
5. R. Düren, U. Lackschewitz, S. Milošević and H. J. Waldapfel, J. Chem. Soc., Faraday Trans. 2, 1989, 85, 1017–1025.
6. R. Düren, U. Lackschewitz, S. Milošević, H. Panknin and N. Schirawski, Chem. Phys. Lett., 1988, 143, 45–50.
7. R. Düren, U. Lackschewitz and S. Milošević, Chem. Phys., 1988, 126, 81–91.
8. R. Düren, D. M. Segal, F. Rebentrost, H. C. W. Beijerinck, S. Leone, L. Kovalenko, M. Glass-Maujean, J. A. Beswick, J. P. Simons and A. J. McCaffery, et al., J. Chem. Soc., Faraday Trans. 2, 1989, 85, 1027–1058.
9. X. Y. Chang, R. Ehlich, A. J. Hudson, P. Piecuch and J. C. Polanyi, Faraday Discuss., 1997, 108, 411–425.
10. M. Shapiro and Y. Zeiri, J. Chem. Phys., 1979, 70, 5264–5270.
11. M. Paniagua, J. M. Garcia De La Vega, J. R. Alvarez Collado, J. C. Sanz, J. M. Alvariño and A. Laganà, J. Mol. Struct., 1986, 142, 525–528.
12. A. Sevin, P. C. Hiberty and J. M. Lefour, J. Am. Chem. Soc., 1987, 109, 1845–1852.
13. A. Laganà, M. L. Hernandez Hernandez, J. M. Alvariño, L. Castro and P. Palmieri, Chem. Phys. Lett., 1993, 202, 284–290.
14. A. Laganà, J. M. Alvariño, M. L. Hernandez, P. Palmieri, E. Garcia and T. Martinez, J. Chem. Phys., 1997, 106, 10222–10229.
15. M. S. Topaler, D. G. Truhlar, X. Y. Chang, P. Piecuch and J. C. Polanyi, J. Chem. Phys., 1998, 108, 5349–5377.
16. M. S. Topaler, D. G. Truhlar, X. Y. Chang, P. Piecuch and J. C. Polanyi, J. Chem. Phys., 1998, 108, 5378–5390.
17. A. W. Jasper, M. D. Hack, A. Chakraborty, D. G. Truhlar and P. Piecuch, J. Chem. Phys., 2001, 115, 7945–7952.
18. S. Garashchuk and V. A. Rassolov, Chem. Phys. Lett., 2007, 446, 395–400.
19. A. W. Jasper and D. G. Truhlar, J. Chem. Phys., 2007, 127, 194306.
20. Y. Zeiri, G. Katz, R. Kosloff, M. S. Topaler, D. G. Truhlar and J. C. Polanyi, Chem. Phys. Lett., 1999, 300, 523–528.
21. G. Katz, Y. Zeiri and R. Kosloff, Chem. Phys. Lett., 2002, 359, 453–459.
22. V. Špirko, P. Piecuch and O. Bludský, J. Chem. Phys., 2000, 112, 189–202.
23. L. E. Espinola López, R. Gargano, K. C. Mundim and J. J. Soares Neto, Chem. Phys. Lett., 2002, 361, 271–276.
24. A. W. S. Antunes, W. Ferreira Da Cunha, G. Magela E Silva, J. B. L. Martins and R. Gargano, Int. J. Quantum Chem., 2010, 110, 1070–1079.
25. R. Gargano, S. Crocchianti, A. Laganà and G. A. Parker, J. Chem. Phys., 1998, 108, 6266–6271.
26. A. F. A. Vilela, J. J. Soares Neto, K. C. Mundim, M. S. P. Mundim and R. Gargano, Chem. Phys. Lett., 2002, 359, 420–427.
27. W. Ferreira Da Cunha, L. F. Roncaratti, R. Gargano and G. M. E. Silva, Int. J. Quantum Chem., 2006, 106, 2650–2657.
28. D. Wang, G. Shi, L. Fu, R. Yin and Y. Ji, ACS Omega, 2019, 4, 12167–12174.
29. R. Yin, N. Gao, J. Cao, Y. Li, D. Wang and X. Huang, RSC Adv., 2020, 10, 39226–39240.
30. R. Yin, N. Gao, R. Zhang, D. Wang and X. Huang, Chem. Phys., 2020, 538, 110906.
31. W. Yan, R. S. Tan and S. Y. Lin, J. Phys. Chem. A, 2019, 123, 2601–2609.
32. W. Yan, R. S. Tan and S. Y. Lin, Chem. Phys. Lett., 2019, 730, 378–383.
33. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz and others, MOLPRO, version 2012.1, a package of ab initio programs, https://www.molpro.net.
34. P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1988, 145, 514–522.
35. H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814.
36. S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61–72.
37. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023.
38. P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267.
39. H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053–5063.
40. H. Zhai and S. Y. Lin, Chem. Phys., 2015, 455, 57–64.
41. H. Guo, Int. Rev. Phys. Chem., 2012, 31, 1–68.
42. R. Kosloff, J. Phys. Chem., 1988, 92, 2087–2100.
43. S. K. Gray and G. G. Balint-Kurti, J. Chem. Phys., 1998, 108, 950–962.
44. R. Chen and H. Guo, J. Chem. Phys., 1996, 105, 3569–3578.
45. R. Chen and H. Guo, J. Chem. Phys., 1996, 105, 1311–1317.
46. V. A. Mandelshtam and H. S. Taylor, J. Chem. Phys., 1995, 102, 7390–7399.
47. V. A. Mandelshtam and H. S. Taylor, J. Chem. Phys., 1995, 103, 2903–2907.
48. Y. Huang, D. J. Kouri and D. K. Hoffman, Chem. Phys. Lett., 1994, 225, 37–45.
49. Y. Huang, W. Zhu, D. J. Kouri and D. K. Hoffman, Chem. Phys. Lett., 1993, 214, 451–455.
50. S. Y. Lin, Z. Sun, H. Guo, D. H. Zhang, P. Honvault, D. Xie and S.-Y. Lee, J. Phys. Chem. A, 2008, 112, 602–611.
51. S. Y. Lin and H. Guo, J. Phys. Chem. A, 2009, 113, 4285–4293.
52. A. J. H. M. Meijer, E. M. Goldfield, S. K. Gray and G. G. Balint-Kurti, Chem. Phys. Lett., 1998, 293, 270–276.
53. S. Y. Lin and H. Guo, J. Chem. Phys., 2003, 119, 11602–11608.
54. J. C. Light and T. Carrington, Adv. Chem. Phys., 2000, 114, 263–310.
55. G. C. Corey and D. Lemoine, J. Chem. Phys., 1992, 97, 4115–4126.
56. G. C. Corey and J. W. Tromp, J. Chem. Phys., 1995, 103, 1812–1820.
57. W. M. Haynesr, CRC Handbook of Chemistry and Physics, 96th Edition (Internet Version 2016), CRC Press/Taylor and Francis, Boca Raton, FL. 2016.
58. E. M. Goldfield and A. J. H. M. Meijer, J. Chem. Phys., 2000, 113, 11055–11062.
59. R. S. Tan, H. C. Zhai, W. Yan, F. Gao and S. Y. Lin, J. Chem. Phys., 2017, 146, 164305.
60. Q. Sun, J. M. Bowman, G. C. Schatz, J. R. Sharp and J. N. L. Connor, J. Chem. Phys., 1990, 92, 1677–1686.
61. A. Aguado, M. Paniagua, M. Lara and O. Roncero, J. Chem. Phys., 1997, 107, 10085–10095.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra01885g

---