Open Access Article
Open Access ArticleQuantitative surface free energy with micro-colloid probe pairs†
Ehtsham-Ul Haq *a,
Yongliang Zhanga,
Noel O'Dowdb,
Ning Liua,
Stanislav Leesmentc,
Claude Beckerd,
Edoardo M. Rossie,
Marco Sebastianie,
Syed A. M. Tofaila and
Christophe Silien
*a,
Yongliang Zhanga,
Noel O'Dowdb,
Ning Liua,
Stanislav Leesmentc,
Claude Beckerd,
Edoardo M. Rossie,
Marco Sebastianie,
Syed A. M. Tofaila and
Christophe Silien *a
*a
aDepartment of Physics and Bernal Institute, University of Limerick, Limerick, V94 T9PX, Ireland. E-mail: Ehtsham.U.Haq@ul.ie; Christophe.Silien@ul.ie
bSchool of Engineering and Bernal Institute, University of Limerick, Limerick, V94 T9PX, Ireland
cSpectrum Instruments Ltd., Stewart House, National Technological Park, Limerick, Ireland
dFuncoats SA, Technoport 4B, Rue du Commerce Foetz, Luxembourg
eEngineering Department, Roma Tre University, Via della Vasca Navale 79, Rome, 00146, Italy
First published on 18th January 2023
Abstract
Measurement of the surface free energy (SFE) of a material allows the prediction of its adhesion properties. Materials can have microscale or sub-microscale surface inhomogeneities, engineered or random, which affect the surface macroscopic behaviour. However, quantitative characterization of the SFE at such length scales remains challenging in view of the variety of instruments and techniques available, the poor knowledge of critical variables and parameters during measurements and the need for appropriate contact models to derive the SFE from the measurements. Failure to characterize adhesion correctly may result in defective components or lengthy process optimization costing billions to industry. Conversely, for planar and homogeneous surfaces, contact angle (CA) measurements are standardized and allow for calculating the SFE using for example the Owen–Wendt model, relying only on the properties of the probing liquids. As such, we assessed and report here a method to correlate quantitative measurements of force–distance curves made with an atomic force microscope (AFM) and with silica and polystyrene (PS) colloidal probe pairs, with quantitative CA measurements and CA-derived SFE values. We measured five surfaces (mica, highly oriented pyrolytic graphite, thermally grown silica on silicon, silicon, and silicon with a super-hydrophobic coating), ranging from hydrophilic to super-hydrophobic, and found an excellent classification of the AFM measurements when these are represented by a set of principal components (PCs), and when both silica and PS colloidal probes are considered together. A regression of the PCs onto the CA measurements allows recovery of the SFE at the length scale of the colloidal probes, which is here ca. 1 micron. We found that once the PC-regression model is built, test sets of only ten AFM force–distance curves are sufficient to predict the local SFE with the calibrated silica and PS colloidal probes.
Introduction
Controlling wetting, adhesion, and friction properties is crucial for tribology, photonics, scaffold materials, particles for drug delivery and bio-coatings.1–3 Engineering surfaces with controlled wettability also has applications in anti-icing, self-cleaning, oil-water separation, and anti-biofouling.4–6 Surfaces that can morph to be both super-hydrophilic and super-hydrophobic create new opportunities for surface-tension-controlled diagnostic devices and cell biology.7–10 Development and validation of standardized, quantitative methods to reliably measure surface properties at relevant length scales remains an industry requirement to account for important contact phenomena such as adhesion and friction.11 However, standardization is impeded by the lack of an unambiguous link between the nanoscale and macroscale SFE.11 Macroscopically, for planar and uniform solid surfaces, surface free energy (SFE) can be quantified by contact angle (CA) measurements, typically using a selection of liquid probes of varying polar components,12–14 and estimated from Young's equation using models such as Owens–Wendt, Fowkes, Good–Girifalco, or van Oss–Chaudhury–Good.12–15 Protocols also have been established for performing reliable and reproducible advancing and receding CA measurements.16 However, nano-patterned materials and other non-planar surfaces where adhesion is directly linked to the physicochemical properties of the mating surfaces require alternative measurement and derivation methods to obtain the SFE.10,11Atomic force microscopy (AFM) can reliably measure forces as low as 0.1 nN between a solid nanoscopic or microscopic probe and a solid surface, from the bending of the cantilever on which the probe is attached. Dedicated (probe-surface) contact models have been used to estimate the SFE, for example from the force that is required to break the contact between the probe and the surface, generally referred to as the pull-off force. Although pull-off force measurements are reliable, it is not necessarily the case for the derived SFE values since the models critically rely on properties of the probes that are poorly known, including true contact geometry with the specimen surface and probe surface chemistry and crystallinity, as well as water meniscus,17–20 although noticeable improvements are seen when the AFM-typical, sharp pyramidal probes are replaced by colloidal probes, since the geometry of the latter is better defined and since their surfaces are more reproducible. Colloidal probes are now widely used to probe the mechanical properties of metals, polymers, ceramics, nanocomposites, and protein–protein, protein-surface, and cell mechanics.21–29 Unfortunately, the contact models necessarily over-simplify the probe-surface interaction.30–32 For example, Bradley's model considers the attraction between a rigid sphere and a planar rigid-body surface, neglecting any elastic deformation. The Derjaguin–Muller–Toporov (DMT) model only considers long-range forces outside the probe-surface contact area. The Johnson–Kendall–Roberts (JKR) validity is limited to cases where the elastic surface displacement is larger than the characteristic range of action of the surface forces that follow Lennard-Jones law of molecular interactions.
Acceptance of SFE characterisation on a global scale requires standardization and agreement between the several techniques probing adhesion across the different length scales, such as CA measurements, nano-indentation and AFM.11,20,33–37 These techniques are all well-developed and provide reproducible measurements of adhesion in controlled environment and with controlled probes. The generation of a quantitative, holistic perspective between these techniques should be addressed with innovative protocols to correlate the data collected by these techniques, that is by increasing the reliance on data-based models. Advances in statistics and their application in machine learning (ML) have provided new insights in medicine and diagnostics, as well as in many other fields including material sciences, physics, and probe microscopy, and ML can provide the desired holistic perspective for SFE.
In this work, principal component analysis (PCA)38,39 is used to analyse the sub-microscopic AFM measurements made on a series of planar, test surfaces covering a wide range of adhesion (super-hydrophobic coated Si (sh-Si), HOPG, thermally oxidized SiO2 thin film on Si, clean Si, and mica) using colloidal probes. Macroscopic CA measurements with three liquid probes (deionised water, methylene iodide, and formamide) were made on the same test surfaces, and their SFE values were calculated using the Owen–Wendt model. A data-oriented regression model was then developed to link CA-derived SFE values to the AFM-derived principal components (PCs), bridging the two extreme length scales probed by CA and AFM and derivation of the SFE with only the simplest of the macroscopic contact model. We verified that the data-oriented model can predict the SFE from only ten AFM force–distance (F(d)) curves, suggesting that rapid, multi-length scale and quantitative SFE analysis is possible.
Experiments
AFM spectroscopy and metrics
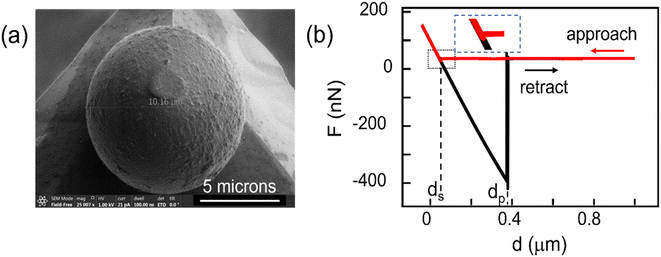
Force − distance, F(d) spectroscopy was performed using a commercial AFM instrument, NTEGRA Spectra II (NT-MDT) equipped with a humidity-controlled environment. We used PS and silica colloidal probes (Applied Nanostructures, Inc. USA) of nominal diameter 10 microns attached to (otherwise probe-less FORTG type) AFM cantilevers. The colloidal probes were used as received. The SEM image of a colloidal probe after measurements is presented in Fig. 1a. It suggests that the actual contact area with the surface is ca. 1 μm2. The apparent deformed surface of the colloid in the contact region could be contaminants from the surfaces as deformation is not expected within our experimental force regime <200 nN. The cantilevers' force constant (with colloid attached to the cantilevers) were determined from the power spectral density of their thermal noise and the Sader method.40,41 Cantilevers with force constant of 1–1.6 N m−1 were selected for measurements. This range of values is adequate for recording forces 1–1000 nN.Inverse optical sensitivities relating cantilevers deflection to actual height changes were measured from the F(d) curve slopes upon contact with a clean Si surface, assumed incompressible.
Before the measurements were made, colloidal probes were installed, samples were mounted onto the sample stage (electrically grounded) and placed in the instrument, the humidity-controlled chamber was filled with N2 (gas flow kept on during the experiment; humidity constant and <7% within 20 min, temperature 21 ± 1 °C constant throughout the experiment), and an additional 30 min of waiting time was applied. For each sample, multiple F(d) curves were measured across grid-mapped points (100–1000 points, grid area 30 μm × 30 μm), repeated on at least three locations across the samples surface. The F(d) curves were acquired with approach-retract velocities of 100 and 1000 nm s−1 (no significant influence of velocity on the F(d) measurements was observed, and the data analysis below is carried out without considering the velocity, ESI Fig. S5†) and an indentation force <200 nN. A waiting time of 100 ms was applied between successive curves measurement.
An F(d) curve represented in Fig. 1b is example of 20 experimental F(d) curves recorded in this study on freshly cleaved HOPG with a silica colloidal probe (100 nm s−1), illustrating the reproducibility of our AFM measurements. In the F(d) curves, F is the force as estimated from the bending of the cantilever and d the relative change in distance between the supporting cantilever and the sample surface, as determined from the piezo scanner. In Fig. 1b, during approach (red curve) the force F initially remains constant with decreasing distance d. The distance ds marks the event where the approach curve exhibits a sudden (small) negative force jump, followed by a linear increase of F with decreasing d that marks the resistance of the surface and colloidal probe against deformation. The distance ds is thus associated with the jump-to-contact or snap-in event between the colloidal probe and the sample surface. Upon retraction (black curve), the colloidal probe remains in contact until the distance reaches dp, with the colloid-surface adhesion interaction bending the cantilever further until the sudden jump-out-of-contact or pull-off event at dp. The change in force at dp measures the force of adhesion between the colloidal probe and the sample.
The experimental F(d) data were automatically processed using MATLAB scripts, to extract a discrete number of metrics (six) from each approach-retract curve pair. We extracted the pull-off force (i.e., force of adhesion, Fpull) at dp and the snap-in force (Fsnap) at ds. Each were extracted using two algorithms to mitigate errors in determining the force baseline (taken as the mean force within the last 10% of the relevant d), the noise at dp and ds, and digitalization and bandwidth limitations. The forces Fpull and Fsnap were thus both computed twice: first, as the minimum of F in the curves with respect to the baseline and, second, as the force difference across the snap-in and pull-off events at ds and dp, with the events ds and dp identified by computing the derivatives of the F(d) curves. We also extracted the work of adhesion (Wadh), defined as the integral below the baseline of the retraction curve, as well as the contact difference Δd = dp − ds. PCA and regressions were performed with MATLAB using built-in functions.
Samples
Mica “Ratan Mica Exports Ltd., India” and highly oriented pyrolytic graphite “HOPG; Agar Scientific” were sourced commercially. Indium-tin-oxide (ITO) coated glass slides with typical resistivity of 50 Ω per square were commercially sourced by “Delta Technologies”. Si and thermally evaporated SiO2 on Si approx. 40 nm thick were provided by “Analog Devices International Limerick, Ireland” and the oxide thickness was measured by ellipsometry. Superhydrophobic coated Si (sh-Si) was prepared using an Atmospheric Pressure Plasma Dielectric Barrier Discharges (APDBD) in open air reactor on one-side polished Si wafers (thickness: approx. 300 μm). In a first step, silicon substrates were subjected to a pre-cleaning procedure using the same APDBD reactor and nitrogen plasma gas to eliminate contaminants and improve coating adhesion. In the second step, a mixture of liquid precursor nanodroplets and nitrogen gas was introduced into the plasma discharge to promote plasma polymerization. Plasma discharge was generated by an AC power supply with a 6 kHz frequency and 100 W of delivered power. The liquid chemical precursor injected into the discharge was 1H,1H,2H,2H-perfluorodecylacrylate from “Sigma Aldrich”. Five surfaces (mica, HOPG, silica, Si and sh-Si) cover a wide range of adhesion properties and are planar, uniform, and free from major defects and therefore chosen as reference surfaces in this study. Before introduction into the humidity-controlled AFM or before CA measurements, mica and HOPG were freshly cleaved and not processed further, while SiO2, Si and sh-Si were cleaned with a spray of deionized water and dried with a nitrogen gas flow.Contact angles
CA measurements followed the standard procedures UNI EN 828, UNI 9752, and ASTM D-5725-99 and were done using a computer-controlled CAM 200 system (KSV instruments). The contact angles were recorded with three liquid probes (deionized water, formamide, and methylene iodide) and the measurements repeated at least five times on different areas of the surfaces. The droplets (5 μL) were deposited on the samples and images of the sessile droplets were captured by a digital camera for 30 s (1 frame/second). The contact angles θi (i = 1, 2, 3 for the 3 probe liquids) were then determined with the CAM software provided by the instrument manufacturer, using contrast enhancement and axisymmetric drop shape analysis. The samples SFE σS was calculated using the commonly used Owens–Wendt model.13 The model assumes that the sample SFE is the sum of polar and dispersive components, σSP and σSD. With the dispersive and polar SFE values of the three liquid probes (σL,iD and σL,iP) known, σSP and σSD can be found by plotting eqn (1) as a line for all three liquids and computing the square of the slope and intercept respectively.
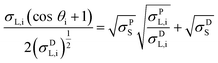 | (1) |
The probe liquids were selected for their varied polar and dispersive components: water a highly polar liquid with a small dispersive component, methylene iodide a highly dispersive liquid with very little polarity and formamide exhibiting similar polar and dispersive components.
Results and discussion
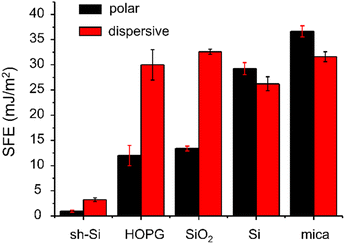
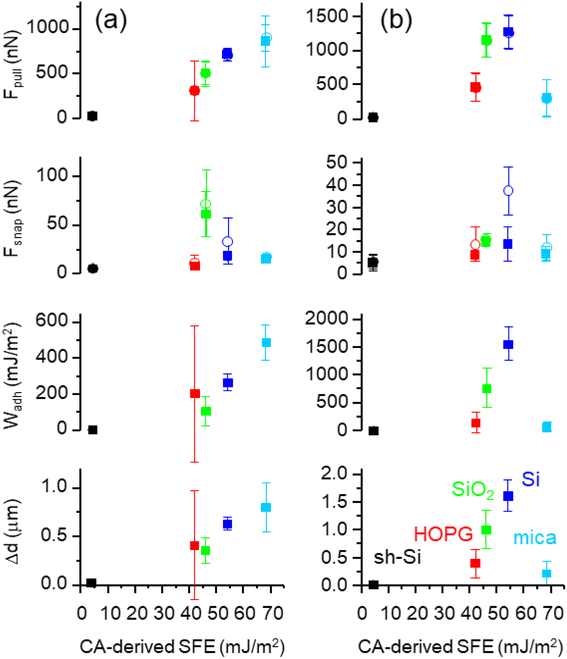
The polar and dispersive components of the SFE for the five test surfaces are presented in Fig. 2 and the measured contact angle values are summarized in Table S1 (ESI†). The total SFE is taken as the sum of the two components. We find that the planar super-hydrophobic sh-Si has the lowest SFE at 4.2 mJ m−2, with water contact angles averaging 162.5°. Mica is the most hydrophilic surface tested here, with an SFE of 68 mJ m−2. The surfaces under test show distinctive polar SFE components, with relatively less variations in their dispersive components (with the exception of sh-Si).Means and standard deviations of Fpull, Fsnap, Wadh and Δd extracted from F(d) (over 300–1000 curves per sample per colloid) are presented in Fig. 3 for both silica and PS colloidal probes, and for the five surfaces under test. The values are plotted as a function of the CA-derived (total) SFE values presented above in Fig. 2. With the PS colloidal probe (Fig. 3a), we observe a monotonically increasing, relatively linear relationship between Fpull, Wadh and Δd and the SFE. These three metrics (in the absence of significant colloidal probe or surface deformation) are indeed expected to scale with the force of adhesion between the colloid and the surfaces and the contact models such as JKR and DMT indeed highlights such a relationship.31,32 Other authors have reported a similar relationship between Fpull and CA-derived polar SFE components with a Si3N4 tip (in ambient atmosphere).20 We note small differences in our data in the Fpull and Fsnap values extracted with the two algorithms, although the mean values for both algorithms are in good agreement with each other as one would expect. Fsnap does not exhibit a linear relationship with the SFE, and this is especially observable with silica and silicon for which the largest values are measured. From a data-oriented perspective, we note that these deviations between AFM-extracted metrics is advantageous, as this will be further discussed below. With the silica colloidal probe (Fig. 3b), the mean values of Fpull, Wadh and Δd exhibit a non-linear relationship with the CA-derived SFE. This is particularly clear for the values measured for mica, which are consistently lower than for the other test surfaces, except for sh-Si. Comparing the magnitudes of these metrics between PS and silica colloidal probes, we observe that, with the exception of mica, Fpull, Wadh and Δd are consistently of higher magnitudes with the silica colloidal probe. With the silica colloidal probe, the Fsnap values are generally lower than with the PS colloidal probe, although silica and silicon again show the largest values. We note that the contact geometry is expected to be similar for the two colloidal probes that have the same nominal diameter. The SFE for PS is expected to be 30–36 mJ m−2 42,43while the reported SFE values for silica significantly vary, from 50 to 259 mJ m−2.44,45 The higher SFE expected for the silica colloidal probe qualitatively justifies thus the larger AFM-derived metrics Fpull, Wadh and Δd values. However, the metrics do not scale linearly between the samples as one expects from contact models. These observations reinforce our proposition to rely on a data-based model to quantify the SFE.
The larger deviation from linearity in force of adhesion (with respect to the SFE) is seen for mica, with the silica colloidal probe. The measured force of adhesion sums Van Der Waals, electrostatic and capillary contributions.20,46 Since our measurements are systematically performed with humidity <7%, capillary forces are not expected to play a major role.47–49 Moreover, PS and silica colloidal probes have similar Hamaker constants50 and also have nominally the same diameter here. As such, one does not expect any significant difference in the Van Der Waals force either. One can speculate thus that electrostatic forces differ. Mica is indeed an excellent dielectric and is largely the least conductive of the samples under test, while the other materials have sufficient bulk electrical conductivity to avoid significant local electrical charging (HOPG, silicon, silica (i.e., 42 nm SiO2/Si), and sh-Si). Mica typically displays (positive) potassium ions and with the propensity of silica colloidal probes to positively charge by triboelectric charging,46,51,52 the electrostatic force between the silica colloidal probe and the mica surface will reduce the measured pull-off force. This is not the case for PS colloidal probes that tend to charge negatively in contact with mica.20,46
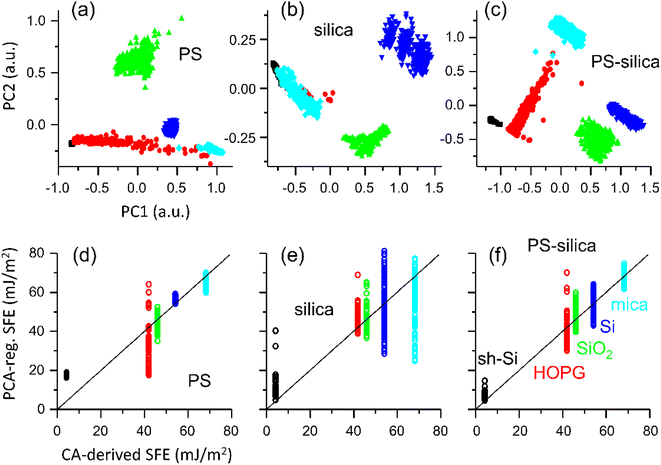
Notwithstanding our speculations on the origin of these deviations from linearity between the AFM-derived metrics and CA-derived SFE, it remains experimentally demonstrated that our AFM measurements do not systematically all agree with contact mechanics models such as DMT and JKR,31,32 and we thus gave preference to develop a data-oriented model by PCA of the six AFM-derived metrics. For the analysis, we randomly set 20% of the data apart for testing. PCA and regressions were computed only on the training set (80% of the data). We studied three datasets: PS colloidal probe, silica colloidal probe, PS and silica colloidal probes combined. For each surfaces and colloidal probes, 200 samples of n × F(d) curves (n = 10 in the main text, see results for n = 1, 5, 10, and 20 in ESI Fig. S3†) were randomly picked from the total population of curves. The median values for each of the six metrics in the samples were calculated and assembled in input vectors for the PCA. For PS colloidal probe and silica colloidal probe analysis, the PCA input vectors were thus made from the six AFM-derived metrics medians, while for the analysis with both PS and silica colloidal probes combined, the PCA input vectors contained twelve values. The PC2 versus PC1 scatter plots are shown in Fig. 4 (top panel) for each of the three datasets, where PC1 and PC2 are respectively the first and second PCs.
With the PS colloidal probe alone (Fig. 4a), we note that along the PC1 axis, the data are clustered alike for the Fpull and Wadh means graphs in Fig. 3a. This is consistent with most of the variance in the datasets seen for these parameters.
The clusters distribution along the PC2 axis is reminiscent of the Fsnap graphs, highlighting the relevance of this metric. The classification is excellent except for HOPG, whose large standard deviation in the datasets remains in the PC1, and the HOPG data partially overlap with those of sh-Si and mica. We note the usefulness of PC2 in separating the SiO2 and Si data. The classification is clearly more ambiguous with the silica colloidal probe alone (Fig. 4b), with a more pronounced overlap between mica, and HOPG and sh-Si. This is expected from the low values of Fpull and Wadh for mica when the silica colloidal probe is used.
By contrast, when both PS and silica colloidal probes are used for a combined analysis, we observe an unambiguous classification for the training set, with well-separated clusters of data for the five specimens under test. This means that measuring ten F(d) curve pairs with each colloidal probe on the same surface is sufficient. The twelve input parameters influence PC1 and PC2, but as expected, the PCs reflect largely a combination of Fpull and Wadh between the two colloidal probes.
We fitted a second-order regression of the first three PCs onto the CA-derived SFE values for each of the training datasets. The scatter plots for the test sets of those regression versus the SFE (mJ m−2) are presented in Fig. 4d–f. The regression with the silica colloidal probe alone performs poorly, especially for silicon and mica that have the largest targeted SFEs (see ESI Fig. S3† for a detailed summary of the R-squared values and where we also list the R-squared values for models built with samples made with 1, 5, 10, and 20 curves). The regression with the PS colloidal probe alone performs better but remains unable to provide a satisfactory fit across all the specimens, especially for sh-Si and HOPG. The regression based on the PCs computed for both colloidal probes combined provides a better fit to the SFE, avoiding the cases where PS and silica colloidal probes perform the poorest (i.e., sh-Si and HOPG, and mica, respectively). Since these regressions are built using the median values of ten F(d) curves for each colloidal probe, we can reasonably expect good predictability of the SFE from such a limited number of measurements, if both PS and silica colloidal probes are used together. For comparison, we show in Fig. S2 (ESI†) the regressions (second order) based on Fpull alone for PS and silica colloidal probes and list in Fig. S3† the corresponding R-squared values. The performances are clearly more limited, again especially for the silica colloidal probe.
We further validate our approach by quantifying the microscale SFE of an ITO coated glass. The F(d) were recorded with the same PS and silica colloidal probes and the metrics for ITO were introduced in the PCA and regression models developed from the sh-Si, HOPG, SiO2, Si, and mica reference surfaces. The PC scores maps (PC2 vs. PC1) are reproduced in Fig. S4 (ESI†) with the ITO data included, for the model based on the PS colloidal probe as well as the one based on the PS and silica colloidal probes combined. The ITO data form a cluster in both cases albeit without overlap onto the reference surfaces clusters only for the combined colloidal probes model. When the corresponding regression models are applied on the ITO PCs, we find SFE values of 59 mJ m−2 and 54 mJ m−2 for the PS only, and PS and silica combined models. These SFE are comparable to values reported for ITO in the literature.53
Conclusions
We reported the recording of a large series of sub-microscale F(d) spectra in humidity-controlled environment, for five planar and uniform surfaces of interest with adhesion properties spanning from super-hydrophobic to hydrophilic and using two different colloidal probes (PS and silica). The macroscopic SFE values were derived from the measurement and analysis of CA, using three liquid probes and the Owen–Wendt model. When plotting the means of AFM-derived metrics such as Fpull and Wadh versus the CA-derived SFEs, we found that the quantities vary relatively linearly with the PS colloidal probe but not with the silica colloidal probe. This deviates from predictions of standard contact models such as JKR and DMT. Moreover, the differences in the values recorded with PS and silica colloidal probe do not scale well with the same, despite the large change in the SFE of PS and silica.We thus proposed a data-oriented model, where PCs are computed from six AFM-derived metrics and where the first PCs are used to fit a second-order regression onto the CA-derived SFE. We found that silica and PS colloidal probes data complement well each other and their combination leads to the best predictive SFE model. As such, once the model is trained, the recording of ten F(d) curves with each colloidal probe is sufficient to correctly classify the specimens under test and to determine their SFE.
The demonstration here shows that the SFE can be quantifiably mapped at sub-microscale using macroscopic SFE reference values, without the need thus for local contact model relying on poorly known probe parameters. This work aims at facilitating standardization of SFE values across the various length scales.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This publication has emanated from research conducted with the partial financial support from the European Commission, European project Oyster, grant agreement 760827. The NETGRA-Spectra atomic force microscope was funded by Science Foundation Ireland opportunistic fund for research infrastructure.References
- E. J. Falde, S. T. Yohe, Y. L. Colson and M. W. Grinstaff, Superhydrophobic materials for biomedical applications, Biomaterials, 2016, 104, 87–103 CrossRef CAS PubMed.
- M. Camara-Torres, R. Sinha, P. Scopece, T. Neubert, K. Lachmann and A. Patelli, et al., Tuning Cell Behavior on 3D Scaffolds Fabricated by Atmospheric Plasma-Assisted Additive Manufacturing, ACS Appl. Mater. Interfaces, 2021, 13(3), 3631–3644 CrossRef CAS PubMed.
- V. Barreau, R. Hensel, N. K. Guimard, A. Ghatak, R. M. McMeeking and E. Arzt, Fibrillar Elastomeric Micropatterns Create Tunable Adhesion Even to Rough Surfaces, Adv. Funct. Mater., 2016, 26(26), 4687–4694 CrossRef CAS.
- H. Liu, Y. D. Wang, J. Y. Huang, Z. Chen, G. Q. Chen and Y. K. Lai, Bioinspired Surfaces with Superamphiphobic Properties: Concepts, Synthesis, and Applications, Adv. Funct. Mater., 2018, 28(19), 1707415 CrossRef.
- W. Barthlott and C. Neinhuis, Purity of the sacred lotus, or escape from contamination in biological surfaces, Planta, 1997, 202(1), 1–8 CrossRef CAS.
- T. S. D. Le, J. N. An, Y. Huang, Q. Vo, J. Boonruangkan and T. Tran, et al., Ultrasensitive Anti-Interference Voice Recognition by Bio-Inspired Skin-Attachable Self-Cleaning Acoustic Sensors, Acs Nano, 2019, 13(11), 13293–13303 CrossRef PubMed.
- P. Auad, E. Ueda and P. A. Levkin, Facile and Multiple Replication of Superhydrophilic-Superhydrophobic Patterns Using Adhesive Tape, ACS Appl. Mater. Interfaces, 2013, 5(16), 8053–8057 CrossRef CAS PubMed.
- E. Ueda and P. A. Levkin, Emerging Applications of Superhydrophilic-Superhydrophobic Micropatterns, Adv. Mater., 2013, 25(9), 1234–1247 CrossRef CAS PubMed.
- M. M. Hussain, A. Kunwar, M. K. Majeed, Y. P. Wang, A. Saleem and H. T. Ma, Superhydrophobic Surface and Lubricant-Infused Surface: Implementing Two Extremes on Electrodeposited Ni-TiO2 Surface to Drive Optimal Wettability Regimes for Droplets’ Multifunctional Behaviors, Adv. Eng. Mater., 2021, 23(10), 2100266 CrossRef CAS.
- T. Kajiya, F. Schellenberger, P. Papadopoulos, D. Vollmer and H. J. Butt, 3D Imaging of Water-Drop Condensation on Hydrophobic and Hydrophilic Lubricant-Impregnated Surfaces, Sci. Rep., 2016, 6, 23687 CrossRef CAS PubMed.
- E. P. Koumoulos, S. A. M. Tofail, C. Silien, D. De Felicis, R. Moscatelli and D. A. Dragatogiannis, et al., Metrology and nano-mechanical tests for nano-manufacturing and nano-bio interface: Challenges & future perspectives, Mater. Des., 2018, 137, 446–462 CrossRef CAS.
- R. J. Good, Contact-Angle, Wetting, and Adhesion - a Critical-Review, J. Adhes. Sci. Technol., 1992, 6(12), 1269–1302 CrossRef CAS.
- D. K. Owens and R. C. Wendt, Estimation of Surface Free Energy of Polymers, J. Appl. Polym. Sci., 1969, 13(8), 1741–1747 CrossRef CAS.
- F. M. Etzler, Contact Angle, Wettability and Adhesion, in Characterization of Surface Free Energies and Surface Chemistry of Solids, ed. Mittal K. L., 2003, vol. 3 Search PubMed.
- C. J. Vanoss, L. Ju, M. K. Chaudhury and R. J. Good, Estimation of the Polar Parameters of the Surface-Tension of Liquids by Contact-Angle Measurements on Gels, J. Colloid Interface Sci., 1989, 128(2), 313–319 CrossRef CAS.
- T. Huhtamaki, X. L. Tian, J. T. Korhonen and R. H. A. Ras, Surface-wetting characterization using contact-angle measurements (vol 13, pg 1521, 2018), Nat. Protoc., 2019, 14(7), 2259 CrossRef CAS PubMed.
- J. C. Hooton, C. S. German, S. Allen, M. C. Davies, C. J. Roberts and S. J. B. Tendler, et al., An atomic force microscopy study of the effect of nanoscale contact geometry and surface chemistry on the adhesion of pharmaceutical particles, Pharm. Res., 2004, 21(6), 953–961 CrossRef CAS PubMed.
- J. C. Hooton, C. S. German, S. Allen, M. C. Davies, C. J. Roberts and S. J. B. Tendler, et al., Characterization of particle-interactions by atomic force microscopy: Effect of contact area, Pharm. Res., 2003, 20(3), 508–514 CrossRef CAS PubMed.
- D. M. Schaefer, M. Carpenter, B. Gady, R. Reifenberger, L. P. Demejo and D. S. Rimai, Surface-Roughness and Its Influence on Particle Adhesion Using Atomic-Force Techniques, J. Adhes. Sci. Technol., 1995, 9(8), 1049–1062 CrossRef CAS.
- A. Rana, A. Patra, M. Annamalai, A. Srivastava, S. Ghosh and K. Stoerzinger, et al., Correlation of nanoscale behaviour of forces and macroscale surface wettability, Nanoscale, 2016, 8(34), 15597–15603 RSC.
- H. J. Butt, Measuring Electrostatic, Vanderwaals, and Hydration Forces in Electrolyte-Solutions with an Atomic Force Microscope, Biophys. J., 1991, 60(6), 1438–1444 CrossRef CAS PubMed.
- W. A. Ducker, T. J. Senden and R. M. Pashley, Direct Measurement of Colloidal Forces Using an Atomic Force Microscope, Nature, 1991, 353(6341), 239–241 CrossRef CAS.
- J. J. Valle-Delgado, J. A. Molina-Bolivar, F. Galisteo-Gonzalez, M. J. Galvez-Ruiz, A. Feiler and M. W. Rutland, Adhesion forces between protein layers studied by means of atomic force microscopy, Langmuir, 2006, 22(11), 5108–5114 CrossRef CAS PubMed.
- K. E. Bremmell, P. Kingshott, Z. Ademovic, B. Winther-Jensen and H. J. Griesser, Colloid probe AFM investigation of interactions between fibrinogen and PEG-like plasma polymer surfaces, Langmuir, 2006, 22(1), 313–318 CrossRef CAS PubMed.
- H. J. Griesser, P. G. Hartley, S. L. McArthur, K. M. McLean, L. Meagher and H. Thissen, Interfacial properties and protein resistance of nano-scale polysaccharide coatings, Smart Mater. Struct., 2002, 11(5), 652–661 CrossRef CAS.
- L. Meagher and H. J. Griesser, Interactions between adsorbed lactoferrin layers measured directly with the atomic force microscope, Colloids Surf., B, 2002, 23(2–3), 125–140 CrossRef CAS.
- M. Kopycinska-Muller, R. H. Geiss, J. Muller and D. C. Hurley, Elastic-property measurements of ultrathin films using atomic force acoustic microscopy, Nanotechnology, 2005, 16(6), 703–709 CrossRef CAS.
- U. Rabe, M. Kopycinska, S. Hirsekorn, J. M. Saldana, G. A. Schneider and W. Arnold, High-resolution characterization of piezoelectric ceramics by ultrasonic scanning force microscopy techniques, J. Phys. D: Appl. Phys., 2002, 35(20), 2621–2635 CrossRef CAS.
- E. Dupas, G. Gremaud, A. Kulik and J. L. Loubet, High-frequency mechanical spectroscopy with an atomic force microscope, Rev. Sci. Instrum., 2001, 72(10), 3891–3897 CrossRef CAS.
- B. Derjaguin, Untersuchungen über die Reibung und Adhäsion, IV, Kolloid-Z., 1934, 69, 155–164 CrossRef.
- B. V. Derjaguin, V. M. Muller and Y. P. Toporov, Effect of Contact Deformations on Adhesion of Particles, J. Colloid Interface Sci., 1975, 53(2), 314–326 CrossRef CAS.
- K. L. Johnson, K. Kendall and A. D. Roberts, Surface Energy and Contact of Elastic Solids, Proc. R. Soc. A: Math. Phys. Eng. Sci., 1971, 324(1558), 301–313 CAS.
- S. Khandavalli, P. Rogers and J. P. Rothstein, Roll-to-roll fabrication of hierarchical superhydrophobic surfaces, Appl. Phys. Lett., 2018, 113(4), 041601 CrossRef.
- A. M. Kietziga, M. N. Mirvakilia, S. Kamalb, P. Englezosa and S. G. Hatzikiriakosa, Nanopatterned Metallic Surfaces: Their Wettability and Impact on Ice Friction, J. Adhes. Sci. Technol., 2011, 25(12), 1293–1303 CrossRef.
- E. M. Rossi, P. S. Phani, R. Guillemet, J. Cholet, D. Jussey and W. C. Oliver, et al., A novel nanoindentation protocol to characterize surface free energy of superhydrophobic nanopatterned materials, J. Mater. Res., 2021, 36(11), 2357–2370 CrossRef CAS.
- S. De Santis, E. Rossi, M. Sebastiani, S. Sennato, E. Bemporad and M. Orsini, A Nanoindentation Approach for Time-Dependent Evaluation of Surface Free Energy in Micro- and Nano-Structured Titanium, Materials, 2022, 15(1), 287 CrossRef CAS PubMed.
- A. Cardellini, F. M. Bellussi, E. Rossi, L. Chiavarini, C. Becker and D. Cant, et al., Integrated molecular dynamics and experimental approach to characterize low-free-energy perfluoro-decyl-acrylate (PFDA) coated silicon, Mater. Des., 2021, 208 Search PubMed.
- N. Bonnet, Artificial intelligence and pattern recognition techniques in microscope image processing and analysis, Adv. Imaging Electron Phys., 2000, 114, 1–77 Search PubMed.
- S. Jesse and S. V. Kalinin, Principal component and spatial correlation analysis of spectroscopic-imaging data in scanning probe microscopy, Nanotechnology, 2009, 20(8), 085714 CrossRef PubMed.
- J. E. Sader, J. W. M. Chon and P. Mulvaney, Calibration of rectangular atomic force microscope cantilevers, Rev. Sci. Instrum., 1999, 70(10), 3967–3969 CrossRef CAS.
- R. W. Stark and W. M. Heckl, Higher harmonics imaging in tapping-mode atomic-force microscopy, Rev. Sci. Instrum., 2003, 74(12), 5111–5114 CrossRef CAS.
- J. R. Dann, Forces Involved in Adhesive Process.1 Critical Surface Tensions of polymeric Solids as Determined with Polar Liquids, J. Colloid Interface Sci., 1970, 32(2), 302–320 CrossRef CAS.
- L. H. Lee, Relationships between Surface Wettability and Glass Temperatures of High Polymers, J. Appl. Polym. Sci., 1968, 12(4), 719–730 CrossRef CAS.
- J. M. Chovelon, F. Gaillard, K. Wan and N. Jaffrezic-Renault, Influence of the surface pressure on the organization of mixed Langmuir-Blodgett films of octadecylamine and butyrylcholinesterase. 2. Film transferred onto silica support, Langmuir, 2000, 16(15), 6228–6232 CrossRef CAS.
- S. Brunauer, D. L. Kantro and C. H. Weise, The Surface Energies of Calcium Oxide and Calcium Hydroxide, Can. J. Chem., 1956, 34(6), 729–742 CrossRef CAS.
- H. Kweon, S. Yiacoumi and C. Tsouris, The role of electrostatic charge in the adhesion of spherical particles onto planar surfaces in atmospheric systems, Colloids Surf., A, 2015, 481, 583–590 CrossRef CAS.
- C. Birleanu, M. Pustan, F. Rusu, C. Dudescu, R. Muller and A. Baracu, Relative humidity effect on pull-off forces in MEMS flexible structures measured by AFM, Symposium on Design, Test, Integration and Packaging of Mems/Moems (Dtip 2017), 2017 Search PubMed.
- Y. I. Rabinovich, J. J. Adler, M. S. Esayanur, A. Ata, R. K. Singh and B. M. Moudgil, Capillary forces between surfaces with nanoscale roughness, Adv. Colloid Interface Sci., 2002, 96(1–3), 213–230 CrossRef CAS PubMed.
- R. A. Quon, A. Ulman and T. K. Vanderlick, Impact of humidity on adhesion between rough surfaces, Langmuir, 2000, 16(23), 8912–8916 CrossRef CAS.
- F. L. Leite, C. C. Bueno, A. L. Da Roz, E. C. Ziemath and O. N. Oliveira, Theoretical Models for Surface Forces and Adhesion and Their Measurement Using Atomic Force Microscopy, Int. J. Mol. Sci., 2012, 13(10), 12773–12856 CrossRef CAS PubMed.
- H. K. Christenson and N. H. Thomson, The nature of the air-cleaved mica surface, Surf. Sci. Rep., 2016, 71(2), 367–390 CrossRef CAS.
- F. Ostendorf, C. Schmitz, S. Hirth, A. Kuhnle, J. J. Kolodziej and M. Reichling, Evidence for Potassium Carbonate Crystallites on Air-Cleaved Mica Surfaces, Langmuir, 2009, 25(18), 10764–10767 CrossRef CAS PubMed.
- J. S. Kim, R. H. Friend and F. Caciallia, Surface energy and polarity of treated indium–tin–oxide anodes for polymer light-emitting diodes studied by contact-angle measurements, J. Appl. Phys., 1999, 86(5), 5 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Table S1 contains the recorded contact angle wetting measurements on the five test surfaces, using three solvents. Total (T), polar (P), and dispersive (D) components of the SFE calculated using Owen–Wendt approach. Fig. S2 shows the second-order regression of Fpull on the CA-derived SFE values for the testing set with silica colloidal probe, PS colloidal probe, and PS and silica probes combined (regression coefficients computed on the training set). Fig. S3 shows a R-squared analysis of the performance of the PCs and regression models. Fig. S4 shows PC2 vs. PC1 maps including ITO data. Fig. S5 shows F(d) curves recorded on the mica reference with different probe velocities. See DOI: https://doi.org/10.1039/d2ra05508b |
| This journal is © The Royal Society of Chemistry 2023 |