Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Chemical recycling to monomer: thermodynamic and kinetic control of the ring-closing depolymerization of aliphatic polyesters and polycarbonates†
Linnea
Cederholm
,
Peter
Olsén
 ,
Minna
Hakkarainen
,
Minna
Hakkarainen
 and
Karin
Odelius
and
Karin
Odelius
 *
*
Wallenberg Wood Science Center, WWSC, Department of Fibre and Polymer Technology, KTH Royal Institute of Technology, Teknikringen 56-58, 100 44 Stockholm, Sweden. E-mail: hoem@kth.se
First published on 4th July 2023
Abstract
The thermodynamic equilibrium between ring-opening polymerization and ring-closing depolymerization is influenced by monomer–solvent–polymer interactions, an effect that can be utilized to promote chemical recycling to monomer. Here, the influence of monomer structure on this solvent effect has been investigated, showing that the chemical structure of the monomer influences the power of the solvent to supress the ceiling temperature. The study also demonstrates how catalyst selectivity can be utilized to obtain selective ring-closing depolymerization of one component of a polymer blend, even when the thermodynamics dictate otherwise.
Ring-opening polymerization (ROP) and the reverse ring-closing depolymerization (RcDP) has received a great deal of attention in terms of chemical recycling and the design of closed-loop monomer–polymer systems.1–3 The reversible nature of ROP opens up for chemical recycling to monomer (CRM),1 which is envisioned to play an important role in the future circular polymer economy.2,4,5 However, the thermodynamic control of the equilibrium between monomer and polymer makes the design of polymers for CRM via ROP and RcDP a constant balance between polymerizability, thermal stability and recyclability. The ROP of smaller cyclic monomers is often enthalpy driven, i.e. although there is an unfavourable decrease in entropy upon polymerization (ΔSp), the reaction continuous due to a favourable decrease in enthalpy (ΔHp).6–8 Hence, as long as the monomer concentration [M] can decrease with the total change in Gibb's free energy ΔGp < 0,
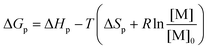 | (1) |
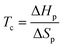 | (2) |
Hence, for CRM via complete RcDP in a closed system, Tc can be considered the lowest possible recycling temperature for complete RcDP. The Tc is closely related to the structure of the monomer, and monomers with a low or moderate Tc are desirable for selective and energy efficient CRM.2,3,9 One strategy when developing polymers for CRM is, therefore, to design the chemical structure of the monomer in a way that generates a desirable Tc. Some examples of when this has been utilized are the development of different fused10–12 or bridged13 bicyclic structures with γ-butyrolactone, the synthesis of δ-lactones with different substituents,14–19 or the benzyl-fused ether/thia-ε-lactones.20–22 In the cases of the bicyclic γ-lactones, the ring-closed substituents function as strain inducing elements that increase the Tc. As an example, the bridged γ-lactone 6-oxabicyclo[3.2.1]oct-3-en-7-one has a Tc (at [M]0 = 1 M) more than 250 °C higher (118 °C)13 compared to the non-substituted γ-butyrolactone (−136 °C).23 The higher Tc, thus, enhances the polymerizability, while the recyclability is maintained. However, substitution may also be used to decrease the Tc, and thereby improve the recyclability, which is the case for the aforementioned δ-lactones and benzyl-fused ether/thia-ε-lactones. Yet, to meet other material requirements without compromising the CRM, a large library of chemically recyclable polymers with varying properties has to be developed. This requires both clever monomer designs, as well as an array RcDP methodologies. One such strategy could be to utilize external factors, factors other than the monomer structure, to manipulate the Tc.
It is well established that the Tc decreases with a decreased [M]0, since the entropy of the system scales with the concentration. Consequently, RcDP can be promoted by dilution. For long, this has been considered a pure effect of concentration, and cases where solvent properties have shown to influence the polymerization thermodynamics have often been treated as individual exceptions rather than a general trend. Although previous observations have indicated otherwise,24 and a relationship between ΔHp and ΔSp and solvent interactions was derived over 50 years ago,25,26 this has been poorly utilized in ROP, and its potential in terms of CRM is fairly unexploited. However, we were recently able to demonstrate how the solvent effects the Tc, where strong monomer–solvent interactions favoured a decrease in Tc.27 This could be utilized to lower the recycling temperature of polylactide (PLA), enabling RcDP to lactide (LA) with high yield and high selectivity, suppressing unwanted side reactions like epimerization to a minimum. We have also exploited RcDP in solution for the design of chemically recyclable A–B–A block copolymers.28 To create a broader and clearer picture of the solvent effect and its potential in terms of CRM, we have here analyzed the influence of solvent on the Tc of three monomers with different chemical features: δ-valerolactone (δVL), trimethylene carbonate (TMC) and LA (Scheme 1). The results for TMC in propylene carbonate (PrC), and for LA in dimethyl sulfoxide (DMSO), dimethylformamide (DMF), γ-valerolactone (GVL), 1,4-dioxane (DX) and chlorobenzene (PhCl), were obtained in earlier studies and have previously been presented elsewhere.27,28 All three monomers are six-membered cyclic structures, but with varying in-ring functionalities: carbonate (TMC), ester (δVL) and diester (LA). Due to their different structural features, their initial polymerization thermodynamic properties are different. However, we hypothesized that the chemical structure of the monomer would influence its ability to interact with the surrounding solvent and, consequently, have an impact on how much the Tc is affected by the solvent properties.
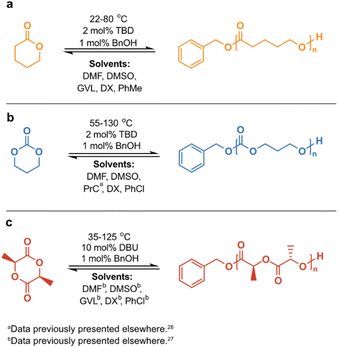 | ||
Scheme 1 Reaction scheme for the calculation of polymerization thermodynamic parameters at [M]0 = 0.5 M of (a) δVL in DMF, DMSO, GVL, DX and PhMe; (b) TMC in DMF, DMSO, PrCa, DX and PhCl; (c) LA in DMFb, DMSOb, GVLb, DXb and PhClb. a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Data previously presented elsewhere.28b Data previously presented elsewhere.28b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Data previously presented elsewhere.27 Data previously presented elsewhere.27 | ||
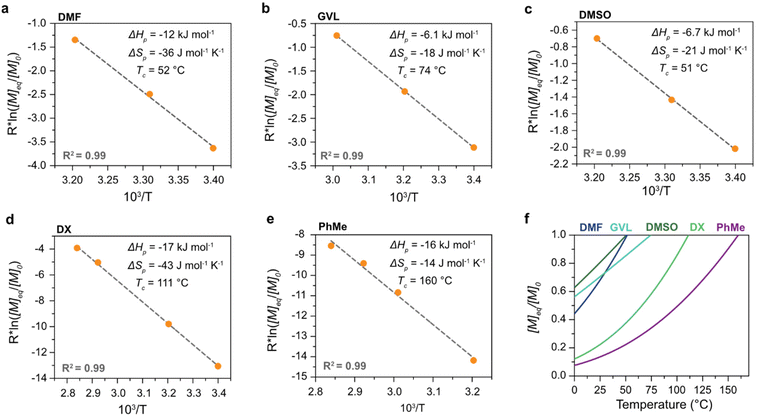
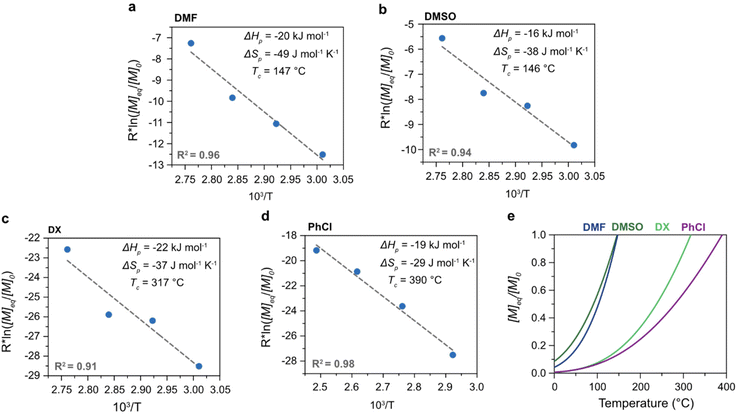
The polymerization thermodynamic parameters ΔHp and ΔSp of δVL were calculated from equilibrium polymerizations in DMSO, DMF, GVL, DX and toluene (PhMe) (Fig. 1), and for TMC in DMSO, DMF, DX and chlorobenzene (PhCl) (Fig. 2). All reactions were performed at [M]0 = 0.5 M with 2 mol% 1,5,7-triazabicyclo[4.4.0]dec-5-ene (TBD) as catalyst (Table S1 and S2 in ESI†). The catalyst was selected based on its activity towards the monomer–polymer system,29–31 to ensure the equilibrium was reached, and should not have an influence on the polymerization thermodynamics. Similar to what was previously observed for LA, the Tc of both δVL and TMC were highly influenced by the solvent: the Tc of δVL was decreased from 160 °C in PhMe (Fig. 1e) to 51 °C in DMSO (Fig. 1c) and the Tc of TMC changed from 422 °C in PhCl (Fig. 2e) to 146 °C in DMSO (Fig. 2b). Thus, the results suggest that the solvent effect on the thermodynamic equilibrium between monomer and polymer cannot be regarded as isolated cases, but rather as a general factor that influences the equilibrium conversion and should, therefore, be considered in the design of both ROP and RcDP systems. This solvent effect on the polymerization thermodynamic equilibrium was described already in the 1960s, when the Flory–Huggins solution theory,32 and the interaction parameters Xms, Xsp and Xmp, were used to derive a relationship between the monomer–polymer equilibrium and the secondary interactions between monomer–solvent–polymer.25,26 In the resulting Ivin–Léonard equation,
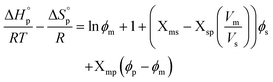 | (3) |
| ϕm + ϕp + ϕs = 1 | (4) |
Thereby, to illustrate the influence of the solvent on the Tc (i.e. ϕp = 0), (4) can be rewritten accordingly,
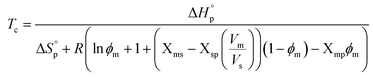 | (5) |
It is worth noting that 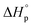 and
and 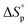 denote the change in enthalpy and entropy at standard conditions ([M]0 = 1 M, 1 atm, 25 °C), i.e. in an ideal environment where all secondary interactions are neglectable. Hence,
denote the change in enthalpy and entropy at standard conditions ([M]0 = 1 M, 1 atm, 25 °C), i.e. in an ideal environment where all secondary interactions are neglectable. Hence, 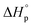 and
and 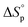 will deviate from ΔHp and ΔSp, which are determined experimentally from (1), depending on the strength of the actual intermolecular forces that are present in the system. In addition, the interactions between solvent and polymer (Xsp) have shown a significant variation with concentration.33,34 Thus, dilution is not a pure entropic effect, which one should be aware of when using thermodynamic experimental data obtained at one [M]0 to explain an equilibrium behaviour at a completely different concentration. Consequently, the thermodynamic data that were utilized in this study originate from equilibrium polymerization experiments all performed at the same initial monomer concentration [M]0.
will deviate from ΔHp and ΔSp, which are determined experimentally from (1), depending on the strength of the actual intermolecular forces that are present in the system. In addition, the interactions between solvent and polymer (Xsp) have shown a significant variation with concentration.33,34 Thus, dilution is not a pure entropic effect, which one should be aware of when using thermodynamic experimental data obtained at one [M]0 to explain an equilibrium behaviour at a completely different concentration. Consequently, the thermodynamic data that were utilized in this study originate from equilibrium polymerization experiments all performed at the same initial monomer concentration [M]0.
Since a small value of, e.g., Xms indicates strong secondary interactions between monomer–solvent, it can be seen from (5) that the Tc of a specific monomer–polymer system, at a constant [M]0 (or ϕs), is decreasing with stronger monomer–solvent interactions and weaker solvent–polymer interactions. However, the variations in Xms with solvent are usually larger compared to Xsp, related to the different mixing processes of small monomers vs. long polymer chains. This is why the monomer–solvent interactions dominate the impact on Tc.35 This was verified by the results from our previous study on LA, where we also showed that the relationship between the Hildebrand solubility parameters of the monomer and solvent (δm − δs)2 and solvent and polymer (δs − δp)2 could be used as valid representations of Xms and Xsp, resulting in (6),27
| Tc = A(δm − δs)2 + B(δs − δp)2 + C | (6) |
Since δm and δp are constant for a specific monomer–polymer system, the influence of δs on the Tc (at a constant [M]0) can be described by (7) (see ESI† for derivation), where the second derivative (8) can be interpreted as the power of the solvent effect,
| Tc = aδs2 + bδs + c | (7) |
| d2Tc/dδs2 = 2a | (8) |
Since (8) is independent δs, the size of d2Tc/dδs2, i.e. how large is the impact of solvent interactions on the polymerization equilibrium, should be a unique property of the monomer–polymer system. It is, hence, reasonable to assume that d2Tc/dδs2 may vary with the chemical structure of the monomer.
As previously reported, the change in Tc of LA with δs was fitted to (7) almost perfectly,27 a trend that, here, was confirmed by the thermodynamic behaviour of δVL and TMC in the different solvents (Fig. 3). To illustrate the importance of using experimental data obtained at the same [M]0, a literature value for TMC in THF,36 recalculated to [M]0 = 0.5 M from experiments performed at [M]0 = 0.03 M, was added to Fig. 3. The calculations are based on the assumption that the influence of concentration is purely entropic, a well-established methodology for calculating and presenting polymerization thermodynamic data. However, as previously mentioned, the Xsp is not independent of concentration, and it has shown to increase with dilution.33,34 Thus, considering (5) and the decreasing effect that a higher Xsp has on the Tc, to calculate a Tc at a certain concentration based on experiments performed at a lower [M]0 would lead to an underestimation of the actual Tc. This could, hence, explain the discrepancy that can be observed between the literature data for TMC and the results obtained from this study (Fig. 3).36
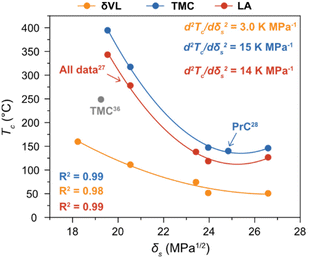 | ||
Fig. 3 Ceiling temperature (Tc) in relation to δs at [M]0 = 0.5 M of δVL ( ) (solvents: DMSO (26.6 MPa1/2), DMF (24.0 MPa1/2), GVL (23.4 MPa1/2), DX (20.5 MPa1/2) and PhMe (18.2 MPa1/2)), TMC ( ) (solvents: DMSO (26.6 MPa1/2), DMF (24.0 MPa1/2), GVL (23.4 MPa1/2), DX (20.5 MPa1/2) and PhMe (18.2 MPa1/2)), TMC ( ) (solvents: DMSO, DMF, PrC (24.8 MPa1/2), DX and PhCl (19.5 MPa1/2)) and LA ( ) (solvents: DMSO, DMF, PrC (24.8 MPa1/2), DX and PhCl (19.5 MPa1/2)) and LA ( ) (solvents: DMSO, DMF, GVL, DX and PhCl). All data for LA,27 and the data for TMC in PrC28 were originally presented elsewhere. The literature data for TMC ( ) (solvents: DMSO, DMF, GVL, DX and PhCl). All data for LA,27 and the data for TMC in PrC28 were originally presented elsewhere. The literature data for TMC ( ) is recalculated form equilibrium polymerization experiments performed at [M]0 = 0.03 M in THF (19.2 MPa1/2).36 ) is recalculated form equilibrium polymerization experiments performed at [M]0 = 0.03 M in THF (19.2 MPa1/2).36 | ||
As hypothesized, the power of the solvent effect varied between the different monomer–polymer systems, where the d2Tc/dδs2 for LA (14 K MPa−1) and TMC (15 K MPa−1) were quite similar, while the d2Tc/dδs2 for δVL was substantially lower (3.0 K MPa−1). Since previous data have shown that the monomer–solvent interactions are the predominant contribution to the solvent effect,35 the proposed explanation to these differences will emanate from the mixing process of monomers in solution. In order for the monomer to form secondary interactions with the solvent (wms) and, thereby, dissolve, the intermolecular bonds between monomer–monomer (wmm) and solvent–solvent (wss) have to be broken. This process usually entails an increase in energy, which is proportional to the enthalpy of mixing,37
| Δw = wms − 0.5(wmm + wss) ∝ ΔHmix | (9) |
The unfavourable increase in ΔHmix is compensated by an increased entropy, though, the larger the ΔHmix is the lower is the solubility of the monomer in the specific solvent. Consequently, monomers with stronger intermolecular forces between monomer–monomer (large negative wmm) show a larger variation in solubility depending on the secondary monomer–solvent interactions. This would explain, why the power of the solvent effect (d2Tc/dδs2) is stronger for the two more polar monomers LA and TMC, as compared to δVL. Consequently, although it is likely that the solvent effect on the thermodynamic equilibrium between monomer–polymer is present in all equilibrium polymerization systems, its relevance and, thereby, potential in terms of CRM depends on the chemical structure of the monomer. This could potentially be utilized in the design of monomers for closed-loop polymer systems.
However, products and polymer waste streams rarely contain one single type of polymer, which adds further complexity to the RcDP system. In a previous study, we showed that PLA could be chemically recycled via solvent triggered RcDP in the presence of other common polymeric materials, like PP, PE, PET and PA6.6, without compromising with the selectivity.27 Though, adding PC to the system resulted in both lower conversion and selectivity in RcDP of PLA to LA. Thus, CRM via RcDP is not purely a matter of thermodynamics, and for RcDP of a mixture of polymers, the catalyst selectivity and kinetical differences can be powerful in terms of selective CRM of mixed polymer waste.
Due to its low toxicity and good performance in the RcDP of PLA, as previously reported,27 GVL was selected as solvent for the mixed polymer RcDP. The RcDP of a mixture of PδVL (26.9 kg mol−1, Đ = 1.82), PTMC (20.9 kg mol−1, Đ = 1.97) and PLA (15.0 kg mol−1, Đ = 1.25) was studied in GVL ([M]0,δVL = [M]0,TMC = [M]0,LA = 0.5 M based on the repeating unit of each polymer, i.e. [M]0,tot = 1.5 M), in the presence of tin(II) 2-ethylhexanoate (SnOct2, [cat] = 0.05 M) as catalyst. This concentration was selected in order to mimic the conditions under which the polymerization thermodynamic parameters ([M]0 = 0.5 M) were calculated. The RcDP was started at 80 °C, and the temperature was, thereafter, increased stepwise by 20 °C up to 140 °C. Interestingly, the experiment resulted in selective RcDP of PLA up to 140 °C (Fig. 4a). The conversion to LA increased stepwise with the increase in temperature, in good agreement with the polymerization thermodynamics of LA in GVL (Fig. 4b). This indicates that the presence of the PδVL and PTMC, and the higher total concentration ([M]0,tot = 1.5 M), did not have strong impact on the thermodynamic equilibrium between PLA and LA. In contrast to PLA, PδVL was stable in the system, although RcDP should be thermodynamically promoted (Tc = 74 °C in GVL). This result was rather unexpected, and quite the opposite to the RcDP behaviour of PδVL ([M]0 = 0.5 M in GVL, 0.05 M SnOct2) at 140 °C without the presence of other polymers in the system (Fig. 4c), where 95% conversion to δVL was reached within 4 h. A similar observation was made for PTMC (Fig. 4d), though the equilibrium conversion to TMC was lower in the single polymer RcDP as compared to δVL due to the higher Tc of TMC in GVL (165 °C, estimated from Fig. 3). These differences between single polymer RcDP and mixed polymer RcDP are similar to observations made for copolymerization systems of LA and ε-caprolactone (εCL), and for LA and TMC, utilizing metal-based transesterification catalysts (e.g. aluminum triisopropoxide,38 or magnesium,39 zinc(II),40 and calcium complexes41). In the case of LA and εCL, it has often been observed that the successful copolymerization via sequential addition is reliant on the order of addition, were the initiation of εCL from PLA often seems prohibited while the reverse (initiation of LA from PεCL) is feasible.38–40 Similarly, one-step copolymerization of LA and εCL (both monomers present form the beginning) resulted in homopolymerization of LA, while εCL stayed unreacted.40 The copolymerization between LA and TMC show a similar, though not as extreme, behaviour, where the polymerization rate of TMC is substantially increased after all LA had been consumed, compared to when unreacted LA units were still left in the system.41 To our knowledge, the reason for this behaviour of copolymerization systems with LA has, not yet, been elucidated. Though, these previous observations could indicate that the catalyst coordinates to the PLA chain end in a way that inhibits or retards the catalysts activity towards ROP of other monomers. A behaviour that also seems to occur during the reverse RcDP. To further explain this interesting phenomenon should be the scope for future studies. Nevertheless, LA could be chemically recycled selectively from PLA (96% selectivity), even in a mixture with PδVL and PTMC, by the use of SnOct2 as a catalyst at 140 °C in GVL. Furthermore, by changing the catalyst, from SnOct2 to diphenyl phosphate (DPP), which has shown a catalytic activity towards ROP of the three monomers in the order δVL ≫ TMC ≫ LA,42,43 the RcDP selectivity could be switched to target PδVL. This enabled selective RcDP to δVL (94% conversion, 97% selectivity) within 23 h at 80 °C (Fig. 4e).
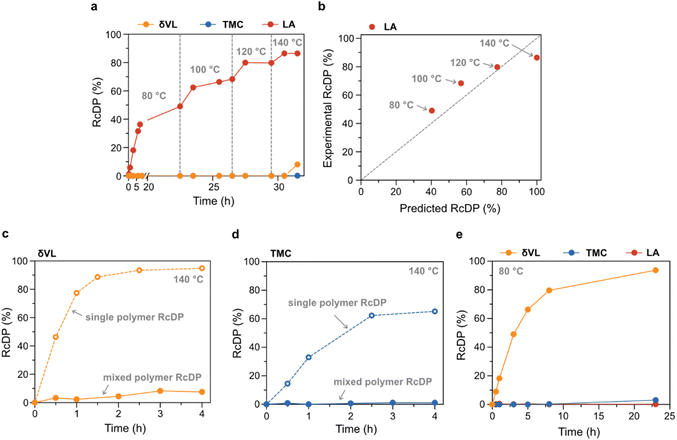 | ||
| Fig. 4 RcDP of polymer mixture of PδVL, PTMC and PLA in GVL ([M]0,δVL = [M]0,TMC = [M]0,LA = 0.5 M). (a) RcDP of polymer mixture from 80–140 °C with SnOct2 (0.05 M) as catalyst. (b) Relationship between experimentally obtained RcDP of PLA to LA during mixed polymer RcDP (SnOct2 (0.05 M) as catalyst) in relation to the predicted RcDP of PLA to LA based on previously reported polymerization thermodynamic parameters.27 (c) Comparison of mixed polymer RcDP and single polymer RcDP of PδVL at 140 °C with SnOct2 (0.05 M) as catalyst. (d) Comparison of mixed polymer RcDP and single polymer RcDP of PTMC at 140 °C with SnOct2 (0.05 M) as catalyst. (e) RcDP of polymer mixture at 80 °C with DPP (0.05 M) as catalyst. | ||
Conclusions
To conclude, this study showed that the power of the solvent effect and its efficiency in decreasing the Tc varies with the chemical structure of the monomer–polymer. The results also support that monomer–solvent–polymer interactions are general influencing factors that affect the thermodynamic equilibrium between ROP and RcDP. Interestingly, the Tc of monomers with a higher polarity show a stronger dependency on the solvent properties. Thus, in combination with the possibility to tune the Tc of cyclic monomers by introducing or reducing ring-strain, monomer structures may be designed to generate stronger monomer–solvent interactions, enabling more efficient Tc depression by the here studied solvent effect. In addition, catalyst selectivity can be utilized to obtain selective RcDP in mixed polyester and polycarbonate streams. Thus, the combination of thermodynamic and kinetic control, adds further possibilities to the design and development of chemically recyclable polymers and CRM systems.Author Contributions
L.C. was main responsible for the concept and methodology development, with contribution from K.O., M.H. and P.O. L.C. performed the experiments and the formal analysis. The work was supervised by K.O., M.H., and P.O. The original manuscript draft was written by L.C., and all authors contributed to the revised manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge funding from the Knut and Alice Wallenberg foundation through Wallenberg Wood Science Center.References
- H. Höcker, J. Macromol. Sci., Part A: Pure Appl. Chem., 1993, 30, 595 CrossRef.
- G. W. Coates and Y. D. Y. L. Getzler, Nat. Rev. Mater., 2020, 5, 501 CrossRef CAS.
- X. Tang and E. Y. X. Chen, Chem, 2019, 5, 284 CAS.
- M. Hong and E. Y. X. Chen, Green Chem., 2017, 19, 3692 RSC.
- D. E. Fagnani, J. L. Tami, G. Copley, M. N. Clemons, Y. D. Y. L. Getzler and A. J. McNeil, ACS Macro Lett., 2021, 10, 41 CrossRef CAS PubMed.
- F. S. Dainton and K. J. Ivin, Nature, 1948, 162, 705 CrossRef CAS.
- F. S. Dainton and K. J. Ivin, Q. Rev., Chem. Soc., 1958, 12, 61 RSC.
- A. V. Tobolsky and A. Eisenberg, J. Am. Chem. Soc., 1960, 82, 289 CrossRef.
- P. Olsén, K. Odelius and A. C. Albertsson, Biomacromolecules, 2016, 17, 699 CrossRef PubMed.
- O. Haba and H. Itabashi, Polym. J., 2014, 46, 89 CrossRef CAS.
- J. B. Zhu, E. M. Watson, J. Tang and E. Y. X. Chen, Science, 2018, 360, 398 CrossRef CAS PubMed.
- J. B. Zhu and E. Y. X. Chen, Angew. Chem., Int. Ed., 2018, 57, 12558 CrossRef CAS PubMed.
- C. Shi, R. W. Clarke, M. L. McGraw and E. Y. X. Chen, J. Am. Chem. Soc., 2022, 144, 2264 CrossRef CAS PubMed.
- X.-L. Li, R. W. Clarke, J.-Y. Jiang, T.-Q. Xu and E. Y. X. Chen, Nat. Chem., 2023, 15, 278 CrossRef CAS PubMed.
- M. Save and A. Soum, Macromol. Chem. Phys., 2002, 203, 2591 CrossRef CAS.
- C. Li, L. Wang, Q. Yan, F. Liu, Y. Shen and Z. Li, Angew. Chem., Int. Ed., 2022, 61, e202207105 Search PubMed.
- Q. Yan, C. Li, T. Yan, Y. Shen and Z. Li, Macromolecules, 2022, 55, 3860 CrossRef CAS.
- M. Xiong, D. K. Schneiderman, F. S. Bates, M. A. Hillmyer and K. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 8357 CrossRef CAS PubMed.
- D. K. Schneiderman, M. E. Vanderlaan, A. M. Mannion, T. R. Panthani, D. C. Batiste, J. Z. Wang, F. S. Bates, C. W. Macosko and M. A. Hillmyer, ACS Macro Lett., 2016, 5, 515 CrossRef CAS PubMed.
- J. P. MacDonald and M. P. Shaver, Polym. Chem., 2016, 7, 553 RSC.
- L.-G. Li, Q.-Y. Wang, Q.-Y. Zheng, F.-S. Du and Z.-C. Li, Macromolecules, 2021, 54, 6745 CrossRef CAS.
- M.-Q. Li, Macromolecules, 2023, 56, 2465 CrossRef CAS.
- M. Hong and E. Y. X. Chen, Nat. Chem., 2016, 8, 42 CrossRef CAS PubMed.
- J. Undin, P. Olsén, J. Godfrey, K. Odelius and A. C. Albertsson, Polymer, 2016, 87, 17 CrossRef CAS.
- K. J. Ivin and J. Leonard, Polymer, 1965, 6, 621 CrossRef CAS.
- K. J. Ivin and J. Léonard, Eur. Polym. J., 1970, 6, 331 CrossRef CAS.
- L. Cederholm, J. Wohlert, P. Olsén, M. Hakkarainen and K. Odelius, Angew. Chem., Int. Ed., 2022, 61, e202204531 CAS.
- L. Cederholm, P. Olsén, M. Hakkarainen and K. Odelius, Macromolecules, 2023, 56, 3641 CrossRef CAS.
- R. C. Pratt, B. G. G. Lohmeijer, D. A. Long, R. M. Waymouth and J. L. Hedrick, J. Am. Chem. Soc., 2006, 128, 4556 CrossRef CAS PubMed.
- B. G. G. Lohmeijer, R. C. Pratt, F. Leibferth, J. E. Logan, A. P. Dove, F. Nederberg, J. Choi, C. Wade, R. M. Waymouth and J. L. Hedrick, Macromolecules, 2006, 39, 8574 CrossRef CAS.
- F. Nederberg, B. G. G. Lohmeijer, F. Leibfarth, R. C. Pratt, J. Choi, A. P. Dove, R. M. Waymouth and J. L. Hedrick, Biomacromolecules, 2007, 8, 153 CrossRef CAS PubMed.
- P. J. Flory, Principles of polymer chemistry, Cornell University Press, 1953 Search PubMed.
- V. T. Bui and J. Léonard, J. Chem. Soc., Faraday Trans. 1, 1985, 81, 1745 RSC.
- V. T. Bui and J. Léonard, J. Chem. Soc., Faraday Trans. 1, 1986, 82, 899 RSC.
- V. T. Bui and J. Léonard, Polym. J., 1989, 21, 185 CrossRef.
- J. Matsuo, K. Aoki, F. Sanda and T. Endo, Macromolecules, 1998, 31, 4432 CrossRef CAS.
- U. W. Gedde and M. S. Hedenqvist, Polymer Solutions, in Fundamental Polymer Science, 2019, p. 113 Search PubMed.
- C. Jacobs, P. Dubois, R. Jérôme and P. Teyssié, Macromolecules, 1991, 24, 3027 CrossRef CAS.
- T. Rosen, I. Goldberg, W. Navarra, V. Venditto and M. Kol, Angew. Chem., Int. Ed., 2018, 57, 7191 CrossRef CAS PubMed.
- I. D'Auria, M. C. D'Alterio, C. Tedesco and C. Pellecchia, RSC Adv., 2019, 9, 32771 RSC.
- D. J. Darensbourg, W. Choi, O. Karroonnirun and N. Bhuvanesh, Macromolecules, 2008, 41, 3493 CrossRef CAS.
- K. Makiguchi, T. Satoh and T. Kakuchi, Macromolecules, 2011, 44, 1999 CrossRef CAS.
- K. Makiguchi, Y. Ogasawara, S. Kikuchi, T. Satoh and T. Kakuchi, Macromolecules, 2013, 46, 1772 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3py00535f |
| This journal is © The Royal Society of Chemistry 2023 |