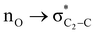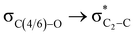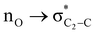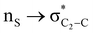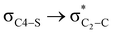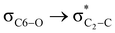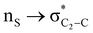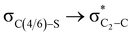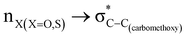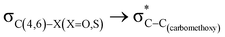Theoretical exploration to the significance of n(S)/n(O) → σ* (C-COOMe) stereoelectronic interactions

Abstract

α-Heterosubstituted 1,3-dioxane and 1,3-dithiane systems have been extensively reported for 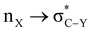(X, Y = heteroatoms) hyperconjugative interactions. However, the definitive interpretation for the conformational analysis of 2-carbomethoxy 1,3-diheterocyclohexane is less explored. The weaker accepting ability of C–C_{(carbomethoxy)} antibonding orbitals in 2-substituted 1,3-diheterocyclohexane makes it an attractive candidate for estimating the role of stereoelectronic effects in such systems. This study explores the conformational preferences of 2-carbomethoxy substituted 1,3-dioxane, 1,3-oxathiane and 1,3-dithiane in the light of stereoelectronic interactions and the contribution of other factors to attain stability in the respective systems using the CBS-QB3 method, at the MP2/6-311+G(d,p)/SMD(chloroform) and B3LYP/6-311+G(d,p)/SMD(chloroform) levels. The DFT calculated results in the solvent phase reveal that the delocalizing interactions operate in all three systems examined; however, ring strain overrides the axial preference of the 2-carbomethoxy substituent on 1,3-dioxane (2-ax) and 1,3-oxathiane (3-ax). The hyperconjugative interaction, lower ring strain and attractive C–H⋯O non-bonded interactions favor the axial (4-ax) over the equatorial (4-eq) isomer of methyl-2-carboxylate-1,3-dithiane.

---

Introduction

The role of the stereoelectronic effect has been widely accepted in controlling the conformational behavior of organic compounds and their reactivity patterns in chemistry.^1,2 The stability of the conformations in X–C–Y (where X has one or more non-bonded lone pair of electrons and Y possesses an electronegative group like –OR, –C≡N, –C≡CR, and –F) arises due to electron transfer between the filled (n or σ) and unfilled (σ*) orbitals.^3–6 Electron delocalization has been achieved more effectively when the best donor orbital is oriented anti-periplanar to the best acceptor orbital.⁷ This subtle stereoelectronic effect is governed by the interplay between kinetic, thermodynamic and solvation effects.⁸ However, the magnitude and origin of such stereoelectronic effects are still a topic of debate and the results have often been confronted with steric and electrostatic effects present in the system.^9,10

The substituted cyclohexane molecules prefer to adopt a chair conformation and equatorial substitutions are energetically more stable than the corresponding axial ones.¹¹ The results obtained in such cases are interpreted in terms of steric effects experienced in the group located at the axial than the equatorial position. Interestingly, α-substituted six-membered saturated heterocyclic ring systems (X–C–Y) occupy an axial position.^12–14 The role of stereoelectronic effects in five-membered rings, e.g., furanose and six-membered rings, e.g., pyranose, have been well documented.^15,16 The presence of lone pairs on heteroatoms in substituted saturated heterocyclic compounds plays an important role in governing the stability of conformers with different substituents. The heteroatoms in heterocyclic rings are in general oxygen, nitrogen and sulfur, whereas a variety of substituents at α-carbon have been studied critically to assess the role of anomeric effects (Scheme 1).^17–20

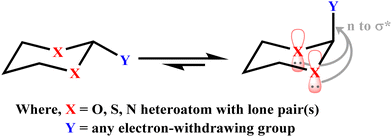Scheme 1 Stereoelectronic interaction involved in 2-substituted 1,3-heterocyclohexane. (For the clarity of the picture, only the axial lone pair is displayed.)

The conformational analysis of saturated heterocycles is important because of their extensive occurrence in nature and their vital role in carbohydrate chemistry.²¹ The presence of α-substituted 1,3-dioxane and 1,3-dithiane have been found in various building blocks for the formation of many important organic compounds and natural products.^1,16,22,23 The conformational behavior of heterocyclic systems with weaker acceptor groups has been less explored despite their greater importance in organic compounds and natural products.^24,25 For example, an Ir-catalyzed asymmetric allylic substitution reaction with 2-alkoxy carbonyl-1,3-dithianes results in new enantioselective α-functionalized products. To control the enantioselectivity of these compounds at C2 carbon, it is important to examine the conformational preferences of Y = –COOMe substitution, which has been found in many organic transformations. Therefore, these two orbital/two electron hyperconjugative interactions with weaker acceptor groups become very important to understand the molecular properties and reactivity in these systems.

With such curiosity, we have examined the conformational preferences of Y = –COOMe substitution on the α-carbon atom of a heterocyclic ring to explore the effect of stereoelectronic interactions. Furthermore, substituent Y at α-carbon does not possess any lone pair for an extra 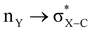type of interaction; thus, the influence of the exo-anomeric effect will be absent in such cases. The magnitude of the anomeric effect for the axial preference in heterocycles is obtained by comparing the corresponding energies for the same substituent in cyclohexane rings. However, the long-standing difficulty with evaluating such an effect is that steric repulsion of axial substitution will differ for cyclohexane and 1,3-diheterocyclohexane. Hence, this study aims to examine the factors responsible for the conformational preferences of such systems and to provide the magnitude of stereoelectronic interactions to adopt an axial or equatorial conformation.

Computational details

Conformational analysis was performed using a conformational search algorithm incorporated in Spartan’08 software with the Merck molecular force field (MMFF).²⁶ The calculations were further performed using the Gaussian 09 program package.²⁷ The geometries were fully optimized using the CBS-QB3²⁸ method, and MP2²⁹ and B3LYP^30,31 functionals with the 6-311+G(d,p)^32–34 basis set. Correction for the solvent effects was executed using a universal solvation model based on density (SMD) considering chloroform (ε = 4.72) as a solvent.³⁵ Electronic structures and hyper-conjugative interactions have been investigated using natural bond orbital (NBO) analysis with version 3.1 of the NBO program as implemented in Gaussian 09.³⁶ In NBO analysis, the delocalizing interactions are calculated either by deletion of relevant off-diagonal elements of the NBO Fock matrix and re-examining of energy (denoted as E_del energies) or by the second-order perturbation approach.^37–39

Bader's theory of atoms in molecules (AIM) analysis was performed by using the wave-function generated at the B3LYP/6-311+G(d,p)/SMD(chloroform) level. AIM analysis was performed using the Multiwfn program package.⁴⁰

Results and discussion

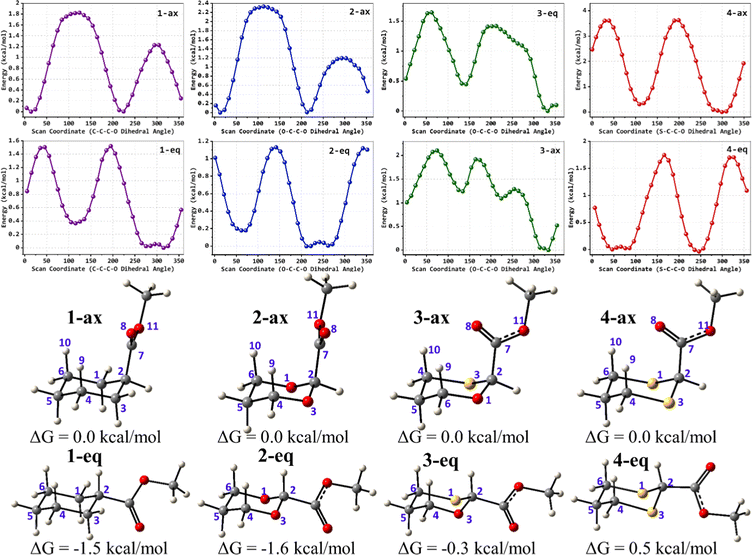
To examine the stereoelectronic and steric interplay for the axial/equatorial preference of the 2-carbomethoxy group in 1,3-diheterocyclohexane rings, we have undertaken three model systems, methyl-1,3-dioxane-2-carboxylate (2), methyl-1,3-oxathiane-2-carboxylate (3) and methyl-1,3-dithiane-2-carboxylate (4) and compared the geometrical parameters with methyl cyclohexanecarboxylate (1) for free energy calculations (Scheme 2 and Table 1). The conformational analysis was performed using a conformational search algorithm with the Merck molecular force field (MMFF).²⁶ Conformational search results generated 4 energetically most favourable conformers and all of them were chair conformers with two conformers having carbomethoxy substitution at axial and two conformers at equatorial positions. Furthermore these conformations were undertaken with the incremental rotation of 10° of the X₃–C₂–C₇–O₈ dihedral angle (where X = O for 2 and 3 and X = S for 4) around the C₂–C₇ bond at the MP2/6-311+G(d,p)/SMD(chloroform) level. The conformational search revealed that the lowest energy conformers of 1-ax and 2-ax have an –X–C–C–O– dihedral angle of ∼0°. However, the –X–C–C–O– dihedral angle from 2-ax to 4-ax increased and leads to the gauche orientation. In the case of 4-ax, the carbonyl oxygen of the carbomethoxy group is oriented towards axial C_4/6-H_9/10 bonds. The equatorial conformations of 1–3 remain similar to the orientation of the carbonyl oxygen syn to the heteroatom present in the ring (Fig. 1). The most stable axial and equatorial conformations were fully optimized without any constraints at the MP2/6-311+G(d,p)/SMD(chloroform) level. The free energy results suggest that equatorial conformations are the most stable for systems 1, 2, and 3 whereas the axial conformation (4-ax) is more stable than the equatorial conformation (4-eq) in the case of methyl-1,3-dithiane-2-carboxylate (4) (Table 1). Furthermore, we have also considered the CBS-QB3 method using the solvation model based on density (SMD) considering chloroform (ε = 4.72) as a solvent to examine the conformational preferences of the systems studied (1–4). The calculated results using the CBS-QB3 method showed that an axial orientation of methyl cyclohexanecarboxylate (1-ax) is energetically less stable by 1.8 kcal mol⁻¹ because of 1,3-diaxial repulsion compared to its corresponding equatorial 1-eq. This result is in good agreement with the experimentally reported energetics (1.3 kcal mol⁻¹) for methyl cyclohexane carboxylate.⁴¹ The experimental reports on conformational equilibria of 2-carbomethoxy substituted 1,3-dioxane and 1,3-oxathiane analogues are not available in the literature; however, 1,3-dithiane analogue showed a predominance of 4-ax by 0.81 ± 0.02 kcal mol⁻¹ in the chloroform solvent.¹⁷ The calculated conformational free energy differences showed stability of 2-eq by 1.6 kcal mol⁻¹ and 0.3 kcal mol⁻¹ for 3-eq (Fig. 1). Interestingly, the free energy difference showed the preference for the axial methyl-1,3-dithiane-2-carboxylate (4-ax) conformer by 0.5 kcal mol⁻¹ at the CBS-QB3 level and was in good agreement with the experimental observations.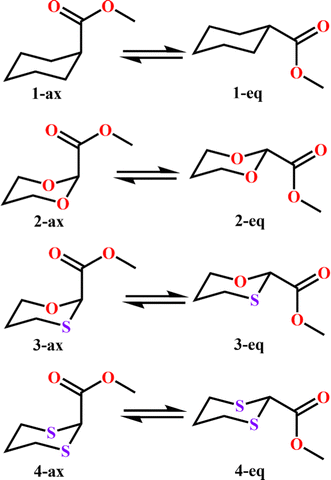

Scheme 2 Chemical equilibration of methyl cyclohexanecarboxylate (1), methyl-1,3-dioxane-2-carboxylate (2), methyl-1,3-oxathiane-2-carboxylate (3) and methyl-1,3-dithiane-2-carboxylate (4).

Table 1 Axial/equatorial conformational free energy differences of 1 (methyl cyclohexanecarboxylate), 2 (methyl 1,3-dioxane-2-carboxylate), 3 (methyl-1,3-oxathiane-2-carboxylate) and 4 (methyl 1,3-dithiane-2-carboxylate) at CBS-QB3, MP2/6-311+G(d,p)/SMD(chloroform) and B3LYP/6-311+G(d,p)/SMD(chloroform) levels. Free energy values are in kcal mol⁻¹

	CBS-QB3		MP2/6-311+G(d,p)		B3LYP/6-311+G(d,p)
	Axial	Equatorial	Axial	Equatorial	Axial	Equatorial
1	0.0	−1.5	0.0	−1.8	0.0	−1.8
2	0.0	−1.6	0.0	−1.8	0.0	−1.7
3	0.0	−0.3	0.0	−0.7	0.0	−0.8
4	0.0	0.5	0.0	0.7	0.0	0.8

---

Fig. 1 Top: MP2/6-311+G(d,p)/SMD(Chloroform) calculated comparative potential energy profiles of the rotation around the X–C–C–O dihedral angle in axial and equatorial conformations of compounds 1–4. Bottom: CBS-QB3 optimized structures of (1) methyl cyclohexanecarboxylate, (2) methyl 1,3-dioxane-2-carboxylate, (3) methyl-1,3-oxathiane-2-carboxylate, and (4) methyl 1,3-dithiane-2-carboxylate in axial (n-ax) and equatorial (n-eq) conformations (n = 1, 2, 3 and 4).

The calculations have also been performed at the B3LYP/6-311+G(d,p)/SMD(chloroform) level and the conformational preferences for 1–4 were found to be in good agreement with the CBS-QB3 and MP2/6-311+G(d,p)/SMD(chloroform) results. These calculations suggest that the computationally less expensive B3LYP/6-311+G(d,p)/SMD(chloroform) level can also be employed for such studies.

The axial C₂–C_{(carbomethoxy)} bond lengths are 1.554 Å (2-ax), 1.529 Å (3-ax) and 1.520 Å (4-ax), whereas the same in the corresponding equatorial conformers are 1.531 Å (2-eq), 1.525 Å (3-eq) and 1.519 (4-eq), respectively. The geometrical parameters (Table 2) calculated using the CBS-QB3 method suggest that C₂–C_{(carbomethoxy)} bond lengths are elongated by 0.03 Å in axial 1,3-dioxane than 1,3-dithiane, suggesting that the donation capacity of oxygen is greater than the sulfur atom present in the ring. Furthermore, the 2-ax/2-eq bond length difference of C₂–C_{(carbomethoxy)} is larger than the differences observed for the corresponding conformers of 3 and 4. The free energy results, however, showed a preference for the formation of equatorial 2-eq and 3-eq for 1,3-dioxane (2) and 1,3-oxathiane (3), respectively and axial 4-ax for 1,3-dithiane (4); hence, the electronic properties have been examined to reveal the preferences observed. Furthermore, similar computational results were observed for 2-diphenylphosphinoyl 1,3-dithiane and 2-trimethylphosphonium-1,3-dithiane with no axial/equatorial bond length difference, but a clear preference for the axial conformer was confirmed with theoretical analysis and crystal structure.⁴² Natural bond orbital (NBO) analysis is a useful method that provides evidence of the stereoelectronic effect as an origin of the conformational preference. It can calculate the magnitude of interaction energies between the participating donor and acceptor orbitals on the studied systems.^43–47

Table 2 Optimized geometrical parameters of methyl 1,3-dioxane-2-carboxylate (2), methyl-1,3-oxathiane-2-carboxylate (3) and methyl 1,3-dithiane-2-carboxylate (4) in axial and equatorial conformations (bond distances in Å)

		CBS-QB3		MP2/6-311+G(d,p)		B3LYP/6-311+G(d,p)
		Axial	Equatorial	Axial	Equatorial	Axial	Equatorial
2	C2–C	1.554	1.531	1.549	1.524	1.557	1.532
	C2–O	1.399–1.405	1.397–1.412	1.399–1.403	1.400–1.409	1.399–1.406	1.407
	C6–O	1.439–1.441	1.438–1.439	1.435–1.439	1.437	1.441–1.444	1.442
	O–C2–O	113.6	112.8	113.7	113.0	113.4	112.5
	C2–O–C4	112.8–113.4	111.0–111.9	111.0–112.3	109.5	112.9–113.9	110.9
3	C2–C	1.529	1.525	1.522	1.518	1.529	1.525
	C2–S	1.860	1.863	1.832	1.833	1.862	1.868
	C2–O	1.396	1.392	1.401	1.399	1.397	1.393
	C4–S	1.838	1.840	1.818	1.820	1.842	1.844
	C6–O	1.446	1.435	1.443	1.434	1.448	1.438
	O–C2–S	114.3	112.8	114.8	113.3	114.3	112.7
	C2–O–C4	97.7	95.7	96.6	111.3	97.7	95.5
	C2–S–C4	118.3	113.5	117.1	94.2	118.5	113.6
4	C2–C	1.520	1.519	1.514	1.514	1.519	1.518
	C2–S	1.831–1.835	1.839	1.813–1.819	1.820	1.835–1.838	1.841–1.845
	C4–S	1.836–1.838	1.837	1.816–1.817	1.818	1.841	1.841
	S–C2–S	114.6	113.2	115.4	113.8	114.9	113.7
	C2–S–C4	100.9–101.4	97.4	100.0–100.7	95.7	101.2–101.5	97.4

---

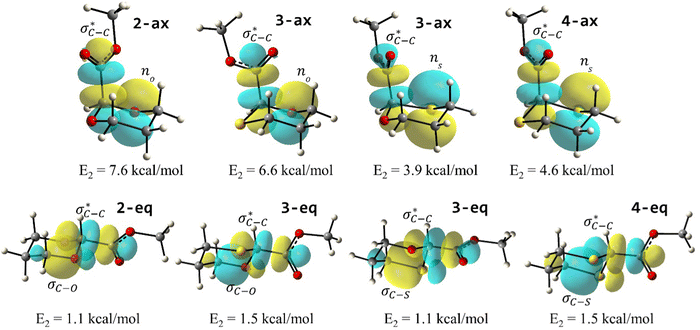
The lower energy difference (ΔE_d/a) between the participating donor and acceptor orbitals shows a higher magnitude of the hyperconjugative interaction. The percentage of polarization of the antibonding C–C bond shows weaker accepting orbitals than the corresponding C–O antibonding orbitals (Table S1, ESI†). The electronic delocalization was largely observed with 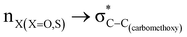stereoelectronic interactions for axial in contrast to the equatorial position of the 2-carbomethoxy group in 1,3-diheterocyclohexane. The donation from oxygen was larger by ∼2.0 kcal mol⁻¹ than the donation observed from sulfur atoms present in 1,3-diheterocyclohexyl rings. This result corroborates well with the bond length elongation observed in the case of 2-ax (Table 2). The anti-periplanar orientation of the interacting donor and acceptor orbitals provides a prominent stereoelectronic interaction in the axial orientation. Therefore, this interaction is responsible for the aforementioned ‘X_(X=O,S) –C–C anomeric effect’ at C₂ in all the systems (Table 3). The 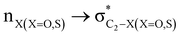hyperconjugative interactions are greater than the 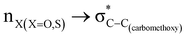delocalization (Table S2, ESI†); however, it is present in both the axial and equatorial conformers. Therefore, this delocalization is equally operative in both the conformers and will not contribute to the overall conformational free energy difference (ΔG) of the 2, 3 and 4 systems. The antiperiplanar 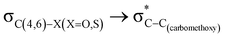hyperconjugative interactions have been observed in equatorial orientations of 2-carbomethoxy-1,3-diheterocyclohexane (2-eq, 3-eq and 4-eq) (Fig. 2). This stereoelectronic interaction may take into account the lengthening of the C₂–C_{(carbomethoxy)} bond in the equatorial conformer as well and the changes in the axial and equatorial bond lengths are marginal in these systems (Table S2, ESI†).

Table 3 Comparison of structural parameters in the optimized geometries of 2-ax, 2-eq, 3-ax, 3-eq, 4-ax and 4-eq with those optimized geometries obtained by NBODEL, when switching off the key NBO Interactions (here, the subscript d in X_d symbolizes the donor atom, where X = O and S)

Methyl 1,3-dioxane-2-carboxylate, 2
	Axial		Equatorial
	Without NBODEL		Without NBODEL
E del	0.0	6.8	0.0	2.3
C2–C	1.540	1.525	1.521	1.518
C2–Od	1.376	1.409	1.381	1.395
C2–O	1.381	1.380	1.381	1.379

---

Methyl-1,3-oxathiane-2-carboxylate, 3
	Axial			Equatorial
	Without NBODEL			Without NBODEL
E del	0.0	6.19	4.33	0.0	2.00	2.08
C2–C	1.524	1.510	1.517	1.520	1.517	1.518
C2–Od	1.379	1.407	1.375	1.377	1.383	1.388
C2–S	1.831	1.840	1.859	1.833	1.833	1.832

---

Methyl 1,3-dithiane-2-carboxylate, 4
	Axial		Equatorial
	Without NBODEL		Without NBODEL
E del	0.0	4.1	0.0	2.1
C2–C	1.517	1.518	1.519	1.517
C2–Sd	1.814	1.845	1.815	1.832
C2–S	1.822	1.807	1.827	1.825

---

Fig. 2 Calculated natural bond orbital profiles of electron densities for the anti-periplanar hyper-conjugation in the axial conformation whereas hyper-conjugation in the equatorial conformation at an iso-surface value of 0.02 a.u.

The magnitude of such interactions depends on the donor ability of the filled (n or σ) orbital, the acceptor ability of the unfilled (σ*) orbital, the energy gap between the donor and acceptor orbitals, the amount of overlap between the orbitals and the directionality of the interacting orbitals. Significant changes in energy values (E_del) were observed by deleting the important two-electron/two-orbital hyperconjugative interactions followed by re-optimizing the geometries by switching off these interactions (Table 3 and Table S2, ESI†).^3,5,42,45,46 The change in geometrical parameters confirms the stereoelectronic interactions that operate in such systems. The deletion of the 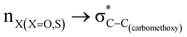orbital interaction leads to the lengthening of C₂–X_d bonds and shortening of C₂–C_{(carbomethoxy)} bonds. Similarly, bond lengthening of C₂–O_d and shortening of C₂–O_a were also observed when the 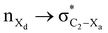orbital interaction in both axial and equatorial conformations was turned off. These results corroborate the presence of stereoelectronic interactions in 2-carbomethoxy-1,3-diheterocyclohexanes (2, 3 and 4).

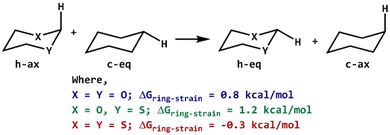
The introduction of heteroatoms in cyclohexyl rings changes the geometrical structure of ring systems and can influence the ring strain energy for axial and equatorial orientations. The strain energy was evaluated as an energy gap between the reactants and products of a homodesmotic reaction.^48–50 In homodesmotic reactions, the number of atoms, type of bonds and valence environment around each atom have been conserved (Scheme 3). The vibrationless calculations^51,52 have been performed using optimized geometries to compute the ring strain involved in such saturated 6-membered rings. The 2-carbomethoxy group was replaced with a hydrogen atom followed by single-point calculations at the same level of theory without any relaxation in geometries. The ring strain energies calculated for 2-ax and 3-ax are higher by 0.8 kcal mol⁻¹ and 1.2 kcal mol⁻¹, respectively compared to 1-ax; however, the ring strain energy of 4-ax is lowered by 0.3 kcal mol⁻¹ compared to that of 1-ax. The higher strain energy of 3-ax can be attributed to two different heteroatoms present in the ring system.

Scheme 3 Homodesmotic reaction for compounds 1–4.

We have also considered the role of dipole–dipole interactions along with the stereoelectronic interaction to govern the conformational preferences of 1–4.^6,14,53–55 However, the systems examined here possess the same substituent and solvent. The dipole moment calculated for the axial and equatorial conformers (1–4) suggests that the latter conformer possesses larger values than the former conformer (Table S4, ESI†). These dipole–diploe results are not aligned with the stability pattern of the conformers observed for systems 1–4 and hence such interactions seem to be not significant in governing conformational preferences shown here.

The lowest energy conformations of 1-ax, 2-ax, 3-ax and 4-ax possess the dihedral angle X₃–C₂–C₇–O₈ at 4.4°, 12.9°, 36.0° and 61.0°, respectively (Fig. 1). The electrostatic repulsion appears to reduce between the ring oxygens and carbomethoxy oxygens with the larger dihedral angle from 2-ax to 3-ax (Fig. S1, ESI†). Furthermore, such changes in the dihedral angle lead to the non-covalent attractive C–H_9/10⋯O₈ interaction in 3-ax and 4-ax, which is absent in 1-ax and 2-ax.

We have further analyzed H-bonding present in the axial conformation of 2-carbomethoxy 1,3-dioxane (2-ax), 1,3-oxathiane (3-ax) and 1,3-dithiane (4-ax) systems using Bader's theory of atoms in molecules (AIM)^56,57 analysis by taking the wave function generated at the B3LYP/6-311+G(d,p)/SMD(Chloroform) level of theory. Topological properties like the Laplacian gradient of the electron density (∇²r), the total energy (H(r)), potential energy (V(r)), and Lagrangian kinetic energy (G(r)) can characterize the nature of the bonding.^58–61 The shared interactions have ρ(r) > 0.1 a.u. whereas closed–shell interactions have ρ(r) ≈ 0.01 a.u. The calculated intramolecular C–H⋯O interactions have ρ(r) less than 0.1 a.u. indicating characteristics for closed–shell interactions. The AIM analysis shows one non-covalent weak hydrogen bonding in 3-ax and two in 4-ax from topological analysis like laplacian gradient of the electron density ∇²ρ(r) > 0, total energy density H(r) > 0 and |V(r)|/G(r) < 1 (Fig. 3 and Table 4). These results suggest that the ring strain effect contributes to overriding the stereoelectronic interactions present in 2-ax and 3-ax, whereas lower ring strain and attractive C–H⋯O interactions also contribute to the stereoelectronic effect to attain the stability of 4-ax compared to the 4-eq conformer.

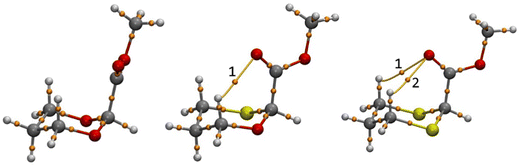Fig. 3 AIM picture showing (a) no, (b) one and (c) two (3,−1) critical points for 2-ax, 3-ax and 4-ax, respectively.

Table 4 AIM values for the (3,−1) critical points of 3-ax and 4-ax

	CP	ρ(r)	V(r)	G(r)	H(r)	∇^2r	V(r)/G(r)
3-ax	1	0.01313	−0.00845	0.00983	0.00137	0.04480	0.8596
4-ax	1	0.00823	−0.00511	0.00591	0.00080	0.02683	0.8646
	2	0.00854	−0.00539	0.00615	0.00082	0.02790	0.8764

---

Conclusions

The role of the stereoelectronic effect in the conformational analysis of methyl-2-carboxylate-1,3-dioxane (2), methyl-2-carboxylate-1,3-oxathiane (3) and methyl-2-carboxylate-1,3-dithiane (4) systems has been examined using the CBS-QB3 method, at the MP2/6-311+G(d,p)/SMD(chloroform) and B3LYP/6-311+G(d,p)/SMD(chloroform) levels. The better accepting ability of the C–X (X = heteroatom) bond in the saturated heterocyclic ring is well explored in governing the conformational preferences; however, the C–C bond with poor accepting ability has received less attention. The experimentally reported methyl-2-carboxylate substituent on the 1,3-dithiane ring system at the axial position makes it an interesting candidate to examine the role of stereoelectronic interactions. It is widely accepted that the lone pair of sulfur has weaker donating ability than the corresponding oxygen atom.^3,5,62,63 Therefore, we examined methyl-2-carboxylate-1,3-dioxane (2) to ascertain the preference for axial or equatorial orientations. The free energies calculated with CBS-QB3 suggest that the equatorial orientation (2-eq) is 1.8 kcal mol⁻¹ more stable than the corresponding axial orientation (2-ax) of methyl-2-carboxylate-1,3-dioxane. The calculations performed at MP2/6-311+G(d,p)/SMD(chloroform) and B3LYP/6-311+G(d,p)/SMD(chloroform) levels were found to be in good agreement with the CBS-QB3 results. The NBO analysis confirmed the presence of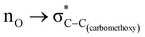 delocalizing interaction (6.8 kcal mol⁻¹) and switching it off resulted in structural changes corresponding to the shortening of the C–C_{(carbomethoxy)} bond. The stability gained by the hyperconjugative interaction appears to be overridden by the ring strain effect induced in the 1,3-dioxane system. The energy difference between the axial and the equatorial orientations for methyl-2-carboxylate-1,3-oxathiane (3) was reduced compared to methyl-2-carboxylate-1,3-dioxane (2) due to hyperconjugation and attractive C–H⋯O interactions. The preference for the axial conformer of methyl-2-carboxylate-1,3-dithiane (4) is complemented by the 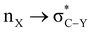delocalizing interaction, lowered ring strain and attractive C–H⋯O interactions. This study sheds light on the conformational preferences of carbomethoxy substituted six-membered saturated heterocyclic ring systems and factors governing such preferences with a change in heterocyclic ring systems.

Author contributions

Sana Jindani: conceptualization; investigation; methodology; validation; visualization; and writing–original draft. Bishwajit Ganguly: conceptualization; resources; software; supervision; and writing–review and editing.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

S. J. acknowledges the CSIR (New Delhi, India) for a senior research fellowship (SRF) and the Academy of Scientific & Innovative Research (AcSIR), Ghaziabad, Uttar Pradesh-201002, India, for enrolment in the PhD program. CSIR-CSMCRI registration number 217/2022. We thank the reviewers for their valuable suggestions that have helped us to improve the manuscript.

References

1. I. V. Alabugin, Stereoelectronic effects: a bridge between structure and reactivity, John Wiley & Sons, 2016.
2. I. V. Alabugin, L. Kuhn, N. V. Krivoshchapov, P. Mehaffy and M. G. Medvedev, Chem. Soc. Rev., 2021, 50, 10212–10252.
3. E. Juaristi and R. Notario, J. Org. Chem., 2016, 81, 1192–1197.
4. N. Hasanzadeh, D. Nori-Shargh, H. Yahyaei, S. N. Mousavi and S. Kamrava, J. Phys. Chem. A, 2017, 121, 5548–5560.
5. E. Juaristi and R. Notario, J. Org. Chem., 2018, 83, 10326–10333.
6. E. Juaristi and Y. Bandala, in Adv. Heterocycl. Chem., ed. A. Katritzky, Academic Press, 2012, vol. 105, pp. 189–222.
7. P. Deslongchamps, Stereoelectronic effects in organic chemistry, Pergamon, 1983.
8. E. Buncel and I.-H. Um, Tetrahedron, 2004, 60, 7801.
9. Y. Mo, Nat. Chem., 2010, 2, 666–671.
10. C. Wang, F. Ying, W. Wu and Y. Mo, J. Am. Chem. Soc., 2011, 133, 13731–13736.
11. J. Clayden, N. Greeves and S. Warren, Organic chemistry, Oxford University Press, 2012.
12. P. P. Graczyk and M. Mikolajczyk, Top. Stereochem., 1994, 21, 159–349.
13. C. Wang, Z. Chen, W. Wu and Y. Mo, Chem. – Eur. J., 2013, 19, 1436–1444.
14. K. B. Wiberg, W. F. Bailey, K. M. Lambert and Z. D. Stempel, J. Org. Chem., 2018, 83, 5242–5255.
15. M. Miljkovic, Electrostatic and stereoelectronic effects in carbohydrate chemistry, Springer, 2014.
16. I. V. Alabugin, L. Kuhn, M. G. Medvedev, N. V. Krivoshchapov, V. A. Vil, I. A. Yaremenko, P. Mehaffy, M. Yarie, A. O. Terent’ev and M. A. Zolfigol, Chem. Soc. Rev., 2021, 50, 10253–10345.
17. E. Juaristi, J. Tapia and R. Mendez, Tetrahedron, 1986, 42, 1253–1264.
18. E. Juaristi and G. Cuevas, Acc. Chem. Res., 2007, 40, 961–970.
19. E. Juaristi and Y. Bandala, Adv. Heterocycl. Chem., 2012, 105, 189–222.
20. E. Juaristi and R. Notario, Stereochemistry and Global Connectivity: The Legacy of Ernest L. Eliel Volume 2, ACS Publications, 2017, pp. 3–18.
21. M. Yus, C. Nájera and F. Foubelo, Tetrahedron, 2003, 59, 6147–6212.
22. J. Janssens, M. D. Risseeuw, J. Van der Eycken and S. Van Calenbergh, Eur. J. Org. Chem., 2018, 6405–6431.
23. S. Pathania, R. K. Narang and R. K. Rawal, Eur. J. Med. Chem., 2019, 180, 486–508.
24. A. Kondoh, M. Oishi, T. Takeda and M. Terada, Angew. Chem., Int. Ed., 2015, 54, 15836–15839.
25. P. Wang, Q. Jiang, R. Zhao, X. Xie, S. Tang and X. Wang, J. Org. Chem., 2020, 85, 12456–12467.
26. Spartan’08 Wavefunction, Inc., Irvine, CA, 2008.
27. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013.
28. J. A. Montgomery, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 1999, 110, 2822–2827.
29. M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 275–280.
30. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Chem. Phys., 1994, 98, 11623–11627.
31. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
32. M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269.
33. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
34. A. McLean and G. Chandler, J. Chem. Phys., 1980, 72, 5639–5648.
35. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
36. E. D. Glendening, A. E. Reed, J. E. Carpenter and F. Weinhold, NBO Version 3.1, University of Wisconsin, Madison, WI, 1988.
37. A. E. Reed and F. Weinhold, J. Chem. Phys., 1985, 83, 1736–1740.
38. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
39. F. Weinhold, Natural Bond Orbital Methods, in Encyclopedia of Computational Chemistry, ed. P. v. R. Schleyer, N. L. Allinger, T. Clark, J. Gasteiger, P. A. Kollman, H. F. Schaefer III and P. R. Schreiner, John Wiley & Sons, Chichester, UK, 1998, vol. 3, pp. 1792–1811.
40. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
41. H. Booth, J. M. Dixon and K. A. Khedhair, Tetrahedron, 1992, 48, 6161–6174.
42. E. Juaristi and R. Notario, J. Org. Chem., 2015, 80, 2879–2883.
43. A. E. Reed and F. Weinhold, Isr. J. Chem., 1991, 31, 277–285.
44. V. Pophristic and L. Goodman, Nature, 2001, 411, 565–568.
45. G. dos Passos Gomes, A. Terent’ev and I. V. Alabugin, Chem. Sci., 2015, 6, 6783–6791.
46. E. Juaristi and R. Notario, J. Org. Chem., 2018, 83, 3293–3298.
47. I. V. Alabugin, J. Org. Chem., 2000, 65, 3910–3919.
48. W. J. Hehre, W. J. Hehre, L. Radom, P. v R. Schleyer and J. Pople, AB INITIO Molecular Orbital Theory, Wiley, 1986.
49. S. E. Wheeler, K. N. Houk, P. v R. Schleyer and W. D. Allen, J. Am. Chem. Soc., 2009, 131, 2547–2560.
50. G. dos Passos Gomes and I. Alabugin, Stereoelectronic effects: Analysis by computational and theoretical methods, 2018.
51. S. T. Howard, J. Am. Chem. Soc., 2000, 122, 8238–8244.
52. A. Singh and B. Ganguly, New J. Chem., 2009, 33, 583–587.
53. D. Nori-Shargh, S. N. Mousavi, R. Tale and H. Yahyaei, Struct. Chem., 2016, 27, 1753–1768.
54. T. Harabe, T. Matsumoto and T. Shioiri, Tetrahedron, 2009, 65, 4044–4052.
55. R. U. Lemieux, Pure Appl. Chem., 1971, 25, 527–548.
56. R. F. Bader, J. Phys. Chem. A, 1998, 102, 7314–7323.
57. R. F. W. Bader and R. F. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, 1990.
58. M. T. Carroll and R. F. Bader, Mol. Phys., 1988, 65, 695–722.
59. M. T. Carroll, C. Chang and R. F. Bader, Mol. Phys., 1988, 63, 387–405.
60. U. Koch and P. L. Popelier, J. Chem. Phys., 1995, 99, 9747–9754.
61. R. Parthasarathi, V. Subramanian and N. Sathyamurthy, J. Phys. Chem. A, 2006, 110, 3349–3351.
62. P. v R. Schleyer, E. D. Jemmis and G. W. Spitznagel, J. Am. Chem. Soc., 1985, 107, 6393–6394.
63. U. Salzner and P. v R. Schleyer, J. Am. Chem. Soc., 1993, 115, 10231–10236.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nj03861g

---