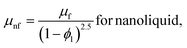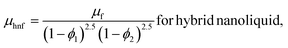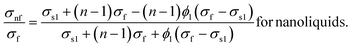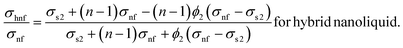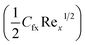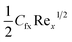DOI:
10.1039/D3NA00441D
(Paper)
Nanoscale Adv., 2023,
5, 6135-6147
KHA model comprising MoS4 and CoFe2O3 in engine oil invoking non-similar Darcy–Forchheimer flow with entropy and Cattaneo–Christov heat flux†
Received
21st June 2023
, Accepted 11th September 2023
First published on 18th October 2023
Abstract
Objective: Nanoliquid flows are widely utilized in industrial, petroleum, engineering, and pharmaceutical applications including electric cooling, drug delivery, nuclear reactor cooling, solar collectors, heat exchangers, magnetohydrodynamic power generators, aerospace, porous media, thermal storage systems, and many others. Darcy–Forchheimer magnetized hybrid nanoliquid subjected to a stretchable cylinder was addressed, and the Cattaneo–Christov heat flux analysis was considered. Herein, disulfido (dithioxo) molybdenum (MoS4) and cobalt ferrite (CoFe2O4) were considered as nanoparticles, and engine oil as a conventional liquid. The thermal relationship of heat generation and radiation was discussed, and the influence of the entropy rate was addressed. Methodology: Governing expressions were transformed into dimensionless forms. Simulation by the ND-solve technique was implemented. Conclusions: Features for the entropy rate, liquid flow, and temperature against emerging variables for nanoliquid (MoS4/engine oil) and hybrid nanoliquid (MoS4 + CoFe2O4/engine oil) were explored. The numerical results of the coefficient of skin friction and thermal transport rate for nanoliquid (MoS4/engine oil) and hybrid nanoliquid (MoS4 + CoFe2O4/engine oil) were examined. Reduction in velocity clearly occurred through a magnetic field, whereas the reverse impact held for the entropy rate. The thermal field and entropy rate against the curvature parameter were enhanced. A decrease in liquid flow occurred for higher porosity variables. An enhancement in the entropy rate was witnessed for radiation and porosity parameters. Higher radiation and thermal relaxation time variables resulted in enhancement of the thermal transport rate.
1. Introduction
Considerable research has been conducted on nanomaterials due to their significance in pharmaceutical, industrial, chemical, and engineering activities. Nanomaterial is basically created by the insertion of small-size (1–100 nm) particles in conventional liquid, which results in thermal conductivity enhancement. Nanomaterials play a key role in heat-related equipment, cooling and heating systems, radiators, nuclear reactors, fuel chambers, space technology, and caloric control. The initial investigations into nanofluids were conducted by Choi1 and Eastman et al.2 The distributed ultrafine particles efficiently strengthen the viscosity and thermal conductivity of nanomaterial and enhance its competence in energy exchange.3,4 Thermal conductivity and viscosity may vary with the temperature of the nanofluid mixture, nanoparticle size, and volume fraction.
The thermal conductivity of metallic nanoparticles is higher than that of conventional materials, such as water and bio-particles with a lower density and thermal conductivity than that of traditional heat transfer fluids (HTFs). Sivasankaran et al.5 addressed magnetohydrodynamic hybrid nanoliquid flow between stretchable parallel plates. Heat transport in the electromagnetohydrodynamic flow of Casson nanoliquid considering the heat source/sink was explored by Hussain et al.6 Mixed convective flow of hybrid nanomaterial was explored by Patil and Shankar.7 Çiçek et al.8 explored the convective flow of hybrid nanofluid considering particle deposition inside a square cavity. There have been numerous investigations that have been conducted to explore nanofluid flow.9–13
A hybrid nanoliquid is the combination of two or more small size metallic nanoparticles with different chemical characteristics in conventional materials. Hybrid nanomaterials are useful to augment the advantages of nanoliquid such as heat transport transmission and enhancement processes. Because hybrid nanomaterials are advantageous for thermal conductivity enhancement, they are widely used in nuclear reactor cooling processes, biomedical applications, solar energy, the automotive industry, automobile generators, space technology, and heat exchangers.
Thermal enhancement of convectional material by insertion of single particles and hybrid nanoparticles was given in Jana et al.14 Bhatti et al.15 discussed the magnetohydrodynamic flow of hybrid nanomaterial by a circular non-Darcy surface. Wahid et al.16 analyzed heat transfer in hybrid nanomaterial subject to a Riga plate. Slip impacts in the convection stagnation point flow of hybrid nanoliquid were reported by Zangooee et al.17 Khan et al.18 explored entropy in a radiating flow of hybrid nanoliquid through the Darcy–Forchheimer relation. Zainal et al.19 deliberated the influence of Arrhenius kinetics in hybrid nanomaterial flow by a shrinking and stretching surface with radiation. It should be noted that there have been few attempts to study hybrid nanoliquid flow.20–30
Entropy generation is the measurement of energy wastage during any thermal process. Entropy always increases in an irreversible process, and therefore, entropy generation is a positive quantity. Entropy generation is also a non-conserved property. There is no existence of conservation of entropy. Therefore, the entropy of the universe is continuously increasing. Joule heating, fluid flow friction between solid surfaces, molecular vibration, liquid viscosity, and diffusion are sources that produce entropy generation. In fact, Bejan discovered entropy optimization for convective flow with thermal convection.31,32 Entropy for the radiative magnetized flow of a hybrid nanoliquid due to a stretchable rotating disk is presented in Khan et al.33 Kumawat et al.34 analyzed magnetized entropy-optimized flow with variable viscosity. Nonlinear radiation in hybridized nanoliquid flow with a convectively heated surface was explored by Ashwinkumar et al.35 Rajkumar et al.36 examined Cattaneo–Christov flux in the radiative flow of micropolar nanofluid with entropy optimization. Similar studies on entropy have been conducted.37–42
The main theme here is to communicate the Cattaneo–Christov heat flux for the magnetohydrodynamic flow of hybrid (MoS4 + CoFe2O4/engine oil) nanoliquid towards a stretchable cylinder. The Darcy–Forchheimer relation is used for porous space. Disulfido (dithioxo) molybdenum (MoS4) and cobalt ferrite (CoFe2O4) are considered as nanoparticles, and engine oil as a conventional fluid. Cattaneo–Christov heat flux was deliberated, and radiation and heat generation were considered. Entropy optimization was also considered. Related equations were converted into dimensionless versions. The ND-solve technique was implemented for solution of nonlinear non-dimensional systems. Fluid flow, entropy rate, and temperature via the involved variables for nanoliquid (MoS4/engine oil) and hybrid nanoliquid (MoS4 + CoFe2O4/engine oil) were graphically analyzed. The numerical results illustrating the impacts of influential variables on physical quantities for nanoliquid (MoS4/engine oil) and hybrid nanoliquid (MoS4 + CoFe2O4/engine oil) are presented.
2. Formulation
The hydromagnetic flow of hybrid (MoS4 + CoFe2O4/engine oil) nanomaterial by stretchable porous cylinder was examined. The Darcy–Forchheimer expression was used for porous space. Cattaneo–Christov heat flux was carried out. Disulfido (dithioxo) molybdenum (MoS4) and cobalt ferrite (CoFe2O4) were considered as nanoparticles, and engine oil as a conventional material. Radiation and heat generation were present in the energy equation, and entropy modeling was carried out. A constant magnetic field (B0) perpendicular to the liquid flow was applied. The radius of a cylinder was considered as (R), and stretching velocity 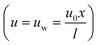 (l shows characteristics length). The flow configuration is sketched in Fig. 1.
(l shows characteristics length). The flow configuration is sketched in Fig. 1.
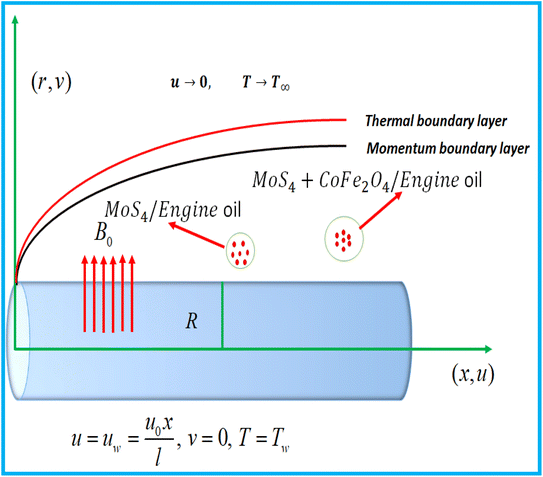 |
| | Fig. 1 Physical model. | |
Under these considerations, the related expressions are:43–48
| | 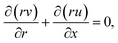 | (1) |
| | 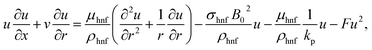 | (2) |
| | 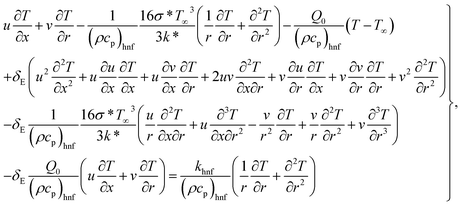 | (3) |
with
| | 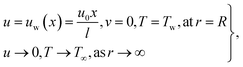 | (4) |
in which (
u,
v) represent velocity components,
μhnf the dynamic viscosity,
σhnf the electrical conductivity, (
x,
r) the cylindrical coordinates,
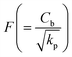
the inertia coefficient,
ρhnf the density,
kp the porous space permeability,
vhnf the kinematic viscosity,
Cb the drag force coefficient,
T the temperature, (
Cp)
hnf specific heat,
Q0 > 0 the heat generation coefficient,
σ* Stefan Boltzmann constant,
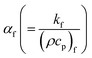
thermal diffusivity,
k* mean absorption coefficient,
khnf the thermal conductivity,
δE the thermal relaxation time,
Tw the wall temperature,
u0 the reference velocity, and
T∞ the ambient temperature.
2.1. Thermophysical characteristics
The thermophysical characteristics were determined by Hamilton–Crosser relations for the nanomaterial and hybrid nanomaterial (Table 1).49
Table 1 Values of nanoparticles and base liquid50–53
| Physical property |
ρ
f (kg m−3) |
(Cp)f (J kg−1 K−1) |
σ
f (S m−1) |
k
f (W m−1 K−1) |
| Engine oil |
884 |
1910 |
10−11 to 2 × 10−9 |
0.1410 |
| MoS4 |
5060 |
397.21 |
2.09 × 104 |
904.4 |
| CoFe2O4 |
4907 |
700 |
5.51 × 109 |
3.7 |
2.1.1. Viscosity.
| |
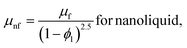
| (5) |
| |
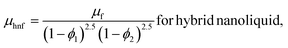
| (6) |
2.1.2. Density.
| | |
ρ
nf = (1 − ϕ1)ρf + ϕ1ρs1 for nanoliquid,
| (7) |
| | |
ρ
hnf = (1 − ϕ2)[(1 − ϕ1)ρf + ϕ1ρs1] + ϕ2ρs2 for hybrid nanoliquid.
| (8) |
2.1.3. Electrical conductivity.
| |
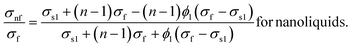
| (9) |
| |
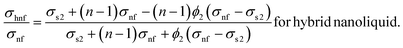
| (10) |
2.1.4. Specific heat capacity.
| | |
(ρcp)nf = (1 − ϕ1)(ρcp)f + ϕ1(ρcp)s1 for nanoliquid,
| (11) |
| | |
(ρcp)hnf = (1 − ϕ2)[(1 − ϕ1)(ρcp)f + ϕ1(ρcp)s1] + ϕ2(ρcp)s2 for hybrid nanoliquid.
| (12) |
2.1.5. Thermal conductivity.
| |
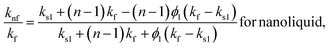
| (13) |
| |
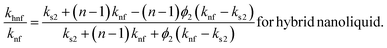
| (14) |
Considering transformations
| | 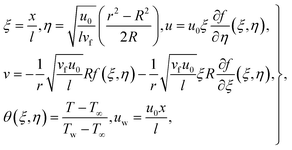 | (15) |
| | 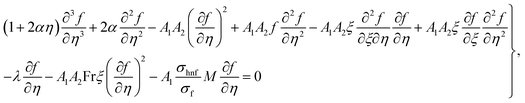 | (16) |
| | 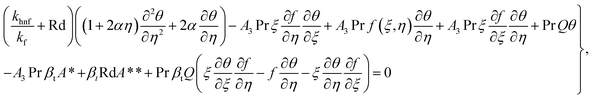 | (17) |
withwe have
| | 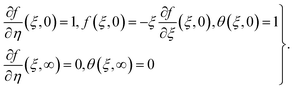 | (18) |
In the above expressions, 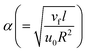 indicates the curvature variable,
indicates the curvature variable, 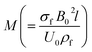 the magnetic parameter,
the magnetic parameter, 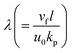 the porosity variable,
the porosity variable, 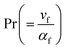 the Prandtl number,
the Prandtl number, 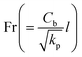 the Forchheimer number,
the Forchheimer number, 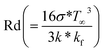 the radiation parameter,
the radiation parameter, 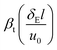 the thermal relaxation time variable, and
the thermal relaxation time variable, and 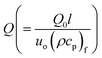 . A*, A**, A1, A2 and A3 are
. A*, A**, A1, A2 and A3 are
| | 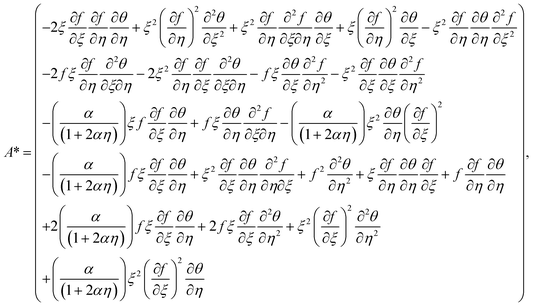 | (19) |
| | 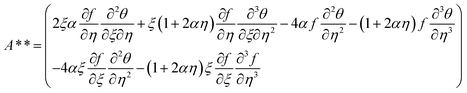 | (20) |
| | | A1 = (1 − ϕ1)2.5(1 − ϕ2)2.5 | (21) |
| | 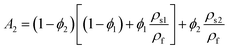 | (22) |
| | 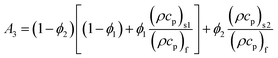 | (23) |
3. Quantities under interest
Skin friction coefficient 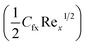 and Nusselt number (NuxRe−1/2x) are
and Nusselt number (NuxRe−1/2x) are| | 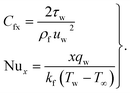 | (24) |
Shear stress (τw) and heat flux (qw) satisfy
| | 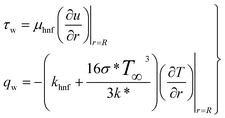 | (25) |
One may write eqn (27) and (28) as
| | 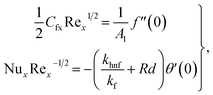 | (26) |
where
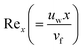
shows the local Reynolds number.
4. Expression for entropy
Mathematically, entropy is expressed as| | 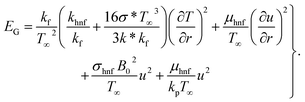 | (27) |
The above expression can be reduced as
| | 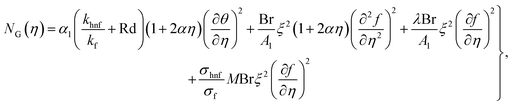 | (28) |
where
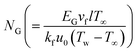
characterizes the entropy rate,
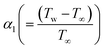
the temperature difference variable, and
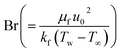
the Brinkman number.
5. Solution development
5.1. Local similar solution
To obtain a local similar solution, we suppose that 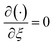 and denote
and denote 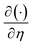 by prime in eqn (16)–(18). We have
by prime in eqn (16)–(18). We have| | 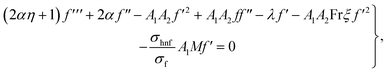 | (29) |
| | 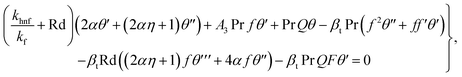 | (30) |
| | 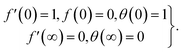 | (31) |
5.2. Local non-similar solution
To construct the local non-similar solution, we suppose that 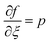 ,
, 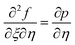 ,
, 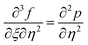 ,
, 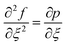 ,
, 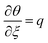 ,
, 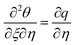 ,
, 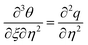 ,
, 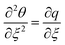 in eqn (16)–(18). One obtains
in eqn (16)–(18). One obtains| | 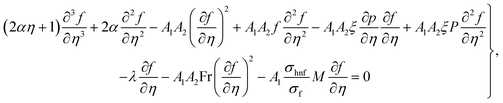 | (32) |
| | 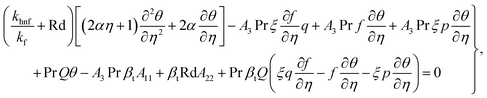 | (33) |
| | 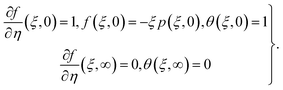 | (34) |
In the above equations, A11 and A22 are defined as
| | 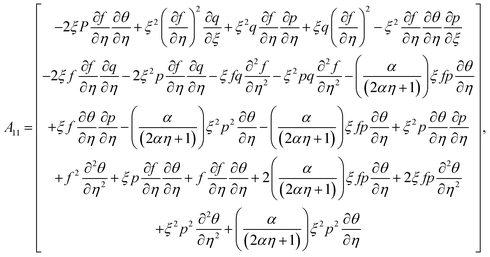 | (35) |
| | 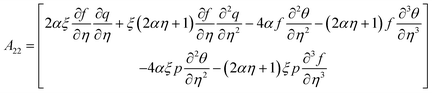 | (36) |
We take the derivative of eqn (32)–(34) with respect to “ξ” and representing 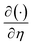 by prime. Suppose that
by prime. Suppose that 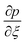 ,
, 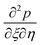 ,
, 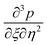 ,
, 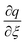 ,
, 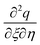 ,
, 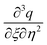 ,
, 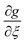 ,
, 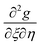 ,
, 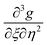 become zero. We obtain
become zero. We obtain
| | 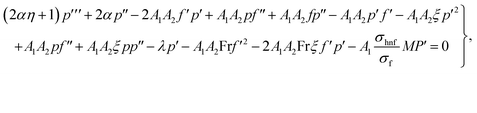 | (37) |
| | 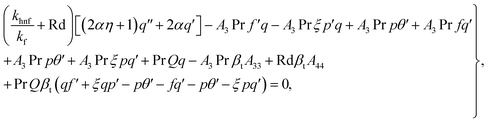 | (38) |
| | 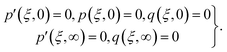 | (39) |
In the above equation, A33 and A44 are expressed as
| | 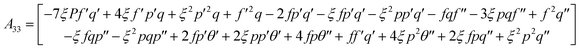 | (40) |
| | 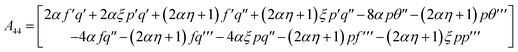 | (41) |
6. Discussion
Fluid flow, temperature, and entropy rate for sundry parameters regarding nanoliquid (MoS4/engine oil) and hybrid nanoliquid (MoS4 + CoFe2O4/engine oil) are presented. In these graphs, the solid lines denote the nanoliquid impact, and the dashed lines represent hybrid nanoliquid behavior. The numerical results for coefficient of skin friction (Cfx) and the thermal transport rate (Nux) for nanoliquid (MoS4/engine oil) and hybrid nanoliquid (MoS4 + CoFe2O4/engine oil) were examined.
6.1. Velocity
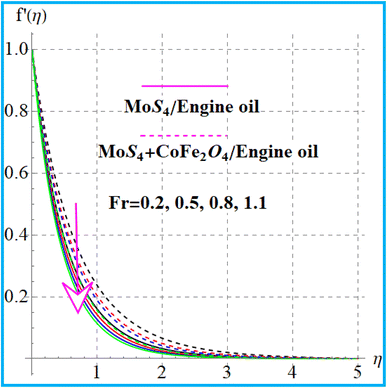
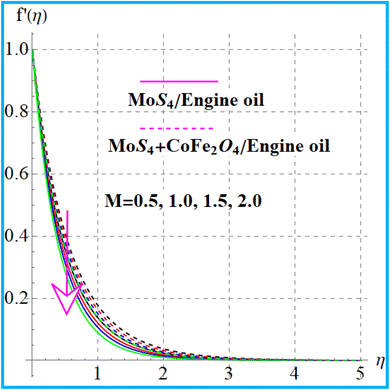
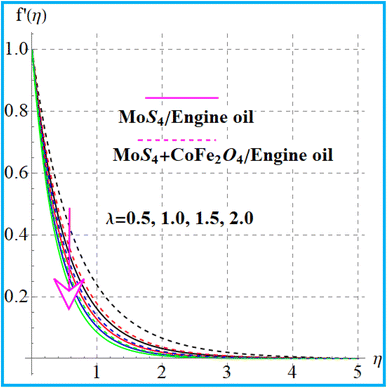
Fig. 2 shows the variation in the curvature variable for liquid flow. A larger approximation of curvature (α) variable leads to a decreased radius of curvature, which shrinks the region of the cylinder in contact with liquid. Consequently, resistance decreases, which hence boosts fluid flow. Fig. 3 indicates the impact of Forchheimer number on velocity. An augmentation in the Forchheimer number corresponds to a decrease in the liquid flow for nanoliquid (MoS4/engine oil) and hybrid nanoliquid (MoS4 + CoFe2O4/engine oil). Fig. 4 depicts the influence of the magnetic effect on liquid flow (f′(η)). A physically higher magnetic field leads to resistance to liquid flow, and as a result, velocity decreases. Fig. 5 exhibits the outcomes of the porosity variable for velocity (f′(η)). The flow was enhanced by a higher approximation of the porosity parameter.
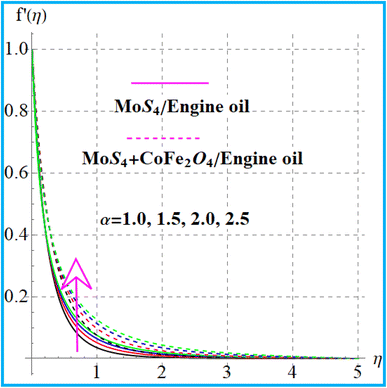 |
| | Fig. 2
f′(η) variation versus α. | |
 |
| | Fig. 3
f′(η) variation versus Fr. | |
 |
| | Fig. 4
f′(η) variation versus M. | |
 |
| | Fig. 5
f′(η) variation versus λ. | |
6.2. Temperature
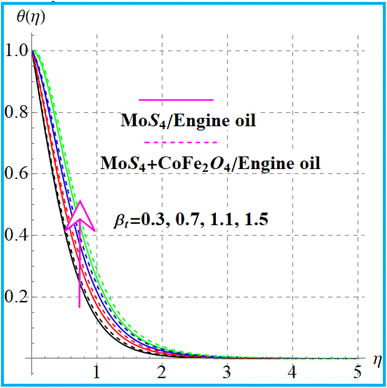
Fig. 6 indicates the temperature variation for thermal relaxation time parameter (βt). An increase in the thermal field occurs versus the higher thermal relaxation time (βt) parameter. The behavior of (θ(η)) versus a higher radiation variable is shown in Fig. 7. Physically higher radiation leads to an additional energy in the system, which increases the thermal field. Fig. 8 displays outcomes of the curvature (α) variable for temperature. Temperature enhances versus a higher curvature parameter. Fig. 9 shows the Prandtl (Pr) number impact for (θ(η)). Physically, (Pr) decreases the thermal diffusivity, and therefore, the temperature decreases. Fig. 10 illustrates the outcomes of heat generation for a thermal field. An increase in temperature against heat generation is possible.
 |
| | Fig. 6
θ(η) variation versus βt. | |
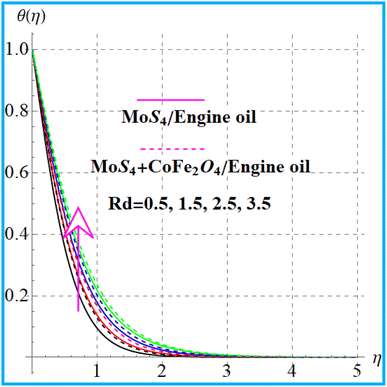 |
| | Fig. 7
θ(η) variation versus Rd. | |
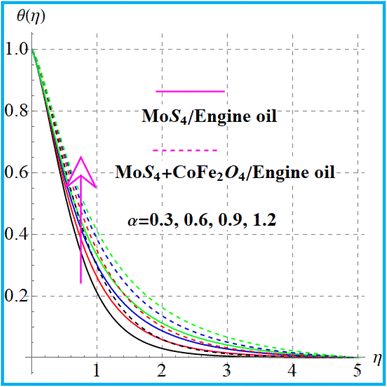 |
| | Fig. 8
θ(η) variation versus α. | |
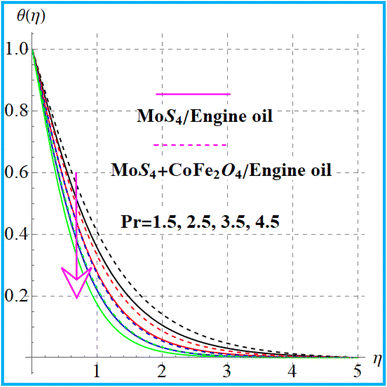 |
| | Fig. 9
θ(η) variation versus Pr. | |
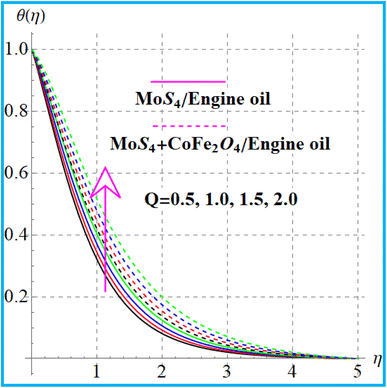 |
| | Fig. 10
θ(η) variation versus Q. | |
6.3. Entropy rate
Fig. 11 depicts the behavior of entropy against a higher magnetic field. A physically higher magnetic force leads to an increasing resistive force, which gives rise to greater energy in the system, and thus, the entropy rate increases. Fig. 12 shows the variation of the porosity (λ) variable against the entropy rate. An increase in the entropy production occurs against a larger approximation of the porosity parameter. Fig. 13 displays the radiation variation for the entropy rate. Physically higher radiation leads to increasing thermal emission, which creates extra energy in a thermal system. As a consequence, the entropy rate increases. Fig. 14 elucidates the impact of curvature on the entropy rate. The entropy production is enhanced for the curvature variable.
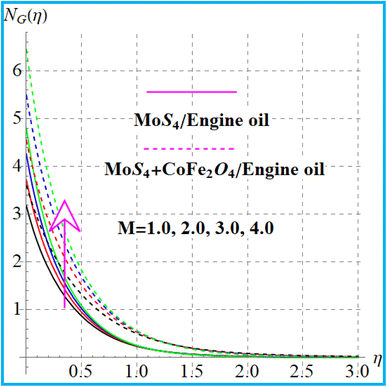 |
| | Fig. 11
N
G(η) variation versus M. | |
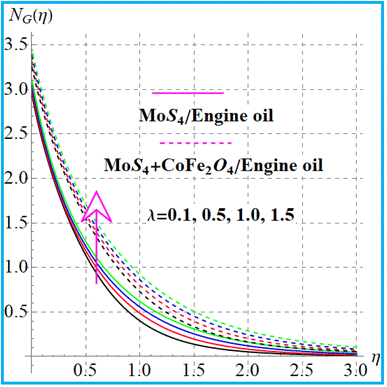 |
| | Fig. 12
N
G(η) variation versus λ. | |
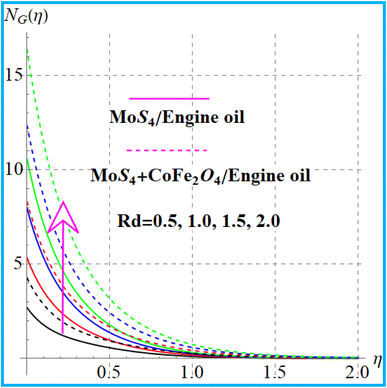 |
| | Fig. 13
N
G(η) variation versus Rd. | |
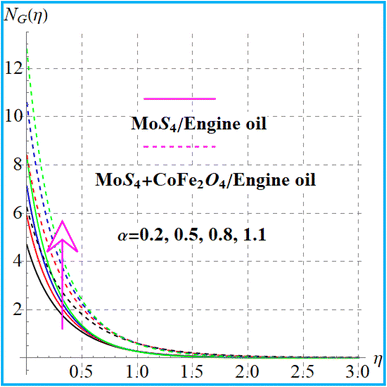 |
| | Fig. 14
N
G(η) variation versus α. | |
6.4. Physical quantities
The numerical results for coefficient of skin friction 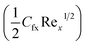 and thermal transport rate (NuxRe−1/2x) for nanoliquid (MoS4/engine oil) and hybrid nanoliquid (MoS4 + CoFe2O4/engine oil) have been sketched in Tables 2 and 3.
and thermal transport rate (NuxRe−1/2x) for nanoliquid (MoS4/engine oil) and hybrid nanoliquid (MoS4 + CoFe2O4/engine oil) have been sketched in Tables 2 and 3.
Table 2 Numerical values of surface drag force 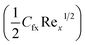
|
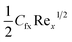
|
| Fr |
M
|
λ
|
MoS4/engine oil |
MoS4 + CoFe2O4/engine oil |
| 0.2 |
0.5 |
0.3 |
1.23154 |
1.65829 |
| 0.6 |
|
|
2.32562 |
3.09652 |
| 1.0 |
|
|
3.09845 |
3.95624 |
| 0.5 |
1.0 |
0.3 |
2.56234 |
3.56329 |
|
|
2.0 |
|
3.69532 |
4.032654 |
|
|
3.0 |
|
4.65892 |
5.01985 |
| 0.2 |
0.5 |
0.5 |
0.96523 |
1.85746 |
|
|
|
1.0 |
1.75632 |
2.89635 |
|
|
|
1.5 |
2.65295 |
3.56982 |
Table 3 Thermal transport rate (NuxRe−1/2x) variation against emerging parameters
| NuxRe−1/2x |
| Rd |
β
t
|
Q
|
MoS4/engine oil |
MoS4 + CoFe2O4/engine oil |
| 1.5 |
0.5 |
1.0 |
3.42352 |
3.89653 |
| 2.0 |
|
|
4.12956 |
5.03256 |
| 2.5 |
|
|
5.45638 |
6.36524 |
| 1.0 |
1.0 |
1.0 |
2.86593 |
3.78654 |
|
|
1.5 |
|
3.58647 |
4.25369 |
|
|
2.0 |
|
4.96583 |
5.65389 |
| 1.0 |
0.5 |
1.5 |
2.54892 |
3.96585 |
|
|
|
2.5 |
3.95862 |
4.65895 |
|
|
|
3.5 |
4.96852 |
5.87562 |
6.4.1. Coefficient of skin friction.
Surface drag force 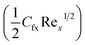 for influential variables is examined in Table 2. Higher magnetic variables lead to intensification of the skin friction coefficient for nanomaterial (MoS4/engine oil) and hybrid nanomaterial (MoS4 + CoFe2O4/engine oil). Clearly, for a larger porosity variable and Forchheimer number, the surface drag force improved.
for influential variables is examined in Table 2. Higher magnetic variables lead to intensification of the skin friction coefficient for nanomaterial (MoS4/engine oil) and hybrid nanomaterial (MoS4 + CoFe2O4/engine oil). Clearly, for a larger porosity variable and Forchheimer number, the surface drag force improved.
6.4.2. Nusselt number.
Physical features of emerging variables of the Nusselt number (NuxRe−1/2x) were constructed in Table 3. An increase in the heat transport rate (NuxRe−1/2x) occurs through radiation and thermal relaxation time parameters. Higher estimation of heat generation variables intensifies the heat transport rate (NuxRe−1/2x) for nanoliquid (MoS4/engine oil) and hybrid nanoliquid (MoS4 + CoFe2O4/engine oil).
7. Concluding remarks
The main results are listed below.
• The fluid flow variation for porosity and curvature variables is reversed.
• The velocity field decayed for a magnetic field, while the opposite holds for the entropy rate and temperature.
• The Forchheimer number results in velocity decrease.
• The curvature parameter variation for entropy and temperature for nanoliquid (MoS4/engine oil) and hybrid nanoliquid (MoS4 + CoFe2O4/engine oil) was the same.
• An enhancement of the temperature and entropy rate against radiation was observed.
• The thermal field decays for a higher Prandtl number in nanoliquid (MoS4/engine oil) and hybrid nanoliquid (MoS4 + CoFe2O4/engine oil).
• A higher thermal relaxation time enhances the temperature in nanoliquid (MoS4/engine oil) and hybrid nanoliquid (MoS4 + CoFe2O4/engine oil).
• Porosity parameter variation increases the entropy rate for nanoliquid (MoS4/engine oil) and hybrid nanoliquid (MoS4 + CoFe2O4/engine oil).
• A higher magnetic field intensifies the surface drag force for nanoliquid (MoS4/engine oil) and hybrid nanoliquid (MoS4 + CoFe2O4/engine oil).
• A larger estimation of the Forchheimer number and porosity variable leads to coefficient of skin friction enhancement for nanomaterial (MoS4/engine oil) and hybrid nanomaterial (MoS4 + CoFe2O4/engine oil).
• A higher radiation variable results in thermal transport rate enhancement for nanoliquid (MoS4/engine oil) and hybrid nanoliquid (MoS4 + CoFe2O4/engine oil).
• A higher thermal relaxation time variable improves the heat transport rate for nanoliquid (MoS4/engine oil) and hybrid nanoliquid (MoS4 + CoFe2O4/engine oil).
• The Nusselt number intensifies for higher heat generation.
• The skin friction coefficient for hybrid nanomaterial (MoS4 + CoFe2O4/engine oil) was more than that of nanoliquid (MoS4/engine oil).
• The thermal transport rate was more dominant for hybrid nanoliquid (MoS4 + CoFe2O4/engine oil) than for nanoliquid (MoS4/engine oil).
Conflicts of interest
There are no conflicts to declare.
References
-
S. U. S. Choi, Enhancing thermal conductivity of fluids with nanoparticles, ASME Publications-Fed, 1995, vol. 231, pp. 99–106 Search PubMed.
- J. A. Eastman, S. U. S. Choi, S. Li, W. Yu and L. J. Thompson, Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles, Appl. Phys. Lett., 2001, 78, 718–720 CrossRef CAS.
- M. J. P. Gallego, L. Lugo, J. L. Legido and M. M. Piñeiro, Enhancement of thermal conductivity and volumetric behavior of FexOy nanofluids, J. Appl. Phys., 2011, 110 DOI:10.1063/1.3603012.
- R. Nasrin, S. Parvin and M. A. Alim, Effect of Prandtl number on free convection in a solar collector filled with nanofluid, Procedia Eng., 2013, 56, 54–62 CrossRef CAS.
- S. Sivasankaran, T. Chandrapushpam, M. Bhuvaneswari, S. Karthikeyan and A. K. Alzahrani, Effect of chemical reaction on double diffusive MHD squeezing copper water nanofluid flow between parallel plates, J. Mol. Liq., 2022, 368 DOI:10.1016/j.molliq.2022.120768.
- M. Hussain, U. Farooq and M. Sheremet, Nonsimilar convective thermal transport analysis of EMHD stagnation Casson nanofluid flow subjected to particle shape factor and thermal radiations, Int. Commun. Heat Mass Transfer, 2022, 137 DOI:10.1016/j.icheatmasstransfer.2022.106230.
- P. M. Patil and H. F. Shankar, Heat transfer attributes of Al2O3-Fe3O4/H2O hybrid nanofluid flow over a yawed cylinder, Propuls. Power Res., 2022, 11, 416–429 CrossRef.
- O. Çiçek, M. A. Sheremet and A. C. Baytaş, Effect of natural convection hybrid nanofluid flow on the migration and deposition of MWCNTFe3O4 in a square enclosure, Int. J. Therm. Sci., 2023, 190 DOI:10.1016/j.ijthermalsci.2023.108318.
- S. A. Khan, T. Hayat and A. Alsaedi, Thermal conductivity performance for ternary hybrid nanomaterial subject to entropy generation, Energy Rep., 2022, 8, 9997–10005 CrossRef.
- M. Hussain and M. Sheremet, Convection analysis of the radiative nanofluid flow through porous media over a stretching surface with inclined magnetic field, Int. Commun. Heat Mass Transfer, 2023, 140 DOI:10.1016/j.icheatmasstransfer.2022.106559.
- S. A. Abdollahi, A. Alizadeh, I. C. Esfahani, M. Zarinfar and P. Pasha, Investigating heat transfer and fluid flow betwixt parallel surfaces under the influence of hybrid nanofluid suction and injection with numerical analytical technique, Alex. Eng. J., 2023, 70, 423–439 CrossRef.
- M. Shanmugapriya, R. Sundareswaran, P. S. Kumar and G. Rangasamy, Impact of nanoparticle shape in enhancing heat transfer of magnetized ternary hybrid nanofluid, Sustain. Energy Technol. Assess., 2022, 53 DOI:10.1016/j.seta.2022.102700.
- M. Arif, P. Kumam, W. Kumam and Z. Mostafa, Heat transfer analysis of radiator using different shaped nanoparticles water-based ternary hybrid nanofluid with applications: A fractional model, Case Stud. Therm. Eng., 2022, 31 DOI:10.1016/j.csite.2022.101837.
- S. Jana, A. S. Khojin and W. H. Zhong, Enhancement of fluid thermal conductivity by the addition of single and hybrid nano-additives, Thermochimica, 2007, 462, 45–55 CrossRef CAS.
- M. M. Bhatti, R. Ellahi and M. H. Doranehgard, Numerical study on the hybrid nanofluid (Co3O4-Go/H2O) flow over a circular elastic surface with non-Darcy medium: Application in solar energy, J. Mol. Liq., 2022, 361 DOI:10.1016/j.molliq.2022.119655.
- N. S. Wahid, N. M. Arifin, N. S. Khashi'ie, I. Pop, N. Bachok and M. E. H. Hafidzuddin, Hybrid nanofluid stagnation point flow past a slip shrinking Riga plate, Chin. J. Phys., 2022, 78, 180–193 CrossRef CAS.
- M. R. Zangooee, K. Hosseinzadeh and D. D. Ganji, Hydrothermal analysis of hybrid nanofluid flow on a vertical plate by considering slip condition, Theor. App. Mech. Lett., 2022, 12 DOI:10.1016/j.taml.2022.100357.
- S. A. Khan, T. Hayat and A. Alsaedi, Entropy optimization for nanofluid flow with radiation subject to a porous medium, J. Pet. Sci. Eng., 2022, 217 DOI:10.1016/j.petrol.2022.110864.
- N. A. Zainal, I. Waini, N. S. Khashi'ie, A. R. M. Kasim, K. Naganthran, R. Nazar and I. Pop, Stagnation point hybrid nanofluid flow past a stretching/shrinking sheet driven by Arrhenius kinetics and radiation effect, Alex. Eng. J., 2023, 68, 29–38 CrossRef.
- S. R. R. Reddy, C. S. K. Raju, S. R. Gunakala, H. T. Basha and S. J. Yook, Bio-magnetic pulsatile CuO-Fe3O4 hybrid nanofluid flow in a vertical irregular channel in a suspension of body acceleration, Int. Commun. Heat Mass Transfer, 2022, 135 DOI:10.1016/j.icheatmasstransfer.2022.106151.
- M. I. Khan, S. A. Khan, T. Hayat, M. Waqas and A. Alsaedi, Modeling and numerical simulation for flow of hybrid nanofluid (SiO2/C3H8O2) and (MoS2/C3H8O2) with entropy optimization and variable viscosity, Int. J. Numer. Methods Heat Fluid Flow, 2020, 22, 3939–3955 Search PubMed.
- A. Z. Ullah, X. Guo, T. Gul, I. Ali, A. Saeed and A. M. Galal, Thin film flow of the ternary hybrid nanofluid over a rotating disk under the influence of magnetic field due to nonlinear convection, J. Magn. Magn. Mater., 2023, 573 DOI:10.1016/j.jmmm.2023.170673.
- X. Wang, Q. Wen, J. Yang, S. Shittu, X. Wang, X. Zhao and Z. Wang, Heat transfer and flow characteristic of a flat confined loop thermosyphon with ternary hybrid nanofluids for electronic devices cooling, Appl. Therm. Eng., 2023, 221 DOI:10.1016/j.applthermaleng.2022.119758.
- M. Yasir, M. Khan, A. S. Alqahtani and M. Y. Malik, Mass transpiration effect on rotating flow of radiative hybrid nanofluid due to shrinking surface with irregular heat source/sink, Case Stud. Therm. Eng., 2023, 44 DOI:10.1016/j.csite.2023.102870.
- A. S. Alnahdi, S. Nasir and T. Gul, Couple stress ternary hybrid nanofluid flow in a contraction channel by means of drug delivery function, Math. Comput. Simul., 2023, 210, 103–119 CrossRef.
- X. Jiang, M. Hatami, A. Abderrahmane, O. Younis, B. M. Makhdoum and K. Guedri, Mixed convection heat transfer and entropy generation of MHD hybrid nanofluid in a cubic porous cavity with wavy wall and rotating cylinders, Appl. Therm. Eng., 2023, 226 DOI:10.1016/j.applthermaleng.2023.120302.
- J. Shelton, N. K. Saini and S. M. Hasan, Experimental study of the rheological behavior of TiO2-Al2O3/mineral oil hybrid nanofluids, J. Mol. Liq., 2023, 380 DOI:10.1016/j.molliq.2023.121688.
- K. N. Sneha, G. Bognar, U. S. Mahabaleshwar, D. K. Singh and O. P. Singh, Magnetohydrodynamics effect of Marangoni nano boundary layer flow and heat transfer with CNT and radiation, J. Magn. Magn. Mater., 2023, 575 DOI:10.1016/j.jmmm.2023.170721.
- K. Mausam, A. Pare, S. K. Ghosh and A. K. Tiwari, Thermal performance analysis of hybrid-nanofluid based flat plate collector using Grey relational analysis (GRA): An approach for sustainable energy harvesting, Therm. Sci. Eng. Prog., 2023, 37 DOI:10.1016/j.tsep.2022.101609.
- R. Vinoth, B. Sachuthananthan, A. Vadivel, S. Balakrishnan and A. G. S. Raj, Heat transfer enhancement in oblique finned curved microchannel using hybrid nanofluid, Int. J. Therm. Sci., 2023, 183 DOI:10.1016/j.ijthermalsci.2022.107848.
- A. Bejan, A study of entropy generation in fundamental convective heat transfer, J. Heat Transfer, 1979, 101, 718–725 CrossRef.
- A. Bejan, Entropy generation through heat and fluid flow, J. Appl. Mech., 1983, 50 DOI:10.1115/1.3167072.
- M. I. Khan, S. A. Khan, T. Hayat, M. I. Khan and A. Alsaedi, Entropy optimization analysis in MHD nanomaterials (TiO2-GO) flow with homogeneous and heterogeneous reactions, Comput. Methods Programs Biomed., 2020, 184 DOI:10.1016/j.cmpb.2019.105111.
- C. Kumawat, B. K. Sharma, Q. M. A. Mdallal and M. R. Gorji, Entropy generation for MHD two phase blood flow through a curved permeable artery having variable viscosity with heat and mass transfer, Int. Commun. Heat Mass Transfer, 2022, 133 DOI:10.1016/j.icheatmasstransfer.2022.105954.
- G. P. Ashwinkumar, S. P. Samrat and N. Sandeep, Convective heat transfer in MHD hybrid nanofluid flow over two different geometries, Int. Commun. Heat Mass Transfer, 2021, 127 DOI:10.1016/j.icheatmasstransfer.2021.105563.
- D. Rajkumar, A. S. Reddy, P. V. S. Narayana, K. Jagadeshkumar and A. J. Chamkha, Pulsating magnetohydrodynamic flow of Fe3O4-blood based micropolar nanofluid between two vertical porous walls with Cattaneo–Christov heat flux and entropy generation, J. Magn. Magn. Mater., 2023, 571 DOI:10.1016/j.jmmm.2023.170564.
- U. M. Zahid, Y. Akbar and F. M. Abbasi, Entropy generation analysis for peristaltically driven flow of hybrid nanofluid, Chin. J. Phys., 2020, 67, 330–348 CrossRef CAS.
- A. Mahesh, S. V. K. Varma, C. S. K. Raju, M. J. Babu, K. Vajravelu and W. Al-Kouz, Significance of non-Fourier heat flux and radiation on PEG – Water based hybrid Nanofluid flow among revolving disks with chemical reaction and entropy generation optimization, Int. Commun. Heat Mass Transfer, 2021, 127 DOI:10.1016/j.icheatmasstransfer.2021.105572.
- J. Chen, R. Zhao, Y. L. Nian and W. L. Cheng, Numerical study on the effects of cylindrical roughness on heat transfer performance and entropy generation of supercritical carbon dioxide in vertical tubes, Int. J. Heat Mass Transfer, 2023, 208 DOI:10.1016/j.ijheatmasstransfer.2023.124060.
- L. S. Sundar and H. K. Mewada, Experimental entropy generation, exergy efficiency and thermal performance factor of CoFe2O4/Water nanofluids in a tube predicted with ANFIS and MLP models, Int. J. Therm. Sci., 2023, 190 DOI:10.1016/j.ijthermalsci.2023.108328.
- S. A. Khan, T. Hayat, A. Alsaedi and B. Ahmad, Melting heat transportation in radiative flow of nanomaterials with irreversibility analysis, Renewable Sustainable Energy Rev., 2021, 140 DOI:10.1016/j.rser.2021.110739.
- P. S. Salimath and I. S. Ertesvåg, Local entropy generation and entropy fluxes of a transient flame during head-on quenching towards solid and hydrogen-permeable porous walls, Int. J. Hydrogen Energy, 2021, 46, 26616–26630 CrossRef CAS.
- L. S. Sundar, S. Mesfin, E. V. Ramana, Z. Said and A. C. M. Sousa, Experimental investigation of thermo-physical properties, heat transfer, pumping power, entropy generation, and exergy efficiency of nanodiamond + Fe3O4/60:40% water-ethylene glycol hybrid nanofluid flow in a tube, Therm. Sci. Eng. Prog., 2021, 21 DOI:10.1016/j.tsep.2020.100799.
- P. Barnoon, D. Toghraie, F. Eslami and B. Mehmandoust, Entropy generation analysis of different nanofluid flows in the space between two concentric horizontal pipes in the presence of magnetic field: Single-phase and two-phase approaches, Comput. Math. Appl., 2019, 77, 662–692 CrossRef.
- S. Das, N. Mahato, A. Ali and R. N. Jana, Dynamical behaviour of magneto-copper-titania/water-ethylene glycol stream inside a gyrating channel, Chem. Phys. Lett., 2022, 793 DOI:10.1016/j.cplett.2022.139476.
- Z. Mahmood, U. Khan, S. Saleem, K. Rafique and S. M. Eldin, Numerical analysis of ternary hybrid nanofluid flow over a stagnation region of stretching/shrinking curved surface with suction and Lorentz force, J. Magn. Magn. Mater., 2023, 573 DOI:10.1016/j.jmmm.2023.170654.
- N. A. Zainal, I. Waini, N. S. Khashi'ie, A. R. M. Kasim, K. Naganthran, R. Nazar and I. Pop, Stagnation point hybrid nanofluid flow past a stretching/shrinking sheet driven by Arrhenius kinetics and radiation effect, Alex. Eng. J., 2023, 68, 29–38 CrossRef.
- B. Saleh and L. S. Sundar, Entropy generation and exergy efficiency analysis of ethylene glycol-water based nanodiamond + Fe3O4 hybrid nanofluids in a circular tube, Powder Technol., 2021, 380, 430–442 CrossRef CAS.
- A. Alsaedi, K. Muhammad and T. Hayat, Numerical study of MHD hybrid nanofluid flow between two coaxial cylinders, Alex. Eng. J., 2022, 61, 8355–8362 CrossRef.
- I. Waini, U. Khan, A. Zaib, A. Ishak and I. Pop, Inspection of TiO2-CoFe2O4 nanoparticles on MHD flow toward a shrinking cylinder with radiative heat transfer, J. Mol. Liq., 2022, 361 DOI:10.1016/j.molliq.2022.119615.
- M. A. Qureshi, A case study of MHD driven Prandtl-Eyring hybrid nanofluid flow over a stretching sheet with thermal jump conditions, Case Stud. Therm. Eng., 2021, 28 DOI:10.1016/j.csite.2021.101581.
- H. Waqas, S. M. R. S. Naqvi, M. S. Alqarni and T. Muhammad, Thermal transport in magnetized flow of hybrid nanofluids over a vertical stretching cylinder, Case Stud. Therm. Eng., 2021, 27 DOI:10.1016/j.csite.2021.101219.
- H. Waqas, M. Fida, D. Liu, U. Manzoor and T. Muhammad, Numerical simulation of entropy generation for nanofluid with the consequences of thermal radiation and Cattaneo–Christov heat flux model, Int. Commun. Heat Mass Transfer, 2022, 137 DOI:10.1016/j.icheatmasstransfer.2022.106293.
Footnote |
| † KHA stands for Khan, Hayat and Alsaedi. |
|
| This journal is © The Royal Society of Chemistry 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
T.
Hayat
a and
A.
Alsaedi
*a,
T.
Hayat
a and
A.
Alsaedi
 b
b
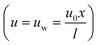 (l shows characteristics length). The flow configuration is sketched in Fig. 1.
(l shows characteristics length). The flow configuration is sketched in Fig. 1.
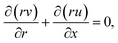
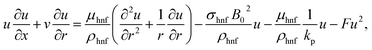
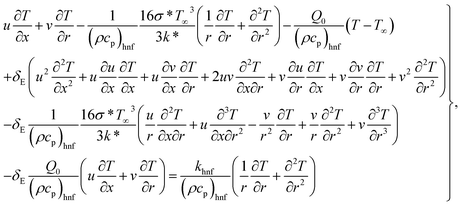
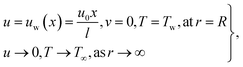
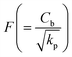 the inertia coefficient, ρhnf the density, kp the porous space permeability, vhnf the kinematic viscosity, Cb the drag force coefficient, T the temperature, (Cp)hnf specific heat, Q0 > 0 the heat generation coefficient, σ* Stefan Boltzmann constant,
the inertia coefficient, ρhnf the density, kp the porous space permeability, vhnf the kinematic viscosity, Cb the drag force coefficient, T the temperature, (Cp)hnf specific heat, Q0 > 0 the heat generation coefficient, σ* Stefan Boltzmann constant, 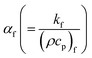 thermal diffusivity, k* mean absorption coefficient, khnf the thermal conductivity, δE the thermal relaxation time, Tw the wall temperature, u0 the reference velocity, and T∞ the ambient temperature.
thermal diffusivity, k* mean absorption coefficient, khnf the thermal conductivity, δE the thermal relaxation time, Tw the wall temperature, u0 the reference velocity, and T∞ the ambient temperature.
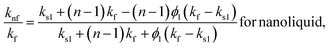
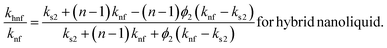
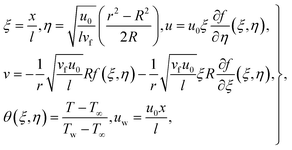
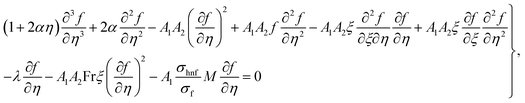
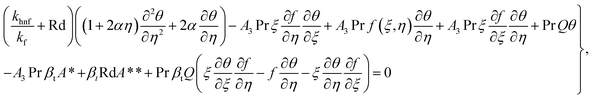
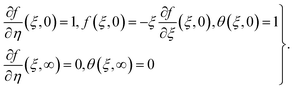
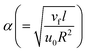 indicates the curvature variable,
indicates the curvature variable, 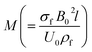 the magnetic parameter,
the magnetic parameter, 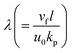 the porosity variable,
the porosity variable, 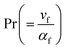 the Prandtl number,
the Prandtl number, 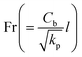 the Forchheimer number,
the Forchheimer number, 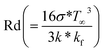 the radiation parameter,
the radiation parameter, 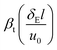 the thermal relaxation time variable, and
the thermal relaxation time variable, and 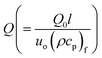 . A*, A**, A1, A2 and A3 are
. A*, A**, A1, A2 and A3 are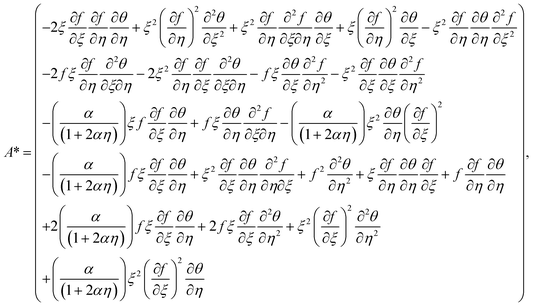
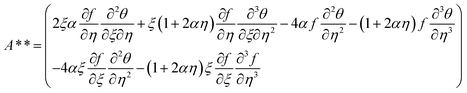
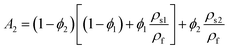
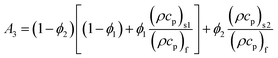
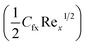 and Nusselt number (NuxRe−1/2x) are
and Nusselt number (NuxRe−1/2x) are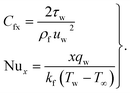
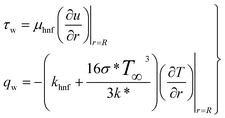
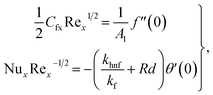
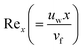 shows the local Reynolds number.
shows the local Reynolds number.
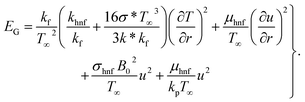
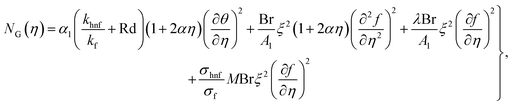
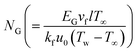 characterizes the entropy rate,
characterizes the entropy rate, 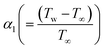 the temperature difference variable, and
the temperature difference variable, and 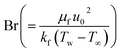 the Brinkman number.
the Brinkman number.
 and denote
and denote 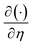 by prime in eqn (16)–(18). We have
by prime in eqn (16)–(18). We have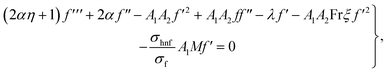
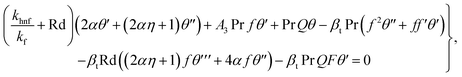
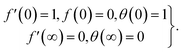
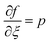 ,
, 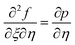 ,
, 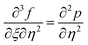 ,
, 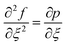 ,
, 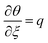 ,
, 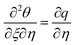 ,
, 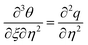 ,
, 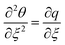 in eqn (16)–(18). One obtains
in eqn (16)–(18). One obtains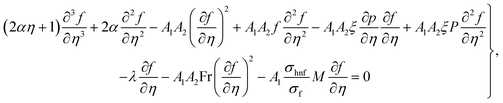
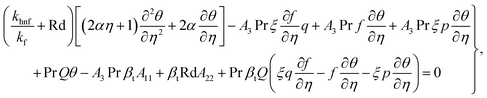
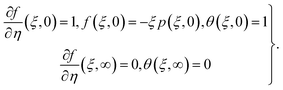
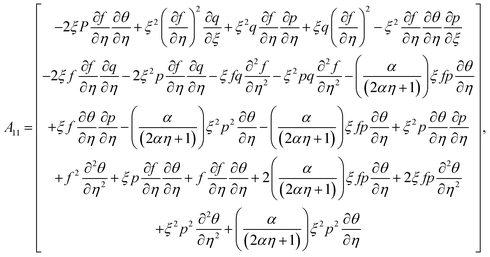
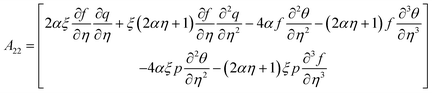
 by prime. Suppose that
by prime. Suppose that  ,
,  ,
, 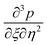 ,
, 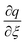 ,
, 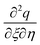 ,
, 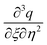 ,
, 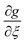 ,
, 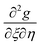 ,
, 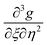 become zero. We obtain
become zero. We obtain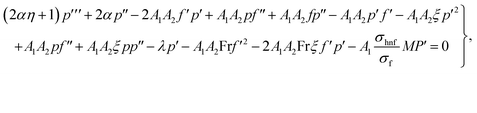
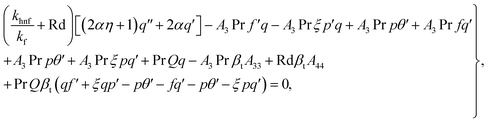
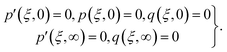
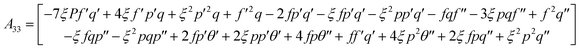
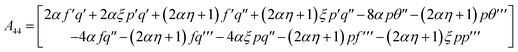
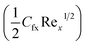 and thermal transport rate (NuxRe−1/2x) for nanoliquid (MoS4/engine oil) and hybrid nanoliquid (MoS4 + CoFe2O4/engine oil) have been sketched in Tables 2 and 3.
and thermal transport rate (NuxRe−1/2x) for nanoliquid (MoS4/engine oil) and hybrid nanoliquid (MoS4 + CoFe2O4/engine oil) have been sketched in Tables 2 and 3.
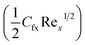 for influential variables is examined in Table 2. Higher magnetic variables lead to intensification of the skin friction coefficient for nanomaterial (MoS4/engine oil) and hybrid nanomaterial (MoS4 + CoFe2O4/engine oil). Clearly, for a larger porosity variable and Forchheimer number, the surface drag force improved.
for influential variables is examined in Table 2. Higher magnetic variables lead to intensification of the skin friction coefficient for nanomaterial (MoS4/engine oil) and hybrid nanomaterial (MoS4 + CoFe2O4/engine oil). Clearly, for a larger porosity variable and Forchheimer number, the surface drag force improved.