Open Access Article
Open Access ArticleComputational assessment of the potential of cross-catalytic coprecipitating systems for the bottom-up design of nanocomposites†
Joti
Rouillard
 *a,
Britta
Maier
b,
Helmut
Cölfen
*a,
Britta
Maier
b,
Helmut
Cölfen
 b and
Juan-Manuel
García-Ruiz
*c
b and
Juan-Manuel
García-Ruiz
*c
aCAS Key Laboratory of Crust-Mantle Materials and Environments, School of Earth and Space Sciences, University of Science and Technology of China, Jinzhai Road 96, 230026 Hefei, China. E-mail: joti@ustc.edu.cn; joti.rouillard@gmail.com
bPhysical Chemistry, Department of Chemistry, University of Konstanz, Universitätsstraße 10, 78457 Konstanz, Germany
cLaboratorio de Estudios Cristalográficos, Instituto Andaluz de Ciencias de la Tierra, CSIC-Universidad de Granada, Av. de las Palmeras, 4, 18100 Armilla, Granada, Spain
First published on 18th October 2023
Abstract
The production of nanocomposites is often economically and environmentally costly. Silica-witherite biomorphs, known for producing a wealth of life-like shapes, are nanocomposites entirely formed through self-organization processes. Behind these precipitates are two precipitation reactions that catalyze each other. Using a simple computational approach, we show here that this type of chemical system – defined here as Cross-Catalytic Coprecipitating Systems (CCCSs) – is of great interest to material design. Provided that cross-catalytic effects are sufficient to overcome the precipitation thresholds for each phase, all CCCSs can be expected to self-organize into nanocomposite materials through a one-pot, one-step synthesis protocol. Symmetry-breaking events generating various complex, ordered textures are predicted in CCCSs involving crystalline phases. While high levels of stochasticity lead to a loss of ordering, coprecipitation is found to be robust to diffusion or advection in the solution. This model shows that a couple of chemical reactions can generate a range of complex textures – with possibly distinct physical/chemical properties. Cross-catalytic coprecipitating systems consequently represent a promising avenue for producing nanocomposites with complex textures at reduced economic and environmental costs.
Introduction
Every year, new types of nanocomposites are designed in various fields of technology.1–11 Because of their enhanced capabilities, they can help to solve critical technological challenges, among which the production of electricity from light6 or heat,3 energy storage1,4,5 and pollution treatment2,8 are some prominent examples. However, a general issue is that the production of these materials is complicated, energy-consuming and costly. This represents a hindrance for scaling up production.One approach generally adopted to produce nanomaterials with reduced economic and environmental costs, the bottom-up synthesis approach, relies on harnessing the self-organization capabilities of certain chemical systems.12–14 Inorganic nanoparticles, for example, can spontaneously co-orient to form the so-called mesocrystals.15,16 It was also found experimentally that reaction-diffusion processes occurring during the synthesis of organic membranes or during crystal growth can generate Turing-like patterns at the nanoscale.17,18 Yet, the self-organization of different phases into a nanocomposite appears more difficult than the self-organization of a single type of nanoparticle. It usually requires separate steps and specialized devices.3,7 Apart from some recent notable exceptions, such as the preparation of binary mesocrystals19 and ternary metallic heterojunctions,20 for most nanocomposites, the synthesis of the constituent phases and their assembly into the desired material are separate. The one-pot, one-step self-organization of molecular reactants into the final material remains a critical challenge.
Incidentally, a chemical system studied for several decades can represent a formidable inspiration in this regard: silica-witherite biomorphs.21 They are self-organized nanocomposites of crystalline witherite and amorphous silica that are well known for the diverse, life-like morphologies they display.22–24 It has been demonstrated that the complex morphogenetic mechanisms underlying biomorph growth are primarily due to the interplay between the precipitation of both phases (Fig. 1-A).25–27 Witherite precipitation under alkaline conditions locally decreases pH. This pH drop increases the saturation of silica and triggers its precipitation. Silica precipitation, in turn, leads to a local increase of pH and an increase of the saturation of witherite. Consequently, the precipitation of each phase, owing to pH changes, favors the precipitation of the other phase, leading to a complex cyclic coprecipitation (Fig. 1-A).
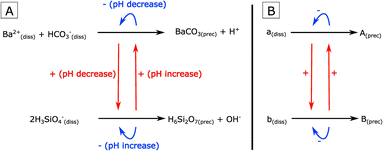 | ||
| Fig. 1 (A) Schematic drawing of the cyclic coprecipitation underlying silica-witherite biomorph growth.25–27 (B) Schematic drawing of the general principle of a cross-catalyzed coprecipitating system. One dissolved species (a(diss)) precipitates to form a condensed phase (A(prec)). A second dissolved species (b(diss)) precipitates to form a distinct condensed phase (B(prec)). Cross-catalysis between the two reactions is depicted by red arrows. Self-inhibition of each reaction is depicted by blue arrows. Modalities of enhancement and inhibition may vary depending on the actual system. | ||
Silica-carbonate biomorphs thus demonstrate the possibility for two distinct inorganic phases to organize into a complex 3D nanocomposite while they precipitate, due to the interaction between both precipitation reactions. Research suggests that the control of environmental parameters such as pH or temperature grants a fine control on the precipitated textures.28,29 Silica-witherite biomorphs could thus reveal highly useful for the design of new optical devices or microcarriers.30–32
In general, we define here this type of system as a Cross-Catalytic Coprecipitating System (abbreviated in the following as CCCS). CCCSs consist in two parallel precipitation reactions, forming two distinct condensed phases, that catalyze each other (Fig. 1-B). This definition is very general, since there are no constraints on the nature of the phases precipitated – they may be organic or inorganic, crystalline or amorphous – and no constraints on the modalities of cross-catalysis. CCCSs may consequently involve different types of chemical species and exist in various contexts.
In this study, we tested the general capabilities of CCCSs for material design using a numerical model. Among the different computational approaches that have been developed for modelling nucleation and growth processes (see e.g. the work of L. Gránásy and coworkers33,34), it was decided to use a simple, two-dimensional model inspired by cellular automata35,36 that focuses on the core of the process of cross-catalyzed coprecipitation. An overview of the model is given in the Experimental section of this paper. The code is given in the ESI.†
Experimental
The principle of the model revolves around three major elements:(1) Two parallel reactions of precipitation – a(diss) → A(prec) and b(diss) → B(prec) – exist. Precipitation is constrained in a square crystallographic lattice. a(diss), A(prec), b(diss) and B(prec) are respectively abbreviated to a, b, A and B in the following.
(2) The precipitation of phases A or B occurs when the concentration in a or b (resp. noted [a] and [b]) reaches a certain threshold T.37–40 To model nucleation energy barriers, two thresholds were introduced for each phase, one for growth (Ta,g and Tb,g) and one, higher, for nucleation (Ta,n and Tb,n).
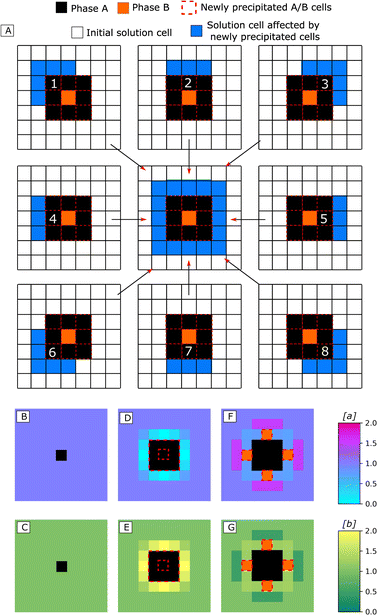
(3) The precipitation of one phase increases locally the saturation levels for the other phase and decreases locally the saturation levels for this phase – this is depicted in Fig. 2-A. The intensity of these cross-catalysis and self-inhibition effects is represented by parameters Oa and Ob. The precipitation of phase A releases a quantity Oa of b and consumes a quantity Oa of a in the solution cells surrounding the newly precipitated cell. The precipitation of phase B releases (respectively consumes) an amount Ob of a (respectively b) in the solution cells surrounding the newly precipitated cell. Oa and Ob values are correlated to the amplitude of concentration oscillations in the solution cells.
In this model, the focus is given to cross-catalysis, and it is assumed that no further interactions between the four chemical species a(diss), A(prec), b(diss) and B(prec) exist. It must be noted however that variable supplementary interactions between these species may exist in a real system (for example, both precipitated species may react together). Depending on their nature, such interactions could significantly alter precipitation and should be taken into account in relevant systems.
Results and discussion
Starting from a single nucleus of phase A, simulations were run using various values for growth thresholds (Ta,g and Tb,g37–40) and for the amplitude of cross-catalysis effects (Oa and Ob). The results show that depending on these parameters, cross-catalytic systems may display several behaviors drastically different from each other, referred to here as Regimes 0 to 5, and shown in Fig. 3-A. Maintained coprecipitation, the desired target for the one-pot/one-step synthesis of nanocomposites, corresponds to Regime 5. We also note that under certain conditions, due to the self-inhibition, single-phase porous precipitates can be obtained (Regime 4). While we do not discuss them further in this work, which is focused on nanocomposites, those porous precipitates can be of high interest to the engineering of molecular sieves.41–43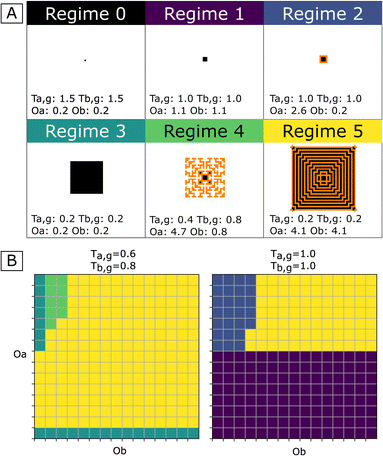 | ||
| Fig. 3 (A) Main growth regimes of CCCSs. For each regime, one example precipitate is shown with its corresponding parameters (see the corresponding videos in the ESI†). Phase A depicted in black and phase B in orange. All simulations initiated with a single cell of phase A as the nucleus, initial [a] and [b] of 1, and nucleation thresholds Ta,n = Tb,n = 2. The simulations last ten timesteps, with different combinations of conditions of values for the growth thresholds Ta,g and Tb,g and intensities of cross-catalysis effects Oa and Ob. In Regime 0, growth does not occur (initial [a] and [b] are lower than Ta,g and Tb,n respectively). Regime 1: growth arrested after one timestep of A precipitation, due to complete self-inhibition. Regime 2: concomitant growth of both phases is arrested after a few timesteps. Regime 3: continuous growth of one phase. Regime 4: growth of porous single-phase precipitates due to partial self-inhibition. Regime 5: concomitant, continuous growth of both phases. (B) Illustration of the dependency of observed regimes on parameters Ta,g, Oa and Ob for a single cell of phase A as the nucleus. Oa and Ob range from 0.2 to 4.7. The color chart corresponds to the color of regimes shown in panel A. | ||
The results indicate that a system of two reactions, although it behaves in a cross-catalytic manner, may never produce nanocomposites if it does not fulfill supplementary conditions. The domain of the parameter space where Regime 5 was observed in the simulations can be seen in Fig. 3-B (yellow) for two different couples of values for growth thresholds Ta,g and Tb,g. In order to observe maintained coprecipitation, the chemical oscillations due to A and B precipitation (Oa and Ob) must be sufficient so that both growth thresholds Ta,g and Tb,g are overcome – i.e., cross-catalysis is effective for both reactions. Regime 5 is consequently observed only above minimal values of Oa and Ob; these minimal values increase when Ta,g or Tb,g values are increased (Fig. 3-B).
One could intuitively predict that in Regime 5, coprecipitation would always result in both phases precipitating alternatively, layer by layer. Interestingly, due to the underlying lattice constraining precipitation, this is not the case. Indeed, the local concentration changes in the solution around the growing precipitate are smaller on the corners than on the sides (see Fig. 2-A for a graphical explanation of this effect). Due to this ‘corner effect’, saturation levels may reach the precipitation thresholds only in some of the solution cells surrounding the precipitate (Fig. 2-D and E). If this occurs, it represents a symmetry-breaking event that increases the geometric complexity of the obtained precipitate and creates new gradients of concentration in the surrounding solution (Fig. 2-F and G). Those gradients can then reverberate into other symmetry-breaking events. This result suggests more generally that, provided at least one of the precipitated phases in a CCCS follows a crystallographic lattice, symmetry-breaking events can occur and nanocomposites with complex textures are formed.
In composite materials obtained using a CCCS, geometry is not controlled by crystal facet energy – as is the case in many classical crystalline systems44 – but by spatial heterogeneities in concentrations in the solution surrounding the precipitate. The history of symmetry-breaking events, and therefore the texture and shape of the precipitate, is thus highly sensitive to the values of the precipitation thresholds and the amplitude of chemical oscillations. With this simple model, by varying these parameters, it was found that a very large variety of nanocomposite materials may be obtained in a CCCS. A glimpse of the diversity obtained after ten timesteps from a single cell nucleus of phase A and for different combinations of Ta,g, Tb,g, Oa and Ob is shown in Fig. 4A–F.
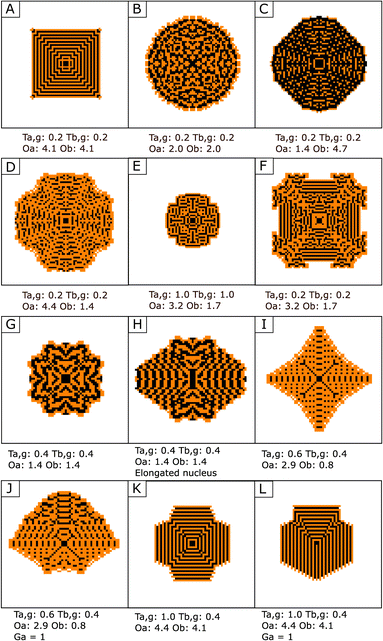 | ||
| Fig. 4 Examples of textures from Regime 5 obtained after ten timesteps, with nucleation thresholds of Ta,n = Tb,n = 2. See the corresponding videos in the ESI.† Phase A depicted in black and phase B in orange. Only a small subset of observed diversity is shown. The parameters used for obtaining each precipitate are written below. (A and B) Effect of a decrease of both Oa and Ob. (C and D) Effect of a change of the relative values of Oa and Ob. (E and F) Effect of an increase of both Ta,g and Tb,g. (G and H) Effect of a change of the nucleus symmetry – here, rectangle (H) instead of square (G). See also Fig. S3.† (I to L) Effect of a gradient of concentration in the solution. (I and K) No gradient. (J and L) The same conditions, but with a gradient of [a], ranging from 0.5 to 1.5 from the bottom to the top of the simulation space. See also Fig. S4.† | ||
For constant values of Ta,g and Tb,g, high values for both Oa and Ob lead logically to more complete rounds of precipitation of A and B at each timestep, and the obtained textures are close to a simple layer-by-layer precipitation (Fig. 4-A). Lower values for Oa and/or Ob are correlated to increased occurrences of symmetry-breaking events and an increased complexity in the obtained textures (Fig. 4-B). A higher chemical oscillation for one phase – α – than for the other phase – β – favors a larger volume of phase β in the precipitate, since smaller volumes of α precipitated are necessary to reach thresholds for β precipitation. Therefore, the ratio Oa/Ob is negatively correlated with the ratio of A volume precipitated to B volume precipitated – see Fig. 4-C and D and S1.† As can be expected, for constant values of chemical oscillation Oa and Ob, an increase in growth thresholds Ta,g and Tb,g overall slows down precipitation, and precipitates obtained after the same number of time steps are smaller – see Fig. 4-E and F and S2.†
Another factor controlling growth is the morphology and nature of the seed. While using a different seed appears to have a rather limited influence on simple textures (Fig. S3-B and C†), it can drastically alter the precipitation history of more complex textures (Fig. S3-D–F†). Noticeably, a change of the symmetry of the seed may be reverberated and modify the symmetry of the obtained precipitates (Fig. 4-G,H and S3-D†).
The spatial gradients of concentration also have an effect, by introducing an axis of polarity in the precipitates (Fig. 4-I–L and S4†). The spatial gradients of concentrations can lead consequently to a supplementary degree of morphologic and textural complexity in the obtained nanocomposite.
Studying self-assembly processes from the nano- to the micro-scale is a notorious technical challenge.45,46 Experiments were not undertaken in this study, that instead focuses on finding general conditions for obtaining nanocomposites with complex textures. Regarding the silica-witherite biomorphs system described in Introduction of this article, the pH-mediated cross-catalysis mechanism has been demonstrated using pH-sensitive dyes,25,27 but the internal texture of these nanocomposites has revealed difficult to characterize at the nanometer scale. Yet, the textures reported in this study of CCCSs can be compared to patterns observed in natural and experimental crystalline materials (Fig. 5). The growth of single crystals can lead to the formation of ordered compositional patterns. Let us mention the cases of oscillatory zoning correlated with cyclic compositional changes (Fig. 5-A),47–49 or the zoning in experimentally grown “dyed” crystals, generally due to the incorporation of light-absorbing molecules in preferential growth sectors (Fig. 5-B–D).50–52 Precipitation may also create ordered patterns at the scale of several crystals. Prominent examples are wave-like compositional patterns referred to generally as “Liesegang rings” (Fig. 5-E) or the orientational patterns formed during spherulitic growth (Fig. 5-F) – very common phenomena that occur in a number of natural and experimental settings.17,53–57 Processes behind these patterns are disparate and arguably quite different from CCCSs. However, they confirm that ordered compositional patterns may frequently form during the growth of crystalline materials.
 | ||
| Fig. 5 Examples of compositional (A to E) or orientational (F) ordering that may occur during the growth of single (A to D) or multiple (E and F) crystals and reported in previous works. (A) (Br,Sr)SO4 solid solution crystal (ref. 46). Darkness in the crystal is correlated to the relative proportions of Sr and Ba. (B) Phthalic acid crystal grown in the presence of methyl green dye (ref. 47). (C) Phthalic acid crystal grown in the presence of Nile red dye (ref. 49). (D) AgBr crystals grown in the presence of Maskasky dye (ref. 48). (E) Concentric rings formed by self-organization of BaCO3 crystals during their growth (ref. 17). (F) Spherulitic growth and orientational pattern observed during the crystallization of hippuric acid at 80 °C (ref. 50). | ||
There are two important factors that may prevent coprecipitation and/or ordering in CCCSs and that need to be discussed. The first is molecular diffusion in the solution. Diffusion around growing precipitates leads in principle to a dilution of the cross-catalytic effect in the solution. To test the effect of diffusion, simulations were run where the diffusion of a and b molecules in the solution was modelled, following Fick's Law:
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) i = D*∇[i] i = D*∇[i] |
![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) i the flux of molecules i, ∇[i] the gradient of concentration of molecule i, and D a diffusion constant. The results indicate that the coprecipitation behavior in the CCCS is robust to diffusion (Fig S5,† first three columns). It is only for very high D values (D = 0.3) that coprecipitation was consistently lost (Fig. S5,† last column). The complexity of precipitated textures however tends to be reduced for D values of 0.1 and higher (Fig. S5,† third column). These findings are consistent with previous observations made on silica-witherite biomorphs. In this system, nanocomposites were obtained even when the solution was stirred mechanically up to 350 rpm (ref. 58) – note that, similarly to molecular diffusion, mechanical stirring creates a dilution of the cross-catalytic chemical effect in the vicinity of the growing biomorph.
i the flux of molecules i, ∇[i] the gradient of concentration of molecule i, and D a diffusion constant. The results indicate that the coprecipitation behavior in the CCCS is robust to diffusion (Fig S5,† first three columns). It is only for very high D values (D = 0.3) that coprecipitation was consistently lost (Fig. S5,† last column). The complexity of precipitated textures however tends to be reduced for D values of 0.1 and higher (Fig. S5,† third column). These findings are consistent with previous observations made on silica-witherite biomorphs. In this system, nanocomposites were obtained even when the solution was stirred mechanically up to 350 rpm (ref. 58) – note that, similarly to molecular diffusion, mechanical stirring creates a dilution of the cross-catalytic chemical effect in the vicinity of the growing biomorph.
The second factor that may prevent ordering in the CCCS is stochasticity. The model used here is purely deterministic, with “hard” thresholds determining whether precipitation occurs or not. However, some amount of randomness may exist in the CCCS. In the case of silica-witherite biomorphs, for example, silica precipitation is related to its polymerization in solution, which follows stochastic rules.59 Random fluctuations in the space and time of the reactant's concentration may also exist,60 and impurities can be randomly integrated during synthesis processes.61 To account for those phenomena and test the effect on the obtained textures, a batch of simulations was run where the hard thresholds were replaced by soft thresholds – i.e., the probability that precipitation occurs P depends on saturation s, following a sigmoidal law centered on the precipitation threshold T:
P = 1/(1 − L*![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(T − s)) exp(T − s)) |
The results show that for L values of 105, the ordering obtained with a purely deterministic behavior is not altered (Fig. S7,† first column). When L is decreased to 100, the ordering is significantly altered (Fig. S7,† second column). Higher amounts of randomness, with an L value of 10, lead to complete obliteration of any ordering (Fig. S7,† third column).
In order to make use of the potential of the CCCS for nanocomposite synthesis in the future, a first step will be to look for couples of precipitation reactions that can interact in a cross-catalytic manner and involve at least the precipitation of one crystalline phase. The challenge is that this interaction may be straightforward – e.g. if the product of one reaction is the reactant of the other, or more indirect – as is the case for example in silica-witherite nanocomposites. It could be envisioned to look for such interactions using network analysis on large databases of chemical reactions.
Screening experiments should then be conducted on the systems previously found in order to search for CCCS behavior. In coprecipitation experiments, chelators could be used with various concentrations in order to modify effective precipitation thresholds Ta,g and Tb,g. Increased viscosity of the mother solution could also be tested (provided that the medium remains inert), since it could slow down diffusion and increase effective Oa/Ob. A rigorous confrontation of the model with experimental results would ideally require to (1) image ongoing precipitation at the nanometre scale and (2) analyze the evolution of local solution properties around the precipitates. However, this is technically very difficult.45,46 While liquid cell TEM is a promising tool to image nanoscale precipitation mechanisms, it is still a relatively young technique that has not yet been applied in this context. The measurement of solution properties at the nanoscale remains a technical challenge.25,62 Consequently, as of now, it may be easier to evaluate potential CCCSs through the characterization of final precipitates.
Promising precipitates will present a high anisotropy that could be evidenced using X-ray diffraction. The texture (as well as physical and chemical properties) of these precipitates should be carefully investigated using e.g. transmission electron microscopy. In order to verify that the system indeed is a CCCS, one should assess how changes in precipitation thresholds, the amplitude of cross-catalysis, and the nucleus shape affect the obtained precipitate, and compare it with the general observations made in Fig. 4.
Alternatively, first principles simulations, already used in the context of precipitation reactions,63 could in the future lead to a fine prediction of the behavior of potential CCCSs. This could circumvent some experimental difficulties and give information about cross-catalysis parameters Oa and Ob – parameters otherwise difficult to assess experimentally.
As a supplementary note, the mechanical stability of materials obtained through coprecipitation can be a concern in some cases.64 Although this particular problem was not considered here, the assessment of the material stability outside of the solvent should be conducted on experimentally obtained precipitates.
Conclusions
Depending on the type of behavior wanted for a specific CCCS, this study shows that several requirements exist:(1) In order to obtain a nanocomposite through maintained coprecipitation, the cross-catalysis effects (Oa and Ob) must be sufficient to overcome successively the precipitation thresholds of A and B (Ta, Tb).
(2) In order to obtain ordered nanocomposites, besides the previous requirement, the degree of randomness must be moderate (L > 100).
(3) In order to obtain nanocomposites displaying complex textures due to symmetry-breaking events, besides previous requirements, it is required that at least one of the phases A or B follows a crystallographic lattice (see Fig. 2).
Although this model is simple, it captures the most general and critical behaviors that may be expected in cross-catalytic coprecipitating systems and illustrates their important potential. These systems are able to produce various nanocomposites with a highly complex texture through a single-pot, single-step process. While precipitation was constrained in a square crystallographic lattice in this model, phases precipitated may be either crystalline or amorphous; they also could be organic or inorganic. Besides, if precipitation thresholds and the amplitude of chemical oscillations are adjustable, a single couple of chemical reactions can produce several types of materials, potentially displaying distinct physical/chemical properties. Such systems are therefore most promising for reducing the economic and environmental costs of nanocomposite production. We hope that this study will trigger new experimental studies looking for the patterns anticipated by our computational approach.
Author contributions
J. R.: conceptualization, methodology, software, validation, writing – original draft, writing – review and editing, and visualization. B. M.: conceptualization and writing – review and editing. H. C.: conceptualization, writing – review and editing, and supervision. J. M. G. R.: conceptualization, writing – review and editing, supervision, and funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. R. thanks the Chinese Academy of Sciences Pioneer Hundred Talents Program for its financial support.References
- M. Genovese and K. Lian, Curr. Opin. Solid State Mater. Sci., 2015, 19, 126–137 CrossRef CAS.
- M. Shahadat, T. T. Teng, M. Rafatullah and M. Arshad, Colloids Surf., B, 2015, 126, 121–137 CrossRef CAS PubMed.
- S. Ortega, M. Ibáñez, Y. Liu, Y. Zhang, M. V. Kovalenko, D. Cadavid and A. Cabot, Chem. Soc. Rev., 2017, 46, 3510–3528 RSC.
- D. Demirocak, S. Srinivasan and E. Stefanakos, Appl. Sci., 2017, 7, 731 CrossRef.
- Y. Liang, W. Lai, Z. Miao and S. Chou, Small, 2018, 14, 1702514 CrossRef PubMed.
- F. W. Low and C. W. Lai, Renewable Sustainable Energy Rev., 2018, 82, 103–125 CrossRef CAS.
- A. V. Rane, K. Kanny, V. K. Abitha and S. Thomas, in Synthesis of Inorganic Nanomaterials, Elsevier, 2018, pp. 121–139 Search PubMed.
- Md. R. Awual, Chem. Eng. J., 2017, 307, 456–465 CrossRef CAS.
- F. Kotz, A. S. Quick, P. Risch, T. Martin, T. Hoose, M. Thiel, D. Helmer and B. E. Rapp, Adv. Mater., 2021, 33, 2006341 CrossRef CAS PubMed.
- B. Ates, S. Koytepe, A. Ulu, C. Gurses and V. K. Thakur, Chem. Rev., 2020, 120, 9304–9362 CrossRef CAS PubMed.
- X. Sun, C. Huang, L. Wang, L. Liang, Y. Cheng, W. Fei and Y. Li, Adv. Mater., 2021, 33, 2001105 CrossRef CAS PubMed.
- H. Cölfen and S. Mann, Angew. Chem., Int. Ed., 2003, 42, 2350–2365 CrossRef PubMed.
- G. J. de A. A. Soler-Illia, C. Sanchez, B. Lebeau and J. Patarin, Chem. Rev., 2002, 102, 4093–4138 CrossRef PubMed.
- E. Nakouzi and O. Steinbock, Sci. Adv., 2016, 2, e1601144 CrossRef PubMed.
- H. Cölfen and M. Antonietti, Angew. Chem., Int. Ed., 2005, 44, 5576–5591 CrossRef PubMed.
- L. Zhou and P. O'Brien, Small, 2008, 4, 1566–1574 CrossRef CAS PubMed.
- T. Wang, A.-W. Xu and H. Cölfen, Angew. Chem., Int. Ed., 2006, 45, 4451–4455 CrossRef CAS PubMed.
- Z. Tan, S. Chen, X. Peng, L. Zhang and C. Gao, Science, 2018, 360, 518–521 CrossRef CAS PubMed.
- C. Jenewein, J. Avaro, C. Appel, M. Liebi and H. Cölfen, Angew. Chem., Int. Ed., 2022, 61(2), e202112461 CrossRef CAS PubMed.
- R. Geng, J. Yin, J. Zhou, T. Jiao, Y. Feng, L. Zhang, Y. Chen, Z. Bai and Q. Peng, Nanomaterials, 2019, 10, 1 CrossRef PubMed.
- J. M. García-Ruiz and J. L. Amorós, J. Cryst. Growth, 1981, 55, 379–383 CrossRef.
- J.-M. Garcia-Ruiz, S. T. Hyde, A. M. Carnerup, A. G. Christy, M. Van Kranendonk and N. J. Welham, Science, 2003, 302, 5648 CrossRef PubMed.
- J. M. García Ruiz, A. Carnerup, A. G. Christy, N. J. Welham and S. T. Hyde, Astrobiology, 2002, 2, 353–369 CrossRef PubMed.
- J. Rouillard, J.-M. García-Ruiz, J. Gong and M. A. van Zuilen, Geobiology, 2018, 16, 279–296 CrossRef CAS PubMed.
- M. Montalti, G. Zhang, D. Genovese, J. Morales, M. Kellermeier and J. M. García-Ruiz, Nat. Commun., 2017, 8, 14427 CrossRef CAS PubMed.
- J. M. García-Ruiz, E. Melero-García and S. T. Hyde, Science, 2009, 323, 362–365 CrossRef PubMed.
- J. Opel, M. Hecht, K. Rurack, J. Eiblmeier, W. Kunz, H. Cölfen and M. Kellermeier, Nanoscale, 2015, 7, 17434–17440 RSC.
- W. L. Noorduin, A. Grinthal, L. Mahadevan and J. Aizenberg, Science, 2013, 340, 832–837 CrossRef CAS PubMed.
- G. Zhang, C. Verdugo-Escamilla, D. Choquesillo-Lazarte and J. M. García-Ruiz, Nat. Commun., 2018, 9, 5221 CrossRef CAS PubMed.
- L. Helmbrecht, M. Tan, R. Röhrich, M. H. Bistervels, B. O. Kessels, A. F. Koenderink, B. Kahr and W. L. Noorduin, Adv. Funct. Mater., 2020, 30, 1908218 CrossRef CAS.
- J. Opel, L.-C. Rosenbaum, J. Brunner, A. Staiger, R. Zimmermanns, M. Kellermeier, T. Gaich, H. Cölfen and J.-M. García-Ruiz, J. Mater. Chem. B, 2020, 8, 4831–4835 RSC.
- J. Opel, J. Brunner, R. Zimmermanns, T. Steegmans, E. Sturm, M. Kellermeier, H. Cölfen and J. García-Ruiz, Adv. Funct. Mater., 2019, 29, 1902047 CrossRef.
- L. Gránásy, T. Pusztai, T. Börzsönyi, J. A. Warren and J. F. Douglas, Nat. Mater., 2004, 3, 645–650 CrossRef PubMed.
- L. Gránásy, G. I. Tóth, J. A. Warren, F. Podmaniczky, G. Tegze, L. Rátkai and T. Pusztai, Prog. Mater. Sci., 2019, 106, 100569 CrossRef.
- J. von Neumann, in Theory of Self-Reproducing Automata, University of Illinois Press, Urbana&London., 1966, p. 377 Search PubMed.
- S. Wolfram, Rev. Mod. Phys., 1983, 55, 601–644 CrossRef.
- J. J. D. Yoreo and P. G. Vekilov, Rev. Mineral. Geochem., 2003, 54, 37 CrossRef.
- H. K. Henisch and J. M. García Ruiz, J. Cryst. Growth, 1986, 75(2), 203–211 CrossRef CAS.
- M. Prieto, L. Fernandez-Diaz and S. Lopez-Andes, J. Cryst. Growth, 1989, 98, 14 CrossRef.
- V. K. LaMer and R. H. Dinegar, J. Am. Chem. Soc., 1950, 72, 4847–4854 CrossRef CAS.
- R. K. Kankala, Y.-H. Han, H.-Y. Xia, S.-B. Wang and A.-Z. Chen, J. Nanobiotechnol., 2022, 20, 126 CrossRef CAS PubMed.
- S. E. Lehman and S. C. Larsen, Environ. Sci.: Nano, 2014, 1, 200–213 RSC.
- M. Vallet-Regí, F. Schüth, D. Lozano, M. Colilla and M. Manzano, Chem. Soc. Rev., 2022, 51(13), 5365–5451 RSC.
- G. Wulff, Z. für Kristallogr. - Cryst. Mater., 1901, 34, 449–530 CrossRef CAS.
- N. Jongen, P. Bowen, J. Lemaître, J.-C. Valmalette and H. Hofmann, J. Colloid Interface Sci., 2000, 226, 189–198 CrossRef CAS.
- D. Gebauer, J. D. Gale and H. Cölfen, Small, 2022, 18, 2107735 CrossRef CAS PubMed.
- M. Shore and A. D. Fowler, Can. Mineral., 1996, 34, 17 Search PubMed.
- S. L. L. Barker and S. F. Cox, Geofluids, 2011, 11, 48–56 CrossRef CAS.
- A. Putnis, L. Fernandez-Diaz and M. Prieto, Nature, 1992, 358, 743–745 CrossRef CAS.
- B. Kahr and R. W. Gurney, Chem. Rev., 2001, 101, 893–952 CrossRef CAS PubMed.
- J. E. Maskasky, Photogr. Sci. Eng., 1984, 28, 202–207 CAS.
- M. Kurimoto, L. D. Bastin, D. Fredrickson, P. Gustafson, S.-H. Jang, W. Kaminsky, S. Lovell, C. A. Mitchell, J. Chmielewski and B. Kahr, in Materials Research Society Symposium, Cambridge University Press, San Francisco, 2000, vol. 620 Search PubMed.
- A. G. Shtukenberg, Y. O. Punin, E. Gunn and B. Kahr, Chem. Rev., 2012, 112, 1805–1838 CrossRef CAS PubMed.
- L. Gránásy, T. Pusztai, G. Tegze, J. A. Warren and J. F. Douglas, Phys. Rev. E, 2005, 72, 011605 CrossRef PubMed.
- I. L'Heureux, Philos. Trans. R. Soc., A, 2013, 371, 20120356 CrossRef PubMed.
- R. E. Liesegang, Naturwiss. Wochenschr., 1896, 11(30), 353 Search PubMed.
- E. Nakouzi and O. Steinbock, Sci. Adv., 2016, 2, e1601144 CrossRef PubMed.
- M. Kellermeier, E. Melero-García, W. Kunz and J. M. García-Ruiz, J. Colloid Interface Sci., 2012, 380, 1–7 CrossRef CAS PubMed.
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, Ithaca, New York, 1958 Search PubMed.
- J. W. Cahn and J. E. Hilliard, J. Chem. Phys., 1958, 28, 258–267 CrossRef CAS.
- S. J. Urwin, G. Levilain, I. Marziano, J. M. Merritt, I. Houson and J. H. Ter Horst, Org. Process Res. Dev., 2020, 24, 1443–1456 CrossRef CAS PubMed.
- M. H. Bistervels, M. Kamp, H. Schoenmaker, A. M. Brouwer and W. L. Noorduin, Adv. Mater., 2022, 34, 2107843 CrossRef CAS PubMed.
- H. Liu, I. Papadimitriou, F. X. Lin and J. LLorca, Acta Mater., 2019, 167, 121–135 CrossRef CAS.
- Z. Dong, A. Chatterji, H. Sandhu, D. S. Choi, H. Chokshi and N. Shah, Int. J. Pharm., 2008, 355, 141–149 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00271c |
| This journal is © The Royal Society of Chemistry 2023 |