Open Access Article
Open Access ArticleInsight into the electronic structure of the centrosymmetric skyrmion magnet GdRu2Si2†
S. V.
Eremeev
 *a,
D.
Glazkova
b,
G.
Poelchen
*a,
D.
Glazkova
b,
G.
Poelchen
 c,
A.
Kraiker
d,
K.
Ali
e,
A. V.
Tarasov
bi,
S.
Schulz
c,
K.
Kliemt
c,
A.
Kraiker
d,
K.
Ali
e,
A. V.
Tarasov
bi,
S.
Schulz
c,
K.
Kliemt
 d,
E. V.
Chulkov
d,
E. V.
Chulkov
 bfgh,
V. S.
Stolyarov
ijk,
A.
Ernst
bfgh,
V. S.
Stolyarov
ijk,
A.
Ernst
 l,
C.
Krellner
l,
C.
Krellner
 d,
D. Yu.
Usachov
d,
D. Yu.
Usachov
 bik and
D. V.
Vyalikh
bik and
D. V.
Vyalikh
 *hm
*hm
aInstitute of Strength Physics and Materials Science, Russian Academy of Sciences, 634055 Tomsk, Russia. E-mail: eremeev@ispms.tsc.ru
bSt. Petersburg State University, 7/9 Universitetskaya Nab., St. Petersburg, 199034, Russia
cInstitut für Festkörper- und Materialphysik, Technische Universität Dresden, D-01062 Dresden, Germany
dKristall- und Materiallabor, Physikalisches Institut, Goethe-Universität Frankfurt, Max-von-Laue Strasse 1, D-60438 Frankfurt am Main, Germany
eDepartment of Microtechnology and Nanoscience, Chalmers University of Technology, Göteborg, 41296, Sweden
fDepartamento de Polímeros y Materiales Avanzados: Física, Química y Tecnología, Facultad de Ciencias Químicas, Universidad del País Vasco UPV/EHU, 20080 San Sebastián/Donostia, Spain
gCentro de Física de Materiales (CFM-MPC), Centro Mixto CSIC-UPV/EHU, 20018 San Sebastián/Donostia, Spain
hDonostia International Physics Center (DIPC), 20018 Donostia-San Sebastián, Spain. E-mail: denis.vyalikh@dipc.org
iMoscow Institute of Physics and Technology, Institute Lane 9, Dolgoprudny, Russia
jDukhov Research Institute of Automatics (VNIIA), Moscow, 127055, Russia
kNational University of Science and Technology MISIS, Moscow, 119049, Russia
lInstitute for Theoretical Physics, Johannes Kepler University, Linz, Austria
mIKERBASQUE, Basque Foundation for Science, 48011 Bilbao, Spain
First published on 18th October 2023
Abstract
The discovery of a square magnetic-skyrmion lattice in GdRu2Si2, with the smallest so far found skyrmion size and without a geometrically frustrated lattice, has attracted significant attention. In this work, we present a comprehensive study of surface and bulk electronic structures of GdRu2Si2 by utilizing momentum-resolved photoemission (ARPES) measurements and first-principles calculations. We show how the electronic structure evolves during the antiferromagnetic transition when a peculiar helical order of 4f magnetic moments within the Gd layers sets in. A nice agreement of the ARPES-derived electronic structure with the calculated one has allowed us to characterize the features of the Fermi surface (FS), unveil the nested region along kz at the corner of the 3D FS, and reveal their orbital compositions. Our findings suggest that the Ruderman–Kittel–Kasuya–Yosida interaction plays a decisive role in stabilizing the spiral-like order of Gd 4f moments responsible for the skyrmion physics in GdRu2Si2. Our results provide a deeper understanding of electronic and magnetic properties of this material, which is crucial for predicting and developing novel skyrmion-based systems.
1 Introduction
The centrosymmetric antiferromagnet GdRu2Si2 (TN of ∼46 K), which crystallizes in the ThCr2Si2 structure with I4/mmm symmetry1–3 is well known from the early 1980s. Recently, it has returned to the focus of research efforts with the discovery of a square magnetic skyrmion lattice without a geometrically frustrated lattice.4 This skyrmion phase appears in an external magnetic field of 2–2.5 T at temperatures below 20 K. Although the magnetic properties of GdRu2Si2 have been studied in great detail over the years,1–3,5–9 the appearance of the skyrmion phase has renewed and intensified the discussions about this material, especially concerning the reason and origin of skyrmion physics.4,10–13 It is worth noting that the discovered square skyrmion lattice has a constant of 1.9 nm, the smallest skyrmion size observed to date, which makes it attractive for the development of next-generation high-density, low-power magnetic memory devices.4,11For further studies on the properties of this material and prediction of possible candidates which could reveal unusual magnetic-skyrmion properties as well, detailed information about surface and bulk electronic structures and, most importantly, on how the electronic structure gets modified upon the antiferromagnetic transition is highly desirable. The latter can be derived from momentum-resolved photoemission (ARPES) measurements combined with ab initio calculations. The curious question here is in how far it is possible to detect the stabilization of the helical long-range in-plane magnetic order of Gd 4f moments appearing at the zero magnetic field in the ARPES patterns. The next essential question is about the Fermi surface (FS) and its intrinsic properties. Recently, contradicting results were presented for the properties of the three-dimensional (3D) FS. In a recent theoretical study,10 the nested region near the Γ-point was manifested and it was declared to be responsible for the skyrmion physics in GdRu2Si2. However, the results of ref. 14, which also present a detailed overview of the actual discussion about the properties of GdRu2Si2, do not confirm the nested region near the Γ-point. This calls for a direct experimental visualization of the Fermi surface and further exploration of its properties via ARPES measurements.
Here, we present a detailed study of the electronic structure and discuss FS properties for GdRu2Si2 obtained from ARPES measurements and ab initio density functional theory (DFT) calculations. The latter has been performed for the bulk and for a finite system (slab) that allows us to distinguish surface resonances and surface states for different surface terminations and separate them from the bulk states. Note that most of the surface electron states were observed for the Si-terminated surface of GdRu2Si2, where the topmost Gd layer is hidden by the Si–Ru–Si surface trilayer block. In our study, this surface will be the main focus.
First, our analysis of GdRu2Si2 will be focused on the characterization of the electronic structure in the paramagnetic phase, which shows a good agreement between experiment and theory. In the AFM ordered phase, our ARPES measurements reveal a pseudogap which is seen as a kind of a “sickle-moon” feature near the Fermi level (EF) in the structure of the bulk projected bands taken along the ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) –
–![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) direction of the surface Brillouin zone (BZ). Our theoretical analysis indicates that this feature is directly linked with the formation of a spiral structure of Gd 4f moments within the basal plane. Furthermore, the agreement between the ARPES-derived electronic structure and the one based on DFT calculations enables a comprehensive characterization of bulk and surface states, including their properties and orbital compositions. Here, we found that in contrast to earlier predictions the FS near the Γ-point does not exhibit nesting properties. Instead, nesting occurs near the corner of the BZ with a vector along [100]([010]), which connects kz-dispersion-less states with essential Gd d contribution. The size of the nesting vector fits well to describe the properties of the spiral magnetic structure. This indicates that the electronic states in this BZ region are most essential for a RKKY-mediated coupling of Gd 4f moments via Gd d states at the Fermi level. These results are in line with those recently reported in ref. 14. Lastly, we discuss the results of a theoretical modelling with stretching of the unit cell within the basal plane, analysing the modifications of the corner-nested region of the BZ. The obtained results allow us to propose the most plausible scenario for the emergence of the helical AFM phase in GdRu2Si2.
direction of the surface Brillouin zone (BZ). Our theoretical analysis indicates that this feature is directly linked with the formation of a spiral structure of Gd 4f moments within the basal plane. Furthermore, the agreement between the ARPES-derived electronic structure and the one based on DFT calculations enables a comprehensive characterization of bulk and surface states, including their properties and orbital compositions. Here, we found that in contrast to earlier predictions the FS near the Γ-point does not exhibit nesting properties. Instead, nesting occurs near the corner of the BZ with a vector along [100]([010]), which connects kz-dispersion-less states with essential Gd d contribution. The size of the nesting vector fits well to describe the properties of the spiral magnetic structure. This indicates that the electronic states in this BZ region are most essential for a RKKY-mediated coupling of Gd 4f moments via Gd d states at the Fermi level. These results are in line with those recently reported in ref. 14. Lastly, we discuss the results of a theoretical modelling with stretching of the unit cell within the basal plane, analysing the modifications of the corner-nested region of the BZ. The obtained results allow us to propose the most plausible scenario for the emergence of the helical AFM phase in GdRu2Si2.
2 Results
2.1 Calculated electronic structure of the paramagnetic GdRu2Si2 (001) surfaces
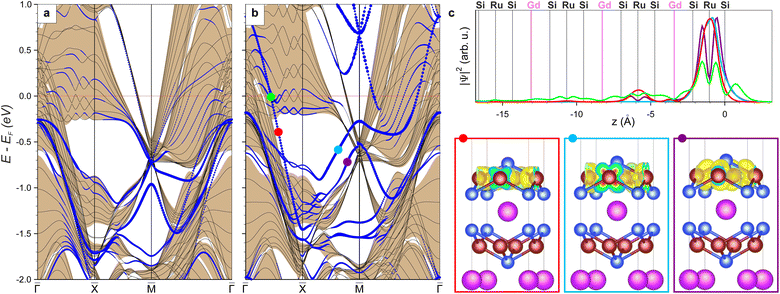
We begin with a theoretical analysis of the surface electronic structure of the paramagnetic GdRu2Si2 obtained from ab initio DFT calculations. Similar to many other RET2Si2 materials,15 the predominant cleavage plane of a single crystal of GdRu2Si2 (001) is between Si- and Gd-atomic layers,11 leaving behind either a Si- or Gd-terminated surface. Therefore, to determine surface electron states and separate them from bulk electron bands, an asymmetric slab terminated by Si and Gd on either side was used allowing us to trace bulk-like bands, band gaps as well as surface-related states for both terminations. Thus, in this way, theoretically derived electron states for the Gd and Si surfaces of GdRu2Si2 (001) are shown in Fig. 1a and b, respectively. The surface electron states are shown in blue overlaid with the tan-colored kz-projected bulk states. The latter are obtained by projecting the bulk electron bands of the paramagnetic spectrum (see ESI, Section A†) onto the (001) surface, perpendicular to the z direction. The strongly localized Gd 4f orbitals were treated as a frozen core approximation.Both surfaces reveal a number of surface-related electron states. While some of them overlap strongly with the bulk bands, others reside within large projected band gaps. As we will see further, the theoretically derived spectral patterns agree well with those obtained in the momentum-resolved photoemission experiment. The in-gap surface states seen for the Si surface are almost fully localized within the topmost trilayer Si–Ru–Si block and are mainly composed of Ru 4d orbitals with different symmetries (lower panel of Fig. 1c). We mark a few examples of such states by using the colored (red, light blue and purple) circles in Fig. 1b and present their density profiles |Ψ2| in the upper panel of Fig. 1c. The lack of their overlap with the Gd layer makes these surface states rather insensitive to the stabilization of a spin-spiral magnetic order in the AFM phase of GdRu2Si2. However, other surface states considerably overlap with the bulk projected states and penetrate into their continuum. Hence, it is reasonable to anticipate that those states, like the one labelled in green situated between ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) and
and ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) close to the EF, should get modified when the exotic magnetic order on the Gd sublattice sets in. We will discuss the sensitivity of these states to the magnetic order in detail later in comparison with our experimental ARPES results.
close to the EF, should get modified when the exotic magnetic order on the Gd sublattice sets in. We will discuss the sensitivity of these states to the magnetic order in detail later in comparison with our experimental ARPES results.
2.2 ARPES
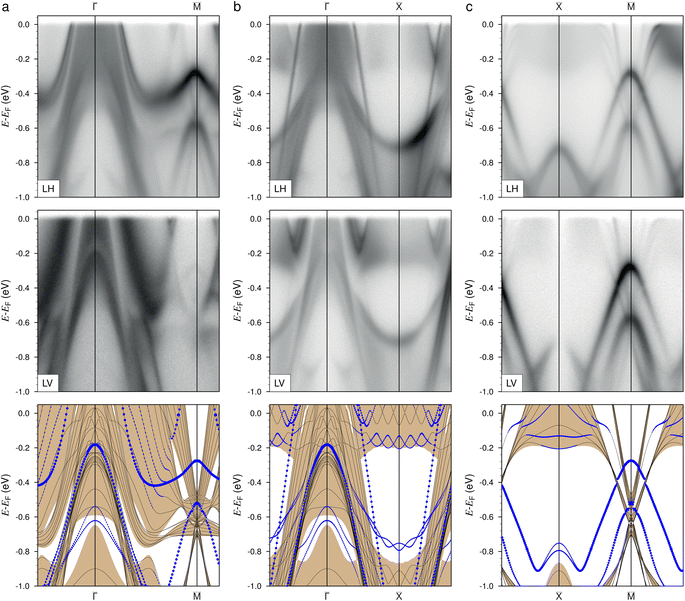
To comprehensively explore the complex electronic structure of paramagnetic GdRu2Si2, we performed detailed ARPES measurements and compared the obtained results with those derived from our first principles calculations. In the first two rows of Fig. 2, we present the experimentally derived electronic structure taken from the Si-termination of a freshly cleaved GdRu2Si2 single crystal at 50 K along the![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) ,
, ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) and
and ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) –
–![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) directions of the surface BZ. The ARPES pattern was obtained at a photon energy of 50 eV with horizontal (LH) and vertical (LV) polarizations shown in the first and second row of Fig. 2, respectively. In the third row, we display the kz-projected bulk states along the same high-symmetry directions as in the experiment. Similar to Fig. 1, the tan-colored bulk states are overlaid with the slab-derived surface and surface-resonant states depicted in blue for the paramagnetic, Si-terminated GdRu2Si2 (001) surface.
directions of the surface BZ. The ARPES pattern was obtained at a photon energy of 50 eV with horizontal (LH) and vertical (LV) polarizations shown in the first and second row of Fig. 2, respectively. In the third row, we display the kz-projected bulk states along the same high-symmetry directions as in the experiment. Similar to Fig. 1, the tan-colored bulk states are overlaid with the slab-derived surface and surface-resonant states depicted in blue for the paramagnetic, Si-terminated GdRu2Si2 (001) surface.
The good agreement between experiment and theory allows us to easily identify and differentiate between the surface-related bands and the bulk-projected electronic structure in the ARPES patterns. This gives us a good starting point for the subsequent evaluation of how these states evolve when the peculiar spiral magnetic order of Gd 4f moments stabilizes in the AFM phase of GdRu2Si2. First, we will focus on the bulk states close to EF, their properties and orbital composition. Based on ref. 10, special attention will be paid to the areas near high-symmetry points and, in particular, the center of the BZ. Secondly, we will investigate the behavior of the surface-related states which overlap with the bulk states (labelled in green in Fig. 1b). Lastly, we can then discuss and analyse the whole Fermi surface as derived from ARPES measurements and DFT calculations.
2.3 Effect of the spin spiral on the electronic structure of GdRu2Si2
After cooling the GdRu2Si2 sample below the spiral-AFM phase transition to a temperature of 19 K, we found that the ARPES patterns did not reveal large modifications of the electronic structure. Nevertheless, a number of subtle changes could be observed. One of the most visible changes is the emergence of a narrow bright feature (“pseudogap”) in the bulk-projected spectrum, which can be seen as a kind of “sickle-moon” feature near EF. This feature is presented in Fig. 3a in the ARPES data taken along the![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) –
–![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) direction of the surface BZ with the “pseudogap” being indicated by a blue arrow. For comparison, in Fig. 3b we show the projection of the calculated bulk states for the paramagnetic phase onto the same
direction of the surface BZ with the “pseudogap” being indicated by a blue arrow. For comparison, in Fig. 3b we show the projection of the calculated bulk states for the paramagnetic phase onto the same ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) –
–![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) direction of the surface BZ. This clearly demonstrates a homogeneous density of bulk states near the
direction of the surface BZ. This clearly demonstrates a homogeneous density of bulk states near the ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) point in the discussed vicinity of the Fermi level. Having observed the ARPES-derived signature of the spiral-AFM order of the Gd 4f moments, our next aim was a corresponding appropriate theoretical modeling. Being able to compute and achieve good agreement with the experiment would allow us to understand the ground state on the basis of first principles calculations the reasons for such a peculiar magnetic order in the AFM phase of GdRu2Si2.
point in the discussed vicinity of the Fermi level. Having observed the ARPES-derived signature of the spiral-AFM order of the Gd 4f moments, our next aim was a corresponding appropriate theoretical modeling. Being able to compute and achieve good agreement with the experiment would allow us to understand the ground state on the basis of first principles calculations the reasons for such a peculiar magnetic order in the AFM phase of GdRu2Si2.
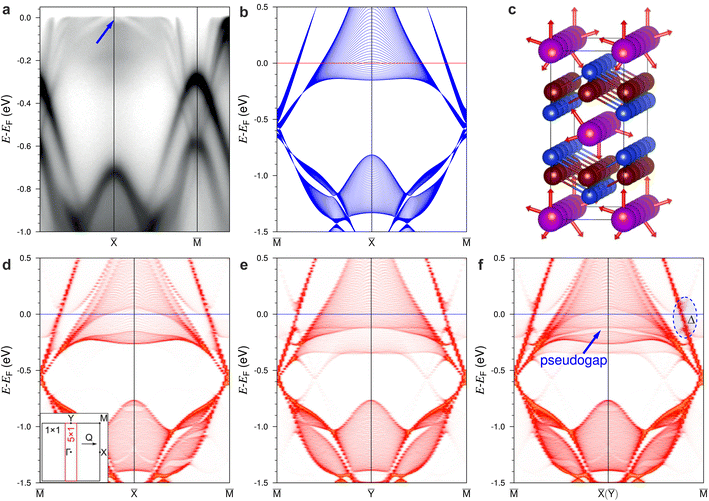 | ||
Fig. 3 (a) Low-temperature ARPES data taken at 19 K along the ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) – –![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) – –![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) direction of the surface BZ in the AFM phase of GdRu2Si2. A blue arrow indicates the “sickle-moon” shaped pseudogap which appears in the bulk continuum states below TN. (b) Bulk electron states for paramagnetic GdRu2Si2 computed along the direction of the surface BZ in the AFM phase of GdRu2Si2. A blue arrow indicates the “sickle-moon” shaped pseudogap which appears in the bulk continuum states below TN. (b) Bulk electron states for paramagnetic GdRu2Si2 computed along the ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) – –![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) – –![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) direction and projected along kz. (c) The 5 × 1 × 1 supercell of GdRu2Si2 in the ordered phase where the Gd 4f moments are rotated within the yz-plane with a propagation vector of Q = 0.2 (in units 2π/a), along the x direction. (d) The bulk-projected electron structure of the spiral-AFM ordered GdRu2Si2 calculated within the 5 × 1 supercell with the spin spiral propagated along x unfolded onto the direction and projected along kz. (c) The 5 × 1 × 1 supercell of GdRu2Si2 in the ordered phase where the Gd 4f moments are rotated within the yz-plane with a propagation vector of Q = 0.2 (in units 2π/a), along the x direction. (d) The bulk-projected electron structure of the spiral-AFM ordered GdRu2Si2 calculated within the 5 × 1 supercell with the spin spiral propagated along x unfolded onto the ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) – –![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) – –![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) direction of the original 1 × 1 BZ. The inset shows the 1 × 1 (black) and 5 × 1 (red) BZs projected on (001). (e) The same as in panel (d) but for the direction of the original 1 × 1 BZ. The inset shows the 1 × 1 (black) and 5 × 1 (red) BZs projected on (001). (e) The same as in panel (d) but for the ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) –Ȳ– –Ȳ–![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) direction. (f) Superposition of the bulk projected electron states shown in panels (d) and (e). The meaning of the highlighted Δ will be discussed later (see Fig. 6d and e). direction. (f) Superposition of the bulk projected electron states shown in panels (d) and (e). The meaning of the highlighted Δ will be discussed later (see Fig. 6d and e). | ||
To simulate the spiral-AFM phase, we constructed a bulk 5 × 1 × 1 supercell, in which the spin spiral corresponding to Q = 0.20 (in units 2π/a) is defined as schematically shown in Fig. 3c. In this supercell the spin magnetic moment on each subsequent Gd plane along the x direction is rotated by ϕ = 40°. Note that it is slightly different from ϕ = 36° which corresponds to the experimentally derived incommensurate spiral propagation vector of Q = 0.22(2π/a).4 As we will see below, the small difference of Q = 0.20 from Q = 0.22 is not essential for the following analysis. The kz-projected bulk band structure unfolded onto the ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) –
–![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) direction (perpendicular to the spin spiral propagation, Fig. 3d) of the original 1 × 1 BZ shows that the main changes compared to the paramagnetic case occur close to the
direction (perpendicular to the spin spiral propagation, Fig. 3d) of the original 1 × 1 BZ shows that the main changes compared to the paramagnetic case occur close to the ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) point and near EF where density of bulk states becomes inhomogeneous, having an increased density at the very bottom and a reduced one at EF. The spectrum calculated along the
point and near EF where density of bulk states becomes inhomogeneous, having an increased density at the very bottom and a reduced one at EF. The spectrum calculated along the ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) –Ȳ–
–Ȳ–![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) direction (along the spin spiral propagation, Fig. 3e) also demonstrates its main changes at Ȳ (which is equivalent to
direction (along the spin spiral propagation, Fig. 3e) also demonstrates its main changes at Ȳ (which is equivalent to ![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) in the original 1 × 1 BZ in the paramagnetic case); however, the reduced density can be found here at lower energies while the increased density lies at higher energies closer to EF. Taking into account that the magnetic spirals along x and y directions must be equiprobable due to symmetry reasons, and that ARPES should acquire a mixture of magnetic domains with different spiral directions, the superposition of the spectra calculated for directions along and perpendicular to the magnetic spiral is presented in Fig. 3f, which shows the presence of a pseudogap in the continuum of the bulk states below EF (a narrow area of a reduced density of the bulk states). This is in excellent agreement with the experiment. Thus, this observation serves as direct photoemission evidence for the presence of the spiral-AFM phase in the low-temperature limit.
in the original 1 × 1 BZ in the paramagnetic case); however, the reduced density can be found here at lower energies while the increased density lies at higher energies closer to EF. Taking into account that the magnetic spirals along x and y directions must be equiprobable due to symmetry reasons, and that ARPES should acquire a mixture of magnetic domains with different spiral directions, the superposition of the spectra calculated for directions along and perpendicular to the magnetic spiral is presented in Fig. 3f, which shows the presence of a pseudogap in the continuum of the bulk states below EF (a narrow area of a reduced density of the bulk states). This is in excellent agreement with the experiment. Thus, this observation serves as direct photoemission evidence for the presence of the spiral-AFM phase in the low-temperature limit.
2.4 Electronic structure of the Si-terminated surface of spiral-AFM GdRu2Si2
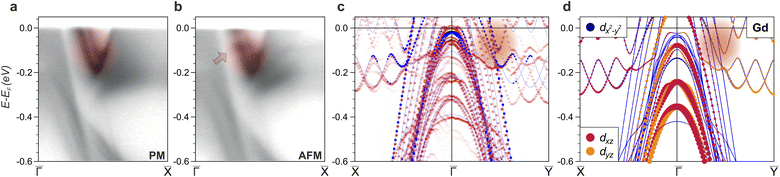
Next we explore how the spin-spiral AFM order is reflected in the properties of the surface electron states, in particular for the Si-terminated surface of GdRu2Si2. Fig. 4a and b show the ARPES data taken along the![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) direction in the paramagnetic and spiral-AFM phase, respectively.
direction in the paramagnetic and spiral-AFM phase, respectively.
The spectra reveal prominent bands located in the energy range of −0.2 eV up to and crossing EF. Our calculations allow us to identify these bands as surface resonances, which penetrate deep into the material overlapping with the bulk band states (Fig. 1b and c, marked in green). Below the spiral-AFM transition these states exhibit notable changes. Particularly, in the paramagnetic phase the photoemission intensity of these states varies smoothly along the spectral structure, while at low temperature an oscillatory modification of the intensity distribution can be observed. To reveal the origin of this intensity redistribution, we expand the 5 × 1 supercell bulk calculation to a supercell slab calculation for the spiral-AFM phase. Fig. 4c shows the spectrum of the Si-terminated (001) surface of GdRu2Si2 unfolded onto the ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) (along the propagation of the spin spiral) and the
(along the propagation of the spin spiral) and the ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –Ȳ (perpendicular to the spin spiral) directions of the 1 × 1 BZ. Compared to the band structure of the paramagnetic phase (blue lines in Fig. 4c), both electronic structures almost coincide for the direction of the spiral propagation (
–Ȳ (perpendicular to the spin spiral) directions of the 1 × 1 BZ. Compared to the band structure of the paramagnetic phase (blue lines in Fig. 4c), both electronic structures almost coincide for the direction of the spiral propagation (![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) ), whereas in the perpendicular direction (
), whereas in the perpendicular direction (![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –Ȳ) the band distribution considerably changes.
–Ȳ) the band distribution considerably changes.
Near EF, the Gd 5d contribution to these states is almost equally determined by dx2−y2 and dxz(dyz) orbitals (see Fig. 4d). With the spin spiral propagating along the x direction, the spin rotates in the yz-plane and clearly affects the dyz orbitals but seems to have no influence on the dxz orbital. Hence, when the surface resonant state penetrates into these bulk states, where the weight of Gd 5d orbitals is considerable, it should experience the effect of spiral-AFM order in the bulk. Again, due to the mixture of x- and y-spiral magnetic domains, in ARPES this modification manifests itself in both −![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) –
–![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) and
and ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) directions leading to a subtle but clearly notable effect.
directions leading to a subtle but clearly notable effect.
2.5 Fermi surface and possible origin of the spin spiral
In ref. 10, the properties of the three-dimensional FS were intensively discussed. There, it was argued that nesting properties found in the center of the BZ are the key points for the formation of the spin-spiral magnetic order in the AFM phase of GdRu2Si2 and define the skyrmion physics in this material. To explore this point in detail, we present the calculated FS for the paramagnetic phase of GdRu2Si2 (Fig. 5a and b) with the experimentally derived FS from ARPES measurements (part of Fig. 5c). To simplify the analysis, we combine the ARPES data with the calculated band structure projected along the kz direction onto the (001) surface as shown in the left side of Fig. 5c. Based on this comparison, we see a close to perfect agreement between experiment and theory, indicating that our calculations reliably describe all bands in the vicinity of EF. The four bands which form the FS are labeled as 1–4.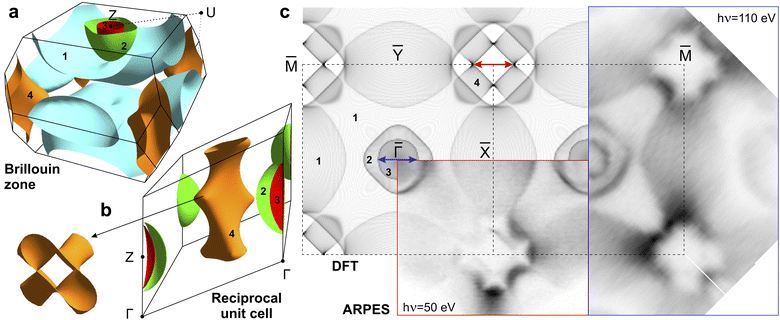 | ||
| Fig. 5 Fermi surface (FS) for GdRu2Si2 in the paramagnetic phase presented for the first BZ (a) and for the reciprocal lattice unit (b). In panel (b), band 1 is not shown for simplicity; the left outset shows the top perspective view of band 4. (c) Projection of the calculated FS on the (001) surface. The red and blue framed parts show the ARPES-derived FS maps obtained with photon energies of hν = 50 eV and hν = 110 eV, respectively. The red arrow indicates the proposed nested region in the 3D FS while the blue arrow shows the region near the center of the BZ, which was discussed in ref. 10. | ||
In ref. 10 it was proposed that band 3, which is highlighted in red in Fig. 5a and b, is mostly barrel-shaped and therefore provides good nesting conditions where the diameter of the barrel fits well to the wave number Q = 0.22(2π/a) of the spin spiral. We indicate the respective region by using a blue arrow around the ![[capital Gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0ba.gif) point in Fig. 5c. However, based on our DFT results, we offer a different interpretation. First, we find that band 3 differs considerably more from a barrel-like shape than previously proposed and instead looks more ellipsoidal with a significant kz dispersion centered around the Z-point of the BZ. In this regard, our calculations suggest that there are no strong nesting properties for this band.
point in Fig. 5c. However, based on our DFT results, we offer a different interpretation. First, we find that band 3 differs considerably more from a barrel-like shape than previously proposed and instead looks more ellipsoidal with a significant kz dispersion centered around the Z-point of the BZ. In this regard, our calculations suggest that there are no strong nesting properties for this band.
On the other hand, our calculations indicate that band 4, which is situated around the ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) point, reveals nesting properties. This band shows almost no kz-dispersion in the
point, reveals nesting properties. This band shows almost no kz-dispersion in the ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) lateral direction. To better visualize this fact, we present in the outset of Fig. 5b the discussed band 4 from the top perspective. In this top view projection, it is clearly visible that the
lateral direction. To better visualize this fact, we present in the outset of Fig. 5b the discussed band 4 from the top perspective. In this top view projection, it is clearly visible that the ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) –
–![[X with combining macron]](https://www.rsc.org/images/entities/i_char_0058_0304.gif) cuts have no kz dispersion since they meet in single points. This nesting vector is highlighted by a red arrow at the corner of BZ in the FS shown in Fig. 5c. Furthermore, it is important to note that these points have a high density of states and possess a strong contribution from Gd 5d states, which are essential for the exchange interaction and will be discussed next.
cuts have no kz dispersion since they meet in single points. This nesting vector is highlighted by a red arrow at the corner of BZ in the FS shown in Fig. 5c. Furthermore, it is important to note that these points have a high density of states and possess a strong contribution from Gd 5d states, which are essential for the exchange interaction and will be discussed next.
To understand the relation between the spiral period and the features of the band structure, we analyze the orbital composition of the bands 1–4 at EF. As illustrated in Fig. 6a, bands 1 and especially 4 have strong contributions from Gd 5d states, while bands 2 and 3 are mainly composed of Ru states with only a small contribution from Gd states (see detailed analysis of the orbital composition in ESI, Section A†). This allows us to conclude that band 4 not only fulfills the nesting condition, but also has the most significant admixture from Gd 5d-states, and thus is the most likely origin for the peculiar magnetic structure of GdRu2Si2.
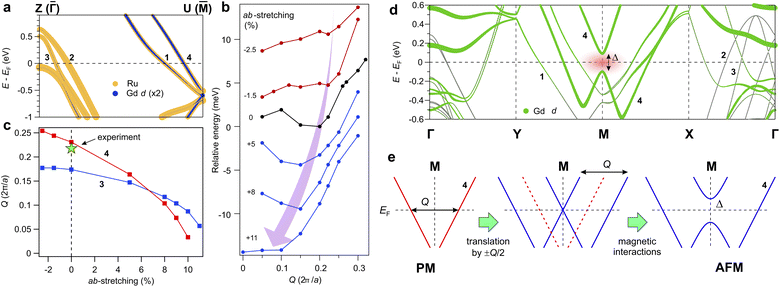 | ||
Fig. 6 (a) Electron band structure near the EF calculated along the Z–U direction of the BZ (see Fig. 5a); the size of the colored symbols represents the weight of all states of Ru and 5d states of Gd, where the weight for the latter is multiplied by a factor of two. (b) The evolution of the total energy of the tetragonal cell as a function of the spin-spiral wave number Q. The cartoon arrow indicates how the minimum of total energy evolves upon lattice stretching. (c) Calculated evolution of the lengths of the red and blue 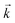 vectors shown in Fig. 5c for bands 3 and 4 at EF. (d) Band structure of the spiral-AFM state with Q = 0.22(2π/a), calculated using the tetragonal unit cell (the spiral vector vectors shown in Fig. 5c for bands 3 and 4 at EF. (d) Band structure of the spiral-AFM state with Q = 0.22(2π/a), calculated using the tetragonal unit cell (the spiral vector 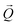 is parallel to the Γ–X and Y–X directions). (e) Schematic illustration of the formation of band 4 in the direction along the spiral. is parallel to the Γ–X and Y–X directions). (e) Schematic illustration of the formation of band 4 in the direction along the spiral. | ||
Next, we will test the relation between the nesting vector and the spiral period. For this, we performed a series of ab initio calculations where the crystal lattice was stretched or compressed within the ab plane. Such deformations may lead to significant changes in the band structure as well as the spiral period, providing a possibility to explore the relationship between them. Fig. 6b demonstrates how the total energy evolves as a function of the spiral wave number Q for different values of stretching. Note that the shown curves are arbitrarily shifted in the energy scale for better comparison. For the case of the equilibrium lattice (black curve), the energy minimum is located at Q = 0.20, which is very close to the experimental value of Q = 0.22. Upon expansion of the lattice the minimum shifts to lower Q values until the system becomes ferromagnetic which happens at 11% of stretching. Upon compression of the lattice the global energy minimum turns to a local minimum, which shifts towards higher Q values and almost disappears at 2.5% of compression.
We can now determine how the band structure evolves under lattice deformation. For this, we will look in detail at the two most interesting bands, namely band 4, which we propose to be responsible for the spiral-AFM order since it exhibits strong nesting properties, and band 3, which was proposed in ref. 10. What we observe as a result of stretching is that band 4 shifts up in energy, while band 3 gets shifted down to lower energies. In both cases the related nesting vector becomes shorter, which is illustrated in Fig. 6c where the lengths of the proposed nesting vectors are shown as a function of stretching. The nesting vectors were measured along the Z–U direction of the BZ shown in Fig. 5a. Our results indicate a qualitative correlation between the length of the nesting vectors and the wave number of the spiral. Upon stretching, the nesting vector gets shorter for both bands 3 and 4, while in the same way the spiral wave number becomes smaller. However, the experimental value of the wave number Q = 0.22(2π/a) for the equilibrium lattice fits better to the nesting vector of band 4 than that of band 3 (experimental value shown as a green star in Fig. 6c). Additionally, the stretching value at which band 4 shifts above EF coincides with the stretching value of 11% where the calculated Q becomes zero. Thus, in agreement with our previous statements about band 4, this band seems to be the probable candidate for the formation of the spin spiral via d–f hybridization.
To understand further the role of band 4 in the stabilization of the spiral state, we present the theoretical band structure of the spiral-AFM state in Fig. 6d. These calculations were performed using the so-called generalized Bloch conditions. In this formalism, for the case of a rotating spin, the wave function has the form of the following spinor
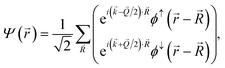 | (1) |
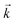 gains an additional quantity of
gains an additional quantity of 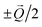 that results in the respective translation of bands in the reciprocal space. This is schematically illustrated in Fig. 6e. In the paramagnetic phase, the states of band 4 at EF at the two sides of the M point are separated by the nesting vector
that results in the respective translation of bands in the reciprocal space. This is schematically illustrated in Fig. 6e. In the paramagnetic phase, the states of band 4 at EF at the two sides of the M point are separated by the nesting vector 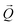 which coincides with the spin spiral wave vector. Upon translation by
which coincides with the spin spiral wave vector. Upon translation by 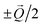 the two sides of the band cross at the M point. The exchange interaction results in the opening of a magnetic gap Δ at the M point. The related decrease in the energy of the occupied states results in stabilization of the spiral. At the same time, bands 2 and 3 remain almost unchanged due to the small contribution of the Gd 5d orbitals.
the two sides of the band cross at the M point. The exchange interaction results in the opening of a magnetic gap Δ at the M point. The related decrease in the energy of the occupied states results in stabilization of the spiral. At the same time, bands 2 and 3 remain almost unchanged due to the small contribution of the Gd 5d orbitals.
It is worth noting that an experimental observation of the predicted magnetic gap with ARPES is very challenging. First, the band structure in Fig. 6d cannot be directly compared with ARPES data because of the redefinition of the quasimomentum 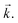 The experimental measurements have to be compared with the unfolded bands from the supercell calculations shown in Fig. 3f. One can see that the discussed gap Δ in band 4 is present in the supercell calculation, although it appears shifted by
The experimental measurements have to be compared with the unfolded bands from the supercell calculations shown in Fig. 3f. One can see that the discussed gap Δ in band 4 is present in the supercell calculation, although it appears shifted by 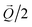 from the
from the ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) point. Moreover, it does not look like a real gap since it is formed only between the low-intensity replica bands which cannot be reliably detected in our ARPES data. Instead, we were able to detect the aforementioned pseudogap formed in band 1 that is of magnetic origin and thus indicates the formation of the spiral-AFM state.
point. Moreover, it does not look like a real gap since it is formed only between the low-intensity replica bands which cannot be reliably detected in our ARPES data. Instead, we were able to detect the aforementioned pseudogap formed in band 1 that is of magnetic origin and thus indicates the formation of the spiral-AFM state.
2.6 Magnetic interaction
To understand in more detail the nature of magnetic interaction in the system, we calculated exchange coupling constants from first-principles calculations applying the magnetic force theorem as it is implemented within the multiple scattering theory.16,17 The exchange coupling constants, Jij represent the direct and indirect overlap between wave functions participating in the magnetic interaction between atoms i and j. A full Fourier transform,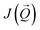 is proportional to the total energy, whose minimum, i.e. the ground state, corresponds to the maximum of
is proportional to the total energy, whose minimum, i.e. the ground state, corresponds to the maximum of 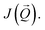 To determine the ground state,
To determine the ground state, 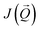 was computed along high symmetry directions of the BZ using various density functional approximations. The HSE06 hybrid functional is the best approach for describing the magnetic bulk band structure of GdRu2Si2 (see the discussion in ESI, Section A†). Unfortunately, this method is not yet implemented within the multiple scattering theory. Therefore, we used a GGA + U functional to obtain exchange coupling constants. It should be noted that previously reported first-principles studies of this system were carried out using a bare GGA functional.10,12 Unfortunately, the GGA + U approximation cannot fully reproduce the band structure obtained with the HSE06 hybrid functional. Nevertheless, the Gd 4f states are pushed down in energy within this approach and the band structure in the Fermi level vicinity with the exception of several features looks similar to that obtained within the HSE06 functional (ESI, Section A†).
was computed along high symmetry directions of the BZ using various density functional approximations. The HSE06 hybrid functional is the best approach for describing the magnetic bulk band structure of GdRu2Si2 (see the discussion in ESI, Section A†). Unfortunately, this method is not yet implemented within the multiple scattering theory. Therefore, we used a GGA + U functional to obtain exchange coupling constants. It should be noted that previously reported first-principles studies of this system were carried out using a bare GGA functional.10,12 Unfortunately, the GGA + U approximation cannot fully reproduce the band structure obtained with the HSE06 hybrid functional. Nevertheless, the Gd 4f states are pushed down in energy within this approach and the band structure in the Fermi level vicinity with the exception of several features looks similar to that obtained within the HSE06 functional (ESI, Section A†).
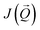 calculated along the high symmetry directions show three peaks: one is between Γ and X, the second is between X and M, and the third is between Γ and Z (see ESI, Section B and Fig. S2a†). The global maximum, which corresponds to the total energy minimum, determines a spiral magnetic structure within the Gd layer. The Q vector of this maximum is in a good agreement with our calculations within generalized Bloch conditions and experiments. However the presence of two other peaks with similar magnitudes indicates a competition between three various magnetic orders: two intra- and one inter-layer spirals. We point out here that the results might be not fully correct, since the approximation used does not provide a full agreement with the HSE06 hybrid functional calculations. Another approach we have tried, a self-interaction correction (SIC) method, delivers a similar picture (see ESI, Fig. S2b†), although
calculated along the high symmetry directions show three peaks: one is between Γ and X, the second is between X and M, and the third is between Γ and Z (see ESI, Section B and Fig. S2a†). The global maximum, which corresponds to the total energy minimum, determines a spiral magnetic structure within the Gd layer. The Q vector of this maximum is in a good agreement with our calculations within generalized Bloch conditions and experiments. However the presence of two other peaks with similar magnitudes indicates a competition between three various magnetic orders: two intra- and one inter-layer spirals. We point out here that the results might be not fully correct, since the approximation used does not provide a full agreement with the HSE06 hybrid functional calculations. Another approach we have tried, a self-interaction correction (SIC) method, delivers a similar picture (see ESI, Fig. S2b†), although 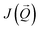 is about two times smaller than that obtained within the GGA + U approach. The latter fact is because the SIC method usually overestimates the localization of SI-corrected orbitals. However, both approaches predict a similar magnetic structure.
is about two times smaller than that obtained within the GGA + U approach. The latter fact is because the SIC method usually overestimates the localization of SI-corrected orbitals. However, both approaches predict a similar magnetic structure.
The next question arises about the origin of spirals in GdRu2Si2. A structurally similar system, GdRh2Si2, exhibits a robust layerwise antiferromagnetic ordering with a relatively high Néel temperature of 107 K.18 We think there are two main reasons for such a strong difference between these two AFM materials. First, Rh has one 4d electron more than Ru. Therefore, Rh–Si hybridization is essentially distinct from that between Ru and Si atoms. The additional Rh 4d electron weakens the Gd–Si coupling and Gd has more 5d electrons for the intra-layer magnetic coupling between the Gd 4f local moments, which results in a strong ferromagnetic order within the Gd layers. Indeed, the magnetic interaction between the nearest Gd moments in GdRh2Si2 is much stronger than that in GdRu2Si2: 5.1 meV vs. 0.7 meV, while the inter-layer magnetic coupling in both systems is of a similar magnitude. The second reason for the stronger intra-layer coupling in GdRh2Si2 is the slight difference in the lattice parameters in these materials. Lanthanides are well known for a sensitive dependence of their magnetic properties on the structure. Thus, a strong reduction of the intra-layer magnetic interaction in GdRu2Si2 leads to magnetic frustration and spiral formation in this material. Our analysis indicates that the magnetic interaction between Gd 4f local moments is mainly mediated by conduction electrons. Although our ARPES experiments and DFT calculations do not confirm the nesting found in ref. 10, the magnitude of the respective vector which was discussed in ref. 10 is similar to that of the nesting vector at the corner of the BZ which was found in our study. Combining our finding and the discussion made in ref. 10 we conclude that the RKKY interaction is the dominant mechanism for helical magnetism in this system. The helical magnetic order arises due to a competition of in-plane and out-of-plane antiferromagnetic interactions, which could lead to a skyrmion formation without a strong spin–orbit coupling in the system.19
3 Conclusions
In summary, applying momentum-resolved photoemission measurements and ab initio DFT calculations, we explored the bulk and surface electronic structure of the helical antiferromagnetic material GdRu2Si2. The ARPES-derived data, taken for GdRu2Si2 in the paramagnetic phase, reveal sharp patterns containing the surface and bulk-projected electron states which allow the exploration of how these states are modified upon the PM–AFM phase transition. Comparison of the ARPES data taken from the AFM phase of GdRu2Si2 with the results of ab initio DFT calculations allowed us to identify the bulk-related states which are intrinsic for the spiral order of 4f moments. Namely, we detected a pseudogap within the bulk continuum states close to EF which is seen as a “sickle-moon” shaped spectral feature. A rather good agreement of experimental and theoretical results allowed us to characterize in detail the properties and orbital composition of the Fermi surface of GdRu2Si2. Note that our results do not confirm the prediction of the existence of the nested three-dimensional barrel-shaped FS near the Γ-point which was reported recently.10 Instead, we found a nested FS sheet at the corner of the BZ, supporting the recent results reported in ref. 14. Our theoretical analysis suggests that this feature possesses a strong admixture of 5d-states of Gd. We show that stretching or compressing the crystal lattice within the ab plane essentially influences the Gd 5d states nesting vector and consequently changes the period of the magnetic spiral in the Gd 4f spin channel. The obtained results allow us to conclude that the RKKY interaction is the most plausible mechanism which defines the spiral magnetic order in GdRu2Si2 and is responsible for the emergence of skyrmions in this material. Although in GdRu2Si2 the skyrmion phase emerged at rather low temperature the deep understanding of the underlying skyrmion physics in the centrosymmetric systems may help to predict novel materials where the nano-size skyrmions may appear at essentially higher temperature, and perhaps even at room temperature. Essentially, in this centrosymmetric type of compound with the ThCr2Si2 structure type, multiple magnetic systems with d- and f-magnetic moments exist, partially with rather high ordering temperatures (for a review see M. Shatruk20). In particular, in the discussed class of materials there are some antiferromagnets, like CeCo2P2 with a rather high temperature of the magnetic order (TN = 440 K).21,22 Since magnetism in most of the rare earth compounds with a centrosymmetric crystal structure is mainly driven by the RKKY interaction, these systems can be promising to develop magnetic skyrmions without a strong Dzyaloshinskii–Moriya interaction.4 Methods
Single crystals of GdRu2Si2 were grown from indium flux using high purity starting materials Gd (99.9%, EvoChem), Ru (99.95%, EvoChem), Si (99.9999%, Wacker) and In (99.9995%, Schuckard) and a modified Bridgman method as described in ref. 23. Gd, Ru, Si, and In were used in the ratio of Gd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ru
Ru![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Si
Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) In = 1
In = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 24. The crystal growth was performed in a vertical furnace (GERO HTRV 70-250/18) (Tmax = 1600 °C), with a slow cooling period with a rate of 1–4 K h−1 down to 850 °C followed by fast cooling to room temperature with 300 K h−1. The crystals were separated from the flux by etching in hydrochloric acid. We obtained platelet-shaped crystals with typical dimensions of 3 mm × 3 mm and a thickness of 50–100 μm.
24. The crystal growth was performed in a vertical furnace (GERO HTRV 70-250/18) (Tmax = 1600 °C), with a slow cooling period with a rate of 1–4 K h−1 down to 850 °C followed by fast cooling to room temperature with 300 K h−1. The crystals were separated from the flux by etching in hydrochloric acid. We obtained platelet-shaped crystals with typical dimensions of 3 mm × 3 mm and a thickness of 50–100 μm.
ARPES experiments were performed at the ULTRA endstation of the SIS-X09LA beamline, Swiss Light Source, and at the BLOCH beamline, MAX-IV laboratory in Lund. Both ARPES endstations were equipped with a Scienta R4000 analyser. The single-crystal samples of GdRu2Si2 were cleaved in situ under ultra-high vacuum conditions better than 10−10 mbar.
Electronic structure calculations were carried out within the density functional theory using the projector augmented-wave (PAW) method24,25 as implemented in the VASP code.26 The exchange–correlation energy was treated using the generalized gradient approximation27 for most calculations. The Gd potential when strongly localized valence 4f electrons are treated as core states was used for non-magnetic calculations. The standard Gd potential in which the 4f electrons are treated as valence states was used for spin-polarized calculations of magnetic phases. To correctly describe the highly correlated Gd 4f electrons, we include the correlation effects within both the HSE06 screened hybrid functional28 and the GGA + U method.29 The values of U and J parameters were taken to be 6.7 eV and 0.7 eV, respectively, which give a good agreement with the HSE06 band structure. Additionally we use the Slater-type DFT-1/2 self-energy correction method30,31 with a partially (quaternary) ionized silicon potential for better describing hybridization between deep Gd f and Si pxy orbitals. To simulate the spiral magnetic state we consider spin spirals with two different methods. The first is to explicitly construct the spiral in a supercell using noncollinear magnetic moments in the yz-plane, perpendicular to the spin spiral propagation vector (along the x direction) and the second approach is to use a spin spiral method to simulate spirals in the unit cell with generalized Bloch conditions.32 In the first case we use BandUP code33,34 to unfold the supercell band structure onto the 1 × 1 BZ. Additional band structure calculations for the paramagnetic phase (Fig. 5c) were performed with the Gd 4f states in the core using FPLO-18.00-52 code (improved version of the original FPLO code by K. Koepernik and H. Eschrig35). The results are in perfect agreement with those obtained with the VASP code. All presented ball-and-stick atomic structures were visualized with VESTA.36 The Fermi surface was determined on a dense 27 × 27 × 23 k-point mesh and visualized by using FermiSurfer.37
Author contributions
S. V. E. – conceptualization, formal analysis, methodology, project administration, writing – original draft, writing – review & editing; D. G. – investigation, data curation, formal analysis; G. P. – investigation, data curation, formal analysis; A. K. – investigation, data curation, formal analysis; K. A. – investigation, data curation, formal analysis; A. V. T. – investigation, data curation, formal analysis; S. S. – investigation, data curation, formal analysis; K. K. – investigation, resources, data curation, formal analysis; E. V. C. – investigation, funding acquisition; V. S. S. – investigation, funding acquisition; A. E. – investigation, software, writing – review & editing; C. K. – conceptualization, investigation, resources, project administration, writing – review & editing, funding acquisition; D. Y. U. – conceptualization, investigation, project administration, writing – original draft, writing – review & editing; D. V. V. – conceptualization, investigation, project administration, writing – original draft, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the German Research Foundation (DFG) for the support through the grants no. KR3831/5-1, no. LA655/20-1, SFB1143 (project no. 247310070), and TRR288 (no. 422213477, project no. A03). The density functional theory calculations were supported by the Government research assignment for ISPMS SB RAS (project FWRW-2022-0001). E. V. C. acknowledges support from Saint Petersburg State University (project ID no. 94031444). V. S. S. and D. Y. U. work was partially supported by the Ministry of Science and Higher Education of the Russian Federation (no. FSMG-2023-0014) and RSF 23-72-30004. The calculations were partially performed using the equipment of the Shared Resource Center “Far Eastern Computing Resource” of IACP FEB RAS (https://cc.dvo.ru) and Joint Supercomputer Center of the Russian Academy of Sciences (https://rscgroup.ru/en/project/jscc). We also thank the Paul Scherrer Institut, Villigen, Switzerland, for the allocation of ARPES experiments at the ULTRA endstation of the SIS-X09LA beamline of the Swiss Light Source. We acknowledge MAX IV Laboratory for experimental time on beamline BLOCH under proposal 20211066. Research conducted at MAX IV, a Swedish national user facility, was supported by the Swedish Research Council under contract 2018-07152, the Swedish Governmental Agency for Innovation Systems under contract 2018-04969, and Formas under contract 2019-0249.References
- M. Ślaski and A. Szytuła, J. Less-Common Met., 1982, 87, L1–L3 CrossRef.
- K. Hiebl, C. Horvath, P. Rogl and M. J. Sienko, J. Magn. Magn. Mater., 1983, 37, 287–296 CrossRef CAS.
- M. Ślaski, A. Szytuła, J. Leciejewicz and A. Zygmunt, J. Magn. Magn. Mater., 1984, 46, 114–122 CrossRef.
- N. D. Khanh, T. Nakajima, X. Yu, S. Gao, K. Shibata, M. Hirschberger, Y. Yamasaki, H. Sagayama, H. Nakao, L. Peng, K. Nakajima, T. Takagi, R. Arima, Y. Tokura and S. Seki, Nat. Nanotechnol., 2020, 15, 444–449 CrossRef CAS PubMed.
- A. Garnier, D. Gignoux, N. Iwata, D. Schmitt, T. Shigeoka and F. Zhang, J. Magn. Magn. Mater., 1995, 140–144, 899–900 CrossRef CAS.
- M. Rotter, M. Doerr, M. Zschintzsch, A. Lindbaum, H. Sassik and G. Behr, J. Magn. Magn. Mater., 2007, 310, 1383–1385 CrossRef CAS.
- T. Samanta, I. Das and S. Banerjee, J. Appl. Phys., 2008, 104, 123901 CrossRef.
- A. Garnier, D. Gignoux, D. Schmitt and T. Shigeoka, Phys. B, 1996, 222, 80–86 CrossRef CAS.
- J. Prokleška, J. Vejpravová and V. Sechovský, J. Phys.: Conf. Ser., 2006, 51, 127 CrossRef.
- J. Bouaziz, E. Mendive-Tapia, S. Blügel and J. B. Staunton, Phys. Rev. Lett., 2022, 128, 157206 CrossRef CAS PubMed.
- Y. Yasui, C. J. Butler, N. D. Khanh, S. Hayami, T. Nomoto, T. Hanaguri, Y. Motome, R. Arita, T. Arima, Y. Tokura and S. Seki, Nat. Commun., 2020, 11, 5925 CrossRef CAS PubMed.
- T. Nomoto, T. Koretsune and R. Arita, Phys. Rev. Lett., 2020, 125, 117204 CrossRef CAS PubMed.
- S. Hayami and Y. Motome, Phys. Rev. B, 2021, 103, 024439 CrossRef CAS.
- N. Matsuyama, T. Nomura, S. Imajo, T. Nomoto, R. Arita, K. Sudo, M. Kimata, N. D. Khanh, R. Takagi, Y. Tokura, S. Seki, K. Kindo and Y. Kohama, Phys. Rev. B, 2023, 107, 104421 CrossRef CAS.
- G. Bihlmayer, P. Noel, D. V. Vyalikh, E. V. Chulkov and A. Manchon, Nat. Rev. Phys., 2022, 4, 642 CrossRef.
- A. Liechtenstein, M. Katsnelson, V. Antropov and V. Gubanov, J. Magn. Magn. Mater., 1987, 67, 65–74 CrossRef CAS.
- M. Hoffmann, A. Ernst, W. Hergert, V. N. Antonov, W. A. Adeagbo, R. M. Geilhufe and H. B. Hamed, Phys. Status Solidi B, 2020, 257, 1900671 CrossRef CAS.
- M. Güttler, A. Generalov, M. M. Otrokov, K. Kummer, K. Kliemt, A. Fedorov, A. Chikina, S. Danzenbächer, S. Schulz, E. V. Chulkov, Y. M. Koroteev, N. Caroca-Canales, M. Shi, M. Radovic, C. Geibel, C. Laubschat, P. Dudin, T. K. Kim, M. Hoesch, C. Krellner and D. V. Vyalikh, Sci. Rep., 2016, 6, 24254 CrossRef PubMed.
- T. Okubo, S. Chung and H. Kawamura, Phys. Rev. Lett., 2012, 108, 017206 CrossRef PubMed.
- M. Shatruk, J. Solid State Chem., 2019, 272, 198–209 CrossRef CAS.
- G. Poelchen, I. P. Rusinov, S. Schulz, M. Güttler, M. Mende, A. Generalov, D. Y. Usachov, S. Danzenbächer, J. Hellwig, M. Peters, K. Kliemt, Y. Kucherenko, V. N. Antonov, C. Laubschat, E. V. Chulkov, A. Ernst, K. Kummer, C. Krellner and D. V. Vyalikh, ACS Nano, 2022, 16, 3573–3581 CrossRef CAS PubMed.
- G. Poelchen, J. Hellwig, M. Peters, D. Y. Usachov, K. Kliemt, C. Laubschat, P. M. Echenique, E. V. Chulkov, C. Krellner, S. S. P. Parkin, D. V. Vyalikh, A. Ernst and K. Kummer, Nat. Commun., 2023, 14, 5422 CrossRef CAS PubMed.
- K. Kliemt, M. Peters, F. Feldmann, A. Kraiker, D.-M. Tran, S. Rongstock, J. Hellwig, S. Witt, M. Bolte and C. Krellner, Cryst. Res. Technol., 2020, 55, 1900116 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954 CrossRef CAS PubMed.
- L. G. Ferreira, M. Marques and L. K. Teles, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 125116 CrossRef.
- L. G. Ferreira, M. Marques and L. K. Teles, AIP Adv., 2011, 1, 032119 CrossRef.
- L. M. Sandratskii, Adv. Phys., 1998, 47, 91–160 CrossRef CAS.
- P. V. C. Medeiros, S. Stafström and J. Björk, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 041407 CrossRef.
- P. V. C. Medeiros, S. S. Tsirkin, S. Stafström and J. Björk, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 041116 CrossRef.
- K. Koepernik and H. Eschrig, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1743–1757 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- M. Kawamura, Comput. Phys. Commun., 2019, 239, 197–203 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details on bulk electronic structure calculations and magnetic interaction. See DOI: https://doi.org/10.1039/d3na00435j |
| This journal is © The Royal Society of Chemistry 2023 |