 Open Access Article
Open Access ArticleMicromagnetic and morphological characterization of heteropolymer human ferritin cores
Thomas
Longo
 a,
Steve
Kim
a,
Steve
Kim
 a,
Ayush K.
Srivastava
a,
Ayush K.
Srivastava
 b,
Lauren
Hurley
a,
Kaixuan
Ji
a,
Arthur J.
Viescas
a,
Nicholas
Flint
b,
Alexandre C.
Foucher
c,
Douglas
Yates
d,
Eric A.
Stach
b,
Lauren
Hurley
a,
Kaixuan
Ji
a,
Arthur J.
Viescas
a,
Nicholas
Flint
b,
Alexandre C.
Foucher
c,
Douglas
Yates
d,
Eric A.
Stach
 c,
Fadi
Bou-Abdallah
c,
Fadi
Bou-Abdallah
 *b and
Georgia C.
Papaefthymiou
*b and
Georgia C.
Papaefthymiou
 *a
*a
aDepartment of Physics, Villanova University, Villanova, PA, USA. E-mail: gcp@villanova.edu
bDepartment of Chemistry, State University of New York, Potsdam, NY, USA. E-mail: bouabdf@potsdam.edu
cDepartment of Materials Science and Engineering, University of Pennsylvania, Philadelphia, PA, USA
dSingh Center for Nanotechnology, University of Pennsylvania, Philadelphia, PA, USA
First published on 15th November 2022
Abstract
The physical properties of in vitro iron-reconstituted and genetically engineered human heteropolymer ferritins were investigated. High-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM), electron energy-loss spectroscopy (EELS), and 57Fe Mössbauer spectroscopy were employed to ascertain (1) the microstructural, electronic, and micromagnetic properties of the nanosized iron cores, and (2) the effect of the H and L ferritin subunit ratios on these properties. Mössbauer spectroscopic signatures indicate that all iron within the core is in the high spin ferric state. Variable temperature Mössbauer spectroscopy for H-rich (H21/L3) and L-rich (H2/L22) ferritins reconstituted at 1000 57Fe/protein indicates superparamagnetic behavior with blocking temperatures of 19 K and 28 K, while HAADF-STEM measurements give average core diameters of (3.7 ± 0.6) nm and (5.9 ± 1.0) nm, respectively. Most significantly, H-rich proteins reveal elongated, dumbbell, and crescent-shaped cores, while L-rich proteins present spherical cores, pointing to a correlation between core shape and protein shell composition. Assuming an attempt time for spin reversal of τ0 = 10−11 s, the Néel–Brown formula for spin-relaxation time predicts effective magnetic anisotropy energy densities of 6.83 × 104 J m−3 and 2.75 × 104 J m−3 for H-rich and L-rich proteins, respectively, due to differences in surface and shape contributions to magnetic anisotropy in the two heteropolymers. The observed differences in shape, size, and effective magnetic anisotropies of the derived biomineral cores are discussed in terms of the iron nucleation sites within the interior surface of the heteropolymer shells for H-rich and L-rich proteins. Overall, our results imply that site-directed nucleation and core growth within the protein cavity play a determinant role in the resulting core morphology. Our findings have relevance to iron biomineralization processes in nature and the growth of designer's magnetic nanoparticles within recombinant apoferritin nano-templates for nanotechnology.
Introduction
Mammalian ferritins are predominantly hetero-polymeric species consisting of 24 structurally similar, but functionally different subunit types named H (for Heavy) and L (for Light).1 The variability in the composition of heteropolymer ferritins is related to the expressions of H and L subunits,2,3 which co-assemble in various H to L ratios, with tissue specific distribution, to form shell-like protein structures of ∼12 nm outer diameter and ∼8 nm inner cavity diameter, where thousands of iron atoms can be sequestered.1,3–5 The human H-subunit has a dinuclear iron center, known as the ferroxidase center, where fast conversion of Fe2+ to Fe3+ occurs. In contrast, the human L-subunit lacks such a center but provides sites for iron cluster nucleation and iron mineralization due to a higher density of carboxyl groups exposed on the inner cavity surface.1,5–7It is generally accepted that after rapid oxidation of Fe2+ at the ferroxidase centers of H-subunits, the Fe3+ ions migrate to the protein cavity and bind at nucleation sites on the L-subunits where iron cluster nucleation and subsequent growth of the iron biomineral core8–12 is initiated. Even though H-subunits lack such nucleation sites, formation of ferritin iron cores inside H-subunit homopolymers does still occur, presumably assisted by acidic residues within the cavity.1,8,11,13,14 Despite the widespread occurrence of heteropolymer ferritins in tissues of vertebrates, very little is known about the complementary roles that H- and L-subunits play within the protein, due to a lack of availability of recombinant heteropolymer experimental systems. In a groundbreaking study, our research group has successfully engineered a novel ferritin expression system to produce recombinant heteropolymer ferritins with different H/L subunit ratios.15 Our unique plasmid design can be easily tuned to allow the synthesis of a full spectrum of heteropolymer ferritins, from H-rich to L-rich ferritins and any combinations in-between (isoferritins). The two ferritin subunits appear to play complementary ferroxidation and mineralization functions, since different mixture of subunits affects the rate and the amount of iron deposited inside the protein cavity.15
Numerous investigations on the structure and morphology of the iron mineral inside ferritin16–23 have been reported, but a systematic study of the iron cores in human heteropolymer ferritins has not, yet, been performed. Natural ferritins with different H to L subunit ratios associated with different organs correlate with different rates of ferritin biomineral formation, and likely, with biomineral order, degree of crystallinity, and iron turnover.3,24,25 In theory, fewer ferroxidase centers decrease the rate of iron oxidation, and therefore the rate of iron deposition and core formation and should lead to more crystalline iron cores. However, studies have reported that the low percentage of catalytic sites in L-rich ferritins (such as liver ferritin) contributed to a less crystalline and low mineral order iron core.26 Interestingly, ferritins which had amorphous iron cores when isolated from natural sources formed crystalline ferrihydrite cores upon reconstitution, that is when the iron core is reconstituted in vitro using native ferritin stripped of iron.3,27–29 Once oxidized, ferric ions are stored inside the ferritin cavity as an inorganic hydrated iron oxide ferrihydrite30,31 (5Fe2O3·9H2O), the morphology of which has been typically investigated by electron microscopy.16–20 It was reported that the iron nanoparticles formed inside recombinant homopolymer human H-ferritin (HuHF) are not discrete and exhibited poor contrast, whereas those inside human L-ferritin (HuLF) homopolymers exhibited discrete, electron-dense cores with well-defined spherical shapes.19 These differences between natural ferritins and recombinant homopolymer ferritins suggest that the morphology of the ferritin iron core depends on the protein shell composition, and the number of nucleation sites present on the protein.19
Ferrihydrite occurs in nature as a nano-phase material with no bulk counterpart.31 The iron ions are in the high spin ferric state (Fe3+, S = 5/2) octahedrally (∼80%) and/or tetrahedrally (∼20%) coordinated to oxygen ions and super-exchange-coupled to produce an antiferromagnetically ordered material of various degrees of crystallinity, referred to as 2-line and 6-line ferrihydrite, based on XRD structure determination.32 The antiferromagnetically ordered ferritin core possesses a net magnetic moment due to spin non-compensation at the surface and the possible presence of defects within the interior of the core, as originally proposed by Néel for single-magnetic-domain antiferromagnetic particles.33–35 The magnetic moment of the ferritin core of horse spleen ferritin has been measured to be only 300 μB,36 where μB is the Bohr magneton. The process of biomineralization in ferritin has been exploited in materials science to produce monodispersed metal and metal-oxide magnetic nanoparticles by biomimetic synthesis within protein cages and viral capsids.37,38 The first magnetic material synthesized within horse spleen apoferritin cages was magnetite39 or maghemite, both of which are ferrimagnetically ordered, and therefore exhibit high magnetization. This material has properly been coined “magnetoferritin” and has found multiple biomedical applications.40 The availability of recombinant human heteropolymer apoferritin nanocages of various L/H ratios, made possible via our novel ferritin expression system in E. coli, afford materials scientists additional protein nano-templates to produce biocompatible magnetic nanoparticles within the confined space of their cavities. Biocompatible magnetic nanoparticles have important applications in nanomedicine and nanobiotechnology for MRI imaging enhancement, magnetically targeted drug delivery, non-viral cell transfection, magnetic hyperthermia, and cell separation applications.41,42 In many medical and biotechnological applications, the magnetization and magnetic relaxation properties of the resulting nanoparticles are of interest, as they must be tailored to specific applications. Mössbauer spectroscopy has uniquely contributed to elucidating the electronic and micromagnetic properties of ferritin, magnetoferritin, and other apoferritin derived magnetic nanoparticles,43–48 while bioanalytical applications of Mössbauer spectroscopy have been recently reviewed.49
Herewith, we present high resolution images obtained via high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) of recombinant human H-rich heteropolymer (H21/L3) ferritin, and recombinant human L-rich heteropolymer (H2/L22) ferritin reconstituted to 1000 Fe/protein, to better understand the effect of protein composition on the shape and crystallinity of the core. We complement these measurements with EELS and 57Fe Mössbauer spectroscopy45 to ascertain the iron oxidation state in the biomineral cores and probe their micromagnetic properties. We hypothesize that differences in structural details observed by high resolution electron microscopy ought to be reflected in the micromagnetic properties of the cores, which determine their superparamagnetic properties.42 Manipulation of the magnetic relaxation properties of biocompatible magnetic nanoparticles is very desirable for applications in nanomedicine. As expected, the results point to correlations between the microstructural morphology of the derived iron cores and their micromagnetic properties.
Electron microscopy
Fig. 1 compares representative STEM images obtained for the L-rich and H-rich proteins reconstituted at 1000 Fe/protein. Distinctly different core shapes are observed in the two ferritin heteropolymers. The L-rich proteins promote the formation of spherical core shapes (Fig. 1A). In contrast, the H-rich proteins (Fig. 1B) present non-spherical cores; various shapes are seen dominated by elongated, dumbbell, and crescent-shaped cores. Furthermore, the H-rich proteins show a higher degree of crystallinity, as evidenced by the more clearly resolved lattice fringes, which indicated increased crystalline order. Fig. 2 gives the histograms of the particle size distributions, assuming spherical cores. For the L-rich ferritin cores, the estimated average core diameter, based on 100 particles count and Gaussian particle-size distribution was 〈dL-rich〉 = (5.9 ± 1.0) nm, while that for the H-rich proteins was 〈dH-rich〉 = (3.7 ± 0.6) nm (Fig. 2). This indicates that under identical iron reconstitution conditions, the L-rich heteropolymers promote the formation of larger and more spherical iron cores compared to H-rich heteropolymers. | ||
| Fig. 2 Histograms of the particle size distributions of the ferrihydrite mineral cores grown in (A) L-rich heteropolymers and (B) H-rich heteropolymers, reconstituted to 1000 Fe/protein. | ||
As expressed in E. coli, purified recombinant heteropolymer ferritins contained a small iron core of ≈100 Fe/protein as determined by an iron reductive mobilization assay.50 To further probe the observed difference in the morphology of the cores, and to image the initial stages of iron nucleation, we obtained HAADF-STEM micrographs of the heteropolymer H-rich and L-rich ferritins containing these small and nascent iron cores. The images are shown in Fig. 3 and the histograms of the corresponding size distributions are shown in Fig. 4. It is noted that the distinct difference in morphology has an early onset as it is already apparent in the nascent cores of mean average diameters of 〈dL-rich〉 = (2.9 ± 1.0) nm and 〈dH-rich〉 = (1.8 ± 0.5) nm. This early difference in iron accumulation and core morphology appears to be caused by site-directed iron cluster nucleation51,52 at specific nucleation sites on the interior cavity surface of the heteropolymers. The presence of nucleation sites on the interior surface of L-rich proteins produce a crown-looking nascent core, as shown in Fig. 3A. The nucleated iron ions appear to grow from the surface of the interior cavity while the center is void of iron. Upon further core growth, iron nucleation expands towards the central region to produce the spherical shapes observed in Fig. 1A. Our data corroborate a previously proposed iron-core-growth mechanism influenced by the L/H ratio in heteropolymer proteins.19 The image shown in Fig. 3A also resembles that of hepatic mineral core obtained from thin sections of a liver biopsy18 from a patient with hereditary haemochromatosis. It is well known that hepatic ferritin is an L-rich ferritin. In contrast, the nascent mineral core for the H-rich protein is smaller in size and appears to grow from a single nucleation site (Fig. 3B), suggesting a role for the ferritin shell and/or subunit composition as a template for core morphology.
 | ||
| Fig. 4 Histograms of the particle size distributions of the ferrihydrite mineral cores grown in (A) L-rich heteropolymers and (B) H-rich heteropolymers, containing ∼100 Fe/protein. | ||
Electron energy-loss spectroscopy (EELS) was also performed on the H-rich and L-rich samples shown in Fig. 5. The O K edge shows 3 distinctive peaks at 529 eV, 540 eV and 564 eV loss. The shape of the O K edges combined with the ratio of the L3/L2 peaks for Fe are consistent with iron in the ferric state.53,54 This agrees with the Mössbauer results given in the following section.
Mössbauer spectroscopy
Fig. 6 and 7 present selected Mössbauer spectra of L-rich and H-rich proteins, respectively, fit to the core/shell model of the ferrihydrite mineral core of ferritin.55 This model treats the core as the superposition of two phases; an interior antiferromagnetically spin-ordered ferrihydrite phase (core) surrounded by a spin disordered phase (shell) on the surface of the mineral core. At room temperature, both samples present a simple Mössbauer quadrupolar absorption at the central region of the velocity axis range. As the temperature is lowered the spectra become complex, broaden, and eventually split into a six-line magnetic hyperfine absorption spectrum, extending over the full range of the velocity axis. This temperature spectral profile is typical of an ensemble of magnetically ordered, small magnetic particles undergoing superparamagnetic relaxation processes relative to the uniaxial magnetic anisotropy axis of the particle.56 | ||
| Fig. 6 Selected Mössbauer spectra for the L-rich heteropolymer ferritin reconstituted at 1000 57Fe/protein at various temperatures fitted to the core/shell model of the ferritin biomineral core (see site legend). Selected values of fitted parameters are given in Table 1. | ||
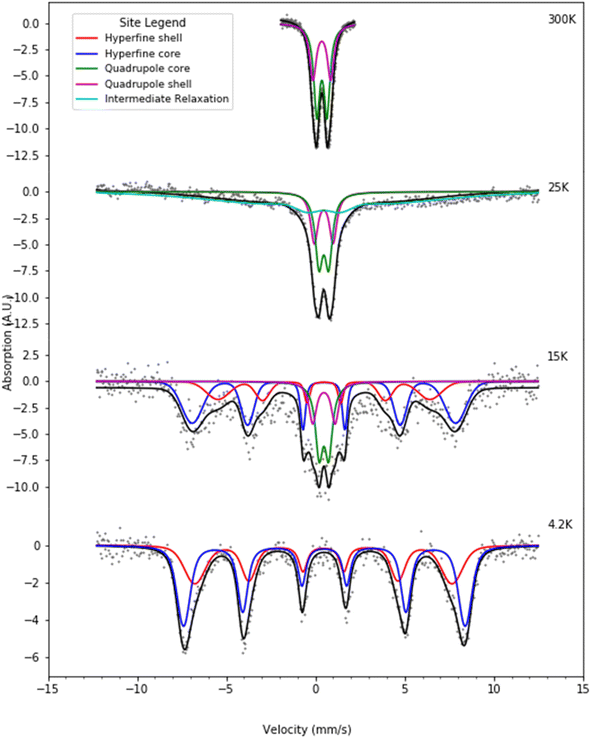 | ||
| Fig. 7 Selected Mössbauer spectra for the H-rich heteropolymer ferritin reconstituted at 1000 57Fe/protein at various temperatures fitted to the core/shell model of the ferritin biomineral core (see site legend). Selected values of fitted parameters are given in Table 2. | ||
At room temperature Mössbauer absorption spectra were fit to the superposition of two quadrupole doublet distributions, corresponding to the ordered interior core phase (green trace) and the disordered shell phase on the surface (purple trace), giving the fitted parameters of the average isomer shift (δ) and average quadrupole splitting (ΔEq) for each phase, tabulated in Table 1 for the L-rich proteins, and Table 2 for the H-rich proteins. It is seen that at room temperature all phases share the same isomer shift δ ≈ 0.36 mm s−1, which indicates that iron is in the ferric high spin (Fe3+, S = 5/2) state. The EELS spectra also indicated iron in the Fe3+ state. The smaller quadrupole splitting values ΔEq ≈ (0.50–0.57) mm s−1 are associated with interior iron atoms, and are consistent with higher coordination symmetry, while the larger values of quadrupole splitting ΔEq ≈ (0.87–0.99) mm s−1 are associated with lower coordination symmetry of iron ions on/or close to the surface (shell), where the ion coordination symmetry gets increasingly distorted as one approaches the surface. This is due to the interruption of the crystallographic order at the surface of the ferrihydrite biomineral core, or the core/protein interface. Thus, the average quadrupole splitting of the outer iron ions on the shell (or surface) are consistently larger compared to those in the interior of the core. At room temperature, for the L-rich protein 60% of the absorption area is associated with iron ions on the shell (Table 1) with distorted coordination symmetry, while for the H-rich proteins only 40% of sites are distorted (Table 2). This is consistent with a higher crystallinity for the H-rich cores compared to the L-rich cores.
| T (K) | Site | δ (mm s−1) | ΔEq (mm s−1) | H hf (kOe) | Area (%) | Core or shell |
|---|---|---|---|---|---|---|
| a Sites 1 and 2 are associated with quadrupolar spectra (green and purple traces in Fig. 6). The reported parameters correspond to the average values of fitted quadrupole distributions. Sites 3 and 4 are associated with magnetic hyperfine spectra (blue and red traces in Fig. 6). The reported parameters correspond to the average values of fitted hyperfine field distributions. Estimated uncertainties: δ (±0.02 mm s−1), ΔEq (±0.04 mm s−1), Hhf (±2 kOe), area (±3%). | ||||||
| 300 | 1 | 0.37 | 0.50 | 0 | 39.8 | Core |
| 2 | 0.36 | 0.87 | 0 | 60.2 | Shell | |
| 25 | 1 | 0.49 | 0.46 | 0 | 23.5 | Core |
| 2 | 0.49 | 0.98 | 0 | 25.8 | Shell | |
| 3 | 0.49 | 0 | 484.2 | 19.1 | Core | |
| 4 | 0.49 | 0 | 434.2 | 31.7 | Shell | |
| 4.2 | 3 | 0.51 | 0 | 495.5 | 43.6 | Core |
| 4 | 0.46 | 0 | 461.6 | 56.4 | Shell | |
| T (K) | Site | δ (mm s−1) | ΔEq (mm s−1) | H hf (kOe) | Area (%) | Core or shell |
|---|---|---|---|---|---|---|
| a Sites 1 and 2 are associated with quadrupolar spectra (green and purple traces in Fig. 7). The reported parameters correspond to the average values of fitted quadrupole distributions. Sites 3 and 4 are associated with magnetic hyperfine spectra (blue and red traces in Fig. 7). The reported parameters correspond to the average values of fitted hyperfine field distributions. Estimated uncertainties: δ (±0.02 mm s−1), ΔEq (±0.04 mm s−1), Hhf (±2 kOe), area (±3%). | ||||||
| 300 | 1 | 0.36 | 0.57 | 0 | 59 | Core |
| 2 | 0.36 | 0.99 | 0 | 41 | Shell | |
| 15 | 1 | 0.48 | 0.54 | 0 | 19.4 | Core |
| 2 | 0.48 | 1.25 | 0 | 11.6 | Shell | |
| 3 | 0.48 | 0 | 484.2 | 46.9 | Core | |
| 4 | 0.48 | 0 | 434.2 | 22.2 | Shell | |
| 4.2 | 3 | 0.50 | 0 | 488.2 | 59.5 | Core |
| 4 | 0.45 | 0 | 446.0 | 40.5 | Shell | |
As the temperature of the sample is decreased, the spectra pass slowly from quadrupolar (two-line) to magnetic (six-line). The smaller particles in the distribution, primarily lying at the core/protein interface, are the last to pass into the magnetic six-line regime, while the larger particles are the first to do so. At room temperature, thermal energy kT prevents observation of the antiferromagnetic order of the ferric ion spins within the crystallographic lattice of the mineral core. The spins fluctuate or flip coherently and continuously between opposite directions of the uniaxial anisotropy axis of the core, with a relaxation time τs shorter than the characteristic measuring time for Mössbauer spectroscopy τMöss, (τs < τMöss, fast relaxation). In this case the nucleus records an average internal magnetic field of zero, resulting in two-line quadrupolar spectra. However, upon lowering the temperature the magnetic order of the mineral is revealed (τs > τMöss, slow relaxation). In this case the electronic spin direction, and therefore the internal magnetic fields, persist long enough for the nucleus to record the internal magnetic field before it flips into the opposite direction. This results in a six-line pattern Zeeman-split Mössbauer spectrum. The characteristic measuring time for Mössbauer, τMöss, is given by the Larmor precession time of the iron nuclear spin in the hyperfine magnetic field experienced by the nucleus, due to correlated electronic spins in its vicinity, τMöss = τL = 10−8 s. Interior core ions experience on average a larger value of hyperfine magnetic field compared to the shell. Thus, the spectra at 4.2 K are also fit with the superposition of two hyperfine field distribution subsites (core/shell). The relative % absorption areas of the average hyperfine fields for the two subsites are preserved, compared to those observed at room temperature for the quadrupolar subsite % absorption areas (Tables 1 and 2). At intermediate temperatures the spectra are more complex due to the superposition of quadrupolar (fast relaxation), magnetic (slow relaxation) and intermediate relaxation (τs ≈ τMöss) processes arising from the presence of particle size distributions (Fig. 2). The temperature spectral profiles observed in Fig. 6 and 7 are characteristic of superparamagnetic particles; they allow estimation the blocking temperature, TB, of the nanoparticle ensembles.
Experimentally, TB is defined as the temperature at which the spectral absorption area is equally divided between quadrupolar and magnetic subsites. We calculate TB (L-rich) = 28 K and TB (H-rich) = 19 K. Theoretically, spin relaxation in magnetically isolated (non-interacting) nanoparticle ensembles, as is the case for ferritin samples, is governed by the Néel–Brown formula:57,58
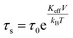 | (1) |
Here, τs is the spin relaxation time, τ0 is an attempt time for spin reversal characteristic of the material, Keff is the effective uniaxial magnetic anisotropy density of the particle, V is its volume, kB is Boltzmann's constant, and T is the temperature in degrees Kelvin. Thus, theoretically, the blocking temperature of a nanoparticle ensemble relative to a measurement technique with characteristic measurement time τm is given by the Néel–Brown formula when τs = τm (10−8 s for Mössbauer spectroscopy). In addition to Mössbauer many other techniques, of different characteristic measuring times, have been applied to the study of the superparamagnetic properties of ferritin, such as AC susceptibility36 with τm = (1 × 10−2 – 3 × 10−4) s and SQUID magnetization measurements59 with τm = (1–100) s. Using the value τ0 = 10−11 s previously reported for ferritin36 based on AC susceptibility measurements, we can use eqn (1) to estimate the effective magnetic anisotropy densities of the two heteropolymer iron cores.
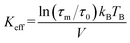 | (2) |
Eqn (2) yields Keff(L-rich) = 2.75 × 104 J m−3 and Keff(H-rich) = 6.83 × 104 J m−3. The value of the magnetic anisotropy density of the H-rich heteropolymer ferritins is larger than that of the L-rich heteropolymer. Considering the different contributions to Keff![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60
60
| Keff = Kmc + Ks + Ksh + Kσ | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 61 and should be more pronounced in the H-rich cores. Ksh is present only in the case of non-spherical particles and must contribute significantly to the H-rich cores, which possess a non-spherical morphology, with some of the cores appearing to have an effective acicularity as large as 1.9. The various contributions to the effective magnetic anisotropy may reinforce or oppose each other, making it difficult to calculate their individual contributions to Keff. The different anchoring topology of the cores onto the cavity surface for the L-rich vs. the H-rich heteropolymers implies different values of Kσ for the two cases. Assuming similar ferrihydrite phases within the cores, contributing similar magneto-crystalline anisotropies, the last three terms must be responsible for the difference in Keff.
61 and should be more pronounced in the H-rich cores. Ksh is present only in the case of non-spherical particles and must contribute significantly to the H-rich cores, which possess a non-spherical morphology, with some of the cores appearing to have an effective acicularity as large as 1.9. The various contributions to the effective magnetic anisotropy may reinforce or oppose each other, making it difficult to calculate their individual contributions to Keff. The different anchoring topology of the cores onto the cavity surface for the L-rich vs. the H-rich heteropolymers implies different values of Kσ for the two cases. Assuming similar ferrihydrite phases within the cores, contributing similar magneto-crystalline anisotropies, the last three terms must be responsible for the difference in Keff.
Conclusion
Nucleation and growth of magnetic nanoparticles by self-assembly within confined spaces of biological templates is a challenging area of research, but of great current interest due to the many applications in nanotechnology and biomedicine.24,42,62–64 In this study we have applied high resolution electron microscopy, electron energy-loss spectroscopy, and Mössbauer spectroscopy to better understand the process of iron biomineralization in two types of recombinant human heteropolymer ferritins (an H-rich and an L-rich), and to characterize the resulting micromagnetic properties of the iron biomineral cores. We observed that data obtained from the three techniques correlate in their findings. Our novel expression system will allow the synthesis of heteropolymer ferritin molecules of any H/L ratio, thus adding to the experimenter's tool kit an additional degree of freedom to probe iron biomineralization in ferritin. The study of these novel experimental systems promises to elucidate the structure–function relationships of different heteropolymer ferritins, which mimic those present in various tissues and organs. Our heteropolymer ferritin templates might be of great interest to nanomedicine and nanobiotechnology and allow researchers the ability to synthesize various metal and metal-oxide nanoparticles, with tailored morphology and magnetic anisotropy densities that dictate the superparamagnetic properties of such nano-systems.Materials and methods
Ferritin expression and purification
Samples were prepared at the State University of New York, Potsdam, NY. The H-rich and L-rich recombinant human heteropolymer ferritins were produced in E. coli Rosetta-gami B strain using a recently engineered pWUR-FtH-TetO-FtL plasmid and different concentrations of inducers.15 Protein purification and quantification was performed according to established protocols using size exclusion chromatography (Akta Go, GE Healthcare), native and SDS-PAGE, and capillary gel electrophoresis (7100 model from Agilent Technologies).15 The concentration of protein was determined using the Micro BCA Protein Assay Kit (Thermo Scientific).Ferritin reconstitution with 57Fe
Ferritin reconstitution was performed at SUNY, Potsdam with 100% iron-57 enriched salts (57FeSO4). The 57FeSO4 solution was prepared by dissolving 5.9 mg of 57Fe metal (95.1 atom%; U.S. Service, Inc. Summit, NJ, USA) in 500 μL of 0.2 M H2SO4 over a period of 3 days, to produce a final solution of 0.207 M FeSO4, pH ∼ 2.0. Three 57Fe injections of 6.5 μL each (1.34 mM or ∼335 Fe/shell), 20 min apart, were made to each ferritin sample (4 μM prepared in an aqueous buffer solution of 200 mM Mops, 50 mM NaCl, pH 7.2) to give a total of 1000 57Fe/shell, equivalent to 0.228 mg of 57Fe. The ferritin samples were then lyophilized (through freeze-drying) and analyzed by Mössbauer spectroscopy.Electron microscopy
HAADF-STEM images at 0.63 nm resolution were obtained at the Singh Center for Nanotechnology at the University of Pennsylvania, Philadelphia, PA using an aberration corrected JEOL NEOARM instrument operating at 200 kV. Electron energy-loss spectroscopy (EELS) was performed with a K2 Summit camera provided by Gatan Inc. For STEM imaging, the camera length was 4 cm with a probe current of 150 pA. For EELS, the camera length was 2 cm, and the probe current was 500 pA.Mössbauer spectroscopy
Mössbauer spectra on freeze-dried, reconstituted heteropolymer ferritins loaded with 1000 57Fe/protein were collected at Villanova University, Villanova, PA with a SEE Co constant acceleration spectrometer, calibrated with a 6 μm thin metal iron foil enriched in 57Fe. All isomer shifts are referenced to metallic iron. Sample temperature variation from 4.2 to 300 K was achieved using a Janis Veri-Temp cryostat by Janis Research Co and a Lake Shore temperature controller. The radioactive source was 57Co deposited in a Rh matrix (E-mail: gamma@seeco.com.us). The source was maintained at room temperature. Spectral fits were performed using the WMOSS fitting software package commercially available from SEE Co, Edina, Minnesota.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Institute of Health Grant R15GM104879 (F. B.-A.), the National Science Foundation, Division of Molecular and Cellular Biosciences (MCB) Award 1934666 (F. B.-A.), and a Cottrell Instrumentation Supplements Award from the Research Corporation for Science Advancement award #27452 (F. B.-A.). The STEM work was carried out in part at the Singh Center for Nanotechnology, which is supported by the NSF National Nanotechnology Coordinated Infrastructure Program under grant NNCI-2025608. Additional support to the Nanoscale Characterization Facility at the Singh Center has been provided by the Laboratory for Research on the Structure of Matter (MRSEC) supported by the National Science Foundation (DMR-1720530).References
- F. Bou-Abdallah, The Iron Redox and Hydrolysis Chemistry of the Ferritins, Biochim. Biophys. Acta, 2010, 1800(8), 719–731 CrossRef CAS PubMed.
- J. Wilkinson IV, X. Di, K. Schonig, J. L. Buss, N. D. Kock, J. M. Cline, T. L. Saunders, H. Bujard, S. V. Torti and F. M. Torti, Tissue-specific expression of ferritin H regulates cellular iron homoeostasis in vivo, Biochem. J., 2006, 395, 501–507 CrossRef PubMed.
- P. M. Harrison and P. Arosio, Ferritins: Molecular Properties, Iron Storage Function and Cellular Regulation, Biochim. Biophys. Acta, 1996, 1275, 161–203 CrossRef PubMed.
- P. Aisen, C. Enns and M. Wessling-Resnick, Chemistry and Biology of Eukaryotic Iron Metabolism, Int. J. Biochem. Cell Biol., 2001, 33, 940–959 CrossRef CAS PubMed.
- E. C. Theil, T. Tosha and R. K. Behera, Solving Biology's Iron Chemistry Problem with Ferritin Protein Nanocages, Acc. Chem. Res., 2016, 49, 784–791 CrossRef CAS PubMed.
- M. Mehlenbacher, M. Poli, P. Arosio, P. Santambrogio, S. Levi, N. D. Chasteen and F. Bou-Abdallah, Iron Oxidation and Core Formation in Recombinant Heteropolymeric Human Ferritins, Biochemistry, 2017, 56, 3900–3912 CrossRef CAS PubMed.
- F. Bou-Abdallah, N. Flint, T. Wilkinson, S. Salim, A. K. Srivastava, M. Poli, P. Arosio and A. Melman, Ferritin Exhibits Michaelis-Menten Behavior with Oxygen but not with Iron During Iron Oxidation and Core Mineralization, Metallomics, 2019, 11(4), 774–783 CrossRef CAS PubMed.
- T. Tosha, M. R. Hasana and E. C. Theil, The ferritin Fe2 site at the diiron catalytic center controls the reaction with O2 in the rapid mineralization pathway, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18182–18187 CrossRef CAS PubMed.
- J. D. Lopez-Castro, J. J. Delgado, J. A. Perez-Omil, N. Galvez, R. Cuesta, R. K. Watt and J. M. Domınguez-Vera, A new approach to the ferritin iron core growth: influence of the H/L ratio on the core shape, Dalton Trans., 2012, 41, 1320–1324 RSC.
- C. Pozzi, S. Ciambellotti, C. Bernacchioni, F. Di Pisa, S. Mangani and P. Turano, Chemistry at the protein–mineral interface in L-ferritin assists the assembly of a functional (μ3-oxo)Tris[(μ2-peroxo)] tri-iron(III) cluster, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 2580–2585 CrossRef CAS PubMed.
- F. Bou-Abdallah, G. Zhao, G. Biasiotto, M. Poli, P. Arosio and N. D. Chasteen, Facilitated diffusion of iron (II) and dioxygen substrates into human H-chain ferritin. A fluorescence and absorbance study employing the ferroxidase center substitution Y34W, J. Am. Chem. Soc., 2008, 130(52), 17801–17811 CrossRef CAS PubMed.
- F. Bou-Abdallah, P. Arosio, P. Santambrogio, X. Yang, C. Janus-Chandler and N. D. Chasteen, Ferrous ion binding to recombinant human H-chain ferritin. An isothermal titration calorimetry study, Biochemistry, 2002, 41(37), 11184–11191 CrossRef CAS PubMed.
- C. Pozzi, P. F. Di, D. Lalli, C. Rosa, E. Theil, P. Turano, S. Mangani, F. Di Pisa, D. Lalli, C. Rosa, E. Theil, P. Turano and S. Mangani, Time-lapse anomalous X-ray diffraction shows how Fe(2+) substrate ions move through ferritin protein nanocages to oxidoreductase sites, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2015, 71, 941–953 CrossRef CAS PubMed.
- C. Pozzi, F. Di Pisa, C. Bernacchioni, S. Ciambellotti, P. Turano and S. Mangani, Iron binding to human heavy-chain ferritin, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2015, 71, 1909–1920 CrossRef CAS PubMed.
- A. K. Srivastava, P. Arosio, M. Poli and F. Bou-Abdallah, A Novel Approach for the Synthesis of Human Heteropolymer Ferritins of Different H to L Subunit Ratios, J. Mol. Biol., 2021, 433(19), 167198 CrossRef CAS PubMed.
- S. Narayanan, E. Firlar, Md G. Rasul, T. Foroozan, N. Farajpour, L. Covnot, R. Shahbazian-Yassar and T. Shokuhfar, On the structure and chemistry of iron oxide cores in human heart and human spleen ferritins using graphene liquid cell electron microscopy, Nanoscale, 2019, 11, 16868 RSC.
- N. Jian, M. Dowle, R. D. Horniblow, C. Tselepis and R. E. Palmer, Morphology of the ferritin iron core by aberration corrected scanning transmission electron microscopy, Nanotechnology, 2016, 27, 46LT02 CrossRef PubMed.
- Y.-H. Pan, K. Sader, J. J. Powell, A. Bleloch, M. Gass, J. Trinick, A. Warley, A. Li, R. Brydson and A. Brown, 3D morphology of the human hepatic ferritin mineral core: new evidence for a subunit structure revealed by single particle analysis of HAADF-STEM images, J. Struct. Biol., 2009, 166, 22–31 CrossRef CAS PubMed.
- J. D. Lopez-Castro, J. J. Delgado, J. A. Perez-Omil, N. Galvez, R. Cuesta, R. K. Watt and J. M. Dominguez-Vera, A new approach to the ferritin iron core growth: influence of the H/L ratio on the core shape, Dalton Trans., 2012, 41, 1320–1324 RSC.
- S. Narayanan, R. Shahbazian-Yassar and T. Shokuhfar, Transmission electron microscopy of the iron oxide core in ferritin proteins: current status and future directions, J. Phys. D: Appl. Phys., 2019, 52, 453001 CrossRef CAS.
- Y. Cai, C. Cao, X. He, C. Yang, L. Tian, R. Zhu and Y. Pan, Enhanced magnetic resonance imaging and staining of cancer cells using ferrimagnetic H-ferritin nanoparticles with increasing core size, Int. J. Nanomed., 2015, 10, 2619–2634 CAS.
- N. Galvez, B. Fernandez, P. Sanchez, R. Cuesta, M. Ceolin, M. Clemente-Leon, S. Trasobares, M. Lopez-Haro, J. J. Calvino, O. Stephan and J. M. Dominguez-Vera, Comparative Structural and Chemical Studies of Ferritin Cores with Gradual Removal of their Iron Contents, J. Am. Chem. Soc., 2008, 130(25), 8062–8068 CrossRef CAS PubMed.
- I. V. Alenkina, M. I. Oshtrakh, Y. V. Klepova, S. M. Dubiel, N. V. Sadovnikov and V. A. Semionkin, Comparative study of the iron cores in human liver ferritin, its pharmaceutical models and ferritin in chicken liver and spleen tissues using Mössbauer spectroscopy with a high velocity resolution, Spectrochim. Acta, Part A, 2013, 100, 88–93 CrossRef CAS PubMed.
- E. C. Theil, Ferritin protein nanocages use ion channels, catalytic sites, and nucleation channels to manage iron/oxygen chemistry, Curr. Opin. Chem. Biol., 2011, 15, 304–311 CrossRef CAS PubMed.
- T. St Pierre, K. C. Tran, J. Webb, D. J. Macey, B. R. Heywood, N. H. Sparks, V. J. Wade, S. Mann and P. Pootrakul, Organ-specific crystalline structures of ferritin cores in beta-thalassemia/hemoglobin E, Biol. Met., 1991, 4(3), 162–165 CrossRef CAS PubMed.
- E. C. Theil, Ferritin: The Protein Nanocage and Iron Biomineral in Health and in Disease, Inorg. Chem., 2013, 52(21), 12223–12233 CrossRef CAS PubMed.
- S. Mann, J. M. Williams, A. Treffry and P. M. Harrison, Reconstituted and native iron-cores of bacterioferritin and ferritin, J. Mol. Biol., 1987, 198, 405–416 CrossRef CAS PubMed.
- V. J. Wade, A. Treffry, J.-P. Laulhere, E. R. Bauminger, M. I. Cleton, S. Mann, J.-F. Briat and P. M. Harrison, Structure and composition of ferritin cores from pea seed (Pisum sativum), Biochim. Biophys. Acta, 1993, 1161, 91–96 CrossRef CAS PubMed.
- S. Mann, J. M. Williams, A. Treffry and P. M. Harrison, Reconstituted and native iron-cores of bacterioferritin and ferritin, J. Mol. Biol., 1988, 198(3), 405–416 CrossRef PubMed.
- F. M. Michel, V. Barrón, J. Torrent, M. P. Morales, J. Serna, J. F. Boily, Q. Liu, A. Ambrosini, A. C. Cismasu and G. E. Brown, Ordered ferrimagnetic form of ferrihydrite reveals links among structure, composition, and magnetism, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 2787–2792 CrossRef CAS PubMed.
- F. M. Michel, L. Ehm, S. M. Antao, P. L. Lee, P. J. Chupas, G. Liu, D. R. Strongin, M. A. A. Schoonen, B. L. Phillips and J. B. Parise, The Structure of Ferrihydrite, A Nanocrystalline Material, Science, 2007, 316(5832), 1726–1729 CrossRef CAS PubMed.
- V. A. Drits, B. A. Sakarov, A. L. Salyn and A. Manceau, Structural Model for Ferrihydrite, Clay Miner., 1993, 28, 185–207 CrossRef CAS.
- L. Néel, Comptes Rendus, Acad. Sci., 1961, 252, 4075–4081 Search PubMed , translated in Selected Works of Louis Néel, ed. N. Kurti, pp. 107–110, Godon and Breach, New York, 1988..
- L. Néel, Comptes Rendus, Acad. Sci., 1961, 253, 203–208 Search PubMed , translated in Selected Works of Louis Néel, ed. N. Kurti, pp. 114–117, Godon and Breach, New York, 1988..
- L. Néel, Comptes Rendus, Acad. Sci., 1961, 253, 1286–1291 Search PubMed , translated in Selected Works of Louis Néel, ed. N. Kurti, pp. 118–121, Godon and Breach, New York, 1988..
- S. H. Kilcoyne and R. Cywinski, Ferritin: a model superparamagnet, J. Magn. Magn. Mater., 1995, 140–144(2), 1466–1467 CrossRef CAS.
- G. C. Papaefthymiou and E. Devlin, Bio-inspired Magnetic Nanoparticles, in Nanobiomaterials, Development and Applications, ed. D. K. Yi and G. C. Papaefthymiou, Series: Advances in Materials Science and Engineering, CRC Press Taylor & Francis Group, 2014, ch. 1, ISBN 13: 978-1-4398-7641-1 Search PubMed.
- G. C. Papaefthymiou, Biogenic and Biomimetic Magnetic Nanoparticles and their Assemblies, in Magnetic Nanoparticle Assemblies, ed. K. N. Trohidou, Pan Stafford Publishing, 2014, ch. 1, ISBN 978-981-4411-96-7 Search PubMed.
- F. C. Meldrum, B. R. Heywood and S. Mann, Magnetoferritin: in vitro synthesis of a novel magnetic protein, Science, 1992, 257, 522–523 CrossRef CAS PubMed.
- L. Le Xue, D. Deng and J. Sun, Magnetoferritin: Process, Prospects, and Their Biomedical Applications, Int. J. Mol. Sci., 2019, 20, 2426 CrossRef PubMed.
- G. Jutz, P. van Rijn, B. Santos Miranda and A. Böker, Ferritin: A Versatile Building Block for Bionanotechnology, Chem. Rev., 2015, 115, 1653–1701 CrossRef CAS PubMed.
- G. C. Papaefthymiou, Nanomagnetism: An Interdisciplinary Approach, CRC Press, Taylor & Francis Group, 2022, ISBN 978-1-439-81846-6 Search PubMed.
- A. A. Kamnev and A. V. Tugarova, Sample treatment in Mössbauer spectroscopy for protein-related analyses: nondestructive possibilities to look inside metal-containing biosystems, Talanta, 2017, 174, 819–837 CrossRef CAS PubMed.
- K. H. Ebrahimi, P.-L. Hagedoorn and W. R. Hagen, Unity in the Biochemistry of the Iron-Storage Proteins Ferritin and Bacterioferritin, Chem. Rev., 2015, 115, 295–326 CrossRef PubMed.
- G. C. Papaefthymiou, The Mössbauer and magnetic properties of ferritin cores, Biochim. Biophys. Acta, 2010, 1800, 886–897 CrossRef CAS PubMed.
- J. D. Wofford, M. Chakrabarti and P. A. Lindahl, Mössbauer Spectra of Mouse Hearts Reveal Age-dependent Changes in Mitochondrial and Ferritin Iron Levels, J. Biol. Chem., 2017, 292, 5546–5554 CrossRef CAS PubMed.
- E. R. Bauminger, A. Treffry, M. A. Quail, Z. Zhao, I. Nowik and P. M. Harrison, Stages in Iron Storage in the Ferritin of Escherichia coli (EcFtnA): Analysis of Mössbauer Spectra Reveals a New Intermediate, Biochemistry, 1999, 38, 7791–7802 CrossRef CAS PubMed.
- G. D. Watt, R. D. Frankel and G. C. Papaefthymiou, Reduction of mammalian ferritin, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 3640–3643 CrossRef CAS PubMed.
- A. A. Kamnev and A. V. Tugarova, Bioanalytical applications of Mössbauer spectroscopy, Russ. Chem. Rev., 2021, 90(11), 141–1453 CrossRef.
- F. Bou-Abdallah, J. J. Paliakkara, G. Melman and A. Melman, Reductive Mobilization of Iron from Intact Ferritin: Mechanisms and Physiological Implication, Pharmaceuticals, 2018, 11(4), 120 CrossRef CAS PubMed.
- B. R. Heywood and S. Mann, Template-directed nucleation and growth of inorganic materials, Adv. Mater., 1994, 6, 9–20 CrossRef CAS.
- P. J. M. Smeets, A. R. Finney, W. J. E. M. Habraken, A. J. M. Sommerdijk and et al., A Classical View on Nonclassical Nucleation, published online, September 5, 2017, https://www.pnas.org/doi/epdf/10.1073/pnas.1700342114 Search PubMed.
- C. Wang, et al., Structure versus properties in α-Fe2O3 nanowires and nanoblades, Nanotechnology, 2016, 27, 035702 CrossRef PubMed.
- H. Tan, J. Verbeeck, A. Abakumov and G. Van Tendeloo, Oxidation state and chemical shift investigation in transition metal oxides by EELS, Ultramicroscopy, 2012, 116, 24–33 CrossRef CAS.
- R. A. Brooks, J. Vymazal, R. B. Goldfarb, J. W. Bulte and P. Aisen, Relaxometry and magnetometry of ferritin, Magn. Reson. Med., 1998, 40, 227–235 CrossRef CAS PubMed.
- G. C. Papaefthymiou, Nanoparticle magnetism, Nano Today, 2009, 4, 438–447 CrossRef CAS.
- L. Néel, Originally published in 1949 as “Théorie du traînage magnétique des ferromagnétiques en grains fins avec application aux terres cuites”, Ann. Geophys., 5, 99–136 Search PubMed , Selected Works of Louis Néel, ed. N. Kurti, Gordon and Breach Science Publishers, 1988, pp. 405–427, ISBN 2-88124-300-2..
- W. F. Brown, Thermal fluctuations of a single-domain particle, Phys. Rev., 1963, 130(5), 1677–1686 CrossRef.
- S. A. Makhlouf, F. T. Parker and A. E. Berkowitz, Magnetic hysteresis anomalies in ferritin, Phys. Rev. B, 1997, 55, R14717(R) CrossRef.
- G. C. Papaefthymiou, Nanomagnetism: An Interdisciplinary Approach, CRC Press, Taylor & Francis Group, 2022, p. 150, ISBN 978-1-439-81846-6 Search PubMed.
- F. Bødker, S. Mørup and S. Lideroth, Surface Effects in Metallic Iron Nanoparticles, Phys. Rev. Lett., 1994, 72, 282 CrossRef PubMed.
- Y. Jin, J. He, K. Fan and X. Yan, Ferritin variants: inspirations for rationally designing protein nanocarriers, Nanoscale, 2019, 11, 12449 RSC.
- B. Issa, I. M. Obaidat, B. A. Albiss and Y. Haik, Magnetic Nanoparticles: Surface Effects and Properties Related to Biomedicine Applications, Int. J. Mol. Sci., 2013, 14, 21266–21305 CrossRef CAS PubMed.
- N. Song, J. Zhang, J. Zhai, J. Hong, C. Yuan and M. Liang, Ferritin: A Multifunctional Nanoplatform for Biological Detection, Imaging Diagnosis, and Drug Delivery, Acc. Chem. Res., 2021, 54(17), 3313–3325 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |



