Open Access Article
Open Access ArticleSingle-bonded nitrogen chain and porous nitrogen layer via Ce–N compounds†
Chi
Ding
 ,
Jianan
Yuan
,
Xiaomeng
Wang
,
Tianheng
Huang
,
Yunlong
Wang
,
Jianan
Yuan
,
Xiaomeng
Wang
,
Tianheng
Huang
,
Yunlong
Wang
 and
Jian
Sun
*
and
Jian
Sun
*
National Laboratory of Solid State Microstructures School of Physics and Collaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing, 210093, China. E-mail: jiansun@nju.edu.cn
First published on 30th March 2023
Abstract
Cerium ions can exist in the trivalent or tetravalent forms such as in Ce2O3 and CeO2, respectively. Therefore, they can provide different chemical environments for stabilizing novel polymeric nitrogen species. This article explored the phase diagram of binary Ce–N compounds under pressures of up to 150 GPa using the crystal structure prediction method MAGUS. In this work, we find that nitrogen atoms can exist in the form of N2, N4, N5, N6, and N8 units. In addition, we identified an infinite helical N4 chain in I41/a CeN4 at about 100 GPa. Differing from the well-known zigzag or armchair nitrogen chains which are mixed with single and double bonds, the helical N4 chain is purely single-bonded. Moreover, it can be quenched to ambient pressure and exhibit excellent denotation properties. We also identified a layered porous nitrogen network in CeN8. After the removal of cerium atoms, the nitrogen network is also dynamically stable in the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase, which has a lower energy than the previously identified P
phase, which has a lower energy than the previously identified P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) phase. For the pentazolate salts, the I4/m CeN10 exhibits ferromagnetism, while the C2 and P21212 CeN15 exhibit anti-ferromagnetism. Overall, the newly discovered Ce–N compounds with polymeric nitrogen exhibit fascinating structural and electronic characteristics, which may lead to potential application in areas such as explosives or catalysis.
phase. For the pentazolate salts, the I4/m CeN10 exhibits ferromagnetism, while the C2 and P21212 CeN15 exhibit anti-ferromagnetism. Overall, the newly discovered Ce–N compounds with polymeric nitrogen exhibit fascinating structural and electronic characteristics, which may lead to potential application in areas such as explosives or catalysis.
Introduction
The element nitrogen plays an important role on earth. It takes the valence configuration of s2p3 which needs three extra electrons to fill the 2p shell. The easiest way is to share six electrons with another nitrogen atom forming the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N triple bond. Alternatively, it can form N–N single bonds with other nitrogen atoms to constitute three-coordinated nitrogen frameworks. Most strikingly, there exists a large energy difference between a single bond (∼160 kJ mol−1) and a triple bond (∼954 kJ mol−1).1 Therefore, a great amount of chemical energy will be released when single-bonded nitrogen compounds are broken down into nitrogen gases, and polymeric nitrogen has potential application values in the energy-storage field or as explosives or propellants.2,3
N triple bond. Alternatively, it can form N–N single bonds with other nitrogen atoms to constitute three-coordinated nitrogen frameworks. Most strikingly, there exists a large energy difference between a single bond (∼160 kJ mol−1) and a triple bond (∼954 kJ mol−1).1 Therefore, a great amount of chemical energy will be released when single-bonded nitrogen compounds are broken down into nitrogen gases, and polymeric nitrogen has potential application values in the energy-storage field or as explosives or propellants.2,3
Researchers have predicted a series of stable nitrogen allotropes under high pressure, from the molecular crystals to the single-bonded cubic-gauge nitrogen in 1992 (cg-N),4 and then to the layered Pba2 phase in 2009,5 a cage-like diamondoid structure in 2012,6 and metallic salts in 2013.7 In addition, some metastable all-nitrogen polymeric structures are also predicted, such as the N6 unit in 2016, N8 in 2014, N10 in 2020,8–10 the chain-like Cmcm phase in 2003 and 2004,11,12 and the layered black phosphorous structure in 2005.13 Because the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N triple bond is one of the strongest chemical bonds on earth, we need a large amount of energy to break it before forming polymerized structures. Extreme conditions such as high pressure and high temperature are inevitable for the experimental synthesis of pure polynitrogen. Although cubic gauge nitrogen (cg-N)4 has been proposed for a long time, the first experimental breakthrough was made by Eremets et al. in 2004.14 They synthesized cg-N under a high pressure of 110 GPa and a high temperature of over 2000 K. After that, people managed to acquire more polymeric nitrogen allotropes under higher pressure, including LP-N in 2014, HLP-N in 2019, and BP-N (black phosphorous phase) in 2020.15–18 However, none of these polymeric phases have been recovered under ambient pressure, which limits their applications.
N triple bond is one of the strongest chemical bonds on earth, we need a large amount of energy to break it before forming polymerized structures. Extreme conditions such as high pressure and high temperature are inevitable for the experimental synthesis of pure polynitrogen. Although cubic gauge nitrogen (cg-N)4 has been proposed for a long time, the first experimental breakthrough was made by Eremets et al. in 2004.14 They synthesized cg-N under a high pressure of 110 GPa and a high temperature of over 2000 K. After that, people managed to acquire more polymeric nitrogen allotropes under higher pressure, including LP-N in 2014, HLP-N in 2019, and BP-N (black phosphorous phase) in 2020.15–18 However, none of these polymeric phases have been recovered under ambient pressure, which limits their applications.
As an alternative way, people began to explore nitrogen-rich compounds that might be stabilized at much lower pressure. Among them, a variety of novel polynitrogen species were identified in alkali and alkaline-earth metal nitrides, for example, the azide N3− unit in XN3 (X = Li, Na, and K),19–21 the pentazolate N5− ring in LiN5 in 2020,22 the cis-N4 unit in Mg2N4 in 2019,23 and the infinite one-dimensional (1D) armchair poly-N4 chain in XN4 (X = Be predicted in 2021, Mg in 2019, etc.).23,24 These poly-nitrogen units are likely to capture extra electrons to fill the nitrogen 2p orbitals, thus serving as anions, while alkali or alkali-earth metals provide extra electrons, thus serving as cations. The alkali-earth metals can also form salts with pentazolates.25–27 The transition metal elements with larger chemical valences and ionic radius can help attract more nitrogen species to reach larger energy densities.2,28–32 For example, trivalent metal pentazolate salts (AlN15, GaN15, YN15, etc.)31 predicted in the year 2020 have a much larger energy density (>4.5 kJ g−1) than monovalent pentazolate salts LiN5 (∼0.5 kJ g−1).22 So are many other transition metal pentazolate salts that possess large energy densities.29 On the other hand, the chain-like polymeric units in these compounds are just one or two-coordinated, and most of the bonds are mixed with single and double bonds. The first purely single-bonded polymeric nitrogen chain was experimentally realized in h-WN6 in the form of an armchair-like N6 ring in 2021.33 It not only possesses very high energy density but also exhibits superhard properties.34 With these concerns, we believe that nitrides with transition metal elements with large chemical valences might capture more nitrogen species or help form novel nitrogen configurations with striking properties.
Cerium is a typical rare-earth element and has the highest abundance among them on earth. It can exist in the trivalent and tetravalent forms just as in Ce2O3 and CeO2, respectively.35 Therefore, cerium might provide different chemical environments for stabilizing novel nitrogen species. However, only cerium pnictides have been widely studied to date,36–39 and other stoichiometries have been paid little attention. In this work, we made full use of crystal structure search methods to explore the phase binary diagram of Ce–N compounds under high pressures of up to 150 GPa. We discovered the common N2, N4, N5, N6, and N8 nitrogen units in these phases. In addition, we identified a novel purely single-bonded nitrogen chain in tetragonal CeN4 that can be quenched to ambient pressure. It possesses a large energy density with detonation pressures close to 100 GPa. In addition, we identified a layered nitrogen configuration in CeN8. After the removal of these cerium atoms, the pure nitrogen framework with the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space group can be recovered under ambient pressure, and it has a lower energy than the previously predicted P
space group can be recovered under ambient pressure, and it has a lower energy than the previously predicted P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) phase which has a different stacking way.
phase which has a different stacking way.
Results and discussion
1. Convex hull and phase diagrams
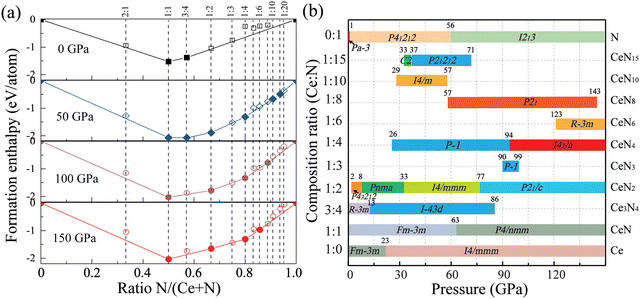
First-principles structure predictions were performed to explore the most stable Ce–N compounds at specific pressures of 0, 50, 100, and 150 GPa. To systematically investigate the potential Ce–N compounds and find novel nitrogen species, we performed fixed-composition crystal structure predictions for nitrogen-rich integer stoichiometries (CeNn and CeN2m with n, m = 1–5). Molecular crystal structure predictions with pentazolates (N5) were then performed for Ce(N5)n with n = 1–4. Moreover, to explore tetravalent cerium nitrides and cerium-rich compounds, we also take into account the stoichiometries of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 and 2
4 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Most of the identified structures are discussed below, and some crystal structures are present in Fig. S1 (ESI†). As a result, Fig. 1(a) displays the final obtained convex hull curves at specific pressures. The curves are plotted according to the formation enthalpies, which are defined as ΔH = [H(CexNy) − xH(Ce) − yH(N)]/(x + y). The enthalpies for pure nitrogen or cerium are calculated with the most stable phases at corresponding pressures. For nitrogen, it is α-N (Pa
1. Most of the identified structures are discussed below, and some crystal structures are present in Fig. S1 (ESI†). As a result, Fig. 1(a) displays the final obtained convex hull curves at specific pressures. The curves are plotted according to the formation enthalpies, which are defined as ΔH = [H(CexNy) − xH(Ce) − yH(N)]/(x + y). The enthalpies for pure nitrogen or cerium are calculated with the most stable phases at corresponding pressures. For nitrogen, it is α-N (Pa![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ), P21/c, P41212, and cg-N (I213) at pressure sequences.40 For cerium, it has been found that cerium transforms from the α phase (space group Fm
), P21/c, P41212, and cg-N (I213) at pressure sequences.40 For cerium, it has been found that cerium transforms from the α phase (space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) to monoclinic α′′ phase (space group C2/m) at about 5 GPa and then to the body-centered-tetragonal (bct) phase (spacegroup I4/mmm) at about 12 GPa with pressure increasing at zero temperature,41,42 and the bct-Ce maintains the most stable phase up to at least 208 GPa.41,43 We then calculated the pressure-dependent enthalpy curves of the α, α′′, and bct phases at the PBE level, as plotted in Fig. S1 (ESI†). The α′′ phase has a similar enthalpy curve as the bct phase. The α phase will transform into the bct phase at about 10 GPa at the PBE level. In addition, the PBE functional underestimates the lattice constants of the α phase (Table S1, ESI†). For the CeN compounds, it has been found that the B1 phase will transform into the B10 phase at about 65 GPa. But the calculated phase transition pressure at the PBE level is only about 45 GPa (see Table S2, ESI†). Due to the f electrons of cerium being very localized, it is necessary to employ the DFT+U method. We further employed the PBE+U method with a series of U values, while keeping the exchange parameters J at 0 eV, by which the phase transition pressure can be raised to a more reasonable value. The PBE+U with U = 3.5 gives a phase transition pressure of 63 GPa, which is close to the experimental value of 65 GPa. In the following, we employed both the PBE and PBE+U method for enthalpy calculations.
m) to monoclinic α′′ phase (space group C2/m) at about 5 GPa and then to the body-centered-tetragonal (bct) phase (spacegroup I4/mmm) at about 12 GPa with pressure increasing at zero temperature,41,42 and the bct-Ce maintains the most stable phase up to at least 208 GPa.41,43 We then calculated the pressure-dependent enthalpy curves of the α, α′′, and bct phases at the PBE level, as plotted in Fig. S1 (ESI†). The α′′ phase has a similar enthalpy curve as the bct phase. The α phase will transform into the bct phase at about 10 GPa at the PBE level. In addition, the PBE functional underestimates the lattice constants of the α phase (Table S1, ESI†). For the CeN compounds, it has been found that the B1 phase will transform into the B10 phase at about 65 GPa. But the calculated phase transition pressure at the PBE level is only about 45 GPa (see Table S2, ESI†). Due to the f electrons of cerium being very localized, it is necessary to employ the DFT+U method. We further employed the PBE+U method with a series of U values, while keeping the exchange parameters J at 0 eV, by which the phase transition pressure can be raised to a more reasonable value. The PBE+U with U = 3.5 gives a phase transition pressure of 63 GPa, which is close to the experimental value of 65 GPa. In the following, we employed both the PBE and PBE+U method for enthalpy calculations.
We then calculated the detailed enthalpies of these stable phases and some metastable structures in the pressure range of 0–150 GPa with an interval of 5 GPa. The detailed phase transition pressure and thermodynamical stability ranges are determined with an accuracy of 1 GPa through the interpolated enthalpy curves as plotted in Fig. S2 (ESI†). Specifically, the cerium mononitride CeN stays thermodynamically stable throughout the pressure range studied. At ambient pressure, it exists in the typical NaCl-type B1 structure with the space-group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. The phases on the convex hull are thermodynamically stable, while those close to the convex hulls which are dynamically stable might also be synthesized in the experiments. We also explored some of these metastable phases with an energy window not larger than those of the convex hulls by 200 meV.44 The calculated lattice parameters and enthalpy results are presented in Tables S3 and S4 (ESI†), respectively. We also present the results for pure nitrogen, cerium, and CeN phases in Table S5 (ESI†). The calculated phonon spectra of these structures are displayed in Fig. S3 and S4 (ESI†), and the phonon spectra of some of the structures quenched to ambient pressure are displayed in Fig. S5 and S6 (ESI†).
m. The phases on the convex hull are thermodynamically stable, while those close to the convex hulls which are dynamically stable might also be synthesized in the experiments. We also explored some of these metastable phases with an energy window not larger than those of the convex hulls by 200 meV.44 The calculated lattice parameters and enthalpy results are presented in Tables S3 and S4 (ESI†), respectively. We also present the results for pure nitrogen, cerium, and CeN phases in Table S5 (ESI†). The calculated phonon spectra of these structures are displayed in Fig. S3 and S4 (ESI†), and the phonon spectra of some of the structures quenched to ambient pressure are displayed in Fig. S5 and S6 (ESI†).
2. The Ce2N compound
Firstly, we looked into the Ce2N compounds. The P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 phase is thermodynamically stable at around 45 GPa at the PBE level, but it is not thermodynamically stable when taking into account the Hubbard U as shown in Fig. S2 (ESI†). However, its enthalpy is higher than that of the convex hull with a value of 80 meV per atom at about 60 GPa at the PBE+U level. The calculated phonon spectrum exhibits no imaginary frequency indicating its dynamical stability. The P
m1 phase is thermodynamically stable at around 45 GPa at the PBE level, but it is not thermodynamically stable when taking into account the Hubbard U as shown in Fig. S2 (ESI†). However, its enthalpy is higher than that of the convex hull with a value of 80 meV per atom at about 60 GPa at the PBE+U level. The calculated phonon spectrum exhibits no imaginary frequency indicating its dynamical stability. The P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 phase is composed of the sandwiched Ce2N layers as shown in Fig. S1 (ESI†). The calculated electronic density of states predicts the P
m1 phase is composed of the sandwiched Ce2N layers as shown in Fig. S1 (ESI†). The calculated electronic density of states predicts the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 phase to be metallic (see the density of states in Fig. S7, ESI†). It has been found that the Ba2N compound also crystalizes in the P
m1 phase to be metallic (see the density of states in Fig. S7, ESI†). It has been found that the Ba2N compound also crystalizes in the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 structure, which is predicted to be an electride with interstitial electrons.25 However, no interstitial electrons are found in the electron localization function (ELF) of the P
m1 structure, which is predicted to be an electride with interstitial electrons.25 However, no interstitial electrons are found in the electron localization function (ELF) of the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 Ce2N phase, and thus it should not be an electride.
m1 Ce2N phase, and thus it should not be an electride.
3. The Ce3N4 compound
Except for the CeN compounds, we discovered another thermodynamically stable compound at ambient pressure with a stoichiometry of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 as shown in Fig. 2. It takes the space group of R
4 as shown in Fig. 2. It takes the space group of R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, and there are two types of layers in the unit cell, the sandwiched CeN2 layer, which is isostructural to the trigonal transition metal dichalcogenide such as 1T-WS2; and the double-layered Ce2N2 structure. The calculated electronic band structure predicts the R
m, and there are two types of layers in the unit cell, the sandwiched CeN2 layer, which is isostructural to the trigonal transition metal dichalcogenide such as 1T-WS2; and the double-layered Ce2N2 structure. The calculated electronic band structure predicts the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m Ce3N4 to be an insulator with a band gap of about 1 eV at 0 GPa. This phase is thermodynamically stable from 0 GPa to 13 GPa, above which it will transform into the I
m Ce3N4 to be an insulator with a band gap of about 1 eV at 0 GPa. This phase is thermodynamically stable from 0 GPa to 13 GPa, above which it will transform into the I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3d Ce3N4 which is thermodynamically stable in the pressure range of 13–86 GPa. The I
3d Ce3N4 which is thermodynamically stable in the pressure range of 13–86 GPa. The I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3d Ce3N4 is isostructural to I
3d Ce3N4 is isostructural to I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3d Sn3N4.45 However, the band gaps of I
3d Sn3N4.45 However, the band gaps of I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3d Ce3N4 decrease with increasing pressure as displayed in Fig. S8 (ESI†), which is different from Sn3N4.
3d Ce3N4 decrease with increasing pressure as displayed in Fig. S8 (ESI†), which is different from Sn3N4.
4. The CeN2 compound
For the CeN2 compound, there are only two stable phases at the PBE level, that is the P43212 phase and the Pnma phase. However, when taking into account the Hubbard U, the I4/mmm and P21/c phases also turn out to be thermodynamically stable. At the PBE+U level, the P43212 phase is thermodynamically stable from 2 GPa to 8 GPa, after that, it will transform into the Pnma phase at about 8 GPa, and then to the I4/mmm phase at about 33 GPa, and finally to the P21/c phase at about 77 GPa, which remains thermodynamically stable up to at least 150 GPa. Nitrogen atoms exist in the form of diatomic configurations in these phases. It has been found that such diatomic configurations can possess a formal charge of −4 with tetravalent cations M4+(N2)4−, which are called pernitrides and has a typical N–N bond length of 1.42 Å;46 or they exhibit a formal charge of −2 with divalent cations M2+(N2)2−, which are called dinitrides and has a typical double bond length of about 1.22 Å.47,48 However, for these CeN2 phases, the nitrogen bond length is around 1.35 Å, and the calculated bond orders run from 1.43 to 1.87 as listed in Table S6 (ESI†). Both the bond length and bond orders indicate that these bonds are between single and double bonds, which are different from those of the pernitrides or dinitrides. The nitrogen bond lengths in CeN2 are closer to those in LaN2 and YN2 systems, which are 1.30 Å and 1.33 Å, respectively.49 The La and Y atoms exist in the form of trivalent cations, and the N2 configuration has a formal charge of −3. For the LaN2 or YN2 phases, 3/4 of the two degenerate anti-bonding π* orbitals of the diatomic N2 unit are occupied by 3 electrons, and therefore they exhibit metallic properties. For the P43212 CeN2, we presented the –COHP results of two pz orbitals from the N1–N2 unit, more than half of the anti-bonding state is occupied as shown in Fig. 3(b). The total two anti-bonding orbitals should also be occupied by three electrons, but contrary to the LaN2 structure, the CeN2 phase exhibits semiconducting properties as shown in Fig. 3(c). Such separated anti-bonding orbitals might be attributed to the local environment of the N2 units, which are not located in the middle of the cavities surrounded by cerium atoms. The Pnma and I4/mmm phases exhibit metallic properties, while the P21/c phase is a semiconductor as shown in Fig. S7 (ESI†).5. The P![[1 with combining macron]](https://www.rsc.org/images/entities/h3_char_0031_0304.gif) CeN3
CeN3
For the CeN3 compound, it is thermodynamically stable in the pressure range of 90–99 GPa (PBE+U) with the space group of P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) . There are two nitrogen configurations in it: the diatomic N2 and trans-N4. The bond length in diatomic N2 is 1.30 Å and the bond order is 1.59, both of which are similar to that in the CeN2 phase. The diatomic N2 in CeN3 should also acquire three electrons. For the trans-N4, the bond lengths are all 1.31 Å. The bond order between the terminal N2 atom and the two-coordinated internal N3 atom (Table S6, ESI†) is 1.46, and the bond order between the internal N3 and N3′ is 1.25, both of which are between those of the single and double bonds. There are totally four pz orbitals for the N4 unit, forming two bonding π orbitals and two anti-bonding π* orbitals. The neutral N4 unit has 2 electrons occupying these pz orbitals. If the N4 unit acquires 4 electrons, the total 6 electrons will occupy two bonding π orbitals and one anti-bonding π* orbital, the total bond order for these π orbitals should be one. Taking three single σ bonds into account, the perfect [N4]4− unit should possess one double bond and two single bonds. Such a situation has been identified in many alkaline-earth metal nitrides.50,51 Take the CaN2 compound as an example,50 the bond between the terminal and internal atoms has an order of 1.67, which is considered as a double bond. But the bond between two internal atoms has an order of 1.01, which is assigned as a single bond. The former bond order is larger than the latter, and the total bond order is 3.69, less than 4 of the perfect [N4]4− unit. For the N4 unit in the CeN3, the bond order between two internal atoms is 1.25, but the bond order between the terminal atom and the internal atom is 1.46, and the former bond order is smaller than the latter; such situation is different from that in CaN2. Moreover, the total bond order of the N4 unit in CeN3 is 4.17, larger than 4 of the perfect [N4]4− unit. As a rational explanation, the N4 unit in CeN3 is more likely to acquire 3 electrons, and the total 5 pz electrons occupy two bonding orbitals and 1/4 of two anti-bonding orbitals, which should give a bond order larger than 4, consistent with the calculated bond order of 4.17. The calculated density of states predicts the P
. There are two nitrogen configurations in it: the diatomic N2 and trans-N4. The bond length in diatomic N2 is 1.30 Å and the bond order is 1.59, both of which are similar to that in the CeN2 phase. The diatomic N2 in CeN3 should also acquire three electrons. For the trans-N4, the bond lengths are all 1.31 Å. The bond order between the terminal N2 atom and the two-coordinated internal N3 atom (Table S6, ESI†) is 1.46, and the bond order between the internal N3 and N3′ is 1.25, both of which are between those of the single and double bonds. There are totally four pz orbitals for the N4 unit, forming two bonding π orbitals and two anti-bonding π* orbitals. The neutral N4 unit has 2 electrons occupying these pz orbitals. If the N4 unit acquires 4 electrons, the total 6 electrons will occupy two bonding π orbitals and one anti-bonding π* orbital, the total bond order for these π orbitals should be one. Taking three single σ bonds into account, the perfect [N4]4− unit should possess one double bond and two single bonds. Such a situation has been identified in many alkaline-earth metal nitrides.50,51 Take the CaN2 compound as an example,50 the bond between the terminal and internal atoms has an order of 1.67, which is considered as a double bond. But the bond between two internal atoms has an order of 1.01, which is assigned as a single bond. The former bond order is larger than the latter, and the total bond order is 3.69, less than 4 of the perfect [N4]4− unit. For the N4 unit in the CeN3, the bond order between two internal atoms is 1.25, but the bond order between the terminal atom and the internal atom is 1.46, and the former bond order is smaller than the latter; such situation is different from that in CaN2. Moreover, the total bond order of the N4 unit in CeN3 is 4.17, larger than 4 of the perfect [N4]4− unit. As a rational explanation, the N4 unit in CeN3 is more likely to acquire 3 electrons, and the total 5 pz electrons occupy two bonding orbitals and 1/4 of two anti-bonding orbitals, which should give a bond order larger than 4, consistent with the calculated bond order of 4.17. The calculated density of states predicts the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) CeN3 to be metallic as shown in Fig. S7 (ESI†).
CeN3 to be metallic as shown in Fig. S7 (ESI†).
6. The P![[1 with combining macron]](https://www.rsc.org/images/entities/h3_char_0031_0304.gif) CeN4
CeN4
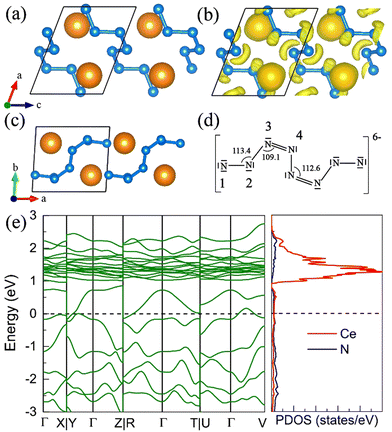
The P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) CeN4 with molecular N8 units becomes thermodynamically stable above 26 GPa at the PBE+U level. The calculated phonon spectrums of this phase at both high pressure and ambient pressure exhibit no imaginary frequency, indicating its dynamical stability. The N8 unit is centrosymmetric with the nitrogen atoms from the terminal to the internal denoted as N1, N2, N3, and N4, respectively. Such N8 configuration has been found in Sn–N phases.45 It has a formal charge of −8 in the P
CeN4 with molecular N8 units becomes thermodynamically stable above 26 GPa at the PBE+U level. The calculated phonon spectrums of this phase at both high pressure and ambient pressure exhibit no imaginary frequency, indicating its dynamical stability. The N8 unit is centrosymmetric with the nitrogen atoms from the terminal to the internal denoted as N1, N2, N3, and N4, respectively. Such N8 configuration has been found in Sn–N phases.45 It has a formal charge of −8 in the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) SnN4 with two double bonds in the Lewis structure, while it has a formal charge of −6 in the P
SnN4 with two double bonds in the Lewis structure, while it has a formal charge of −6 in the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) SnN5 with only one double bond in the middle of the N8 unit for the Lewis structure. For the P
SnN5 with only one double bond in the middle of the N8 unit for the Lewis structure. For the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) CeN4, six internal nitrogen atoms take the normal armchair-like structure with little rotation, while the two terminal atoms N1 have a large deviation from the armchair configuration. Bader charges analysis52 reveals that the N1 atom acquires 0.85e, N2 acquires 0.46e, and the remaining nitrogen atoms each acquire approximately 0.36e. To reveal the bonding properties, we calculated the electron localized function53 (ELF) (Fig. 4(b)), the high localization around each nitrogen atom represents electron lone pairs, which take the crescentic shape for the six internal nitrogen atoms, and the disk shape pointing to the terminal N1 atom. There are four different bonds in the N8 unit differentiated by their lengths, which are 1.35 Å, 1.40 Å, 1.32 Å, and 1.38 Å at 50 GPa from the terminal to the internal. The corresponding bond orders are 1.42, 1.12, 1.34, and 1.16, respectively. As a result, the N2–N3 and N4–N4′ bonds are close to the single bond, while the N1–N2 or N3–N4 bonds are between the single and double bonds. The calculated total bond order for the N8 unit with 7 bonds is about 8.9, and thus it is more likely for the Lewis structure of the N8 unit to possess two double bonds instead of one. As the bonds between N3 and N4 possess the shortest length, a reasonable Lewis structure might be constructed as shown in Fig. 4(d), in which the double bond only appears between the N3 and N4 atoms. As a result, the two coordinated N2, N3, and N4 nitrogen atoms belong to the AX2E2, AX2E1, and AX2E1, respectively. Therefore, this nitrogen configuration presents a bent geometry according to the VSEPR. According to the bond orders, another possible Lewis structure might be constructed as shown in Fig. S9 (ESI†), in which the N1–N2 bond is assigned as a double bond. The electronic band structure calculation shows that the P
CeN4, six internal nitrogen atoms take the normal armchair-like structure with little rotation, while the two terminal atoms N1 have a large deviation from the armchair configuration. Bader charges analysis52 reveals that the N1 atom acquires 0.85e, N2 acquires 0.46e, and the remaining nitrogen atoms each acquire approximately 0.36e. To reveal the bonding properties, we calculated the electron localized function53 (ELF) (Fig. 4(b)), the high localization around each nitrogen atom represents electron lone pairs, which take the crescentic shape for the six internal nitrogen atoms, and the disk shape pointing to the terminal N1 atom. There are four different bonds in the N8 unit differentiated by their lengths, which are 1.35 Å, 1.40 Å, 1.32 Å, and 1.38 Å at 50 GPa from the terminal to the internal. The corresponding bond orders are 1.42, 1.12, 1.34, and 1.16, respectively. As a result, the N2–N3 and N4–N4′ bonds are close to the single bond, while the N1–N2 or N3–N4 bonds are between the single and double bonds. The calculated total bond order for the N8 unit with 7 bonds is about 8.9, and thus it is more likely for the Lewis structure of the N8 unit to possess two double bonds instead of one. As the bonds between N3 and N4 possess the shortest length, a reasonable Lewis structure might be constructed as shown in Fig. 4(d), in which the double bond only appears between the N3 and N4 atoms. As a result, the two coordinated N2, N3, and N4 nitrogen atoms belong to the AX2E2, AX2E1, and AX2E1, respectively. Therefore, this nitrogen configuration presents a bent geometry according to the VSEPR. According to the bond orders, another possible Lewis structure might be constructed as shown in Fig. S9 (ESI†), in which the N1–N2 bond is assigned as a double bond. The electronic band structure calculation shows that the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) CeN4 is a semimetal as shown in Fig. 4(e).
CeN4 is a semimetal as shown in Fig. 4(e).
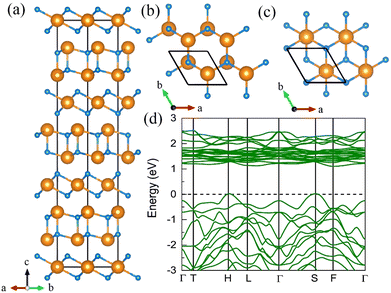
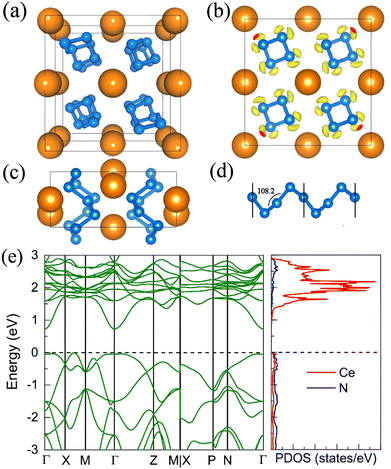
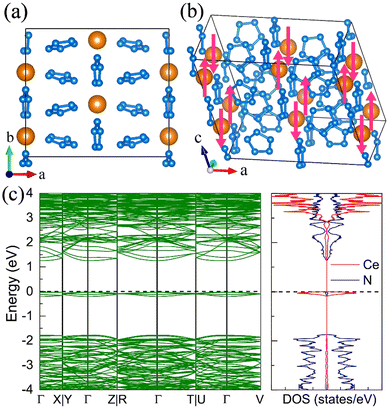
7. The I41/a CeN4
With increasing pressure to 94 GPa, the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) CeN4 will be energetically substituted by a tetragonal I41/a phase which is composed of cerium ions and infinite nitrogen chains (Fig. 5). This kind of chain possesses a helical structure with four nitrogen atoms in one period along the c direction. To the best of our knowledge, armchair and zigzag-like polymeric nitrogen chains have been widely studied in many systems,54,55 but the helical chains have not been studied up to now. The infinite spiral chain has been predicted for the oxygen and realized in sulfur and selenium element phases.56,57 All the nitrogen atoms in this chain have equivalent Wyckoff positions, and there is only one type of bond, which is calculated to be 1.36 Å at 120 GPa. The bond length is similar to that in cg-N, and the helical-N4 chain should be purely single-bonded. In addition, the distance between cerium and nitrogen is 2.45 Å, and the angle between two adjacent bonds is 108° at 120 GPa. Bader charge analysis shows that each nitrogen atom captures 0.48e from cerium atoms, revealing their ionic interactions. Furthermore, ELF calculations show that two electron lone pairs exist around each nitrogen atom (Fig. 5(b)). The nitrogen atoms in the helical-N4 chain should be sp3-hybridized such that two of these orbitals are single-bonded with two adjacent nitrogen atoms and the remaining two orbitals are occupied by two electron lone pairs. Each nitrogen atom in the helical-N4 chain should acquire one extra electron, and the cerium atoms exhibit tetravalent properties. The bent configuration of the helical chain can also be explained by the VSEPR that every nitrogen atom belongs to the AX2E2.
CeN4 will be energetically substituted by a tetragonal I41/a phase which is composed of cerium ions and infinite nitrogen chains (Fig. 5). This kind of chain possesses a helical structure with four nitrogen atoms in one period along the c direction. To the best of our knowledge, armchair and zigzag-like polymeric nitrogen chains have been widely studied in many systems,54,55 but the helical chains have not been studied up to now. The infinite spiral chain has been predicted for the oxygen and realized in sulfur and selenium element phases.56,57 All the nitrogen atoms in this chain have equivalent Wyckoff positions, and there is only one type of bond, which is calculated to be 1.36 Å at 120 GPa. The bond length is similar to that in cg-N, and the helical-N4 chain should be purely single-bonded. In addition, the distance between cerium and nitrogen is 2.45 Å, and the angle between two adjacent bonds is 108° at 120 GPa. Bader charge analysis shows that each nitrogen atom captures 0.48e from cerium atoms, revealing their ionic interactions. Furthermore, ELF calculations show that two electron lone pairs exist around each nitrogen atom (Fig. 5(b)). The nitrogen atoms in the helical-N4 chain should be sp3-hybridized such that two of these orbitals are single-bonded with two adjacent nitrogen atoms and the remaining two orbitals are occupied by two electron lone pairs. Each nitrogen atom in the helical-N4 chain should acquire one extra electron, and the cerium atoms exhibit tetravalent properties. The bent configuration of the helical chain can also be explained by the VSEPR that every nitrogen atom belongs to the AX2E2.
We further calculated the electronic band structure of this novel phase at 120 GPa. It turns out to be a semiconductor with an indirect bandgap of approximately 1 eV. The nitrogen orbitals and cerium orbitals contribute most to the valence bands, while the conduction bands are only contributed by cerium orbitals. There are no imaginary frequencies found in the phonon spectrum at both 0 GPa and 120 GPa, indicating that this phase might be quenched to ambient pressure. We also employed the AIMD simulations for it at 0 GPa, which remains stable at 300 K, but some N2 units split from the helical chains at 400 K (see Fig. S10, ESI†). The bond length between nitrogen atoms in the helical-N4 chain is calculated to be 1.42 Å at 0 GPa, close to that of the single bond. Thus, the I41/a CeN4 might be a good candidate for high-energy-density materials. Although the cerium atoms are rather heavy and the abundance of nitrogen is not high in I41/a CeN4, it still possesses a large gravimetric energy density of 1.81 kJ g−1 with the decomposition products of Ce3N4 and N2. By using the Kamlet–Jacobs empirical equations, its detonation pressure is calculated to be approximately 100 GPa (see Table 1), which is about 5 times TNT (∼19.0 GPa) and 2.5 times HMX (∼39.3 GPa).58 However, it is worth noting that the cerium dioxide which should be the product of the Ce–N compounds in the atmospheric environment is toxic, and that the Ce–N compounds cannot be used as safe HEDMs. The energy density properties with other decomposition products are also presented in Table S7 (ESI†). The single-bonded nitrogen configuration has been realized in WN6 with armchair like N6 rings, and in TaN5 with infinite chains. We believe that the CeN4 with all single-bonded nitrogen chains is likely to be synthesized in the near future.
| Materials | ρ (g cm−3) | E g (kJ g−1) | E v (kJ cm−3) | V d (km s−1) | P d (GPa) |
|---|---|---|---|---|---|
| I41/a CeN4 | 6.43 | 1.81 | 11.62 | 11.69 | 98.6 |
| TNT | 1.64 | 4.30 | 7.05 | 6.90 | 19.0 |
| HMX | 1.90 | 5.70 | 10.83 | 9.10 | 39.3 |
8. The R![[3 with combining macron]](https://www.rsc.org/images/entities/h3_char_0033_0304.gif) m CeN6
m CeN6
The R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m CeN6 becomes thermodynamically stable above 123 GPa. It is isostructural to h-WN6 or MoN6 with a 6-membered ring in a chair conformation as shown in Fig. S1 (ESI†).32,34 However, unlike h-WN6, the R
m CeN6 becomes thermodynamically stable above 123 GPa. It is isostructural to h-WN6 or MoN6 with a 6-membered ring in a chair conformation as shown in Fig. S1 (ESI†).32,34 However, unlike h-WN6, the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m CeN6 is calculated to be metallic. We calculated the bond properties of this phase at 140 GPa. The obtained bond lengths are 1.34 Å, which is close to the bond length of cg-N (1.33 Å) at the same pressure. The calculated bond order in the N6 unit is 1.13 at 140 GPa, which is also close to that of the single bond. For the N6 ring, six pz orbitals form three bonding π orbitals and three anti-bonding π* orbitals. The neutral N6 ring has 6 electrons occupying these orbitals. Thus, the cerium atoms are likely to lose four electrons to the N6 ring and the total 10 π electrons can satisfy the 4n + 2 (n = 2) Hückel rule. Six of the 10 π electrons will occupy 3 bonding states, and four of the 10 π electrons will occupy 2 anti-bonding states. As a result, the total bond order for the N6 ring should be about 7 (take six σ bonds into account), and the average bond order should be 1.17 which is close to the calculated values of 1.13. There should be an energy gap between the occupied two degenerate π* levels and the unoccupied π* levels according to the molecular orbital analysis.59 We then calculated the band structure of the CeN6 phase at 140 GPa. It is metallic at the PBE+U level but becomes a semimetal at the HSE06 level (Fig. S11, ESI†). However, this phase should be a semiconductor at a much lower pressure. (Fig. S12, ESI†), consistent with the molecular orbital analysis. The very high pressure induces the gap closing in this phase.
m CeN6 is calculated to be metallic. We calculated the bond properties of this phase at 140 GPa. The obtained bond lengths are 1.34 Å, which is close to the bond length of cg-N (1.33 Å) at the same pressure. The calculated bond order in the N6 unit is 1.13 at 140 GPa, which is also close to that of the single bond. For the N6 ring, six pz orbitals form three bonding π orbitals and three anti-bonding π* orbitals. The neutral N6 ring has 6 electrons occupying these orbitals. Thus, the cerium atoms are likely to lose four electrons to the N6 ring and the total 10 π electrons can satisfy the 4n + 2 (n = 2) Hückel rule. Six of the 10 π electrons will occupy 3 bonding states, and four of the 10 π electrons will occupy 2 anti-bonding states. As a result, the total bond order for the N6 ring should be about 7 (take six σ bonds into account), and the average bond order should be 1.17 which is close to the calculated values of 1.13. There should be an energy gap between the occupied two degenerate π* levels and the unoccupied π* levels according to the molecular orbital analysis.59 We then calculated the band structure of the CeN6 phase at 140 GPa. It is metallic at the PBE+U level but becomes a semimetal at the HSE06 level (Fig. S11, ESI†). However, this phase should be a semiconductor at a much lower pressure. (Fig. S12, ESI†), consistent with the molecular orbital analysis. The very high pressure induces the gap closing in this phase.
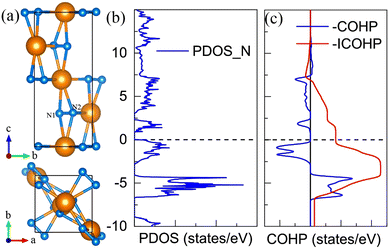
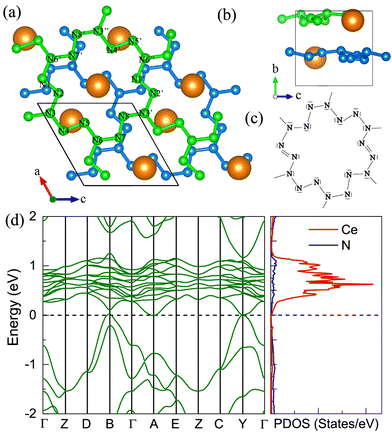
9. P21 CeN8
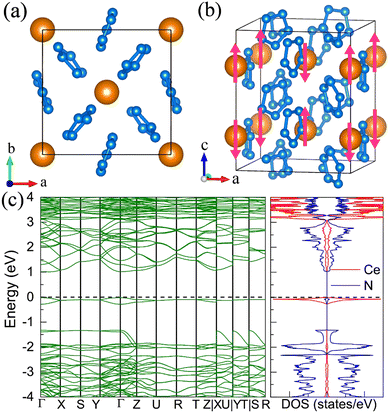
The P21 CeN8 turns out to be thermodynamically stable above 58 GPa. It is composed of two atomically thick CeN8 layers in the unit cell. There are two types of nitrogen atoms by the coordination numbers. Six 3-coordinated atoms and twelve 2-coordinated nitrogen atoms are combined to form the extended covalent two-dimensional networks with 18-membered hexagonal rings, and the cerium atoms are rightly located in the center of the hexagonal hole. It is worth noting that such kind of poly-nitrogen network has been first predicted in K2N16 by Steele and Oleynick in 2017,60 and then in high-pressure XeN8 and Xe(N8)2(N2) solid-state compounds,61 and then in YN8 in 2022.62 For the P21 CeN8, the average distance between two adjacent layers is about 2.38 Å at 60 GPa. The top layer has a shift of about half the lattice along the [101] direction as compared to the bottom layer. This kind of shift results in the non-equivalence of the 2-coordinated nitrogen atoms. We have presented the ELF results in Fig. S13 (ESI†); there are electrons localized outside the two-coordinated nitrogen atoms, indicating the electron lone pairs. Bader charge analysis reveals that the two-coordinated N1 (N2), N4 (N5), and N7 (N8) atoms each capture about 0.29e, 0.46e, and 0.23e, respectively; the three-coordinated nitrogen atoms each acquire electrons less than 0.1e. The calculated bond orders for the bonds between two two-coordinated nitrogen atoms of N1–N2, N4–N5, and N7–N8 are 1.32, 1.21, and 1.27, respectively, which are between the single and double bonds indicating a strong π delocalization. The bond orders for the bonds between the two-coordinated and three-coordinated atoms run from 1.0 to 1.1, which indicates the single bonds. Given these bonding properties, we propose a possible Lewis structure as shown in Fig. 6(c), in which the N4–N5 and N7–N8 are assigned as a single bond and N1–N2 as the double bond. Given the similarities between the N1–N2 and N7–N8 bonds, other Lewis structures might be drawn. With this configuration, each ring possesses 14 π electrons. The eight two-coordinated N4 (N5, N4′, and N5′) and N7 (N8, N7′, and N8′) atoms each denote one π lone pair shared by two rings (8 × 1/2 π pairs), the two bonds N1–N2 (N1′–N2′) each denote one π pair also shared by two rings (2 × 1/2 π pairs), and the six three-coordinated atoms each denote one π lone pair shared by three rings (6 × 1/3 π pairs). Wang et al. have identified a similar 2D polynitrogen with the 18-membered ring in Xe–N systems, and they proposed that each ring has formally 10 π electrons, which follow the Hückel rule with 4n + 2 π electrons and can be classified as an aromatic. As to the CeN8, each nitrogen ring has 14 π electrons, which also follow the Hückel rule with n = 3. Such a configuration possesses the formal charge −4. In addition, the two coordinated N1 (N2) and N4 (N5, N7, and N8) atoms belongs to the AX2E1 and AX2E2, respectively. Therefore, this nitrogen configuration presents a bent geometry according to the VSEPR. The strong π electron delocalization makes the trigonal geometry planar, the same as in the Xe–N systems. The calculated band structure at the PBE+U level predicted the P21 CeN8 to be a semimetal with a Dirac point at the Y point, The HSE06 calculation does not change the semimetal properties of this phase as shown in Fig. S14 (ESI†). The PBE+U+SOC calculation opens the Dirac point at the Y point.10. The metastable R![[3 with combining macron]](https://www.rsc.org/images/entities/h3_char_0033_0304.gif) CeN8
CeN8
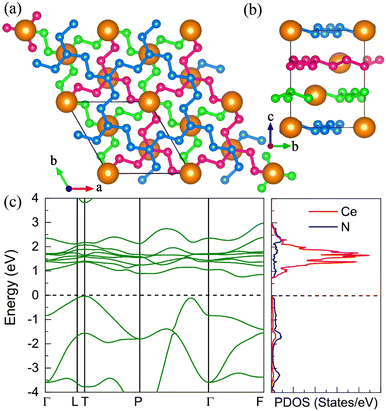
On the other hand, we found the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) CeN8 has higher energy than the P21 CeN8 below 150 GPa. The R
CeN8 has higher energy than the P21 CeN8 below 150 GPa. The R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase is also composed of the above-mentioned porous polynitrogen but in a different stacking way. There are three layers in the unit cell, as painted with three colors in Fig. 7. Within this configuration, the two-coordinated atoms are all equivalent. The bond length between N1 and N2 (see Table S6, ESI†) is approximately 1.32 Å at 120 GPa, and the distance between the two-coordinated N2 and N2′ atoms is 1.35 Å. The nitrogen bond lengths in the R
phase is also composed of the above-mentioned porous polynitrogen but in a different stacking way. There are three layers in the unit cell, as painted with three colors in Fig. 7. Within this configuration, the two-coordinated atoms are all equivalent. The bond length between N1 and N2 (see Table S6, ESI†) is approximately 1.32 Å at 120 GPa, and the distance between the two-coordinated N2 and N2′ atoms is 1.35 Å. The nitrogen bond lengths in the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase are also between those of the single and double bonds, indicating strong delocalization. The electronic band structure and density of states show that the R
phase are also between those of the single and double bonds, indicating strong delocalization. The electronic band structure and density of states show that the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase is a semiconductor with an indirect bandgap of approximately 0.8 eV. We further calculated the band structure of the R
phase is a semiconductor with an indirect bandgap of approximately 0.8 eV. We further calculated the band structure of the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase at 60 GPa at the HSE06 level (Fig. S15, ESI†) for comparison with the P21 phase. The HSE06 functional also predicts the R
phase at 60 GPa at the HSE06 level (Fig. S15, ESI†) for comparison with the P21 phase. The HSE06 functional also predicts the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase to be a band insulator. The band gap increases from the P21 phase to the R
phase to be a band insulator. The band gap increases from the P21 phase to the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase. We looked into the band structure of the P21 phase, the conduction and valence bands get close to each other at the B(0, 0, 0.5) and Y(0.5, 0, 0) points, which means that the metallic properties are almost along the a and c directions, that is within the CeN8 layers. We then compared the geometric structures of these two structures at 60 GPa. The average distance between the cerium atoms and the adjacent nitrogen atoms within the same layer in the P21 phase is about 2.368 Å, but the result is 2.441 Å in the R
phase. We looked into the band structure of the P21 phase, the conduction and valence bands get close to each other at the B(0, 0, 0.5) and Y(0.5, 0, 0) points, which means that the metallic properties are almost along the a and c directions, that is within the CeN8 layers. We then compared the geometric structures of these two structures at 60 GPa. The average distance between the cerium atoms and the adjacent nitrogen atoms within the same layer in the P21 phase is about 2.368 Å, but the result is 2.441 Å in the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase. The closer distance between the cerium and nitrogen atoms makes the cerium orbitals overlap more with electron lone pairs outside the two-coordinated nitrogen atoms. As a result, the contribution of cerium orbitals into the valence band increases it and decreases the band gaps.
phase. The closer distance between the cerium and nitrogen atoms makes the cerium orbitals overlap more with electron lone pairs outside the two-coordinated nitrogen atoms. As a result, the contribution of cerium orbitals into the valence band increases it and decreases the band gaps.
After the removal of the cerium atoms, the nitrogen networks in the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) phase remain in the same symmetry, and its phonon spectrum exhibits no imaginary frequency at ambient pressure indicating its dynamical stability. We also presented the AIMD results for its bulk and monolayer forms in Fig. S16 and S17 (ESI†), respectively. We found that the R
phase remain in the same symmetry, and its phonon spectrum exhibits no imaginary frequency at ambient pressure indicating its dynamical stability. We also presented the AIMD results for its bulk and monolayer forms in Fig. S16 and S17 (ESI†), respectively. We found that the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) nitrogen phase has lower energy than the previously identified P
nitrogen phase has lower energy than the previously identified P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) phase by about 9 meV per atom at the SCAN + rvv10 level.61 The energy results from other pure nitrogen phases are also listed in Table S8 (ESI†).
phase by about 9 meV per atom at the SCAN + rvv10 level.61 The energy results from other pure nitrogen phases are also listed in Table S8 (ESI†).
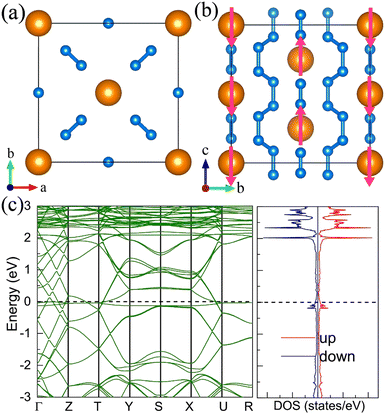
11. Pentazolate salts
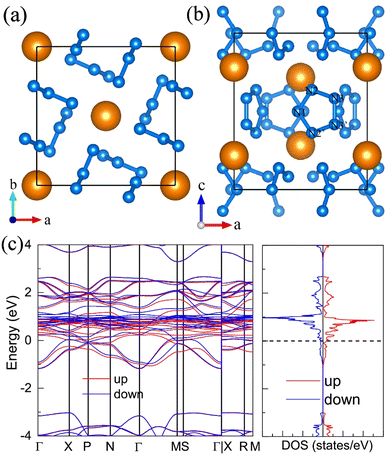
For the molecular crystals with nitrogen pentazolates, the I4/m CeN10 is thermodynamically stable from 29 GPa to 57 GPa. The DOS calculation predicts it to be metallic as shown in Fig. S7 (ESI†). These pentazolates are parallel to the lattice axis c. Most interestingly, the spin-polarized calculations predict the I4/m CeN10 to be iterant ferromagnetic (see Fig. 8) with the magnetic moment being 0.2μB per formula unit at about 50 GPa at the PBE+U level. For the CeN15 phases, the C2 phase is not thermodynamically stable at the PBE level, but it turns out to be thermodynamically stable from 33 GPa to 37 GPa at the PBE+U level (see Fig. S2, ESI†). The pentazolates are almost parallel along the c-axis and the cerium atoms take hexagonal arrays in the ab plane. The spin-nonpolarized calculations predict this phase to be metallic. However, the antiferromagnetic (AFM) configuration is found to possess the lowest energy as displayed in Fig. 9 by magenta arrows, which exhibits a zigzag-type anti-ferromagnetism within the ab plane and anti-ferromagnetism along the c-axis. The AFM phase is insulating with a band gap of about 1.23 eV. The highest occupied valence bands are mostly projected to the cerium orbitals as shown in Fig. 9, and the calculated magnetic moment is about 1μB per cerium atom at about 35 GPa at the PBE+U level. As a result, one of the f-orbitals of the cerium atom is half-filled, and that cerium atom exhibits trivalent properties. When pressure is increased above 37 GPa, the C2 phase will transform into the P21212 phase, which also exhibits antiferromagnetic properties (see Fig. 10).12. The metastable Immm CeN10
The I4/m CeN10 is thermodynamically stable above 29 GPa, but the Immm CeN10 phase has a lower enthalpy than the I4/m phase below 25 GPa at which the enthalpy of the Immm phase is about 19 meV per atom higher than the convex hull. Moreover, the Immm phase is dynamically stable (Fig. S4, ESI†). Therefore, it is metastable and likely to be synthesized. As shown in Fig. 11, this phase should be isostructural to the Immm HfN10 with isolated nitrogen diatomic molecules and infinite armchair chains parallel to the c-axis.2 The calculated bond length of the diatomic N2 is 1.11 Å, and the bond order is 2.45 at 20 GPa, which predicts a bond length between double and triple bond. The calculated bond lengths for the N2–N3 and N3–N4 (see Table S7, ESI†) within the armchair chains are 1.31 Å and 1.33 Å, respectively. The corresponding bond orders are 1.45 and 1.35, respectively. These bonds should be between the single and double bonds with strongly delocalized π electrons. In addition, the Immm CeN10 is calculated to the spin-polarized, and the enthalpy lowest magnetic configuration is displayed in Fig. 11(b), in which the cerium atom is ferromagnetic along the c-axis, while the nearest cerium atoms in the ab plane are anti-ferromagnetic. The spin-polarized band structure also predicts the Immm CeN10 to be metallic.Conclusions
In summary, we performed a systematic crystal structure prediction for Ce–N compounds under high pressures of up to 150 GPa. A variety of nitrogen-rich phases are predicted to be thermodynamically stable at specific pressures. Among them, the infinite helical nitrogen chain is discovered for the first time within the I41/a CeN4, in which the cerium atom exhibits tetravalent properties and the nitrogen chains are purely single-bonded. This phase can be recovered under ambient conditions. Although the cerium atoms are rather heavy in I41/a CeN4, it still possesses a large gravimetric energy density of 1.81 kJ g−1 when broken down into Ce3N4 and N2. Moreover, its detonation pressure is close to 100 GPa, which is about 5 times TNT (∼19.0 GPa) and 2.5 times HMX (∼39.3 GPa).58 In addition, we identified two CeN8 phases with the space group of P21 and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , in which the cerium atoms are embedded in the porous nitrogen frameworks. After the removal of these cerium atoms, the pure nitrogen framework with R
, in which the cerium atoms are embedded in the porous nitrogen frameworks. After the removal of these cerium atoms, the pure nitrogen framework with R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) symmetry is still stable and has a lower energy than the previously identified P
symmetry is still stable and has a lower energy than the previously identified P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) phase at ambient pressure. Moreover, we found that the I4/m CeN10 with pentazolates exhibits iterant ferromagnetism while the C2 and P21212 CeN15 exhibit antiferromagnetic properties with one of the cerium f-orbitals half-filled, in which the cerium atoms exhibit trivalent properties.
phase at ambient pressure. Moreover, we found that the I4/m CeN10 with pentazolates exhibits iterant ferromagnetism while the C2 and P21212 CeN15 exhibit antiferromagnetic properties with one of the cerium f-orbitals half-filled, in which the cerium atoms exhibit trivalent properties.
Computational details
First-principles structure predictions were performed at pressure points of 0, 50, 100, and 150 GPa using our recently developed machine learning and graph theory accelerated crystal structure prediction software MAGUS.34,63 This method has been successfully applied in many systems.64–67 Variable composition searches are carried out with the unit cell containing up to 40 atoms. Fixed composition non-molecular crystal structural searches were employed for given compositions, in which the unit cells contain up to four corresponding CexNy formula units. For the molecular crystal structure predictions, we adopted up to 5 formula units for CeN5, 3 formula units for CeN10 and CeN15, and 2 formula units for CeN20. 40 random structures were generated in the first generation and subsequent generations contain 30 structures. Structural optimizations and electronic structure analysis were performed according to density functional theory (DFT) within the generalized gradient approximation (GGA) using Perdew–Burke–Ernzerhof (PBE) functionals68 as implemented in the VASP package.69 Due to the f-electrons of cerium atoms being very localized, we employed the PBE+U method with U = 3.5 to have a better description of the electronic properties of Ce–N compounds. The projector augmented wave (PAW)70 potentials were used with core electrons for cerium and nitrogen being [Kr]4d10 and [He], respectively. We used the Monkhorst–Pack71 scheme to sample the Brillouin Zone with a grid spacing of 2π × 0.03 Å−1 and a kinetic energy cutoff of 1050 eV for plane-wave expansion. The DFT-D3 scheme was used to describe the van der Waals (vdW) interactions within the layered configuration.72 We optimized these novel structures with convergence criteria 2 × 10−4 eV Å−1 and 1 × 10−5 eV for force and total energy per atom, respectively. The bond orders are calculated from Manz's bond order equation with DDEC6 partitioning as employed in the Chargemol program.73–77 All the phonon frequencies were calculated using the finite displacements method as implemented in the PHONOPY package.78 The energy reduction from the solid nitrogen phase to the gaseous state is taken as 0.25 eV per atom. We check the thermal stability of these phases at finite temperatures by ab initio molecular dynamics (AIMD) simulations. The simulations were performed for 10 ps with an interval of 1 fs using the NVT ensemble with a Nosè–Hoover thermostat.79,80 Crystal structure visualization was performed through VESTA software.81Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
J. S. gratefully acknowledges the financial support from the National Natural Science Foundation of China (grant no. 12125404, 11974162, and 11834006) and the Fundamental Research Funds for the Central Universities. The calculations were carried out using supercomputers at the High-Performance Computing Center of Collaborative Innovation Center of Advanced Microstructures, the high-performance supercomputing center of Nanjing University.References
- M. I. Eremets, M. Y. Popov, I. A. Trojan, V. N. Denisov, R. Boehler and R. J. Hemley, Polymerization of nitrogen in sodium azide, J. Chem. Phys., 2004, 120, 10618–10623 CrossRef CAS PubMed.
- J. Zhang, A. R. Oganov, X. Li and H. Niu, Pressure-stabilized hafnium nitrides and their properties, Phys. Rev. B, 2017, 95, 020103 CrossRef.
- K. O. Christe, Recent advances in the chemistry of N5+N5− and high-oxygen compounds, Propellants, Explos., Pyrotech., 2007, 32, 194–204 CrossRef CAS.
- C. Mailhiot, L. H. Yang and A. K. McMahan, Polymeric nitrogen, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 14419–14435 CrossRef CAS PubMed.
- Y. Ma, A. R. Oganov, Z. Li, Y. Xie and J. Kotakoski, Novel High Pressure Structures of Polymeric Nitrogen, Phys. Rev. Lett., 2009, 102, 065501 CrossRef PubMed.
- X. Wang, Y. Wang, M. Miao, X. Zhong, J. Lv, T. Cui, J. Li, L. Chen, C. J. Pickard and Y. Ma, Cagelike Diamondoid Nitrogen at High Pressures, Phys. Rev. Lett., 2012, 109, 175502 CrossRef PubMed.
- J. Sun, M. Martinez-Canales, D. D. Klug, C. J. Pickard and R. J. Needs, Stable All-Nitrogen Metallic Salt at Terapascal Pressures, Phys. Rev. Lett., 2013, 111, 175502 CrossRef PubMed.
- M. J. Greschner, M. Zhang, A. Majumdar, H. Liu, F. Peng, J. S. Tse, Y. Yao and A. New, Allotrope of Nitrogen as High-Energy Density Material, J. Phys. Chem. A, 2016, 120, 2920–2925 CrossRef CAS PubMed.
- B. Hirshberg, R. B. Gerber and A. I. Krylov, Calculations predict a stable molecular crystal of N8, Nat. Chem., 2014, 6, 52–56 CrossRef CAS PubMed.
- S. Liu, L. Zhao, M. Yao, M. Miao and B. Liu, Novel All-Nitrogen Molecular Crystals of Aromatic N10, Adv. Sci., 2020, 7, 1902320 CrossRef CAS PubMed.
- M. M. G. Alemany and J. L. Martins, Density-functional study of nonmolecular phases of nitrogen: Metastable phase at low pressure, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 024110 CrossRef.
- W. D. Mattson, D. Sanchez-Portal, S. Chiesa and R. M. Martin, Prediction of New Phases of Nitrogen at High Pressure from First-Principles Simulations, Phys. Rev. Lett., 2004, 93, 125501 CrossRef PubMed.
- F. Zahariev, A. Hu, J. Hooper, F. Zhang and T. Woo, Layered single-bonded nonmolecular phase of nitrogen from first-principles simulation, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 214108 CrossRef.
- M. I. Eremets, A. G. Gavriliuk, I. A. Trojan, D. A. Dzivenko and R. Boehler, Single-bonded cubic form of nitrogen, Nat. Mater., 2004, 3, 558–563 CrossRef CAS PubMed.
- C. Ji, A. A. Adeleke, L. X. Yang, B. Wan, H. Y. Gou, Y. S. Yao, B. Li, Y. Meng, J. S. Smith, V. B. Prakapenka, W. J. Liu, G. Y. Shen, W. L. Mao and H. K. Mao, Nitrogen in black phosphorus structure, Sci. Adv., 2020, 6, eaba9206 CrossRef CAS PubMed.
- D. Laniel, B. Winkler, T. Fedotenko, A. Pakhomova, S. Chariton, V. Milman, V. Prakapenka, L. Dubrovinsky and N. Dubrovinskaia, High-Pressure Polymeric Nitrogen Allotrope with the Black Phosphorus Structure, Phys. Rev. Lett., 2020, 124, 216001 CrossRef CAS PubMed.
- D. Tomasino, M. Kim, J. Smith and C. S. Yoo, Pressure-Induced Symmetry-Lowering Transition in Dense Nitrogen to Layered Polymeric Nitrogen (LP-N) with Colossal Raman Intensity, Phys. Rev. Lett., 2014, 113, 205502 CrossRef PubMed.
- D. Laniel, G. Geneste, G. Weck, M. Mezouar and P. Loubeyre, Hexagonal Layered Polymeric Nitrogen Phase Synthesized near 250 GPa, Phys. Rev. Lett., 2019, 122, 066001 CrossRef CAS PubMed.
- K. Ramesh Babu and G. Vaitheeswaran, Ab initio study of structural and vibrational properties of KN3 under pressure, Chem. Phys. Lett., 2012, 533, 35–39 CrossRef CAS.
- X. Wang, J. Li, J. Botana, M. Zhang, H. Zhu, L. Chen, H. Liu, T. Cui and M. Miao, Polymerization of nitrogen in lithium azide, J. Chem. Phys., 2013, 139, 164710 CrossRef PubMed.
- X. Wang, J. Li, H. Zhu, L. Chen and H. Lin, Polymerization of nitrogen in cesium azide under modest pressure, J. Chem. Phys., 2014, 141, 044717 CrossRef PubMed.
- W. Yi, X. Jiang, T. Yang, B. Yang, Z. Liu and X. Liu, Crystalline Structures and Energetic Properties of Lithium Pentazolate under Ambient Conditions, ACS Omega, 2020, 5, 24946–24953 CrossRef CAS PubMed.
- D. Laniel, B. Winkler, E. Koemets, T. Fedotenko, M. Bykov, E. Bykova, L. Dubrovinsky and N. Dubrovinskaia, Synthesis of magnesium-nitrogen salts of polynitrogen anions, Nat. Commun., 2019, 10, 4515 CrossRef PubMed.
- M. Bykov, T. Fedotenko, S. Chariton, D. Laniel, K. Glazyrin, M. Hanfland, J. S. Smith, V. B. Prakapenka, M. F. Mahmood, A. F. Goncharov, A. V. Ponomareva, F. Tasnádi, A. I. Abrikosov, T. Bin Masood, I. Hotz, A. N. Rudenko, M. I. Katsnelson, N. Dubrovinskaia, L. Dubrovinsky and I. A. Abrikosov, High-Pressure Synthesis of Dirac Materials: Layered van der Waals Bonded BeN4 Polymorph, Phys. Rev. Lett., 2021, 126, 175501 CrossRef CAS PubMed.
- B. Huang and G. Frapper, Barium–Nitrogen Phases Under Pressure: Emergence of Structural Diversity and Nitrogen-Rich Compounds, Chem. Mater., 2018, 30, 7623–7636 CrossRef CAS.
- K. Xia, X. Zheng, J. Yuan, C. Liu, H. Gao, Q. Wu and J. Sun, Pressure-Stabilized High-Energy-Density Alkaline-Earth-Metal Pentazolate Salts, J. Phys. Chem. C, 2019, 123, 10205–10211 CrossRef CAS.
- J. Yuan, K. Xia, J. Wu and J. Sun, High-energy-density pentazolate salts: CaN10 and BaN10, Sci. China: Phys., Mech. Astron., 2020, 64, 218211 Search PubMed.
- M. Bykov, E. Bykova, A. V. Ponomareva, I. A. Abrikosov, S. Chariton, V. B. Prakapenka, M. F. Mahmood, L. Dubrovinsky and A. F. Goncharov, Stabilization of Polynitrogen Anions in Tantalum–Nitrogen Compounds at High Pressure, Angew. Chem., Int. Ed., 2021, 60, 9003–9008 CrossRef CAS PubMed.
- B. Huang, B. Wang, S. Wu, F. Guégan, W. Hu and G. Frapper, Predicted Polymeric and Layered Covalent Networks in Transition Metal Pentazolate M(cyclo-N5)x Phases at Ambient and High Pressure: Up to 20 Nitrogen Atoms per Metal, Chem. Mater., 2021, 33, 5298–5307 CrossRef CAS.
- X. Du, Y. Yao, J. Wang, Q. Yang and G. Yang, IrN4 and IrN7 as potential high-energy-density materials, J. Chem. Phys., 2021, 154, 054706 CrossRef CAS PubMed.
- K. Xia, J. Yuan, X. Zheng, C. Liu, H. Gao, Q. Wu and J. Sun, Predictions on High-Power Trivalent Metal Pentazolate Salts, J. Phys. Chem. Lett., 2019, 10, 6166–6173 CrossRef CAS PubMed.
- Q. Wei, C. Zhao, M. Zhang, H. Yan and B. Wei, High-pressure phases and pressure-induced phase transition of MoN6 and ReN6, Phys. Lett. A, 2019, 383, 2429–2435 CrossRef CAS.
- N. P. Salke, K. Xia, S. Fu, Y. Zhang, E. Greenberg, V. B. Prakapenka, J. Liu, J. Sun and J.-F. Lin, Tungsten Hexanitride with Single-Bonded Armchairlike Hexazine Structure at High Pressure, Phys. Rev. Lett., 2021, 126, 065702 CrossRef CAS PubMed.
- K. Xia, H. Gao, C. Liu, J. N. Yuan, J. Sun, H. T. Wang and D. Y. Xing, A novel superhard tungsten nitride predicted by machine-learning accelerated crystal structure search, Sci. Bull., 2018, 63, 817–824 CrossRef CAS PubMed.
- N. V. Skorodumova, R. Ahuja, S. I. Simak, I. A. Abrikosov, B. Johansson and B. I. Lundqvist, Electronic, bonding, and optical properties of CeO2 and Ce2O3 from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 115108 CrossRef.
- V. Kanchana, G. Vaitheeswaran, X. Zhang, Y. Ma, A. Svane and O. Eriksson, Lattice dynamics and elastic properties of the 4f electron system: CeN, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 205135 CrossRef.
- T. Y. Lee, D. Gall, C. S. Shin, N. Hellgren, I. Petrov and J. E. Greene, Growth and physical properties of epitaxial CeN layers on MgO(001), J. Appl. Phys., 2003, 94, 921–927 CrossRef CAS.
- M. B. Nielsen, D. Ceresoli, J.-E. Jørgensen, C. Prescher, V. B. Prakapenka and M. Bremholm, Experimental evidence for pressure-induced first order transition in cerium nitride from B1 to B10 structure type, J. Appl. Phys., 2017, 121, 025903 CrossRef.
- J. S. Olsen, J. E. Jørgensen, L. Gerward, G. Vaitheeswaran, V. Kanchana and A. Svane, Compressibility and structural stability of CeN from experiment and theory. The B1–B2 transition, J. Alloys Compd., 2012, 533, 29–32 CrossRef CAS.
- C. J. Pickard and R. J. Needs, High-Pressure Phases of Nitrogen, Phys. Rev. Lett., 2009, 102, 125702 CrossRef PubMed.
- J. S. Olsen, L. Gerward, U. Benedict and J. P. Itié, The crystal structure and the equation of state of cerium metal in the pressure range 0–46 Gpa, Physica B+C, 1985, 133, 129–137 CrossRef CAS.
- M. I. McMahon and R. J. Nelmes, Different Results for the Equilibrium Phases of Cerium above 5 GPa, Phys. Rev. Lett., 1997, 78, 3884–3887 CrossRef CAS.
- Y. K. Vohra, S. L. Beaver, J. Akella, C. A. Ruddle and S. T. Weir, Ultrapressure equation of state of cerium metal to 208 GPa, J. Appl. Phys., 1999, 85, 2451–2453 CrossRef CAS.
- W. Sun, C. J. Bartel, E. Arca, S. R. Bauers, B. Matthews, B. Orvañanos, B.-R. Chen, M. F. Toney, L. T. Schelhas, W. Tumas, J. Tate, A. Zakutayev, S. Lany, A. M. Holder and G. Ceder, A map of the inorganic ternary metal nitrides, Nat. Mater., 2019, 18, 732–739 CrossRef CAS PubMed.
- B. Wang, R. Larhlimi, H. Valencia, F. Guégan and G. Frapper, Prediction of Novel Tin Nitride SnxNy Phases Under Pressure, J. Phys. Chem. C, 2020, 124, 8080–8093 CrossRef CAS.
- J. C. Crowhurst, A. F. Goncharov, B. Sadigh, C. L. Evans, P. G. Morrall, J. L. Ferreira and A. J. Nelson, Synthesis and Characterization of the Nitrides of Platinum and Iridium, Science, 2006, 311, 1275–1278 CrossRef CAS PubMed.
- G. V. Vajenine, G. Auffermann, Y. Prots, W. Schnelle, R. K. Kremer, A. Simon and R. Kniep, Preparation, Crystal Structure, and Properties of Barium Pernitride, BaN2, Inorg. Chem., 2001, 40, 4866–4870 CrossRef CAS PubMed.
- G. Auffermann, Y. Prots and R. Kniep, SrN and SrN2: Diazenides by Synthesis under High N2-Pressure, Angew. Chem., Int. Ed., 2001, 40, 547–549 CrossRef CAS PubMed.
- M. Wessel and R. Dronskowski, Nature of N–N Bonding within High-Pressure Noble-Metal Pernitrides and the Prediction of Lanthanum Pernitride, J. Am. Chem. Soc., 2010, 132, 2421–2429 CrossRef CAS PubMed.
- S. Zhu, F. Peng, H. Liu, A. Majumdar, T. Gao and Y. Yao, Stable Calcium Nitrides at Ambient and High Pressures, Inorg. Chem., 2016, 55, 7550–7555 CrossRef CAS PubMed.
- S. Wei, L. Lian, Y. Liu, D. Li, Z. Liu and T. Cui, Pressure-stabilized polymerization of nitrogen in alkaline-earth-metal strontium nitrides, Phys. Chem. Chem. Phys., 2020, 22, 5242–5248 RSC.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- A. Savin, R. Nesper, S. Wengert and T. F. Fässler, ELF: The Electron Localization Function, Angew. Chem., Int. Ed. Engl., 1997, 36, 1808–1832 CrossRef CAS.
- C. Ding, J. Wang, Y. Han, J. Yuan, H. Gao and J. Sun, High Energy Density Polymeric Nitrogen Nanotubes inside Carbon Nanotubes, Chin. Phys. Lett., 2022, 39, 036101 CrossRef.
- J. Yuan, K. Xia, C. Ding, X. Wang, Q. Lu and J. Sun, High-energy-density metal nitrides with armchair chains, Matter Radiat. Extremes, 2022, 7, 038402 CrossRef CAS.
- L. Zhu, Z. Wang, Y. Wang, G. Zou, H.-K. Mao and Y. Ma, Spiral chain O4 form of dense oxygen, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 751–753 CrossRef CAS PubMed.
- H. Fujihisa, Y. Akahama, H. Kawamura, H. Yamawaki, M. Sakashita, T. Yamada, K. Honda and T. Le Bihan, Spiral chain structure of high pressure selenium-II′ and sulfur-II from powder X-ray diffraction, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 134106 CrossRef.
- M. J. Kamlet and C. Dickinson, Chemistry of Detonations. III. Evaluation of the Simplified Calculational Method for Chapman-Jouguet Detonation Pressures on the Basis of Available Experimental Information, J. Chem. Phys., 1968, 48, 43–50 CrossRef CAS.
- S. Yu, B. Huang, Q. Zeng, A. R. Oganov, L. Zhang and G. Frapper, Emergence of Novel Polynitrogen Molecule-like Species, Covalent Chains, and Layers in Magnesium–Nitrogen MgxNy Phases under High Pressure, J. Phys. Chem. C, 2017, 121, 11037–11046 CrossRef CAS.
- B. A. Steele and I. I. Oleynik, Novel Potassium Polynitrides at High Pressures, J. Phys. Chem. A, 2017, 121, 8955–8961 CrossRef CAS PubMed.
- B. Wang, F. Guégan and G. Frapper, Putting xenon and nitrogen under pressure: towards new layered and two-dimensional nitrogen allotropes with crown ether-like nanopores, J. Mater. Chem. C, 2022, 10, 10374–10381 RSC.
- F. Wang, Q. Rui, Q. Jiang, J. Li, H. Zhu, Q. Wang and X. Wang, Stable nitrogen-rich yttrium nitrides under high pressure, Solid State Commun., 2022, 358, 115001 CrossRef CAS.
- H. Gao, J. Wang, Y. Han and J. Sun, Enhancing crystal structure prediction by decomposition and evolution schemes based on graph theory, Fundam. Res., 2021, 1, 466–471 CrossRef CAS.
- H. Gao, C. Liu, A. Hermann, R. J. Needs, C. J. Pickard, H.-T. Wang, D. Xing and J. Sun, Coexistence of plastic and partially diffusive phases in a helium-methane compound, Natl. Sci. Rev., 2020, 7, 1540–1547 CrossRef CAS PubMed.
- H. Gao, C. Liu, J. Shi, S. Pan, T. Huang, X. Lu, H.-T. Wang, D. Xing and J. Sun, Superionic Silica-Water and Silica-Hydrogen Compounds in the Deep Interiors of Uranus and Neptune, Phys. Rev. Lett., 2022, 128, 035702 CrossRef CAS PubMed.
- C. Liu, H. Gao, Y. Wang, R. J. Needs, C. J. Pickard, J. Sun, H.-T. Wang and D. Xing, Multiple superionic states in helium–water compounds, Nat. Phys., 2019, 15, 1065–1070 Search PubMed.
- C. Liu, J. Shi, H. Gao, J. Wang, Y. Han, X. Lu, H.-T. Wang, D. Xing and J. Sun, Mixed Coordination Silica at Megabar Pressure, Phys. Rev. Lett., 2021, 126, 035701 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Kresse and J. Furthmuller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- T. A. Manz and D. S. Sholl, Methods for Computing Accurate Atomic Spin Moments for Collinear and Noncollinear Magnetism in Periodic and Nonperiodic Materials, J. Chem. Theory Comput., 2011, 7, 4146–4164 CrossRef CAS PubMed.
- T. A. Manz and N. G. Limas, Introducing DDEC6 atomic population analysis: part 1. Charge partitioning theory and methodology, RSC Adv., 2016, 6, 47771–47801 RSC.
- T. A. Manz, Introducing DDEC6 atomic population analysis: part 3. Comprehensive method to compute bond orders, RSC Adv., 2017, 7, 45552–45581 RSC.
- N. G. Limas and T. A. Manz, Introducing DDEC6 atomic population analysis: part 4. Efficient parallel computation of net atomic charges, atomic spin moments, bond orders, and more, RSC Adv., 2018, 8, 2678–2707 RSC.
- T. Chen and T. A. Manz, Bond orders of the diatomic molecules, RSC Adv., 2019, 9, 17072–17092 RSC.
- A. Togo, F. Oba and I. Tanaka, First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- W. G. Hoover, Canonical dynamics: Equilibrium phase-space distributions, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ma01012g |
| This journal is © The Royal Society of Chemistry 2023 |