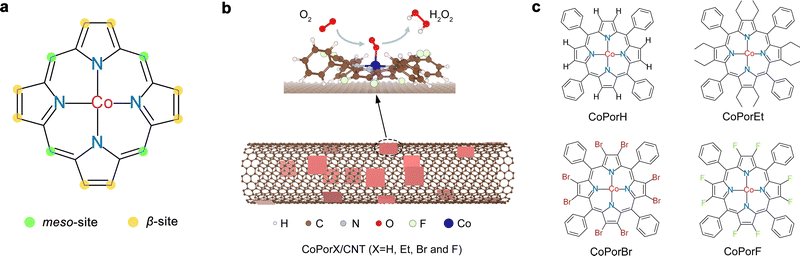
Heterogeneous molecular Co–N–C catalysts for efficient electrochemical H2O2 synthesis†
Chang
Liu
a,
Zixun
Yu
ab,
Fangxin
She
a,
Jiaxiang
Chen
 a,
Fangzhou
Liu
a,
Jiangtao
Qu
a,
Fangzhou
Liu
a,
Jiangtao
Qu
 c,
Julie M.
Cairney
c,
Chongchong
Wu
c,
Julie M.
Cairney
c,
Chongchong
Wu
 d,
Kailong
Liu
e,
Weijie
Yang
d,
Kailong
Liu
e,
Weijie
Yang
 e,
Huiling
Zheng
f,
Yuan
Chen
e,
Huiling
Zheng
f,
Yuan
Chen
 *a,
Hao
Li
*a,
Hao
Li
 *b and
Li
Wei
*b and
Li
Wei
 *a
*a
aSchool of Chemical and Biomolecule Engineering, The University of Sydney, Sydney, New South Wales, Australia. E-mail: yuan.chen@sydney.edu.au; l.wei@sydney.edu.au
bAdvanced Institute for Materials Research (WPI-AIMR), Tohoku University, Sendai, Japan. E-mail: li.hao.b8@tohoku.ac.jp
cAustralian Centre for Microscopy and Microanalysis, The University of Sydney, Sydney, New South Wales, Australia
dDepartment of Chemical and Petroleum Engineering, University of Calgary, Calgary, Alberta, Canada
eSchool of Energy, Power and Mechanical Engineering, North China Electric Power University, Baoding, 071003, China
fState Key Laboratory of Clean and Efficient Coal Utilization, Taiyuan University of Technology, Taiyuan 030024, China
First published on 29th November 2022
Abstract
Sustainable hydrogen peroxide can be produced via the oxygen reduction reaction catalyzed by single-atom cobalt–nitrogen–carbon catalysts. However, the precise catalyst atomic structure tailoring remains difficult, limiting the a priori design and activity improvement. We address this limitation by constructing heterogeneous molecular catalysts from cobalt porphyrins adsorbed on a carbon nanotube substrate. Based on the explicit atomistic models, our first-principle calculation suggested that porphyrin β-substituents and the carbon substrate can synergistically modulate Co properties and catalytic activity. An octafluoro-substituted catalyst was predicted as optimal and further validated by experiments, exhibiting >94% H2O2 selectivity and a high turnover frequency of 3.51 per second at an overpotential of 200 millivolts in an acid electrolyte. It can reach a maximum H2O2 productivity of 10.76 molH2O2 gcat−1 h−1 in a two-electrode electrolyzer, delivering pure H2O2 solutions that can be used directly for water treatment and chemical production.
Broader contextElectrochemical hydrogen peroxide synthesis via the two-electron transferred oxygen reduction reaction (2e−-ORR) holds great promise to replace the energy and emission-intensive anthraquinone process. Nitrogen coordinated single atom cobalt in carbon matrix (Co–N–C) catalysts have been recognized as potential candidates. Their performance depends strongly on the local atomic structure of the Co active site, implying that explicit catalyst structure engineering should be the key to realizing high-performance H2O2 synthesis. Heterogeneous molecular catalysts (HMCs), which bring the atomic structure explicitly of molecular catalysis to the heterogeneous catalysts, can be a feasible solution. Cobalt porphyrin molecules can resemble the Co–N–C structure and offer versatile structure tunability. Herein, a series of β-substituted cobalt porphyrin molecules were synthesized and used to prepare HMCs with a catalytic inert carbon substrate. The β-substituents could impact the 2e−-ORR performance substantially. Theoretical and experimental studies found the F-substituents as the optimal, which could optimize ORR free energy scheme towards H2O2 formation and stabilize the molecule structure alternation to improve the catalyst stability. The resulting catalyst exhibits an over 90% H2O2 selectivity in a wide potential range and a high turnover frequency of 3.51 s−1 at an overpotential of 200 mV. It can further reach H2O2 productivity of 10.76 molH2O2 gcat−1 h−1 in a two-electrode electrolyzer, delivering an ion-free aqueous H2O2 solution suitable for water treatment and chemical synthesis. This work presents an effective strategy for the design and synthesis of structure well-defined electrocatalysts for H2O2 electrochemical synthesis and beyond. |
Introduction
Hydrogen peroxide (H2O2) is an essential chemical with wide applications.1 Global H2O2 production is dominated by the unsustainable and energy-intensive anthraquinone redox (AO) process, which relies on expensive palladium (Pd) catalysts and leaves a large amount of organic waste.2 Electrochemical H2O2 production via the two-electron oxygen reduction reaction (2e−-ORR: O2 + 2H+ + 2e− → H2O2, E0 = 0.68 V) is a promising alternative approach for H2O2 production.3 Efficient electrocatalysts play a pivotal role in this process. They are expected to deliver a large current while maintaining a high H2O2 selectivity by suppressing the competitive four-electron ORR (4e−-ORR: O2 + 4H+ + 4e− → 2H2O, E0 = 1.23 V). Various ORR catalysts for electrochemical H2O2 synthesis have been investigated. Noble metal-based catalysts (e.g., Au–Pd, Pt–Hg, and Pd–Hg) exhibit high H2O2 selectivity but are limited by their high cost.4–6 Oxidized carbon materials, including graphene oxide, carbon black, and carbon nanotubes (CNT), perform well only in alkaline electrolytes, where H2O2 will decompose spontaneously.7–9Nevertheless, valuable catalyst design principles extracted from these studies suggest that an efficient catalyst should exhibit an optimal binding strength for various ORR intermediates (e.g., *O2, *OOH, and *HOOH, * denotes the active site). This principle also applies to the design and synthesis of four-nitrogen coordinated single-atom cobalt catalysts (Co–N4), which have been identified as a promising candidate for H2O2 synthesis.10–12 Recent studies further discovered a strong dependence of the Co center performance on the surrounding functional groups.13,14 It is crucial to realize precise catalyst atomic structure control to realize a high-performance catalyst. However, this remains a challenging task for conventional thermal annealing-based synthesis methods.
Cobalt porphyrins, which readily resemble ORR active Co–N4 sites, can be used to construct electrocatalysts for H2O2 synthesis.15 Their structure can be precisely tuned by replacing the H atoms at the meso- and β-site with different functionalities via rigorous organic synthesis (Fig. 1(a)). Cobalt porphyrins with various meso-substituents have been extensively investigated, and their varied ORR performance is largely attributed to the steric or co-factor effects of the substituents.16–18 Alternatively, β-substituents can modify the porphyrin π-electron system and tune the Co electronic properties,19 offering an excellent opportunity to precisely optimize the Co properties toward H2O2 synthesis. The resulting β-substituted porphyrins can adsorb on catalytic inert carbon nanotube (CNT) surface by van der Waals interaction, forming heterogeneous molecular electrocatalysts (HMCs, Fig. 1(b)) with explicit and tunable atomic structures.
In this work, we combined theoretical design and experimental synthesis to prepare a series HMCs for efficient electrochemical H2O2 production. We replaced all eight β-H atoms of a cobalt tetraphenyl porphyrin with an electron-donating ethyl (Et) or electron-withdrawing bromo (Br) and fluoro (F) substituents (denoted as CoPorX, where X = H, Et, Br and F, Fig. 1(c)) and constructed the corresponding HMCs using a CNT substrate (CoPorX/CNT). We predicted the relationship between β-substituents and the properties and ORR activities of the Co centers by density functional theory (DFT) calculations. The experimental results showed excellent agreement with our prediction. CoPorF/CNT catalyst has been identified as the optimal, exhibiting a >94% H2O2 selectivity and a turnover frequency (TOF) of 3.51 s−1 at an overpotential of 200 mV. In a two-electrode electrolyzer, it can reach H2O2 productivity up to 10.76 molH2O2 gcat−1 h−1 and produce an electrolyte-free H2O2 solution over 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm, which is ideal for water treatment and chemical production, as exemplified by synthesizing dihydroxybenzenes from phenol hydroxylation reaction.
000 ppm, which is ideal for water treatment and chemical production, as exemplified by synthesizing dihydroxybenzenes from phenol hydroxylation reaction.
Results and discussion
Theoretical prediction of catalyst properties and activities
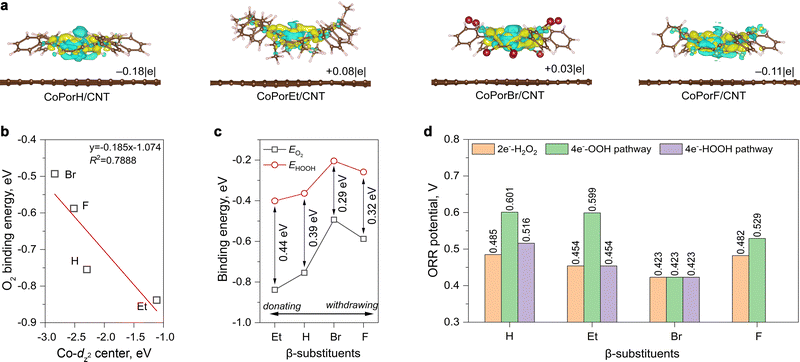
We firstly investigated the electronic structure of the different β-substituted porphines (H2PorX, X = H, Et, Br and F) and the corresponding cobalt porphyrins. The calculated delocalized π-electrons distribution at the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbitals (LUMO) exhibit obvious differences (Fig. S1 in the ESI†). Compared to the base-form H2PorH and the metalated CoPorH molecules, the ethyl substitution could increase electron density, and the delocalized π-orbitals can extend to the meso-phenyl groups. On the contrary, the Br and F substituents accumulate electrons from the porphyrin core, consistent with their electron-withdrawing capability. Consequently, the molecular orbital energy levels of these porphines and cobalt porphyrins exhibit a similar trend (Fig. S2 and Table S1, ESI†), resulting in varied Co d-electron distribution as found from their calculated spin-polarized partial density of state (pDOS, Fig. S3, ESI†).Explicit atomistic models of the HMCs were created by adsorbing a porphyrin molecule on a graphene sheet. All (between 239 to 297) atoms were allowed to relax freely for structure optimization, ensuring calculation accuracy. The overlapping between porphyrin π-electrons and graphene pz-orbitals can result in significant charge transfer phenomena between the two components and alter the cobalt properties consequently.20 After adsorption, differential charge density (Δq, Fig. 2(a)) calculations suggested the Co atom in CoPorH/CNT (Δq = −0.18|e|) and CoPorF/CNT (−0.11|e|) have become more positive by losing electrons. Oppositely, CoPorBr/CNT and CoPorEt/CNT became electron-rich by accepting 0.03|e| and 0.08|e|, respectively. These Δq values are comparable to that observed on Co–N4 catalyst models with neighboring carbon atoms functionalized with O atoms.13 Subsequently, the Co electronic spin moment (µs) also shifted by 0.1–0.3µB to a comparable value between 0.908–1.060µB after adsorption (Table S2, ESI†), except for CoPorF/CNT. Its much greater change of 1.012µB (from 0.007 to 1.019µB) is indicative of possible Co spin transition, which can significantly alter the electronic properties and catalytic activity of CoPorF/CNT. Therefore, the CNT substrate can tweak the Co properties synergistically with the β-substituents.
We then predicted the ORR activity of these catalyst models by analyzing the interaction between the Co center and different ORR intermediates. In the preferential edge-on adsorption model, the Co–O interaction will be governed by the σ-type bond formed by the non-bonding Co-dz2 orbital and the oxygen π* anti-bonding orbital.21,22 We performed a qualitative comparison using the Co-dz2 orbital center (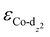 ) determined from their spin-polarized pDOS (Fig. S4, ESI†). The
) determined from their spin-polarized pDOS (Fig. S4, ESI†). The 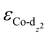 of the HMC models exhibit a monotonous correlation to the binding energies of the *O2 (EO2, * denotes the adsorption site, Fig. 2(b)) and other intermediates (e.g., *OOH, EOOH and *HOOH, EHOOH, Fig. S5, ESI†). The electron-donating ethyl substituent shifted the
of the HMC models exhibit a monotonous correlation to the binding energies of the *O2 (EO2, * denotes the adsorption site, Fig. 2(b)) and other intermediates (e.g., *OOH, EOOH and *HOOH, EHOOH, Fig. S5, ESI†). The electron-donating ethyl substituent shifted the 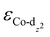 (−1.12 eV) closer to the Fermi level than CoPorH/CNT (−2.30 eV), leading to the strongest O2 affinity among the HMCs with the most negative intermediate binding energies (EO2 = −0.84 eV, Fig. 2(c), all binding energy values are listed in Table S3, ESI†). The electron-withdrawing substituents lower the
(−1.12 eV) closer to the Fermi level than CoPorH/CNT (−2.30 eV), leading to the strongest O2 affinity among the HMCs with the most negative intermediate binding energies (EO2 = −0.84 eV, Fig. 2(c), all binding energy values are listed in Table S3, ESI†). The electron-withdrawing substituents lower the 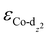 of CoPorBr/CNT (−2.84 eV) and CoPorF/CNT (−2.52 eV) and reduce their intermediate binding strength. Based on our previous theoretical and experimental observation, the adsorption of *O2 and *HOOH should be neither too strong nor too weak for efficient reactant and product turnover, which suggested that a near-zero binding energy difference between *O2 and *HOOH (ΔE = |EO2 − EHOOH|) should benefit H2O2 formation.10 The smallest ΔE found on CoPorBr/CNT (0.29 eV, Fig. 2(c)) suggested it should exhibit the highest H2O2 selectivity, followed by CoPorF/CNT (0.32 eV), CoPorH/CNT (0.39 eV), and CoPorEt/CNT (0.44 eV). This trend also agreed well with the less expanded O–O bond found in the geometry-optimized CoPorBr/CNT (1.278 Å) and CoPorF/CNT models (1.279 Å), as shown in Fig. S6 (ESI†), which can suppress O2 dissociation and benefit H2O2 formation.23
of CoPorBr/CNT (−2.84 eV) and CoPorF/CNT (−2.52 eV) and reduce their intermediate binding strength. Based on our previous theoretical and experimental observation, the adsorption of *O2 and *HOOH should be neither too strong nor too weak for efficient reactant and product turnover, which suggested that a near-zero binding energy difference between *O2 and *HOOH (ΔE = |EO2 − EHOOH|) should benefit H2O2 formation.10 The smallest ΔE found on CoPorBr/CNT (0.29 eV, Fig. 2(c)) suggested it should exhibit the highest H2O2 selectivity, followed by CoPorF/CNT (0.32 eV), CoPorH/CNT (0.39 eV), and CoPorEt/CNT (0.44 eV). This trend also agreed well with the less expanded O–O bond found in the geometry-optimized CoPorBr/CNT (1.278 Å) and CoPorF/CNT models (1.279 Å), as shown in Fig. S6 (ESI†), which can suppress O2 dissociation and benefit H2O2 formation.23
We further compared the theoretical ORR potentials in Fig. 2(d) from the calculated Gibbs free energy (G) schemes along the 2e−-ORR and the 4e−-associative and 4e−-dissociative ORR pathways (the elementary steps are provided in the Experimental section). The calculated G values obtained at U = 0 V are listed in Table S4 (ESI†), and the energy diagrams obtained at different U are compared in Fig. S7–S11 in ESI.†
We firstly examine the 2e−-ORR activity of the HMCs. CoPorH/CNT and CoPorF/CNT exhibit a comparable theoretical potential of 0.485 V and 0.482 V, respectively. This performance is superior to CoPorEt/CNT and CoPorBr/CNT catalysts. The potential determining step (PDS) of the CoPorEt/CNT catalyst has changed from the *OOH formation to the *HOOH formation due to its strong binding strength to the intermediates, leading to a decreased theoretical potential of 0.454 V. CoPorBr/CNT catalyst exhibits the smallest ORR potential of 0.423 V among the HMCs. Its weak intermediate binding capability further imposes a 0.147 eV barrier for the initial O2 adsorption.
All HMCs models can proceed with the 4e−-OOH dissociative pathway, affording a similar trend in the theoretical potentials to that of the 2e−-ORR pathway (Fig. 2(d)). The activities of CoPorH/CNT (0.601 V) and CoPorEt/CNT (0.599 V) are comparable. They exhibit a large potential difference between the 2e−-ORR and 4e−-ORR of 0.116 V and 0.145 V, respectively, suggesting they would initiate 4e−-ORR at a more positive potential and afford a lower selectivity toward H2O2. On the contrary, this potential difference is much smaller for CoPorF/CNT (0.047 V) and CoPorBr/CNT (0 V). It is also notable that the O–O bond breakage step (*OOH → *O + OH*) would apply a thermodynamic barrier, forming a rate-determining step (RDS) for all catalysts (Fig. S11, ESI†).24 CoPorEt/CNT exhibited the greatest barrier of 1.31 eV in this step, resulting in significantly lower catalytic activity even though it has the second-lowest ORR overpotential along the 4e−-OOH dissociative pathway. We also found that the 4e−-HOOH dissociative pathway is prohibited on CoPorF/CNT since it cannot stabilize two *OH adsorbed simultaneously. Therefore, the electron-withdrawing β-substituents, i.e., F and Br, can weaken the Co–O interaction, affording a near-optimal intermediate adsorption energy scheme for H2O2 formation. In terms of the substituent types, our calculation results predict a qualitative ORR activity trend that H ≈ F > Et > Br and an H2O2 selectivity trend that Br > F > H > Et.
Synthesis and characterization of heterogeneous molecular catalysts
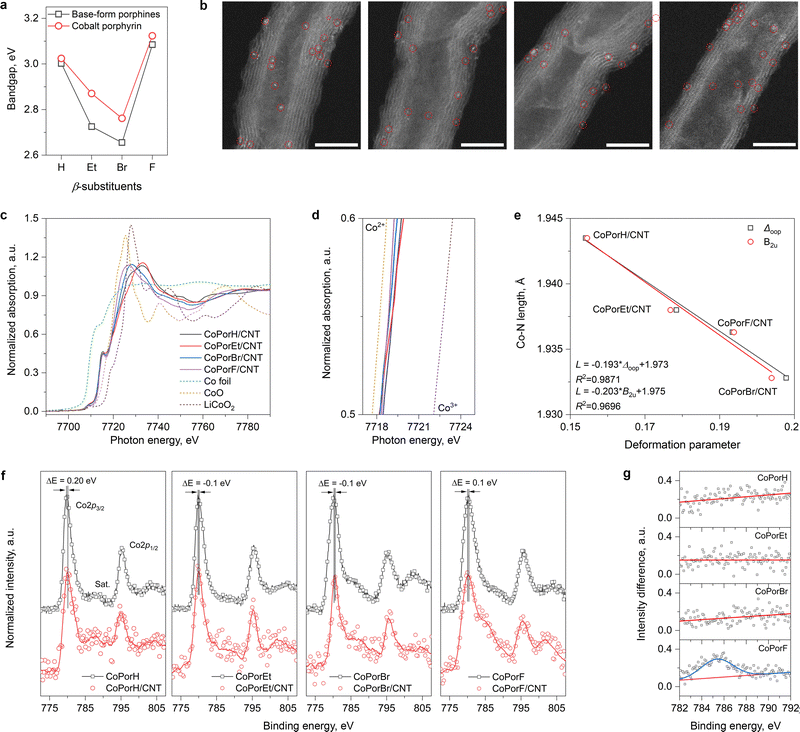
Guided by our theoretical rationales, the β-substituted porphines and cobalt porphyrins were synthesized accordingly (details in the Experimental section). Ultraviolet-visible absorption spectra (UV-vis) of the porphines exhibit a strong Soret peak at ∼400 nm and quadruple Q-band peaks between 500–700 nm (Fig. S12a, ESI†). After cobalt metalation, the Soret peaks blue-shift by different extents and quadruple Q-band peaks degenerate into a single peak due to the improved molecule symmetry (Fig. S12b, ESI†). The bandgap estimated from the Soret peak (Fig. 3(a)) and its changes before and after metallation agree well with our calculation (Table S5, ESI†). The work functions of the cobalt porphyrins (4.6 to 4.9 eV) and the CNT substrate (5.1 eV) determined from ultraviolet photoelectron spectra (UPS, Fig. S13, ESI†) are comparable, allowing efficient electron transfer.Heterogeneous molecular catalysts are then prepared by loading the cobalt porphyrins on a carbon nanotube substrate in N,N′-dimethylformamide (DMF), followed by filtration and washing (details in Experimental section). The purities of the CNT substrate are confirmed by electron microscopic and spectroscopic tests (Fig. S14, ESI†). These HMCs show identical N2 physisorption isotherms (Fig. S15a, ESI†) and a comparable specific surface area of about 180 m2 g−1. Inductively coupled plasma atomic emission spectroscopy measurements further offer a similar Co loading of around 0.2 wt% (Fig. S15b and c, ESI†). Their X-ray diffraction patterns (XRD) only exhibit peaks that can be assigned to the graphitic carbon of the CNT substrates. These physicochemical properties are summarized in Table S6 (ESI†). The high-angle annular dark-field scanning transmission electron microscopic (HAADF-STEM) images of the HMCs are displayed in Fig. 3(b). Highly dispersed bright dots correspond to the individual cobalt atom in porphyrin molecules, while no porphyrin aggregates can be observed. Their corresponding energy-dispersive X-ray spectroscopic elemental mapping results (EDX, Fig. S16, ESI†) further confirm the uniform elemental distribution in these HMCs.
The normalized Co K-edge X-ray near-edge absorption spectra (XANES) of the HMCs are compared in Fig. 3(c) with Co foil, CoO, and LiCoO2 references. The pre-edge peak at 7715 eV (1s → 4p transition) is indicative of Co with a D4h symmetry in the porphyrin cores. The magnified edge region displayed in Fig. 3(d) suggests the Co valence state in different β-substituted porphyrins is close to 2+ with a slight difference. The extended X-ray absorption fine structures (EXAFS) of these catalysts are further analyzed. Compared to Co-foil, the wavelet-transformed EXAFS contour plots of the HMCs all exhibit a strong single peak in the first shell (Fig. S17a, ESI†). The R-space fitting results also confirm that the Co-atoms are atomically dispersed with a Co–N4 structure (Fig. S17b fitting parameters are listed in Table S6, ESI†). Compared to CoPorH/CNT, the slightly reduced Co–N bond length found in other HMCs (Table S6, ESI†) are consistent with our theoretical models, which can be attributed to the porphyrin conformation changes induced by the β-substituents.25 It should be noted that such porphyrin conformation change will not impact the Co center symmetry. As shown in Fig. 3(e), we can establish good correlations between the Co–N bond length and the porphyrin core distortion parameter (Δoop, Table S7, ESI†) determined from the normal-coordinate structural decomposition analysis.26,27 Further analysis suggests that the porphyrin core deformation is mainly caused by the saddle distortion (B2u, Fig. 3(e)), which becomes more significant with a β-substituent of greater size and/or molecule weight.
We further collected the high-resolution Co 2p X-ray photoelectron spectra (XPS, Fig. 3(f)) of the porphyrins before and after loading on the CNT substrate. All spectra exhibit the spin–orbit split 2p3/2 and 2p1/2 peaks at about 780 eV and 795 eV. A small peak shift of about 0.1–0.2 eV was found for all Co porphyrins after adsorption on the CNT substrate. CoPorH/CNT and CoPorF/CNT, which would lose 0.08–0.11|e|, would have their 2p3/2 peaks shift to higher binding energy, while CoPorEt/CNT and CoPorBr/CNT exhibited an opposite trend. This observation agrees with earlier works,13 confirming the strong electronic interaction between the adsorbed porphyrin molecules and the CNT substrate. Interestingly, only CoPorF/CNT exhibits significant line shape change in the satellite peak region before and after adsorption on the CNT substrate. The spectra differences in the 2p3/2 satellite peak region are calculated and compared in Fig. 3(g). The emergence of a prominent 2p3/2 satellite peak at ca. 785 eV for the CoPorF sample is indicative of a possible Co spin crossover,28,29 which is consistent with our theoretical calculation results.
ORR performance in three-electrode test
The HMC ORR performance was assessed on a calibrated rotary platinum ring-glassy carbon disk electrode (RRDE) at an optimal loading of 0.01 mg cm−2 (Experimental section, Fig. S18, ESI†). The linear sweep voltammetry (LSV) curves collected in an acidic 0.1 M HClO4 were displayed in Fig. 4(a). All HMCs exhibit prominent ring and disk currents after 0.7 volts versus a reversible hydrogen electrode (VRHE). Compared to the negligible activity of the CNT substrate, the catalytic currents of the HMCs can be assigned to the Co sites. CoPorF/CNT exhibits a small onset potential difference of 20 mV to CoPorH/CNT (Table 1). CoPorEt/CNT and CoPorBr/CNT show higher ORR onset potentials (Table 1) and smaller disk and ring currents, which agrees well with our theoretically predicted catalytic activity trend among them, i.e., H ≈ F > Et > Br.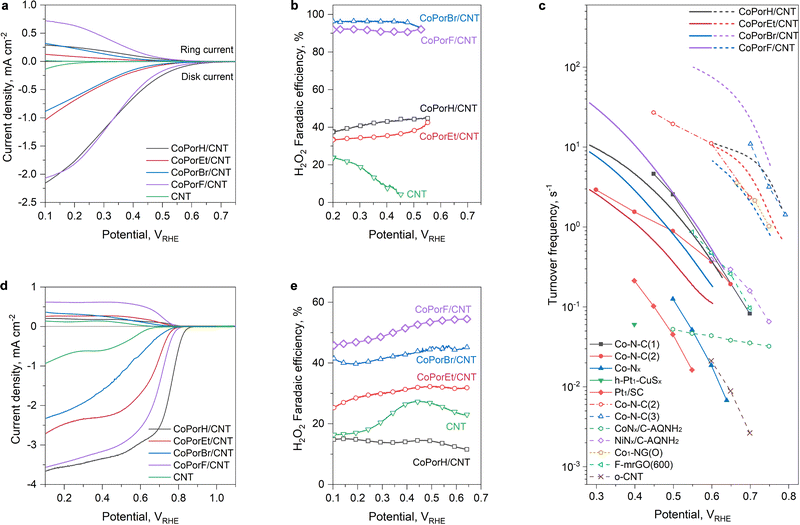 | ||
| Fig. 4 ORR performance obtained from three-electrode measurement. (a) LSV curves and (b) the corresponding H2O2 faradaic efficiency obtained in an O2-saturated 0.1 M HClO4 electrolyte (scan rate: 5 mV s−1, rotation speed: 1600 rpm, without iR-correction). (c) Turnover frequency of the HMCs compared to some recently reported catalysts. Solid line/symbol: from acidic electrolytes; dashed line/open symbol: from alkaline electrolytes. The TOF value of reference single-atom catalysts was either cited directly or calculated using the same method for the HMCs based on their metal content and catalyst loadings (details listed in Tables S8 and S9, ESI†). All metals in these catalysts were assumed active sites, which is also applied to the HMCs. For carbon-based catalysts, the number of active sites was estimated based on oxygen content in the –C–O–C– configuration, which has been recognized as the key ORR active site.7,8 (d) LSV curves and (e) the corresponding H2O2 faradaic efficiency obtained in an O2-saturated 0.1 M KOH electrolyte. | ||
| ORR disk onset potential,a VRHE | ORR ring onset potential,a VRHE | Faradaic efficiency,b % | H2O2 molar fraction,b % | Turnover frequency,b s−1 | Mass activity,b A gcat−1 | Mass activity,b A gCo−1 | |
|---|---|---|---|---|---|---|---|
| a Defined as the potential required to reach a disk or ring current density of 0.025 mA cm−2. b Calculated at an overpotential of 200 mV (or 0.48 VRHE). | |||||||
| CoPorH/CNT | 0.64 | 0.54 | 44.3 ± 1.8 | 61.4 ± 2.1 | 2.08 ± 0.08 | 14.62 | 6647 |
| CoPorEt/CNT | 0.56 | 0.40 | 36.0 ± 1.9 | 52.9 ± 1.7 | 0.47 ± 0.03 | 2.62 | 1540 |
| CoPorBr/CNT | 0.54 | 0.46 | 95.0 ± 1.2 | 97.4 ± 1.3 | 1.05 ± 0.05 | 5.51 | 3443 |
| CoPorF/CNT | 0.62 | 0.56 | 89.3 ± 1.6 | 94.3 ± 1.8 | 3.51 ± 0.06 | 22.01 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 584 584 |
We further calculated the H2O2 selectivity of these HMCs, as compared in Fig. 4(b). With a more than doubled ring current, CoPorF/CNT exhibited a higher H2O2 faradaic efficiency (FE) of 89.3 ± 1.66% (with a corresponding H2O2 molar fraction of 94.3 ± 1.8% at an overpotential of 200 mV) than CoPorH/CNT (FE of 44.3 ± 1.8%, and H2O2 molar fraction of 61.4 ± 2.1%). As predicted, CoPorBr/CNT exhibits the highest H2O2 FE, over 95%, while CoPorEt/CNT is the worst with a FE of ∼36%. The experimentally observed H2O2 selectivity trend of the HMCs is in excellent agreement with our calculated binding energy differences between *O2 and *HOOH (Fig. S19, ESI†). The ORR activity of the catalysts is further compared quantitatively by computing their H2O2 specific turnover frequency (TOF) per Co site and the total mass activity or Co-specific mass activity. CoPorF/CNT can deliver a turnover frequency (TOF) of 3.51 ± 0.06 s−1 at an overpotential of 200 mV, which is superior to other HMCs and recently reported atomic cobalt and other single-atom metal catalysts as compared in Fig. 4(c) (see details in Table S8, ESI†).10–12,16,30–33 It also exhibited a total and Co-specific mass activity of 22.01 A gcat−1 and 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 584 A gCo−1, respectively (Fig. S20, ESI†). These performance descriptors can further reach 13.35 ± 0.11 s−1, 82.95 A gcat−1, and 43
584 A gCo−1, respectively (Fig. S20, ESI†). These performance descriptors can further reach 13.35 ± 0.11 s−1, 82.95 A gcat−1, and 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 656 A gCo−1 at an η of 300 mV.
656 A gCo−1 at an η of 300 mV.
The kinetic performance of the HMCs is further assessed by Tafel analysis (Fig. S21, ESI†) and the reaction orders to O2 and proton concentration (Fig. S22 and S23, ESI†). The results suggest that a proton-coupled electron transfer step (*O2 + H+ + e− → *OOH) can be assigned as the rate-determining step (RDS) for CoPorH/CNT based on its Tafel slope of 114 mV dec−1 and a zero reaction order to H+.11 The RDS gradually switches to the O2 adsorption for CoPorF/CNT (128 mV dec−1) and CoPorBr/CNT (195 mV dec−1). CoPorEt/CNT exhibits the slowest O2 adsorption kinetics with the largest Tafel slope of 226 mV dec−1 and an O2 reaction order of 0.84. We attribute its slow oxygen adsorption mechanism to the hindrance of the extruding+ ethyl substituents, which also results in the greatest onset potential increment in thiocyanate poisoning tests (Fig. S24, ESI†).
All HMCs exhibit improved ORR currents but reduced H2O2 selectivity in an alkaline electrolyte (0.1 M KOH, Fig. 4(d) and (e)). This observation is consistent with earlier reports disclosing the pH-dependent ORR activities of single atom ORR catalysts.34 CoPorF/CNT remains optimal, delivering the highest ring current density (0.62 mA cm−2 at 0.4 VRHE) and an ∼50% H2O2 faradaic efficiency between 0.7 to 0.1 VRHE. It also exhibits the highest TOF (e.g., 85.78 s−1 at 200 mV overpotential, Fig. 4(c)) and mass activity (533.04 A gcat−1 and 280![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 546 A gCo−1) among the HMCs, delivering one of the best performances among recently reports (Fig. S20 and Table S9, ESI†).7,8,13,33,35 Notably, the HMCs exhibit varied performance differences in acidic and alkaline electrolytes, as quantified by the ORR kinetic current densities ratios (jk-alkaline/jk-acid, Fig. S25a, ESI†). We discovered a monotonous correlation between the performance difference and the HMC dipole moment change (Δµ, Fig. S25b and Table S10, ESI†) before and after an oxygenous intermediate adsorption,36 which can guide ORR catalyst design.
546 A gCo−1) among the HMCs, delivering one of the best performances among recently reports (Fig. S20 and Table S9, ESI†).7,8,13,33,35 Notably, the HMCs exhibit varied performance differences in acidic and alkaline electrolytes, as quantified by the ORR kinetic current densities ratios (jk-alkaline/jk-acid, Fig. S25a, ESI†). We discovered a monotonous correlation between the performance difference and the HMC dipole moment change (Δµ, Fig. S25b and Table S10, ESI†) before and after an oxygenous intermediate adsorption,36 which can guide ORR catalyst design.
H2O2 production performance in a two-electrode electrolyser
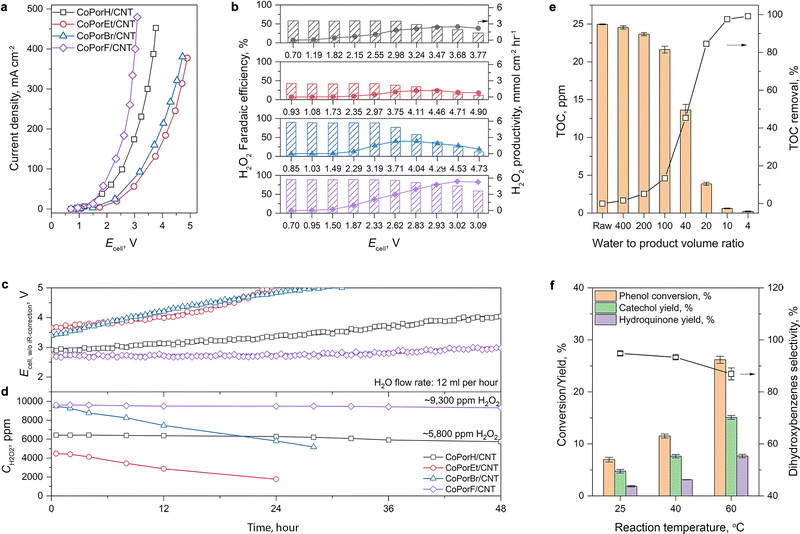
We then assessed the H2O2 production performance of the HMCs in a two-electrode flow cell electrolyzer (Fig. S26a and b, ESI†). The cathode is a 4 cm2 gas-diffusion electrode loaded with 0.5 mg cm−2 catalysts. The anode is IrO2 nanoparticles hot-pressed on a Nafion 212 membrane, which provides protons by anodic oxygen evolution reaction in a 0.5 M H2SO4 electrolyte. A cation-exchange polymer bead (Fig. S26c and d, ESI†) is used as a porous solid-state electrolyte, allowing us to produce an electrolytic ion-free H2O2/water solution from the electrolyzer by using deionized water as the flowing phase.37 The H2O2 concentration in the product is determined by Ce3+/4+ titration (Fig. S27, ESI†).The current–voltage response of the HMCs is compared in Fig. 5(a), and the performance trend is consistent with that obtained from RRDE tests. The optimal CoPorF/CNT surpasses CoPorH/CNT when the cell voltage (Ecell, with 80%-iR corrected) is above 1.6 V, reaching a current density of 464 mA cm−2 at 3.32 V (or 10 V without iR-correction, Fig. S28a, ESI†). It can maintain an over 70% H2O2 faradaic efficiency (Fig. 5(b), or ∼80% H2O2 molar fraction, Fig. S28b and c, ESI†) up to 300 mA cm−2. Meanwhile, no H2 can be detected from the gas stream leaving the cathode chamber by gas chromatography. At an Ecell of 3.02 V, CoPorF/CNT can reach its maximum H2O2 specific current density of 288 mA cm−2 at a device energy efficiency of 6.3% (or 18.2% without iR-correction), which corresponds to H2O2 productivity of 5.38 mmolH2O2 cm−2 h−1 (or 10.76 molH2O2 gcat−1 h−1). Further increasing operation potential will lead to slightly reduced H2O2 selectivity.
The H2O2 production performance and stability of the HMCs are then assessed at a constant current density of 50 mA cm−2. After discharging continuously for 48 hours, the optimal CoPorF/CNT exhibits the smallest Ecell increment of 11% among the HMCs (Fig. 5(c)). At a water flow rate of 12 mL h−1, a 9300 ppm H2O2 solution can be produced continuously, as shown in Fig. 5(d). By reducing the water flow rate, the H2O2 concentration can reach about 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 and 33
400 and 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 ppm at 6 or 3 mL h−1, respectively (Fig. S29, ESI†). The slightly reduced H2O2 concentration can be attributed to the shifted equilibrium of 2e−-ORR to the competing 4e−-ORR pathway at a higher H2O2 concentration.37 Other HMCs show inferior performance and stability. After the 48 hour test, CoPorH/CNT exhibits a 39% Ecell increment, much greater than the CoPorF/CNT. It can produce a ∼5800 ppm H2O2 product at 12 mL h−1 due to its lower H2O2 selectivity, which is about 60% of that obtained from the CoPorF/CNT catalyst. We further evaluated the stability of CoPorF/CNT at a higher current density of 100 mA cm−2 (Fig. S30, ESI†). An H2O2 solution of 18
400 ppm at 6 or 3 mL h−1, respectively (Fig. S29, ESI†). The slightly reduced H2O2 concentration can be attributed to the shifted equilibrium of 2e−-ORR to the competing 4e−-ORR pathway at a higher H2O2 concentration.37 Other HMCs show inferior performance and stability. After the 48 hour test, CoPorH/CNT exhibits a 39% Ecell increment, much greater than the CoPorF/CNT. It can produce a ∼5800 ppm H2O2 product at 12 mL h−1 due to its lower H2O2 selectivity, which is about 60% of that obtained from the CoPorF/CNT catalyst. We further evaluated the stability of CoPorF/CNT at a higher current density of 100 mA cm−2 (Fig. S30, ESI†). An H2O2 solution of 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 ppm can be produced stably over 48 hours continuously at a flow rate of 12 mL h−1, while the voltage has increased by ∼17.1%. The slightly dropped faradaic efficiency may be caused by the higher local H2O2 concentration, which is similar to that observed when a reduced water flow rate was used.
200 ppm can be produced stably over 48 hours continuously at a flow rate of 12 mL h−1, while the voltage has increased by ∼17.1%. The slightly dropped faradaic efficiency may be caused by the higher local H2O2 concentration, which is similar to that observed when a reduced water flow rate was used.
Meanwhile, CoPorEt/CNT and CoPorBr/CNT not only exhibit much inferior performance. They require a higher cell voltage and deactivate quickly. They reach the 5 V cut-off limit at ∼33 and 24 hours, respectively. We further characterized the post-test catalysts to understand their deactivation mechanisms. SEM images and the corresponding EDX mapping results of the post-test catalyst showed negligible surface morphology change (Fig. S31, ESI†), indicating the catalyst deactivation should take place at a molecular level. The post-test XPS measurements exhibited negligible carbon conformation changes (Fig. S32, ESI†). Meanwhile, the nitrogen content remained identical (Fig. S32a, ESI†), suggesting the porphyrin molecules should remain adsorbed on the CNT substrate and excluding the porphyrin desorption as the cause of deactivation. However, the high-resolution N 1s spectra of the HMCs exhibit varied lineshape changes (Fig. S33c–f, ESI†). Deconvolution results suggest an obvious increment of protonated N species (–NH–) in CoPorEt/CNT and CoPorBr/CNT, corresponding to ∼30 at% of the total N population (Fig. S33b, ESI†). The protonated N atoms break the Co–N bond and destabilize the Co center. We observe much weakened Co pre-edge peaks in the post-test XANES measurement and reduced Co–N coordination numbers in these two samples (3.2 and 3.4, Fig. S34 and Table S11, ESI†). Consequently, a 45 at% and 37 at% Co loss has been found for CoPorEt/CNT and CoPorBr/CNT by ICP-AES measurement (Fig. S35, ESI†). The greater size of the Et and Br substituents could result in heavier porphyrin molecule distortion.38 We also calculated the deformation parameters of the porphyrin cores with different ORR intermediate adsorbed. Our results suggest that the intermediates adsorbed CoPorEt and CoPorBr models exhibit much more significant porphyrin core distortion along the ORR pathways (from *O2, *OOH, *O + *OH, to 2*OH adsorption, Fig. S36, ESI†). On the contrary, CoPorF/CNT models become flattened with improved structural integrity, suggesting the β-substituents can also control the Co–N4 active site stability for electrochemical H2O2 synthesis.
We can directly utilize the H2O2 solution produced by the CoPorF/CNT catalyst for various applications. This solution can be used for water treatment, for example, reducing the total organic carbon (TOC) in groundwater or organic dye removal by the Fenton-like reaction. We mixed the H2O2 solution (ca., 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm) produced from the 4 cm2 electrolyzer (operating at 50 mA cm−2 and a water flow rate of 6 mL h−1) with groundwater at different volume ratios and measured the remnant TOC. A maximum treatment capacity of 21.5 mL groundwater per square centimeter of electrode per hour (mL cm−2electrode h−1) can be obtained, reducing the TOC from 25 ppm to below 2 ppm to comply with the US drinking water level (volume ratio obtained by interpolation Fig. S37, ESI†) at ambient temperature (about 5–15 °C for wintertime at Sydney, Australia).37 This capacity can further increase to 37.9 mL cm−2electrode h−1 if tested at a controlled temperature of 25 °C. This solution can also oxidize high-concentration organic dyes via the Fenton reaction. For example, we added 1 mL of the H2O2 solution (produced at 50 mA cm−2 and a water flow rate of 6 mL h−1) to 5 mL of acidified 100 ppm methylene blue (MB), orange G (OG), or rhodamine B (RB) dye solutions containing 2 mM Fe2+. After brief mixing, the dye solutions quickly fade (Fig. S38a and b, ESI†). After 30 min, UV-vis measurements suggest that over 99% of the dye molecules can be effectively removed (Fig. S38c, ESI†).
000 ppm) produced from the 4 cm2 electrolyzer (operating at 50 mA cm−2 and a water flow rate of 6 mL h−1) with groundwater at different volume ratios and measured the remnant TOC. A maximum treatment capacity of 21.5 mL groundwater per square centimeter of electrode per hour (mL cm−2electrode h−1) can be obtained, reducing the TOC from 25 ppm to below 2 ppm to comply with the US drinking water level (volume ratio obtained by interpolation Fig. S37, ESI†) at ambient temperature (about 5–15 °C for wintertime at Sydney, Australia).37 This capacity can further increase to 37.9 mL cm−2electrode h−1 if tested at a controlled temperature of 25 °C. This solution can also oxidize high-concentration organic dyes via the Fenton reaction. For example, we added 1 mL of the H2O2 solution (produced at 50 mA cm−2 and a water flow rate of 6 mL h−1) to 5 mL of acidified 100 ppm methylene blue (MB), orange G (OG), or rhodamine B (RB) dye solutions containing 2 mM Fe2+. After brief mixing, the dye solutions quickly fade (Fig. S38a and b, ESI†). After 30 min, UV-vis measurements suggest that over 99% of the dye molecules can be effectively removed (Fig. S38c, ESI†).
Moreover, we demonstrate that the H2O2 produced from the CoPorF/CNT can be further activated in situ for the selective phenol hydroxylation reaction. Ferrocene molecules are adsorbed on the polymer beads at a concentration of 0.3 wt%, serving as the H2O2 activation catalyst.39 We operate the electrolyzer at 50 mA cm−2 and a reduced water flow rate of 1.5 mL h−1 to increase the local H2O2 concentration and extend the resident time to about 10 min. After stabilizing the electrolyzer for 30 min, the DI water stream is switched to an aqueous phenol solution (50 mg mL−1) for 1 hour. Catechol and hydroquinone are identified as the main products in the effluent by liquid chromatography. The phenol conversion can reach 7.0% at 25 °C and gradually increase to 11.5% and 26.2% at a higher reaction temperature of 40 and 60 °C, respectively (Fig. 5(f)). The catechol yield is 15.1% at 60 °C. However, the overall selectivity towards dihydroxybenzene (catechol and hydroquinone) has dropped slightly from 94.7% to 86.9% at a higher reaction temperature. Meanwhile, the molar ratio between catechol and hydroquinone slightly decreased from 2.2 to 1.36. No Co (from the CoPorF/CNT catalyst) or Fe (from the ferrocene-adsorbed polymer beads) can be detected from the effluent, showing great promise for integrating H2O2 electrochemical synthesis with chemical production processes.
Conclusion
In summary, we demonstrate a structure explicit heterogeneous molecular catalyst from β-substituted cobalt porphyrin and carbon nanotube substrate for high-performance electrochemical H2O2 synthesis. Our theoretical calculation shows that the β-site substituents can effectively control the electronic properties and catalytic activity of the Co active center with the carbon nanotube substrate. An electron-withdrawing fluoro substituent has been predicted as optimal and further validated by our experimental catalytic assessments. We also find that the β-substituents can also impact the stability of the catalysts by affecting the porphyrin conformation changes. The optimal CoPorF/CNT catalyst exhibits a large turnover frequency of 3.51 and 85.1 s−1 for H2O2 synthesis in acidic and alkaline electrolytes, respectively. It can reach a mass activity of 10.76 molH2O2 gcat−1 h−1 in a two-electrode electrolyzer, producing a pure H2O2 water solution ideal for water treatment and chemical synthesis. Our catalyst synthesis strategy demonstrated here offers an excellent opportunity to understand the fundamentals between the catalytic performance of a single-atom active center and its local environment, which can be expanded to develop high-performance catalysts for reactions beyond ORR.Experimental section
Computational method
The molecule orbitals of the porphyrin molecules used in this study were calculated using Gaussian 09 program at the B3LYP/6-311++G(d,p) level with the geometry optimized models. Spin-polarised DFT calculations were performed using the Vienna Ab initio Simulation Package (VASP), where the valence electrons were considered by the Kohn–Sham wave functions expanded in a plane-wave basis set.40 Electron correlations were considered by the generalized gradient approximation method with the functional developed by Perdew, Burke, and Ernzerhof.41,42 Core electrons were considered by the projector augmented-wave method.43The geometries of the models were considered fully relaxed when all the forces became lower than 0.05 eV Å−1. The Brillouin zone was sampled by the Γ-point. Entropic contributions (with a temperature of 298 K) and zero-point energy corrections were added to the free energy calculations, with the data referred from ref. 44. The Co d-orbital centers were calculated from their partial density of states in the range of −5 to 5 eV. The binding energies of O2 and HOOH were respectively calculated by referring to the total energies of O2 and HOOH in vacuum.
Based on the computational hydrogen electrode method,44 we computed the ORR free energy diagrams along three-different pathways, including 2e−-ORR towards H2O2 formation, 4e−-OOH dissociative, and 4e−-HOOH dissociative pathways towards H2O formation. The optimized geometries are displayed in Fig. S7–S9 (ESI†). The following elementary steps were analyzed, where * denotes the active site.10 Shared elementary steps:
| O2 + * → *O2 | (1) |
| *O2 + H+ + e− → *OOH | (2) |
| *OOH + H+ + e− → *HOOH | (3) |
For 2e−-ORR:
| *HOOH → H2O2 + * | (4) |
For 4e−-OOH dissociative ORR pathway:
| *OOH + H+ + e− → *O + *OH | (5) |
| *O + *OH + H+ + e− → *O + H2O | (6) |
| *O + H+ + e− + H2O → *OH + H2O | (7) |
| *OH + H+ + e− + H2O → *H2O + H2O | (8) |
For 4e−-HOOH dissociative ORR pathway:
| *HOOH → 2*OH | (9) |
| *2OH + H+ + e− → *OH + H2O | (10) |
| *OH + H+ + e− + H2O → *H2O + H2O | (11) |
Chemicals
5,10,15,20-Tetraphenyl porphine (PorH, ≥99%), dichloromethane (CH2Cl2, anhydrous), boron trifluoride diethyl etherate (BF3·OEt2, ≥46.5% BF3 basis), 2,3-dichloro-5,6-dicyano-1,4-benzoquinone (DDQ, 98%), cobalt(II) acetate (99.99% trace metals basis), sodium sulfate (Na2SO4, anhydrous, ≥99%), potassium nitrate (KNO3, anhydrous, ≥99%), potassium hydroxide (semiconductor grade, pellets, 99.99% trace metals basis), potassium thiocyanate (KSCN, ≥99%), cerium sulfate tetrahydrate (Ce(IV)(SO4)2, ≥98%), potassium ferricyanide(III) (K3Fe(CN)6, ≥99%), N,N′-dimethylformamide (DMF, ≥99%), methanol (anhydrous, 99.8%), isopropanol (IPA, ≥99.5%), chloroform-d (CDCl3, 99.96% D), toluene (anhydrous, 99.8%), methylene blue (MB, ≥97.0%), rhodamine B (RB, ≥95%), orange G (OG, 80%), ferrocene (FeCp2, 98%), phenol (≥99%), 1,2-dihydroxybenzene (catechol, ≥99%), hydroquinone (≥99%), hydrochloric acid (HCl, 37%), perchloric acid (HClO4, 70%), phosphoric acid (H3PO4, 85 wt% in H2O), and Nafion 117 solution (∼5% in a mixture of lower aliphatic alcohols and water) were obtained from Sigma-Aldrich. 3,4-Diethyl-1H-pyrrole (≥95%), 3,4-dibromo-1H-pyrrole (≥95%) and 3,4-difluoro-1H-pyrrole (98%) were obtained from AmBeed Inc. Chemicals were used without purification. Deionized water (18 MΩ cm−1) was produced from a Milli-Q Simplicity UV water purification system. Oxygen (O2, 99.999%), argon (Ar, 99.999%), and 5% hydrogen in argon (H2/Ar) mixture gas was purchased from BOC Limited. Iridium oxide (IrO2) and Nafion 211 membrane were obtained from the Fuel Cell Store. A cation exchange polymer resin (Purolite® CT275, batch no. 126S/19/6) was gifted from Purolite® Pty Ltd. Multi-walled carbon nanotubes with a diameter of 10–20 nm were obtained from CNano Inc. and purified by sonication in 3 M HCl aqueous solution for 30 mins, followed by refluxing in the acid for 6 h. The nanotubes were then recovered by filtration and washed with a large amount of deionized (DI) water. After drying under vacuum, the nanotubes were further thermal annealed at 1500 °C for 3 h in a 5% H2/Ar flow.Synthesis of β-substituted porphines
The ethyl-substituted 2,3,7,8,12,13,17,18-octaethyl-5,10,15,20-tetraphenyl porphine (H2PorEt) was synthesized following a reported method at a reduced scale.45 Briefly, an equal mole of 3,4-diethyl-1H-pyrrole (123.2 mg, 1 mmol) and benzaldehyde was added in 100 mL anhydrous CH2Cl2 under Ar protection. After 15 min stirring, 40 µL BF3·OEt2 was added. The mixture was further stirred for one hour in the dark before DDQ (160 mg, 0.66 mmol) was added and stirred under reflux for 30 min, affording a green solution. After concentration, the solid product was recovered by filtration and further purified by silica gel column chromatography using a 2 vol% CH3OH/CH2Cl2 solution. The green portion was recovered and dried under vacuum, affording H2PorEt as deep-blue crystals with a yield of 42%. 1H NMR (CDCl3, 500 MHz): δ = −2.01 (s, 2H, NH), 0.44 (t, 24H, CH3), 1.90 and 2.61 (m, 16H, CH2), 7.66 (m, 8H, m-H), 7.72 (m, 4 H, p-H), 8.32 (m, 8H, o-H).Bromo-substituted 2,3,7,8,12,13,17,18-octabromo-5,10,15,20-tetraphenyl porphine (H2PorBr) and fluoro-substituted 2,3,7,8,12,13,17,18-octafluoro-5,10,15,20-tetraphenyl porphine (H2PorF) were synthesized following a reported method that is similar to the synthesis of H2PorEt.46 While all chemicals and steps were kept the same, 3,4-dibromo-1H-pyrrole (225 mg, 1 mmol) or 3,4-difluoro-1H-pyrrole (102 mg, 1 mmol) was used instead of 3,4-diethyl-1H-pyrrole. The crude compound obtained from concentration and filtration was further purified by silica gel column chromatography, yielding H2PorBr and H2PorF in the form of brownish crystals with a yield of 53% and 66%, respectively. H2PorBr 1H NMR (CDCl3, 500.1 MHz,): δ = −4.20 (s, 2H, NH), 7.68 (t, 8H, m-H), 7.72 (t, 4H, p-H), 8.01 (d, 8H, o-H); H2PorF 1H NMR (CDCl3, 500.1 MHz): δ = −4.20 (s, 2H, NH), 7.67 (t, 8H, m-H), 7.71 (t, 4H, p-H), 8.01 (d, 8H, o-H).
Synthesis of cobalt metallated porphyrins
The metallation was achieved by dissolving the porphines (200 mg) and cobalt(II) acetate (200 mg, 1.130 mmol) in 20 mL methanol. Afterwards, 90 mL CHCl3 and 30 mL DMF were added, and the mixture was stirred at 80 °C under Ar for 24 h. After cooling to room temperature, the mixture was washed with DI water (3 × 100 mL) in a separatory funnel before the organic layer was collected and dried over anhydrous Na2SO4. The solid product was further dried under vacuum to afford cobalt metallated porphyrins, and the products were denoted as CoPorH, CoPorEt, CoPorBr and CoPorF.Synthesis of heterogeneous molecular catalysts
The catalyst was then prepared by loading the metalated porphyrins on purified carbon nanotubes. Briefly, about 3 mg of the metalated porphyrins and 20 mg of purified MWCNT were dissolved in 20 mL DMF. After 30 min ultrasonication, the mixture solution was further stirred under Ar protection for 24 hours before the solids were recovered from filtration. The solids were washed with DMF and ethanol before being dried under vacuum at 80 °C overnight.Physiochemical characterization
UV-vis absorption spectra were collected on a Shimadzu UV-3600 spectrometer by dissolving the porphines and porphyrins in CH2Cl2 with a 10 mm light path length quartz cuvette. NMR results were obtained on a Bruker Avance III spectrometer. SEM images were collected on a Zeiss Ultraplus microscope. HAADF-STEM images were obtained on an FEI Themis-Z microscope. The metal loading of catalysts was determined by inductively coupled plasma optical emission spectroscopy (ICP-AES) on a PerkinElmer Avio 500 spectrometer. Samples were digested in concentrated HNO3 and diluted accordingly for tests. UPS and XPS measurement was performed on a Thermo Scientific K-Alpha+ spectrometer. A He(I) line (21.2 eV) was used for UPS, and an Al Kα source (1486.3 eV) was used for XPS. UPS spectra were collected at an energy step of 0.05 eV. The XPS survey scans were collected at an energy step of 1 eV in CAE mode, with a pass energy of 200 eV. The high-resolution scans were collected at a step of 0.1 eV with a pass energy of 50 eV. The spectra were then deconvoluted following the reported parameters.47 Synchrotron-illuminated XAS spectra were collected in fluorescence mode at the BL-12B2 beamline at Taiwan National Synchrotron Radiation Research Center. Chromatic energies were tuned by a double crystal Si (111) monochromator, and the fluorescence signals were recorded using a Lytle detector. The near-edge spectra and Fourier-transform extended X-ray absorption fine structure spectra analysis and fitting were performed in the Demeter Software package using the FEFF 9.0 code.Porphyrin core conformation assessment
The distortion parameters of the porphyrin core confirmation were determined by the normal-coordinate structural decomposition method developed by Liptak et al.26,27 Structural files were created from the geometry-optimized porphyrin models. The square root of the sum of squares of out-of-plane distortions, Δoop, can be used as a single overall parameter to compare the distortion level of the porphyrin cores. Four principal modes of porphyrin core out-of-plane deformation were considered in terms of the saddle (B2u), ruffle (B1u), dome (A2u), and wave (Eg(x) or Eg(y)) were computed.25 Results listed in Table S6 (ESI†) suggest that the out-of-plane saddle-shaped deformation dominated porphyrin distortion.Electrochemical test
The electrochemical ORR activity was evaluated under a conventional three-electrode configuration on a CHI760 electrochemical workstation. A rotary ring-disk electrode (RRDE, E6R2, Pine Instrument, collection efficiency N = 0.379 as calibrated by a Fe(CN)62+/3+ redox method, Fig. S19, ESI†) was used as the working electrode. The glassy carbon disk and Pt ring area were 0.2375 and 0.2355 cm2, respectively. A pre-calibrated Ag/AgCl electrode (3 M KCl filling, Basi, MF-2056) and a Hg/HgO (0.1 M KOH filling) were used as a reference in acidic (0.1 M HClO4) and alkaline (0.1 M KOH) electrolytes, respectively. The counter electrode is a graphite rod electrode (Pine, AFCTR3B). All reported potential was corrected versus the reversible hydrogen electrode (VRHE).The catalyst ink was prepared by dispersing 5 mg catalyst in 1 mL water/isopropanol solution (1/9 = v/v, containing 0.05% Nafion 117) by 30 min bath sonication. The ink was drop-casted on the disk electrode at an optimal mass loading of 0.01 mg cm−2. ORR measurement was performed in O2 saturated electrolyte, and the linear sweep voltammetry (LSV) polarization curves on the disk (idisk) were recorded at 5 mV s−1 without iR-compensation, while the ring current (iring) was collected by biasing the Pt-ring electrode at 1.2 VRHE. The currents were corrected with the background currents obtained in Ar-saturated electrolytes. The H2O2 faradaic efficiency (FE, %) under the RRDE configuration was determined using eqn (12) from a reported method:48
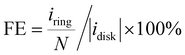 | (12) |
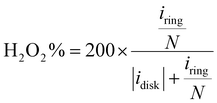 | (13) |
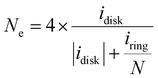 | (14) |
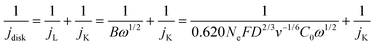 | (15) |
| jK-H2O2 = jK·FE | (16) |
| TOF = jK-H2O2/(0.01·Co wt%/MwCo)/n·F | (17) |
| Mass activitytotal = jK-H2O2/0.01 | (18) |
| Mass activityCo = Mass activitytotal/Co wt% | (19) |
Kinetic analysis was performed based on the calculated jK-H2O2. Reaction order analysis was performed by tuning O2 concentration and electrolyte pH. The O2 concentration was controlled by using Ar to dilute the O2 gas stream at a flow rate ratio of 0 (pure O2), 1/3 (75% O2), 1 (50% O2), and 3 (25% O2). The reaction order to H+ was measured in a series of pH-controlled phosphoric acid buffers.49 Briefly, the KOH pellet and concentrated KOH solution were added to a 0.1 M H3PO4 solution to tune the electrolyte pH to ∼1.5, 2.0, 2.5 and 3.0. ORR LSV curves were then obtained at different conditions with a rotation speed of 1600 rpm and a scan rate of 5 mV s−1.
Flow-cell electrolyzer test
The catalyst ink was spray-coated on a gas diffusion electrode (2 × 2 cm2) at a loading of 0.5 mg cm−2, and it was used as the cathode for ORR. IrO2 nanoparticles were deposited on a Nafion 211 membrane at 0.5 mg cm−2 as the anode to catalyze the oxygen evolution reaction using a 0.5 M H2SO4 solution circulating in the anode chamber at 20 mL h−1. A cation exchange polymer resin, Purolite® CT275 (batch# 126S/19/6), was gifted from Purolite Pty Ltd and used to fill the gap between cathode and anode (2 × 2 × 0.25 cm3) to form a porous solid-state electrolyte. The H+ produced at the anode was transduced to the cathode across the Nafion membrane and the proton-conductive solid-state electrolyte. DI water was supplied to this porous electrolyte using a peristaltic pump at a tunable flow rate to wash out the as-produced H2O2. The iR-corrected electrolyzer voltage (Ecell) was calculated at an 80% level (to avoid over-correction) using eqn (20):Ecell = Ecell,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) w/o w/o![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) iR-correction − 80%·I·R iR-correction − 80%·I·R | (20) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) w/o
w/o![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) iR-correction is the applied voltage, I is the corresponding current, and R is the ohmic resistance measured from electrochemical impedance spectroscopy test at different operating conditions. Subsequently, the device energy efficiency was calculated by:
iR-correction is the applied voltage, I is the corresponding current, and R is the ohmic resistance measured from electrochemical impedance spectroscopy test at different operating conditions. Subsequently, the device energy efficiency was calculated by:Energy efficiency = ΔE0/Ecell,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) w/o w/o![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) iR-correction iR-correction | (21) |
After the stability test, the used catalysts were recovered by dissembling the electrolyzer and bath sonicating the gas diffusion electrode in ethanol for 30 min. The solids were recovered by centrifuge and used for ICP-AES and XAS measurements.
H2O2 concentration determination and catalyst productivity calculation
A Ce4+/3+ titration method was used to determine H2O2 concentration (CH2O2). The standard curve is displayed in Fig. S27 (ESI†).| 2Ce4+ + H2O2 → 2Ce3+ + 2H+ + O2 | (22) |
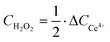 | (23) |
By using the experimentally determined H2O2 concentration, the FE (%) and the H2O2 productivity (in terms of electrode area or catalyst mass) of the electrolyzer were calculated using eqn (24)–(26):
| FE = 2·CH2O2·v·F·t/Q·100% | (24) |
| H2O2 productivity [mmol h−1 cm−2] = CH2O2·(v·10−3)/A | (25) |
| H2O2 productivity [mol h−1 g−1] = CH2O2·(v·10−3)/(A·m) | (26) |
Examples of H2O2 product utilization
We adopted three examples to demonstrate the applications of the H2O2 produced from the optima catalyst.Example 1, groundwater TOC reduction. Groundwater sample was collected from the pond in the School of Chemical and Biomolecular Engineering Building, The University of Sydney. The water was filtered through a 0.22 µm filter disc to remove large particles. The initial total organic carbon (TOC) was determined to be 24.96 ± 0.06 ppm on a Shimadzu TOC-LCSH instrument. The H2O2 solution was produced from the CoPorF/CNT loaded electrolyzer operating at 50 mA cm−2 and a water flow rate of 6 mL h−1. The product was mixed with groundwater at different volumetric ratios (Vwater![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) VH2O2), i.e., 500, 250, 100, 50, 25, 10, 5, 2.5, and 1. The H2O2 concentration in the mixture solution was diluted accordingly, ranging from 18.1 to 9300 ppm. The solution was further stirred for 24 hours before the residue TOC was measured.
VH2O2), i.e., 500, 250, 100, 50, 25, 10, 5, 2.5, and 1. The H2O2 concentration in the mixture solution was diluted accordingly, ranging from 18.1 to 9300 ppm. The solution was further stirred for 24 hours before the residue TOC was measured.
Example 2, organic dye removal via Fenton reaction. Three organic dyes, MB, RB, and OG were dissolved in water to reach 100 ppm at pH = ∼3 with 2 mM Fe2+. About 1 mL of the H2O2 solution (produced at 50 mA cm−2 and a water flow rate of 6 mL h−1) was added to 5 mL of the dye solutions under stirring (volumetric ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the H2O2 was diluted by 6 times to about 3000 ppm). After 30 min reaction, the remnant dye concentration was quantified by UV-vis measurement.
1, the H2O2 was diluted by 6 times to about 3000 ppm). After 30 min reaction, the remnant dye concentration was quantified by UV-vis measurement.
Example 3, in situ phenol hydroxylation reaction. Ferrocene was loaded on the polymer beads as the catalyst for the phenol hydroxylation reaction. About 5 g polymer beads were added to 10 mL toluene with 50 mg ferrocene under stirring for 1 hour. The beads were recovered by filtration and washed with ethanol before they were dried in an oven overnight at 80 °C. The Fe content in the polymer beads was determined by ICP-AES to be 0.30 wt%. These beads were packed in the electrolyzer as a porous solid electrolyte. The electrolyzer loaded with CoPorF/CNT was operated at 50 mA cm−2 and stabilized at 3 mL h−1 DI H2O for 30 min before the flowing phase was switched to a 50 mg mL−1 phenol solution. The volume of the void between the cathode and anode is about 1 cm3. By estimating a porosity of 26% (closely packed equal spheres), the resident time is about 10.4 min. The reaction was tested at 25, 40, and 60 °C by supplying a temperature-controlled reactant solution. The flow was maintained for 1 hour, and the phenol, catechol, and benzoquinone concentration in the effluent were analyzed by high-performance liquid chromatography (HPLC, Shimadzu, LC-20AD) with a reversed-phase column (Kinetex® EVO C18, 100 Å, 150 × 4.6 mm, 5 µm) and a UV detector at 270 nm. Each injection volume is 10 µL, and a 3/7 (v/v) MeOH/H2O solution was used as the mobile phase at a flow rate of 1 mL min−1.50 The phenol conversion rate, catechol and 1,2-benzoquinone yield, and dihydroxybenzene selectivity are calculated using the following equations:
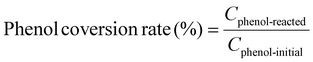 | (27) |
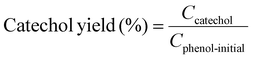 | (28) |
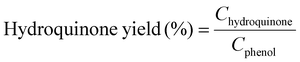 | (29) |
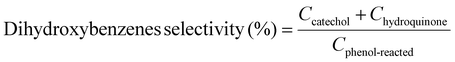 | (30) |
Author contributions
Conceptualization: CL, HL, YC, LW; DFT calculation: CCW, KL, WY, HZ, HL, LW; methodology: CL, ZY, FXS, JXC, JQ, JMC, SZ, LW; funding acquisition: YC, LW; writing – original draft, review & editing: CL, HL, YC, LW.Conflicts of interest
Authors declare no competing interests.Acknowledgements
This work was supported by the Australian Research Council under the Future Fellowship (FT180100232, FT210100218), the University of Sydney for the Commercial Development and Industry Partnerships Fund (CDIP33-2020) and the SDG International Collaboration Program, State Key Laboratory of Clean and Efficient Coal Utilization of Taiyuan University of Technology (SKL2022001). The authors acknowledge the technical and scientific assistance of Sydney Microscopy & Microanalysis, the University of Sydney node of Microscopy Australia, and the computational support from Compute Canada. H. L. acknowledges the Center for Computational Materials Science, Institute for Materials Research, Tohoku University for the use of MASAMUNE-IMR (Project No. 202208-SCKXX-0211) and the Institute for Solid State Physics (ISSP) at the University of Tokyo for the use of their supercomputers. We acknowledge Purolite® Pty Ltd for gifting the resin.References
- R. Ciriminna, L. Albanese, F. Meneguzzo and M. Pagliaro, ChemSusChem, 2016, 9, 3374–3381 CrossRef PubMed
.
-
G. Goor, J. Glenneberg, S. Jacobi, J. Dadabhoy and E. Candido, Ullmann's Encyclopedia of Industrial Chemistry, 2020, pp. 1–40 DOI:10.1002/14356007.a13_443.pub3
.
- S. C. Perry, D. Pangotra, L. Vieira, L.-I. Csepei, V. Sieber, L. Wang, C. Ponce de León and F. C. Walsh, Nat. Rev. Chem., 2019, 3, 442–458 CrossRef CAS
.
- J. S. Jirkovský, I. Panas, E. Ahlberg, M. Halasa, S. Romani and D. J. Schiffrin, J. Am. Chem. Soc., 2011, 133, 19432–19441 CrossRef PubMed
.
- S. Siahrostami, A. Verdaguer-Casadevall, M. Karamad, D. Deiana, P. Malacrida, B. Wickman, M. Escudero-Escribano, E. A. Paoli, R. Frydendal, T. W. Hansen, I. Chorkendorff, I. E. L. Stephens and J. Rossmeisl, Nat. Mater., 2013, 12, 1137–1143 CrossRef CAS PubMed
.
- A. Verdaguer-Casadevall, D. Deiana, M. Karamad, S. Siahrostami, P. Malacrida, T. W. Hansen, J. Rossmeisl, I. Chorkendorff and I. E. L. Stephens, Nano Lett., 2014, 14, 1603–1608 CrossRef CAS PubMed
.
- Z. Lu, G. Chen, S. Siahrostami, Z. Chen, K. Liu, J. Xie, L. Liao, T. Wu, D. Lin, Y. Liu, T. F. Jaramillo, J. K. Nørskov and Y. Cui, Nat. Catal., 2018, 1, 156–162 CrossRef CAS
.
- H. W. Kim, M. B. Ross, N. Kornienko, L. Zhang, J. Guo, P. Yang and B. D. McCloskey, Nat. Catal., 2018, 1, 282–290 CrossRef
.
- Z. Wang, Q.-K. Li, C. Zhang, Z. Cheng, W. Chen, E. A. McHugh, R. A. Carter, B. I. Yakobson and J. M. Tour, ACS Catal., 2021, 2454–2459, DOI:10.1021/acscatal.0c04735
.
- C. Liu, H. Li, F. Liu, J. Chen, Z. Yu, Z. Yuan, C. Wang, H. Zheng, G. Henkelman, L. Wei and Y. Chen, J. Am. Chem. Soc., 2020, 142, 21861–21871 CrossRef CAS
.
- J. Gao, H. b Yang, X. Huang, S.-F. Hung, W. Cai, C. Jia, S. Miao, H. M. Chen, X. Yang, Y. Huang, T. Zhang and B. Liu, Chem, 2020, 6, 658–674 CAS
.
- Y. Sun, L. Silvioli, N. R. Sahraie, W. Ju, J. Li, A. Zitolo, S. Li, A. Bagger, L. Arnarson, X. Wang, T. Moeller, D. Bernsmeier, J. Rossmeisl, F. Jaouen and P. Strasser, J. Am. Chem. Soc., 2019, 141, 12372–12381 CrossRef CAS PubMed
.
- E. Jung, H. Shin, B.-H. Lee, V. Efremov, S. Lee, H. S. Lee, J. Kim, W. Hooch Antink, S. Park, K.-S. Lee, S.-P. Cho, J. S. Yoo, Y.-E. Sung and T. Hyeon, Nat. Mater., 2020, 19, 436–442 CrossRef CAS PubMed
.
- Q. Zhang, X. Tan, N. M. Bedford, Z. Han, L. Thomsen, S. Smith, R. Amal and X. Lu, Nat. Commun., 2020, 11, 4181 CrossRef PubMed
.
- W. Zhang, W. Lai and R. Cao, Chem. Rev., 2017, 117, 3717–3797 CrossRef CAS
.
- P. T. Smith, Y. Kim, B. P. Benke, K. Kim and C. J. Chang, Angew. Chem., Int. Ed., 2019, 59, 4902–4907 CrossRef
.
- R. Zhang and J. J. Warren, J. Am. Chem. Soc., 2020, 142, 13426–13434 CrossRef CAS
.
- S. Dey, B. Mondal, S. Chatterjee, A. Rana, S. Amanullah and A. Dey, Nat. Rev. Chem., 2017, 1, 0098 CrossRef CAS
.
- R. Kumar and M. Sankar, Inorg. Chem., 2014, 53, 12706–12719 CrossRef CAS PubMed
.
- C. F. Hermanns, K. Tarafder, M. Bernien, A. Krüger, Y.-M. Chang, P. M. Oppeneer and W. Kuch, Adv. Mater., 2013, 25, 3473–3477 CrossRef CAS PubMed
.
- K. Liu, Y. Lei and G. Wang, J. Chem. Phys., 2013, 139, 204306 CrossRef PubMed
.
- K. A. Moltved and K. P. Kepp, ChemPhysChem, 2020, 21, 2173–2186 CrossRef CAS PubMed
.
- A. Kulkarni, S. Siahrostami, A. Patel and J. K. Nørskov, Chem. Rev., 2018, 118, 2302–2312 CrossRef CAS PubMed
.
- K. Liu, G. Wu and G. Wang, J. Phys. Chem. C, 2017, 121, 11319–11324 CrossRef CAS
.
- C. J. Kingsbury and M. O. Senge, Coord. Chem. Rev., 2021, 431, 213760 CrossRef CAS
.
- A. B. Graves, M. T. Graves and M. D. Liptak, J. Chem. Phys. B, 2016, 120, 3844–3853 CrossRef CAS PubMed
.
- W. Jentzen, X.-Z. Song and J. A. Shelnutt, J. Chem. Phys. B, 1997, 101, 1684–1699 CrossRef CAS
.
- Y. G. Borod’ko, S. I. Vetchinkin, S. L. Zimont, I. N. Ivleva and Y. M. Shul’ga, Chem. Phys. Lett., 1976, 42, 264–267 CrossRef
.
- T. Ivanova, A. Naumkin, A. Sidorov, I. Eremenko and M. Kiskin, J. Electron Spectrosc. Relat. Phenom., 2007, 156–158, 200–203 CrossRef CAS
.
- I. Yamanaka, R. Ichihashi, T. Iwasaki, N. Nishimura, T. Murayama, W. Ueda and S. Takenaka, Electrochim. Acta, 2013, 108, 321–329 CrossRef CAS
.
- R. Shen, W. Chen, Q. Peng, S. Lu, L. Zheng, X. Cao, Y. Wang, W. Zhu, J. Zhang, Z. Zhuang, C. Chen, D. Wang and Y. Li, Chem, 2019, 5, 2099–2110 CAS
.
- C. H. Choi, M. Kim, H. C. Kwon, S. J. Cho, S. Yun, H.-T. Kim, K. J. J. Mayrhofer, H. Kim and M. Choi, Nat. Commun., 2016, 7, 10922 CrossRef CAS PubMed
.
- X. Li, S. Tang, S. Dou, H. J. Fan, T. S. Choksi and X. Wang, Adv. Mater., 2022, 34, 2104891 CrossRef CAS
.
- W. Zhong, Z. Wang, S. Han, L. Deng, J. Yu, Y. Lin, X. Long, M. Gu and S. Yang, Cell Rep. Phys. Sci., 2020, 1, 100115 CrossRef
.
- H. Gong, Z. Wei, Z. Gong, J. Liu, G. Ye, M. Yan, J. Dong, C. Allen, J. Liu, K. Huang, R. Liu, G. He, S. Zhao and H. Fei, Adv. Funct. Mater., 2022, 32, 2106886 CrossRef CAS
.
- H. Li, S. Kelly, D. Guevarra, Z. Wang, Y. Wang, J. A. Haber, M. Anand, G. T. K. K. Gunasooriya, C. S. Abraham, S. Vijay, J. M. Gregoire and J. K. Nørskov, Nat. Catal., 2021, 463–468, DOI:10.1038/s41929-021-00618-w
.
- C. Xia, Y. Xia, P. Zhu, L. Fan and H. Wang, Science, 2019, 366, 226–231 CrossRef CAS PubMed
.
- M. O. Senge and I. Bischoff, Eur. J. Org. Chem., 2001, 1735–1751 CrossRef CAS
.
- A. Dubey, M. Choi and R. Ryoo, Green Chem., 2006, 8, 144–146 RSC
.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed
.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef
.
- K. M. Barkigia, M. D. Berber, J. Fajer, C. J. Medforth, M. W. Renner and K. M. Smith, J. Am. Chem. Soc., 1990, 112, 8851–8857 CrossRef CAS
.
- J. Leroy, A. Bondon, L. Toupet and C. Rolando, Chem. – Eur. J., 1997, 3, 1890–1893 CrossRef CAS
.
- M. Viera, J. Riquelme, C. Aliaga, J. F. Marco, W. Orellana, J. H. Zagal and F. Tasca, Front. Chem., 2020, 8, 00022 CrossRef CAS PubMed
.
- C. Xia, J. Y. Kim and H. Wang, Nat. Catal., 2020, 3, 605–607 CrossRef CAS
.
- M. Huynh, D. K. Bediako and D. G. Nocera, J. Am. Chem. Soc., 2014, 136, 6002–6010 CrossRef CAS PubMed
.
- A. D. Salazar-Aguilar, G. Vega, J. A. Casas, S. M. Vega-Díaz, F. Tristan, D. Meneses-Rodríguez, M. Belmonte and A. Quintanilla, Catalysts, 2020, 10, 172 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ee02734h |
| This journal is © The Royal Society of Chemistry 2023 |