2-Isopropyl-1,3-dimethylimidazolium as a versatile structure-directing agent in the synthesis of zeolites

Abstract

An organic cation lacking specificity in its structure-directing action offers the possibility, through the screening of other structure-directing parameters, to synthesize a variety of zeolites. In this work we show that the organic structure-directing agent 2-isopropyl-1,3-dimethylimidazolium (2iPr13DMI) can produce up to seven different zeolite phases depending on water concentration, the presence of inorganic impurities, crystallization temperature and time, and germanium molar fraction. The obtained phases are very different in terms of pore system, connectivity of the zeolite structure and structural units. At the pure SiO₂ side, ZSM-12 and SSZ-35 dominate, with ZSM-12 being favored by the presence of potassium impurities and by less concentrated conditions. The introduction of Ge at low levels favors SSZ-35 over ZSM-12 and as the Ge fraction increases it successively affords CSV, -CLO and two distinct UOS zeolites, HPM-11 and HPM-6. These two zeolites have the same topology but distinct chemical compositions and display powder X-ray diffraction patterns that are much different from each other and from that of as-synthesized IM-16 (UOS reference material). They also show different symmetry at 96 K. Rietveld refinements of the three as-made UOS materials mentioned are provided. HPM-6 and HPM-11 are produced in distinct, non-adjacent crystallization fields. The frequent cocrystallization of the chiral STW zeolite, however, did not afford its synthesis as a pure phase. Molecular mechanics simulations of the location of the organic cation and host–guest interactions fail to explain the observed trends, but also considering the intrinsic stability of the zeolites and the effect of germanium help to rationalize the results. The study is completed by DFT calculations of the NMR chemical shifts of ¹³C in UOS (helping to understand splittings in the spectrum) and ¹⁹F in CSV (supporting the location of fluoride inside the new [4⁴5²], which is an incomplete double 4-ring).

---

Introduction

Zeolites are microporous crystalline materials with interesting commercial applications that critically depend on their structures and compositions.⁵ The crystalline structure enables control of access in and out of the intrazeolitic pore space and, in this respect, pores ranging from small,⁶ to medium,⁷ to large⁸ and extralarge⁹ sizes all find interesting applications. On the other hand, the zeolite composition determines properties such as chemical, thermal and hydrothermal stability, cation exchange,¹⁰ acidity,¹¹ redox activity¹² and hydrophilicity vs. organophilicity characteristics,¹³ which may prove valuable in different applications.¹⁴ The wide variability in structures and compositions of zeolites offers opportunities to select and fine tune materials to maximize the performance in a given process. This has led to huge research efforts to control the structure, composition and textural properties of zeolites. Organic cations, usually referred to as organic structure-directing agents (OSDAs), are among the most critical factors allowing the synthesis of a particular zeolite. However, they may exert a structuring/crystallizing role with varying degrees of specificity, from a close to key-and-lock templating effect all the way down to mere pore filling.¹⁵ The latter typically produces “default structures”,¹⁶i.e., zeolites that are rather stable by themselves and that, thus, are not very in need of additional stabilization by a host–guest interaction with the OSDA. As a consequence, default materials can be obtained using a very large number of different OSDAs. By contrast, OSDAs that truly act as templates may afford unique materials.

When an OSDA is unspecific in its structure-directing action, other synthesis parameters may come into play to control the output of crystallization.¹⁷ Among them, the use of fluoride anions,¹⁸ the concentration of the synthesis mixture,¹⁹ the presence of heteroatoms²⁰ and temperature²¹ can all make a large difference. As we show here, the presence of inorganic impurities should be added to this list. With regard to the role of heteroatoms, it is interesting to realize that, on occasion, a given heteroatom (for instance Ge) can have absolutely no structure-directing effect, producing instead a solid solution over the whole range of Ge_f = Ge/(Ge + Si) = 0–1 molar fractions,²² while in other cases a structure-directing effect definitely exists.^20,23 Thus, for unspecific OSDAs, a screening of synthesis conditions by varying the above factors may be of interest and provide opportunities for discovery.²⁴ Here we show that 2-isopropyl-1,3-dimethylimidazolium (2iPr13DMI) is a rather unspecific OSDA that can produce up to seven different zeolite phases. Interestingly, two of these phases possess the same UOS topology but distinctly different compositions and are produced in significantly different, non-adjacent crystallization fields [bold three letter codes refer to zeolite framework type codes approved by the Structure Commission of the International Zeolite Association and, when preceded by a dash, they correspond to “interrupted frameworks”].²⁵ Due to different symmetries and unit cell parameters, the PXRD diagrams of these zeolites differ from that of IM-16 zeolite, the reference UOS material, the monoclinic structure of which in the as-synthesized form is also reported here for the first time.²⁶

Experimental section

Synthesis of the OSDA

Method A. The first synthesis attempts were carried out through single step nucleophilic substitution reactions, following a methodology similar to the ones we previously used for the synthesis of other imidazolium cations. This consisted of full methylation at the N positions of imidazole compounds using methyl iodide in the presence of potassium carbonate sesquihydrate as a proton scavenger. However, in this case, the organic salt obtained (2iPr13DMI⁺I⁻) showed low solubility in chloroform (as well as in other organic solvents) so separation of the solid resulting from the use of K₂CO₃·1.5H₂O was very difficult. To overcome this problem, after filtering the reaction mixture, the solid residues were washed with methanol and the salt was obtained by rotary evaporation. However, it turned out that methanol eventually also dissolved some potassium compound (coming from the potassium carbonate) and, while its amount was very small according to CHN analysis (which suggested that the particular OSDA analyzed was close to 100% pure, see Table S1†), it very significantly affected the subsequent zeolite synthesis experiments (see below).

Method B. We then changed the synthesis to a two-step methylation that avoided the solubility problem. First 0.075 mol of 2-isopropylimidazole (Aldrich or Alfa Aesar, 98%) was dissolved in around 100 mL chloroform (Aldrich, 99%). Then, 0.0825 mol of iodomethane (Aldrich, 99%) was added to the solution in the presence of 0.206 mol of finely ground K₂CO₃·1.5H₂O (Aldrich, 99%). After 3 days under magnetic stirring at RT, the solution was filtered and the solid was washed with chloroform. Then, an excess of iodomethane was added to the chloroform solution, and the reaction was left for a further three days under magnetic stirring. The solvent was removed by rotary evaporation and the organic salt was washed with acetone. The overall yield was generally close to 80% and the nature and purity of the cation were confirmed by ¹H and ¹³C NMR and chemical analysis (see below).

For both synthesis methods, the obtained iodide salt was converted into the organic hydroxide form by anion exchange using Dowex Monosphere 550A (OH) anion exchange resin (Sigma Aldrich). The hydroxide solution, 2iPr13DMIOH (aq), was concentrated by rotary evaporation to achieve a final concentration of around 1.2 mol kg⁻¹. The concentration before and after rotary evaporation was determined by titration with HCl 0.1 N (Aldrich) using phenolphthalein as an indicator.

Zeolite synthesis

Tetraethylorthosilicate (TEOS 98%, Aldrich) and GeO₂ (Aldrich, 99+%) were used as the silicon and germanium sources, respectively. Appropriate amounts of these reagents were hydrolyzed at room temperature under stirring in the aqueous 2iPr13DMIOH solution. Evaporation of all the ethanol produced and as much water as needed was allowed and monitored by weight. Finally, hydrofluoric acid (HF 48%, Aldrich) was added (caution: work under a fume hood), followed by manual stirring using a spatula for approximately 15 minutes. The highly viscous gel so obtained was placed inside the inner Teflon vessels of stainless steel autoclaves. For crystallization, temperatures of 423, 448, 458 and 468 K were used, under tumbling (rotation speed ca. 54 rpm). The final composition of the gel was (1 − x)SiO₂ : xGeO₂ : 0.5OSDAF : wH₂O, where x = Ge_f = Ge/(Si + Ge) was the molar fraction of germanium to germanium and silicon and was varied from 0 to 1 and w was varied in the 2.9 to 6.7 range for the pure SiO₂ syntheses and kept fixed at 4 for the syntheses containing Ge. After predefined times, the autoclaves were removed from the oven, cooled with water, then the final pH was checked and the solids were washed with deionized water and then dried in an oven at 373 K. The reference material IM-16 was prepared hydrothermally at 443 K for 14 days according to the procedure published by Lorgouilloux et al. with 3-ethyl-1-methyl-3H-imidazol-1-ium as the OSDA.²⁶

Characterization

Powder X-ray diffraction (PXRD) was performed using a Bruker D8 Advance diffractometer, with Cu Kα radiation. C, N, H analyses were performed with a LECO CHNS-932 instrument. ¹⁹F, ²⁹Si and ¹³C MAS NMR experiments were recorded on a Bruker AV 400WB spectrometer, as described elsewhere.²⁷ Field emission scanning electron microscopy (FE-SEM) images were obtained on an FEI NOVA NANOSEM 230 instrument without metal coating. Thermogravimetric (TG) analyses were achieved with an SDT Q600 TA Instruments device at a heating rate of 10 K min⁻¹ under an air flow of 100 mL min⁻¹. Synchrotron PXRD (SPXRD) data for HPM-6 and HPM-11 were collected at the bl04 MSPD beamline of the Spanish synchrotron light source (ALBA, Cerdanyola del Vallès, Barcelona), in capillary mode (0.6–0.8 mm diameter). The PXRD pattern of as-synthesized IM-16 was collected on a PANalytical MPD X'Pert Pro diffractometer in the Debye–Scherrer geometry equipped with a capillary sample holder, a hybrid mirror monochromator (λ = 1.5406 Å), which gave the mono-chromatic parallel beam geometry, and an X'Celerator real-time multiple strip detector (active length = 2.122°, 2θ).

Electron diffraction data collection, structure solution and Rietveld refinement

Electron diffraction data on as-made HPM-6 and HPM-11 were collected at 96 K using the continuous rotation method (cRED) on a JEOL JEM2100 TEM (LaB₆ filament) instrument operating at 200 kV and equipped with a quad hybrid pixel detector (Timepix). The reciprocal space reconstruction (Figs. S1 and S2†) was carried out using the program REDp,²⁸ and the reflection intensity extraction was conducted by the program XDS.²⁹Ab inito structure solution was performed using ShelxT,³⁰ then refined with atomic scattering factors for electrons by Olex 2.³¹ The final structures of as-made HPM-6 and HPM-11 were refined against the SPXRD data using TOPAS-V6.³² The model from cRED data was used as the initial model, although for HPM-11 we then had to change symmetry (see below). The positions of OSDAs were determined by using a combination of simulated annealing (global optimization) and Rietveld refinement using a previously described procedure.³³ The structure of as-synthesized IM-16 was refined using the GSASII suite of programs.³⁴ The initial model of the framework was generated from the structure of the orthorhombic unit cell (space group Cmcm)²⁶ of the calcined sample transformed into the monoclinic subunit cell (space group P2₁/m) using the program PowderCell.³⁵ Two OSDA molecules were placed on a mirror plane, as revealed by difference Fourier maps. The structure was minimized with the Forcite module of Materials Studio³⁶ before Rietveld refinement.

Computational details

Molecular mechanics simulations were performed in order to find the most stable location of 2iPr13DMI cations within the different frameworks; simulations were carried out using the Forcite module implemented in Materials Studio,³⁶ using the Dreiding forcefield.³⁷ Suitable supercells were built for each system in pure silica composition. 2iPr13DMI cations were manually docked in the framework in different positions/orientations, and the most stable location was obtained by simulated annealing (200 cycles). Due to the distinct porosity and framework density of different zeolite structures (and hence of the different organic contents per Si) as well as the different intrinsic stabilities of the frameworks as a function of network composition, direct comparison of the total interaction energies is meaningless. Hence, in order to analyze the intrinsic fitting of the cation in the different zeolite frameworks, the interaction energies were normalized to the free volume available, and these values (which were referred to as the normalized interaction energy, N.I.E.) were used to estimate the structure-directing ability of the organic cation for the different frameworks. Free volumes were calculated with a probe radius of 1.0 Å. Lattice energies were calculated using the GULP code,³⁸ with the potential developed by Catlow³⁹ and Gale and Henson, and taking that of SiO₂-quartz from ref. 40. In this way, the final stability of the host–guest zeolite systems was assessed by comparing both the relative framework stability through the lattice energy and the structure-directing ability of the organic cation through the normalized interaction energy.

The DFT relative framework stability as well as the theoretical ¹³C and ¹⁹F NMR chemical shifts were studied by full geometry optimization of zeolite models with DFT+D methods, which were performed with the CASTEP code,⁴¹ using plane waves (with an energy cut-off of 571.4 eV) and the PBE functional (including the Grimme dispersion term).⁴² In the case of the theoretical NMR calculations, F anions were located in the d4r units (for UOS) and in the [4⁴5²] cages (for CSV). Calculation of the ¹³C and ¹⁹F NMR chemical shieldings was carried out with the gauge-including projector augmented-wave method (GIPAW) developed by Pickard and Mauri,⁴³ as implemented in the CASTEP code. The chemical shift for a nucleus at a given position (δ(r)) is defined as δ(r) = σ_ref − σ(r), where σ(r) is the isotropic shielding obtained in the calculations. For comparison with experimental chemical shifts, σ_ref values of 174 ppm (for ¹³C) and 91.6 ppm (for ¹⁹F) were used, so that the experimental and theoretical values roughly coincided.

Results and discussion

Synthesis results

The results for the synthesis of pure silica zeolites using 2iPr13DMI obtained by the two different methodologies under varying H₂O/SiO₂ ratios and temperatures are listed in the first eighteen rows of Table S2.† Using the OSDA obtained by the first methodology at 423 K, the only zeolite that crystallized was the default phase ZSM-12 (structure code MTW) for any H₂O/SiO₂ ratios tried. We also occasionally observed the coprecipitation of a K₂SiF₆ impurity (Fig. S3†), which revealed contamination by K⁺ for the OSDA prepared by method A. Thus, further experiments were done using only the OSDA prepared by method B.

When the OSDA obtained by method B was used at low H₂O/SiO₂ ratios and 423 or 448 K, it resulted in the crystallization of pure silica SSZ-35 (structure code STF), another zeolite without high demand for specificity. This phase was also obtained in a pure silica composition using 2iPr13DMI by Schmidt et al.⁴⁴ SSZ-35 tends to be replaced by ZSM-12 over time (suggesting ZSM-12 is thermodynamically more stable than SSZ-35), which is further favored as the concentration decreases. These observations are in accordance with Villaescusa's rule (the experimental observation that less dense zeolites tend to appear at higher concentrations),¹⁹ since STF is less dense than MTW (FD_Si = 16.9 vs. 18.2 T per 1000 ų).⁴⁵

Thus, under the reported conditions, 2iPr13DMI does not appear to be a very interesting OSDA, merely yielding two different default structures. It was however interesting that the presence of minute amounts of potassium affected the selectivity of crystallization, since, when the OSDA synthesized by method A was used, only ZSM-12 was obtained, even under conditions in which SSZ-35 should have prevailed. Possibly, either K⁺ plays a structure directing role towards the crystallization of ZSM-12 zeolite in a short crystallization time or the crystallization of ZSM-12 is caused by fluoride depletion in solution resulting from the precipitation of highly insoluble K₂SiF₆. We reckon that the second possibility is more likely because the low solubility of potassium hexafluorosilicate would largely impede potassium from acting in solution. Also, the amount of this salt cannot be very large so it is unlikely that it may somehow promote the nucleation of ZSM-12 on its surface. Upon the introduction of germanium into the synthesis gel, the scenario changes drastically (see Fig. 1). First, very small Ge fractions (around 0.01) stabilize the SSZ-35 structure with regard to its transformation into ZSM-12, suggesting that the accommodation of Ge within the MTW topology is more difficult. Slightly increasing the Ge content to just around 0.1 at 448 K consistently produces CIT-7, a recently discovered zeolite to which the CSV code has been assigned.⁴⁶ With a further increase in Ge, the system enters a region of very low specificity where three additional zeolites, to which we assigned lab codes HPM-10, HPM-6 and HPM-11, appear, most frequently as mixtures and with HPM-1 (STW) in minor proportions. The first one, HPM-10, the zeolite with lowest framework density obtained in this system, tends to appear at low Ge_f (0.2) in this region and transforms into CIT-7, which in turn starts to transform into HPM-1 during long runs. As Ge_f increases further (0.4), CIT-7 is no longer observed and HPM-10 starts to transform over time into HPM-1 and, with more Ge (0.6), into HPM-6. With a further increase in Ge_f to 0.7, HPM-10 disappears from the field and HPM-6 dominates until Ge_f = 1. An increase in temperature to 458 K at Ge_f = 0.4 favors the transformation of initially crystallized HPM-10 into another phase, to which we assign the lab code HPM-11, and then its mixtures with CSV, while pure HPM-11 can be obtained with a further increase in temperature to 468 K, although small amounts of GeO₂ argutite tend to precipitate over long crystallization times. All the phase transformations observed are towards denser phases. The structural features of all the zeolites obtained are listed in Table 1. The group of zeolites synthesized in this work using 2iPr13DMI is very much heterogeneous from any point of view, as it contains a very low-density interrupted framework (-CLO) and five true, fully connected zeolites of varying density, pore apertures and building units. It is true, however, that the materials requiring a higher Ge_f (>0.1) all contain double four membered ring (d4r) units in their structures. The observed -CLO and UOS phases received an HPM lab code because their true nature remained unknown for some time (see below).

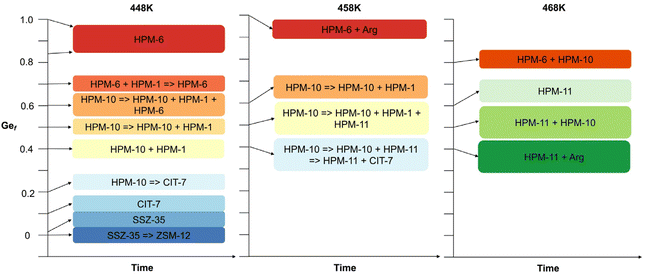Fig. 1 Schematic representation of the synthesis results at H₂O/SiO₂ = 4 and 448, 458 and 468 K (see Table S2†).

Table 1 Structural characteristics of the materials synthesized in this work using 2iPr13DMI⁴⁵

Zeolite	ZFT^a	Channel system^b	FDSi ^c	CBU^d
a Zeolite framework types. b Dimensionality and number of tetrahedra in the window limiting diffusion along the pore. c Framework density (FD, tetrahedra per 1000 Å^3). d Composite building units.
ZSM-12	MTW	1D 12 MR	18.2	jbw, cas, bik, mtw
SSZ-35	STF	1D 10 MR	16.9	stf, cas
CIT-7	CSV	2D 10 × 8 MR	16.2	sti, cas, mtw
HPM-10	-CLO	3D 20 × 20 × 20 + 8 × 8 × 8 MR	11.1	d4r, clo, lta
HPM-1	STW	3D 10 × 8 × 8 MR	16.4	d4r
HPM-6, HPM-11	UOS	3D 10 × 8 × 8 MR	17.6	d4r, mtw

---

Powder X-ray diffraction

The PXRD patterns of the six zeolitic phases prepared in pure form in this work are presented in Fig. 2. They could be assigned to the MTW, STF, -CLO, CSV and UOS zeolite structure types but it was not immediately clear in the case of -CLO (HPM-10) and UOS (HPM-6 and HPM-11). In Figs. S4 and S5† we compare the PXRD patterns of these three materials with the patterns simulated with the program VESTA for -CLO and UOS,⁴⁷ respectively, using the cif files provided in the IZA's database of zeolite structures and a single average Cu Kα wavelength, λ = 1.5418 Å.⁴⁵ In the case of HPM-10, the very low intensity of its reflections, its most frequent appearance in mixtures (with HPM-1, HPM-6 or CIT-7, see Table S2†) and the omission of the first reflection around 2θ = 3.2° under our then standard PXRD measurements prevented its identification for months. Fig. S4† clearly demonstrates, however, that HPM-10 has the -CLO framework type and is thus similar to the recently reported germanosilicate PKU-12.⁴⁸ The comparatively broad and weak reflections are probably a consequence of its nanocrystalline nature (see below). In the case of HPM-6, its high Ge content (Ge_f ≥ 0.7 for any pure solid in Table S2† that we have analyzed, compared to 0.43 in the original IM-16 (UOS) report²⁶ and up to 0.8 claimed in the patent⁴⁹) together with a change in symmetry (see below and Fig. S5†) changed the PXRD pattern greatly enough so as to prevent identification of this phase. Then, its structure was solved in space group Pbma (no. 57) using EXPO2009 and conventional PXRD data for a phase with Ge_f = 1.⁵⁰ First a partial solution lacking some Ge atoms in d4r was obtained and these units were then completed manually to yield the fully connected zeolite. Only then was HPM-6 identified as belonging to the UOS type through the use of KRIBER with an up-to-date version of the coseq file.⁵¹ As far as we know, this is the first report of a pure germanate with UOS topology. Finally, HPM-11, synthesized at a higher temperature but with a lower Ge_f (around 0.4 in the gel), appeared to be related but distinctly different from HPM-6 and from the reported IM-16. For instance, IM-16 has 5 peaks below 12° while HPM-11 has only 3 with much different relative intensities (Fig. S5†). This is attributed to its slightly larger Ge_f (0.58 compared to 0.42, although the Ge_f in the gel was lower for HPM-11 than for IM-16) and a change in symmetry from Cmcm in the reported calcined IM-16 to Pbcm in as-made HPM-11. In Fig. S5†, we have included the simulated PXRD pattern of ECNU-16 (EOS), a very recently reported zeolite, to show that these two zeolites (reported as having different but closely related zeolite framework types)⁵² display patterns (simulated from the corresponding cif files) that are very similar to each other but greatly differ from those of HPM-11 and HPM-6. The sharp differences in PXRD patterns between HPM-11 and HPM-6 contrast with the fact that data for materials identified as HPM-6 but synthesized from quite different Ge_f (0.7, 0.85, 1.0) hardly change (Fig. S6†). This is likely due, in part, to the fact that the measured Ge_f in the HPM-6 solid is in a narrower range (0.88, 0.96 and 1.0) than in the gel. We have confirmed beyond doubt by cRED that both HPM-11 and HPM-6 samples indeed have UOS topology. Interestingly, there is a difference in symmetry between them at the temperature of the electron diffraction experiments (96 K). cRED data for eleven crystals of HPM-11 indicated Pmcm symmetry (Fig. S2†), but the PXRD pattern at room temperature showed several reflections that could not be indexed to that symmetry. The whole pattern could be indexed instead to a Pbcm cell with a doubling of the b parameter. In the case of HPM-6, both cRED (Fig. S1†) and PRXD agreed on Pbcm symmetry with double b. Thus, there must be a phase transition in HPM-11 between RT and 96 K that does not occur in the higher Ge_f analog HPM-6. The Rietveld refinements of HPM-11 and HPM-6 against RT synchrotron PXRD data were performed under Pbcm symmetry with double b (see results in Figs. S7 and S8 and Tables S3–S8†). For completeness, the Rietveld refinement results for as-made IM-16 are shown in Fig. S9 and Tables S9–S11.†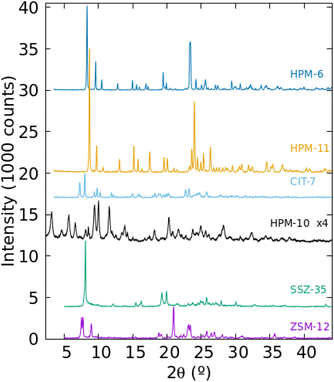

Fig. 2 Powder XRD of the six zeolitic phases synthesized as pure phases in this work as Ge_f in the gel increases (from bottom to top).

Table 2 lists crystallographic data for several phases prepared in this work and Fig. S10† shows that the volume per tetrahedral atom in the topologically related materials we discuss here (IM-16, HPM-6, HPM-11 and ECNU-16) roughly increases as Ge_f increases. This tendency is clearly more linear for the samples synthesized with the same OSDA (2iPr13DMI in HPM-6 and HPM-11). In summary, the distinct patterns of HPM-6 and HPM-11, compared to UOS, which are particularly obvious in the 2θ = 20–30° range, are a consequence of their different symmetries and chemical compositions, which for HPM-6 and HPM-11 arise from different synthesis conditions using the same OSDA.

Table 2 Crystallographic data of materials relevant to this work

Zeolite (T/K)	ZFT	Gef^c	Space group	a/Å	b/Å	c/Å	α/°	β/°	γ/°	Vol Å^3/T
a By Le Bail fitting (others by Rietveld refinement). b From ref. 52. c Gef in zeolite, determined by EDS (the value for the gel is listed inside parentheses).
CIT-7^a (448)	CSV	0.22(0.2)	P1̄	12.949	11.233	9.388	92.89	107.14	103.04	63.06
HPM-10^a (458)	-CLO	0.51(0.6)	Pm3̄m	26.179	26.179	26.179	90	90	90	93.4
IM-16 (443)	UOS	0.43(0.5)	P21/m	11.82694	19.95425	11.71845	90	99.71	90	56.79
ECNU-16^b (443)	EOS	0.48(0.5)	C2/m	17.83400	15.12600	10.67100	90	108.56	90	56.85
HPM-11 (468)	UOS	0.58(0.4)	Pbcm	7.6212	18.1181	20.2859	90	90	90	58.36
HPM-11^a (468)	UOS	0.66(0.6)	Pbcm	7.644	18.114	20.410	90	90	90	58.88
HPM-6 (448)	UOS	0.88(0.7)	Pbcm	7.66042	18.07804	20.72105	90	90	90	59.78
HPM-6 (448)^a	UOS	0.96(0.85)	Pbcm	7.677	18.095	20.822	90	90	90	60.26
HPM-6 (448)	UOS	1(1)	Pbcm	7.68166	18.10273	20.89530	90	90	90	60.54

---

Elemental and thermal analyses. The CHN analysis of the relevant zeolites in this study are listed in Table 3. The C/N and H/N molar ratios are close to, but generally a bit higher and lower, respectively, than the theoretical and experimental ratios for the pristine OSDA cation (Table S1†). The total organic content (based on N analysis and assuming the charge is balanced by fluoride) indicates that close to 2 OSDAs per unit cell are occluded in CIT-7. In HPM-6 and HPM-11, there are four OSDAs in the Pbcm double unit cell. In HPM-10, there are 24 per cell, due not only to the much larger cell of -CLO (192 T atoms compared to 20 for CSV and 24 for UOS), but also to its significantly more open character (FD_Si = 11.1 T per 1000 ų for -CLO compared to 16.2 and 17.6 for CSV and UOS, respectively).⁴⁵ The calculated amount of OSDAs in all these phases, if balanced by fluoride in d4r cages, suggests a total occupancy of d4r cages in -CLO (24 d4r/u.c.) and UOS (4 d4r/u.c. in Pbcm symmetry) and also a total occupancy of the two [4⁴5²] cages per cell in CSV (see below).

Table 3 Elemental and thermal analysis data of relevant as-made zeolites prepared in this work

Sample	ZFT	Gef	C/%	H/%	N/%	C/N^a	H/N^a	Residue^b/%	Empirical formula per cell^c
a Theoretical C/N = 4.0 and H/N = 7.5. b TG residue at 1000 °C. In parentheses, the TO2 weight percent in the empirical formula (note that the residue will be altered if GeO sublimation occurs during thermal analysis). c Calculated from the N content and assuming the OSDA is balanced by F anions. In the case of -CLO, a 2.5% weight lost at low T is accounted for by including 27 H2O molecules per cell.
ZSM-12	MTW	0	5.50	1.23	1.57	4.1	11.1	88.6 (87.7)	[SiO2]28(C8H15N2F)1.1(H2O)3.7
SSZ-35	STF	0	8.16	1.14	2.39	4.0	6.7	84.8 (86.5)	[SiO2]32(C8H15N2F)1.9
CIT-7	CSV	0.22	11.01	1.66	3.16	4.1	7.3	79.9 (82.1)	[Ge0.22Si0.78O2]20(C8H15N2F)1.9
HPM-10	-CLO	0.42	12.88	1.91	3.53	4.3	7.5	75.2 (77.6)	[Ge0.42Si0.58(OH)0.12O1.94F0.12]192(C8H15N2)24.6(H2O)27.1
HPM-11	UOS	0.58	8.53	1.31	2.45	4.1	7.4	86.0 (86.2)	[Ge0.58Si0.42O2]48(C8H15N2F)4.2
HPM-6	UOS	0.88	7.39	0.99	2.04	4.2	6.7	86.4 (88.5)	[Ge0.88Si0.12O2]48(C8H15N2F)3.9
HPM-6	UOS	1.0	6.81	0.92	1.93	4.1	6.7	88.9 (89.1)	[GeO2]48(C8H15N2F)3.9

---

The thermogravimetric (TG) and differential thermal analyses (DTA) of the five germanosilicate phases are shown in Fig. S11,† where in addition to the large weight loss presented by HPM-10, the most noticeable feature is observed in the thermograms of the phases synthesized with a higher Ge_f (HPM-6 with Ge_f = 0.7 and 1), where two weight gaining stages are observed, starting at around 660–680 and 900–940 °C, respectively (see arrows in Fig. S11†). The temperatures of both weight gaining events are close to those we observe in the case of pure GeO₂-AST phases,⁵³ despite the large difference in pore apertures of the 6MR windows in AST and the 10 + 8 MR pores in UOS. This is due to the fact that the gaining steps are not related to diffusion along the pores but to reoxidation of previously reduced framework Ge(IV).⁵³ Also, in HPM-11, a much smaller but clear weight gaining event is observed by the end of the thermal trace.

The noted reduction itself cannot be directly observed, but it has an influence on the corresponding DTA trace: instead of the large exothermic DTA peak observed in the remaining cases, due to OSDA combustion, the materials that present large weight gaining steps show minor and endothermic DTA variations associated with the weight loss steps and a small exothermic peak at the onset of the weight gaining step, very similarly to our previous observations in the GeO₂-AST system.⁵³ This kind of DTA feature is likely due to the fact that there is no OSDA combustion with oxygen but, at least partly, an organothermal reduction of the framework GeO₂. We warn that, even when weight gaining is not clearly seen by TG/DTA (as in the case of CSV, HPM-10 and HPM-11), reduction and reoxidation of Ge, and even sublimation of GeO, may still occur and pass unnoticed.⁵³ This is because germanium monoxide, which may be produced by the reaction of metallic Ge with GeO₂, sublimates at temperatures above 480–490 °C,^54,55i.e. at a temperature below the first weight loss in all five germanosilicates. Given that -CLO has two independent channel systems and one of them is just a small 8MR pore, it is not surprising that thermal reduction also occurs in these small pores. This emphasizes our previous warning that much caution is needed in the interpretation of thermal events for germanosilicate zeolites.⁵³

Multinuclear NMR

The ¹³C CPMAS NMR spectra of the six pure phases (Fig. 3) show, in every case, signals close to the expected positions corresponding to the five unique C atoms in 2iPr13DMI, strongly suggesting the cations are occluded intact in the zeolites. This happens even when phase transformations occur, showing that during the transformations, which are likely driven by the increased density/stability of the framework, the OSDA continues to act as a pore filler (under the conditions of this study, it is highly unlikely that a zeolite could crystallize without an organic compound helping to stabilize the void space). However, in several zeolites, some signal splittings are evident. For SSZ-35, the signal corresponding to the methyl groups of the isopropyl moiety are split, suggesting that both methyl groups are not equivalent in the occluded cation. In the case of HPM-6, the signals that can be assigned to C̲H groups of the imidazolium ring (around 123 ppm) and to NC̲H₃ (around 37 ppm) are both split into two signals of about equal intensity. These splittings indicate the zeolites impose unequal environments for C atoms that would otherwise be, in principle, equivalent. In the case of isostructural HPM-11, the significantly broadened resonances, which can result from the heterogeneity of Si–Ge occupancies of sites, show no splitting except for the resonance around 37 ppm, which splits into two resonances of unequal intensities. For the remaining as-made zeolites, the NMR signals are significantly broader but there are, however, clear indications of signal splittings at least in ZSM-12 and HPM-10. The ²⁹Si MAS NMR spectra of the samples containing silica are shown in the ESI (Fig. S12†). The only remarkable features appear in the pure silica SSZ-35 material, which shows very high resolution of crystallographic sites (not less than 10, possibly 14 tetrahedrally coordinated sites) plus a doublet at −147 ppm characteristic of pentacoordinated silicon (SiO_4/2F⁻ units) with a J coupling of around 175 Hz.⁵⁸ This agrees with previous results obtained for SSZ-35 zeolites prepared using unrelated OSDAs,^59–61 although the resolution and evidence of SiO_4/2F⁻ units are not always as clear in the ²⁹Si MAS NMR spectra of as-made SSZ-35 zeolites as they are here.⁶² In contrast, as-made pure silica ZSM-12 displays a poorly resolved spectrum, as commonly observed for this zeolite structure type.⁶³ On the other hand, the poorly resolved spectra of the Ge-containing materials is not surprising, since they are not pure SiO₂ materials and, hence, Si(OT)₄ is expected to be spread over a wide chemical shift range.

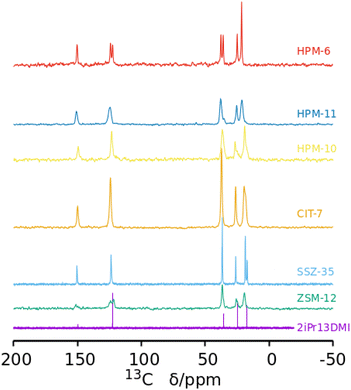Fig. 3 ¹³C NMR spectrum of 2iPr13DMI iodide in D₂O solution and ¹³C MAS NMR spectra of six as-made phases prepared in this work as Ge_f increases (from bottom). In the bottom spectrum, the C at position 2 of the aromatic ring (between both N) is barely visible at around 150 ppm. That carbon typically displays a very small relative intensity in the proton-decoupled ¹³C NMR spectra of this kind of compound.^56,57

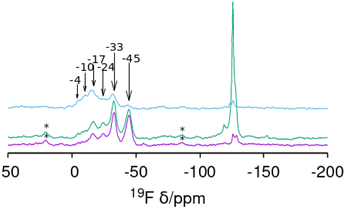
Of most interest are the ¹⁹F MAS NMR spectra (Fig. 4). Fluoride occluded in small cages of zeolites displays ¹⁹F resonances with chemical shifts in ranges that typically depend on the fluoride–framework interaction, which in turn is a function of the composition and type of cage in which it is occluded. In pure silica zeolites, the typical chemical shifts can span from −35/−42 ppm in the small [4⁶] cages (d4r) to over −80 ppm in larger cages.⁶⁴ The pure silica ZSM-12 and SSZ-35 phases display resonances in the typical range for fluoride occluded in cages of silica zeolites: −75 and −78 ppm in ZSM-12 and −80 ppm in SSZ-35. ZSM-12 also shows sharp resonances at higher fields (−119, −126 and −127 ppm) that are ascribed to penta- and/or hexa(oxofluoro)silicate impurities. Several of the other spectra in Fig. 4 also present broad resonances in this region, although with much lower intensity. The germanium containing zeolites show, in contrast, resonances at significantly lower fields, which typically indicate strong F–Ge interactions and which depend on the Ge content and distribution in addition to the enclosing cage. Both Ge and fluoride typically favor the formation of d4r in zeolites.^18,19,22,23 The sharp and single resonance at −13.5 ppm in pure Ge HPM-6 has to be ascribed to fluoride occluded in d4r made of germanium (GeO₂-d4r), which agrees with previous reports on chemical shifts of F@GeO₂-d4r whether as discreet units,⁶⁵ or in zeolites.²² Interestingly, the isostructural HPM-11 synthesized with a significantly lower Ge content (Ge_f = 0.4 in gel, 0.58 in the zeolite) has a single resonance in the close chemical shift of −12.7 ppm. This resonance, however, cannot be assigned in this case to fluoride occluded in d4r made only of germanium because this would require a much higher Ge content even if there were an absolute preference for Ge to occupy d4r sites (16 out of the 24 tetrahedral sites in a unit cell, or Ge_f = 0.67). For Ge_f = 0.58 (13.9 Ge per unit cell) that signal needs to be assigned to fluoride occluded in d4r units containing Ge in closed clusters, i.e., with at least one Ge having three Ge as next nearest neighbors in the d4r unit. For this a minimum of 4 Ge per unit cell are needed; this is indeed achievable for this Ge content. This agrees with our proposition that the main factor determining the chemical shift of ¹⁹F in Ge-containing d4r is not the total Ge content in the d4r but the number of Ge–O–Ge pairs resulting in four categories of resonances: with no Ge (I), non-paired Ge (II), Ge pairs without larger clusters (III) and with larger clusters (IV).²² For HPM-10, a single resonance at −9.2 ppm is assigned to fluoride occluded in d4r units of the -CLO structure with between 2 and 6 Ge atoms forming pairs but no larger clusters (i.e., resonance type III where no Ge has three Ge neighbors in the d4r unit). This chemical shift contrasts with the one reported for PKU-12, −4.3 ppm.⁴⁸ It is interesting that for both HPM-10 and PKU-12 there is a single and symmetrical ¹⁹F resonance despite the fact that there are two different types of d4r in the -CLO structure: one is a “normal” unit in which each T atom is oxygen-bridged to 4 T atoms; the other contains two “dangling” T–O bonds where the structure is interrupted. In both PKU-12 and HPM-10, there is likely to be full occupancy of both types of d4r. For HPM-10, this is deduced from the CHN analysis and charge balance considerations (see above).

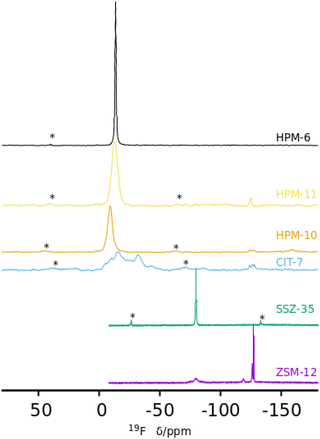Fig. 4 ¹⁹F MAS NMR spectra of six as-made phases prepared in this work: ZSM-12, SSZ-35, CIT-7, HPM-10, HPM-11 and HPM-6 (Ge_f 0.88 and 1.0) (from bottom).

The reported ¹⁹F spectrum of as-made silica CIT-7 displays an asymmetric resonance around −45 ppm, which is not specifically assigned.⁴⁶CSV is the first zeolite containing the [4⁴5²] cage, which is composed of an sti unit with an additional T atom inserted between the open corners. However, similar tiling containing the sti unit exists in other fluoride-containing materials: the truly open and interrupted “[4⁴6]” cage, which is not properly a tile but half the [4⁸8²] tile, in the layered germanosilicate PKU-22, with no T atom between the open corners,⁶⁶ and the [4⁴6²] cage with 2 T atoms inserted between the open corners in the interrupted germanosilicate PKU-26,⁶⁷ see Fig. 5. Reported ¹⁹F resonances at 1.0 and 0.3 ppm in PKU-22 and PKU-26, respectively, have been assigned to F occluded in the sti unit with a direct very short F–Ge bond (2.206 and 2.20 Å, respectively) to a specific Ge site. Interestingly, the ¹⁹F spectrum of our CSV germanosilicate contains at least six overlapped resonances in the 0 to −45 ppm range, which we attribute to fluoride occluded in the [4⁴5²] units of the structure because of its similarity to the d4r ([4⁶]), within which ¹⁹F spans a similar chemical shift range depending on the Ge content and distribution. Also, the range in our germanosilicate CSV is between that of pure silica CIT-7 and those of Ge-containing PKU-22 and PKU-26 with short F–Ge bonds in the sti units. Thus, we propose that the multiple resonances that can be discerned in the spectrum correspond to different Ge contents and distributions in the [4⁴5²] cage and, possibly, to fluoride interacting with different crystallographic sites within that cage (see calculations below).

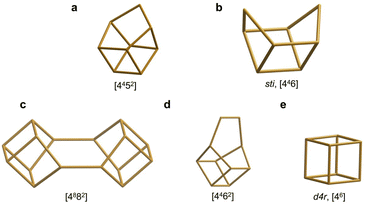Fig. 5 Several cages that can be formally considered as being derived from the d4r cage by modification at one corner and which may provide similar environments for fluoride at the opposite side. They appear in CSV (a), STI (b), PKU-22 (c), PKU-26 (d) and, among others, AST (e).⁶⁸

FE-SEM

Fig. S13† shows FE-SEM micrographs of the germanosilicate phases. HPM-10 is nanocrystalline in nature (crystal size below 50 nm), while all the other phases are microcrystalline with sizes ranging from up to 3 µm for CIT-7, up to 15 µm for HPM-11 and up to 40 µm and 80 µm for HPM-6 synthesized at Ge_f = 0.7 and 1, respectively. In the last sample we observed a considerable amount of smaller particles in the shape of circular wafers of around 0.8 µm. This impurity phase was not apparent in the powder XRD data, which was fully indexed.

Computational results

Pore-filling and interaction energies. We then analyzed the most stable location of the 2iPr13DMI cations within the different frameworks by molecular mechanics calculations in order to understand their structure-directing ability for the different zeolite structures. Due to the complexity of the -CLO host–guest system, with 24 cations per unit cell with a high degree of freedom, which might result in non-reliable results associated with local minima, this system was excluded from the calculations. Two 2iPr13DMI cations per unit cell (1 per cavity) were loaded in the STF framework (Fig. 6, top-left), with the organic cations sited in the center of the SSZ-35 cavities, showing good geometric host–guest complementarity between its molecular shape and that of the cavity. Indeed, 99.7% of the void pore volume is filled upon occlusion of this cation, showing efficient pore filling, with a N.I.E. of −1.08 kJ mol⁻¹ Å⁻³ (Table 4).

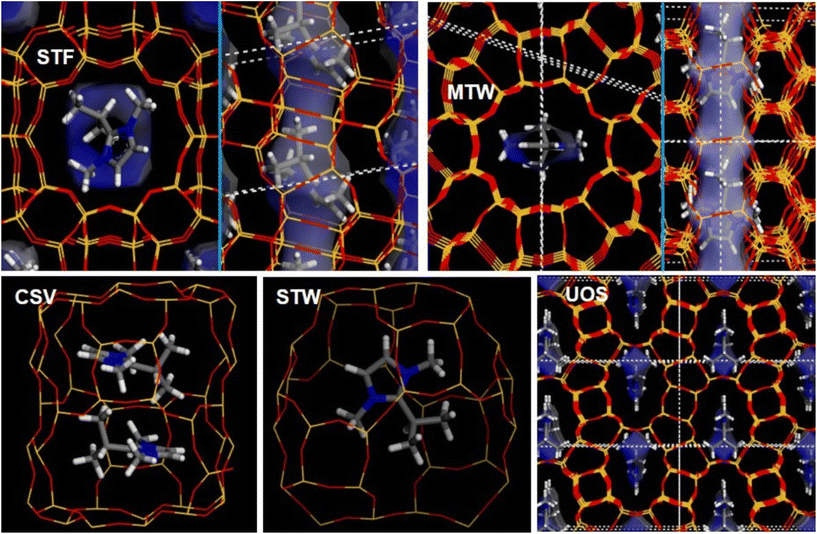Fig. 6 Location of 2iPr13DMI within the different frameworks studied. Void volume is shown as a transparent white/blue surface to facilitate pore visualization.

Table 4 Different parameters studied for the 2iPr13DMI cations in different frameworks

ZFT (u.c.)	SDA per		Free volume (Å^3/Si)	Pore filling (%)	I.E. (kJ mol^−1 Si)	N.I.E. (kJ mol^−1 Å^−3 of free V)	GULP	DFT
	u.c.	Si					(kJ mol^−1 Si)
STF (Si32O64)	2	0.0625	9.756	99.7	−10.51	−1.08	13.17	11.29
MTW (Si56O112)	2	0.0357	5.186	92.3	−5.37	−1.04	8.13	7.32
CSV (Si20O40)	2	0.1000	12.544	100	−15.34	−1.22	16.63	12.03
STW (Si60O120)	6	0.1000	9.867	99.9	−15.50	−1.57	19.94	14.06
UOS (Si24O48)	2	0.0833	6.056	100	−12.52	−2.07	15.48	11.41

---

In the case of the ZSM-12 structure (MTW), two 2iPr13DMI cations per Si₅₆O₁₁₂ unit cell were loaded; higher loadings were also tried, but these led to unstable situations. As can be seen in Fig. 6 (top-right), 2iPr13DMI cations are located within the 12MR channels of the ZSM-12 framework, with the imidazolium ring aligned with the channel direction, and the C3 methyl groups bonded to N sited in the lateral side pockets of the framework, showing once again a good geometric host–guest fit. However, in this case, a lower pore-filling efficiency is observed (92.3%) because one of each of the two side-pockets remains free, and this results in a relatively low N.I.E. of −1.04 kJ mol⁻¹ Å⁻³.

Two 2iPr13DMI cations per unit cell were loaded in the CSV framework, corresponding to two cations per CSV cavity. The most stable location of the cations (Fig. 6, bottom-left) shows that the CSV cavity has the appropriate dimensions to host two OSDA cations parallel to each other, siting the bulky isopropyl groups of the two cations on opposite sides to avoid steric repulsion interactions. In this case, the high pore-filling efficiency of 2iPr13DMI in this framework (100%) and the good host–guest geometric fit brings an improvement in the N.I.E. to −1.22 kJ mol⁻¹ Å⁻³, suggesting a good structure-directing efficiency of the cation towards this cavity-based framework. We then analyzed the location of the cation within the chiral STW framework, despite it not being obtained as a pure phase experimentally. Each cavity can host one cation, resulting in a high N.I.E. of −1.57 kJ mol⁻¹ Å⁻³, indicating a good geometric host–guest match for this system (99.9% of pore-filling efficiency), as can be seen in Fig. 6 (bottom-middle).

Finally, two 2iPr13DMI cations were loaded per UOS unit cell, giving 100% pore-filling efficiency. In this case, a clear geometrical match between the molecular cross-like shape of the imidazolium cation and the void space of the UOS framework is also apparent (Fig. 6, bottom-right). This framework shows the best host–guest fit for the 2iPr13DMI cations, giving a N.I.E. of −2.07 kJ mol⁻¹ Å⁻³ (Table 4), the highest value found among all the frameworks, suggesting a high specificity towards the UOS framework, independently of the inherent structural framework stability of the distinct zeolites.

Thus, our results suggest that the 2iPr13DMI cation has a molecular shape that can fit within all these zeolite frameworks, possibly favored by the conformational freedom of the isopropyl group, although this must be significantly limited by steric hindrance. However, by themselves, the N.I.E. results fail to explain the observed experimental trends in structure direction since STW, which displays the second-highest N.I.E. value (after UOS), should appear as a frequent framework, but it is only marginally observed as a competing phase at high Ge loadings. The lack of strong specificity of this cation implies that other factors come into play to determine the phase selectivity of crystallization. The best calculated fit (in terms of pore-filling efficiency) is UOS = CSV > STW > STF > MTW while the NIE is in the order UOS > STW > CSV > STF > MTW. Both orders are in pretty good agreement, except for CSV and STW. The fact that our theoretical results cannot be straightforwardly correlated with the experimental results is attributed to the different intrinsic stabilities of the different topologies and the strong effect of Ge on them. Although most zeolites typically exhibit a clear correlation between stability and density,⁶⁹ this is not the case for the phases involved in this work because of the existence of d4r units in several of them. The d4r units are strained in pure silica zeolites,⁷⁰ and require the presence of F and/or Ge for flexibilization.⁷¹ In fact, the density (FD_Si) of the phases involved decrease in the order MTW > UOS > STF > STW > CSV, while, based on previous reports, we can consider MTW and STF as default structures but UOS is clearly not (there has been, so far, only a single reported synthesis of UOS, and it required the presence of Ge).²⁶ The density of STW is also close to that of STF, but, while it cannot be considered a very stable zeolite, it was once considered unfeasible.⁷² Thus, the discussion must take into account the energies of the SiO₂ phases plus the likely effect of F and Ge on the synthesis. To account for the intrinsic stability of the different topologies, we have calculated their energies as pure silica polymorphs relative to quartz using both interatomic potentials (with GULP code) and DFT methodologies and the results are included in Table 4. Both GULP and DFT provide the same order of relative stabilities (MTW > STF > UOS > CSV > STW), which agree with our previous considerations (MTW and STF as default structures and STW as the least stable phase among those considered here). In the absence of Ge, STF is the phase that first crystallizes, which agrees with a fairly good host–guest match and with its known stability (default structure). It tends to transform into MTW, which is denser and, hence, this agrees with the expected stability trend. The predominance of MTW when the OSDA is prepared by method A suggests that, under these conditions (the presence of K, precipitation of K₂SiF₆), the phase with higher thermodynamic stability prevails, possibly because fluoride depletion is a catalyst to promote thermodynamic over kinetic control.

When Ge is introduced into the synthesis, the phase selectivity landscape changes dramatically. For Ge_f equal to or above 0.4, UOS is clearly the dominant phase, which agrees with its not too low intrinsic stability as a pure SiO₂ zeolite, the stabilization effect of F and Ge on d4r units and the excellent fit and strongest host–guest interaction with the OSDA used. This does not happen for STW, which is never obtained in this system as a pure phase; this is likely due to its lower host–guest stabilization energy and, especially, to its lower intrinsic stability, which may require a relatively high Ge_f, for which it competes with UOS, which has a stronger interaction energy. The appearance of CSV and -CLO at fairly low Ge_f suggests they are not as highly unstable as STW and UOS, which, in the case of CSV may be easily understood, since it does not contain d4r but the more open and presumably more flexible sti cages.

Comparison with other OSDA systems may be illustrative. In the synthesis of HPM-1 (pure silica STW) using 2-ethyl-1,3,4-trimethylimidazolium, 2E134TMI, the OSDA was able to stabilize the pure silica material and, since STW contained d4r, the introduction of Ge did not change the phase selectivity and the whole solid solution series from Ge_f 0 to 1 could be synthesized. Other examples from the literature show how this is not always the case and totally different phases are obtained as Ge_f is systematically varied.⁷³ Thus, an interesting point to consider is that, when no single structure-directing effect dominates, the opportunities for discovery arise. This is the case for HPM-8, an intergrown zeolite of the Beta family largely enriched in polymorph E, which has a niche crystallization field with a low Ge_f (around 0.1 or 0.15).⁷⁴

Theoretical prediction of ¹³C and ¹⁹F NMR. We then wanted to gain some insights into the splitting of the ¹³C NMR signals observed for the unsubstituted C of the imidazolium ring (C̲H) and the methyl groups attached to N (NC̲H₃) as a function of Ge content in the UOS framework. Starting from the location of the 2iPr13DMI cations found previously by molecular mechanics, four different 2iPr13DMI/UOS systems were built: (i) with all T atoms being Si (Ge_f = 0), (ii) with 8 Ge and 16 Si atoms per unit cell, siting 4 Ge in each d4r, having one Ge surrounded by 3 Ge (Ge clusters) (Ge_f = 0.33), (iii) with 16 Ge and 8 Si atoms per unit cell, with all d4r atoms being Ge (Ge_f = 0.67), and (iv) with all T atoms being Ge (Ge_f = 1). All these systems were DFT geometry optimized with variable unit cell parameters, and then the ¹³C NMR shieldings were calculated by the GIPAW method (Table 5).

Table 5 Predicted ¹³C NMR shifts as a function of the Ge content, and unit cell parameters and volume of the optimized unit cell

Gef	N2C̲C	C̲H		NC̲H3		C̲C3		CC̲H3	V (Å^3)	a	b	c
0	151.0	127.6	129.1	41.4	40.6	28.5	20.7	20.7	1378.08	9.114	19.994	7.563
0.33	151.7	127.2	128.8	40.7	40.2	28.3	21.2	20.5	1430.83	9.19	20.154	7.725
0.66	150.7	127.5	129.4	40.8	37.9	28.0	22.2	22.2	1456.41	9.169	20.344	7.809
1	151.6	127.7	128.6	40.9	37.2	28.8	22.8	22.8	1536.13	9.273	21.076	7.867

---

Interestingly, the results show that an increase of the Ge fraction involves a larger splitting of the NC̲H₃ signals: they have very similar shifts for Ge-poor systems (with chemical shift differences of 0.8 and 0.5 ppm for Ge_f = 0 and 0.33, respectively), while showing larger differences for Ge-rich systems (2.9 and 3.7 ppm for Ge_f = 0.67 and 1, respectively) because of a high field displacement of one of the NC̲H₃ chemical shifts from ∼40 to ∼37 ppm. This change is probably associated with the change in the unit cell upon incorporation of Ge, where the unit cell volume and specifically the c parameter, are notably increased, and the pores become slightly larger as well. Indeed, such a distortion of the unit cell might explain the splitting of the NC̲H₃ NMR signal, since when Ge_f is low (0.33), the environment of both NC̲H₃ atoms seems more similar (Fig. S14, left†) than when Ge_f is high (1) (Fig. S14, right†), where the distortion of the unit cell slightly changes the orientation of the organic cation, possibly involving a different environment for both NC̲H₃. In contrast, we do not observe a clear trend as a function of Ge_f for the two C̲H signals, which are always slightly split (0.9 to 1.9 ppm, Table 5). However, we need to take into account that these are just simplified systems with regular Ge distributions, while in the real case a more heterogeneous Ge distribution must be present, in particular for HPM-11, which may explain its broader ¹³C resonances.

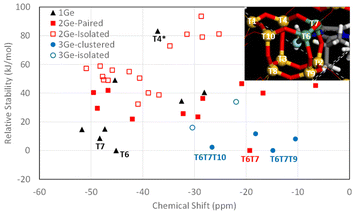
On the other hand, since the ¹⁹F NMR spectrum of F⁻ occluded in the [4⁴5²] cages of the CSV framework was reported only recently, and no specific assignations have been provided yet, we calculated the ¹⁹F NMR chemical shift of the system with different Ge configurations in order to test our above assignation. Systems with 1, 2 or 3 Ge per cage (giving overall Ge_f of 0.1, 0.2 and 0.3, respectively) were studied by DFT geometry optimization, and the theoretical ¹⁹F chemical shifts were calculated. For Ge_f = 0.1, each [4⁴5²] cage contained 1 Ge and all the different configurations were tried. F⁻ was initially located in the center of the cage, and the systems were geometry optimized (keeping P1̄ symmetry, i.e. both [4⁴5²] cages are symmetry-equivalent); in all cases, F bonded to Ge instead of Si upon geometry optimization (see Fig. 7 caption), evidencing higher stability of the Ge–F bonds (the only exception was T4, marked with * in Fig. 7, where F–Ge4 was very unstable, and instead bonded to Si7, also resulting in a very unstable system). Results are shown in Fig. 7, where the relative stability (calculated independently for systems with the same Ge_f) is plotted against the theoretical ¹⁹F NMR chemical shift. Energy results show that the most stable position for 1 Ge is T6 (see inset), followed by T7 (8.6 kJ mol⁻¹ u.c.); calculations predict a ¹⁹F NMR signal at around −45 ppm for cages with 1 Ge in T6; indeed, all the more stable 1 Ge systems gave shifts close to this (−45 to −52 ppm). We then included a second Ge in the cage (red squares) (Ge_f = 0.2); in this case, a notably higher stability for systems with Ge in adjacent positions (Ge-paired, solid red squares) was found (compared with isolated Ge, empty red squares), clearly showing a trend to form Ge–O–Ge bonds in these silicogermanate systems. The most stable system corresponds to a paired Ge–O–Ge position with Ge in contiguous T6 and T7 positions with F bonded to T6 (Fig. 7, inset), which correspond to the most stable T sites found for 1 Ge systems. In this case, a broad dispersion of chemical shifts is observed, with signals ranging from −6 to −50 ppm, and with the most stable system (T6T7) giving a chemical shift of −19 ppm. We finally studied systems with 3 Ge in the cage (Ge_f = 0.3), with two of them in the more stable and contiguous T6 and T7 positions, varying the location of the third Ge. Once again, energy results evidence the tendency of Ge to cluster since the most stable systems correspond to Ge bonded to T6 in the T6T7T9 and T6T7T10 positions, both forming GeOGeOGe clusters, and giving theoretical ¹⁹F NMR chemical shifts at −15 and −27 ppm, respectively. These results agree well with the experimental chemical shifts found for CSV materials with different Ge_f (Fig. 8).

Fig. 7 Relative stability vs.¹⁹F NMR chemical shift for F⁻ in [4⁴5²] cages with 1 Ge (black triangles), 2 Ge (red squares) in paired (solid) or isolated (empty) positions and 3 Ge (blue circles) in clustered (solid) or non-clustered (empty) positions. Relative stabilities are calculated independently for 1Ge, 2Ge and 3Ge systems. The inset shows the labels for the T atoms in the [4⁴5²] cage, with 2Ge in T6 and T7 positions.

Fig. 8 ¹⁹F MAS NMR spectra of CSV samples synthesized at Ge_f equal to (from bottom) 0.09, 0.1 and 0.2. The resonances around −115 to −130 ppm are assigned to impurities. Spinning side bands are marked with ‘*’. Measured chemical shifts are signaled by arrows.

When compared with the experimental ¹⁹F NMR spectra observed for the CSV samples, the overall trends observed in our computational results can provide a tentative explanation for the bands observed (although the exact chemical shifts are not the same, trends can be appreciated). At low Ge_f (0.09 and 0.1), two more intense signals are observed at −33 and −45 ppm, which can be assigned to F bonded to Ge in cages with 1 Ge at positions T6 and T7, respectively. When Ge_f is increased to 0.2, the former bands decrease their intensity, and a higher intensity in the low-field region is observed, with a band at around −20 ppm now displaying the highest intensity, which according to our computational results should be ascribed to F bonded to Ge in cages with 2 paired Ge at positions T6–T7, which increases its intensity because of the higher Ge content.

Conclusions

This work shows how the complex interplay between different factors determines the phase selectivity of zeolite crystallization when the structure direction exerted by the OSDA is not highly specific and strong enough. When using 2iPr13DMI as the OSDA, several phases might be stabilized but they differ in their intrinsic stability and in the effect of Ge (and F) on that stability. Here, only two default, intrinsically stable, zeolites (ZSM-12 and SSZ-35) were obtained under pure silica conditions. When Ge is added to the synthesis mixtures, up to four additional zeolites can be obtained: HPM-10 (-CLO), HPM-1 (STW, although we never got it as a pure phase), CIT-7 (CSV) and HPM-11 and HPM-6 (intermediate and high Ge_fUOS, respectively). These two UOS materials have PXRD patterns that are markedly different from each other and from that of as-synthesized IM-16 (reference UOS material with lower Ge content) due to the different Ge_f and symmetries. Calculations suggest 2iPr13DMI may rather comfortably fit in all the obtained phases, providing some moderate stabilization, likely helped by the flexibility, though limited, provided by the isopropyl group.

Calculations also shine some light on ¹³C MAS NMR resonances that split in UOS when the Ge_f increases, although this is more clearly observed for the methyl groups attached to N than the imidazolium C–H. Finally, multiple overlapped ¹⁹F resonances in the −5 to −45 ppm range in germanosilicate CSV are ascribed to F occluded in the [4⁴5²] cage interacting with different crystallographic sites and with different contents and distributions of Ge atoms. This is supported by comparison with similar systems and by DFT calculations.

Author contributions

H. Y., A. R., Z. R. G. and L. A. V.: synthesis and physicochemical characterization; L. G. H.: calculations; J. L.: structural characterization; J.-L. P.: synthesis, structural characterization; M. A. C.: supervision, physicochemical characterization, writing-original draft. All the authors discussed the results and revised the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the Spanish Research Agency, MCIN/AEI/10.13039/501100011033, and the European Union for funding (Projects PID2019-105479RB-I00, PID2019-107968RB-I00, and PID2021-128141OB-C22, FEDER and TED2021-131223B-I00, “NextGenerationEU”/PRTR). H. Y. is grateful to the China Scholarship Council (CSC) for a PhD fellowship. L. A. V. also thanks the Generalitat Valenciana (PROMETEO CIPROM/2021/007).

References

1. H. Yu, A. Rojas, Z. R. Gao, L. Gómez-Hortigüela, L. A. Villaescusa, J. Li, J.-L. Paillaud and M. A. Camblor, CCDC 2276644: Experimental Crystal Structure Determination, 2023,  DOI:10.5517/ccdc.csd.cc2gf143.
2. H. Yu, A. Rojas, Z. R. Gao, L. Gómez-Hortigüela, L. A. Villaescusa, J. Li, J.-L. Paillaud and M. A. Camblor, CCDC 2280872: Experimental Crystal Structure Determination, 2023,  DOI:10.5517/ccdc.csd.cc2gkfj0.
3. H. Yu, A. Rojas, Z. R. Gao, L. Gómez-Hortigüela, L. A. Villaescusa, J. Li, J.-L. Paillaud and M. A. Camblor, CCDC 2280873: Experimental Crystal Structure Determination, 2023,  DOI:10.5517/ccdc.csd.cc2gkfk1.
4. H. Yu, A. Rojas, Z. R. Gao, L. Gómez-Hortigüela, L. A. Villaescusa, J. Li, J.-L. Paillaud and M. A. Camblor, CCDC 2280874: Experimental Crystal Structure Determination, 2023,  DOI:10.5517/ccdc.csd.cc2gkfl2.
5. J. D. Sherman, Synthetic zeolites and other microporous oxide molecular sieves, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 3471–3478.
6. Z. Cao, N. D. Anjikar and S. Yang, Small-pore zeolite membranes: A review of gas separation applications and membrane preparation, Separations, 2022, 9, 47; J. B. Lim, J. Shin, N. H. Ahn, I. Heo and S. B. Hong, Selective catalytic reduction of NO with CH₄ over cobalt-exchanged cage-based, small-pore zeolites with different framework structures, Appl. Catal., B, 2020, 267, 118710.
7. J. H. Lee and S. B. Hong, Dehydration of 1,3-butanediol to butadiene over medium-pore zeolites: Another example of reaction intermediate shape selectivity, Appl. Catal., B, 2021, 280, 119446; V. G. Komvokis, E. F. Iliopoulou, I. A. Vasalos, K. S. Triantafyllidis and C. L. Marshall, Development of optimized Cu–ZSM-5 deNOx catalytic materials both for HC-SCR applications and as FCC catalytic additives, Appl. Catal., A, 2007, 325, 345–352.
8. H. Lee, J. Shin, K. Lee, H. J. Choi, A. Mayoral, N. Y. Kang and S. B. Hong, Synthesis of thermally stable SBT and SBS/SBT intergrowth zeolites, Science, 2021, 373, 104–107.
9. Q.-F. Lin, Z. R. Gao, C. Lin, S. Zhang, J. Chen, Z. Li, X. Liu, W. Fan, J. Li, X. Chen, M. A. Camblor and F.-J. Chen, A stable aluminosilicate zeolite with intersecting three-dimensional extra-large pores, Science, 2021, 374, 1605–1608; J. Li, Z. R. Gao, Q.-F. Lin, C. Liu, F. Gao, C. Lin, S. Zhang, H. Deng, A. Mayoral, W. Fan, S. Luo, X. Chen, H. He, M. A. Camblor, F.-J. Chen and J. Yu, A 3D extra-large-pore zeolite enabled by 1D-to-3D topotactic condensation of a chain silicate, Science, 2023, 379, 283–287.
10. Y. Kakutani, P. Weerachawanasak, Y. Hirata, M. Sano, T. Suzuki and T. Miyake, Highly effective K-Merlinoite adsorbent for removal of Cs⁺ and Sr²⁺ in aqueous solution, RSC Adv., 2017, 7, 30919–30928.
11. J. Chen, T. Liang, J. Li, S. Wang, Z. Qin, P. Wang, L. Huang, W. Fan and J. Wang, Regulation of Framework Aluminum Siting and Acid DistributionH-MCM-22 by Boron Incorporation and its Effect on the Catalytic Performance in Methanol to Hydrocarbons, ACS Catal., 2016, 6, 2299–2313.
12. R. Millini, G. Bellussi, P. Pollesel, C. Rizzo and C. Perego, Beyond TS-1: Background and recent advances in the synthesis of Ti-containing zeolites, Microporous Mesoporous Mater., 2022, 346, 112286.
13. Z. Zhu, H. Xu, J. Jiang, H. Wu and P. Wu, Hydrophobic nanosized all-silica beta zeolite: Efficient synthesis and adsorption application, ACS Appl. Mater. Interfaces, 2017, 9, 27273–27283.
14. M. A. Camblor, A. Corma, P. Esteve, A. Martínez and S. Valencia, Epoxidation of unsaturated fatty esters over large-pore Ti-containing molecular sieves as catalysts: important role of the hydrophobic–hydrophilic properties of the molecular sieve, Chem. Commun., 1997, 795–796; M. A. Camblor, A. Corma, S. Iborra, S. Miquel, J. Primo and S. Valencia, Beta zeolite as a catalyst for the preparation of alkyl glucoside surfactants: The role of crystal size and hydrophobicity, J. Catal., 1997, 172, 76–84.
15. M. E. Davis and R. F. Lobo, Zeolite and molecular sieve synthesis, Chem. Mater., 1992, 4, 756–768.
16. A. Moini, K. D. Schmitt, E. W. Valyocsik and R. F. Polomski, The role of diquaternary cations as directing agents in zeolite synthesis, Zeolites, 1994, 14, 504–511; F.-J. Chen, Z. R. Gao, J. Li, L. Gómez-Hortigüela, C. Lin, L. Xu, H.-B. Du, C. Márquez-Álvarez, J. Sun and M. A. Camblor, Structure-direction towards the new large pore zeolite NUD-3, Chem. Commun., 2021, 57, 191–194; P. Lu, L. Gómez-Hortigüela, Z. Gao and M. A. Camblor, Synthesis of a germanosilicate zeolite HPM-12 using a short imidazolium-based dication: structure-direction by charge-to-charge distance matching, Dalton Trans., 2019, 48, 17752–17762; P. Lu, L. Gómez-Hortigüela and M. A. Camblor, Synthesis of pure silica MWW zeolite in fluoride medium by using an imidazolium-based long dication, Chem. – Eur. J., 2019, 25, 1561–1572.
17. M. A. Camblor and S. B. Hong, in Porous Materials, Ed. D. W. Bruce, D. O'Hare and R. I. Walton, Wiley, Chichester, 2011, pp. 265–325.
18. P. Caullet, J.-L. Paillaud, A. Simon-Masseron, M. Soulard and J. Patarin, The fluoride route: a strategy to crystalline porous materials, C. R. Chim., 2005, 8, 245–266; L. A. Villaescusa and M. A. Camblor, The Fluoride Route to New Zeolites, Recent Res. Dev. Chem., 2003, 1, 93–141.
19. M. A. Camblor, L. A. Villaescusa and M. J. Díaz-Cabañas, Synthesis of all-silica and high-silica molecular sieves in fluoride media, Top. Catal., 1999, 9, 59–76; P. Lu, L. A. Villaescusa and M. A. Camblor, Driving the crystallization of zeolites, Chem. Rec., 2018, 18, 713–723.
20. H. Li and O. M. Yaghi, Transformation of germanium dioxide to microporous germanate 4-connected nets, J. Am. Chem. Soc., 1998, 120, 10569–10570; T. Conradsson, M. S. Dadachov and X. D. Zou, Synthesis and structure of (Me₃N)₆[Ge₃₂O₆₄]·(H₂O)_4.5, a thermally stable novel zeotype with 3D interconnected 12-ring channels, Microporous Mesoporous Mater., 2000, 41, 183–191; A. K. Cheetham, H. Fjellvg, T. E. Gier, K. O. Kongshaug, K. P. Lillerud and G. D. Stucky, Stud. Surf. Sci. Catal., 2001, 135, 788; A. Corma and M. E. Davis, Issues in the synthesis of crystalline molecular sieves: towards the crystallization of low framework-density structures, ChemPhysChem, 2004, 5, 305–313; M. A. Camblor and M. E. Davis, ²⁹Si MAS NMR spectroscopy of tectozincosilicates, J. Phys. Chem., 1994, 98, 13151–13156; S. H. Park, P. Daniels and H. Gies, RUB-23: a new microporous lithosilicate containing spiro-5 building units, Microporous Mesoporous Mater., 2000, 37, 129–143; S.-H. Park, J. B. Parise, H. Gies, H. Liu, C. P. Grey and B. H. Toby, A new porous lithosilicate with a high ionic conductivity and ion-exchange capacity, J. Am. Chem. Soc., 2000, 122, 11023–11024.
21. H. Gies and B. Marker, The structure-controlling role of organic templates for the synthesis of porosils in the systems SiO₂/template/H₂O, Zeolites, 1992, 12, 42–49.
22. R. T. Rigo, S. R. G. Balestra, S. Hamad, R. Bueno-Perez, A. R. Ruiz-Salvador, S. Calero and M. A. Camblor, The Si–Ge substitutional series in the chiral STW zeolite structure type, J. Mater. Chem. A, 2018, 6, 15110–15122.
23. S. Valencia, PhD Thesis, Universidad Politecnia de Valencia, Valencia, 1997; Y. Mathieu, J.-L. Paillaud, P. Caullet and N. Bats, Synthesis and characterization of IM-10: a new microporous silicogermanate with a novel topology, Microporous Mesoporous Mater., 2004, 75, 13–22; J.-L. Paillaud, B. Harbuzaru, J. Patarin and N. Bats, Extra-large-pore zeolites with two-dimensional channels formed by 14 and 12 rings, Science, 2004, 304, 990–992.
24. Z. R. Gao, S. R. G. Balestra, J. Li and M. A. Camblor, Synthesis of extra-large pore, large pore and medium pore zeolites using a small imidazolium cation as the organic structure-directing agent, Chem. – Eur. J., 2021, 27, 18109–18117.
25. Zeolite Database Help, https://europe.iza-structure.org/IZA-SC/DatabaseHelp_Structures.html, (accessed July 11, 2023).
26. Y. Lorgouilloux, M. Dodin, J.-L. Paillaud, P. Caullet, L. Michelin, L. Josien, O. Ersen and N. Bats, IM-16: A new microporous germanosilicate with a novel framework topology containing d4r and mtw composite building units, J. Solid State Chem., 2009, 182, 622–629.
27. A. Rojas, E. Martínez-Morales, C. M. Zicovich-Wilson and M. A. Camblor, Zeolite synthesis in fluoride media: structure direction toward ITW by small methylimidazolium cations, J. Am. Chem. Soc., 2012, 134, 2255–2263.
28. W. Wan, J. Sun, J. Su, S. Hovmöller and X. Zou, Three-dimensional rotation electron diffraction: software RED for automated data collection and data processing, J. Appl. Crystallogr., 2013, 46, 1863–1873.
29. W. Kabsch, XDS, Acta Crystallogr., 2010, 66, 125–132.
30. G. M. Sheldrick, SHELXT - integrated space-group and crystal-structure determination, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8.
31. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, OLEX2: a complete structure solution, refinement and analysis program, J. Appl. Crystallogr., 2009, 42, 339–341.
32. A. A. Coelho, TOPAS and TOPAS-Academic: an optimization program integrating computer algebra and crystallographic objects written in C++, J. Appl. Crystallogr., 2018, 51, 210–218.
33. S. Smeets, L. B. McCusker, C. Baerlocher, S. Elomari, D. Xie and S. I. Zones, Locating organic guests in inorganic host materials from X-ray powder diffraction data, J. Am. Chem. Soc., 2016, 138, 7099–7106.
34. B. H. Toby and R. B. Von Dreele, GSAS-II: the genesis of a modern open-source all purpose crystallography software package, J. Appl. Crystallogr., 2013, 46, 544–549.
35. PowderCell for Windows, Version 2.4 8.03.2000, Berlin, Germany.
36. Forcite Module. Material Studio 2019, BIOVIA.
37. S. L. Mayo, B. D. Olafson and W. A. Goddard, DREIDING: a generic force field for molecular simulations, J. Phys. Chem., 1990, 94, 8897–8909.
38. J. D. Gale and A. L. Rohl, The general utility lattice program (GULP), Mol. Simul., 2003, 29, 291–341.
39. K.-P. Schröder, J. Sauer, M. Leslie, C. Richard, A. Catlow and J. M. Thomas, Bridging hydrodyl groups in zeolitic catalysts: a computer simulation of their structure, vibrational properties and acidity in protonated faujasites (H-Y zeolites), Chem. Phys. Lett., 1992, 188, 320–325.
40. J. D. Gale and N. J. Henson, Derivation of interatomic potentials for microporous aluminophosphates from the structure and properties of berlinite, J. Chem. Soc., Faraday Trans., 1994, 90, 3175.
41. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, First principles methods using CASTEP, Z. Kristallogr. – Cryst. Mater., 2005, 220, 567–570.
42. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
43. C. J. Pickard and F. Mauri, All-electron magnetic response with pseudopotentials: NMR chemical shifts, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245101.
44. J. E. Schmidt, M. A. Deimund, D. Xie and M. E. Davis, Synthesis of RTH-type zeolites using a diverse library of imidazolium cations, Chem. Mater., 2015, 27, 3756–3762.
45. Database of Zeolite Structures, https://www.iza-structure.org/databases/, (accessed July 11, 2023).
46. J. E. Schmidt, D. Xie, T. Rea and M. E. Davis, CIT-7, a crystalline, molecular sieve with pores bounded by 8 and 10-membered rings, Chem. Sci., 2015, 6, 1728–1734.
47. K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276.
48. J. Su, Y. Wang, J. Lin, J. Liang, J. Sun and X. Zou, A silicogermanate with 20-ring channels directed by a simple quaternary ammonium cation, Dalton Trans., 2013, 42, 1360–1363.
49. Y. Lorgouilloux, J. L. Paillaud, P. Caullet, J. Patarin and N. Bats, FR2918979A1, 2009.
50. A. Altomare, M. Camalli, C. Cuocci, C. Giacovazzo, A. Moliterni and R. Rizzi, EXPO2009: structure solution by powder data in direct and reciprocal space, J. Appl. Crystallogr., 2009, 42, 1197–1202.
51. R. Bialek, Kriber v. 1.0, ETH, Zurich, 1991.
52. L. Xu, L. Zhang, J. Li, K. Muraoka, F. Peng, H. Xu, C. Lin, Z. Gao, J.-G. Jiang, W. Chaikittisilp, J. Sun, T. Okubo and P. Wu, Crystallization of a novel germanosilicate ECNU-16 provides insights into the space-filling effect on zeolite crystal symmetry, Chem. – Eur. J., 2018, 24, 9247–9253.
53. L. A. Villaescusa and M. A. Camblor, Framework Reduction of GeO₂ Zeolites During Calcination, Chem. Mater., 2016, 28, 7544–7550.
54. Y. Pauleau and J.-C. Remy, Kinetics of the formation and sublimation of germanium monoxide, J. Less-Common Met., 1975, 42, 199–208.
55. S. K. Sahari, A. Ohta, M. Matsui, K. Mishima, H. Murakami, S. Higashi and S. Miyazaki, Kinetics of thermally oxidation of Ge(100) surface, J. Phys.: Conf. Ser., 2013, 417, 012014.
56. A. Rojas, M. L. San-Roman, C. M. Zicovich-Wilson and M. A. Camblor, Host–guest stabilization of a zeolite strained framework: In situ transformation of zeolite MTW into the less dense and more strained ITW, Chem. Mater., 2013, 25, 729–738.
57. A. Rojas, O. Arteaga, B. Kahr and M. A. Camblor, Synthesis, structure, and optical activity of HPM-1, a pure silica chiral zeolite, J. Am. Chem. Soc., 2013, 135, 11975–11984.
58. H. Koller, A. Wölker, L. A. Villaescusa, M. J. Díaz-Cabañas, S. Valencia and M. A. Camblor, Five-coordinate silicon in high-silica zeolites, J. Am. Chem. Soc., 1999, 121, 3368–3376.
59. C. A. Fyfe, D. H. Brouwer, A. R. Lewis, L. A. Villaescusa and R. E. Morris, Combined solid state NMR and X-ray diffraction investigation of the local structure of the five-coordinate silicon in fluoride-containing as-synthesized STF zeolite, J. Am. Chem. Soc., 2002, 124, 7770–7778.
60. B. Harbuzaru, M. Roux, J. L. Paillaud, F. Porcher, C. Marichal, J. M. Chézeau and J. Patarin, Synthesis and characterisation of Mu-26 a fluorinated all-silica zeolite with the SSZ-35 framework topology: Evidence for a triclinic symmetry, Chem. Lett., 2002, 31, 616–617.
61. S. I. Zones, S.-J. Hwang, M. M. Olmstead, S. J. Teat, A. Jackowski, A. W. Burton and C. Kim, A most unusual zeolite templating: Cage to cage connection of one guest molecule, J. Phys. Chem. C, 2010, 114, 8899–8904.
62. Y. M. Variani, A. Rojas, L. Gómez-Hortigüela and S. B. C. Pergher, Study of the performance of imidazolium-derived cations as structure directing agents in the synthesis of zeolites in fluoride media, New J. Chem., 2016, 40, 7968–7977.
63. A. Rojas, L. Gómez-Hortigüela and M. A. Camblor, Benzylimidazolium cations as zeolite structure-directing agents. Differences in performance brought about by a small change in size, Dalton Trans., 2013, 42, 2562–2571.
64. M. A. Camblor, P. A. Barrett, M.-J. Díaz-Cabañas, L. A. Villaescusa, M. Puche, T. Boix, E. Pérez and H. Koller, High silica zeolites with three-dimensional systems of large pore channels, Microporous Mesoporous Mater., 2001, 48, 11–22.
65. L. A. Villaescusa, P. Lightfoot and R. E. Morris, Synthesis and structure of fluoride-containing GeO₂ analogues of zeolite double four-ring building units, Chem. Commun., 2002, 2220–2221.
66. Y. Chen, S. Huang, X. Wang, L. Zhang, N. Wu, F. Liao and Y. Wang, Synthesis and Characterization of a Layered Silicogermanate PKU-22 and Its Topotactic Condensation to a Three-Dimensional STI-type Zeolite, Cryst. Growth Des., 2017, 17, 5465–5473.
67. Y. Chen, N. Ma, S. Huang, X. Du, F. Liao, Y. Zhu, J. Sun and Y. Wang, An interrupted zeolite PKU-26 and its transformation to a fully four-connected zeolite PKU-27 upon calcination, Chem. – Eur. J., 2019, 25, 3219–3223.
68. P. Caullet, J. L. Guth, J. Hazm, J. M. Lamblin and H. Gies, Synthesis, Characterization and Crystal Structure of the New Clathrasil Phase Octadecasil, Eur. J. Solid State Inorg. Chem., 1991, 28, 345–361.
69. P. M. Piccione, C. Laberty, S. Yang, M. A. Camblor, A. Navrotsky and M. E. Davis, Thermochemistry of pure-silica zeolites, J. Phys. Chem. B, 2000, 104, 10001–10011.
70. C. M. Zicovich-Wilson, F. Gándara, A. Monge and M. A. Camblor, In situ transformation of TON silica zeolite into the less dense ITW: structure-direction overcoming framework instability in the synthesis of SiO₂ zeolites, J. Am. Chem. Soc., 2010, 132, 3461–3471.
71. C. M. Zicovich-Wilson, M. L. San-Román, M. A. Camblor, F. Pascale and J. S. Durand-Niconoff, Structure, vibrational analysis, and insights into host-guest interactions in as-synthesized pure silica ITQ-12 zeolite by periodic B3LYP calculations, J. Am. Chem. Soc., 2007, 129, 11512–11523.
72. G. Sastre and A. Corma, Predicting structural feasibility of silica and Germania zeolites, J. Phys. Chem. C, 2010, 114, 1667–1673.
73. Z. R. Gao, S. R. G. Balestra, J. Li and M. A. Camblor, HPM–16, a stable interrupted zeolite with a multidimensional mixed medium–large pore system containing supercages, Angew. Chem., Int. Ed., 2021, 60, 20249–20252.
74. P. Lu, A. Mayoral, L. Gómez-Hortigüela, Y. Zhang and M. A. Camblor, Synthesis of 3D large-pore germanosilicate zeolites using imidazolium-based long dications, Chem. Mater., 2019, 31, 5484–5493.

---

Footnotes

† Electronic supplementary information (ESI) available: 3D ED and supplementary PXRD patterns, Rietveld refinement plots, characterization data, supplementary calculation figures, detailed synthesis results, and crystallographic tables. Structures for as-synthesized IM-16, HPM-6 (Ge_f = 1), HPM-6 (Ge_f = 0.88) and HPM-11 (Ge_f = 0.58) were previously published as CCDC Communications (ref. 1–4). See DOI: https://doi.org/10.1039/d3dt02414h

‡ These authors contributed equally to this work.

§ Current address: Department of Chemical and Biomolecular Engineering, Institute for NanoBioTechnology, Johns Hopkins University, Baltimore, MD 21218, USA.

---