Role of molecular symmetry in the magnetic relaxation dynamics of five-coordinate Dy(III) complexes

Abstract

A new family of low-coordinate mononuclear Dy^III single-molecule magnets [(Trapen^TMS)Dy(L^B)] (Trapen = tris(2-aminobenzyl)amine; TMS = SiMe₃; L^B = THF 1, pyridine 2, ONMe₃3) has been synthesized and structurally characterized by single crystal X-ray diffraction. The five-coordinate Dy^III ions exhibit distorted triangular bipyramidal geometries, among the different neutral ligands L^B on the apex and the same Trapen^TMS ligand, making the pyramid base of the trigonal bipyramid. Magnetic data analysis reveals that 1–3 are characteristic of SMM behaviors without a dc field, accompanying an unambiguous quantum tunneling of magnetization. Under an extra dc field of 500 Oe, field-induced slow magnetic relaxation behaviors occur with Raman and/or QTM processes. Ab initio calculations were also performed to rationalize the observed discrepancy in the magnetic behaviors, and the result illustrates that the SMM behavior could be effectively manipulated by the axial symmetry of the triangular bipyramidal Dy^III motifs.

---

Introduction

Single-molecule magnets (SMMs), a kind of molecular material capable of retaining unquenched spin information, have attracted much attention in the fields of molecular spintronics, high-density data storage, and quantum information processing.^1–3 Since the first discovery of the superparamagnetic behavior in {TbPc₂} (Pc = phthalocyanine) below a blocking temperature,^4,5 there have been many remarkable developments in the synthesis and study of monometallic lanthanide SMMs, also named single-ion magnets (SIMs).

It is worth noting that dysprosium-based SIMs become an ideal candidate in the construction of SMMs owing to their large unquenched orbital momentum as well as high magnetic anisotropy and the strong spin–orbital coupling effect of the Dy^III ions.^6–10 Theoretical and experimental studies have shown that the magnetic dynamics of dysprosium SIMs can be tailored by the coordination geometries and ligand fields around the Dy^III centers and have provided perspectives that might be of assistance in the design of superior Dy-SIMs.^11–13 The strong axial ligand field, short Dy–L_axial bond length and weak equatorial donors favor stabilizing the oblate-shaped |±15/2〉 Kramers doublet, thereby yielding strong anisotropy. In past studies, some high symmetry and high coordination number (CN > 6) Dy^III complexes have been dominating the molecular magnetism field.^12,14–19 However, as a new benchmark in molecule-based magnets, a mononuclear dysprosium SMMs with nearly linear geometry, [(Cp^iPr5)Dy(Cp*)]⁺, has been reported to boost the U_eff record to 1541 cm⁻¹ and the blocking temperature (T_B) to 80 K.²⁰ This groundbreaking work opens up a new direction for the development of single-molecule magnets. Meanwhile, theoretical investigations showed that Dy-base SIMs, with a low coordination number, can induce the building of large crystal field (CF) splitting.²¹ Even so, from the perspective of synthetic chemistry, the construction of a low-coordinated (CN < 6) Dy^III complex is a highly challenging task, owing to a particular preference for large coordination numbers and flexible geometric configuration. This requires appropriate steric hindrance ligands and strict experimental conditions. To date, previous work shows that five-coordinate triangular bipyramidal Dy^III SIMs with local D_3h symmetry are extremely rare.^22–24 Thus, the study of this system can not only expand the family of Dy^III-based SMMs, but also contribute to an in-depth understanding of the magneto-structural correlation and detailed theoretical elucidations of the dynamic magnetic behaviors in five-coordinate Dy^III SIMs.

In this context, we decided to construct a family of five-coordinate triangular bipyramidal mononuclear Dy^III complexes with local D_3h symmetry, designed in such a way that the Dy^III coordination sphere can be selectively varied at a single position to deeply explore the relationships among the coordination geometry, steric effect, electronic effect and magnetic properties. Herein, we used the sterically demanding tris(2-aminobenzyl)amine (Trapen) as a ligand to limit the coordination number at the Dy^III centre. Fortunately, three monometallic dysprosium complexes, [(Trapen^TMS)Dy(L^B)] (L^B = THF 1, Pyridine 2, ONMe₃3), have been successfully isolated by alternating the coordination units at the axial position of one side of the Dy^III centre (Scheme 1). As a result, subtle structural modulations around the Dy^III ions caused by ligand field effects contribute to noticeable changes in the magnetic dynamics for three complexes that could be elucidated by the investigation of magnetism and ab initio calculations.

Scheme 1 Synthesis of the five-coordinate mononuclear Dy^III ions of 1–3.

Experimental

Materials and physical measurements

All experimental manipulations were carried out under an inert atmosphere of dry argon using a standard Schlenk line and glovebox (<1 ppm of O₂, <1 ppm of H₂O). All solvents were dried using sodium and degassed before use, distilled, and stored in Young ampule sodium mirrors. [(Trapen^TMS)(Li)₃] and DyCl₃(THF)_2.7 were prepared according to the literature procedure.^25,26 Other reagents were purchased from Energy Chemical, J&K, and other companies. Elemental analysis (C, H, and N) was performed with a Vario EL III elemental analyzer at Peking University. The phase purity of complexes 1–3 was confirmed by powder X-ray diffraction (PXRD) measurements on the same portions of microcrystalline samples at room temperature, equipped with a Rigaku RU200 diffractometer at Cu-Kα radiation (λ = 1.5406 Å) with a step size of 0.02° in 2θ and a scan speed of 5° min⁻¹. The crystalline sample was ground into fine powder in the glove box, and then packaged in a special sealed container for measurement. The theoretical simulation of PXRD was performed on Mercury 2020.3.0, and the single crystal data of 1–3 were used as the simulation basis. Magnetic measurements on the polycrystalline samples were accomplished using a Quantum Design MPMS-XL7 SQUID magnetometer (restrained in eicosane to prevent torquing at high fields). The measured magnetic data were corrected for the diamagnetic susceptibility by means of Pascal's constants and sample-holder calibration.

Synthesis of [(Trapen^TMS)Dy(THF)] (1)

Inside an argon glovebox, 10 mL of THF was added to the mixture of [(Trapen^TMS)(Li)₃] (283 mg, 0.5 mmol) and DyCl₃(THF)_2.7 (25 mg, 0.55 mmol) at −30 °C. The materials were gradually dissolved, and the color of the solution changed from colorless to light yellow. The reaction mixture was warmed up to room temperature and stirred for 12 h. The solvent was removed under reduced pressure, and the residue was extracted with toluene (15 mL) and filtered to obtain a colorless solution. The solution was concentrated to about 1 mL, and then stored at −30 °C for several days, to obtain colorless crystals of 1. The crystals were washed with cold hexane (2 mL) and then dried to get a clean, colorless solid (252 mg, 0.323 mmol, 65%). Anal. calcd for C₃₄H₅₃N₄OSi₃Dy: C, 52.32; H, 6.84; N, 7.18. Found: C, 52.20; H, 6.51; N, 7.03.

Synthesis of [(Trapen^TMS)Dy(Pyridine)] (2)

Complex 1 (78 mg, 0.1 mmol) was dissolved in 5 mL of pyridine. Then the solution was slowly volatilized for more than 5 days at room temperature. A few colorless crystals were precipitated from the solution. The mixtures were stored at −30 °C to obtain more colorless crystals of 2, which were suitable for the single-crystal X-ray diffraction analysis. The crystals were washed with cold hexane (1 mL) and then dried to obtain a colorless solid (47 mg, 0.060 mmol, 61%). Anal. calcd for C₃₄H₅₃N₄OSi₃Dy: C, 53.45; H, 6.28; N, 8.90. Found: C, 53.12; H, 6.14; N, 8.78.

Synthesis of [(Trapen^TMS)Dy(ONMe₃)] (3)

At −30 °C, the pre-cooled THF (10 mL) was added to complex 1 (156 mg, 0.2 mmol) and ONMe₃ (15 mg, 0.2 mmol) under vigorous stirring. The solution was warmed to room temperature and then stirred for 12 h. The solvent was removed under reduced pressure, and the residue was extracted with toluene (10 mL). The toluene solution was filtered and then concentrated to 0.5 mL and stored at −30 °C by slow evaporation, yielding 3 as colorless crystals (94 mg, 0.120 mmol, 60%). The molecular structures of the crystals were confirmed by single-crystal X-ray diffraction analysis. Anal. calcd for C₃₄H₅₃N₄OSi₃Dy: C, 50.58; H, 6.95; N, 8.94. Found: C, 50.37; H, 6.51; N, 8.74.

X-ray crystallography

Suitable crystals of all complexes were selected for X-ray measurements. Crystal structure data were collected with a Bruker D8 VENTURE X-ray CMOS diffractometer using graphite monochromated Mo-K_α radiation (λ = 0.71073 Å) at 150 K for 1 and 170 K for 3, and the Cu-K_α X-ray source (λ = 1.54178 Å) at 170 K for 2. Using Olex2, the structure was solved with the XT structural solution program using Intrinsic Phasing and refined with the XL²⁷ refinement package using least squares minimization. All non-hydrogen atoms were refined with anisotropic thermal parameters. All hydrogen atoms were placed in calculated positions and refined isotropically. Crystallographic data for all complexes are provided in Table S1.† Selected bond lengths and angles are listed in Table S2.†

Theoretical methods

Complete-active-space self-consistent field (CASSCF) calculations on mononuclear five-coordinate complexes 1a, 1b, 2, and 3 (Fig. S10†) on the basis of single-crystal X-ray determined geometries were carried out with the OpenMolcas²⁸ program package. The basis sets for all atoms are atomic natural orbitals from the OpenMolcas ANO-RCC library: ANO-RCC-VTZP for Dy^III; VTZ for close N and O; and VDZ for distant atoms. The calculations employed the second-order Douglas–Kroll–Hess Hamiltonian, where scalar relativistic contractions were taken into account in the basis set and the spin–orbit couplings were handled separately in the restricted active space state interaction (RASSI-SO) procedure.^29,30 For complexes 1–3, active electrons in 7 active orbitals include all f electrons (CAS(9, 7)) for Dy^III in the CASSCF calculations. To exclude all the doubts, we calculated all the roots in the active space and mixed the maximum number of a spin-free state, which was possible with our hardware (all from 21 sextets, 128 from 224 quadruplets, 130 from 490 doublets) for them. The SINGLE_ANISO^31–33 program was used to obtain the energy levels, g tensors, magnetic axes, etc. based on the above CASSCF/RASSI-SO calculations.

Results and discussion

Crystal structures

The molecular structures of 1, 2, and 3 were confirmed using X-ray single-crystal diffraction analysis. The crystal data and structure refinement for three complexes are depicted in Table S1 in the ESI.† Complex 1 crystallized in the monoclinic P2₁ space group, whilst 2 and 3 pertain to the monoclinic P2₁/c space group. The PXRD patterns correspond with those simulated from single-crystal X-ray diffraction data, confirming that the bulk polycrystalline samples for these complexes are pure (Fig. S4–S6†).

As shown in Fig. 1, complexes 1–3 [(Trapen^TMS)Dy(L^B)] (L^B = THF 1, pyridine 2, ONMe₃3) have similar coordination geometrical configurations, containing a mononuclear Dy^III ion in a rare penta-coordinate distorted trigonal bipyramidal geometry, having a neutral molecule L^B at the apex of the trigonal bipyramid and a Trapen^TMS ligand making the pyramid base. It is worth noting that the unit cell of 1 contains two crystallographically independent Dy^III atoms (Dy1 and Dy2, Fig. 1a). For 1, 2, and 3, three N atoms of the Trapen^TMS ligand coordinate to the central Dy^III ions at the equatorial sites; the other nitrogen atom of the ligand further occupies an axial position of the Dy^III center. The coordination units L^B at another axial position of Dy^III central to these three complexes are different (L^B = THF 1, pyridine 2, ONMe₃3). A comparison of the structural data for the above three complexes is shown in Table 1. The Dy–N_equatorial distances (1a: 2.249(5), 2.263(5), 2.249(4) Å; 1b: 2.265(5), 2.247(5), 2.242(5) Å; 2: 2.258(3), 2.242(3), 2.253(3) Å) of the equatorial plane and the Dy–N_axial bond lengths (1a: 2.499(5) Å; 1b: 2.527(5) Å; 2: 2.500(2) Å) of the axial position for 1 and 2 are almost equal, respectively. Compared to 1 and 2, the Dy–N_equatorial and the Dy–N_axial bond lengths become longer in 3, but the Dy–O_axial distance of 3 is significantly shorter than that of the corresponding Dy–O bond length in 1. This may be due to the strong bonding ability of ONMe₃ with the metal atom. Overall, the lengths of two Dy–N bonds on the equatorial plane in 1 and 3 are nearly equal, but slightly shorter than the other Dy–N bond length, respectively. But the two roughly equal Dy–N bond lengths in 2 are slightly longer than the third Dy–N bond. Meanwhile, based on the structural parameters of these complexes, the geometrical configuration of the Dy^III center in 1–3 was investigated using the SHAPE 2.1 software. As listed in Table S9,† the calculated Dy^III centers of 1–3 are best described as having a trigonal bipyramidal (D_3h) geometry with different distortions from the ideal geometry (CShMs parameters: 0.835 (1a), 0.890 (1b), 0.737 (2), and 0.531 (3)). The average N–Dy–N angles of 1–3 are all nearly 118°, indicating that the three N atoms of the Trapen^TMS ligand with the Dy atom are approximately coplanar. The shortest intermolecular Dy⋯Dy distances in the crystal lattice of 1–3 are 10.0282 Å, 9.9063 Å, and 10.050 Å (Fig. S1–S3†), respectively, implying spatial isolation of the mononuclear motifs.

Fig. 1 Coordination environment of the Dy^III center and polyhedra around the Dy^III ions for 1–3 (a–d). Hydrogen atoms and free solvent molecules are omitted for clarity.

Table 1 Comparison of partial structural data for 1–3

Bond length/angle	1a	1b	2	3
Dy–Nequatorial [Å]	2.249(5)	2.247(5)	2.258(3)	2.2684(17)
	2.263(5)	2.265(5)	2.242(3)	2.2904(18)
	2.249(4)	2.242(5)	2.253(3)	2.2720(17)
Dy–Naxial [Å]	2.499(5)	2.527(5)	2.500(2)	2.5884(17)
Dy–Oaxial [Å]	2.425(4)	2.409(5)	—	2.1686(14)
Dy–Npy [Å]	—	—	2.532(3)	—
Average N–Dy–N [°]	118.81	118.55	118.95	117.55

---

Static (dc) magnetic properties

The direct-current (dc) magnetic susceptibility was measured as a function of temperature (2–300 K) in a field of 1 kOe on the polycrystalline samples of 1, 2, and 3 (Fig. 2). At 300 K, the χ_MT values for 1, 2 and 3 are, respectively, 13.72, 13.57 and 13.87 cm³ K mol⁻¹, lower than that expected for a free Dy^III ion (14.17 cm³ K mol⁻¹), due to the splitting of the ⁶H_15/2 ground state.³¹ Upon cooling, the χ_MT plots gradually drop to 11.66, 10.58, and 11.76 for 1–3 at 2 K, respectively. Such a tendency is mainly attributed to the progressive depopulation of the Kramers doublets (KDs) of the Dy^III ion or weak antiferromagnetic dipolar coupling between the mononuclear groups.³⁴ The field-dependent magnetization (M) exhibits a sharp increase in the low fields and then slowly increases to 4.40Nβ for 1, 4.24Nβ for 2, and 4.57Nβ for 3 at 2 K and 5T (Fig. 2, inset), which prominently deviates from the saturated value of 10Nβ. The unsaturation of M at 5 T supports the onset of strong magnetic anisotropy and/or low-lying excited states (Fig. S7†).³⁵

Fig. 2 Plots of χ_MT vs. T for 1 (a), 2 (b), and 3 (c). Inset: plots of M vs. H at indicated temperatures.

Furthermore, the dc magnetic data of the Dy^III ion for three complexes were analyzed with crystal field theory using the PHI program,³⁶ for qualitative comparison with the experimental data. The crystal field Hamiltonian is expressed in the following equation:

where σ_i^k is the orbital reduction parameters, B_k^q is the crystal field parameters (CFPs) in Steven's notation, θ_k is the operator equivalent factors, and Ô_ki^q is the operator equivalents. To fit the magnetic susceptibility and magnetization data, the CFPs were employed for all complexes. It is gratifying that the theoretically simulated data on the isolated mononuclear molecules correspond reasonably well with the experimental results (Fig. 2), which suggests significant magnetic anisotropy of the Dy^III ion and very weak dipole–dipole interactions. With the obtained fitting parameters (CFPs) (Table S10†), the magnetic data of the three complexes were simulated to obtain the energy levels and g-tensors. From the simulation of the ground state multiplet ⁶H_15/2 (energy levels are listed in Table S11†), the energy gaps between the ground state Kramers doublets and the first excited states are 128 cm⁻¹, 91 cm⁻¹, and 107 cm⁻¹ for 1–3, respectively. The local g-tensors on the ground doublets of the Dy sites show large g_z values, g_z = 19.7734, g_z = 18.8536, and g_z = 19.0064, for 1–3 (ideally g_x = g_y = 0, g_z = 20), respectively, indicating the distinct easy axial magnetic anisotropies of 1–3.

Dynamic (ac) magnetic properties

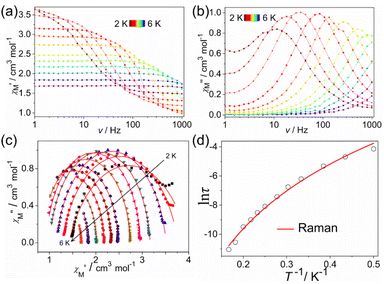
For alternating-current (ac) measurements without an external dc field, although no maximum appears from 2.0 to 6.0 K for 1 and 2 as well as from 2.0 to 5.0 K for 3, both the in-phase (χ′) and out-of-phase (χ′′) signals are observed in all complexes (Fig. S8 and S9†), suggesting the SMM behavior exists in all complexes at zero dc field. It is expected that the quantum tunneling magnetization (QTM) effect plays an important role. For the purpose of selecting a proper dc field, the ac data for all complexes were recorded under various static fields, giving an optimum dc field of 500 Oe. Therefore, temperature-dependent ac data for all complexes were performed under 500 Oe (Fig. S10†). Both the real and imaginary susceptibilities indicate clear temperature dependence, pointing out the slow magnetic relaxation in all complexes. At 1000 Hz, the peaks of temperature-dependent χ′′ appear at about 5 K for 1, 3 K for 2, and 3.5 K for 3.

In addition, the frequency dependencies of the ac susceptibility were measured under an applied dc field of 500 Oe (Fig. 3–5). Both the χ′ and χ′′ signals of all complexes appear to be frequency-dependent, indicative of slow magnetic relaxation. As the temperature increases, the peaks of χ′′ in 1 and 3 gradually shift from low frequencies to high frequencies at ac frequencies up to 1000 Hz. However, for complex 2, the evident χ′′ peaks are only observed at the lowest temperature. Obviously, the QTM is still through the spin-reversal barrier despite being under an applied dc field. Cole–Cole plots of the in-phase versus out-of-phase signals appear as broad asymmetric semicircles, suggesting the overlap of more than one relaxation process. The severity of this overlap precluded the extraction of precise relaxation time data for distinct processes. Instead, the Cole–Cole plot data for all complexes were approximately fitted using a single modified Debye model,^37–39 yielding values for the relaxation time, τ, at each temperature. The resulting fitted parameter is the α value, which provides a measure of the uniformity of relaxation and ranges from 0 to 1, with smaller values corresponding to relaxation dominated by a single process. The resulting α values are in the ranges of 0.014–0.266 for 1, 0.074–0.437 for 2, and 0.258–0.372 for 3 (Tables S3–S5†), suggesting a narrow distribution of the times for 1 and 3. A wide distribution of the relaxation times for 2 and values of α as high as 0.4–0.5 at the lowest temperature for 2 confirm the presence of multiple relaxation processes. To evaluate the occurrence of possible magnetization dynamic pathways, τ vs. T⁻ⁿ plots on a log–log scale were plotted (Fig. S11†). The log₁₀–log₁₀ representation is employed because temperature dependence is linear and thus n can simply be determined from the slope. The fitting slopes of 5.61(2) and 5.85(1) for 1, as well as 6.00(2) and 5.78(2) for 3, indicate that only the Raman process is dominant. The slopes of 0.96(8) and 6.48(3) for 2 suggest that the magnetic relaxation goes through QTM and Raman processes.^40,41 It is necessary to add that, at the lowest temperature of a few Kelvin, the dominant relaxation mechanism is usually QTM (quantum tunnelling of the magnetisation), which is governed by environmental factors, such as the presence of nuclear spins and dipolar coupling. QTM between magnetic ground states is naturally temperature-independent, hence the relaxation rate is often well described by τ_QTM⁻¹ = B₁/(1 + B₂H²),⁴² where B₁ and B₂ are the empirical parameters and H represents the applied dc field. The Raman relaxation process is a non-resonant scattering process involving the simultaneous absorption and emission of two phonons. In this process, the microscopic particles absorb a phonon energy to the virtual state, and then emit a phonon energy to gradually decay. They cannot achieve a true relaxation transition, so there is no contribution of the energy barrier. The studies suggest that the process is temperature dependent and determined by the parameter C and the exponential n, τ_Raman⁻¹ = CTⁿ (where T is the temperature), which appears linear when plotted on a log₁₀–log₁₀ plot. For a two-phonon Raman process, an exponent n = 9 was predicted for Kramers ions. Additionally, R. Orbach found that n = 7 was also in the Raman region and n = 5 was in the low-temperature part of the Raman region. Experimentally the Tⁿ power law was indeed found with an exponent deviating from ideal values.^43,44 Thus, the QTM (n ≤ 1) and Raman (4 ≤ n ≤ 9)⁴⁵ spin reversal processes are presumed reasonable, while the Orbach relaxation process is similar to the Raman relaxation process, in that it is also an absorption and emission process of two phonons, but it experiences a real intermediate energy state. This relaxation process is a real relaxation transition process, which reflects the relaxation kinetic behavior of a single molecule magnet. Meanwhile, the relaxation time and temperature of the Orbach relaxation process conform to the Arrhenius relationship, which is a relaxation process showing an effective energy barrier, τ_Orbach⁻¹ = τ₀⁻¹exp(−Δ_CF/k_BT), where Δ_CF is an intermediate crystal-field parameter. Hence, the Orbach relaxation process is related to temperature, but not to an external magnetic field. It is the intrinsic relaxation behavior of the monomolecular magnet. The direct relaxation process is a monotonic process, and the values are related to the energy level difference between −M_J and +M_J. This process depends on the temperature, but is more closely related to magnetic fields. Its strength is determined by the parameter A and the exponential n, τ_direct⁻¹ = AHⁿT, where n is 2 for non-Kramers ions and 4 for Kramers ions.^46,47

Fig. 3 Frequency dependence of the in-phase (a) and out-of-phase (b) ac susceptibility for complexes 1 under a 500 Oe dc field. (c) Cole–Cole plots at a dc field of 500 Oe for 1; the solid lines fit the generalized Debye equation. (d) Magnetization relaxation time, ln τ vs. T⁻¹ plot under a 500 Oe dc field. The red line represents the Raman fit relaxation process.

Fig. 4 Frequency dependence of the in-phase (a) and out-of-phase (b) ac susceptibility for complexes 2 under a 500 Oe dc field. (c) Cole–Cole plots at a dc field of 500 Oe for 2; the solid lines fit to the generalized Debye equation. (d) Magnetization relaxation time, ln τ vs. T⁻¹ plot under a 500 Oe dc field. The red line represents the Raman and QTM fit relaxation processes.

Fig. 5 Frequency dependence of the in-phase (a) and out-of-phase (b) ac susceptibility for complexes 3 under a 500 Oe dc field. (c) Cole–Cole plots at a dc field of 500 Oe for 3; the solid lines fit to the generalized Debye equation. (d) Magnetization relaxation time, ln τ vs. T⁻¹ plot under a 500 Oe dc field. The red line represents the Raman fit relaxation process.

According to the above analysis results, the best fittings of the temperature-dependent relaxation times according to eqn (2) give C = 0.50(12), n = 6.41(18) for 1, τ_QTM = 4.03(46) × 10⁻⁴ s, C = 0.02(0.1), n = 9.3 (fixed) for 2, close to n = 9 for the Raman relaxation of Kramers ions, and C = 1.73(37), n = 5.52(16) for 3, indicating that at least one Raman relaxation mechanism, a spin–lattice relaxation process that occurs through virtual magnetic excited states, likely dominates in the examined temperature and frequency range for 1 and 3, and the QTM is still existent for 2.

τ⁻¹ = CTⁿ + τ_QTM⁻¹. (2)

Theoretical calculations

To gain further insight into the magneto-structural effect of all complexes, ab initio calculations were carried out. Complete-active-space self-consistent field (CASSCF) calculations on the four mononuclear five-coordinate 1a, 1b, 2, and 3 (Fig. S12†) on the basis of X-ray determined geometries were carried out with OpenMoclcas²⁸ and SINGLE_ANISO^31–33 programs (see the ESI† for details). The energy levels (cm⁻¹), g (g_x, g_y, g_z) tensors, and the predominant m_J values of the lowest eight Kramers doublets (KDs) of complexes 1–3 are shown in Table S6,† where the predominant m_J is equal to ±15/2 in their ground KDs. For 1a, 1b, and 3, the ground g_z is close to 20.00, showing nearly perfect axial anisotropies for them. But the ground g_z for 2 = 16.514, illustrating a poor axial anisotropy. The mixed m_J components for the lowest eight KDs for them are all composed of m_J = ±15/2 (92.9%|±15/2〉 for 1a, 94.0%|±15/2〉 for 1b, 70.8%|±15/2〉 for 2 and 88.1%|±15/2〉 for 3) and the first excited KDs are a mixture of several m_J states, leading to the large transversal magnetic moments shown in Fig. 6. The transversal magnetic moments in the ground KDs for 1a and 2 are 0.10 and 0.80μ_B, respectively, allowing a fast quantum tunneling of magnetization (QTM) at low temperatures. However, for 1b and 3, their ground transversal magnetic moments are 0.67 × 10⁻¹ and 0.74 × 10⁻¹μ_B, respectively. Therefore, the QTM in their ground KDs may be suppressed at low temperatures if applying an external field, while the transversal magnetic moments in their first excited states are 1.20 and 0.48μ_B, respectively, leading to a fast thermal-assisted QTM. Therefore, the calculated energy barriers of 1b and 3 are equal to 160.7 and 83.8 cm⁻¹, respectively (Table S6†). Due to the unfavourable effects, such as harmonic phonons, Raman magnetic relaxation, QTM, etc., on the energy barrier, the experimental effective energy barriers (U_eff) are usually smaller than the calculated ones.^48–52 In order to further confirm the relaxation, fitting the high-temperature data using the Arrhenius law τ = τ₀ exp(U_eff)/k_BT affords the following values of U_eff and pro-factor τ₀: U_eff = 36.45(25) K and τ₀ = 4.00(54) × 10⁻⁸ s for 1; and U_eff = 18.37(53) K and τ₀ = 2.18(16) × 10⁻⁶ s for 3 (Fig. S13†). These values are much lower than the calculated energy barriers of 1 and 3, suggesting that the Orbach process could not be considered as the dominant relaxation pathway in the considered temperature range. As shown in Table S8,† the weights of the axial crystal-field (CF) parameter B (2, 0) for 2 and 3 are 9.96% and 10.86%, respectively, which are lower than those of the non-axial B (2, 2) of 2 (16.07%) and B (4, 4) of 3 (14.58%), indicating a poor axial symmetry for all of them. Meanwhile for 1a and 1b, the weights of the axial CF parameters B (2, 0) are 13.89% and 16.23%, respectively, which are larger than the non-axial ones. Thus, the axial symmetry for complex 1 is higher than those of the others. The main magnetic axes on the Dy^III ions of 1–3 in their ground KDs are indicated in Fig. 7.

Fig. 6 Magnetization blocking barriers for complexes 1a (a), 1b (b), 2 (c), and 3 (d). The thick black lines represent the KDs as a function of their magnetic moment along the magnetic axis. The blue lines correspond to the diagonal matrix elements of the transversal magnetic moment; the green lines represent the Orbach relaxation processes. The path shown by the red arrows represents the most probable path for magnetic relaxation in the corresponding compounds. The numbers at each arrow stand for the mean absolute value of the corresponding matrix element of the transition magnetic moment.

Fig. 7 Calculated orientations of the local main magnetic axes on Dy^III ions of complexes 1a (a), 1b (b), 2 (c), and 3 (d) in their ground KDs.

Magneto-structural correlation

To understand the nature of the magneto-structure correlation of complexes 1–3, it is necessary to provide a structural comparison of the coordination spheres for the three mononuclear complexes. Geometrically, complexes 1 and 3 present DyN₄O chromophore, 2 exhibits a DyN₅ chromophore, with obvious distortion (CShMs parameters: 0.835 (1a), 0.890 (1b), 0.737 (2), and 0.531 (3)) from the corresponding ideal geometry. However, the magnetic properties for 1–3 are different (1 > 3 > 2), although 2 has a similar distortion to 1 and 3 in its geometry. Therefore, the geometric distortion and magnetic properties are not really interrelated. First, for 1–3, the discrepancies in the magnetic anisotropy depend critically on the different coordination groups on one side. Second, they are closely related to the bond lengths of Dy–N/Dy–O in the axis (1a: Dy–N_axial 2.499(5), Dy–O_axial 2.425(4) Å; 1b: Dy–N_axial 2.527(5), Dy–O_axial 2.409(5) Å; 2: Dy–N_axial 2.500(2), Dy–N_py 2.532(3) Å; 3: 2.5884(17), Dy–O_axial 2.1686(14) Å). In contrast, 2 has a longer axial distance in these three complexes, a shorter axial distance and a higher symmetry for 1. The weights of the axial crystal-field (CF) parameters B (2, 0) of 1–3 (1: 16.23%; 2: 9.96%; 3: 10.86%) can also confirm that the axial symmetry of 1 is higher than those of the two others. In addition, the ground g_z is close to 20.00 showing nearly perfect axial anisotropies for 1 and 3. But the ground g_z of 2 deviates from the ideal value 20.00, illustrating a poor axial anisotropy. Obviously, the influence of the ligand effect on the single-ion magnetic behaviour is very important, and the coordination of oxygen-containing ligands is conducive to promoting the Dy^III single-ion anisotropy and the slow relaxation of the magnetization, thus achieving enhanced magnetism. Theoretical calculation in-depth elucidates the intrinsic differences in magnetic anisotropy of complexes 1–3, which are in good agreement with the experimental results.

Conclusions

In summary, we have successfully constructed and characterized a series of five-coordinate triangular bipyramidal mononuclear Dy^III SMMs with local D_3h symmetry, [(Trapen^TMS)Dy(THF)] (1), [(Trapen^TMS)Dy(py)] (2) and [(Trapen^TMS)Dy(ONMe₃)] (3), and systematically investigated the effect of the coordination unit alterations on the magnetism of the Dy^III center in the same direction as the trigonal–bipyramidal geometry. Architecturally, the coordination spheres of 1–3 are similar in the equatorial plane, whereas the significant difference lies in the bond lengths of Dy–N/Dy–O at the axial position (in the sequence 1 > 3 > 2). Under a zero dc field, 1a and 2 exhibit a fast QTM at low temperatures. In contrast, for 1b and 3, due to smaller ground transversal magnetic moments, the QTM in their ground KDs may be suppressed at low temperatures if applying an external field. Further magnetic results demonstrate that three complexes present field-induced slow magnetic relaxation with the obvious Raman relaxation processes. Therefore, this work suggests that the magneto-structural relationship, such as non-Orbach processes and geometrical symmetry, would be vital for observing field-induced SMM behaviors. This contributes to a better understanding of environment-mediated magnetic relaxation mechanisms.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 22176191, 21863009, and 22266026), the National Science Fund for Distinguished Young Scholars (No. 21925603), and the Natural Science Foundation of Ningxia Province (2021BEB04062 and 2022AAC05002).

References

1. K. S. Pedersen, A.-M. Ariciu, S. McAdams, H. Weihe, J. Bendix, F. Tuna and S. Piligkos, Toward molecular 4f single-ion magnet qubits, J. Am. Chem. Soc., 2016, 138, 5801–5804.
2. M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M.-A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Magnetic memory of a single-molecule quantum magnet wired to a gold surface, Nat. Mater., 2009, 8, 194–197.
3. F. D. Natterer, K. Yang, W. Paul, P. Willke, T. Choi, T. Greber, A. J. Heinrich and C. P. Lutz, Reading and writing single-atom magnets, Nature, 2017, 543, 226–228.
4. N. Ishikawa, M. Sugita, T. Ishikawa, S.-y. Koshihara and Y. Kaizu, Lanthanide double-decker complexes functioning as magnets at the single-molecular level, J. Am. Chem. Soc., 2003, 125, 8694–8695.
5. N. Ishikawa, M. Sugita, N. Tanaka, T. Ishikawa, S.-y. Koshihara and Y. Kaizu, Upward temperature shift of the intrinsic phase lag of the magnetization of bis(phthalocyaninato)terbium by ligand oxidation creating an S = 1/2 spin, Inorg. Chem., 2004, 43, 5498–5500.
6. C. Benelli and D. Gatteschi, Magnetism of lanthanides in molecular materials with transition-metal ions and organic radicals, Chem. Rev., 2002, 102, 2369–2388.
7. A. Chakraborty, Simple models of magnetism, Oxford graduate texts, by Ralph Skomski, Contemp. Phys., 2013, 54, 298–299.
8. D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Lanthanide single-molecule magnets, Chem. Rev., 2013, 113, 5110–5148.
9. P. Zhang, Y.-N. Guo and J. Tang, Recent advances in dysprosium-based single molecule magnets: Structural overview and synthetic strategies, Coord. Chem. Rev., 2013, 257, 1728–1763.
10. L. Sorace, C. Benelli and D. Gatteschi, Lanthanides in molecular magnetism: Old tools in a new field, Chem. Soc. Rev., 2011, 40, 3092–3104.
11. Y. Ma, Y.-Q. Zhai, Q.-C. Luo, Y.-S. Ding and Y.-Z. Zheng, Ligand fluorination to mitigate the Raman relaxation of Dy^III single-molecule magnets: A combined terahertz, far-IR and vibronic barrier model study, Angew. Chem., Int. Ed., 2022, 61, e202206022.
12. M. Feng and M.-L. Tong, Single ion magnets from 3d to 5f: Developments and strategies, Chem. – Eur. J., 2018, 24, 7574–7594.
13. Y.-S. Ding, T. Han, Y.-Q. Zhai, D. Reta, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, A study of magnetic relaxation in dysprosium(III) single-molecule magnets, Chem. – Eur. J., 2020, 26, 5893–5902.
14. S.-D. Jiang, B.-W. Wang, G. Su, Z.-M. Wang and S. Gao, A mononuclear dysprosium complex featuring single-molecule-magnet behavior, Angew. Chem., Int. Ed., 2010, 49, 7448–7451.
15. N. F. Chilton, S. K. Langley, B. Moubaraki, A. Soncini, S. R. Batten and K. S. Murray, Single molecule magnetism in a family of mononuclear β-diketonate lanthanide(III) complexes: Rationalization of magnetic anisotropy in complexes of low symmetry, Chem. Sci., 2013, 4, 1719–1730.
16. F. Pointillart, K. Bernot, S. Golhen, B. Le Guennic, T. Guizouarn, L. Ouahab and O. Cador, Magnetic memory in an isotopically enriched and magnetically isolated mononuclear dysprosium complex, Angew. Chem., Int. Ed., 2015, 54, 1504–1507.
17. Y. Bi, Y.-N. Guo, L. Zhao, Y. Guo, S.-Y. Lin, S.-D. Jiang, J. Tang, B.-W. Wang and S. Gao, Capping ligand perturbed slow magnetic relaxation in dysprosium single-ion magnets, Chem. – Eur. J., 2011, 17, 12476–12481.
18. J. Wu, O. Cador, X.-L. Li, L. Zhao, B. Le Guennic and J. Tang, Axial ligand field in D_4d coordination symmetry: Magnetic relaxation of Dy SMMs perturbed by counteranions, Inorg. Chem., 2017, 56, 11211–11219.
19. K. R. Meihaus and J. R. Long, Magnetic blocking at 10 K and a dipolar-mediated avalanche in salts of the Bis(η⁸-cyclooctatetraenide) complex [Er(COT)₂]⁻, J. Am. Chem. Soc., 2013, 135, 17952–17957.
20. F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Magnetic hysteresis up to 80 Kelvin in a dysprosium metallocene single-molecule magnet, Science, 2018, 362, 1400–1403.
21. L. Ungur and L. F. Chibotaru, Strategies toward high-temperature lanthanide-based single-molecule magnets, Inorg. Chem., 2016, 55, 10043–10056.
22. V. S. Parmar, D. P. Mills and R. E. P. Winpenny, Mononuclear dysprosium alkoxide and aryloxide single-molecule magnets, Chem. – Eur. J., 2021, 27, 7625–7645.
23. Z. Zhu, X. Ying, C. Zhao, Y.-Q. Zhang and J. Tang, A new breakthrough in low-coordinate Dy(III) single-molecule magnet, Inorg. Chem. Front., 2022, 9, 6061–6066.
24. V. S. Parmar, F. Ortu, X. Ma, N. F. Chilton, R. Clérac, D. P. Mills and R. E. P. Winpenny, Probing relaxation dynamics in five-coordinate dysprosium single-molecule magnets, Chem. – Eur. J., 2020, 26, 7774–7778.
25. K. Liu, J.-P. Yu, Q.-Y. Wu, X.-B. Tao, X.-H. Kong, L. Mei, K.-Q. Hu, L.-Y. Yuan, Z.-F. Chai and W.-Q. Shi, Rational design of a tripodal ligand for U(IV): Synthesis and characterization of a U–Cl species and insights into its reactivity, Organometallics, 2020, 39, 4069–4077.
26. G. B. Deacon, T. Feng, P. C. Junk, B. W. Skelton, A. N. Sobolev and A. H. White, Preparation and X-ray crystal structures of tetrahydrofuran-complexed rare earth chlorides – A structurally rich series, Aust. J. Chem., 1998, 51, 75–89.
27. G. M. Sheldrick, Crystal structure refinement with SHELXL, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
28. I. F. Galván, I. F. M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovačević, E. Källman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. Å. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesołowski, P.-O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, OpenMolcas: From source code to insight, J. Chem. Theory Comput., 2019, 15, 5925–5964.
29. P. Å. Malmqvist, B. O. Roos and B. Schimmelpfennig, The restricted active space (RAS) state interaction approach with spin-orbit coupling, Chem. Phys. Lett., 2002, 357, 230–240.
30. B. A. Heß, C. M. Marian, U. Wahlgren and O. A. Gropen, Mean-field spin-orbit method applicable to correlated wavefunctions, Chem. Phys. Lett., 1996, 251, 365–371.
31. L. F. Chibotaru, L. Ungur and A. Soncini, The origin of nonmagnetic Kramers doublets in the ground state of dysprosium triangles: Evidence for a toroidal magnetic moment, Angew. Chem., Int. Ed., 2008, 47, 4126–4129.
32. L. Ungur, W. Van den Heuvel and L. F. Chibotaru, Ab initio investigation of the non-collinear magnetic structure and the lowest magnetic excitations in dysprosium triangles, New J. Chem., 2009, 33, 1224–1230.
33. L. F. Chibotaru, L. Ungur, C. Aronica, H. Elmoll, G. Pilet and D. Luneau, Structure, magnetism, and theoretical study of a mixed-valence Co^II₃Co^III₄ heptanuclear wheel: Lack of SMM behavior despite negative magnetic anisotropy, J. Am. Chem. Soc., 2008, 130, 12445–12455.
34. Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, Symmetry-supported magnetic blocking at 20 K in pentagonal bipyramidal Dy(III) single-ion magnets, J. Am. Chem. Soc., 2016, 138, 2829–2837.
35. X. Liu, X. Ma, W. Yuan, P. Cen, Y.-Q. Zhang, J. Ferrando-Soria, G. Xie, S. Chen and E. Pardo, Concise chemistry modulation of the SMM behavior within a family of mononuclear Dy(III) complexes, Inorg. Chem., 2018, 57, 14843–14851.
36. N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes, J. Comput. Chem., 2013, 34, 1164–1175.
37. M. Grahl, J. Kotzler and I. Sessler, Correlation between domain-wall dynamics and spin–spin relaxation in uniaxial ferromagnets, J. Magn. Magn. Mater., 1990, 90, 187–188.
38. Y. N. Guo, G. F. Xu, Y. Guo and J. K. Tang, Relaxation dynamics of dysprosium(III) single molecule magnets, Dalton Trans., 2011, 40, 9953–9963.
39. N. F. Chilton , CC-fit model, The University of Manchester.
40. L. E. Darago, M. D. Boshart, B. D. Nguyen, E. Perlt, J. W. Ziller, W. W. Lukens, F. Furche, W. J. Evans and J. R. Long, Strong ferromagnetic exchange coupling and single-molecule magnetism in MoS₄³⁻-bridged dilanthanide complexes, J. Am. Chem. Soc., 2021, 143, 8465–8475.
41. Q. Yang, G. L. Wang, Y. Q. Zhang and J. Tang, Self-assembly of fish-bone and grid-like Co II-based single-molecule magnets using dihydrazone ligands with NNN and NNO pockets, Dalton Trans., 2022, 51, 13928–13937.
42. A. Fort, A. Rettori, J. Villain, D. Gatteschi and R. Sessoli, Mixed quantum-thermal relaxation in Mn₁₂ acetate molecules, Phys. Rev. Lett., 1998, 80, 612–615.
43. R. Orbach and M. Blume, Spin-lattice relaxation in multilevel spin systems, Phys. Rev. Lett., 1962, 8, 478.
44. K. S. Pedersen, L. Ungur, M. Sigrist, A. Sundt, M. S. Magnussen, V. Vieru, H. Mutka, S. Rols, H. Weihe, O. Waldmann, L. F. Chibotaru, J. Bendix and J. Dreiser, Modifying the properties of 4f single-ion magnets by peripheral ligand functionalisation, Chem. Sci., 2014, 5, 1650–1660.
45. J. M. Zadrozny, M. Atanasov, A. M. Bryan, C.-Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Slow magnetization dynamics in a series of two-coordinate iron(II) complexes, Chem. Sci., 2013, 4, 125–138.
46. S. G. McAdams, A.-M. Ariciu, A. K. Kostopoulos, J. P. S. Walsh and F. Tuna, Molecular single-ion magnets based on lanthanides and actinides: Design considerations and new advances in the context of quantum technologies, Coord. Chem. Rev., 2017, 346, 216–239.
47. S. T. Liddle and J. v. Slageren, Improving f-element single molecule magnets, Chem. Soc. Rev., 2015, 44, 6655–6669.
48. M. Wang, Y. Guo, Z. Han, X. Cheng, Y.-Q. Zhang, W. Shi and P. Cheng, Impact of ligand substituents on the magnetization dynamics of mononuclear Dy^III single-molecule magnets, Inorg. Chem., 2022, 61, 9785–9791.
49. A. Lunghi, F. Totti, R. Sessoli and S. Sanvito, The role of anharmonic phonons in under-barrier spin relaxation of single molecule magnets, Nat. Commun., 2017, 8, 14620.
50. F. Lu, M.-M. Ding, J.-X. Li, B.-L. Wang and Y.-Q. Zhang, Why lanthanide Er^III SIMs cannot possess huge energy barriers: A theoretical investigation, Dalton Trans., 2020, 49, 14576–14583.
51. M.-M. Ding, T. Shang, R. Hu and Y.-Q. Zhang, Understanding the magnetic anisotropy for linear sandwich [Er(COT)]⁺-based compounds: a theoretical investigation, Dalton Trans., 2022, 51, 3295–3303.
52. F. Lu, W.-X. Guo and Y.-Q. Zhang, Largely enhancing the blocking energy barrier and temperature of a linear cobalt(II) complex through the structural distortion: A theoretical exploration, Inorg. Chem., 2022, 61, 295–301.

---

Footnotes

† Electronic supplementary information (ESI) available: Experimental details, additional figures, tables, etc. Fig. S1–S13, Tables S1–S9. CCDC 2210770 (1), 2210771 (2) and 2210772 (3). For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3dt00095h

‡ These authors contributed equally to this work.

---