Magnetic and optical studies of a new family of multidimensional and multiproperty PO-lanthanide(III) derived systems

Abstract

A new family of lanthanide compounds has been synthesized using 1,2-bis(diphenylphosphino)ethane dioxide (dppeO₂) as an O-donor ligand through the phosphoryl group to lanthanide(III) cations and structurally, magnetically and optically studied. Depending on the lanthanide, two different topologies appear: the two-dimensional structure [Ln^III(dppeO₂)_1.5(NO₃)₃(H₂O)_0.5]_n (Ln = Ce (1), Sm (2) and Dy (6)) and the one-dimensional structure [Ln(dppeO₂)(NO₃)₃DMF]_n (Ln = Eu (3), Gd (4) and Tb (5)). Some of the Ln-derived complexes have been used as structural probes, while others have been synthesized to use the specific characteristics of each cation to take advantage of their magnetic/luminescence properties. Complex 6 presents slow relaxation of the magnetization while 2, 3 and 5 present emitting properties in the visible range.

---

Introduction

During the last few years, molecular lanthanide(III)-derived compounds climbed to the top of different new applications like luminescent sensors,^1,2 slow-relaxing magnetic systems^3,4 spintronics^5,6 or anticounterfeit technologies.^7,8 One of the most exploited applications of lanthanide molecular compounds is their use as potential Single Molecule Magnets (SMMs) or Single Ion Magnets (SIMs) due to their comparatively high single ion anisotropy arising from their Spin–Orbit Coupling (SOC) and from the crystal field splitting of the lowest J multiplet when they are forming a coordination complex.^4,9,10 Among this, lanthanide cations present extraordinary emitting properties originating from the electronic transitions within the partially filled 4f orbitals except for Ce^III, which presents 5d–4f electronic transitions. However, due to the very low sensitivity of lanthanide(III) to their surroundings, their hybridization is limited and, consequently, Ln^III exhibits very narrow emission lines, which can be considered as a fingerprint of each cation. The main drawback of this approach to the luminescence of lanthanide-derived complexes is that transitions in-between 4f orbitals are partially Laporte-forbidden. Therefore, any strategy to increase the luminescence of lanthanide coordination compounds must consider the sensitization of lanthanide(III) cations.^11,12 To this end, a useful procedure is the coordination of lanthanide(III) ions to phosphine oxides, known to be excellent ligands.¹³ Phosphine oxides are ideal for this purpose because they can be easily prepared by oxidation of the parent phosphines, a huge family of ligands extensively studied due to their application in organometallic homogeneous catalysis. Hence, this kind of ligand allows the fine-tuning of the system's properties.

Some extended systems derived from the diphosphine oxide bis(diphenylphosphino)ethane dioxide (dppeO₂), Scheme 1, were previously reported by other authors^14–19 but their magnetic properties remain practically unexplored.

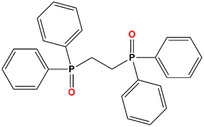Scheme 1 Structural formula of the ligand employed in this work, 1,2-bis(diphenylphosphino)ethane dioxide (dppeO₂).

Noteworthily, the stereochemistry or dimensionality of the dppO₂/Ln^III system can show a multifactorial dependence on factors such as the size of the cation, the counterions present in the reaction media, reaction conditions or the solvent employed.²⁰ In the present paper, we report a new family of Ln-derived systems using dppeO₂. Single crystal X-ray diffraction demonstrated that two different structures could be obtained with no changes in the reaction conditions: bidimensional networks with the general formula [Ln^III(dppeO₂)_1.5(NO₃)₃(H₂O)_0.5]_n (Ln = Ce (1), Sm (2) and Dy (6)) and monodimensional compounds with the general formula [Ln(dppeO₂)(NO₃)₃DMF]_n (Ln = Eu (3), Gd (4) and Tb (5)), which are apparently independent of the above-mentioned factors affecting the final structures. Complexes 1, 3 and 4 were used as structural probes to test the isostructurality with other family members by X-ray powder diffraction. Noteworthily, the reported systems provide the first examples of 1-D arrangement for the dppeO₂/Ln^III system. The anisotropic derivative 6 has been magnetically characterized (both statically and dynamically) while complexes 2, 3 and 5, the typical visible-range emitters, have been studied to check their emitting properties.

Experimental

X-ray crystallography

White (1, 3 and 4) prism-like specimens were used for single crystal X-ray crystallographic analysis. The X-ray intensity data were measured on a D8 Venture system equipped with a multilayer monochromator and a Mo microfocus (Table 1).

Table 1 Crystal data, collection and structure refinement details for the X-ray structure determination of complexes 1, 3 and 4

	1	3	4
Formula	C78H74Ce2N6O25P6	C29 H31EuN4O12P2	C29 H31GdN4 O12 P2
FW	1961.49	841.48	846.77
System	Trigonal	Monoclinic	Monoclinic
Space group	R3̄c	P21/c	P21/n
a/Å	15.5252(3)	9.1723(5)	17.0768(7)
b/Å	15.5252(3)	17.776(1)	9.9525(5)
c/Å	60.112(2)	20.858(1)	20.509(1)
α/°	90	90	90
β/°	90	102.952(2)	104.076(2)
γ/°	120	90	90
V/Å^3	12 547.9(7)	3314.4(3)	3380.9(3)
Z	6	4	4
T, K	100(2)	100(2)	100(2)
λ(MoKα), Å	0.71073	0.71073	0.71073
p cal, g cm^−3	1.557	1.686	1.664
μ(MoKα), mm^−1	1.269	2.057	2.123
R	0.0480	0.0316	0.0271
ωR^2	0.1138	0.0724	0.0530

---

The frames were integrated with the Bruker SAINT software package using a narrow-frame algorithm. The structures were solved and refined using the Bruker SHELXTL software.²¹

Powder X-ray diffraction was performed with a PANalytical X'Pert PRO MPD θ/θ powder diffractometer of 240 millimetre radius, in a configuration of the convergent beam with a focalizing mirror and a transmission geometry with flat samples sandwiched between low absorbing films and Cu Kα radiation (λ = 1.5418 Å). Comparison between the calculated spectrum from the single crystal structures of 1 and 4 and the experimental powder X-ray spectrum for compounds 2, 5 and 6 confirms the isostructurality among the two different groups, Fig. S1.†

Crystal data and refinement details for complexes 1, 3 and 4 are summarized in Table 1. Further crystallographic details can be found in the corresponding CIF files provided in the ESI.†

Physical measurements

Magnetic susceptibility measurements were carried out on pressed polycrystalline samples with an MPMS5 Quantum Design susceptometer working in the range 30–300 K under magnetic fields of 0.3 T and under a field of 0.03 T in the 30–2 K range to avoid saturation effects at low temperature. Diamagnetic corrections were estimated from Pascal Tables. Infrared spectra (4000–400 cm⁻¹) were recorded from KBr pellets on a Bruker IFS-125 FT-IR spectrophotometer.

Solid-state fluorescence spectra of compounds 2, 3 and 5 were recorded on a Horiba Jobin Yvon SPEX Nanolog fluorescence spectrophotometer (Fluorolog-3 v3.2, HORIBA Jovin Yvon, Cedex, France) equipped with a three-slit, double-grating excitation and emission monochromator with dispersions of 2.1 nm mm⁻¹ (1200 grooves per mm) at room temperature. The steady-state luminescence was excited with unpolarized light from a 450 W xenon CW lamp and detected at an angle of 22.5° for solid-state measurement with a red-sensitive Hamamatsu R928 photomultiplier tube. The instrument was adjusted to obtain the highest background-to-noise ratio. The sample was mounted between two quartz plates. Spectra were corrected for both the excitation source light intensity variation (lamp and grating) and the emission spectral response (detector and grating). Lifetime decay curves were measured in the same instrument monitored in the phosphoresce mode using a 450 W xenon pulsed lamp (1.5 ns pulse). The measured decays were analysed using the OriginPro 8 software package. The decay curves of compounds 3 and 5 and the fit quality were determined by the χ² method of Pearson. A band pass of 0.5 nm was employed in order to not surpass 10⁶ CPS to make sure that we are not measuring in the non-linear optical zone.

The ¹H and ³¹P{¹H} NMR spectra of dppeO₂ were recorded at room temperature in a cryoprobe-equipped, 400 MHz Bruker Avance III spectrometer in dmso-d₆.

Syntheses

1,2-Bis(diphenylphosphino)ethane dioxide (dppeO₂). A 30% aqueous solution of H₂O₂ (1.0 mL, 9.8 mmol) was added dropwise to a THF solution (20 mL) of dppe (2.0 g, 5.0 mmol) with stirring and ice-cooling. When the exothermal process finished the solvent was concentrated under vacuum. A white powder was formed, which was filtered and washed with diethyl ether. Yield: 1.90 g, 88%. ¹H NMR (CDCl₃, δ ppm): 7.72–7.67 (m, 8H, C₆H₅), 7.54–7.42 (m, 12H, C₆H₅), 2.51 (d, J = 2.7 Hz, 4H, CH₂CH₂). ³¹P{¹H} NMR (CDCl₃, δ ppm): 32.88 (s), which matched the published data.²²

[Ln^III(dppeO₂)_1.5(NO₃)₃(H₂O)_0.5]_n (Ln = Ce (1), Sm (2), Dy (6) and [Ln^III(dppeO₂)(NO₃)₃(DMF)]_n (Ln = Eu (3), Gd (4) and Tb (5)). As a general procedure: In a mixture of 15 ml of MeOH/2 ml of DMF, the corresponding lanthanide nitrate salt (0.2 mmol) and dppeO₂ (0.2 mmol/0.086 g) were added. The reaction mixture was refluxed for 1 h and filtered. After one day, white crystals, suitable for X-ray diffraction, were formed by layering with diethyl ether. CHN for C₃₉H₃₆CeN₃O_12.5P₃: calc.: C, 47.81; H, 3.70; N, 4.29, found C, 47.66; H, 3.54; N, 4.38; C₃₉H₃₆SmN₃O₁₃P₃: calc.: C, 46.93; H, 3.64; N, 4.21, found C, 46.21; H, 3.71; N, 4.25; C₃₉H₃₆DyN₃O₁₃P₃: calc.: C, 46.37; H, 3.59; N, 4.16, found C, 45.97; H, 3.62; N, 4.08; C₂₉H₃₁EuN₄O₁₂P₂: calc.: C, 41.39; H, 3.71; N, 6.65, found C, 41.12; H, 3.53; N, 6.70; C₂₉H₃₁GdN₄O₁₂P₂: calc.: C, 41.13; H, 3.69; N, 6.61, found C, 41.42; H, 3.52; N, 6.52; C₂₉H₃₁TbN₄O₁₂P₂: calc.: C, 41.05; H, 3.68; N, 6.60, found C, 40.93; H, 3.47; N, 6.38. IR spectra for the two kinds of complexes are shown in Fig. S2.†

Results and discussion

Description of the structures

[Ce^III(dppeO₂)_1.5(NO₃)₃(H₂O)_0.5]_n (1). The structure consists of a 2D layer of Ce^III cations linked by bis-monodentate dppeO₂ ligands. The Ce^III cation links three bidentate nitrato ligands, three O-donors from three dppeO₂ ligands and one water molecule along the C₃ symmetry axis with an occupancy of 50% and for the 50% of the molecules one of the nitrato anions is placed in a more axial position resulting ennea- and decacoordinated environments Fig. 1, top. The main bond parameters are reported in Table 2. The ligands show a fac-arrangement, symmetrically placed around the cation due to the C₃ symmetry axis along the O5–Ce bond. The dppeO₂ ligands act in its bis-monodentate coordination mode and the symmetrical in-plane arrangement, Fig. 1, allows for a 2D honeycomb network, Fig. 2. The short Ce–O distances correspond to the Ce–O_phosphine (2.428 Å) bonds whereas the larger one is the Ce–O5 bond (2.74 Å). SHAPE²³ analysis of the coordination sphere around the Ce^III cation shows that it is far from any ideal polyhedron due to the low bite of the nitrato ligands, as indicated by a minimum CShM value of 3.49. The simplified environment referred to the seven ligands and assuming the position of the nitrate ligands as the mean position between the two O_nitrato donors reveals an intermediate between a capped octahedron and one capped trigonal prismatic arrangement, Fig. 1, left.

Fig. 1 Top, labelled plot of the Ce^III environment for complex 1. Bottom, intermediate O_h/TP polyhedron around the decacoordinated Ce^III cation and in-plane arrangement of the dppeO₂ ligands. Color key for all figures, Ce^III, light blue; Gd^III, firebrick; P, orange; O, red; N, navy; and C, black. The positions indicated as green balls correspond to the mean position between the two O-donors of each bidentate nitrate ligand.

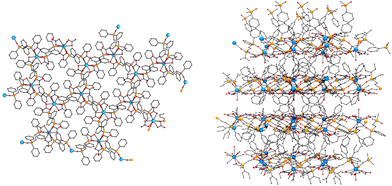Fig. 2 Left, a view of the honeycomb layers of 1 along the c-axis; right, view of the network along the a-axis.

Table 2 Selected bond distances (Å) and angles (°) of complex 1

Ce1–O1	2.641(4)	Ce1–O1′	2.35(1)
Ce1–O2	2.592(5)	Ce1–O3′	2.52(3)
Ce1–O5	2.74(1)	Ce1–O4	2.428(2)
P(1)–O(4)	1.503(2)
O1–Ce1–O2	48.5(1)	O1–Ce1–O5	63.36(8)
O1–Ce1–O4	68.49(9)	O2–Ce1–O5	76.3(1)
O2–Ce1–O4	75.0(2)	P(1)–O(4)–Ce(1)	165.2(2)
O4–Ce1–O5	131.71(6)	O4–Ce1–O4′	80.55(9)

---

[Ln^III(dppeO₂)(NO₃)₃(DMF)]_n, Ln = Eu^III (3) and Gd^III (4). Due to the similarity between the two structures and to avoid repetitive descriptions, only the structure of complex 4 will be described. The main bond parameters for the two compounds are summarized in Table 3.

Table 3 Selected bond distances (Å) and angles (°) of complexes 3 and 4

	(3) Ln = Eu	(4) Ln = Gd
Ln(1)–O(1)	2.315(2)	2.313(1)
Ln(1)–O(2)	2.323(2)	2.314(1)
Ln(1)–O(3)	2.531(3)	2.473(2)
Ln(1)–O(5)	2.503(3)	2.468(2)
Ln(1)–O(6)	2.498(3)	2.525(2)
Ln(1)–O(7)	2.538(3)	2.439(2)
Ln(1)–O(9)	2.474(3)	2.573(2)
Ln(1)–O(10)	2.523(3)	2.506(2)
Ln(1)–O(12)	2.386(3)	2.338(2)
P(1)–O(1)	1.508(2)	1.505(1)
P(2)–O(2)	1.506(3)	1.503(1)
O(1)–Ln(1)–O(2)	149.27(8)	149.26(5)
O(1)–Ln(1)–O(12)	84.13(9)	85.41(5)
O(2)–Ln(1)–O(12)	85.05(9)	83.97(5)
P(1)–O1–Ln(1)	166.4(2)	153.46(9)
P(2)–O(2)–Ln(1)	168.9(2)	166.43(9)

---

The structure consists of a 1D arrangement of Gd^III cations bridged by bis-monodentate dppeO₂ ligands. The enneacoordinated environment around the Gd^III cation is formed by three bidentate nitrato ligands, two O-donors from two dppeO₂ ligands and one dimethylformamide molecule. The two dppO₂ ligands are coordinated in trans positions to the lantanoid cation (O–Gd–O bond angle of 149.3°) whereas the nitrato and DMF ligands are roughly linked in the equatorial plane, Fig. 3-top. The Gd–O bond distances are in the range of 2.313–2.506 Å, with the shorter ones being those involving the O_phosphine bonds. The dppeO₂ ligands link the Gd^III cations resulting in a zig-zag chain along the a-axis of the cell, Fig. 3. SHAPE²³ analysis of the coordination sphere around the Gd^III cation shows that, as for 1, the minimum CShM value of 1.79 indicates a strong distortion from any ideal polyhedron whereas with regard to the six ligands, their arrangement is clearly octahedral, Fig. 3, right.

Fig. 3 Top, partially labelled plot and polyhedral environment of complex 4. Bottom, plot of the 1D chain of GdIII cations (left) and network arrangement of the chains along the a-axis of the unit cell.

Structural and synthetic comments

The chemistry of bis(diphenylphosphine)-dioxide ligands with lanthanide cations is strongly dependent on several factors that can modify the denticity of the ligands and/or the dimensionality of the resulting complexes. This kind of ligand can act as a bidentate or bis-monodentate donor Scheme 2-top, allowing for molecular or extended systems, respectively. The length of the flexible (CH₂)_n spacer between the phosphor atoms is a determinant resulting in always a bidentate coordination for n = 1 and consequently exclusively molecular compounds have been reported whereas both modes have been characterized for n = 2–4. Interestingly, the bis-monodentate mode is preferred for the n = 2 case yielding 2D networks whereas the bidentate mode is preferred for the n = 4 case due to the flexibility of the butane spacer.

Scheme 2 Top, bidentate (left) and bis-monodentate (right) coordination modes of the dppeO₂ ligand. Bottom, previously reported fac (a) and mer (b) arrangement of the ligands around the lanthanide cations. Arrangement of the ligands for the 2D (c) and 1D (d) structures reported in this paper. X for (a) and (b): O,O′-NO₃⁻ or Cl⁻ allowing for coordination 9 or 6, respectively; X for (c) and (d): O,O′-NO₃⁻; P=O represent one of the donors of the dppeO₂ ligand; S: solvent molecule.

The simultaneous presence of both coordination modes has been found in dinuclear systems for the dppeO₂ ligand and Pr^III, Dy^III and Lu^III cations¹⁸ but all the remainder complexes are 2D systems with exclusive presence of the bis-monodentate mode, Table 4. These 2D networks with the [Ln(dppeO₂)_1.5(X)₃]_n formula are equally found for X = O,O′-NO₃⁻ (resulting LnO₉ coordination), or for X = Cl⁻, (resulting LnO₃Cl₃) hexacoordination. In the two cases the arrangement of the ligands can adopt a fac- or mer-arrangement around the lanthanide (Scheme 2a and b), which allows for different 2D network architectures (parquet-floor, brick-wall or honeycomb).

Table 4 Summary of the arrangement, coordination numbers (C. N.) and dimensionality (n-D) of the reported n-D systems derived from dppO₂ and Ln^III cations

Ln^III cation	Arrang.	Anion	C. N./n-D	Ref.
Dy	FAC	Cl^−	6 – 2D	18
Nd, Pr	FAC	NO^3−	9 – 2D	15
La, Nd, Eu, Gd, Dy	MER	Cl^−	6 – 2D	14, 15, 17 and 18
Nd, Pr, Sm, Eu, Dy	MER	NO^3−	9 – 2D	15–17
Dy	FAC/MER	Cl^−	6 – 3D	18
Ce, Sm, Dy	FAC	NO^3−	9/10 – 2D	This work
Eu, Gd, Tb	MER	NO^3−	9 – 1D	This work

---

As can be extracted from Table 4, any relationship can be extracted from factors like the cation size or the size or denticity of the coordinated anions. In the same way, the syntheses under soft conditions (room temperature) or solvothermal conditions at high temperatures and large reaction times become also irrelevant.¹⁸ In light of these data, the solvent employed as reaction medium becomes a determinant as was proposed by Spichal et al.¹⁵ This assumption has been corroborated by means of the MeOH/DMF medium employed in the present work that allows for unprecedented coordination numbers or dimensionality of the reported systems, Table 4.

Magnetic properties

Static measurements. DC magnetic susceptibility (χ_M) data for 1, 4, 5 and 6 were measured on polycrystalline and pressed samples in the 2–300 K temperature range and plotted as χ_MT vs. T (Fig. 4).

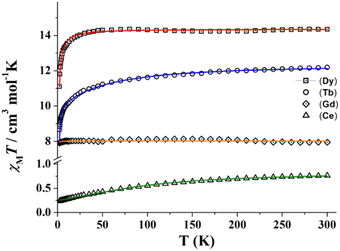Fig. 4 χ _M T vs. temperature plots of complexes 1 (triangles), 3 (diamonds), 5 (circles) and 6 (squares). Solid lines show the best fit of the experimental data.

Due to the topology of all the studied structures, the magnetic behaviour of the paramagnetic carriers in the compounds corresponds to single ion contributions. χ_MT values for complexes 1, 5 and 6 are very close to the corresponding values for the isolated lanthanide cations ²F_5/2 (Ce^III, 0.80 cm³ mol⁻¹ K), ⁷F₆ (Tb^III, 11.82 cm³ mol⁻¹ K), and ⁶H_15/2 (Dy^III, 14.17 cm³ mol⁻¹ K), respectively. For these three compounds, χ_MT slowly decreases when lowering the temperature due to the progressive depopulation of the m_J levels, with a more pronounced decay below 50 K, probably due to antiferromagnetic intramolecular interactions in-between the extended structures. The isotropic compound 4 (Gd^III, ⁸S_7/2) shows a room temperature χ_MT value of 7.95 cm³ mol⁻¹ K close to the expected value of 7.875 cm³ mol⁻¹ K that follows a Curie law down to low temperature.

Experimental data from Fig. 4 was fitted using PHI software²⁴ and using a simple, but effective model reported by Lloret and co-workers for axial symmetry environments in lanthanide derived compounds, which has been previously used by us.^25,26 For compounds 1, 5 and 6, the used Hamiltonian (eqn (1)), in which Ŝ are the spin operators, L is the orbit operator, and λ is the spin–orbit coupling, while Δ describes the energy gap between m_L components. The value for the orbital reduction parameter (κ) was assumed as 1 (lanthanide ions behave as purely ionic). The important point about this fitting is the different shapes of the χ_MT curves depending on the sign of Δ: if Δ is greater than 0, the smallest value of m_L corresponds to the ground states, so the lowest m_L will be the ground state. For Δ smaller than 0, occurs the opposite and the highest m_L corresponds to the ground state. The fact that only the shape of the curve is relevant here is because the low symmetry of the compounds tends to mix the ground state. The first term of the Hamiltonian describes the spin–orbit coupling, while the second term is related to the ligand field around the lanthanide cation while the third term describes the Zeeman effect.

H = (λŜL) + Δ[L_z² − L(L + 1)/3] + [βH(−κL + 2Ŝ)] (1)

A very good fit of the experimental data was obtained (solid lines in Fig. 4) with Δ parameters of −8.3, −12.1 and −6.2 cm⁻¹, for 1, 5 and 6, respectively. Magnetization experiments performed at 2 K show quasi saturated plots with Nμ_β values of 1.05 (1), 4.83 (5) and 5.31 (6) that confirm the negative Δ value for these cations and 7.09 for the isotropic gadolinium system (4).

Dynamic measurements. Preliminary alternate current measurements showed that no signals were found for any of the compounds at zero field. Measurements under static or increasing magnetic fields revealed weak tails of out-of-phase signals for 1 and 5 (Fig. S3†), but well defined χ′′_M(T) peaks with a similar intensity in the 0.1–0.6 T range for complex 6 (Fig. 5-top). The absence of an ac response at zero field is usually attributed to quantum tunnelling of the magnetization (QTM) which can be suppressed by removing the ±m_J degeneration when an external dc field is applied. As is shown in Fig. 5, complex 6 shows temperature and frequency-dependent behaviour both in χ′_M and χ′′_M revealing slow magnetic relaxation behaviour, and it can be considered a Single Ion Magnet (SIM).

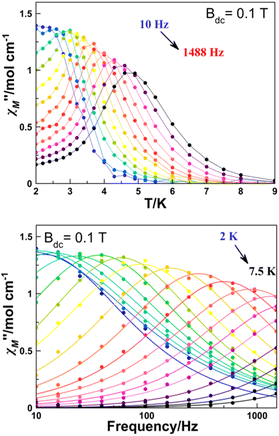Fig. 5 Temperature (top) and frequency (bottom) dependence of χ′′_M of complex 6 at an optimal applied external magnetic field of 0.1 T.

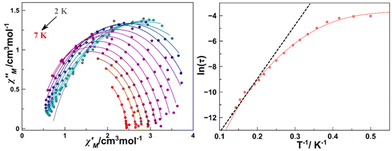
Plots of the maxima of χ′′_Mvs. inverse of the temperature, the so-called Arrhenius plot, evidence that their dependence is not linear and only a rough linearity can be found for higher temperatures, indicating the presence of more than one relaxation mechanism (Fig. S4†). Because for a Kramers ion the magnetic relaxation should occur through excited Kramers doublets with a sequential number of transitions induced by an emission of a quantum of energy lattice (a phonon), a preliminary fit of the high temperature region using the equation ln(1/(2πω) = ln(1/τ₀) − U_eff/(k_BT) yields in the fitting parameters U_eff = 21.77 K and reasonable τ₀ = 2.00 10⁻⁷ s (Fig. S4†). However, on one hand, these values are poorly precise due to the low number of points in the linear region and on the other hand, the low U_eff values are probably much lower than the gap with the Dy^III first excited doublet.

A more precise analysis of the χ′_M and χ′′_M behaviour was performed using the generalized Debye model,^27,28 where these two variables are analysed jointly with τ (the relaxation rate) and α (the parameter that defines the broadness of the spectra involving the distribution in the relaxation times) represented as Argand plots (Fig. 6, left).

Fig. 6 Left, Argand plot of the magnetic susceptibility of 6. Right, temperature dependence of the relaxation time as a function of the temperature plotted as ln(τ) vs. inverse of T. Solid lines show the best fit of the experimental data (Orbach plus Raman fitting) and dotted lines show the slope of the Orbach high temperature regime.

The data extracted from the fitting (CCfit program), is represented in the form of ln(τ) vs. 1/T (Fig. 6, right). Two different relaxations can be observed: the data were simulated following the combination of Orbach and Raman relaxations because the high temperature region clearly follows an Arrhenius-like behaviour while the low temperature region follows the two-phonon relaxation path (eqn (2)).

τ⁻¹ = τ₀⁻¹e^−Ea/KT + CTⁿ (2)

The alpha parameter has a value of 0.06, indicating a narrow distribution of the relaxation times, while the Orbach parameters U_eff and τ₀ of 21.77 K and 2.0 × 10⁻⁷ s are in good agreement with those obtained from the χ′′_M(T⁻¹) fit. The Raman relaxation path was fitted with C = 0.06 and n = 7.3. This value of the Raman coefficient is close to the ones expected for Kramers ions (typically 9–11). However, lower Raman coefficients have been reported commonly relating them to the participation of optical phonons in the spin–phonon interaction.^29,30

To demonstrate the intervention of the lattice in the magnetic relaxation of complex 6, ultra-low frequency Raman measurements have been performed (Fig. 7).^31,32 The spectrum evidences the presence of low frequency vibrations appearing at 27, 59 and 84 cm⁻¹, which are compatible with the energy required for a spin–phonon relaxation path.

Fig. 7 Ultralow frequency Raman spectrum of complex 6 showing low energy vibrations.

Photoluminescence characterization

The emissive properties of compounds 2, 3 and 5 have been studied in polycrystalline samples. As a previous step, the first absorption and emission of the free ligand, dppeO₂, was measured in a chloroform solution (Fig. S5†). The phosphine oxide ligand shows an absorption band at 265 nm. Additionally, the excitation and emission spectra of the free ligand have been recorded at an excitation wavelength (λ_exc) of 270 nm (an λ_exc of 260 nm cannot be used due to instrumental limitations) and at an emission wavelength (λ_em) of 320 nm, respectively.

Excitation of the lanthanide samples at 270 nm induces an emission response for the three measured compounds leading to the characteristic luminescence for each lanthanide cation. Nevertheless, the sensitization effect is not efficient since the emission intensity is rather low. Furthermore, in the excitation spectra recorded at λ_em values of 597 nm (⁴G_5/2 → ⁶H_7/2) for 2, 619 nm (⁵D₀ → ⁷F₂) for 3 and 545 nm (⁵D₄ → ⁷F₅) for 5 the signals arising from the excitation f–f transitions are more intense and can be well differentiated with respect to the bands corresponding to the π–π* and n–π* transitions from the benzene groups of the ligand moieties. Also, the free ligand absorption and emission wavelengths are found in the 270–300 nm UV range suggesting that the phosphine molecule in each Ln^III compound would also absorb light in this range. Then, the whole excitation of the ligand under 300 nm is difficult to observe in all the excitation spectra due to instrumental limitations.

Besides, the energy gaps between the excited singlet and triplet states of the ligand and the respective lanthanide emitting state ions (⁵D₀ for Eu^III, ⁴D₄ for Tb^III, ⁴G_5/2 for Sm^III) are too large. Nevertheless, the distortion due to crystal field perturbation in these structures makes the f–f transitions less forbidden by Laporte's rule and excitation of each sample at their respective f–f excitation transitions, induced more intense emission signals than when exciting the sample in the ligand excitation wavelength, especially for the Eu^III and Tb^III compounds that the emission color could be seen in the naked eye (Fig. S6†).^33,34

Compound 2 (Sm^III). The excitation spectrum recorded at the emission wavelength of 597 nm (⁴G_5/2 → ⁶H_7/2) for compound 2 is presented in Fig. 8. The band in the 270–300 nm range is attributed to the excitation of the ligands present in the structure. Then, in the near UV range, a series of bands appear belonging to the excitation of Laporte forbidden transitions from the f orbitals of the Sm^III ion. The most intense band in the spectra appears at 403 nm and it is assigned to the ⁶H_5/2 → ⁴F_7/2 transition followed by the bands at 345, 363 and 375 nm that are assigned to ⁶H_5/2 → ⁴H_9/2, ⁶H_5/2 → ⁴D_3/2 and ⁶H_5/2 → ⁴D_1/2 transitions, respectively.^35,36 Moreover, the sharp band at 296 nm agrees with the residual ½ harmonic signal from the lamp's instrument. By exciting the Sm^III sample at the ligand excitation wavelength of 275 nm, an emission spectrum with a poor signal is obtained.

Fig. 8 Excitation (top) and emission (bottom) spectra of compound 2.

Nevertheless, when 2 is excited at 403 nm, corresponding to the ⁶H_5/2 → ⁴F_7/2 excitation transition, a more intense spectrum with the expected Sm^III emission bands is acquired, Fig. 8. In this manner, there is a rapid non-radiative deactivation from the ⁴F_7/2 energy level to the emitting ⁴G_5/2 state due to the closely spaced energy levels of these spectroscopic terms. Then the ⁴G_5/2 → ⁶H_5/2–11/2 radiative transitions take place. The band at 564 nm is assigned to ⁴G_5/2 → ⁶H_5/2 which is a pure magnetic dipole transition (ΔJ = 0). The more intense signal at 597 nm corresponds to ⁴G_5/2 → ⁶H_7/2 (ΔJ = ± 1) and along with the selection rule, the transition is partially magnetic and partially forced electric dipole allowed. Next the electric dipole transition (ΔJ = ± 2) ⁴G_5/2 → ⁶H_9/2, more susceptible to the crystal field (hypersensitive transition), is discerned at 643 nm followed by ⁴G_5/2 → ⁶H_11/2 as a low intensity band. It is known that the intensity ratio between the magnetic dipole and electric dipole transitions can be an indicator of the symmetry site of the lanthanide cation inside the structure. For compound 2, the integrated area of the ⁴G_5/2 → ⁶H_9/2 band is larger than that of the ⁴G_5/2 → ⁶H_5/2 band, indicating certain asymmetry in the Sm^III coordination environment^37–39 (the symmetry point group of the coordination polyhedron of 2 does not present an inversion symmetry).

Compound 3 (Eu^III). For compound 3, the excitation spectra at 280 nm show an increase of the signal, suggesting the excitation of the ligand (Fig. 9). Measurements above 270 nm cannot be performed due to instrumental limitations. Then, the signals observed at a higher wavelength correspond to the f–f centred transitions from the Eu^III cation and are assigned to ⁵D₄ ← ⁷F₀ at 375 nm and the more intense band at 394 nm corresponds to ⁵L₆ ← ⁷F₀ and at 464 nm to ⁵D₂ ← ⁷F₀ transitions.

Fig. 9 Excitation (top) and emission (bottom) spectra of compound 3.

When the sample is excited at the ligand excitation wavelength (270 nm) the emission spectrum (shown in Fig. 9, top) is recorded. The signal to noise ratio is high and only two bands are observed. Still, when the λ_exc employed is 394 nm, corresponding to the highest metal centred f–f excitation transition ⁵L₆ ← ⁷F₀, an emission spectrum with a higher resolution could be recorded (Fig. 9, bottom). The bands corresponding to the emission from the ⁵D₀ emitting energy level at 580, 592, 619, 654 and 696 nm are in good agreement with the ⁵D₀ → ⁷F_(0–4) transitions. The magnetic dipole ⁵D₀ → ⁷F₁ transition, the intensity of which is independent of its environment, is split due to the crystal field in the spectrum recorded at λ_exc = 270 nm. This splitting is manifested as a shoulder for the λ_exc = 394 nm spectrum. Next, the most intense band corresponding to the electric dipole ⁵D₀ → ⁷F₂ transition presents a small split due to the crystal field effect and the ⁵D₀ → ⁷F₂/⁵D₀ → ⁷F₁ ratio is 4.7, suggesting that the Eu^III cation does not belong to a point group with inversion symmetry inside the structure. When exciting the sample at 394 nm, the ⁵D₄ excited level deactivates through radiationless transitions to the ⁵D₀ emitting level, leading to the above-mentioned transitions. In addition, radiative transitions take place from the ⁵D₁ energy level, higher in energy than the ⁵D₀ level. The bands corresponding to these transitions are located at 539 nm corresponding to ⁵D₁ → ⁷F₁ and at 649 nm, they overlapped with the ⁵D₀ → ⁷F₃ transition, assigned to ⁵D₁ → ⁷F₅.⁴⁰

Luminescence lifetime decay was measured for the europium compound. The experiment was monitored at an emission wavelength of 614 nm and the sample was excited at 395 nm. The decay curve presented in the semi-log plot is shown in Fig. 10 and it could be fitted with a mono-exponential equation (eqn (3)) which is consistent with one deactivation mechanism. The luminescence lifetime (τ_obs) of 3 is 1.65 ms. Furthermore, the pure magnetic dipole character of europium's ⁵D₀ → ⁷F₁ transition allows the calculation of the radiative rate constant k_rad from the corrected emission spectrum, using a simplified equation presented by Werts et al. (eqn (4)).⁴¹ The τ_rad (k_rad = 1/τ_rad) parameter accounts for the lifetime of luminescence deactivation from the emitting level if all the deactivation transitions were of radiative nature and for 4 it was found to be 2.9 ms. The calculated τ_rad value is higher than the observed lifetime obtained from the measurement elucidating that faster non-radiative deactivation processes take place reducing the τ_obs. Additionally, the ratio between the radiative rate and the luminescence deactivation rate of the compound defines the intrinsic quantum yield (ϕ^Ln_Ln) which is the emission efficiency once the Eu^III emitting level is populated. For 3, (ϕ^Ln_Ln) is 55%.

Fig. 10 Luminescence lifetimes curves of compounds 3 and 5. Solid lines represent mono-exponential fittings using eqn (3).

Compound 5 (Tb^III). Finally, in the excitation spectra of compound 5, excitation transitions from terbium's f⁸ orbitals arise in the 300 to 400 nm range, Fig. 11. The bands corresponding to the excitation transitions from the ⁷F₆ ground state are assigned as follows: ⁷F₆ → ⁵D₁, ⁵D₀, ⁵G_J, ⁵D₂, ⁵G_J, ⁵L₁₀, and ⁵D₃ at 318, 325, 340, 351, 359, 368 and 378 nm, respectively.³⁹ Furthermore, an increase of the signal intensity is perceived below 300 nm corresponding to ligand excitation that cannot be entirely seen since ligand absorption occurs at a lower wavelength in the UV range added to the poor sensitization effect in these systems. Nevertheless, f–f centred excitation transitions from the lanthanide ion are well defined and intense enough to record the emission spectrum of compound 5 (Fig. 11). Exciting the sample at 270 nm (ligand excitation) induced the emission of 5 and the expected bands from f–f transitions are discerned at 490, 545, 586 and 623 nm, consistent with the radiative transitions from the ⁵D₄ emitting energy level to the ⁷F_6–3 ground state, respectively. Among this, very weak bands corresponding to ⁵D₄ → ⁷F_2–1 transitions are perceived in the 650–700 nm range. Furthermore, when the emission measurement is monitored at an λ_exc of 350 nm, corresponding to the highest in intensity ⁷F₆ → ⁵D₂ f–f excitation transition, the same terbium emission bands are recorded using the λ_exc that corresponds to the intraconfigurational 4f–4f transition of Tb^III leading to luminescence higher in intensity.^42–44

Fig. 11 Excitation (top) and emission (bottom) spectra of compound 5.

The luminescence lifetime decay of 5, monitored at an emission wavelength of 545 nm and at an excitation wavelength of 350 nm that agrees with the Tb^III centred ⁷F₆ → ⁵D₂ transition, yielded 1.51 ms. For the terbium compound, the decay curve also followed a mono-exponentially function suggesting a single deactivation mechanism as the Eu^III compound.

Conclusions

A new family of phosphine oxide lanthanide-derived compounds has been synthesized and characterized by structural, magnetic and luminescence techniques. Two different structures can be achieved while using the same synthesis, and the final topology of the products seems independent of the previously proposed factors like lanthanide size or co-ligands but determined by the solvents. Moreover, the first monodimensional chain-like structure has been achieved for dppeO₂ lanthanide coordination compounds. All the family members have been magnetically characterized, but only Dy presents a field-induced SIM response following an Orbach-like plus Raman relaxation path. Among these, the visible emitters Sm^III, Eu^III and Tb^III systems have been studied in their specific emission range, and all of them present good emission properties.

Author contributions

E. P.: synthesis, magnetic measurements, and data analysis; A. T.: luminescence measurements, data analysis, and original draft writing; M. F.-B.: single crystal X-ray crystallography; S. S.: preliminary luminescence spectra; A. E.: structural analysis, conceptualization, writing and editing. A. G.: funding acquisition and project administration; and J. M.: supervision of the experimental work and measurements, final manuscript writing, and conceptualization.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

JM and AE are thankful for the funding from MICINN (Project PGC2018-094031-B-100). AG is thankful for the support from MICINN (Project PID2020-115658GB-I00) and IN²UB (Project ART_2021_3).

References

1. C. M. G. Dos Santos, A. J. Harte, S. J. Quinn and T. Gunnlaugsson, Coord. Chem. Rev., 2008, 252, 2512.
2. S. Shinoda and H. Tsukube, Analyst, 2011, 136, 431.
3. A. Dey, P. Kalita and V. Chandrasekhar, ACS Omega, 2018, 3, 9462.
4. R. A. Layfield and M. Murugesu, Lanthanides and Actinides in Molecular Magnetism, John Wiley & Sons, 2015.
5. R. Marin, G. Brunet and M. Murugesu, Angew. Chem., Int. Ed., 2021, 60, 1728.
6. L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179.
7. A. M. Kaczmaret, Y.-Y. Liu, C. Wang, B. Laforce, L. Vincze, P. Van Der Vort, K. Van Hecke and R. Van Deun, Adv. Funct. Mater., 2017, 27, 1700258.
8. W. Ren, G. Lin, C. Clarke, J. Zhou and D. Jin, Adv. Mater., 2020, 32, 1901430.
9. L. Sorace, C. Benelli and D. Gatteschi, Chem. Soc. Rev., 2011, 40, 3092.
10. J. Luzón and R. Sessoli, Dalton Trans., 2012, 41, 13556.
11. H. Zhang, Z.-H. Chen, X. Liu and F. Zhang, Nano Res., 2020, 13, 1795.
12. A. D'Aléo, F. Pointillart, L. Ouahab, C. Andraud and O. Maury, Coord. Chem. Rev., 2012, 256, 1604.
13. A. W. G. Platt, Coord. Chem. Rev., 2017, 340, 62.
14. R. D. Bannister, W. Levason, G. Reid and W. Zhang, Polyhedron, 2017, 133, 264.
15. Z. Spichal, M. Necas and J. Pinkas, Inorg. Chem., 2005, 44, 2074.
16. Z. Spichal, M. Nekas, J. Pankas and J. Novosad, Inorg. Chem., 2004, 43, 2776.
17. P. Pekarkova, Z. Spichal, P. Taborsky and M. Nekas, Luminescence, 2011, 26, 650.
18. W. Q. Lin, D. R. Wang, W. J. Long, L. S. Lin, Z. X. Tao, J. L. Liu, Z. Q. Liu and J. D. Leng, Dalton Trans., 2022, 51, 5159.
19. S. A. Cotton and P. R. Raithby, Coord. Chem. Rev., 2017, 340, 220.
20. A. M. J. Lees and A. W. G. Platt, Inorg. Chem., 2003, 42, 4673.
21. G. M. Sheldrick, SHELXL-2014/7: Program for the Solution of Crystal Structures, University of Göttingen, Göttingen, Germany, 2014.
22. F. Marchetti, C. Pettinari, A. Pizzabiocca, A. A. Drozdov, S. I. Troyanov, C. O. Zhuravlev, S. N. Semenov, Y. A. Belousov and I. G. Timokhin, Inorg. Chim. Acta, 2010, 363, 4038.
23. M. Lunell, D. Casanova, J. Cirera, P. Alemany and S. Alvarez, SHAPE v.2.0, Barcelona, 2010. The program can be obtained by request to the authors.
24. N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164.
25. M. V. Marinho, D. O. Reis, W. X. C. Oliveira, L. F. Marques, H. O. Stumpf, M. Déniz, J. Pasán, C. Ruíz-Pérez, J. Cano, F. Lloret and M. Julve, Inorg. Chem., 2017, 56, 2108.
26. A. Worrell, D. Sun, J. Mayans, C. Lampropoulos, A. Escuer and T. C. Stamatatos, Inorg. Chem., 2018, 57, 13944.
27. K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341.
28. P. Debye, Phys. Z., 1938, 39, 616.
29. L. Gu and R. Wu, Phys. Rev. B, 2021, 103, 01441.
30. K. N. Shivatava, Phys. Status Solidi B, 1983, 117, 437.
31. M. Atzori, S. Benci, E. Morra, L. Tesi, M. Chiesa, R. Torre, L. Sorace and R. Sessoli, Inorg. Chem., 2018, 57, 731.
32. M. Briganti, F. Santanni, L. Tesi, F. Totti, R. Sessoli and A. Lunghi, J. Am. Chem. Soc., 2021, 143, 13633.
33. Y.-S. Meng, Y.-S. Qiao, Y.-Q. Zhang, S.-D. Jiang, Z.-S. Meng, B.-W. Wang, Z.-M. Wang and S. Gao, Chem. – Eur. J., 2016, 22, 4704.
34. M. Latva, H. Takalo, V. M. Mukkala, C. Matachescu, U. J. C. Rodríguez-Ubis and J. Kankare, J. Lumin., 1997, 75, 149.
35. F. A. Mautner, F. Bierbaumer, R. Vicente, S. Speed, A. Tubau, R. C. Fischer and S. S. Massoud, Magnetochemistry, 2022, 8, 72.
36. C. K. Jayasankar and E. Rukmini, Opt. Mater., 1997, 8, 193.
37. R. Yu, N. Xue, T. Wang, Z. Zhao, J. Wang, Z. Hei, M. Li, H.-M. Noh and J.-H. Jeong, Ceram. Int., 2015, 41, 6030.
38. J. Bolton, J. Lumin., 2021, 231, 117717.
39. I. J. Al-Busaidi, R. Ilmi, D. Zhang, J. D. L. Dutra, W. F. Oliveira, N. K. Al Rasbi, L. Zhou, W.-Y. Wong, P. R. Raithby and M. S. Kahn, Dyes Pigm., 2022, 197, 109879.
40. K. Binnemans, Coord. Chem. Rev., 2015, 295, 1.
41. M. H. V. Werts, R. T. F. Jukes and J. W. Verhoeven, Phys. Chem. Chem. Phys., 2002, 4, 1542.
42. Y.-C. Li, Y.-H. Chang, Y.-J. Lin and C.-H. Laing, J. Phys. Chem. C, 2007, 111, 210682.
43. A. J. Kanimozdhi and V. Alexander, Dalton Trans., 2017, 46, 8562.
44. X. Zhou, X. Zhao, Y. Wang, B. Wu, J. Shen, L. Li and Q. Li, Inorg. Chem., 2014, 53, 12275.

---

Footnote

† Electronic supplementary information (ESI) available: Structural and magnetic data. CCDC 2215834–2215836. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2dt03621e

---