First ternary tungsten tellurate(IV) WTe₂O₇ with unique crystal structure type

Abstract

At multianvil high-pressure/high-temperature conditions of 10 GPa and 1273 K, the first ternary tungsten tellurate WTe₂O₇ is formed, starting from a stoichiometric mixture of WO₃ and TeO₂. The compound crystallizes triclinic in a hitherto unknown crystal structure type with the space group P1̄; (no. 2), and was refined from single-crystal X-ray diffractometer data: a = 538.3(1), b = 687.5(1), c = 802.3(1) pm, α = 72.4(1)°, β = 85.7(1)°, γ = 68.1(1)°, wR₂ = 0.0323, GooF = 1.048, 3157 F² values, and 106 variables. The main motifs of the crystal structure are pairs of edge-linked [WO₆]⁶⁻ octahedra and fourfold oxygen-coordinated Te⁴⁺ atoms. The oxidation state of W⁶⁺ and Te⁴⁺ was further verified by measuring the characteristic binding energy values for the W 4f and the Te 3d core levels via X-ray photoelectron spectroscopy (XPS). In addition, DFT calculations of the structure, the associated electron localisation functions (ELF) and vibrational spectra have been carried out. The theoretical data clearly demonstrates the impact of the residual electron density located at the Te⁴⁺ ions, which can be directly interpreted as the presence of lone electron pairs within the solid structure.

---

I. Introduction

For various reasons, tellurate compounds have attracted increasing interest in recent years. From a structural point of view, tellurium with its +IV and +VI oxidation states in oxotellurates reveals a diverse variety of coordination environments and Te–O bond lengths.^1,2 A comprehensive overview about the structural abundance of oxotellurates(IV) and -(VI) has recently been provided by Christy et al.³ Moreover, the Te⁴⁺ atom and the electron lone pair (Ψ) have a decisive contribution to the structural diversity of tellurates. Low symmetrical and one-sided open coordination polyhedra (space requirement of the Ψ) are the consequence and also the origin of the highly interesting physicochemical properties of oxotellurates. The low symmetric and polar structure-directing building blocks often lead to non-centrosymmetric crystal structures with non-linear optical, pyro-, piezo-, or ferroelectrical properties,^4–7 which is one of the main reasons, why tellurates are currently attracting a lot of interest.

Our approach to expand the broad field of oxotellurates by further representatives is to add and vary another synthetic parameter – namely pressure. By multianvil high-pressure/high-temperature (HP/HT) experiments, maximum conditions of 1700 K and 15 GPa are accessible for us. The high-pressure influences coordination environments, oxidation states and bond lengths as well as physicochemical properties.^8–13 In addition to high-pressure phase transformations and the synthesis of polymorphs, new compositions can also be stabilized that would not be accessible at ambient pressure conditions.^14–16 Using this technique, we recently reported on the synthesis of HP-Mg₃TeO₆, an SHG active and UV-transparent material,¹⁷ HP-Sc₂TeO₆,¹⁸ and HP-Co₃TeO₆,¹⁹ which shows magnetoelectric behavior. All the aforementioned tellurates are oxotellurates(VI) without exception, because a stabilization of oxotellurates(IV) at HP/HT conditions is challenging. Within this work, we accomplished the synthesis of an oxotellurate(IV), namely WTe₂O₇, the first ternary tungsten tellurate. To the best of our knowledge, we are not aware of any structurally investigated ternary tungsten tellurate. This is all the more astonishing, since several representatives of the almost identically sized molybdenum are known. From Mo₅TeO₁₆ ²⁰ and MoTe₂O₇,^21,22 a monoclinic as well as an orthorhombic modification were synthesized. Via a hydrothermal route, MoTe₂O₇ (Pna2₁) and MoTeO₅,²¹ a third composition in the ternary system was accessible. Remarkably, a rare tetravalent cation conduction of Te⁴⁺ ions is observed for monoclinic MoTe₂O₇.²² In this work, we report about the multianvil HP/HT synthesis, structural elucidation and theoretical calculations of the first oxotellurate(IV) WTe₂O₇.

II. Results and discussion

At ambient pressure conditions, no reaction of WO₃ occurred in combination with Te(OH)₆ or TeO₂. Telluric acid dehydrated to TeO₃ and decomposed to TeO₂ and O₂. Using corundum crucibles, side reactions and the insertion of aluminum was observed. By adding the synthesis parameter pressure, the title compound WTe₂O₇ was synthesized from WO₃ and TeO₂ at 1273 K and 10 GPa in closed platinum capsules. EDX analyses confirmed the elemental composition of WTe₂O₇, in particular concerning the tungsten to tellurium ratio. No additional elemental impurities were visible. The respective data can be found in the Experimental section.

II.1 Crystal structure of WTe₂O₇

The compound WTe₂O₇ crystallizes triclinic in the space group P1̄ (no. 2) with the corresponding lattice parameters a = 539(1), b = 689(1), c = 803(1) pm, α = 72.4(1)°, β = 85.6(1)°, γ = 68.1(1)° and a volume of V = 0.263(1) nm³ (selected crystallographic data are listed in Table 1).

Table 1 Selected crystallographic data and details of the structure determination of WTe₂O₇

Empirical formula	WTe2O7
Molar mass, g mol^−1	551.05
Crystal system	Triclinic
Space group	P1̄ (no. 2)
Powder data
Powder diffractometer	Stoe Stadi P
Radiation	Mo-Kα1 (λ = 70.93 pm)
a, pm	538.650(6)
b, pm	688.515(8)
c, pm	802.649(9)
α, °	72.41(1)
β, °	85.62(1)
γ, °	68.06(1)
V, nm^3	0.263(1)
T, K	293(2)
Single-crystal data
Single-crystal diffractometer	Bruker D8 quest, photon 100
Radiation	Mo-Kα (λ = 71.073 pm)
a, pm	538.31(2)
b, pm	687.49(3)
c, pm	802.30(4)
α, °	72.44(1)
β, °	85.70(1)
γ, °	68.11(1)
V, nm^3	0.2624(1)
Formula units per cell, Z	2
Calculated density, g cm^−3	6.97
Temperature, K	223(2)
Absorption coefficient, mm^−1	32.88
F(000), e	468
2θ range, °	2.67–39.42
Range in hkl	±9, ±12, ±14
Total no. of reflections	22468
Independent reflections/Rint	3157/0.0324
Reflections with I > 2σ(I)	2932
Data/ref. parameters	3157/106
Goodness-of fit on Fo^2	1.048
Absorption correction	Multi-scan
Final R1/wR2 (I ≥ 2σ(I))	0.0155/0.0316
Final R1/wR2 (all data)	0.0187/0.0323
Largest diff. peak/hole, e Å^−3	1.93/−1.88

---

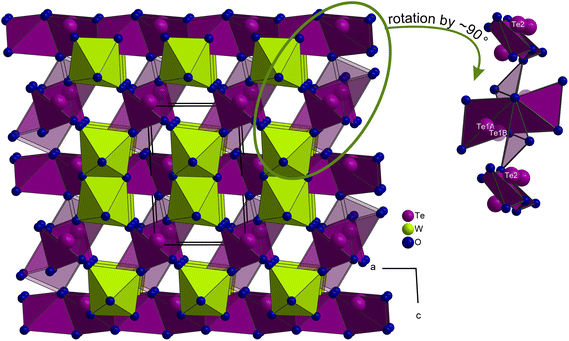
A unit cell of WTe₂O₇ comprises two formula units and 20 atoms. The main motifs of the crystal structure are pairs of edge-linked [WO₆]⁶⁻ octahedra and fourfold oxygen-coordinated tellurium atoms. The tungsten site revealed a minor positional disorder of about 1.9%. Consequently, the W–W distance within the [W₂O₁₀]⁸⁻ pairs varies from majority W_AA = 316 pm to W_AB = 330 pm to possible W_BB = 347 pm, and is thus significantly longer than the W–W distance of 273 pm in metallic tungsten.²³ There are two crystallographically distinct tellurium positions Te1 and Te2, of which the Te1 position has also been refined as a split position with Te1A and Te1B occupying 96.8% and 3.2%, respectively. Despite the low splitting, refinement of the split positions significantly improved the residual electron density and the quality of the final results. Possible refinement of disordered oxygen positions, resulting from the displacement of the W and Te atoms was omitted, since this enhanced the quality factors of the structure optimization only marginally. All Te⁴⁺ sites show fourfold oxygen coordination in a first approximation with Te–O distances from 190 pm to 230 pm. The next and fifth coordinated oxygen atoms, involved in secondary bonding interactions (SBIs), are found only at the following distances: Te1A–O1 = 248 pm, Te1B–O6 = 264 pm and Te2–O7 = 247 pm. An exact determination of the threshold value for a coordination is difficult and was made on the basis of MAPLE (Madelung part of lattice energy) calculations, which showed only a negligible coordinative contribution to the respective tellurium atom for a fifth oxygen atom. More details on the MAPLE calculations can be found below. Christy et al. also proposed a cut off at 245 pm in their review about the structural architecture of tellurium oxy-compounds.³ Coordination geometries and distances are shown in Fig. 1. Table SI1† contains the atomic coordinates, site occupation, and isotropic displacement parameters. Anisotropic displacement parameters, bond length and angles are given in Tables SI2–SI4 of the ESI.†

Fig. 1 (top) Common and single coordination spheres of Te1A and Te1B atoms. (bottom) Te2 is also coordinated bisphenoidal and tungsten shows a distorted octahedral oxygen environment. All Te atoms exhibit a unilateral coordination with corresponding free space for the positioning of the electron lone pair. Te1B and W1B atoms with occupancies of 3.2% and 1.9%, respectively, are plotted in transparent. Bond lengths are given in pm.

Fig. 1 (top center) displays the common coordination geometry of the disordered atoms Te1A and Te1B. According to the lower site-occupation, the Te1B atom is drawn in transparent mode. Both Te⁴⁺ atoms together show a unilateral nutshell-shaped coordination, whereas each individual atom has a distorted trigonal bipyramidal coordination with one of the equatorial positions left unoccupied, creating free space for the electron lone pair of Te⁴⁺ (Fig. 1, top left and top right). The Te2 atoms exhibit a comparable bisphenoidal coordination geometry. Within these units, three shorter and one longer Te⁴⁺–O contacts are observed. Since Te⁴⁺ has a wide range of bond lengths and coordination geometries to oxygen, reference is made here to a comprehensive review.³

The tungsten atoms are surrounded octahedrally by six oxygen atoms. Due to second-order Jahn–Teller (SOJT) distortions, for which d⁰ W⁶⁺ cations are predisposed, the tungsten cations are off-center coordinated. SOJT effects occur from mixing of vacant cation d orbitals with the filled p orbitals of the ligands.^24,25 The geometrical changes of the coordination polyhedra are not predictable but depend on the extended structure of the crystal. For WTe₂O₇, this is evident in three ‘short’ (173–189 pm) and three ‘long’ (195–229 pm) W1A–O bonds and in the case of the octahedral W1B out-of-center coordination it is apparent in two ‘short’ (168 and 183 pm) and four ‘longer’ (201–213 pm) spacings. The distances agree well with the bond lengths reported in literature for triclinic WO₃ (176 pm to 218 pm)²⁶ or W₁₇O₄₇ (143 pm to 239 pm).²⁷

A database search in the ICSD²⁸ based on the Wyckoff sequence i10 yielded 152 hits of triclinic compounds. To the best of our knowledge, none of these compounds showed pairs of edge-linked octahedrally coordinated atoms in combination with bisphenoidal atomic coordinations. Consequently, the crystal structure of the title compound WTe₂O₇ can be considered as a unique structure.

After this description of the local configuration, the topology of the crystal structure is described in more detail. In Fig. 2, the WTe₂O₇ structure with view along the crystallographic a- and c-axis is depicted. Here, isolated [W₂O₁₀]⁸⁻ units can be identified as well as single chains built up from bisphenoidal coordinated and edge linked Te2 atoms running along the a-axis. These are so-called zweier edge-sharing chains of CN4 Te forming electrostatically neutral chains [Te₂O₄]⁰. Fig. 3 shows more clearly the chains described according to Christy et al.³ in the terminology of Liebau²⁹ as (… = ◊ = ◊ = …), where ◊ and = each represent a [TeO₄]⁴⁻ unit with edge-sharing of such units.

Fig. 2 Crystal structure of WTe₂O₇ with view along the a- (top) and c-axis (bottom). Along a, the pairs of edge-linked [W₂O₁₀]⁸⁻ units can be identified, which are connected by dimers of bisphenoidal coordinated Te1A polyhedra ([Te₂O₆]⁴⁻ units, (Liebau:²⁹ (◊ = ◊)). In addition, the polyhedra of the Te1B dimers are also depicted, but with higher transparency. With view along the c-axis, the zweier edge-sharing chains of CN4 Te2 atoms ([Te₂O₄]⁰ units, (… = ◊ = ◊ = …)) are shown.

Fig. 3 Crystal structure of WTe₂O₇ with view along the b-axis. [W₂O₁₀]⁸⁻ dimers as well as zweier edge-sharing chains of Te2 atoms running along a are depicted. By increased transparency, the disorder of the Te1 atoms is highlighted and leads to a z-shaped linkage of the chains. On the right side, a structural detail of this linkage is shown.

A similar structural feature is known from the compound Ag(TeO₂)(NO₃) ≡ Ag₂(Te₂O₄)(NO₃)₂ ³⁰ with chains parallel to the c-axis. Due to the higher symmetry of the compound Ag(TeO₂)(NO₃) (S.G. Pbcn), the Te–O distances within the chains are more uniformly distributed and are determined as 192 pm and 207 pm, respectively. The Te1 atoms in WTe₂O₇ form edge-sharing dimers of bisphenoidal [TeO₄]⁴⁻. The resulting [Te₂O₆]⁴⁻ units (Liebau:²⁹ (◊ = ◊)) are isolated and share corners with the [W₂O₁₀]⁸⁻ octahedral dimers (see Fig. 2 (top), 3) and in the case of [(Te1B)₂O₆]⁴⁻ dimers, additional linkages to the O1 atoms of the chains are formed (see Fig. 3). Comparable [Te₂O₆]⁴⁻ units can also be found in the mixed-metal oxide halide material Pb₃Te₂O₆X₂ (X = Cl, Br).³¹ Te–O distances in this compound are reported from 194 pm to 205 pm. In the following a closer look on the disorder in the WTe₂O₇ crystal structure is given. It is noteworthy that the occupancies of W1B (1.9%) and Te1B (3.2%) are comparable, indicating a possible mutual dependence and the formation of a local alternative structural arrangement. Fig. 4 (top) illustrates the changing situation in the coordination environments with different occupation of the A- and B-sites. The top right part shows the most common situation and the top left part of Fig. 4 the exclusive occupation of the B-sites. In between, the superposition of both coordination possibilities is given, because not always both A or B atoms of the [Te₂O₆]⁴⁻ units have to be present, but also an A and B occupation is possible.

Fig. 4 (top) Illustration of the different coordination environments when switching from only occupied B-sites (top left) to only occupied A-sites (top right). The center of the top figure shows the overlay of the two coordination options. The secondary bonding interactions (Te⁴⁺⋯O²⁻) formed in WTe₂O₇ are given as dashed bonds. All distances are given in pm. (bottom) Layers within the crystal structure of WTe₂O₇ connected via [Te₂O₄]⁰ chains running along a. The disorder takes place within the layers or in the type of stacking disorder.

By switching from A to B sites, the largest structural changes occur at the following locations. The shortest W1A–O4 distance (173 pm) increases to 201 pm for W1B–O4, since O4 is now additionally bonded to Te1B at a distance of 217 pm. The shortest W1B–O distance is now formed to the O2 site (168 pm), which subsequently coordinates only with Te1B at a distance of 277 pm. An additional stabilizing effect by crosslinking of the structure is achieved by the formation of a new connection between Te1B and O1 atoms at a distance of 203 pm. This leads to a z-shaped linkage of the chains running along a (see Fig. 3). Overall, the oxygen surrounding of the tungsten atoms becomes more uniform for the W1B coordination. The long W1A–O5 distance of 229 pm decreases to 203 pm (W1B–O5). Apparently, however, the off-center coordination of tungsten atoms is structurally preferred due to the SOJT effects. If the oxygen surrounding of the Te1 atoms is compared, a similar situation is found. The bisphenoidal coordination is retained and the Te1–O distances become more uniform, too. The average bond length increases from 201 pm (Te1A–O) to 207 pm (Te1B–O). However, due to the unilateral coordination and the open crystal structure, both Te1A- and Te1B-atoms have enough space for the orientation of their lone-pair electrons. The question of the cause for the disorder in the WTe₂O₇ crystal structure is difficult to answer and will be a combination of stabilizing SOJT effects as well as a similar stabilization of the lone-pair electrons in their different orientations. It is obvious that the structural changes all take place within one layer of the crystal structure. As the bottom part of Fig. 4 shows, the layers are connected only by the [Te₂O₄]⁰ chains. These layers can stack differently, which can lead to stacking faults of the heavy atoms’ tellurium and tungsten at its different A- and B-sites with different probabilities. The disorder within one layer or the formation of alternative local structural arrangements (clustering) appear to be purely statistical. Also, no higher order was observed in the sequence of layers, which should have become visible by superstructure reflections or diffuse scattering. In addition, so-called secondary bonding interactions (SBIs) are formed, which also have structure-stabilizing effects. These Te⁴⁺⋯O²⁻ interactions are common in rare-earth metal(III) oxotellurates(IV) such as RE₂Te₃O₉ (RE = La, Ce, Pr, Nd) in a space region of d (Te⋯O) = 250–297 pm.³² Oxotellurate(IV) groups, and in particular the Ψ-bisphenoidal [TeO₄]⁴⁻ groups, are known for their pronounced Te⁴⁺⋯O²⁻ interactions to other [TeO₄]⁴⁻ groups as well as [W₂O₁₀]⁸⁻ octahedral dimers in WTe₂O₇. The theoretical concept of SBIs was established by Alcock et al.,³³ and the bonding interactions originate from the hyperconjugation of a σ*-Te–O molecular orbital with a non-bonded p-orbital of an oxygen atom.³⁴ Another common name for this specific interaction is called “chalcogen bonding”.³⁵Fig. 4 (top) displays these additional Te⋯O contacts in WTe₂O₇. On the right part of the top graphic, the Te1A and Te2 SBIs are shown. The bisphenoidal [(Te1A)O₄]⁴⁻ group establishes a weak interaction with the O1 atom of the [Te(2)O₄]⁴⁻ group in a distance of 248 pm. Vice versa, Te2 also has a secondary bonding interaction via the O7 atom of the [Te₂O₆]⁴⁻ dimer with a distance of 247 pm. Two additional weaker contacts are formed to O4 (288 pm) and O3 (265 pm) of the [W₂O₁₀]⁸⁻ octahedral dimers. In the left part of Fig. 4 (top), the [(Te1B)O₄]⁴⁻ groups are displayed. Even in this case of site occupation, the formation of SBIs can occur.

Concerning the charge distribution in WTe₂O₇, the reliability of the crystal structure model was checked by bond-length/bond-strength (BLBS),^36–38 CHARDI (Charge Distribution),³⁹ and MAPLE^40–42 calculations. The obtained values are in good agreement with the formal charges W⁶⁺, Te⁴⁺, and O²⁻ derived by X-ray crystal structural analysis. The MAPLE value of WTe₂O₇ was calculated and compared to the sum of the MAPLE values of the binary high-pressure polymorphs WO₃ ⁴³ and 2× TeO₂ ⁴⁴ (for details, see Table SI5 of the ESI†). The values are in good agreement with a deviation of 0.55%. For the MAPLE and CHARDI calculations, the disorder of the tungsten and tellurium atoms was neglected, because the method does not support split sites. Consequently, the calculated valences (∑Q) of these atoms are less accurate. The BLBS model was optimized to consider split sites by multiplying the valence contribution of each bond between atoms i and j (v_ij) by the site occupation factor (SOF) of the split site according to . R_ij is the bond valence parameter, b is a “universal” constant and d_ij is the distance between the atoms i and j.³⁶ These results are shown in the Table 2.

Table 2 Charge distribution in WTe₂O₇ (space group P1̄), calculated with the bond-length/bond-strength concept (∑V) and the CHARDI concept (∑Q)

Atom	W1A	W1B	Te1A	Te1B	Te2	O1	O2	O3	O4	O5	O6	O7
∑Q	+6.20		+3.86		+3.93	−2.29	−2.20	−1.65	−1.92	−1.77	−2.25	−1.91
∑V	+6.00	+5.90	+3.93	+3.28	+3.67	−2.13	−2.02	−1.74	−1.68	−1.93	−2.03	−1.93

---

The low BLBS values for the atoms O3 and O4, which show only one coordination to tungsten, are noticeable. Two O3 atoms form the edge linkage between the tungsten octahedra dimers. O4 is a terminal oxygen atom, which just coordinates to W1A and W1B, respectively. If the split position Te1B is occupied, it is also coordinated to O4. The influence of the tellurium lone pair electrons and secondary bonding interactions on the O3 and O4 atoms are not considered in the BLBS calculation and could be an explanation for the low valences.

The crystal structure model of WTe₂O₇ was verified on a powdered sample by Rietveld analysis depicted in Fig. 5. Starting atomic parameters were derived from the single crystal solution. The fitting was performed in good quality and exhibited an almost X-ray pure specimen. Only a marginal unknown side phase, marked with an asterisk, is visible in the diffraction pattern and the difference plot. Refined cell parameters of the powder data are given in Table 1.

Fig. 5 X-ray powder diffraction pattern (Mo-K_α1 radiation) of WTe₂O₇ and Rietveld refinement (measured (black) and calculated (red) patterns). The calculated reflection positions are indicated by the vertical green bars below the difference pattern (R_exp = 1.94%, R_wp = 3.98%, R_p = 3.03%, GooF = 2.05). A small unknown side phase is indicated by an asterisk.

II.2. XPS studies

X-ray photoelectron spectroscopy (XPS) was applied for the determination of the binding energy values of W 4f and Te 3d core levels. To make a reliable statement about the position of the binding energies, the averaged values for the O 1s level in WO₃ and TeO₂ were used to correct for charging effects during the measurement procedure. Detailed information on this can be found in the Experimental Part. In Fig. 6, the characteristic energy core levels for Te 3d and W 4f are depicted. Table 3 lists the results of the peak fits for the respective species.

Fig. 6 XP spectra of the Te 3d (top) and W 4f (bottom) core levels with experimental data (dots) and fit (purple and green, respectively).

Table 3 Detailed listing of the peak fitting values of the Te 3d and W 4f core levels

	Te 3d3/2	Te 3d5/2	W 4f5/2	W 4f7/2
Position/eV	586.41	576.02	37.62	35.44
FWHM	1.81	1.81	1.49	1.49
% Lorentz:Gaussian	65	65	48	48

---

For tellurium, the positions of the 3d core levels are 586.41 eV and 576.02 eV, respectively. The 4f energy core levels for tungsten are located at 37.62 eV and 35.44 eV. In previous studies, the position of the Te 3d5/2 and the W 4f7/2 core levels were determined for tellurium and tungsten oxides. Here, Te 3d5/2 of Te⁴⁺ is positioned in the range of 575.6 eV to 576.9 eV.^45–51 For W 4f7/2 with an oxidation state of W⁶⁺, these values range from 35.2 eV to 36 eV.^47,52–57 By comparing these values to the experimental data obtained under consideration of the overall structural motif of WTe₂O₇, oxidation states of Te⁴⁺ and W⁶⁺ are reasonable. The oxidation states determined agree with those obtained from crystal structure analysis.

II.3 Theoretical calculations and analysis

The optimized lattice parameters a, b and c as well as the lattice angles α, β and γ show good agreement with the experimental measurements and deviate only by ≤2.5% (PBESOL) and 1% (HSESOL), respectively. The associated values are listed and compared to the experimental ones in Table 4. As expected, the range-separated hybrid functional HSESOL leads to slightly better results, which is also reflected in the calculated powder XRD patterns depicted in Fig. SI1.†

Table 4 Comparison of experimental lattice parameters and values derived from DFT optimized structures. Lattice parameters are given in pm

	a	b	c	α	β	γ	V/nm^3
HSESOL	535.38	694.82	795.39	72.58°	85.90°	67.81°	0.2611
PBESOL	538.61	705.83	790.14	72.18°	86.10°	67.38°	0.2635
Single crystal data	538.31(2)	687.49(3)	802.30(4)	72.44(1)°	85.70(1)°	68.11(1)°	0.2624(1)
Powder data	538.650(6)	688.515(8)	802.649(9)	72.41(1)°	85.62(1)°	68.06(1)°	0.2629(1)

---

Band structure and density of states calculations lead to viable results as well, although the band gap values determined by the functionals seems unusual as the employment of the hybrid functional HSESOL leads to a larger band gap (3.49 eV) as observed in case of PBESOL (2.28 eV), which in general tends to overestimate band gap energies. It is likely that the unusual character of the tungsten tellurate(IV) featuring residual electron density (Ψ) at the tellurium atoms is a particular challenge in the calculations. Fig. 7 shows the HSESOL band structure and density of states. The corresponding PBESOL band structure is given in the ESI (see Fig. SI2†). It is evident that the valence band is almost exclusively formed from Te- and O-orbitals, whereas the bottom edge of the conduction bands is dominated by W-, Te-, and O-orbitals, which determine the band gap. The Fermi-level is placed in the center of the band gap, determined as 3.49 eV. From diffuse UV/Vis reflectance data, the optical bandgap was determined experimentally via the Kubelka–Munk function (F(R)). In Fig. SI3,† the UV/Vis spectrum, the plot (F(R)hν)^1/2/(hν) for the indirect band gap (3.0 eV) and the plot (F(R)hν)²/(hν) for the direct band gap (3.3 eV) are depicted. A wide transparency range up to an absorption edge of 260 nm is visible from the spectrum.

Fig. 7 Band structure and density of states (right part of the figure) of WTe₂O₇ determined at the HSESOL/double-zeta level.

To visualize the electron lone pair contributions to the overall electron density, electron localization functions (ELFs) have been calculated, which are depicted in Fig. 8. Three independent values (0.55, 0.65, 0.75) in arbitrary units were chosen for the isosurfaces, resembling the ELF around the atoms in the unit cell. While the oxygen and tungsten atoms feature electron densities resembling a spherical shape centered at the respective core, the residual electron density near the tellurium atom is clearly represented via the hemisphere-like shaped functions pointed at by the arrows in Fig. 8. Due to the associated crystal symmetry, two pairs of tellurium atoms can be distinguished, showing a slightly different residual density (Ψ). Nevertheless, it can be seen that these density contributions do not form bonds within the crystal, but can be interpreted as electron lone pairs being localized within the unit cell. For better comparison, a corresponding structural section is shown in the lower part of Fig. 8. The lone pair electrons point exactly into the non-coordinated region of the tellurium(IV) atoms. Projections of the ELF density as well as an animation of the electron localization function for WTe₂O₇ obtained at HSESOL level is provided at the ESI.†

Fig. 8 (top) Calculated electron localization functions (ELF). (bottom) Corresponding structural section of WTe₂O₇. Residual electron density can be attributed to the lone pair electrons of Te⁴⁺ atoms.

In addition, the results of the infrared and Raman vibration calculations at the optimized geometries are shown in Fig. 9 and SI6.† While the overall shapes of both calculated infrared spectra are similar, the values of the GGA functional PBESOL seem to feature a shift compared to results generated by the more demanding hybrid functional HSESOL (see Fig. SI6,† top). A comparison between experimental and calculated IR spectrum on HSESOL level is depicted in Fig. 9. Again, the overall shape of the spectrum is comparable, but the calculated absorptions are shifted around 90 cm⁻¹ to lower wavenumbers. The observed shifts in the calculated vibrational wavenumbers are not uncommon and also occurred in spectral data of previously investigated systems.^58–60 Both Te atoms in WTe₂O₇ are bisphenoidal coordinated with two longer axial (ax = axial) and two shorter equatorial (eq = equatorial) bonded oxygen atoms forming [TeO₄]⁴⁻ units. A similar situation exists for α-TeO₂, where the stronger Te–O_eq vibrations have been assigned above 600 cm⁻¹, while the weaker Te–O_ax modes appear between 400 and 500 cm⁻¹.⁶¹ The free TeO₂ molecule with two Te=O double bonds (Te=O distance: 184 pm, ∡OTeO: 110°), which is close to the Te–O_2,eq geometry in the [TeO₄]⁴⁻ bisphenoidal units exhibit three normal vibrations at 849, 830 and 292 cm⁻¹.⁶² Therefore, the modes of the two different [TeO₄]⁴⁻ units in WTe₂O₇ can be assigned according to Te–O_eq: 750–880 cm⁻¹ and Te–O_ax: 520–750 cm⁻¹ (see Fig. 9) using the calculated IR spectrum (see Table SI6†). If one takes a closer look, such an assignment is not very meaningful in the case of the special structural situation in WTe₂O₇. The bisphenoidal [TeO₄]⁴⁻ units do not occur in isolation, but are linked via edges to form either chains or pairs in the crystal structure (see Fig. 4). This results in a highly asymmetric bridge Te–_axO_eq–Te and equatorial and axial vibrations are mutually dependent. The infrared spectra of known molybdenum tellurates(IV) are similar.²¹ MoTe₄O₁₁·KCl shows [Te₄O₉]²⁻ chains consisting of alternating [TeO₃]²⁻ trigonal pyramids and [TeO₄]⁴⁻ bisphenoidal units also causing strong bands in the range of 600–800 cm⁻¹, which were attributed to the antisymmetric stretching vibrations of the Te–O bonds. The bands occurring above 900 cm⁻¹ were assigned as antisymmetric stretches of the Mo–O bonds. An analogous assignment of the absorption bands for W–O can also be made here. An exact attribution of the absorption bands to the corresponding symmetric and antisymmetric stretching or bending modes is difficult in the solid state. Therefore, a list of all modes with their equivalent vibrational components derived from the calculated IR spectrum is given in Table SI6.† In addition, the calculated Raman spectrum obtained at PBESOL level is depicted in Fig. SI6† (bottom).

Fig. 9 Comparison of calculated and experimental IR spectrum of WTe₂O₇. The theoretical data are based on the HSESOL functional. A shift of the calculated data towards lower energies is visible.

III. Conclusions

WTe₂O₇ is the first compound in the ternary system W–Te–O and was synthesized via a multianvil high-pressure/high-temperature route. The crystal structure contains edge linked [W₂O₁₀]⁸⁻ octahedra, dimers of bisphenoidal coordinated [Te₂O₆]⁴⁻ units (◊ = ◊), and zweier edge-sharing chains of [Te₂O₄]⁰ units (… = ◊ = ◊ = …). The lone pair character of the two Te⁴⁺ sites was analyzed by ELF and high values appeared in nonbonding regions. A confirmation of the charge distribution according to W⁶⁺, Te⁴⁺, and O²⁻ was done by BLBS and CHARDI as well as experimentally by XPS analysis. Theoretical DFT calculations support the experimental data and band structure calculations indicate that WTe₂O₇ is a wide-band gap semiconducting material.

IV. Experimental section

IV. 1. Synthesis

Bulk material with embedded small single-crystals of WTe₂O₇ was synthesized via a high-pressure/high-temperature synthetic approach. The starting materials WO₃ (Alfa Aesar, Haverhill, USA, 99+%) and TeO₂ (TCI Chemicals, Tokio, Japan, 98+%) were weight in with a stochiometric ratio of 1 : 2 and homogenized in an agate mortar in air. The mixture was filled into a platinum capsule (99.95%, Ögussa, Vienna, Austria), inserted in a boron-nitride crucible (Henze Boron Nitride Products AG, Lauben, Germany) and placed in an 18/11 assembly (further details of the multianvil experiment are described elsewhere^19,63–65). The sample was compressed (1000 t multianvil press, Walker-type module (Max Voggenreiter GmbH, Mainleus, Germany)) to 10 GPa within 275 min, and held at this pressure until the heating phase was completed. For sample heating, the temperature was increased to 1273 K within 10 min, remained for another 15 min at this temperature, and cooled down to 673 K within 30 min. Subsequently, the sample was quenched to room temperature and decompressed within 825 min. Afterwards, it was mechanically separated from the surrounding assembly material. It appeared colourless, polycrystalline and was stable in air.

IV. 2. X-ray structure determination

X-ray powder diffraction analysis of WTe₂O₇ was carried out at ambient temperature using a Stoe Stadi P powder diffractometer in transmission geometry with the WinXPOW 3.07 software package.⁶⁶ Ge(111) monochromated Mo-K_α1 (λ = 70.93 pm) radiation was applied to the sample, mounted between two thin acetate foils with vacuum grease, and diffraction intensities were collected from a Mythen 2 DCS4 detector. The measurement was performed in the 2θ range of 2.0–77.5° with a step size of 0.015° and an exposure time of 30 s per step. Fig. 5 shows the Rietveld refinement plot performed with Diffrac^plus-Topas 4.2 (Bruker AXS, Karlsruhe, Germany). As starting model, the single-crystal structure reported here was used and the peak shapes were modeled using modified Thompson-Cox-Hastings pseudo-Voigt profiles.^67,68 Instrumental contributions on reflection profiles were corrected from the refinement of a LaB₆ standard.⁶⁹ The background was fitted with Chebychev polynomials up to the 12^th order.

Colorless single-crystals were isolated under a polarization microscope using perfluoropolyalkylether (viscosity 1800) and mounted on the tip of MicroMounts™ (MiTeGen, LLC, Ithaca, NY, USA) with a diameter of 30 μm. The intensity data were collected at 223(2) K on a Bruker D8 Quest single-crystal diffractometer (BRUKER, Billerica, USA) with Mo-K_α radiation (λ = 71.073 pm), Incoatec microfocus X-ray tube (Incoatec, Geesthacht, Germany), Photon 100 detector system and Apex3 program package.⁷⁰ The multi-scan absorption correction of the intensity data was performed with Sadabs 2016/2. Because of missing additional symmetry except inversion symmetry, P1̄ (no. 2) was considered and found to be correct for the structure solution and refinement process (SHELXTL-XT-2018/2). Full-matrix least-squares refinements against F² were carried out with Shelxl-2017/1.^71–73 All sites were refined with anisotropic displacement parameters and the refinement process finally led to values of 0.0187 and 0.0323 for R₁ and wR₂ (all data), respectively. A verification of the space group was done with the ADDSYM⁷⁴ routine of the PLATON program package.⁷⁵ In the case of refinement in space group P1, PLATON indicated additional inversion symmetry. Moreover, no weak superstructure reflections or possible diffuse scattering was observed on the diffraction patterns.

IV. 3. Energy-dispersive X-ray spectroscopy (EDX)

EDX investigations on several crystals of WTe₂O₇ were performed in a semiquantitative approach using a scanning electron microscope (JSM-6010LV, Jeol, Freising, Germany) with an energy-dispersive Quantax X-ray detector-system (Bruker AXS GmbH, Billerica, MA, USA) for element identification. The crystals were placed on a carbon platelet on an aluminium sample carrier and sputtered with carbon. Three crystals and several measurement points on each were analyzed for 60 s at an excitation energy of 15 kV in high vacuum regarding to their W to Te ratio. All values were arithmetically averaged. Due to the preparation method and the low sensitivity of light atoms like oxygen next to tellurium and tungsten, only the ratio of the heavy atom was considered, and the absolute values are neglected. The measured ratio of W/Te = 14 ± 2 at% W/31 ± 2 at% Te agrees well with the theoretical ratio of W/Te = 1 : 2 in WTe₂O₇.

IV.4. X-ray photoelectron spectroscopy (XPS)

For XPS measurements, bulky WTe₂O₇ was placed on an adhesive copper foil. Measurements were performed in a multi-chamber UHV system at a pressure of 5 × 10⁻¹⁰ mbar using a Phoibos 100 hemispherical analyzer (Specs). A Mg-K_α anode was used as an excitation source (h × ν = 1252.6 eV, probing depth ∼10 nm).

Due to charging effects during the measurement caused by the low conductivity of the powder sample, the binding energy scale as measured by XPS was shifted to higher values by a few eV. To account for this, the binding energies were corrected in a way that the O 1s energy level is positioned at 530.7 eV. This value was chosen by a careful evaluation of the O 1s binding energy values within WO₃ and TeO₂, which are in the range of 530.30 eV and 530.8 eV for the first, and 530.1 eV to 530.7 eV for the latter (data taken from NIST X-ray Photoelectron Spectroscopy Database,⁷⁶ and from the following publications.^45–57

IV.5. Infrared spectroscopy

Infrared spectra were recorded from powdered samples of WTe₂O₇ in the spectral range of 400–4000 cm⁻¹ using a Bruker Alpha Platinum FTIR-ATR spectrometer (Bruker, Billerica, USA) equipped with a 2 × 2 mm diamond ATR-crystal. A DTGS detector collected the intensity during 24 scans and atmospheric influences were corrected via a reference measurement using the Opus 7.2 software.⁷⁷

IV.6. Quantum chemical calculations, ELF

All DFT calculations of the tungsten tellurate WTe₂O₇ have been carried out using Crystal17 ⁷⁸ employing the dedicated solid-state functionals PBESOL⁷⁹ and HSESOL⁸⁰ in conjunction with the W_cora_1996 ⁸¹ the Te_m-pVDZ-PP_Heyd_2005 ⁸² basis and the O_8-411d11f_mahmoud_2013 ⁸³ basis set for tungsten, tellurium and oxygen, respectively. The convergence criteria for energy and forces were set to 10⁻⁸ Hartree and 4.5 × 10⁻⁴ Hartree bohr⁻¹. In order to ensure the viability of the treatment, Brillouin-zone sampling employing a shrinking factor of 8 was employed. To compare the structures determined by experimental method and theoretical calculation, powder-diffraction patterns of the DFT optimized structures were generated using RIETAN-FP⁸⁴ included in the VESTA program.⁸⁵ To assess the ionic character of the compound, partial charges have been calculated employing a Hirshfeld population analysis⁸⁶ as implemented in Crystal17.

In addition, band structure and density of states (DOS) calculations have been carried out at the optimized geometries using Crystal17. As the tungsten tellurate features residual electron density located near the Te⁴⁺ atom (“lone pair”), electron localization functions (ELFs) have been calculated via the Multiwfn program⁸⁷ and were visualized using VMD.⁸⁸

Infrared and Raman spectra at the optimized geometries have been determined via the harmonic approximation.⁸⁹ As Crystal17 does not support calculations employing coupled-perturbed Hartree–Fock/Kohn–Sham equations in conjunction with range-separated hybrid functionals such as HSESOL, the Raman intensities were only calculated using the PBSESOL functional. A weighted kernel density estimation using a Gaussian kernel was applied to the line spectra for better comparison with the experimental results.⁹⁰

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Martina Tribus for collecting the EDX data and Markus Rödl for measuring the UV/Vis spectrum. Further, we acknowledge H. Huppertz for continuous support and usage of all the facilities of the Institute of General, Inorganic and Theoretical Chemistry, University of Innsbruck.

References

1. J. Zemann, Monatsh. Chem., 1971, 102, 1209–1216.
2. A. V. Marukhnov, D. V. Pushkin and V. N. Serezhkin, Russ. J. Inorg. Chem., 2007, 52, 203–208.
3. A. G. Christy, S. J. Mills and A. R. Kampf, Mineral. Mag., 2016, 80, 415–545.
4. K. M. Ok, E. O. Chi and P. S. Halasyamani, Chem. Soc. Rev., 2006, 35, 710–717.
5. E. O. Chi, K. M. Ok, Y. Porter and P. S. Halasyamani, Chem. Mater., 2006, 18, 2070–2074.
6. B. Vidyavathy and K. Vidyasagar, Inorg. Chem., 1999, 38, 1394–1400.
7. P. S. Halasyamani and W. Zhang, Inorg. Chem., 2017, 56, 12077–12085.
8. C. T. Prewitt and R. T. Downs, Rev. Mineral. Geochem., 1998, 37, 283–317.
9. H. Huppertz, Chem. Commun., 2011, 47, 131–140.
10. P. F. McMillan, Chem. Commun., 2003, 919–923,  10.1039/B300963G.
11. P. F. McMillan, Chem. Soc. Rev., 2006, 35, 855–857.
12. G. Demazeau, H. Huppertz, J. A. Alonso, R. Pöttgen, E. Moran and J. P. Attfield, Z. Naturforsch., B: Chem. Sci., 2006, 61, 1457–1470.
13. U. Schwarz, R. Giedigkeit, R. Niewa, M. Schmidt, W. Schnelle, R. Cardoso, M. Hanfland, Z. Hu, K. Klementiev and Y. Grin, Z. Anorg. Allg. Chem., 2001, 627, 2249–2256.
14. A. Haberer, G. Heymann and H. Huppertz, J. Solid State Chem., 2007, 180, 1595–1600.
15. H. Huppertz and B. von der Eltz, J. Am. Chem. Soc., 2002, 124, 9376–9377.
16. H. Huppertz, S. Altmannshofer and G. Heymann, J. Solid State Chem., 2003, 170, 320–329.
17. E. Selb, L. Declara, L. Bayarjargal, M. Podewitz, M. Tribus and G. Heymann, Eur. J. Inorg. Chem., 2019, 2019, 4668–4676.
18. R. Ziegler, M. Tribus, C. Hejny and G. Heymann, Crystals, 2021, 11, 1554.
19. E. Selb, T. Buttlar, O. Janka, M. Tribus, S. G. Ebbinghaus and G. Heymann, J. Mater. Chem. C, 2021, 9, 5486–5496.
20. S. Vallar and M. Goreaud, J. Solid State Chem., 1997, 129, 303–307.
21. J. Ling, H. Zhang, K. Yuan, D. Burgess, J. Hu and M. Hu, J. Solid State Chem., 2020, 287, 121317.
22. N. Nunotani, S. Tamura and N. Imanaka, Eur. J. Inorg. Chem., 2013, 2013, 4300–4304.
23. H. Hartmann, F. Ebert and O. Bretschneider, Z. Anorg. Allg. Chem., 1931, 198, 116–140.
24. H.-S. Ra, K. M. Ok and P. S. Halasyamani, J. Am. Chem. Soc., 2003, 125, 7764–7765.
25. M. Kunz and I. D. Brown, J. Solid State Chem., 1995, 115, 395–406.
26. P. M. Woodward, A. W. Sleight and T. Vogt, J. Phys. Chem. Solids, 1995, 56, 1305–1315.
27. M. M. Dobson and R. J. D. Tilley, Acta Crystallogr., Sect. B: Struct. Sci., 1988, 44, 474–480.
28. CSD Crystallographic Database, FIZ Karlsruhe GmbH, ICSD Web version 4.7.1, data release 2021.2.
29. F. Liebau, Structural Chemistry of Silicates, Springer Verlag, Berlin, Heidelberg, 1st edn, 1985.
30. C. Olsson, L.-G. Johansson and S. Kazikowski, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1988, 44, 427–429.
31. Y. Porter and P. S. Halasyamani, Inorg. Chem., 2003, 42, 205–209.
32. S.-C. Chou, P. Höss, P. L. Russ, S. Strobel and T. Schleid, Z. Anorg. Allg. Chem., 2021, 647, 134–150.
33. N. W. Alcock, in Advances in Inorganic Chemistry and Radiochemistry, ed. H. J. Emeléus and A. G. Sharpe, Academic Press, 1972, vol. 15, pp. 1–58.
34. A. F. Cozzolino, P. J. W. Elder and I. Vargas-Baca, Coord. Chem. Rev., 2011, 255, 1426–1438.
35. L. Vogel, P. Wonner and S. M. Huber, Angew. Chem., Int. Ed., 2019, 58, 1880–1891.
36. N. E. Brese and M. O'Keeffe, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 192–197.
37. I. D. Brown and D. Altermatt, Acta Crystallogr., Sect. B: Struct. Sci., 1985, 41, 244–247.
38. S. J. Mills and A. G. Christy, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2013, 69, 145–149.
39. R. Hoppe, S. Voigt, H. Glaum, J. Kissel, H. P. Müller and K. Bernet, J. Less-Common Met., 1989, 156, 105–122.
40. R. Hoppe, Angew. Chem., Int. Ed. Engl., 1966, 5, 95–106.
41. R. Hoppe, Angew. Chem., Int. Ed. Engl., 1970, 9, 25–34.
42. R. Hübenthal, MAPLE, Universität Gießen.
43. Y. Xu, S. Carlson and R. Norrestam, J. Solid State Chem., 1997, 132, 123–130.
44. T. G. Worlton and R. A. Beyerlein, Phys. Rev. B: Condens. Matter, 1975, 12, 1899–1907.
45. B. V. R. Chowdari and P. Pramoda Kumari, J. Non-Cryst. Solids, 1996, 197, 31–40.
46. T. S. Sun, S. P. Buchner and N. E. Byer, J. Vac. Sci. Technol., 1980, 17, 1067–1073.
47. Y. A. Teterin, V. I. Nefedov, M. F. Churbanov, A. Y. Teterin, K. I. Maslakov and E. V. Zorin, Inorg. Mater., 2007, 43, 888–896.
48. H. Kong, J.-B. Yeo and H.-Y. Lee, J. Korean Phys. Soc., 2015, 66, 1744–1749.
49. A. B. Christie, I. Sutherland and J. M. Walls, Surf. Sci., 1983, 135, 225–242.
50. F. Garbassi, J. C. J. Bart and G. Petrini, J. Electron Spectrosc. Relat. Phenom., 1981, 22, 95–107.
51. M. F. Al-Kuhaili, S. M. A. Durrani, E. E. Khawaja and J. Shirokoff, J. Phys. D: Appl. Phys., 2002, 35, 910–915.
52. O. Y. Khyzhun, Y. M. Solonin and V. D. Dobrovolsky, J. Alloys Compd., 2001, 320, 1–6.
53. R. J. Colton, A. M. Guzman and J. W. Rabalais, J. Appl. Phys., 1978, 49, 409–416.
54. A. Marin, C. P. Lungu and C. Porosnicu, J. Vac. Sci. Technol., A, 2017, 35, 021403.
55. P. J. C. Chappell, M. H. Kibel and B. G. Baker, J. Catal., 1988, 110, 139–149.
56. V. I. Nefedov, Y. V. Salyn, G. Leonhardt and R. Scheibe, J. Electron Spectrosc. Relat. Phenom., 1977, 10, 121–124.
57. D. D. Sarma and C. N. R. Rao, J. Electron Spectrosc. Relat. Phenom., 1980, 20, 25–45.
58. E. Hinteregger, G. Heymann, T. S. Hofer and H. Huppertz, Z. Naturforsch., B: Chem. Sci., 2012, 67b, 605–613.
59. E. Hinteregger, T. S. Hofer, G. Heymann, L. Perfler, F. Kraus and H. Huppertz, Chem. – Eur. J., 2013, 19, 15985–15992.
60. E. Hinteregger, K. Kocsis, T. S. Hofer, G. Heymann, L. Perfler and H. Huppertz, Z. Naturforsch., B: J. Chem. Sci., 2013, 68, 951–959.
61. A. P. Mirgorodsky, T. Merle-Méjean, J. C. Champarnaud, P. Thomas and B. Frit, J. Phys. Chem. Solids, 2000, 61, 501–509.
62. M. Spoliti, V. Grosso and S. N. Cesaro, J. Mol. Struct., 1974, 21, 7–15.
63. H. Huppertz, Z. Kristallogr., 2004, 219, 330–338.
64. D. Walker, M. A. Carpenter and C. M. Hitch, Am. Mineral., 1990, 75, 1020–1028.
65. D. Walker, Am. Mineral., 1991, 76, 1092–1100.
66. WinXPOW Powder Diffraction Software, STOE & CIE GmbH.
67. P. Thompson, D. E. Cox and J. B. Hastings, J. Appl. Crystallogr., 1987, 20, 79–83.
68. R. A. Young and P. Desai, Arch. Nauki Mater., 1989, 10, 71–90.
69. M. C. Morris, H. F. McMurdie, E. H. Evans, B. Paretzkin, H. S. Parker and N. P. Pyrros, NBS Monogr. (U. S.), 1984, 25, 62.
70. APEX3 (v. 2017.3-0), CELL_NOW (v. 2008/4), SAINT (v. 8.38A), TWINABS (v. 2012/1), and SADABS (v. 2016/2), Bruker AXS GmbH, Karlsruhe (Germany).
71. G. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2015, 71, 3–8.
72. G. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
73. G. M. Sheldrick, ShelXL – Crystal Structure Refinement – Multi-CPU Version, University of Göttingen.
74. Y. Le Page, J. Appl. Crystallogr., 1988, 21, 983–984.
75. A. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155.
76. A. V. Naumkin, A. Kraut-Vass, S. W. Gaarenstroom and C. J. Powell, NIST Standard Reference Database Number 20, National Institute of Standards and Technology, Gaithersburg MD, 20899, 2000, NIST X-ray Photoelectron Spectroscopy Database, (retrieved: 18.08.2022).
77. OPUS (v 7.2), Bruker AXS GmbH.
78. R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360.
79. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
80. L. Schimka, J. Harl and G. Kresse, J. Chem. Phys., 2011, 134, 024116.
81. F. Corà, A. Patel, N. M. Harrison, R. Dovesi and C. R. A. Catlow, J. Am. Chem. Soc., 1996, 118, 12174–12182.
82. J. Heyd, J. E. Peralta, G. E. Scuseria and R. L. Martin, J. Chem. Phys., 2005, 123, 174101.
83. A. Mahmoud, A. Erba, K. E. El-Kelany, M. Rérat and R. Orlando, Phys. Rev. B: Condens. Matter, 2014, 89, 045103.
84. F. Izumi and K. Momma, Solid State Phenom., 2007, 130, 15–20.
85. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
86. F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138.
87. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
88. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
89. Y. Ozaki, K. B. Beć, Y. Morisawa, S. Yamamoto, I. Tanabe, C. W. Huck and T. S. Hofer, Chem. Soc. Rev., 2021, 50, 10917–10954.
90. M. A. Wolters and W. J. Braun, Statistics, 2018, 7, e202.

---

Footnote

† Electronic supplementary information (ESI) available. CSD 2212710. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2dt03419k

---