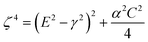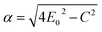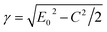Open Access Article
Open Access ArticleTackling data scarcity with transfer learning: a case study of thickness characterization from optical spectra of perovskite thin films†
Siyu Isaac Parker
Tian‡
 ab,
Zekun
Ren§
ab,
Selvaraj
Venkataraj
b,
Yuanhang
Cheng¶
b,
Daniil
Bash
ab,
Zekun
Ren§
ab,
Selvaraj
Venkataraj
b,
Yuanhang
Cheng¶
b,
Daniil
Bash
 c,
Felipe
Oviedo||
d,
J.
Senthilnath
e,
Vijila
Chellappan
c,
Felipe
Oviedo||
d,
J.
Senthilnath
e,
Vijila
Chellappan
 c,
Yee-Fun
Lim
cf,
Armin G.
Aberle
c,
Yee-Fun
Lim
cf,
Armin G.
Aberle
 b,
Benjamin P.
MacLeod
g,
Fraser G. L.
Parlane
g,
Curtis P.
Berlinguette
b,
Benjamin P.
MacLeod
g,
Fraser G. L.
Parlane
g,
Curtis P.
Berlinguette
 g,
Qianxiao
Li
g,
Qianxiao
Li
 h,
Tonio
Buonassisi
*ad and
Zhe
Liu**
ad
h,
Tonio
Buonassisi
*ad and
Zhe
Liu**
ad
aLow Energy Electronic Systems (LEES), Singapore-MIT Alliance for Research and Technology (SMART), 1 Create Way, Singapore 138602, Singapore. E-mail: zhe.liu@nwpu.edu.cn; buonassi@mit.edu
bSolar Energy Research Institute of Singapore (SERIS), National University of Singapore, 7 Engineering Drive, Singapore 117574, Singapore
cInstitute of Materials Research and Engineering (IMRE), Agency for Science, Technology and Research (A*STAR), 2 Fusionopolis Way, Singapore 138634, Singapore
dDepartment of Mechanical Engineering, Massachusetts Institute of Technology (MIT), 77 Massachusetts Ave., Cambridge, MA 02139, USA
eInstitute for Infocomm Research (I2R), Agency for Science, Technology and Research (A*STAR), 1 Fusionopolis Way, Singapore 138632, Singapore
fInstitute of Sustainability for Chemicals, Energy and Environment, Agency for Science, Technology and Research (A*STAR), 1 Pesek Rd, Singapore 627833, Singapore
gDepartment of Chemistry, The University of British Columbia (UBC), 2036 Main Mall, Vancouver, BC V6T 1Z1, Canada
hDepartment of Mathematics, National University of Singapore (NUS), 21 Lower Kent Ridge Rd, Singapore 119077, Singapore
First published on 13th July 2023
Abstract
Transfer learning (TL) increasingly becomes an important tool in handling data scarcity, especially when applying machine learning (ML) to novel materials science problems. In autonomous workflows to optimize optoelectronic thin films, high-throughput thickness characterization is often required as a downstream process. To surmount data scarcity and enable high-throughput thickness characterization, we propose a transfer learning workflow centering an ML model called thicknessML that predicts thickness from UV-Vis spectrophotometry. We demonstrate the transfer learning workflow from a generic source domain (of materials with various bandgaps) to a specific target domain (of perovskite materials), where the target-domain data are from just 18 refractive indices from the literature. While featuring perovskite materials in this study, the target domain easily extends to other material classes with a few corresponding literature refractive indices. With accuracy defined as being within-10%, the accuracy rate of perovskite thickness prediction reaches 92.2 ± 3.6% (mean ± standard deviation) with TL compared to 81.8 ± 11.7% without. As an experimental validation, thicknessML with TL yields a 10.5% mean absolute percentage error (MAPE) for six deposited perovskite films.
1 Introduction
The recent advances in robotic automation in research laboratories have enabled autonomous high-throughput experimentation (HTE) workflows for synthesis, screening, and optimization of new materials.1–10 These HTE workflows can generate new materials in thin-film form at a record rate (e.g., a few minutes per sample),11–13 and therefore downstream materials characterization and data analysis must match the elevated throughput. To accelerate data analysis and knowledge extraction in HTE, ML algorithms are used together with rapid characterization techniques.14–20 For materials in thin-film form, film thickness is among the most essential and yet challenging parameters to measure in a high-throughput non-destructive manner.21–26The state-of-the-art characterization method is optical spectroscopy. However, despite its rapid measurement, optical spectroscopy requires a manual fitting of optical models (a parametric description of the material's wavelength-resolved refractive indices) to obtain thickness. This manual fitting for a new material is slow ranging from a few tens of minutes to hours per sample, and it usually requires much experience on top of trial and error. The refractive indices of different material classes fall into different distributions (domains), reflected by different numbers and types of optical models typically used. For each specific domain (material class), especially newly developed materials such as lead-halide perovskites, readily available refractive-index data are few. This data scarcity poses difficulty to replacing the manual model fitting with the high-throughput ML model across domains (material classes).
To counter the data scarcity prevalent in many materials science applications, the use of transfer learning is gradually rising nowadays. Notable examples lie heavily in materials property prediction, where the learning transfers across properties,27–32 across modes of observation, e.g., from calculated properties to experimental ones,27,30 and across different materials systems,31e.g., from inorganic materials to organic polymers,30 or from alloys to high-entropy alloys.32 Following the same rationale, thin film thickness characterization also presents itself as a suitable field for transfer learning to overcome data scarcity across material classes.
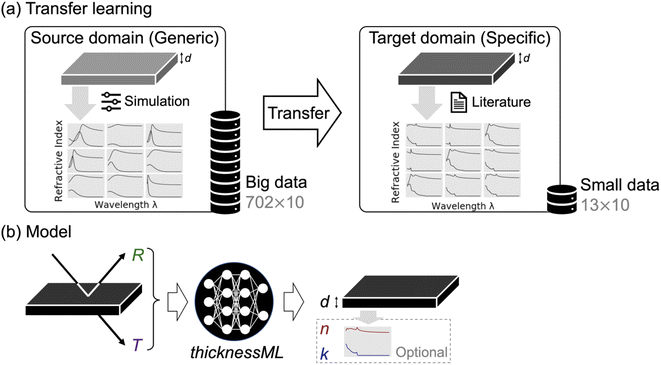
To demonstrate high-throughput thickness characterization with ML across material classes, we propose in this work the following high-throughput transfer learning workflow (Fig. 1) to automatically characterize thickness, i.e., predict film thickness from optical spectra. Without loss of generality, we select lead-halide perovskites as our ultimate material class (target domain) for prediction. Lead-halide perovskites are a family of ABX3 semiconductors with excellent optoelectronic properties, e.g., for photovoltaics, light-emitting diodes, and photodetectors. To ultimately predict thickness for perovskite films, the workflow relies on a transfer learning from the source domain (once-off pre-training) to the target domain (retraining for every individual target domain) as shown in Fig. 1a. The source domain contains generic semiconductor refractive indices; we parametrically simulate 702 refractive indices from a single optical model (Tauc–Lorentz) commonly used for optical materials with an absorption bandgap. We then simulate the optical reflectance/transmittance with 10 thicknesses for every refractive index, constructing a training dataset of 702 × 10. The source domain is “big data”. The target domain contains 13 perovskite semiconductor refractive indices that are experimentally fitted found in the literature. We then repeat the optical reflectance/transmittance simulation with 10 thicknesses per refractive index, obtaining a training dataset of 13 × 10. The target domain is “small data”. Note that the source domain has over 50 times more training data than the target domain. In practice, this chosen perovskite target domain represents the typical data-scarce bottleneck of newly developed materials. This transfer learning workflow enables the target domain to easily extend to other data-scarce material classes with a few literature refractive indices of that material class.
Transfer learning entails two stages of training—(I) once-off pre-training on the source domain and (II) once-every-target-domain retraining. Each training stage features the same model named thicknessML. thicknessML takes optical reflection (R) and transmission (T) spectra as input and outputs thickness (d) and optionally wavelength-resolved refractive indices as shown in Fig. 1b. We denote the real and imaginary parts of refractive indices as n and k respectively.
With the two-stage transfer learning, thicknessML predicts the perovskite film thickness with a mean absolute percentage error (MAPE) of 4.6 ± 0.5% compared to a MAPE of 7.4 ± 4.2% from direct learning (no transfer learning). When validated on six experimentally deposited methylammonium lead iodide (MAPbI3) perovskite films, thicknessML achieves 10.5% MAPE from retraining on only eight most dissimilar literature refractive indices whose perovskite compositions contain no methylammonium.
2 Results and discussion
2.1 Preparation of source and target datasets
For ML datasets, the inputs are wavelength-resolved optical spectra of reflection and transmission. Denoting the wavelength as λ, the optical spectra are respectively R(λ) and T(λ) for reflection and transmission. The outputs (or labels in supervised ML terminology) are thickness d, and optionally wavelength-resolved refractive indices n(λ) and k(λ). The refractive index is complex, and n and k denote the real and imaginary parts respectively, namely ñ(λ) = n(λ) + ik(λ). In physics, the order is inversed, where thickness d (an extensive property of a material) and the refractive index (an intensive property of a material) are inputs, and the optical spectra are outputs (an optical response given by a material film). Therefore, the ML model in essence needs to learn the inverse of the physical optical response. Note that the to-be-learnt physical response is universal for all materials (across material classes). The source/target domains (material classes) only appear due to different underlying distributions of an output (label), namely the refractive index. The different refractive index distributions are a manifestation of the different underlying governing parametric optical models in different material classes.To facilitate transfer learning, we build the source dataset to be generic; practically, we simulate refractive indices with the Tauc–Lorentz (TL) optical model, universal for materials with a band gap. The simulation of refractive indices is analogous to the simulation of materials (possessing the simulated refractive index). Paired with different thicknesses, a set of simulated n, k spectra (a simulated material) can yield the respective optical R, T spectra. This is analogous to measuring the optical response of a batch of thin films (different thicknesses) made of the same material (the same simulated refractive index spectra). The optical response is simulated by the physical transfer-matrix method (TMM). Without loss of generality, we adopt 0° incident angle and a 1 mm glass substrate in the TMM simulations.
In the source dataset, we simulate 1116 n(λ), k(λ) spectra by sampling a grid of parameter values (for A, C, E0, and Eg, with a fixed ε∞ = 1) of a single TL optical model with λ ranging from 350 to 1000 nm. The λ range was chosen to be a common subset of frequent ranges in UV-Vis measurements and reported literature. The 1116 n, k spectra of the source dataset are divided into 702, 302, and 112 for the training, the validation and the test set respectively. Then we randomly choose 10 thicknesses per pair of n, k spectra (per simulated material) in the training and the validation set, and 50 thicknesses per n, k spectra in the test set to obtain the corresponding R, T spectra. The larger number of d per pair of n, k spectra in the test set gives a more stringent and thus reliable evaluation of how well thicknessML performs. The range of d is 10–2010 nm. Three different training-validation-test splits are performed for three ensemble runs, and the randomly selected thicknesses for the same n, k spectra differ in the three splits.
In the target dataset, we obtain 18 perovskite n(λ), k(λ) spectra from the literature.33–37 The 18 n, k spectra of the target dataset are divided into 13 and 5 for the training and the test set. The validation set is not used in the target dataset due to data scarcity. We follow the same convention and simulate the corresponding R, T spectra with the number of d per n, k spectra of 10 and 50 respectively in the training and the test set. To compare with direct learning (no transfer), we also build a dataset for direct learning by assigning 500 d per n, k spectra for training while maintaining the 50 d per n, k spectra for test. The extremely large number of assigned d per n, k spectra is to compensate for the small number of n, k spectra available, ensuring enough training data in learning from scratch. Five training-test splits are performed for ensemble runs. To study transfer learning with varying data quantities, we also build training-test splits with increasing numbers of training n, k spectra from 0 to 17, with the corresponding rest (18 – number of training n, k spectra) in the test set. In these datasets, we preserve the number of d per n, k spectra in the training (10) and the test set (50) as well as the five training-test splits. To prepare for the experimental validation on six deposited MAPbI3 films, we build the target training dataset by selecting the more distinct perovskite materials (not containing methylammonium) out of the 18 literature materials. We follow the number of d per n, k spectra in the training as well as the five training-test splits. We capture the details of the datasets in Table 1.
| Source dataset | |||
|---|---|---|---|
| Training set | Validation set | Test set | |
| Number of n, k spectra | 702 | 302 | 112 |
| Number of d per n, k spectra | 10 | 10 | 50 |
| Resulting number of R, T spectra | 702 × 10 | 302 × 10 | 112 × 50 |
| Target dataset | ||
|---|---|---|
| Training set | Test set | |
| Transfer learning vs. direct learning | ||
| Number of n, k spectra | 13 | 5 |
| Number of d per n, k spectra | 10 (500 for direct learning) | 50 |
| Resulting number of R, T spectra | 13 × 10 (13 × 500 for direct learning) | 5 × 50 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| Transfer learning with varying training data quantities | ||
| Number of n, k spectra | X (0 ≤ X ≤ 17) | 18 − X |
| Number of d per n, k spectra | 10 | 50 |
| Resulting number of R, T spectra | 10X | (18 − X) × 50 |
| Training set | |
|---|---|
| Experimental validation | |
| Number of n, k spectra | 8 (not containing methylammonium) |
| Number of d per n, k spectra | 10 |
| Resulting number of R, T spectra | 8 × 10 |
3 Model: thicknessML
The whole framework of the thickness-predicting model thicknessML is shown in Fig. 2. For thicknessML, we propose a convolutional neural network (CNN) architecture.38–40 CNNs are originally developed for image processing and can capture local spatial information (neighboring pixels) as well as correlation among channels, such as RGB as channels. We used a CNN here to capture R and T segments at adjacent wavelengths and thus capture some spatial features like hills and valleys of R(λ) and T(λ), which are closely related to thickness d. We concatenated R and T channel-wise to capture the correlation.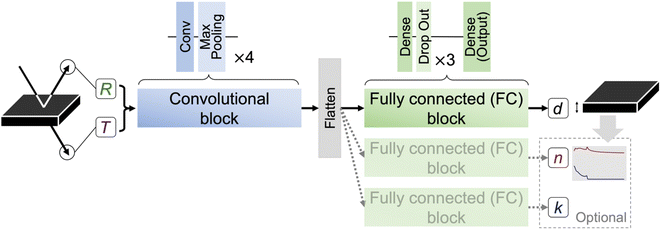 | ||
| Fig. 2 thicknessML framework: thicknessML receives the R(λ) and T(λ) spectra and outputs d (and n(λ), k(λ)) for single task learning (multitask learning). Input R and T spectra first go through four convolutional and max pooling layers for feature extractions and then get flattened to be passed to three fully connected (FC, also “Dense” in Keras43 terminology) and dropout layers, where mappings from extracted features to task targets are drawn. The three dedicated FC blocks for d, n(λ), and k(λ) correspond to MTL implementation. STL implementation has the same architecture without the two FC blocks for n(λ) and k(λ). (The adopted incident angle in UV-Vis is 0°. The inclined beams are drawn to achieve better visual clarity.) The detailed hyperparameters are recorded in Section S1 thicknessML hyperparameters in the ESI.† | ||
Aside from a straightforward RT-to-d architecture, we also explore a multitask learning (MTL) architecture, where n(λ) and k(λ) are additional outputs with d. This is inspired from physics where the determination of d (from R and T) is closely related to the concurrent determination of n and k. Therefore, we reflect such concurrent determinations with MTL, concurrent learning of multiple tasks. In MTL, if the tasks are related, the model benefits from concurrent learning to be more accurate and is less likely to overfit to a specific task (in other words, the learning is more generalized).41,42 As a result, we concurrently learn to predict d as our main task, and n, k as auxiliary tasks in our MTL implementation. The straightforward RT-to-d architecture, framed in a compatible language, becomes single task learning (STL).
In this study, we use the term “thicknessML” to refer to both the ML model per se and the encompassing framework (including the UV-Vis operation) depending on context.
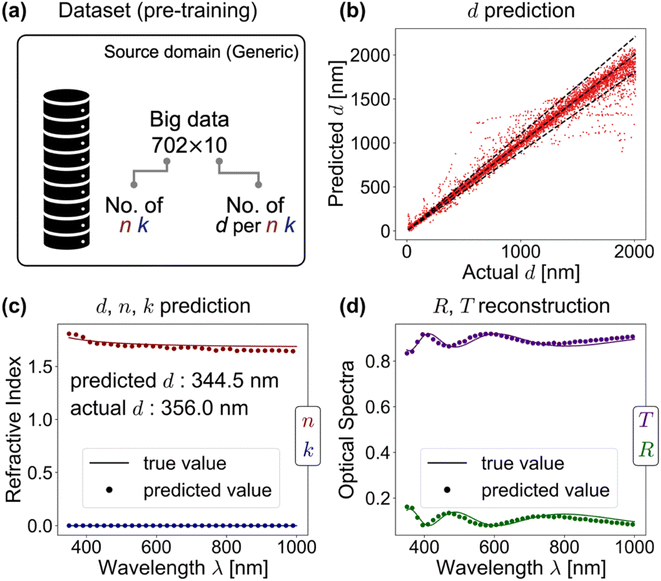
3.1 Stage I: pre-training on the generic source dataset
We tabulate the pre-training performance of thicknessML (STL and MTL) in Table 2 and give some visual performance of thicknessML-MTL in Fig. 3. For d prediction, STL achieves 89.2% accuracy (5.0% MAPE) and MTL 83.3% accuracy (8.0% MAPE). We consider a prediction “accurate” if the prediction deviates less than 10% from the actual value, and the accuracy (%) records the prediction accuracy ratio (what is the proportion of accurate predictions). The choice of defining such an accuracy follows that we intuitively give a larger tolerance of inaccuracy (deviation) to thicker films as the relative error stays small. The performances in Table 2 are averaged across three ensemble runs (three data splits). We observe that STL slightly is better than MTL, which contradicts that MTL promotes more generalized learning and better accuracy. To understand this result, we look at the trade-off between a generalized learning and a task-specific learning: a generalized learning is less likely to overfit and thus may improve performance; however, compared to a task-specific learning, a generalized learning may have worse performance by scattering learning capacity across various tasks (thus losing focus on the intended main task). We believe that thicknessML-MTL in the pre-training has a slightly worse performance due to scattered learning capacity. Further improvements may be gained by a more focused learning on d prediction in the MTL setting, realized by increasing the proportion of d-prediction loss in the overall loss function. For n and k predictions in MTL, accuracies reach 94.2% and 26.8% respectively. Here we expand the accuracy definition to within-10%-deviation quantified across wavelengths on average because n and k are wavelength-resolved. We note the relatively poor performance of k prediction, and we attribute it to several reasons:| d (<10% deviation) | n (<10% deviation) | k (<10% deviation) | |
|---|---|---|---|
| STL | 89.2% | ||
| MTL | 83.3% | 94.2% | 26.8% |
• Many k values on larger wavelengths are near or at zero, e.g., on the magnitude of 10−2. This makes the percentage-based within-10%-deviation accuracy definition unduly stringent. A different choice of absolute-error-based accuracy definition may reflect the k prediction performance more appropriately.
• The many near-zero and at-zero k values bias the output data distribution unfavorably.
• The prediction of wavelength-resolved values is naturally harder than the prediction of a scalar value.
We acknowledge the k prediction limitation of thicknessML-MTL and caution potential users to place more confidence in the d prediction than the n, k prediction when using thicknessML in the MTL setting. Overall, we recommend potential users to use thicknessML in the STL setting for better performance.
Fig. 3 offers some visual performance of thicknessML-MTL: (1) (a) d prediction is considered accurate if it falls between the two side diagonal lines denoting 10% deviation from perfect prediction (predicted value = actual value) as shown in Fig. 3b. (2) An example of thicknessML-MTL outputting predicted d, n, and k is shown in Fig. 3c; and the optical response R and T can be reconstructed from the predicted d, n, and k to compare with the actual values as shown in Fig. 3d.
3.2 Stage II: transfer learning to the perovskite target dataset
Transfer learning takes the pre-trained model (a warm start from the pre-trained weights instead of random initialization) and let weights continue to train partially or fully on a new dataset (retraining). Through the pre-trained model weights, transfer learning44 allows knowledge learnt in the pre-trained task to be transferred to a related new task with much less data and training. In our case, the pre-trained weights carry the knowledge of an inverse mapping of TMM, from R, and T to d, n, and k, and the retraining further adapts the mapping to a dataset comprising perovskite materials whose underlying oscillator models are specific.We propose and run two types of transfer learning: (1) full-weight retraining, to continue updating the weights of both convolutional and FC blocks, and (2) partial-weight retraining, to freeze the weights of the convolutional block (unchanged feature extraction), while updating the FC block. To provide a baseline, we also implement a case of direct learning/training from scratch (from random initialized weights as in pre-training). We first validate the use of transfer learning by comparing against direct learning as shown in Table 3 and Fig. 4b. In this transfer learning vs. direct learning comparison, we use different datasets—for transfer learning, we split the 18 literature n, k spectra into 13 and 5 for training and test (paired with 10 and 50 d per n, k spectra respectively); for direct learning, we preserve the same n, k spectra split (13–5) but pair with 500 and 50 d per n, k spectra respectively for training and test. The details of the datasets are described in Table 1 and the section preparation of source and target datasets. Transfer learning achieves better accuracy (higher mean) and precision (smaller spread) than direct learning regardless of MTL or STL. Within transfer learning, full-weight retraining of the STL setting has the highest performance. We observe that although certain individual runs of direct learning can surpass the transfer learning performance, direct learning is largely affected by specific training-test splits (certain runs having extremely low performance). We point out that the current comparison is based on a 50 times difference in the training data size between transfer learning and direct learning. To conclude, we justify the use of transfer learning (better performance achieved with less data).
| Transfer learning | Direct learning | ||
|---|---|---|---|
| Full-weight retraining | Partial-weight retraining | ||
| a This is the proportion of accurate d predictions, where accuracy is defined as within 10% deviation. | |||
| d accuracya | 92.2 ± 3.6% (STL) | 90.0 ± 2.9% (STL) | 76.9 ± 23.7 (STL) |
| d MAPE | 4.6 ± 0.5% (STL) | 4.9 ± 0.6% (STL) | 10.0 ± 9.6% (STL) |
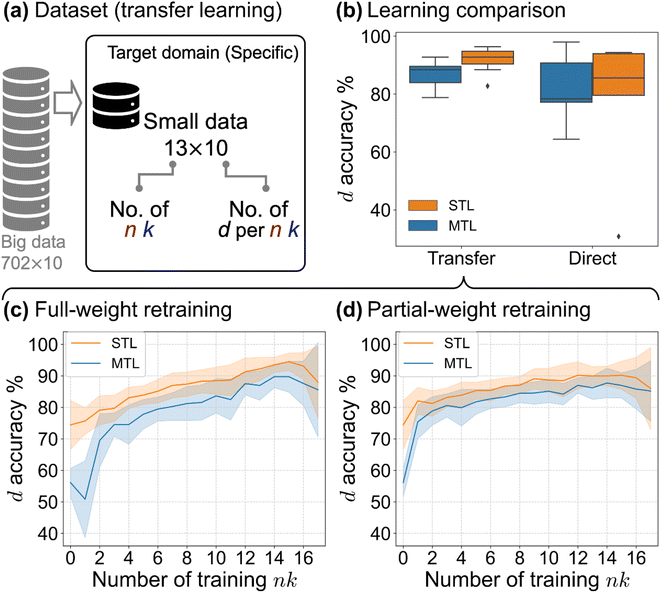 | ||
| Fig. 4 Transfer learning performance of thicknessML. (a) The transfer learning dataset, showing the size of training data. (b) Transfer learning vs. direct learning on predicted d accuracy (%, evaluated on the test set) shown in a box plot: the box plot records the d accuracies of each model in the ensemble runs (3 pre-trained models × 5 data splits). This transfer learning is full-weight retraining due to its better performance. The retraining data are as described in (a). (Table 1 records the dataset in more detail.) To study transfer learning with varying data quantities, we record d accuracy vs. the number of training n, k spectra (out of a total of 18) of (c) full-weight retraining and (d) partial-weight retraining. Solid lines and spreads denote the mean and standard deviation of the performance (d accuracy) from the 3 × 5 ensemble runs. | ||
To consider whether the 13–5 training-test split of the n, k spectra yields reasonable results and to study the effect of the retraining data size on the transfer learning, we conduct transfer learning with an increasing number of retraining n, k spectra. The results are shown in Fig. 4c and d. Here we take an increasing number of retraining n, k spectra from 0 to 17 and leave the rest (in the 18 literature n, k spectra) to test. We preserve the 10 and 50 d per n, k spectra respectively for the training and the test set throughout. The details of the dataset are described in Table 1 and the section preparation of source and target datasets. We observe that the initial transfer at 0 training n, k (without retraining) only yields 50+% and 70+% d accuracy for MTL and STL respectively. Full-weight retraining encounters an initial drop for MTL (or a minimal increase for STL) in performance before showing performance rise with the increase of training data size, while partial-weight retraining immediately shows steady performance rise. However, with larger training data sizes (>11 training n, k) full-weight retraining eventually becomes better than partial-weight retraining and yields better d accuracies. To explain full-weight retraining vs. partial-weight retraining, we look at the difference in the weights to update—compared to partial-weight retraining, full-weight retraining has more weights to update. Thus full-weight retraining is more flexible. Flexibility has both pros and cons: when the number of retraining n, k is small, flexibility more easily steers thicknessML away from the optimal weights (an initial drop or a minimal increase in accuracy); when the number of retraining n, k becomes large enough, flexibility offers a higher learning capacity, and thus a better accuracy. Overall, we recommend the STL implementation in the transfer learning workflow paired with either partial-weight retraining (when the number of retraining n, k is smaller) or full-weight retraining (when the number of retraining n, k is larger). We follow this recommendation in our ensuing experimental validation.
We reiterate the goal of thicknessML, to characterize film thickness across materials classes in high throughput, and we evaluate the transfer learning performance in this section accordingly. Note that thicknessML-STL after transfer learning starts to approach a high d accuracy, e.g., 90% d accuracy, as shown in Fig. 4c and d rapidly with only 1 retraining n, k (taking the better of full-weight and partial-weight retraining). Around 90% d accuracy is achieved when there are ≥9 retraining n, k spectra. Functionally, this means that for any materials class, thicknessML can successfully predict film thickness with high (around 90% in this perovskite case) accuracy given a few (9 in this case) literature n, k spectra via this generic-to-specific transfer learning framework. The impact of thicknessML in the transfer learning workflow is significant for achieving high-throughput film thickness characterization across materials classes; the only requirement is a few literature n, k spectra of the target material class.
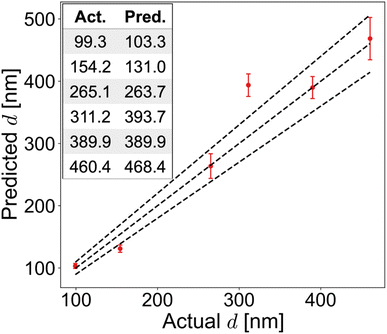
3.3 Experimental validation with six experimental perovskite thin films
We validate our transfer-learning-enabled thickness prediction on experimental perovskite films. We deposited six methylammonium lead iodide (MAPbI3) films with assorted precursor solution concentrations and spin coating speeds recorded in Table 4. We performed UV-Vis and profilometry measurements and compared them with the thicknessML predictions in Fig. 5. The measurement data are shown in Section S4.† Raw Measurements of the Experimentally Deposited MAPbI3 Films. Pre-trained thicknessML (STL) was retrained on the perovskite target dataset with eight retraining n, k spectra using a partial-weight retraining. The choice of eight perovskites was deliberate to be more distinct from MAPbI3 by not containing methylammonium (MA). The resulting predictions have a 10.5% MAPE.| Film no. | Concentration of precursor solution (M) | Spin coating speed (rpm) | Measured thickness (nm) | Predicted thickness (nm) |
|---|---|---|---|---|
| 1 | 0.5 | 3000 | 154.17 | 122.8 |
| 2 | 0.5 | 6000 | 99.29 | 101.3 |
| 3 | 1.25 | 3000 | 389.89 | 418.5 |
| 4 | 1.25 | 6000 | 265.07 | 256.0 |
| 5 | 1.5 | 3000 | 460.35 | 489.9 |
| 6 | 1.5 | 6000 | 311.15 | 373.8 |
To evaluate thicknessML as a high-throughput characterization framework, we also record its throughput. During prediction (when deployed), the thickness prediction of one film is within milliseconds, and the bulk of time (per sample) is spent on UV-Vis. In this study, UV-Vis is performed by using a stand-alone tool with an integrating sphere and takes about 2 minutes per sample to measure R(λ) and T(λ) of 0° incident angle. During training (pre-training and retraining), the once-off pre-training takes about 1.5 hours (STL) and 3.3 hours (MTL) per model, while the retraining completes within minutes, on a desktop equipped with an Intel(R) Core(TM) i7-4790 CPU and NIVIDIA GeForce GTX 1650 GPU.
4 Conclusions
We use transfer learning to tackle data scarcity in the application of high-throughput thin film thickness characterization. Data scarcity in thickness characterization arises from the need to traverse different domains (classes) of materials with different underlying optical models when certain domains, especially newly developed materials such as perovskites, do not have much data. To tackle this data scarcity with transfer learning, we propose a workflow to first pre-train the model thicknessML on a generic source domain of big data and then transfer to a specific target domain of small data to predict film thickness from the UV-Vis measured spectra. We select perovskite materials as the target domain to demonstrate our workflow and model in this study when the target domain can easily extend to other materials classes.On the generic source dataset simulated from the generic Tauc–Lorentz optical model, 89.2% of the predicted d from pre-trained thicknessML fall within 10% deviation (89.2% d accuracy). After transferring to the specific target dataset from 18 literature perovskite refractive indices, retrained thicknessML reaches 92.2 ± 3.6% d accuracy compared to 81.8 ± 11.7% d accuracy of direct learning. Moreover, we demonstrate that just a few (9 in the perovskite case) literature n, k spectra in the target domain are sufficient for this generic-to-specific transfer learning framework to predict target-domain film thickness with high accuracy. This transfer learning workflow yields a 10.5% MAPE when validated on six experimentally deposited MAPbI3 films.
Overall, we demonstrate that our proposed generic-to-specific transfer learning workflow can effectively characterize film thickness in high throughput; it only needs a few literature n, k spectra (tackling data scarcity) to perform high-accuracy thickness prediction across various material classes. We believe that this study opens a new direction of high-throughput thickness characterization and serves as an inspiration for future research encountering data scarcity.
5 Methods
5.1 Refractive index simulation from a single Tauc–Lorentz oscillator
In UV-Vis, estimating thickness relies on fitting underlying oscillator models, which describes the interaction between the impingent electromagnetic wave and electrons within the thin film. Specifically, an oscillator model parameterizes the complex wavelength-resolved refractive index ñ(λ) = n(λ) + ik(λ) via a middleman, the dielectric function, which determines the optical responses R(λ) and T(λ) with film thickness d. Reflecting the variety of materials and their electron densities of states, there are many types of oscillator models, including Tauc–Lorentz, Cauchy, and Drude, among others.45–47 The TL oscillator, widely used for modeling metal oxides, is a default go-to for modeling materials with band gaps, serving as an indispensable building block for semiconductor optical models. Hence, we choose a single TL oscillator to simulate our generic source dataset.The Python implementation of the single Tauc–Lorentz oscillator entails the implementation of the following equations:45
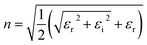 | (1) |
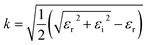 | (2) |
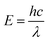 | (3) |
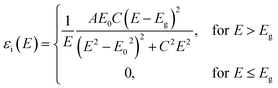 | (4) |
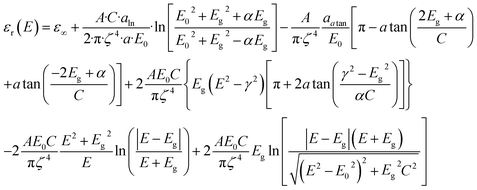 | (5) |
| aln = (Eg2 − E02)E2 + Eg2C2 − E02(E02 + 3Eg2), |
| aatan = (E2 − E02)(E02 + Eg2) + Eg2C2, |
After combining all the above equations, n(λ) and k(λ) are parameterized with five fitting parameters, A, C, E0, Eg, and ε∞. We fix ε∞ = 0 and sample grids for each parameter as follows—A, 10 to 200 with 11 grid nodes; C, 0.5 to 10 with 10 grid nodes; E0, 1 to 10 with 10 grid nodes; Eg, 1 to 5 with 10 grid nodes. After sampling, we randomly select 1116 n, k spectra to be included in our dataset. We describe the selection of these 1116 n, k spectra in more detail in Section S3† selection of 1116 n, k spectra in the generic source dataset.
5.2 Transfer-matrix method simulation
The Python implementation of TMM simulation follows the equations in ref. 48, assuming no roughness and fully coherent layers. The incident angle is 0°, and the incident medium above the films and the exit medium below the glass substrate are air (with infinite thickness). The glass substrate with a thickness of 1 mm corresponds to the actual substrate used in depositing the six MAPbI3 films. An incident angle of around 0° for transmission and 8° for reflectance are also used in the UV-Vis measurement due to the setup of the integrating sphere. The small discrepancy of incidence angles between the measurement and the simulation only causes negligible difference in reflectance spectra.5.3 Convolutional neural network
Designed for image recognition, the classic CNN architecture consists of three main types of layers: convolutional, pooling and fully connected. Convolutional layers connect input and each other through local filters of fixed sizes and extract features within the filter window through convolution. In the convolutional layer, information from local pixels (within the filter window), or the local feature, gets concentrated and passed as a single pixel to the next layer. With the addition of each convolutional layer, features extracted are of a higher and higher level (features that are more global). Thus, the series of convolutional layers becomes a feature extractor, containing features ranging from low to high levels. A pooling layer usually follows convolutional layers, to downsample the spatial dimensions of the given input. Max pooling (retaining the maximum values during downsampling) is the most widely used, which aims to retain the most salient features. Fully connected layers are exactly a multilayer perceptron (MLP), taking the extracted features as input. The name “fully connected” arises from the comparison with convolutional layers, which are locally connected through filters. An MLP is a universal approximator49 to map the input to the output and in the CNN serves to learn the mapping from extracted features to the output. In addition to the three types of layers, thicknessML also adds dropout layers after fully connected layers to prevent overfitting. The detailed layers and hyperparameter of thicknessML can be found in Section S1†thicknessML hyperparameters. As a potential future improvement, a CNN with continuous-filter convolution such as used in SchNet50 might achieve better results as the R, T spectra are intrinsically continuous with respect to wavelength.Section S2† Visualization of thicknessML Activation Maps of an example R, T spectra peeks into the black box of thicknessML and visualizes activation maps of example R, T spectra (from the source dataset). The four rows of activation maps correspond to the outputs of the four convolutional layers (after ReLU activation) respectively (ten filters are randomly chosen for each convolutional layer to produce the activation maps). Certain filters are activated maximally at peaks or valleys of the R, T spectra, which is closely related to film thickness.
5.4 Multitask learning
Multitask learning is the concurrent learning of multiple tasks, where each task can be regression or classification as in supervised learning. This concurrent learning is achieved by parameter sharing, which can be implemented via hard (using the same parameters) or soft (using similar parameters) parameter sharing. Ruder provides a helpful overview of multitask learning in ref. 41. thicknessML-MTL adopts the hard parameter sharing, letting the prediction of d, n, and k share the same parameters of convolutional layers, i.e., the same feature extractor. The shared feature extractor promotes extraction of more generalized features, and the auxiliary tasks also provide regularization by introducing an inductive bias. The three tasks of d, n, and k prediction retain individual fully connected layer blocks to process and map the extracted features to respective values.5.5 Heteroskedastic loss function
To encourage smaller d prediction deviation for smaller thickness (consistent relative error), we adopt a heteroskedastic loss function as shown in eqn (6)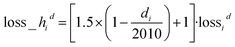 | (6) |
lossid = log(cosh(![[d with combining circumflex]](https://www.rsc.org/images/entities/i_char_0064_0302.gif) i − di)) i − di)) | (7) |
![[d with combining circumflex]](https://www.rsc.org/images/entities/i_char_0064_0302.gif) i denotes the predicted thickness for sample i. Given our d range from 10 nm to 2010 nm, we amplify individual sample loss by how much thinner it is than 2010 nm. If di is 2010 nm, its loss is simply lossid, where lossid is the log-cosh loss for thickness as shown in eqn (7). If di is close to 0 nm, its loss is close to 2.5 × lossid. Here, 1.5 is tunable. This heteroskedastic loss penalizes d prediction deviations for smaller thickness more than d prediction deviations for larger thickness, yielding a more consistent relative error overall. The overall loss is the average over all individual sample heteroskedastic loss los
i denotes the predicted thickness for sample i. Given our d range from 10 nm to 2010 nm, we amplify individual sample loss by how much thinner it is than 2010 nm. If di is 2010 nm, its loss is simply lossid, where lossid is the log-cosh loss for thickness as shown in eqn (7). If di is close to 0 nm, its loss is close to 2.5 × lossid. Here, 1.5 is tunable. This heteroskedastic loss penalizes d prediction deviations for smaller thickness more than d prediction deviations for larger thickness, yielding a more consistent relative error overall. The overall loss is the average over all individual sample heteroskedastic loss los![[s with combining low line]](https://www.rsc.org/images/entities/char_0073_0332.gif) hid as shown in eqn (8)
hid as shown in eqn (8)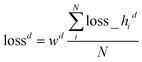 | (8) |
For the n loss function, we adopt a similar heteroskedastic form, 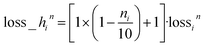 . The prediction deviation of n is proportionally amplified by how much less the actual n is from 10; if ni is close to 0, its loss is close to 2 × lossin. For the k loss function, we simply use the log-cosh loss function without heteroskedasticity because of its many near-zero and zero values. The corresponding loss scalers wn and wk are recorded in Section S1†thicknessML Hyperparameters.
. The prediction deviation of n is proportionally amplified by how much less the actual n is from 10; if ni is close to 0, its loss is close to 2 × lossin. For the k loss function, we simply use the log-cosh loss function without heteroskedasticity because of its many near-zero and zero values. The corresponding loss scalers wn and wk are recorded in Section S1†thicknessML Hyperparameters.
5.6 Transfer learning
Fig. 6 depicts a simplified representation of certain fully connected layers with associated weights and activation functions. Weights are to perform weighted sum with incoming inputs from previous layers, and activation functions are to decide whether to activate with a hard or soft cut-off based on the weighted sum. The convolutional layers follow the same principle except the incoming inputs are spatially arrange, and the weights are in the spatial form of filters. During the pre-training and the direct learning of thicknessML, the weights are randomly initialized, and the weights are updated through training data via backpropagation. The knowledge of an inverse mapping of TMM of an underlying TL oscillator is embedded in the trained weights of the pre-trained thicknessML. This knowledge via the pre-trained weights is then transferred to the perovskite target dataset in two ways—continue to update only the weights of the fully connected layers (partial-weight retraining), or weights of both the convolutional layers and the fully connected layers (full-weight retraining).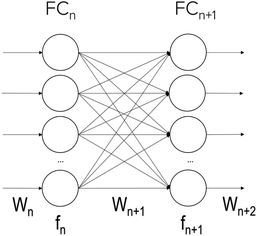 | ||
| Fig. 6 A simplified neuron representation of fully connected layer n and n + 1, where Wn denotes the weights associated with layer n, and fn the activation functions. | ||
5.7 MAPbI3 film deposition, UV-Vis measurement, and profilometry measurement
In the deposition of MAPbI3, we follow the procedures as described in ref. 51 and 52. Six combinations of two thickness-affecting process variables, the concentration of the perovskite precursor solution (PbI2 and MAI with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio), and the spin coating speed, are used and recorded in Table 4. The deposited films are then measured by UV-Vis with an Agilent Cary 7000 UV-Vis-NIR spectrophotometer, and by profilometry with a KLA Tencor P-16 + Plus Stylus Profiler.
1 molar ratio), and the spin coating speed, are used and recorded in Table 4. The deposited films are then measured by UV-Vis with an Agilent Cary 7000 UV-Vis-NIR spectrophotometer, and by profilometry with a KLA Tencor P-16 + Plus Stylus Profiler.
Data availability
Datasets used in this study are provided at https://github.com/PV-Lab/thicknessML and https://doi.org/10.6084/m9.figshare.23501715.v1. The code for pre-training and transfer learning is provided, together with pre-trained thicknessML models, at https://github.com/PV-Lab/thicknessML.Author contributions
Conceptualization: B. P. M., F. G. L. P., F. O., C. P. B. and T. B.; methodology: Z. L., S. I. P. T., Z. R., T. B., Q. L., Y. F. L., J. S., F. O., B. P. M. and F. G. L. P.; software: Z. L. and S. I. P. T.; investigation: S. V., Y. C., D. B., V. C., and S. I. P. T.; writing – original draft: S. I. P. T., and Z. L.; writing – review & editing: Z. L., T. B. and S. I. P. T.; funding acquisition: T. B. and A. G. A.; resources: A. G. A.; supervision: Z. L., T. B., and Q. L.Conflicts of interest
Although our laboratory has IP filed covering photovoltaic technologies and materials informatics broadly, we do not envision a direct COI with this study, the content of which is open sourced. Three of the authors (Z. R., T. B., and Z. L.) own equity in Xinterra Pte Ltd, which applies machine learning to accelerate novel materials development.Acknowledgements
We acknowledge financial support from the National Research Foundation (NRF) Singapore through the Singapore Massachusetts Institute of Technology (MIT) Alliance for Research and Technology's Low Energy Electronic Systems research program, and the Energy Innovation Research Program (grant number, NRF2015EWT-EIRP003-004 and NRF-CRP14-2014-03 and Solar CRP: S18-1176-SCRP), the TOTAL SA research grant funded through MITei, the Accelerated Materials Development for Manufacturing Program at A*STAR via the AME Programmatic Fund by the Agency for Science, Technology and Research under Grant No. A1898b0043, and the Solar Energy Research Institute of Singapore (SERIS), a research institute at the National University of Singapore (NUS) supported by the National University of Singapore (NUS), the National Research Foundation Singapore (NRF), the Energy Market Authority of Singapore (EMA), and the Singapore Economic Development Board (EDB). C. P. B., B. P. M., and F. G. L. P. are grateful to the Canadian Natural Science and Engineering Research Council (RGPIN-2018-06748) and Natural Resources Canada's Energy Innovation Program (EIP2-MAT-001) for financial support. QL is supported by the National Research Foundation, Singapore, under the NRF fellowship (NRFNRFF13-2021-0005).References
- B. A. Rizkin, A. S. Shkolnik, N. J. Ferraro and R. L. Hartman, Combining automated microfluidic experimentation with machine learning for efficient polymerization design, Nat. Mach. Intell., 2020, 2(4), 200–209, DOI:10.1038/s42256-020-0166-5.
- B. Burger, P. M. Maffettone and V. V. Gusev, et al., A mobile robotic chemist, Nature, 2020, 583(7815), 237–241, DOI:10.1038/s41586-020-2442-2.
- K. Abdel-Latif, F. Bateni, S. Crouse and M. Abolhasani, Flow Synthesis of Metal Halide Perovskite Quantum Dots: From Rapid Parameter Space Mapping to AI-Guided Modular Manufacturing, Matter, 2020, 3(4), 1053–1086, DOI:10.1016/j.matt.2020.07.024.
- F. Häse, L. M. Roch, C. Kreisbeck and A. Aspuru-Guzik, Phoenics: A Bayesian Optimizer for Chemistry, ACS Cent. Sci., 2018, 4(9), 1134–1145, DOI:10.1021/acscentsci.8b00307.
- F. Mekki-Berrada, Z. Ren and T. Huang, et al., Two-step machine learning enables optimized nanoparticle synthesis, Npj Comput. Mater., 2021, 7(1), 55, DOI:10.1038/s41524-021-00520-w.
- P. F. Newhouse, D. Guevarra and M. Umehara, et al., Combinatorial alloying improves bismuth vanadate photoanodes: Via reduced monoclinic distortion, Energy Environ. Sci., 2018, 11(9), 2444–2457, 10.1039/c8ee00179k.
- S. Ament, M. Amsler and D. R. Sutherland, et al., Autonomous materials synthesis via hierarchical active learning of nonequilibrium phase diagrams, Sci. Adv., 2021, 7(51), 4930, DOI:10.1126/sciadv.abg4930.
- Z. Liu, N. Rolston, A. C. Flick, T. W. Colburn, Z. Ren, R. H. Dauskardt and T. Buonassisi, Machine learning with knowledge constraints for process optimization of open-air perovskite solar cell manufacturing, Joule, 2022, 6(4), 834–849, DOI:10.1016/j.joule.2022.03.003.
- B. P. MacLeod, F. G. L. Parlane, A. K. Brown, J. E. Hein and C. P. Berlinguette, Flexible automation accelerates materials discovery, Nat. Mater., 2022, 21, 722–726, DOI:10.1038/s41563-021-01156-3.
- A. E. Gongora, B. Xu, W. Perry, C. Okoye, P. Riley, K. G. Reyes, E. F. Morgan and K. A. Brown, A Bayesian experimental autonomous researcher for mechanical design, Sci. Adv., 2020, 6(15), eaaz1708, DOI:10.1126/sciadv.aaz1708.
- B. P. MacLeod, F. G. L. Parlane and T. D. Morrissey, et al., Self-driving laboratory for accelerated discovery of thin-film materials, Sci. Adv., 2020, 6(20), eaaz8867, DOI:10.1126/sciadv.aaz8867.
- X. Du, L. Lüer and T. Heumueller, et al., Elucidating the Full Potential of OPV Materials Utilizing a High-Throughput Robot-Based Platform and Machine Learning, Joule, 2021, 5(2), 495–506, DOI:10.1016/J.JOULE.2020.12.013.
- D. Bash, Y. Cai and V. Chellappan, et al., Multi-Fidelity High-Throughput Optimization of Electrical Conductivity in P3HT-CNT Composites, Adv. Funct. Mater., 2021, 31(36), 2102606, DOI:10.1002/adfm.202102606.
- F. Oviedo, Z. Ren and S. Sun, et al., Fast and interpretable classification of small X-ray diffraction datasets using data augmentation and deep neural networks, Npj Comput. Mater., 2019, 5(1), 1–9, DOI:10.1038/s41524-019-0196-x.
- N. Taherimakhsousi, B. P. MacLeod, F. G. L. Parlane, T. D. Morrissey, E. P. Booker, K. E. Dettelbach and C. P. Berlinguette, Quantifying defects in thin films using machine vision, npj Comput. Mater., 2020, 6(1), 111, DOI:10.1038/s41524-020-00380-w.
- Z. Liu, F. Oviedo, E. M. Sachs and T. Buonassisi, Detecting Microcracks in Photovoltaics Silicon Wafers using Varitional Autoencoder, in Conference Record of the IEEE Photovoltaic Specialists Conference, 2020, pp. 0139–0142, DOI:10.1109/PVSC45281.2020.9300366.
- P. Nikolaev, D. Hooper, F. Webber, R. Rao, K. Decker, M. Krein, J. Poleski, R. Barto and B. Maruyama, Autonomy in materials research: a case study in carbon nanotube growth, npj Comput. Mater., 2016, 2, 16031, DOI:10.1038/npjcompumats.2016.31.
- R. Luo, J. Popp and T. Bocklitz, Deep Learning for Raman Spectroscopy: A Review, Anal., 2022, 3(3), 287–301, DOI:10.3390/ANALYTICA3030020.
- X. Bai, L. Zhang, C. Kang, B. Quan, Y. Zheng, X. Zhang, J. Song, T. Xia and M. Wang, Near-infrared spectroscopy and machine learning-based technique to predict quality-related parameters in instant tea, Sci. Rep., 2022, 12(1), 1–8, DOI:10.1038/s41598-022-07652-z.
- A. Stoll and P. Benner, Machine learning for material characterization with an application for predicting mechanical properties, GAMM Mitt., 2021, 44(1), e202100003, DOI:10.1002/GAMM.202100003.
- T. D. Lee and A. U. Ebong, A review of thin film solar cell technologies and challenges, Renewable Sustainable Energy Rev., 2017, 70, 1286–1297, DOI:10.1016/J.RSER.2016.12.028.
- M. Powalla, S. Paetel, E. Ahlswede, R. Wuerz, C. D. Wessendorf and T. Magorian Friedlmeier, Thin-film solar cells exceeding 22% solar cell efficiency: An overview on CdTe-, Cu(In,Ga)Se2-, and perovskite-based materials, Appl. Phys. Rev., 2018, 5(4), 041602, DOI:10.1063/1.5061809.
- C. Mackin, A. Fasoli, M. Xue, Y. Lin, A. Adebiyi, L. Bozano and T. Palacios, Chemical sensor systems based on 2D and thin film materials, 2D Mater., 2020, 7(2), 022002, DOI:10.1088/2053-1583/AB6E88.
- J. E. Ellis, S. E. Crawford and K. J. Kim, Metal–organic framework thin films as versatile chemical sensing materials, Adv. Mater., 2021, 2(19), 6169–6196, 10.1039/D1MA00535A.
- Y. S. Choi, J. W. Kang, D. K. Hwang and S. J. Park, Recent advances in ZnO-based light-emitting diodes, IEEE Trans. Electron Devices, 2010, 57(1), 26–41, DOI:10.1109/TED.2009.2033769.
- X. Chen, Z. Zhou, Y. H. Lin and C. Nan, Thermoelectric thin films: Promising strategies and related mechanism on boosting energy conversion performance, J. Mater., 2020, 6(3), 494–512, DOI:10.1016/J.JMAT.2020.02.008.
- D. Jha, K. Choudhary, F. Tavazza, W. keng Liao, A. Choudhary, C. Campbell and A. Agrawal, Enhancing materials property prediction by leveraging computational and experimental data using deep transfer learning, Nat. Commun., 2019, 10(1), 1–12, DOI:10.1038/s41467-019-13297-w.
- J. Lee and R. Asahi, Transfer learning for materials informatics using crystal graph convolutional neural network, Comput. Mater. Sci., 2021, 190, 110314, DOI:10.1016/J.COMMATSCI.2021.110314.
- V. Gupta, K. Choudhary, F. Tavazza, C. Campbell, W. keng Liao, A. Choudhary and A. Agrawal, Cross-property deep transfer learning framework for enhanced predictive analytics on small materials data, Nat. Commun., 2021, 121(1), 1–10, DOI:10.1038/s41467-021-26921-5.
- H. Yamada, C. Liu, S. Wu, Y. Koyama, S. Ju, J. Shiomi, J. Morikawa and R. Yoshida, Predicting Materials Properties with Little Data Using Shotgun Transfer Learning, ACS Cent. Sci., 2019, 5(10), 1717–1730, DOI:10.1021/acscentsci.9b00804.
- S. Krawczuk and D. Venturi, Improving Neural Network Predictions of Material Properties with Limited Data Using Transfer Learning, Int. J. Mach. Learn. Comput., 2021, 2(1), 31–47 CrossRef , accessed: Oct. 12, 2022. https://www.begellhouse.com.
- S. Feng, H. Fu, H. Zhou, Y. Wu, Z. Lu and H. Dong, A general and transferable deep learning framework for predicting phase formation in materials, Npj Comput. Mater., 2021, 7(1), 1–10, DOI:10.1038/s41524-020-00488-z.
- H. Fujiwara, N. J. Podraza, M. I. Alonso, M. Kato, K. Ghimire, T. Miyadera and M. Chikamatsu, Organic-inorganic hybrid perovskite solar cells, in Springer Series in Optical Sciences, Springer, Cham, 2018, vol. 212, pp. 463–507, DOI:10.1007/978-3-319-75377-5_16.
- M. Shirayama, H. Kadowaki and T. Miyadera, et al., Optical Transitions in Hybrid Perovskite Solar Cells: Ellipsometry, Density Functional Theory, and Quantum Efficiency Analyses for CH3NH3PbI3, Phys. Rev. Appl., 2016, 5(1), 014012, DOI:10.1103/PhysRevApplied.5.014012.
- S. Manzoor, J. Häusele, K. A. Bush, A. F. Palmstrom, J. Carpenter, Z. J. Yu, S. F. Bent, M. D. Mcgehee and Z. C. Holman, Optical modeling of wide-bandgap perovskite and perovskite/silicon tandem solar cells using complex refractive indices for arbitrary-bandgap perovskite absorbers, Opt. Express, 2018, 26(21), 27441–27460, DOI:10.1364/OE.26.027441.
- J. Werner, G. Nogay and F. Sahli, et al., Complex Refractive Indices of Cesium-Formamidinium-Based Mixed-Halide Perovskites with Optical Band Gaps from 1.5 to 1.8 eV, ACS Energy Lett., 2018, 3(3), 742–747, DOI:10.1021/acsenergylett.8b00089.
- P. Löper, M. Stuckelberger and B. Niesen, et al., Complex refractive index spectra of CH3NH3PbI3 perovskite thin films determined by spectroscopic ellipsometry and spectrophotometry, J. Phys. Chem. Lett., 2015, 6(1), 66–71, DOI:10.1021/jz502471h.
- Y. LeCun, B. Boser, J. S. Denker, D. Henderson, R. E. Howard, W. Hubbard and L. D. Jackel, Backpropagation Applied to Handwritten Zip Code Recognition, Neural Comput., 1989, 1(4), 541–551, DOI:10.1162/NECO.1989.1.4.541.
- L. Cun, J. Henderson, Y. Le Cun, J. S. Denker, D. Henderson, R. E. Howard, W. Hubbard and L. D. Jackel, Handwritten Digit Recognition with a Back-Propagation Network, 1989 Search PubMed.
- K. O’shea and R. Nash, An Introduction to Convolutional Neural Networks, 2015 Search PubMed.
- S. Ruder, An Overview of Multi-Task Learning in Deep Neural Networks, 2017, https://sebastianruder.com/multi-task/index Search PubMed.
- R. Caruana, Multitask Learning, Mach. Learn., 1997, 28, 41–75, DOI:10.1007/978-3-030-01620-3_5.
- F. Chollet, Keras, 2015, https://keras.io Search PubMed.
- K. Weiss, T. M. Khoshgoftaar and D. D. Wang, A survey of transfer learning, J. Big Data, 2016, 3(1), 1–40, DOI:10.1186/S40537-016-0043-6/TABLES/6.
- G. E. Jellison and F. A. Modine, Parameterization of the optical functions of amorphous materials in the interband region, Appl. Phys. Lett., 1996, 69(3), 371–373, DOI:10.1063/1.118064.
- M. Born and E. Wolf, Principles of Optics, Pergamon Press, 1984 Search PubMed.
- P. Drude, C. R. Mann and R. Andrews, The Theory of Optics, Longmans, Green, and Co., New York, 1902 Search PubMed.
- E. Centurioni, Generalized matrix method for calculation of internal light energy flux in mixed coherent and incoherent multilayers, Appl. Opt., 2005, 44(35), 7532–7539, DOI:10.1364/AO.44.007532.
- K. Hornik, M. Stinchcombe and H. White, Multilayer feedforward networks are universal approximators, Neural Netw, 1989, 2(5), 359–366, DOI:10.1016/0893-6080(89)90020-8.
- K. T. Schütt, H. E. Sauceda, P. J. Kindermans, A. Tkatchenko and K. R. Müller, SchNet – A deep learning architecture for molecules and materials, J. Chem. Phys., 2018, 148(24), 241722, DOI:10.1063/1.5019779.
- M. Li, X. Xu, Y. Xie, H.-W. Li, Y. Ma, Y. Cheng and S.-W. Tsang, Improving the conductivity of sol–gel derived NiOx with a mixed oxide composite to realize over 80% fill factor in inverted planar perovskite solar cells, J. Mater. Chem. A, 2019, 7(16), 9578–9586, 10.1039/C8TA10821H.
- Y. Cheng, M. Li and X. Liu, et al., Impact of surface dipole in NiOx on the crystallization and photovoltaic performance of organometal halide perovskite solar cells, Nano Energy, 2019, 61, 496–504, DOI:10.1016/j.nanoen.2019.05.004.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2dd00149g |
| ‡ Now at: Department of Mathematics, National University of Singapore, 10 Lower Kent Ridge Road, Singapore 119076 |
| § Now at: Xinterra, Singapore, 77 Robinson Road, Singapore 068896, Singapore |
| ¶ Now at: Department of Materials Science and Engineering, City University of Hong Kong, Kowloon, Hong Kong, 999077, P. R. China |
| || Now at: Microsoft AI for Good, Redmond, WA 98052, USA |
| ** Now at: School of Materials Science and Engineering, Northwestern Polytechnical University, Xi'an, Shaanxi, 710072, P. R. China |
| This journal is © The Royal Society of Chemistry 2023 |