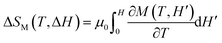Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Neural networks for a quick access to a digital twin of scanning physical property measurements†
Kensei
Terashima
 *a,
Pedro
Baptista de Castro
*a,
Pedro
Baptista de Castro
 ab,
Miren Garbiñe
Esparza Echevarria
ab,
Ryo
Matsumoto
a,
Takafumi D.
Yamamoto
a,
Akiko T.
Saito
ab,
Miren Garbiñe
Esparza Echevarria
ab,
Ryo
Matsumoto
a,
Takafumi D.
Yamamoto
a,
Akiko T.
Saito
 a,
Hiroyuki
Takeya
a and
Yoshihiko
Takano
ab
a,
Hiroyuki
Takeya
a and
Yoshihiko
Takano
ab
aNational Institute for Materials Science, 1-2-1 Sengen, Tsukuba, Japan. E-mail: TERASHIMA.Kensei@nims.go.jp
bUniversity of Tsukuba, 1-1-1 Tennoidai, Tsukuba, Japan
First published on 13th January 2023
Abstract
For performing successful measurements within a limited experimental time, efficient use of preliminary data plays a crucial role. This work shows that a simple feedforward type neural network approach for learning preliminary experimental data can provide a quick access to simulate the experiment within the learned range. The approach is especially beneficial for physical property measurements with scanning on multiple axes, where differentiation or integration of data are required to obtain the objective quantity. Due to its simplicity, the learning process is fast enough for the users to perform learning and simulation on-the-fly by using a combination of open-source optimization techniques and deep-learning libraries. Here such an approach for augmenting the experimental data is proposed, aiming to help researchers decide the most suitable experimental conditions before performing costly experiments in reality. Furthermore, we suggest that this method can also be used from the perspective of taking advantage of reutilizing and repurposing previously published data, accelerating data-driven exploration of functional materials.
1 Introduction
The recent global increase in databases on materials as well as accessible repositories and advanced text mining techniques has led to the evolution of materials informatics as a new paradigm for exploration and design of functional materials.1 Along with the increase in the available crystal structural input data, the emergence of high-throughput first-principles calculation systems has enhanced a variety of materials’ estimated property data useful for statistical analysis.2–4 In addition, the application of machine-learning methods has proved to be quite efficient for dealing with large amounts of materials data,1,5 allowing the extraction of useful information that has been hidden or too complicated for an ordinary human to perceive. As a result of the recent rapid growth of such tools for handling materials data, the process for obtaining candidate materials in cyberspace has been significantly accelerated, while the bottleneck for the discovery of functional materials remains the actual synthesis and experimental evaluation in real space.6 This is because the cost for obtaining experimental data is usually high, especially when researchers have to use a state-of-the-art shared facility with fixed machine time. Furthermore, not only the experiment itself but also its preparation can be time-consuming as sometimes one has to start with optimization of the sample synthesis process, a typical aspect of physics and materials science workflows.Such a costly-in-real situation is even more serious in industrial fields, where the production of “real” items is expensive. To overcome this issue, an idea called the “digital twin” was created, where one builds a simulation model that takes account of the data in real space and tries to optimize the parameters in cyberspace before real manufacturing.7 For being beneficial, the model has to correspond enough to the objective, and the cost for the simulation both in terms of money and time has to be lower than the actual production. Here again, the application of machine-learning methods has greatly reduced the duration required for the execution of simulation as compared to that for performing conventional simulation algorithms. Recently, the use cases of such a digital-twin approach aided by machine learning are becoming popular also in academic research. For instance, machine-learning was used for approximating time-consuming simulation results for fluid dynamics, allowing researchers to perform a quick optimization of the growing conditions of objective crystals.8
In this context, the use of the digital-twin approach is also expected to be effective and highly useful for physics and materials science measurements, where the objective properties are sometimes deduced from experimental data by applying mathematical operations such as differentiation or integration. Especially in physics, the development of new approaches or ideas for data analysis creates an opportunity to revisit or reanalyze previously published data, allowing researchers to draw new insights from this previous knowledge. However, it is quite often that the data are non-evenly spaced along multiple axes due to experimental confinements, and they may contain non-linear responses that cannot be interpolated easily. In such a case, it is quite difficult to estimate the target quantity from preliminary data. On the other hand, artificial neural networks are known to have high flexibility and adaptivity in principle.9,10 It has also been discussed11 that neural network learning can be as efficient as other approximation methods from a viewpoint of minimizing loss by keeping the number of parameters as low as possible. They have proved to be even useful when the objective has inhomogeneity in smoothness12 or when the objective has several discontinuities.13 Thus, approximation using this method is expected to be suitable for materials science and physics experimental data that tend to contain discrete change due to first-order transition and/or multiple peak structures.
In this article, we show that learning preliminary data of materials science using neural networks provides us a way to quickly build a model that can describe the target property dependencies on scanning axes (treated as features). In order to ensure the accuracy of the model that can be built on-the-fly during the experiment, we used several open Python libraries in combination. Once the model is built, the simulation within the learned feature range can be performed instantly, which enables researchers to evaluate the experimental plan as well as its cost (Fig. 1). We propose that such an approach to data augmentation helps researchers use preliminary- or deposited data effectively for performing the data-driven search of functional materials.
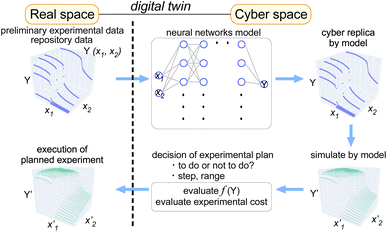 | ||
| Fig. 1 Graphical concept for application of the digital-twin approach to material property measurements for performing efficient experiments using preliminary data as training data. | ||
2 Construction of a neural network model
Our approach relies mainly on 4 open libraries available to the public in addition to the Anaconda package.14 As a machine-learning body, we built fully connected feedforward neural networks, using Keras with the Tensorflow backend (v.2.x).15,16 Keras has several optimizers by default, and among them, we tried stochastic gradient descent, Nesterov accelerated gradient,17 root mean square propagation,18 and adaptive moment estimation (Adam)19 several times on our data shown in Section 3. For our data, Adam tended to be the most stable and fast for minimizing the loss of mean squared error between predicted values and training data (not shown). We set the number of layers, nodes, learning rate, batch size, and regularization methods and factors as hyperparameters to be optimized. Once these hyperparameters are suggested, random weights and biases are given as the initial values in Keras and they are tuned by the optimizer as the epoch proceeds in a single training run. Thus the learned result in a single run varies by the initial random values, even though there could be a general trend for obtaining a moderate set of hyperparameters; for example the case of the learning rate and batch size.20–22 To be quick, we confined the default search space of the hyperparameters to the following range: 2 ≤ number of layers ≤10, 50 ≤ number of nodes ≤200, 5e−4 ≤ learning rate ≤5e−3, and 16 ≤ batch size ≤1024 varying on the data size. To obtain the best possible learned result in a fixed time, we used the Bayesian optimization package Optuna.23 By combining a relational database provided by MySQL,24 Optuna receives each training result with a set of hyperparameters running in parallel, so that it can determine a set of hyperparameters for the next run based on the tree Parzen estimator.25 Typically, the best set of hyperparameters is found after at most ∼30 runs. For visualization of data and controlling multiple Optuna runs in parallel, we used the Streamlit library26 to construct a graphical user interface (GUI) that works on a web browser. For ease of use, we also provide a Jupyter Notebook that does not require the usage of MySQL, without several visualizations.To obtain the best model during the hyperparameter search, we used three functions equipped in the above libraries. The first is early stopping implemented in Keras, with the option of saving the best model in the run, where the maximum epoch number is 500. The second is the learning rate scheduler implemented in Keras, where we change the learning rate to be 5 times smaller than its initial value after 100 epochs. The third is pruning with the asynchronous successive halving algorithm27 implemented in Optuna, where it examines if each run should be pruned based on the comparison of the current score with those of running parallel by 25n epochs where n is an integer greater than or equal to zero.
The approach used here might be primitive as compared to recent state-of-the-art combinations of neural network architectures, optimizers, and other techniques, but we tried to keep the system simple, fast, and easy to use as much as possible since we think that such tools should be convenient if they can be used instantly even during the experiments, where researchers do not necessarily have an access to powerful PCs. As a result, we could quickly finish learning small datasets typical for physical property measurements (number of data ∼ a few thousand) shown in the next section, even without using graphics processing units (GPUs). More details on case studies for the duration and used computers are in the ESI.† A tutorial for how to get ready and perform the neural network learning and simulation shown in this paper will be available at https://www.github.com/kensei-te/mat_interp.
3 Results and discussion
In this section, we show 4 typical use cases as an example. The first is the magnetization curve of a well-known magnetocaloric material ErCo2, where 1st order transition occurs that accompanies a steep change in the magnetization as a function of temperature and the transition temperature migrates by application of an external magnetic field. The second example is the magnetization curve and estimation of magnetocaloric effect in another magnet Fe3Ga4 that shows 1st order transition but whose transition temperature changes more drastically by the applied field than in the first example of ErCo2. The third example is the resistance data of the PdH superconductor which is relatively noisy as compared to the above examples. The fourth example is the mapping data of angle-resolved photoelectron spectroscopy (ARPES) intensity on Fermi energy of a La(O,F)BiS2 superconductor taken above superconducting temperature (Tc) as a demonstration of the application of the method for a two-dimensional intensity map, consisting of a number of peak structures.3.1 M(T, H) of the ErCo2 magnet and estimation of its magnetocaloric effect
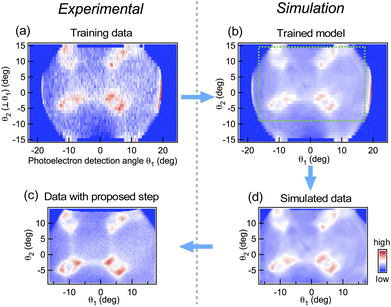
First, we show a case for physical property data that have 1st order transition, namely a steep change in the observed value. ErCo2 is known to be a ferrimagnet with an ordering temperature TCurie of ∼ 35 K.28 It exhibits a 1st order magnetic transition accompanied by magnetostriction, and the material is one of the most popular materials for magnetic refrigeration.29–31 To evaluate the magnitude of magnetic entropy change |ΔSM|, one of the most common ways30 is to measure the magnetization of the sample as a function of temperature and applied magnetic field change ΔH (from 0 to H) either isothermal or isofield, and deduce |ΔSM| by applying the following Maxwell's equation to the observed magnetization data:The equation includes an integration along the applied field (H). Practically, with such discrete experimental data, trapezoidal integration can be applied for a numerical integration, which corresponds to a linear interpolation along the H-axis. However, if we estimate |ΔSM| in this manner from the experimental data shown in Fig. 2(a) taken with a coarse magnetic field step, we end up with extrinsic oscillation of estimated |ΔSM| values shown as a gray solid line in Fig. 2(e). This is simply because of the failure of linear interpolation of data having 1st order transition (see the ESI† for technical details and comparison of approximation methods including several regressors available in Scikit-learn32). To avoid this extrinsic effect for estimation of the target properties, one has to use a finer magnetic field step, so that linear interpolation starts to work well since ∂M/∂T|H between two steps has a finite overlap each other. This means one has to know the appropriate measurement step before the measurement itself. In such a case, neural network simulation based on preliminary data works efficiently as it can perform a non-linear interpolation. Fig. 2(b) shows the predicted magnetization values by a constructed model for the conditions in the training data shown in Fig. 2(a), which correspond well to the training data, indicating that a plausible model has been made. Once such a model is constructed, the model can perform quick predictions for any desired feature value within the learned range. After a couple of trials, we found as shown in Fig. 2(f) that extrinsic oscillation in the simulation is expected to be significantly suppressed when the magnetic field step of the measurement is smaller than 0.2 T. We measured the magnetization in the proposed step as shown in Fig. 2(c), and found as shown in Fig. 2(e) that the experimentally evaluated |ΔSM| corresponds very well to what has been predicted by the simulated model.
3.2 M(T, H) of the Fe3Ga4 magnet and estimation of its magnetocaloric effect
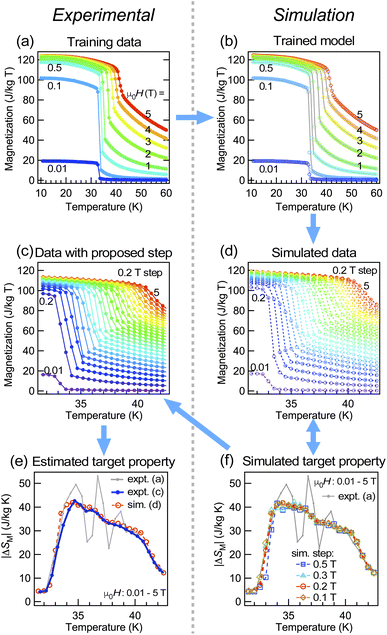
Here we show the case of another magnet Fe3Ga4 and evaluation of its magnetocaloric properties, to show the possibility of applying the neural network study for analyzing literature data. The magnetic properties and magnetization as a function of temperature and magnetic fields have been reported,33 while |ΔSM| of this material has not been reported yet. Fig. 3(a) shows our preliminary experimental data that corresponds well to the literature data,33 but both of them do not have fine enough experimental steps to evaluate |ΔSM| of this material. As shown in Fig. 3(d) and (f), we have performed a simulation of expected |ΔSM| taken on each field step case and found that the extrinsic effect for |ΔSM| would not be observed when we measure magnetization with a magnetic field step of less than 0.1 T for this material. Considering the required experimental time, we chose a 0.075 T step, and the simulated data showed an excellent correspondence with the real experimental data as shown in Fig. 3(c)–(f). The simulation also tells us that the estimated |ΔSM| is at most 0.25 J kg−1 K−1 by a field change of 0–1 T (which is small as compared to those of other magnetocaloric materials30) despite this measurement covering a wide temperature range of 10–200 K with a fine magnetic field step; hence it is expected to take approximately 1 week. Therefore if one is simply looking for a material with high |ΔSM|, the simulation tells us that this material may not be suitable to be synthesized and measured by spending a fair amount of time. In other words, such a simulation is not only useful for analyzing the past preliminary or repository data from a different point of view, but it can also help researchers evaluate the cost of performing the experiment by leveraging the confined knowledge available from preliminary- or literature data.3.3 R(T, H) of the PdH superconductor
Next, we show the case for data with a lower signal-to-noise ratio. For this purpose, we used a part of our resistance data of PdH34 as training data (Fig. 4(a)). As can be seen in Fig. 4(b), the model does not necessarily capture the ultrafine structure coming from noise; however it grabs not only the overall tendency of the lineshape but also several fine structures that might be influenced by noise. The inability of tracking the full noise is because of the fact that the number of layers and nodes in the model is limited and lower than the number of total training data points. Indeed, neural networks are sometimes used for denoising purposes.35,36 On the other hand, our intention here is to simulate the experiment as it is, including the extrinsic effects such as noise and the unique characteristics of the measurement apparatus, based on the non-evenly spaced preliminary data. By comparing the experimental data shown in Fig. 4(c) with simulated data shown in Fig. 4(d), it can be said that the model in the current approach can tell us how the expected lineshapes can be affected by the noise level that appeared in the training data, with a finite and inevitable denoising effect.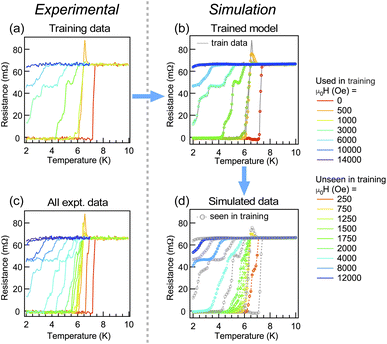 | ||
| Fig. 4 (a) Training data of resistivity measurements for PdH, taken from a part of the whole experimental data in (c). (b) Simulated resistance by the trained model for the conditions in the training data. Gray solid lines show the training data. (c) Experimental data of resistivity measurements for the PdH superconductor.34 (d) Simulated resistance by the trained model for the same conditions as in (c). Gray open circles show the conditions seen by the model during training. | ||
3.4 Angle-resolved photoelectron spectroscopy intensity map of La(O,F)BiS2
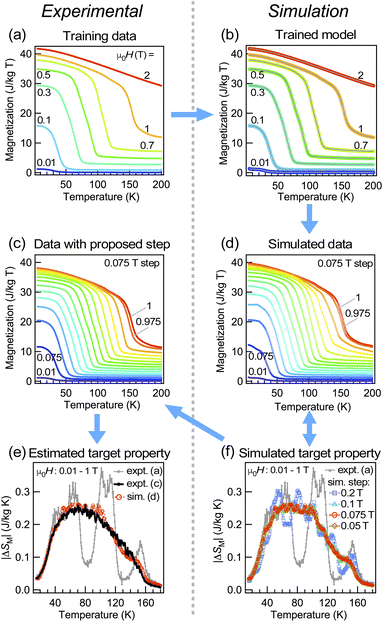
As a last example, we show that our quick and simple approach is also applicable to a two-dimensional intensity map, namely, the ARPES intensity map at Fermi energy in the La(O,F)BiS2 superconductor in a normal state (above Tc). ARPES intensity at fixed energy tends to be high in an angular area where the corresponding electronic state exists, and thus the data consist of a number of peak structures (see the ESI† for the lineshape of each cut). In Fig. 5, the ARPES intensity is shown as a function of two-dimensional angles with respect to the normal angle to the sample surface that corresponds to two-dimensional wave vectors in reciprocal space.37 For constructing such mapping data, it is quite often that one measurement is performed by fixing one of the axes (for instance θ2 in the figure) and keeping concatenating data with different angles of θ2. Therefore a preliminary measurement with a coarse angle step of θ2 (Fig. 5(a)) can be performed before a serious measurement with fine angular steps and better statistics (Fig. 5(c)), so that one can determine the objective measurement area of angles. With the help of neural network learning, we can simulate how the data would become with specific measurement areas and steps as shown in Fig. 5(d); thus the simulation helps researchers make a decision on planning the experiment. Here we note that the simulated pattern captures characteristics of the measurement apparatus, namely high sensitivity at the edge and detection limits in certain angles, so it is suitable for estimating the effect of such instrumental conditions as well. However, the simulated pattern is affected by the presence of sizable noise; hence the pre-processing of training data with other noise reduction methods might help further though such a process may take longer time. Alternatively, it is also possible to take an average of predictions using several models found during the learning process. We also note that although our simple approach is applicable on-the-fly to such mapping data including non-evenly spaced ones, other sophisticated methods such as the super resolution convolutional neural network-based approach38–40 would perform certainly better especially for evenly spaced data such as photographs if one can spare enough time for training and has an access to powerful GPUs.3.5 Scope and limitation of the current approach
Here we note the applicability/inability of our approach. It can quickly learn the data so that one can perform the simulation during the experiment, especially when the total number of data points is kept up to a few tens of thousands. For this reason, it is preferred to keep the dimensions of data (i.e., the number of feature columns) low, even though it can deal with multidimensional data. The approach would be useful mainly in two cases: (i) Simulation of a costly experiment from preliminary experimental data: based on the roughly scanned data, one can simulate how the data and resultant estimated target properties would be, when taken in fixed experimental steps and ranges. Thus it helps researchers plan and perform efficient experiments. This is beneficial especially when the target properties are deduced from mathematical operations on experimental data and hence depend on experimental conditions, as shown in Sections 3.1 and 3.2. (ii) Alignment and augmentation of repository data: there is an increasing number of accessible materials data sets that have been published in the past. It is quite often that one encounters such problems that despite the material being of interest, there is a mismatch or lack in the experimental conditions as compared to what is required in order to perform additional analysis. As the current method can adapt readily to non-evenly spaced data with a non-linear response, it will help researchers judge whether the material is worthy of being examined further by reusing this data for the simulation method proposed here, sparing a certain amount of experimental cost as shown in Section 3.2.It is worth noting here that the method is ultimately a mere interpolation, and thus the signal that is skipped in the training data with too coarse a step will never be predicted in the simulation. Particularly in physical property experiments, the existence of only a few data points (such as sharp peaks) can have great significance for the entire observation. Experimentalists would have a dilemma: the more training data we provide, the more accurate the model becomes, while experimental data are costly to collect. Given these factors, we have used all of the preliminary experimental data as the training data in Sections 3.1–3.4, aiming to build an interpolator that can map the desired relationship and use it to simulate/suggest what steps we should take to accurately measure the properties of interest in a given range. As shown in these examples, the models built here, despite their simple approach, were able to learn well the relationship between the two scanning axes and the target properties, allowing the simulated results to correspond well with the real costly experiments. This shows the potential of its usage in physical disciplines. We also stress that though the simulation helps researchers plan the experiment, the simulated results and estimated values of physical properties themselves should be clearly distinguished from experimental data and be taken with care since it is not certain what will come out in reality until verified by the experiment. As shown in Sections 3.3 and 3.4, the prediction by learned models includes how the data will be affected by unique characteristics of experimental apparatus (sensitivity, detection limit, and so on) and noise that also helps researchers for decision-making on experimental plans. The effect of noise could be examined by comparing several simulated results in different runs (see the ESI† for details). If the researcher aims to suppress the effect of noise rather than simulate it, other noise reduction methods may work better.
4 Conclusions
In this work, we present a simple and quick method to simulate experimental data by learning preliminary data using fully connected feedforward neural networks. The approach is shown to be suitable for materials science experimental data with typical examples. Such a tool would help researchers deal with preliminary- or past repository data efficiently, supporting decision-making during experimental research.Data and code availability statement
A tutorial on how to get ready and perform the neural network learning and simulation shown in this paper, the corresponding Jupyter Notebook file, and the dataset appearing in the paper are available at https://doi.org/10.5281/zenodo.7523510 and https://www.github.com/kensei-te/mat_interp.Author contributions
Conceptualization: KT and PBC; project administration: KT, PBC, ATS, and YT; investigation: KT, PBC, MGEE, RM, and TDY; formal analysis: KT, PBC, and ATS; data curation: KT and PBC; resources: YT and HT; software: KT and PBC; validation: KT, PBC, and MGEE; visualization: KT and PBC; methodology: KT and PBC; supervision: YT; funding acquisition: YT and KT; writing – original draft: KT; writing – review & editing: KT, PBC, RM, TDY, and ATS.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The ARPES measurements were performed at BL28A of the Photon Factory, KEK (proposal No. 2021G686). The authors acknowledge Wei-Sheng Wang and Taku Tou for testing the installation of the code. This work was supported by the JST-Mirai Program (Grant No. JPMJMI18A3), JSPS Bilateral Program (JPJSBP120214602), and JSPS KAKENHI (Grant Nos. 20K05070 and 19H02177). P.B.C. and M.G.E.E. acknowledge the scholarship support from the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan.Notes and references
- V. Stanev, K. Choudhary, A. Kusne, J. Paglione and I. Takeuchi, Commun. Mater., 2021, 2, 105 CrossRef.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, NPJ Comput. Mater., 2015, 1, 1–15 CrossRef.
- S. Curtarolo, W. Setyawan, G. L. Hart, M. Jahnatek, R. V. Chepulskii, R. H. Taylor, S. Wang, J. Xue, K. Yang, O. Levy, M. J. Mehl, H. T. Stokes, D. O. Demchenko and D. Morgan, Comput. Mater. Sci., 2012, 58, 218–226 CrossRef CAS.
- P. B. de Castro, K. Terashima, T. D. Yamamoto, Z. Hou, S. Iwasaki, R. Matsumoto, S. Adachi, Y. Saito, P. Song, H. Takeya and Y. Takano, NPG Asia Mater., 2020, 12, 35 CrossRef.
- Y. Xiong, Q. T. Campbell, J. Fanghanel, C. K. Badding, H. Wang, N. E. Kirchner-Hall, M. J. Theibault, I. Timrov, J. S. Mondschein, K. Seth, R. Katz, A. M. Villarino, B. Pamuk, M. E. Penrod, M. M. Khan, T. Rivera, N. C. Smith, X. Quintana, P. Orbe, C. J. Fennie, S. Asem-Hiablie, J. L. Young, T. G. Deutsch, M. Cococcioni, V. Gopalan, H. D. Abruña, R. E. Schaak and I. Dabo, Energy Environ. Sci., 2021, 14, 2335–2348 RSC.
- F. Tao, H. Zhang, A. Liu and A. Y. C. Nee, IEEE Trans. Ind. Inf., 2019, 15, 2405–2415 Search PubMed.
- Y. Dang, C. Zhu, M. Ikumi, M. Takaishi, W. Yu, W. Huang, X. Liu, K. Kutsukake, S. Harada, M. Tagawa and T. Ujihara, CrystEngComm, 2021, 23, 1982–1990 RSC.
- G. Cybenko, Math. Control Signals Syst., 1989, 2, 303–314 CrossRef.
- H. N. Mhaskar and C. A. Micchelli, Adv. Appl. Mathemat., 1992, 13, 350–373 CrossRef.
- H. N. Mhaskar, Neural Comput., 1996, 8, 164–177 CrossRef.
- T. Suzuki, International Conference on Learning Representations, 2019 Search PubMed.
- M. Imaizumi and K. Fukumizu, Proceedings of the Twenty-Second International Conference on Artificial Intelligence and Statistics, 2019, pp. 869–878 Search PubMed.
- Anaconda Software Distribution, 2020, https://docs.anaconda.com/ Search PubMed.
- F. Chollet, et al., Keras, 2015, https://github.com/fchollet/keras Search PubMed.
- M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, Y. Jia, R. Jozefowicz, L. Kaiser, M. Kudlur, J. Levenberg, D. Mané, R. Monga, S. Moore, D. Murray, C. Olah, M. Schuster, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viégas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu and X. Zheng, TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, 2015, https://www.tensorflow.org/ Search PubMed.
- Y. Nesterov, Sov. Math. -Dokl, 1983, 372 Search PubMed.
- T. Tieleman and G. Hinton, COURSERA: Neural networks for machine learning, 2012, vol. 4, pp. 26–31.
- D. P. Kingma and J. Ba, Adam: a method for stochastic optimization, 2014, arXiv:1412.6980.
- A. Krizhevsky, One weird trick for parallelizing convolutional neural networks, 2014, arXiv:1404.5997.
- P. Goyal, P. Dollár, R. Girshick, P. Noordhuis, L. Wesolowski, A. Kyrola, A. Tulloch, Y. Jia and K. He, Accurate, Large minibatch SGD: training ImageNet in 1 Hour, 2017, arXiv:1706.02677.
- S. Jastrzebski, Z. Kenton, D. Arpit, N. Ballas, A. Fischer, Y. Bengio and A. J. Storkey, ICANN, 2018, vol. 3, pp. 392–402 Search PubMed.
- T. Akiba, S. Sano, T. Yanase, T. Ohta and M. Koyama, Proceedings of the 25rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2019, pp. 2623–2631 Search PubMed.
- M. Widenius, D. Axmark and K. Arno, MySQL Reference Manual: Documentation from the Source, O'Reilly Media, Inc., 2002 Search PubMed.
- J. Bergstra, B. Komer, C. Eliasmith, D. Yamins and D. D. Cox, Computat. Sci. Discov., 2015, 8, 014008 CrossRef.
- Streamlit, https://streamlit.io/ Search PubMed.
- L. Li, K. Jamieson, A. Rostamizadeh, E. Gonina, M. Hardt, B. Recht and A. Talwalkar, A system for massively parallel hyperparameter tuning, 2018, arXiv:1810.05934.
- J. W. Ross and J. Crangle, Phys. Rev., 1964, 133, A509–A510 CrossRef.
- H. Wada, S. Tomekawa and M. Shiga, Cryogenics, 1999, 39, 915–919 CrossRef CAS.
- K. A. GschneidnerJr, V. K. Pecharsky and A. O. Tsokol, Rep. Prog. Phys., 2005, 68, 1479–1539 CrossRef.
- X. Tang, H. Sepehri-Amin, N. Terada, A. Martin-Cid, I. Kurniawan, S. Kobayashi, Y. Kotani, H. Takeya, J. Lai, Y. Matsushita, T. Ohkubo, Y. Miura, T. Nakamura and K. Hono, Nat. Commun., 2022, 13, 1817 CrossRef CAS.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- N. Kawamiya and K. Adachi, J. Phys. Soc. Jpn., 1986, 55, 634–640 CrossRef CAS.
- R. Matsumoto, S. Nakano, S. Yamamoto and Y. Takano, Jpn. J. Appl. Phys., 2021, 60, 090902 CrossRef CAS.
- Y. Kim, D. Oh, S. Huh, D. Song, S. Jeong, J. Kwon, M. Kim, D. Kim, H. Ryu, J. Jung, W. Kyung, B. Sohn, S. Lee, J. Hyun, Y. Lee, Y. Kim and C. Kim, Rev. Sci. Instrum., 2021, 92, 073901 CrossRef CAS PubMed.
- F. Restrepo, J. Zhao and U. Chatterjee, Denoising and feature extraction in photoemission spectra with variational auto-encoder neural networks, 2022, arXiv:2203.07537.
- A. Damascelli, Z. Hussain and Z.-X. Shen, Rev. Mod. Phys., 2003, 75, 473–541 CrossRef CAS.
- J. Kim, J. K. Lee and K. M. Lee, IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016, pp. 1646–1654 Search PubMed.
- X. Chai, H. Gu, F. Li, H. Duan, X. Hu and K. Lin, Sci. Rep., 2020, 10, 3302 CrossRef CAS PubMed.
- H. Peng, X. Gao, Y. He, Y. Li, Y. Ji, C. Liu, S. A. Ekahana, D. Pei, Z. Liu, Z. Shen and Y. Chen, Rev. Sci. Instrum., 2020, 91, 033905 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Technical details of approximations. See DOI: https://doi.org/10.1039/d2dd00124a |
| This journal is © The Royal Society of Chemistry 2023 |