Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unified graph neural network force-field for the periodic table: solid state applications
Kamal
Choudhary
 *ab,
Brian
DeCost
*ab,
Brian
DeCost
 c,
Lily
Major
c,
Lily
Major
 de,
Keith
Butler
de,
Keith
Butler
 e,
Jeyan
Thiyagalingam
e,
Jeyan
Thiyagalingam
 e and
Francesca
Tavazza
e and
Francesca
Tavazza
 c
c
aMaterial Measurement Laboratory, National Institute of Standards and Technology, Gaithersburg, 20899, MD, USA. E-mail: kamal.choudhary@nist.gov
bTheiss Research, La Jolla, 92037, CA, USA
cMaterials Measurement Laboratory, National Institute of Standards and Technology, Gaithersburg, 20899, MD, USA
dDepartment of Computer Science, Aberystwyth University, SY23 3DB, UK
eScientific Computing Department, Rutherford Appleton Laboratory, Science and Technology Facilities Council, Harwell Campus, Didcot, OX11 0QX, UK
First published on 23rd January 2023
Abstract
Classical force fields (FFs) based on machine learning (ML) methods show great potential for large scale simulations of solids. MLFFs have hitherto largely been designed and fitted for specific systems and are not usually transferable to chemistries beyond the specific training set. We develop a unified atomisitic line graph neural network-based FF (ALIGNN-FF) that can model both structurally and chemically diverse solids with any combination of 89 elements from the periodic table. To train the ALIGNN-FF model, we use the JARVIS-DFT dataset which contains around 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 materials and 4 million energy-force entries, out of which 307
000 materials and 4 million energy-force entries, out of which 307![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 113 are used in the training. We demonstrate the applicability of this method for fast optimization of atomic structures in the crystallography open database and by predicting accurate crystal structures using a genetic algorithm for alloys.
113 are used in the training. We demonstrate the applicability of this method for fast optimization of atomic structures in the crystallography open database and by predicting accurate crystal structures using a genetic algorithm for alloys.
Introduction
Large scale atomistic simulation of multi-component systems is a difficult task but they are highly valuable for industrial applications such as designing alloys, designing electrical contacts, touch screens, transistors, batteries, composites and catalysts.1–4 Quantum chemistry methods, such as density functional theory, are obvious approaches to simulate such systems; however, they are computationally very expensive for large systems.5 Classical force-fields, or interatomic potentials, such as the embedded-atom method (EAM),6–8 the modified embedded-atom method (MEAM), reactive bond-order (ReaxFF), charge-optimized many-body (COMB), etc.,9–13 can be used for such simulations, but they are usually parameterized for a very narrow chemical phase-space limiting their applicability and transferability. Moreover, it can be quite strenuous and time consuming to develop such traditional classical FFs.Recently, machine learning based FFs14,15 have been used to systematically improve the accuracy of FFs and have successfully been used for multiple systems. One of the pioneer MLFFs were developed by Behler–Parinello in 2007 using a neural network.16 It was initially used for molecular systems and now has been extended to numerous other applications.17 Although a neural network is one of the most popular regressors, other methods such as Gaussian process-based Gaussian approximation potential (GAP),18 as well as linear regression and basis function-based spectral neighbor analysis potential (SNAP)19 have also been thoroughly used. Such FFs use two and three body descriptors to describe the local environment. Other popular MLFF formalisms include smooth overlap of atomic positions (SOAP),20 moment tensor potential (MTP),21,22 symbolic regression23 and polynomial-based approaches.24 One of the critical issues in developing and maintaining classical force-fields is that they are hard to update with software and hardware changes. Luckily, MLFFs are more transparently developed and maintained compared to other classical FFs. A review article on this topic can be found elsewhere.17 Nevertheless, early-generation MLFFs are also limited to a narrow chemical space and may require hand-crafted descriptors which may take time to be identified. Conventional MLFFs are usually trained on specific chemistry only as the number of parameters (cross-terms) exponentially increases with the number of elements in the system. This is where GNN based methods can be particularly useful for generalizability. We note that the number of model parameters do not scale explicitly with the number of elements, because there are no explicit cross-terms for interactions between different pairs of chemical species. Moreover, the model does not require retraining for new systems. So it could be shared and many researchers can make use of pre-trained models.
Graph neural network (GNN) based methods have shown remarkable improvements over descriptor based machine learning methods and can capture highly non-Euclidean chemical space.15,25–33 GNN FFs have been also recently proposed and are still in the development phase.34,35 We developed an atomistic line graph neural network (ALIGNN) in our previous work36 which can capture many body interactions in graph and successfully models more than 70 properties of materials, either scalar or vector quantities, such as formation energy, bandgap, elastic modulus, superconducting properties, adsorption isotherm, electron and density of states etc.36–41 The same automatic differentiation capability that allows training these complex models allows for physically consistent prediction of quantities such as forces and energies; this enables GNNs to be used in quickly identifying relaxed or equilibrium states of complex systems. However, there is a need for a large and diverse amount of data to train unified force-fields.
In this work, we present a dataset of energy and forces with 4 million entries for around 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 materials in the JARVIS-DFT dataset which have been developed over the past 5 years.42 We extend the ALIGNN model to also predict derivatives that are necessary for FF formalism. There can be numerous applications of such a unified FF; however, in this work we limit ourselves to pre-optimization of structures, genetic algorithm based structure, and molecular dynamics applications. The developed model will be publicly available on the ALIGNN GitHub page (https://github.com/usnistgov/alignn) with several examples and a brief documentation.
000 materials in the JARVIS-DFT dataset which have been developed over the past 5 years.42 We extend the ALIGNN model to also predict derivatives that are necessary for FF formalism. There can be numerous applications of such a unified FF; however, in this work we limit ourselves to pre-optimization of structures, genetic algorithm based structure, and molecular dynamics applications. The developed model will be publicly available on the ALIGNN GitHub page (https://github.com/usnistgov/alignn) with several examples and a brief documentation.
Methodology
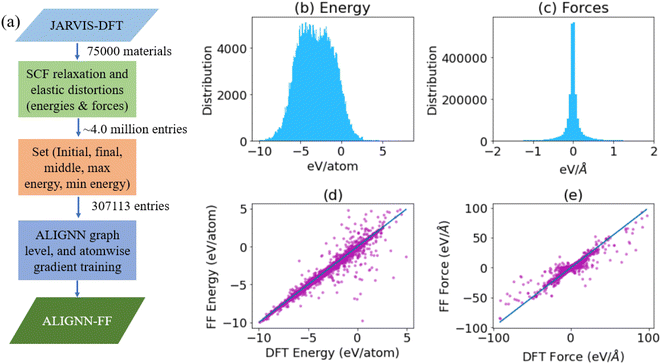
A flow-chart for training an ALIGNN-FF is shown in Fig. 1a. To train the FF, we use a large DFT dataset, JARVIS-DFT, which contains about 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 materials with a variety of atomic structures and chemistry and has been generated over the last 5 years. JARVIS-DFT is primarily based on Vienna Ab initio Simulation Package (VASP)43,44 software and the OptB88vdW45 functional but also contains data obtained using other functionals and methods. In this work, only OptB88vdW-based data have been used. The OptB88vdW functional was shown to be very well applicable to solids in ref. 45 and, ever since, it has been used to model rare-gas dimers and metallic, ionic, and covalent bonded solids, polymers, and small molecular systems.46 Energies and forces are available for each structure optimization and elastic constant calculation runs. The total number of such entries is around 4 million. Although it would be justified to train on the entire dataset, we choose to use only a subset of it because of the computational budget and hardware requirements available to us. Instead of the 4 million datapoints, we use 307
000 materials with a variety of atomic structures and chemistry and has been generated over the last 5 years. JARVIS-DFT is primarily based on Vienna Ab initio Simulation Package (VASP)43,44 software and the OptB88vdW45 functional but also contains data obtained using other functionals and methods. In this work, only OptB88vdW-based data have been used. The OptB88vdW functional was shown to be very well applicable to solids in ref. 45 and, ever since, it has been used to model rare-gas dimers and metallic, ionic, and covalent bonded solids, polymers, and small molecular systems.46 Energies and forces are available for each structure optimization and elastic constant calculation runs. The total number of such entries is around 4 million. Although it would be justified to train on the entire dataset, we choose to use only a subset of it because of the computational budget and hardware requirements available to us. Instead of the 4 million datapoints, we use 307![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 113 points i.e. more than an order of magnitude less, by taking a unique set of first, last, middle, maximum energy and minimum energy structures only. If some snapshots for a run are identical, say the last step and the minimum energy configuration are the same, then we only include one of them. The dataset consists of perfect structures only.
113 points i.e. more than an order of magnitude less, by taking a unique set of first, last, middle, maximum energy and minimum energy structures only. If some snapshots for a run are identical, say the last step and the minimum energy configuration are the same, then we only include one of them. The dataset consists of perfect structures only.
We convert the atomic structures to a graph representation using an atomistic line graph neural network (ALIGNN). Details on the ALIGNN can be found in the related paper.36 In brief, each node in the atomistic graph is assigned 9 input node features based on its atomic species: electronegativity, group number, covalent radius, valence electrons, first ionization energy, electron affinity, block and atomic volume. The inter-atomic bond distances are used as edge features with a radial basis function up to an 8 Å cut-off. We use a periodic 12-nearest-neighbor graph construction. This atomistic graph is then used for constructing the corresponding line graph using interatomic bond-distances as nodes and bond-angles as edge features. The ALIGNN uses edge-gated graph convolution for updating nodes as well as edge features. One ALIGNN layer composes an edge-gated graph convolution on the bond graph with an edge-gated graph convolution on the line graph. The line graph convolution produces bond messages that are propagated to the atomistic graph, which further updates the bond features in combination with atom features.
In this work, we developed the functionality for atomwise and gradient predictions in the ALIGNN framework. Quantities related to gradients of the predicted energy, such as forces on each atom, are computed by applying the chain rule through the automatic differentiation system used to train the GNN. Usually, MLFF datasets are not transferable. We share a large dataset of energy and forces (available on the Figshare repository: https://doi.org/10.6084/m9.figshare.21667874), which can be used for other applications as well. Importantly, this dataset is continuously expanding, making it very systematic and transferable across multiple elements and their combinations. In a closed system, the forces on each atom i depend on its position with respect to every other particle j through a force-field as:
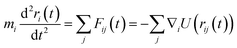 | (1) |
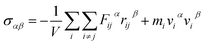 | (2) |
The 307![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 113 data points are split into a 90
113 data points are split into a 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 ratio for training, validation and testing. We train the model for 250 epochs using the same hyper-parameters as in the original ALIGNN model.36 The ALIGNN is based on deep graph library (DGL),48 PyTorch49 and JARVIS-Tools packages.42 We optimize a composite loss function (l) with weighted mean absolute error terms for both forces and energies:
5 ratio for training, validation and testing. We train the model for 250 epochs using the same hyper-parameters as in the original ALIGNN model.36 The ALIGNN is based on deep graph library (DGL),48 PyTorch49 and JARVIS-Tools packages.42 We optimize a composite loss function (l) with weighted mean absolute error terms for both forces and energies:
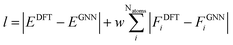 | (3) |
The ALIGNN-FF model has been integrated with an atomic simulation environment (ASE)50 as an energy, force and stress calculator for structure optimization and MD simulations. This calculator can be used for optimizing atomic structures using a genetic algorithm,51 and running molecular dynamics simulations, for example constant-temperature, constant-volume ensemble (NVT) simulations. The structural relaxations are carried out with the fast inertial relaxation engine (FIRE),52 available in ASE. In order to predict the equation of state/energy–volume–curve (EV) simulation, we apply volumetric strains in the range of −0.1 to 0.1 with an interval of 0.01. Although the current implementation is in ASE only, we plan to implement this FF in high-performance MD codes such as LAMMPS53 in the future which can provide significantly better performance.
Results and discussion
Performance on a test set
We find that the energy per atom dataset (with 307![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 113 entries) varies from −9.98 eV per atom to 9.97 eV per atom. The force dataset containing 9
113 entries) varies from −9.98 eV per atom to 9.97 eV per atom. The force dataset containing 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 593
593![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 385 entries (resulting from x, y, z forces on each atom) is mostly centered around zero, but ranges from −591.12 eV Å−1 to 591.40 eV Å−1. The mean absolute deviation (MAD) for energies and forces are 1.80 eV and 0.10 eV Å−1 respectively. The distributions of the energy and force used in training are shown in Fig. 1b and c, respectively. The total dataset was split in 90
385 entries (resulting from x, y, z forces on each atom) is mostly centered around zero, but ranges from −591.12 eV Å−1 to 591.40 eV Å−1. The mean absolute deviation (MAD) for energies and forces are 1.80 eV and 0.10 eV Å−1 respectively. The distributions of the energy and force used in training are shown in Fig. 1b and c, respectively. The total dataset was split in 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 train-validation-test sets. We show the performance on a test set for energies and forces in Fig. 1d and e respectively. We note that these points represent a variety of chemistries and structures unlike usual MLFFs which are usually focused on a specific chemistry. The mean absolute error (MAE) of the predicted energy per atom and force component per atom are 0.086 eV and 0.047 eV Å−1 respectively. In comparison to the previous ALIGNN model for energy only, which has an MAE of 0.03 eV per atom, 0.086 eV per atom might seem high; however, we note that the previous energy model was trained on relaxed structures only while the current model also captures several un-relaxed structures which can be much higher in energy scale. The MAD
5 train-validation-test sets. We show the performance on a test set for energies and forces in Fig. 1d and e respectively. We note that these points represent a variety of chemistries and structures unlike usual MLFFs which are usually focused on a specific chemistry. The mean absolute error (MAE) of the predicted energy per atom and force component per atom are 0.086 eV and 0.047 eV Å−1 respectively. In comparison to the previous ALIGNN model for energy only, which has an MAE of 0.03 eV per atom, 0.086 eV per atom might seem high; however, we note that the previous energy model was trained on relaxed structures only while the current model also captures several un-relaxed structures which can be much higher in energy scale. The MAD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MAE ratios for energies and forces are 20.93 and 2.12, which are high.
MAE ratios for energies and forces are 20.93 and 2.12, which are high.
While the above results are for a force tunable weighting factor of 10, we also train the models with other weighting factors as shown in Table 1. We find that as we increase the weighting factors, the MAEs increase for increase in energies but decrease for forces. As the MAD for forces is 0.1 eV Å−1, we choose to work with the model obtained for the lowest MAE for forces and to analyze its applications in the rest of the paper. Nevertheless, we share model parameters for other weighting factors for those interested in analyzing its effect on property predictions.
| Weight | MAE-Energies (eV per atom) | MAE-Forces (eV Å−1) |
|---|---|---|
| 0.1 | 0.034 | 0.092 |
| 0.5 | 0.044 | 0.089 |
| 1.0 | 0.051 | 0.088 |
| 5.0 | 0.082 | 0.054 |
| 10.0 | 0.086 | 0.047 |
Energy–volume curves
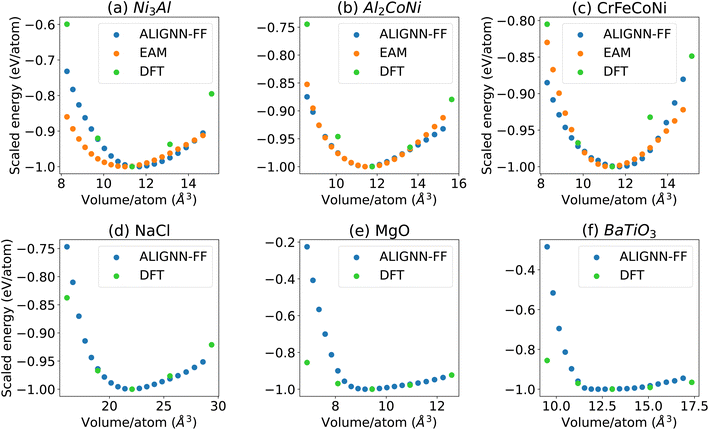
The energy–volume (E–V) curves are crucial to understand the behavior of an FF. We obtain EV-curves for a few test case materials by applying volumetric strains in the range of −0.1 to 0.1 with an interval of 0.01. Specifically, we compare the energy volume curves for Ni3Al (JVASP-14971), Al2CoNi (JVASP-108163), CrFeCoNi (4 atom cell with spacegroup number 216 and a lattice parameter of 4.007 Å), NaCl (JVASP-23862), MgO (JVASP-116), and BaTiO3 (JVASP-8029) using the EAM potential,7,8 GPAW DFT,54 and ALIGNN-FF, as shown in Fig. 2. The energy scales for these methods differ, so we align them with respect to the corresponding minimum energies, for comparison. We used less EV-curve points for a structure in GPAW to save computational cost. We notice that all the EV-curves are parabolic in nature and smooth, indicating a smooth potential energy surface.We find that the EV curves from these methods coincide near the minimum for all systems but for Al2CoNi and CrFeCoNi, the GPAW equilibrium volume is slightly smaller than that for the EAM and ALIGNN-FF, suggesting that the lattice constants for the ALIGNN-FF and EAM might be overestimated compared to those for GPAW. Nevertheless, EAM and ALIGNN-FF data agree well. Comparing the EAM and ALIGN-FF, it's important to remember that GNNs have no fundamental limitation to the number of species they can model (i.e. high chemical diversity), and can, in principle, even extrapolate to species not contained in the training set, which is extremely powerful compared to conventional FFs like the EAM.
Note that there are many other conventional FF repositories available (such as the Inter-atomic Potential Repository55 and JARVIS-FF56) which contain data for a variety of systems. It is beyond the scope of the current work to compare all of them with the ALIGNN-FF; however, it would be an interesting effort for future work.
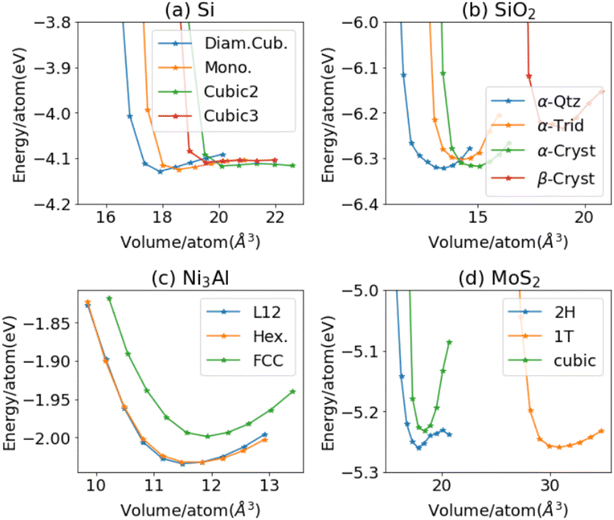
While the above examples are for individual crystals, it is important to distinguish different polymorphs of a composition system for materials simulation (i.e. structural diversity). As shown in Fig. 3, we analyze the energy–volume (EV) curve of four systems and their polymorphs using the ALIGNN-FF. We choose four such example systems because they are representative of different stable structures. In general, however, the EV-curve can be computed for any arbitrary system and structure. In Fig. 3a, we show the EV-curve for 4 silicon materials (JARVIS-IDs: JVASP-1002, JVASP-91933, JVASP-25369, and JVASP-25368) with diamond cubic correctly being the lowest in energy. Similarly, the EV-curve for naturally prevalent SiO2 systems (JARVIS-IDs: JVASP-58349, JVASP-34674, JVASP-34656, and JVASP-58394), binary alloy Ni3Al (JARVIS-IDs: JVASP-14971, JVASP-99749, and JVASP-11979) and vdW bonded material MoS2 (JARVIS-IDs: JVASP-28733, JVASP-28413, and JVASP-58505) all have the correct structure corresponding to the minimum energy. Therefore, while the MAE for our overall energy model is high, such a model is able to distinguish polymorphs of compounds with meV level accuracy which is critical for atomistic applications.
Lattice constants and formation energies
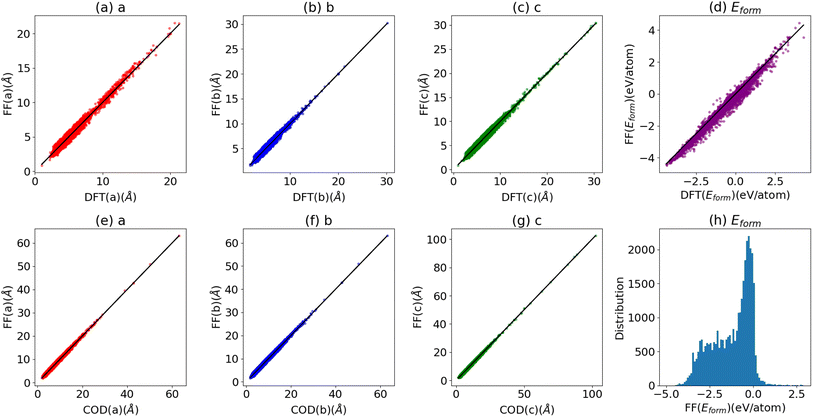
In this section, we compare the lattice constants and formation energies for elemental and multi-component solids from the JARVIS-DFT after optimizing them using the ALIGNN-FF as shown in Fig. 4a–d. For the ALIGNN-FF we choose solids with less than 10 atoms in a cell from the JARVIS-DFT database. We optimize 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 495 such materials, and present the results in Fig. 4a–d. The formation energies require the chemical potential of elemental systems. The energies per atom of elemental solid systems with minimum energy are used as chemical potentials. We optimize the lattices with the FIRE algorithm as implemented in ASE and find reasonable agreement between the DFT and ALIGNN-FF lattice constants. The MAE for a, b, and c lattice constants are 0.11, 0.11 and 0.13 Å respectively. The mean absolute error (MAE) for formation energies between ALIGNN-FF and JARVIS-DFT is 0.08 eV per atom which is reasonable for pre-screening applications. Note that the above validation is different from the performance measurement in Fig. 1 for the 5% test dataset because we optimize the crystals rather than directly predicting the formation energies on unrelaxed structures. Similarly, we apply the ALIGNN-FF on the crystallography open database (COD). The COD contains more than 431
495 such materials, and present the results in Fig. 4a–d. The formation energies require the chemical potential of elemental systems. The energies per atom of elemental solid systems with minimum energy are used as chemical potentials. We optimize the lattices with the FIRE algorithm as implemented in ASE and find reasonable agreement between the DFT and ALIGNN-FF lattice constants. The MAE for a, b, and c lattice constants are 0.11, 0.11 and 0.13 Å respectively. The mean absolute error (MAE) for formation energies between ALIGNN-FF and JARVIS-DFT is 0.08 eV per atom which is reasonable for pre-screening applications. Note that the above validation is different from the performance measurement in Fig. 1 for the 5% test dataset because we optimize the crystals rather than directly predicting the formation energies on unrelaxed structures. Similarly, we apply the ALIGNN-FF on the crystallography open database (COD). The COD contains more than 431![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 778 atomic structures with different types of chemical bondings and environments. We optimize 34
778 atomic structures with different types of chemical bondings and environments. We optimize 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 615 structures in the COD with the number of atoms in a cell less than 50, and the results are shown in Fig. 4e–h. Here, we find the MAE or a, b, and c lattice parameters to be 0.20, 0.20 and 0.23 Å, respectively. Most of the systems in the COD have been derived from experiments, and hence we see many of them have negative formation energies as shown in Fig. 4h.
615 structures in the COD with the number of atoms in a cell less than 50, and the results are shown in Fig. 4e–h. Here, we find the MAE or a, b, and c lattice parameters to be 0.20, 0.20 and 0.23 Å, respectively. Most of the systems in the COD have been derived from experiments, and hence we see many of them have negative formation energies as shown in Fig. 4h.
Genetic algorithm based structure search
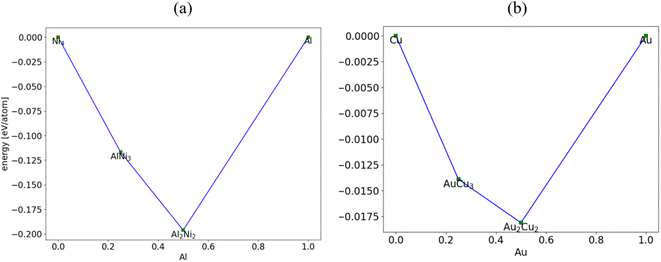
Computational prediction of the ground-state structures of a chemical system is a challenging task. Some of the common methods for this task include genetic algorithm (GA), simulated annealing and basin or minima hopping.57 In the following examples, we show the use of GA together with the ALIGNN-FF to search for crystal structures of Ni–Al and Cu–Al example systems. Genetic algorithms mimic the biological evolution process to solve optimization problems. A GA optimization consists of (1) inheritance, (2) mutation, (3) selection, and (4) crossover operations to produce new structures and search for better survivors from generation to generation based on the “survival of the fittest” idea which in our case would be energetics criteria. While all GAs follow a similar strategy, the details of the individual operations can vary a lot from problem to problem and can be critical to search efficiency. We start with face-centered cubic (FCC) structures of the individual components (FCC Al (JVASP-816) and FCC Ni (JVASP-943) for Ni–Al search and FCC Al and FCC Cu (JVASP-867) for Cu–Al search) as the initial population. We perform relaxation of these systems with the ALIGNN-FF. We choose a population size of 10 individuals and create the initial population by randomly selecting the elements. We use 40 generations to evolve the system and store the entries which are also relaxed with the ALIGNN-FF.After this example GA search for structures, we plot the convex hull diagram of these systems, as shown in Fig. 5. We find that the GA predicts AB and A3B compounds which are in fact observed experimentally in such binary alloys.51,58 Additionally, Ni3Al (spacegroup: Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) is known to be one of the best performing super-alloys51 which is reproduced in the above example. We also found that the formation energy of this structure (−0.47 eV per atom) is similar to Johannesson's51 findings of −0.49 eV per atom. Although the above example is carried out for binary systems, in principle, the same methodology can be applied for any other system as well.
m) is known to be one of the best performing super-alloys51 which is reproduced in the above example. We also found that the formation energy of this structure (−0.47 eV per atom) is similar to Johannesson's51 findings of −0.49 eV per atom. Although the above example is carried out for binary systems, in principle, the same methodology can be applied for any other system as well.
Timing study
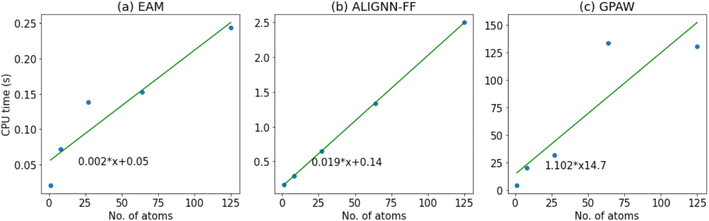
Now, we compare the time for a single step potential energy calculation for FCC aluminum (JVASP-816) with varied supercell sizes with EAM, ALIGNN-FF and GPAW DFT54 methods. All of these calculations are performed on the CPU on a personal laptop; GPU performance scaling may differ, particularly for large cell sizes. We start with a unit cell and start making supercells with [2,2,2], [3,3,3], [4,4,4] and [5,5,5] dimensions. For the GPAW case we use 8 × 8 × 8 k-points and as we make supercells, and we reduce the k-points inversely proportional to the supercell size. As shown in Fig. 6, we find that out of these three, the EAM is the fastest method. The ALIGNN-FF is an order of magnitude slower than the EAM, as expected. While EAM potentials are considerably faster, we note that they are difficult to train for multi-component systems. The GPAW single step calculations are almost 100 times slower than the ALIGNN-FF. As we add multiple electronic and ionic relaxation steps in DFT, the computational cost drastically increases. Note that we chose a very generalized DFT set up with a 330 eV plane wave cutoff and PBE59 exchange correlation functional for GPAW calculations. As we add more k-points and a plane wave cut-off, the computational cost will increase. Moreover, this comparison is only for an elemental system, and as the system complexity (such as the number of elements, number of electrons, vacuum padding etc.) increases, we believe the ALIGNN-FF will get a significantly higher boost in speed. The ALIGNN-FF does not explicitly suffer from DFT parameters such as plane-wave cutoff and k-point settings, which can add much higher computational cost.Conclusion
In summary, we have developed a unified atomistic line graph neural network based force-field (ALIGNN-FF) that can model a diverse set of materials with any combination of 89 elements from the periodic table. Using several test cases, we demonstrate the application of this method to determine several properties such as lattice constants, formation energies, and an EV-curve for different materials including metallic, ionic and van der Waals bonded materials.Although the above examples are based on a few test cases, the ALIGNN-FF can, in principle, be used for several applications such as investigating defective systems, high-entropy alloys, metal–organic frameworks, catalysts, battery designs, etc. and its validity needs to be tested for other applications which is beyond the scope of the present work. Also, as the methods for including larger datasets improve (such as training on millions of data points), and integration of active learning and transfer learning strategies is achieved, we believe we can train more accurate models. Moreover, such a universal FF model can be integrated with a universal tight-binding model60 so that classical and quantum properties can be predicted for large systems. In the current state, such FFs can be very useful for structure optimization; however, there is lot of room for improvement in terms of other physical characteristics such as defects, magnetism, charges, electronic levels, etc. Under-parameterized potentials get drastically better energy and force accuracy, but are much narrower in scope and have much higher training data density in their regions of applicability, based on highly tailored (and expensive) fit-for-purpose dataset generation. Over-parameterized GNNs are currently trained on extremely sparse datasets that are repurposed from high throughput material discovery efforts (e.g. JARVIS-DFT). Their potential to generalize a much greater chemical diversity is good, but a lot of research is needed to close the gap in accuracy with more narrow MLFF methods. A happy path forward for future research is probably intermediate in terms of the breadth of chemical and structural space and dataset density. Additionally, availability of standard benchmark datasets of multi-component systems with important properties such as diffusion coefficients for a diverse set of solute species, stacking fault energies, defect formation energies (solute substitution, vacancy, Schottky/Frenkel, etc), thermal conductivity, mechanical properties, and interface properties would play a pivotal role in the development of universal force-fields.
Integration with an external coding interface such as Alloy Theoretic Automated Toolkit (ATAT),61 calculation of phase diagrams (CALPHAD),62 Universal Structure Predictor (USPEX),63ab initio random structure searching (AIRSS),64 genetic algorithm for structure and phase prediction (GASP),65,66 RASPA,67etc. would further extend the applications for alloy design, structure predictions and designing nanoporous materials in the future. We note that the current force-field has been mainly evaluated for solids only, but in principle can be extended to polymers, and molecular and hybrid systems as well in the future. While there are several areas of improvements for such a unified force-field, we believe that this work would spark interest among materials scientists and engineers to enable a very wide range of atomistic applications.
Data availability
The dataset, code and model used in this work are available at: https://doi.org/10.6084/m9.figshare.21667874. The JARVIS-DFT dataset can also be obtained from the websites: https://jarvis.nist.gov/ and https://jarvistools.readthedocs.io/en/master/databases.ht.Conflicts of interest
There are no conflicts to declare.Acknowledgements
K. C. thanks the National Institute of Standards and Technology for funding and computational support. In addition, K. C thanks Ruth Pachter and Kiet Ngyuen from the Air Force Research Laboratory for helpful discussions. This work was also partially supported by Wave 1 of the UKRI Strategic Priorities Fund under the EPSRC grant EP/T001569/1, particularly the ‘AI for Science’ theme within that grant, by the Alan Turing Institute ad UKRI AnIMLAC CDT, grant no. EP/S023992/1.References
- S. B. Ogale, Thin films and heterostructures for oxide electronics, Springer Science & Business Media, 2006 Search PubMed.
- M. P. Andersson, T. Bligaard, A. Kustov, K. E. Larsen, J. Greeley, T. Johannessen, C. H. Christensen and J. K. Nørskov, Toward computational screening in heterogeneous catalysis: Pareto-optimal methanation catalysts, J. Catal., 2006, 239, 501–506 CrossRef CAS.
- T. Liang, T.-R. Shan, Y.-T. Cheng, B. D. Devine, M. Noordhoek, Y. Li, Z. Lu, S. R. Phillpot and S. B. Sinnott, Classical atomistic simulations of surfaces and heterogeneous interfaces with the charge-optimized many body (COMB) potentials, Mater. Sci. Eng., R, 2013, 74, 255–279 CrossRef.
- X. Li, Y. Zhu, W. Cai, M. Borysiak, B. Han, D. Chen, R. D. Piner, L. Colombo and R. S. Ruoff, Transfer of large-area graphene films for high-performance transparent conductive electrodes, Nano Lett., 2009, 9, 4359–4363 CrossRef CAS PubMed.
- D. J. Srolovitz and V. Vitek, Atomistic Simulation of Materials: Beyond Pair Potentials, Springer Science & Business Media, 2012 Search PubMed.
- M. S. Daw and M. I. Baskes, Semiempirical, quantum mechanical calculation of hydrogen embrittlement in metals, Phys. Rev. Lett., 1983, 50, 1285 CrossRef CAS.
- G. P. Pun, V. Yamakov and Y. Mishin, Interatomic potential for the ternary Ni–Al–Co system and application to atomistic modeling of the B2–L10 martensitic transformation, Modell. Simul. Mater. Sci. Eng., 2015, 23, 065006 CrossRef.
- D. Farkas and A. Caro, Model interatomic potentials for Fe–Ni–Cr–Co–Al high-entropy alloys, J. Mater. Res., 2020, 35, 3031–3040 CrossRef CAS.
- M. S. Daw and M. I. Baskes, Embedded-atom method: Derivation and application to impurities, surfaces, and other defects in metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 6443 CrossRef CAS.
- T. Liang, B. Devine, S. R. Phillpot and S. B. Sinnott, Variable charge reactive potential for hydrocarbons to simulate organic-copper interactions, J. Phys. Chem. A, 2012, 116, 7976–7991 CrossRef CAS PubMed.
- D. W. Brenner, Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 9458 CrossRef CAS PubMed.
- A. C. Van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, ReaxFF: a reactive force field for hydrocarbons, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS.
- D. W. Brenner, The art and science of an analytic potential, Phys. Status Solidi B, 2000, 217, 23–40 CrossRef CAS.
- I. Poltavsky and A. Tkatchenko, Machine learning force fields: Recent advances and remaining challenges, J. Phys. Chem. Lett., 2021, 12, 6551–6564 CrossRef CAS PubMed.
- K. Choudhary, B. DeCost, C. Chen, A. Jain, F. Tavazza, R. Cohn, C. W. Park, A. Choudhary, A. Agrawal and S. J. Billinge, et al., Recent advances and applications of deep learning methods in materials science, npj Comput. Mater., 2022, 8, 1–26 CrossRef.
- J. Behler and M. Parrinello, Generalized neural-network representation of high-dimensional potential-energy surfaces, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- O. T. Unke, S. Chmiela, H. E. Sauceda, M. Gastegger, I. Poltavsky, K. T. Schütt, A. Tkatchenko and K.-R. Müllerr, Machine learning force fields, Chem. Rev., 2021, 121, 10142–10186 CrossRef CAS PubMed.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Gaussian approximation potentials: the accuracy of quantum mechanics, without the electrons, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- M. A. Wood and A. P. Thompson, Extending the accuracy of the SNAP interatomic potential form, J. Chem. Phys., 2018, 148, 241721 CrossRef PubMed.
- A. P. Bartók, R. Kondor and G. Csányi, On representing chemical environments, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- A. V. Shapeev, Moment tensor potentials: A class of systematically improvable interatomic potentials, Multiscale Model. Simul., 2016, 14, 1153–1173 CrossRef.
- I. S. Novikov, K. Gubaev, E. V. Podryabinkin and A. V. Shapeev, The MLIP package: moment tensor potentials with MPI and active learning, Mach. learn.: sci. technol., 2020, 2, 025002 Search PubMed.
- A. Hernandez, A. Balasubramanian, F. Yuan, S. A. Mason and T. Mueller, Fast, accurate, and transferable many-body interatomic potentials by symbolic regression, npj Comput. Mater., 2019, 5, 1–11 CrossRef.
- R. Drautz, Atomic cluster expansion for accurate and transferable interatomic potentials, Phys. Rev. B, 2019, 99, 014104 CrossRef CAS.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, Schnet–a deep learning architecture for molecules and materials, J. Chem. Phys., 2018, 148, 241722 CrossRef PubMed.
- T. Xie and J. C. Grossman, Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties, Phys. Rev. Lett., 2018, 120, 145301 CrossRef CAS PubMed.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Graph networks as a universal machine learning framework for molecules and crystals, Chem. Mater., 2019, 31, 3564–3572 CrossRef CAS.
- C. Chen and S. P. Ong, A universal graph deep learning interatomic potential for the periodic table, arXiv, 2022, preprint, arXiv:2202.02450.
- S. Kearnes, K. McCloskey, M. Berndl, V. Pande and P. Riley, Molecular graph convolutions: moving beyond fingerprints, J. Comput.-Aided Mol. Des., 2016, 30, 595–608 CrossRef CAS PubMed.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, Neural message passing for quantum chemistry, International conference on machine learning, 2017, pp. 1263–1272 Search PubMed.
- J. Klicpera, S. Giri, J. T. Margraf and S. Günnemann, Fast and uncertainty-aware directional message passing for non-equilibrium molecules, arXiv, 2020, preprint, arXiv:2011.14115.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. E. Kozinsky, (3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials, Nat. Commun., 2022, 13, 1–11 Search PubMed.
- A. Musaelian, S. Batzner, A. Johansson, L. Sun, C. J. Owen, M. Kornbluth and B. Kozinsky, Learning Local Equivariant Representations for Large-Scale Atomistic Dynamics, arXiv, 2022, preprint, arXiv:2204.05249.
- C. W. Park, M. Kornbluth, J. Vandermause, C. Wolverton, B. Kozinsky and J. P. Mailoa, Accurate and scalable graph neural network force field and molecular dynamics with direct force architecture, npj Comput. Mater., 2021, 7, 1–9 CrossRef.
- S. Chmiela, H. E. Sauceda, K.-R. Müller and A. Tkatchenko, Towards exact molecular dynamics simulations with machine-learned force fields, Nat. Commun., 2018, 9, 1–10 CrossRef CAS PubMed.
- K. Choudhary and B. DeCost, Atomistic Line Graph Neural Network for improved materials property predictions, npj Comput. Mater., 2021, 7, 1–8 CrossRef.
- K. Choudhary, T. Yildirim, D. W. Siderius, A. G. Kusne, A. McDannald and D. L. Ortiz-Montalvo, Graph neural network predictions of metal organic framework CO2 adsorption properties, Comput. Mater. Sci., 2022, 210, 111388 CrossRef CAS.
- K. Choudhary and K. Garrity, Designing High-Tc Superconductors with BCS-inspired Screening, Density Functional Theory and Deep-learning, arXiv, 2022, preprint, arXiv:2205.00060.
- K. Choudhary and B. G. Sumpter, A Deep-learning Model for Fast Prediction of Vacancy Formation in Diverse Materials, arXiv, 2022, preprint, arXiv:2205.08366.
- P. R. Kaundinya, K. Choudhary and S. R. Kalidindi, Prediction of the electron density of states for crystalline compounds with Atomistic Line Graph Neural Networks (ALIGNN), JOM, 2022, 74, 1395–1405 CrossRef CAS.
- R. Gurunathan, K. Choudhary and F. Tavazza, Rapid Prediction of Phonon Structure and Properties using the Atomistic Line Graph Neural Network (ALIGNN), arXiv, 2022, preprint, arXiv:2207.12510.
- K. Choudhary, K. F. Garrity, A. C. Reid, B. DeCost, A. J. Biacchi, A. R. Hight Walker, Z. Trautt, J. Hattrick-Simpers, A. G. Kusne and A. Centrone, et al., The joint automated repository for various integrated simulations (JARVIS) for data-driven materials design, npj Comput. Mater., 2020, 6, 1–13 CrossRef.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. Klimeš, D. R. Bowler and A. Michaelides, Chemical accuracy for the van der Waals density functional, J. Phys.: Condens. Matter, 2009, 22, 022201 CrossRef PubMed.
- K. Choudhary, G. Cheon, E. Reed and F. Tavazza, Elastic properties of bulk and low-dimensional materials using van der Waals density functional, Phys. Rev. B, 2018, 98, 014107 CrossRef CAS PubMed.
- A. K. Subramaniyan and C. Sun, Continuum interpretation of virial stress in molecular simulations, Int. J. Solids Struct., 2008, 45, 4340–4346 CrossRef.
- M. Wang, D. Zheng, Z. Ye, Q. Gan, M. Li, X. Song, J. Zhou, C. Ma, L. Yu and Y. Gai, et al., Deep graph library: a graph-centric, highly-performant package for graph neural networks, arXiv, 2019, preprint, arXiv:1909.01315.
- A. Paszke, S. Gross, S. Chintala, G. Chanan, E. Yang, Z. DeVito, Z. Lin, A. Desmaison, L. Antiga and A. Lerer, Automatic differentiation in pytorch, 2017 Search PubMed.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Du lak, J. Friis, M. N. Groves, B. Hammer and C. Hargus, et al., The atomic simulation environment—a Python library for working with atoms, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- G. H. Johannesson, T. Bligaard, A. V. Ruban, H. L. Skriver, K. W. Jacobsen and J. K. Nørskov, Combined electronic structure and evolutionary search approach to materials design, Phys. Rev. Lett., 2002, 88, 255506 CrossRef CAS PubMed.
- E. Bitzek, P. Koskinen, F. Gähler, M. Moseler and P. Gumbsch, Structural relaxation made simple, Phys. Rev. Lett., 2006, 97, 170201 CrossRef PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in’t Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen, et al., LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Du lak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola and H. Hansen, et al., Electronic structure calculations with GPAW: a real-space implementation of the projector augmented-wave method, J. Phys.: Condens. Matter, 2010, 22, 253202 CrossRef CAS PubMed.
- C. A. Becker, F. Tavazza, Z. T. Trautt and R. A. B. de Macedo, Considerations for choosing and using force fields and interatomic potentials in materials science and engineering, Curr. Opin. Solid State Mater. Sci., 2013, 17, 277–283 CrossRef CAS.
- K. Choudhary, F. Y. P. Congo, T. Liang, C. Becker, R. G. Hennig and F. Tavazza, Evaluation and comparison of classical interatomic potentials through a user-friendly interactive web-interface, Sci. Data, 2017, 4, 1–12 Search PubMed.
- M. Ji, C.-Z. Wang and K.-M. Ho, Comparing efficiencies of genetic and minima hopping algorithms for crystal structure prediction, Phys. Chem. Chem. Phys., 2010, 12, 11617–11623 RSC.
- A. van de Walle and G. Ceder, Automating first-principles phase diagram calculations, J. Phase Equilib., 2002, 23, 348–359 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- K. F. Garrity and K. Choudhary, Fast and Accurate Prediction of Material Properties with Three-Body Tight-Binding Model for the Periodic Table, arXiv, 2021, preprint, arXiv:2112.11585.
- A. Van De Walle, M. Asta and G. Ceder, The alloy theoretic automated toolkit: A user guide, Calphad, 2002, 26, 539–553 CrossRef CAS.
- Z.-K. Liu, First-principles calculations and CALPHAD modeling of thermodynamics, J. Phase Equilib. Diffus., 2009, 30, 517–534 CrossRef CAS.
- C. W. Glass, A. R. Oganov and N. Hansen, USPEX—Evolutionary crystal structure prediction, Comput. Phys. Commun., 2006, 175, 713–720 CrossRef CAS.
- C. J. Pickard and R. Needs, High-pressure phases of silane, Phys. Rev. Lett., 2006, 97, 045504 CrossRef PubMed.
- B. C. Revard, W. W. Tipton and R. G. Hennig, Structure and stability prediction of compounds with evolutionary algorithms, Prediction and Calculation of Crystal Structures, 2014, pp. 181–222 Search PubMed.
- K. Choudhary, T. Liang, K. Mathew, B. Revard, A. Chernatynskiy, S. R. Phillpot, R. G. Hennig and S. B. Sinnott, Dynamical properties of AlN nanostructures and heterogeneous interfaces predicted using COMB potentials, Comput. Mater. Sci., 2016, 113, 80–87 CrossRef CAS.
- D. Dubbeldam, S. Calero, D. E. Ellis and R. Q. Snurr, RASPA: molecular simulation software for adsorption and diffusion in flexible nanoporous materials, Mol. Simul., 2016, 42, 81–101 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2023 |