Open Access Article
Open Access ArticleMaterials synthesizability and stability prediction using a semi-supervised teacher-student dual neural network
Daniel
Gleaves
 ,
Nihang
Fu
,
Edirisuriya M.
Dilanga Siriwardane
,
Nihang
Fu
,
Edirisuriya M.
Dilanga Siriwardane
 ,
Yong
Zhao
,
Yong
Zhao
 and
Jianjun
Hu
and
Jianjun
Hu
 *
*
Department of Computer Science and Engineering University of South Carolina Columbia, SC 29201, USA. E-mail: jianjunh@cse.sc.edu
First published on 27th January 2023
Abstract
Data driven generative deep learning models have recently emerged as one of the most promising approaches for new materials discovery. While generator models can generate millions of candidates, it is critical to train fast and accurate machine learning models to filter out stable, synthesizable materials with the desired properties. However, such efforts to build supervised regression or classification screening models have been severely hindered by the lack of unstable or unsynthesizable samples, which usually are not collected and deposited in materials databases such as ICSD and Materials Project (MP). At the same time, there is a significant amount of unlabelled data available in these databases. Here we propose a semi-supervised deep neural network (TSDNN) model for high-performance formation energy and synthesizability prediction, which is achieved via its unique teacher-student dual network architecture and its effective exploitation of the large amount of unlabeled data. For formation energy based stability screening, our semi-supervised classifier achieves an absolute 10.3% accuracy improvement compared to the baseline CGCNN regression model. For synthesizability prediction, our model significantly increases the baseline PU learning's true positive rate from 87.9% to 92.9% using 1/49 model parameters. To further prove the effectiveness of our models, we combined our TSDNN-energy and TSDNN-synthesizability models with our CubicGAN generator to discover novel stable cubic structures. Out of the 1000 recommended candidate samples by our models, 512 of them have negative formation energies as validated by our DFT formation energy calculations. Our experimental results show that our semi-supervised deep neural networks can significantly improve the screening accuracy in large-scale generative materials design. Our source code can be accessed at https://github.com/usccolumbia/tsdnn.
Introduction
Machine learning based screening models have emerged as one of the most promising approaches for discovery of new materials either from repositories of known materials1–3 or from hypothetical materials with compositions4–6 or/and structures7,8 generated by generative deep learning models or by crystal structure prediction algorithms.9 While existing materials repositories such as ICSD10 and Materials Project11 can be conveniently used for finding known synthesizable materials with potential new functions, the success rate of discovering materials with extremely novel properties is severely constrained by the limited diversity and the number of known materials: the ICSD has only about 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 crystal materials compared to the almost infinite chemical space. To search for novel materials in uncharted chemical space, it is important to develop the capability to screen stable and synthesizable hypothetical materials12,13 out of the candidates generated by generative models or CSP algorithms and then apply high-performance materials property prediction models to find the desired candidates.14,15
000 crystal materials compared to the almost infinite chemical space. To search for novel materials in uncharted chemical space, it is important to develop the capability to screen stable and synthesizable hypothetical materials12,13 out of the candidates generated by generative models or CSP algorithms and then apply high-performance materials property prediction models to find the desired candidates.14,15
Given a material's structure, its structural stability can be estimated by calculating its formation energy using first-principles computations such as density functional theory (DFT) and the phase stability of a structure can be quantified by using the energy above the hull (Ehull).16 However, DFT based calculation of formation energy or Ehull is too computationally expensive, which leads to a large number of machine learning models for formation energy/enthalpy prediction17,18 based on composition without18–25 or with structures.15,21,26–28 However despite the development of more than a dozen formation energy/enthalpy prediction models, they all suffer from a neglected strong bias from the training data: most of the training samples from the repositories of known materials are stable structures with negative formation energy. For example, out of the 138![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 613 samples of the Materials Project database, only 11
613 samples of the Materials Project database, only 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 340 samples have positive formation energy. This makes it difficult to train good supervised classification or regression models that can differentiate stable materials from the unstable candidates.
340 samples have positive formation energy. This makes it difficult to train good supervised classification or regression models that can differentiate stable materials from the unstable candidates.
These methods usually formulate the formation energy prediction problem as a regression problem with models trained with a majority of negative formation energy. However, such formation energy prediction models are most interesting when they can be used to differentiate stable versus non-stable hypothetical materials, most of which tend to be unstable and have positive formation energy. Despite the claimed high accuracy of these models,17,25 they are mainly evaluated on stable materials with negative formation energy, leading to their questionable extrapolation performance on out-of-distribution non-stable materials with positive formation energy.29 The question here is how we can train ML models with a majority of samples with only negative formation energy while they are expected to differentiate stable materials with negative formation energy from unstable materials with positive formation energy. In addition to this issue, it is argued that the accurate prediction of formation alone does not correspond exactly to high accuracy of predicting stability which can be better measured by the quantity ΔHf and be obtained by a convex hull construction in formation enthalpy (ΔHf)-composition space.25
Synthesizability of a hypothetical material is another important property needed for effective materials screening,30,31 which is challenging to predict accurately.32 It is found that many naive generative models for molecules tend to generate unsynthesizable candidates.31 Unfortunately, synthesizability is much more challenging to be predicted using ML models or other computational methods.32,33 One approach is to predict the synthesis path given a material composition;34–37 however, these methods are newly emerging and cannot yet be applied to the large scale of hypothetical materials. Another option is ML based models for materials synthesizability prediction. For inorganic materials, a recent study using the positive and unlabelled semi-supervised machine learning algorithm (PU-learning)13 has been applied to predict synthesizability with promising results. Davariashtiyani et al. proposed a 3D voxel representation based convolution network for synthesizability classification trained with 600 anomaly samples.38 However, the extrapolation prediction power of their model is expected to be low due to their highly biased and limited selection of anomaly structures.
Semi-supervised learning39,40 has been widely and successfully used in computer vision,41 natural language processing,42 and medical diagnosis43 to mainly address the scarce annotation data issue or just to improve the performance using unlabelled data. However, despite the well-known small data issue in materials ML problems, semi-supervised learning has rarely been used in such problems except in a few studies13,44,45 for materials synthesis classification, microstructure classification, and synthesizability prediction.13
SSL algorithms are developed on several fundamental assumptions40 including (1) the smoothness assumption: two samples close to each other in the input space tend to have similar labels; (2) low-density assumption: the decision boundary should not pass through high-density areas in the input space; (3) manifold assumption: data points on the same low-dimensional manifold should have the same label. These assumptions can be interpreted as specific instances of the cluster assumption: similar points tend to belong to the same group/cluster. There are two main categories of SSL algorithms including graph based transductive methods which focus on label propagation and inductive methods which aim to build a ML model f: x → y by incorporating unlabelled data either in pre-processing steps, directly inside the loss function, or via a pseudo-labeling step. SSL algorithms have demonstrated strong performance especially in the deep learning framework.42
Here we propose a semi-supervised learning (SSL) approach for the materials formation energy and synthesizability prediction problems by considering both the database bias that most samples are stable, synthesizable materials with negative formation energy and the model application scenarios for which we need to apply the models to differentiate stable and unstable hypothetical materials. In this work, we exploit a deep learning based SSL framework, the teacher-student deep neural network (TSDNN),46 to address the lack of negative samples in synthesizability prediction and formation energy prediction. A TSDNN is characterized by a dual-network architecture with a teacher model trained using a supervised signal and an unsupervised feedback signal from the student network to improve the teacher's pseudo-labeling capability. The teacher model provides pseudo-labels for unlabeled data for the student model to learn from. Unlike the previous positive-unlabeled SSL algorithm for synthesizability prediction,13 our TSDNN model has much fewer parameters while achieving 5.3% higher prediction accuracy and improving the positive rate from 87.9% to 92.9% using the same performance evaluation. Extensive experiments on the formation energy classifiers also show that our TSDNN can screen negative formation energies with 7.5% higher precision, a 10.3% higher F1 score, and 9.7% higher accuracy than the CGCNN regression model.
Our contributions in this paper can be summarized as follows:
• We identify the inherent dataset bias in formation energy and synthesizability prediction problems and propose to formulate both as semi-supervised classification problems.
• We exploit a novel teacher-student dual network deep neural network model framework to achieve high-performance semi-supervised learning for both formation energy and synthesizability classification. Compared to previous approaches, our models achieved >10% performance improvement with much simpler model structures and 98% fewer model sizes.
• We evaluate our algorithms on different dataset configurations and demonstrate the effectiveness and advantage of SSL for both problems.
• We apply our TSDNN based formation energy and synthesizability SSL model for screening new materials from the hypothetical cubic crystal materials and identify a set of new stable materials as verified by DFT formation energy calculations.
Results
In many problem domains, particularly materials science, there is a severe lack of quality labeled data. The set is often too small, unbalanced, or has missing data classes. For example, there are only about 2700 crystal materials with labelled thermal conductivity values47 and less than 1700 annotated piezoelectric materials in the Materials Project (MP) database.48 In the same database, only 8.2% of materials have a positive formation energy. As a result, it becomes difficult to train a well-converged machine learning model using these data and obtain adequate performance on out-of-distribution samples. In this work, we propose to combine the TSDNN semi-supervised learning framework shown in Fig. 1 with a crystal graph convolutional neural network (CGCNN)26 (Fig. 2) for structure-based synthesizabiliy and formation energy prediction. The teacher-student deep neural network (TSDNN) leverages unlabeled data to overcome the issues of a small labeled dataset and the severe issue of a lack of negative samples. In this case, we are lacking known unstable samples as they do not exist.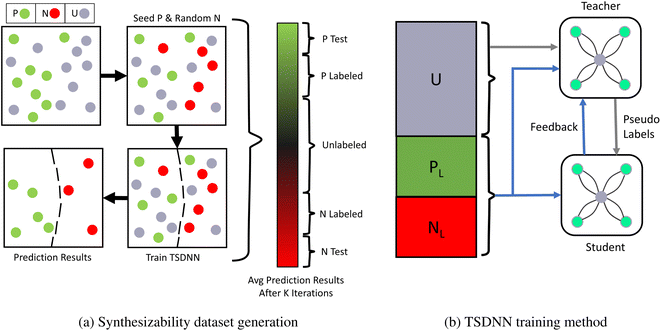 | ||
| Fig. 1 PU-learning based dataset generation and training procedure for the TSDNN framework. (a) The first step of a TSDNN is to cluster positive and negative samples from the unlabeled set. Since there are only positive samples in our raw dataset, we use an iterative PU learning procedure13 to select the most likely negative samples from the unlabeled set. It starts with only positive (green) and unlabeled (gray) samples. It first randomly selects unlabeled samples (equal in number to the positive) as negative ones. A TSDNN model is then trained using these labels and used to classify all samples. This random sampling and prediction process is repeated 5 times and the classification scores are averaged for each material, as shown in the gradient bar. From this, we assemble a complete dataset: 9629 materials with the highest classification scores (P Test) are selected as the positive test set and 9629 lowest (N Test) ones as the negative test set. The labeled training dataset (P labeled and N labeled) is selected as shown, and the middle section of uncertain classifications is left as the unknown set (unlabeled). A final fine-tuned TSDNN model is then trained using this clustered dataset. (b) A TSDNN model is trained using a teacher model and a student model. The teacher model is trained on labeled data (PL + NL) and predicts pseudo-labels (classification score) for the unlabeled data (U). The student model learns from these pseudo-labels exclusively. The teacher model also has a feedback signal46 from the student model based on the student model's loss calculated on the batch of labeled data. This allows for the teacher model to be updated to optimize for the student model's performance. The student model is saved and used for testing and predictions. | ||
Semi-supervised learning based screening models using teacher-student deep neural networks (TSDNNs)
A TSDNN is a semi-supervised learning framework composed of two neural network models (Fig. 1b): a teacher network and a student network. These two models are trained in parallel. The teacher model generates pseudo labels on the unlabelled data which are then used to train the student network. The teacher model is trained with two objectives in our case: labeled data (synthesizability or formation energy classification) performance and a feedback signal46 from the student model based on its performance on the labelled dataset. This feedback signal provides a guide for the teacher model in the case when the unlabeled samples are unlike the labeled data. The student model is trained only on unlabeled data with hard pseudo-labels provided by the teacher model. This leverages unlabeled data to improve further than supervised learning and smooth biases that may be found in the labeled data, such as through dataset imbalances, as seen with formation energy classification.Given a labeled dataset and an unlabeled dataset, the training process of the TSDNN goes as follows: first, a batch of labeled and a batch of unlabeled data are sampled. The teacher's loss is calculated on the labeled batch. The teacher model then provides pseudo-labels for the unlabeled batch for training the student network. The student model's loss is calculated on the labeled data both before and after the student model is updated with the pseudo-labels from the teacher model. The change in this performance from the teacher's pseudo-labels is used to calculate the student model's feedback signal, which is combined with the teacher's loss over labeled data to update the teacher model. This helps the student network to learn the true labels of a large set of unlabeled data by ensuring that the student model is clustering the unlabeled data consistent with the labeled dataset. The benefit of this is that a small labeled dataset can be used and augmented with a much larger unlabeled dataset, resulting in a more robust student model that has been trained on the unlabeled data.
Loss functions of our student and teacher networks include:
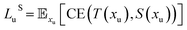 | (1) |
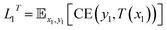 | (2) |
A feedback signal from the student model46 is additionally included to further optimize the teacher model by improving its pseudo-labeling. This reduces labeled data bias by introducing a dynamic teacher; while a static teacher model would replicate implicit biases, this dynamic teacher model is able to adapt to the full context of the unlabeled dataset, which in turn leads to a less biased final model.
In the TSDNN, before training can commence, the dataset must be prepared for our semi-supervised framework. In the case of synthesizability, there are only positive data, so we must first identify candidate negative samples. This is possible by clustering, since synthesizability is defined with respect to other previously synthesized materials. For synthesizability, selecting the most optimal negative labels is integral to assembling an accurate labelled dataset. For formation energy classification, the two greatest challenges to overcome are the high density of materials with near-zero formation energies, as shown in Fig. 3, and the labelled dataset imbalance with relatively few negative samples. Once these issues are resolved, the TSDNN model can be trained.
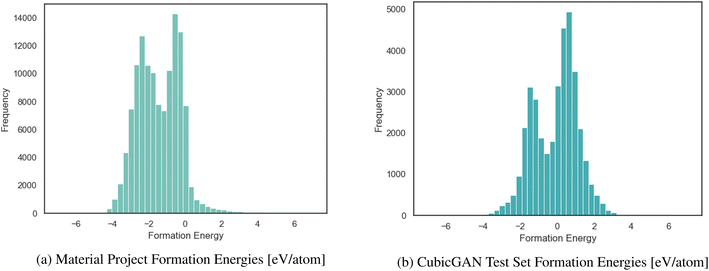 | ||
| Fig. 3 Distribution of formation energy for the MP dataset with few positive values and the Cubic test dataset with many positive energies. | ||
Synthesizability dataset generation using PU learning
Material synthesizability prediction is a positive and unknown (PU) learning problem, meaning that there are only positive samples, materials with ICSD entries which have been previously synthesized, and unlabeled samples, hypothetical materials which may or may not be able to be synthesized. To utilize these unlabelled samples, the PU learning framework was proposed in ref. 13 (Fig. 1a), which we use to cluster the unlabeled data and produce an experimental labeled dataset. By clustering the unlabeled data, we can identify likely synthesizable materials clustered with known synthesizable materials as well as identify the cluster of likely unsynthesizable materials that we can then use as a negative class to fill in a full labeled dataset.The PU learning framework is a modified transductive bagging support vector machine.49 In this framework, a model is trained with a random selection of the unlabeled data set as the negative class equal in size to the positive class. This model then produces predictions on the remaining unlabeled data not chosen as the negative class. After a given number of iterations, the unlabeled scores are averaged, resulting in a final score. The motivation in this is to identify a cluster of samples that lie apart from the positive class. This is useful for identifying the highest and lowest prediction score materials, but still leaves a large amount of uncertain data with a score near the classification boundary. Using our TSDNN semi-supervised framework, we train our final fine-tuned model on the new labeled dataset produced from the PU learning dataset generation step and use it to classify the remaining unknown data.
CGCNN model for structure-based classification
The TSDNN model is a wrapper framework for semi-supervised classification, which can be combined with any material property prediction model architecture. Here we adopt the CGCNN model for structure based synthesizablity and formation energy classification. The CGCNN (Fig. 2) works by converting material structures in their unit cell into crystal graphs by encoding atoms as nodes and bonds as the edges between them. By encoding both the atomic features and bond interactions between atoms, the inherent structural characteristics can be learned. A set of convolutional layers are then built on top of the crystal graphs to extract the feature representations, which are fed to the hidden layers for final classification.TSDNN-syn: a synthesizability screening model using semi-supervised learning models
Our synthesizability screening model (TSDNN-syn) is a binary classification model trained using the above-mentioned semi-supervised teacher-student neural network (TSDNN). We obtained the raw dataset of crystal structures from the Materials Project (MP) database and used the following procedure to prepare the training and testing datasets. First we obtained 125![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 619 materials with 48
619 materials with 48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 146 of them being ICSD entries, which are labeled as positive samples to indicate that they are synthesizable materials. However, there are no ground truth negative samples, the un-synthesizable materials from the downloaded MP dataset. There are only ICSD entries and virtual materials, the latter with an unknown synthesizability status. This lack of negative samples prevents a traditional supervised classification model from being trained as it normally would. To overcome this, we used the positive and unknown (PU) learning method13 discussed above to cluster the unlabeled data and identify materials with low synthesizability scores to be used as negative samples, as discussed above for the initial experimental dataset. We first remove 9629 randomly selected positive samples to be used as the test set prior to any training. Then, we generate the clustered unlabeled dataset as shown in Fig. 1b, where our TSDNN model is trained for 5 independent iterations. In each iteration, a random subset of the unlabeled dataset is selected to be the negative set with a size equal to the number of samples in the positive set. A TSDNN model is then trained on these data. This model makes predictions on the unlabeled samples not selected as the negative set. The final predicted scores are averaged across the 5 iterations to provide the clustered dataset. We then selected the lowest 9629 lowest-scored materials as negative samples to be used in the final test set to ensure our final model accurately classifies the positive and negative set that was determined by clustering. Then, the next 38
146 of them being ICSD entries, which are labeled as positive samples to indicate that they are synthesizable materials. However, there are no ground truth negative samples, the un-synthesizable materials from the downloaded MP dataset. There are only ICSD entries and virtual materials, the latter with an unknown synthesizability status. This lack of negative samples prevents a traditional supervised classification model from being trained as it normally would. To overcome this, we used the positive and unknown (PU) learning method13 discussed above to cluster the unlabeled data and identify materials with low synthesizability scores to be used as negative samples, as discussed above for the initial experimental dataset. We first remove 9629 randomly selected positive samples to be used as the test set prior to any training. Then, we generate the clustered unlabeled dataset as shown in Fig. 1b, where our TSDNN model is trained for 5 independent iterations. In each iteration, a random subset of the unlabeled dataset is selected to be the negative set with a size equal to the number of samples in the positive set. A TSDNN model is then trained on these data. This model makes predictions on the unlabeled samples not selected as the negative set. The final predicted scores are averaged across the 5 iterations to provide the clustered dataset. We then selected the lowest 9629 lowest-scored materials as negative samples to be used in the final test set to ensure our final model accurately classifies the positive and negative set that was determined by clustering. Then, the next 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 517 lowest-scored materials (all scored below 0.33) were selected to match the 38
517 lowest-scored materials (all scored below 0.33) were selected to match the 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 517 positive samples for the labelled dataset. This provides a full labeled dataset with negative labels and a full test set in which accuracy can be determined. The remaining 29
517 positive samples for the labelled dataset. This provides a full labeled dataset with negative labels and a full test set in which accuracy can be determined. The remaining 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 327 samples are considered inconclusive and remain as the unlabeled set to be filtered by the final model.
327 samples are considered inconclusive and remain as the unlabeled set to be filtered by the final model.
This dataset could be directly used to train a supervised or semi-supervised model, which is performed with the balanced TSDNN and supervised CGCNN models. However, since the negatively labeled materials are selected as the result of an imperfect model's predictions, there will be false negatives introduced into the training data. This increases as materials are selected that had prediction scores closer to 0.5 than to 0.0. As a countermeasure to this, we leverage our semi-supervised model to gain insight into the dataset and select optimal negative samples. When trained with our semi-supervised model, the true negative rate is especially low compared to the true positive rate. However, when the threshold for negative samples is moved lower from the 0.33 prediction score, this performance improves. By utilizing this, we are able to determine the optimal negative class threshold to balance the true positive rate and true negative rate, which leads to improved performance of the unbalanced TSDNN.
TSDNN-fe: a formation energy based screener using a semi-supervised TSDNN framework
We design two different TSDNN models for formation energy prediction to overcome biases inherent of previous methods due to having few samples with positive formation energy. We design the first model, a separated TSDNN, to classify whether the formation energy of a material is above or below a threshold of −2.0 eV. We chose this threshold since there are many materials with a slightly negative formation energy (−2.0, 0) that may be very structurally similar to those with slightly positive formation energies (0, 1.0). For this model, we use the materials with formation energies below −2.0 eV (n = 5549) as positive samples in the labeled dataset. We select an equal number of samples with the highest formation energies as negative samples.For the second model, an unseparated TSDNN, we use only materials with positive formation energies (n = 2444) as negative samples and an equal number of randomly selected materials with negative formation energy as positive samples. This is optimized for a representative distribution of positive samples, with the intent of ensuring dataset smoothness and a low density. This allows for improved smoothness by including samples with near-zero eV formation energies while still ensuring a low density near the classification threshold of 0.0 eV. This is a general screener for positive vs. negative formation energy screening as opposed to the first approach, which is optimized for strictly low eV classification. This approach results in a high-precision model, where 78.4% of samples with predicted scores greater than 0.5 have a formation energy of less than −2.0 eV and 99.0% of samples have a negative formation energy. It correctly classifies 57.8% of the possible samples with formation energies less than −2.0 eV.
In both models, we use an unlabeled dataset with 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 CubicGAN-generated structures. These two models ensure that there is a low sample density at the classification threshold. To use the dataset as-is with a threshold of 0.0 eV would result in a very high density of materials at the threshold. As such, we use the different thresholds and data-selection methods to account for this. Each model has distinct benefits that are best suited for different applications, as shown in Fig. 5.
000 CubicGAN-generated structures. These two models ensure that there is a low sample density at the classification threshold. To use the dataset as-is with a threshold of 0.0 eV would result in a very high density of materials at the threshold. As such, we use the different thresholds and data-selection methods to account for this. Each model has distinct benefits that are best suited for different applications, as shown in Fig. 5.
We structure our datasets in this way to correct for biases and inconsistencies that models are ingrained with due to the unbalanced nature of formation energy datasets. As shown in Fig. 3a, the Materials Project has an overwhelming majority of <0 eV materials. If trained from the raw data, it is likely that a model will bias heavily toward predicting >0 eV materials as being <0 eV. For this reason, we seek to combine the benefit of our TSDNN model with a balanced dataset to remove this bias. It is of particular importance that the model be unbiased when used with generated materials, such as those produced by our CubicGAN, as they contain many more >0 eV materials. We seek to apply our method to provide superior screening performance in identifying low formation energy materials.
Datasets
We use inorganic material structures obtained from the Materials Project11,50,51 (MP) database [Version v2020.09.08, accessed 01/28/2021] for both our synthesizability prediction model and our formation energy prediction models. The MP database is a widely used material database consisting of materials obtained from the ICSD10 database or through high-throughput DFT calculations. In the case of synthesizability, we use the MP materials with ICSD entries as the positive dataset and the negative labels selected from the virtual MP materials as described in the TSDNN-syn section. For our formation energy model, we use a combination of the MP database and a custom dataset of material structures generated by our CubicGAN model.8 Our criteria for selecting positive and negative samples are detailed in the TSDNN-fe section. Table 1 shows the source and number of samples in each dataset for each model. To compare the performance of our TSDNN models with that of the baseline PU-learning method, we first prepare a random test dataset in the same way as in previous work,13 which is composed of a random selection of 9629 positive (synthesizable) samples from the labeled set. To validate that our model is able to accurately classify materials structurally different to those in the training set, we prepared a balanced test set composed of the 9629 negative samples with the lowest classification score from the PU learning dataset generation and a group of randomly selected 9629 positive samples. By introducing the negative samples, we are able to ensure that the model does not simply predict all materials as positive and has actually learned the structure features linked to synthesizability.| Synthesizability | Stability (formation energy) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | Labeled | Src | Unlabeled | Src | Model | Labeled | Src | Unlabeled | Src |
| Supervised CGCNN | 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 035 035 |
MP | 0 | N/A | Unseparated FE TSDNN | 4888 | MP | 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
CG |
| Balanced TSDNN | 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 035 035 |
MP | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 327 327 |
MP | Separated FE TSDNN | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 078 078 |
MP | 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
CG |
| Unbalanced TSDNN | 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 165 165 |
MP | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 327 327 |
MP | CGCNN regressor | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 614 614 |
MP | 0 | N/A |
| PU-learning13 | 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 781 781 |
MP | 78![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 734 734 |
MP | |||||
The supervised CGCNN and balanced TSDNN models use the same labeled datasets. The balanced TSDNN model is trained using the remaining samples as the unlabeled set. This uses the unoptimized dataset provided from the dataset generation step. The unbalanced TSDNN uses the optimized labeled dataset from the optimization step discussed in the formation energy classification performance section.
Due to the fact that our CubicGAN generative model produces strictly cubic structures, we utilized only cubic Materials Project structures to train a formation-energy classification model to predict samples with negative formation energies. We used two selections of data for our formation energy models. The first model, the unseparated TSDNN, uses only materials with formation energies lower than 0.0 eV as negative data (n = 2444). We then randomly selected an equal number from the remaining samples as positive data (n = 2444). This allowed for a balanced labeled dataset with the full distribution of negative formation energy samples represented. The second model, the separated TSDNN, is trained using the lowest 25% eV samples (n = 5539) as positive data and the highest eV materials (n = 5539) as negative data. This excludes the range of materials close to 0.0 eV. The motivation for this is to separate the positive and negative classes in the input space. The motivation for this is to train the model to identify only low formation energy materials. The CGCNN regression model is trained using the full cubic training dataset. We validate our formation energy models' performance by testing it on our own dataset of cubic structures produced by the CubicGAN with DFT-calculated formation energies. For each model, we used a test set of 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 847 CubicGAN-generated structures with DFT-calculated formation energies. This test set has 16
847 CubicGAN-generated structures with DFT-calculated formation energies. This test set has 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 407 negative formation energy samples and 20
407 negative formation energy samples and 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440 positive formation energy samples.
440 positive formation energy samples.
Performance evaluation of TSDNN based semi-supervised learning
We compare our TSDNN-syn and TSDNN-fe models against previous structure-based methods for predicting synthesizability and formation energies, respectively. For synthesizability classification, we compare against the previous semi-supervised method of PU learning.13 In the case of formation energy screening, we compare against a CGCNN regression model. We perform additional performance validation of our method by screening 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 545
545![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 713 novel CubicGAN-generated materials and selecting the top 1000 for analysis. We perform DFT calculations to calculate their formation energies to analyze their stability and likely synthesizability.
713 novel CubicGAN-generated materials and selecting the top 1000 for analysis. We perform DFT calculations to calculate their formation energies to analyze their stability and likely synthesizability.
Synthesizability classification performance
Due to the lack of known true negative samples (non-synthesizable samples) for synthesizability prediction, the true positive rate is used here to evaluate the performance of the synthesizability prediction models. We include the accuracy metric for our tests as we utilize our method for selecting high-quality negative samples in addition to the true positive rate. This is to validate that there is not simply a positive bias that results in a high true positive rate, but there is in fact an observable differentiation in the model predictions.We show the results of our synthesizability prediction in Table 2. The balanced TSDNN was trained using the full labeled dataset and a comparatively small unlabeled dataset to compare it to the strictly supervised CGCNN classifier method. These two models have equivalent performance, with the supervised CGCNN achieving an 81.60% TPR and the balanced TSDNN achieving an 81.20% TPR. To improve on this and benefit from semi-supervised learning, we then use the optimized dataset described in the TSDNN-syn method section for training the unbalanced TSDNN model, which achieved the highest accuracy of 94.11% along with a TPR of 92.90%. We also evaluate this model by moving the test data into the unlabeled dataset for the seeded TSDNN test. We use this test to evaluate the pseudo-labeling ability of our teacher model and to show that the true labels of data in the unlabeled set are learned correctly. The seeded TSDNN achieves the highest TPR of 93.80% and an accuracy of 91.48%, which demonstrates accurate teacher pseudo-labelling for unlabeled data. It increased the TPR of the unbalanced TSDNN from 92.90% to 93.80%. This is the best comparison to real-world performance, as the unlabeled data would be the desired data to be classified.
| Model | TPR | Accuracy | Test Set |
|---|---|---|---|
| Supervised CGCNN (baseline) | 81.60% | 62.73% | 9629 holdout |
| Balanced TSDNN (ours) | 81.20% | 56.40% | 9629 holdout |
| Seeded TSDNN (ours) | 93.80% | 91.48% | 9629 unlabeled |
| Unbalanced TSDNN (ours) | 92.90% | 94.11% | 9629 holdout |
| PU-learning (baseline)13 | 87.90% | N/A | 9629 holdout |
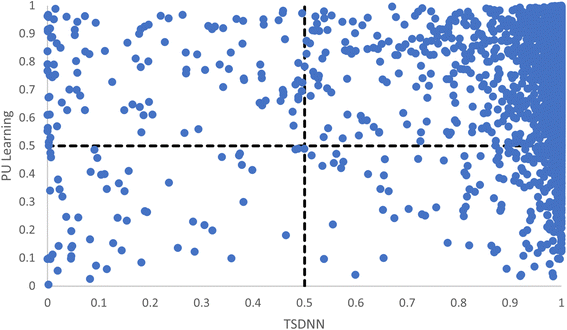
In both the basic PU learning method for synthesizability13 and our TSDNN framework, a decision boundary of 0.5 is used for determining synthesizable vs. unsynthesizable materials for both classifiers. To show the consistency and performance of both models, Fig. 4 plots the probabilities of being stable materials for all the ICSD materials from our test set by the PU learning model against those predicted by our TSDNN model. The figure is divided into quadrants, with each quadrant signifying agreement or disagreement between the PU learning method and our TSDNN framework. The top right quadrant signifies correct agreement between the models, where both models correctly classify the materials as positive. As expected due to the similarity in methods, both models correctly agree for 92.24% of samples. The bottom left quadrant, similarly, denotes the incorrect agreement that the materials should be classified as negative. These are very few, totaling only 0.62% of samples. The bottom right quadrant signifies a disagreement in which the TSDNN model correctly classifies the materials and the PU learning method does not. It can be easily found that the bottom right quadrant contains much more samples compared to the top left quadrant, containing 5.91% and 1.22% of samples, respectively, solidly indicating that there are many materials with very high prediction scores correctly predicted by our TSDNN model but were incorrectly classified by the PU learning method as being unsynthesizable. These results show that while our model has an improved true positive rate, the improvement is not simply a result of materials being classified right at the 0.5 classification boundary.
Further performance validation
To further validate our model's performance, we conducted two additional experiments. We trained the model in the same way as described above but only using data from the Materials Project database [v2021.11.10, accessed 12/10/2022] entered into the database before 2018. We withheld all materials that were entered into the database in 2018 or later. This resulted in a training dataset consisting of 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 047 positive samples and 41
047 positive samples and 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 387 unlabeled samples. The withheld test set contained 15
387 unlabeled samples. The withheld test set contained 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 747 positive samples and 55
747 positive samples and 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 138 unlabeled samples. We used the 15
138 unlabeled samples. We used the 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 747 true positive samples from the post-2018 test set to evaluate our model's performance as it would be used to make predictions for new data.
747 true positive samples from the post-2018 test set to evaluate our model's performance as it would be used to make predictions for new data.
The second experiment was conducted in the same manner but withholding any materials containing the element Mn. This experiment was conducted to evaluate the model's reliance on relating the similarity of materials. The training dataset consisted of 47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 635 positive samples and 85
635 positive samples and 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 393 unlabeled samples that do not include the element Mn. The final test set contained 2159 positive samples and 11
393 unlabeled samples that do not include the element Mn. The final test set contained 2159 positive samples and 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 132 unlabeled samples each containing the element Mn. The results for each experiment are found in Table 3.
132 unlabeled samples each containing the element Mn. The results for each experiment are found in Table 3.
| Model | TPR | |
|---|---|---|
| Time-based splitting | PU-learning (baseline)13 | 86.20% |
| TSDNN (ours) | 91.65% | |
| Element holdout | TSDNN (ours) | 72.67% |
We compare our time-based splitting validation with the standard PU learning method from ref. 13. They use an older version of the training dataset with data pre-2015, so we similarly used the latest 5 years of data for testing to match their dataset splitting. Our model's consistent performance when trained on historical data demonstrates our model's efficacy for use in real-world application for future predictions.
Similarly, with the element holdout experiment, our model demonstrates the expected performance. Though this experiment is orthogonal to real-world material discovery through similarity to existing materials, the model demonstrates that it can still perform well with little knowledge of the interactions of Mn.
Formation energy classification performance
Formation energy based material screening can be performed using either regression models or classification models, depending on the motivation of the screening. For screening hypothetical materials, the first step is identifying potentially stable candidates with negative formation energies. As the exact formation energy is not needed, this can be performed effectively by an accurate formation energy classification model. To evaluate the performance of models for formation energy classification, we consider accuracy, precision, and F1 score, as each metric corresponds to a specific screening motivation. We notably do not use recall as for our problem here, as simply achieving a high recall may not be meaningful on its own because it may include many false positives that are not stable. The F1 score better represents performance in this regard, as it measures the performance with balanced recall and precision. In this situation, predicting few false-positives while still correctly classifying a majority of the actual positive materials is desired. For precision, in situations in which it is imperative that the screened materials be below a given eV threshold (e.g. finding materials with high-confidence stability), a high-precision model is the most optimal choice regardless of its accuracy or F1 score. Precision and F1 score are useful metrics at any eV threshold. Accuracy, however, is only significant with an eV threshold of 0.0 eV for our test set, as we are seeking to classify samples with negative or positive formation energies. With lower eV thresholds, the number of negative samples vastly outweighs the number of positive samples, as shown in Fig. 3b. A model could have a high accuracy at a low eV threshold while correctly classifying few actual positive samples. Accuracy is most useful for identifying >0.0 eV per atom materials. A high-accuracy model with a threshold of 0.0 eV achieves the best balance between correctly identifying actual positive and negative samples.Table 4 shows the classification performance of the three models on our test set of materials. Our unseperated TSDNN model achieves a 74.60% F1 score compared to the CGCNN regression model's F1 score of 64.3%, with a significant absolute 10.3% improvement by using our semi-supervised learning approach. At the same time, this model achieves an accuracy of 74%, with an absolute 9.7% improvement over the CGCNN model. Our separated TSDNN model shows that our approach is able to be tweaked for achieving higher precision by adjusting the training threshold, resulting in a high-confidence model. Here, the table shows that the model can be tuned to achieve 100% precision for identifying candidates which are highly likely to be stable materials.
| Model | Precision | F1 score | Accuracy |
|---|---|---|---|
| CGCNN | 58.60% | 64.30% | 64.30% |
| Unseparated FE TSDNN | 66.10% | 74.60% | 74.00% |
| Separated FE TSDNN | 100.00% | 16.50% | 59.50% |
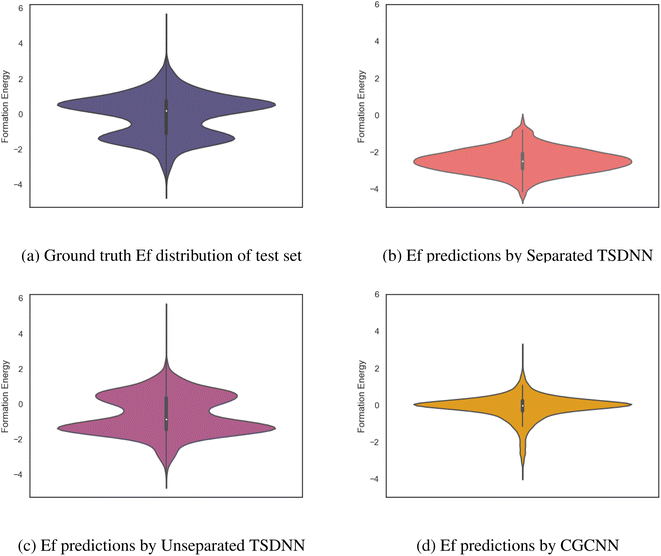
To further illustrate the advantage of our TSDNN models, we show the formation energy distributions of the positively classified samples (with negative formation energies) from our test set by using our classifiers and the baseline CGCNN regression model. As shown in Fig. 5a, our test set contains a large number of samples with positive formation energy to fully test the model's ability to differentiate between samples with positive and negative formation energies. The desired formation energy distribution of screened samples is seen in the bottom group of samples at around −2.0 eV. Fig. 5b shows that our separated TSDNN model has just obtained the desired sample groups with the formation energy distributed around the peak of −2.2 eV, which indicates that our separated FE TSDNN is effective for applications which require a high certainty that a material will have a low formation energy because of its very high precision. For more general screening with an eV threshold of 0.0, our unseparated TSDNN model is more suitable (Fig. 5c). With the vast array of materials with formation energies very close to 0.0 eV, it is very challenging to train a model to accurately differentiate between materials with small positive and small negative formation energies. As shown in Fig. 5d, the CGCNN model is not able to capture the full distribution of negative formation energy materials in the test set and has difficulty in differentiating between samples with positive and negative formation energies. As shown in Table 4, our unseparated TSDNN model is able to improve greatly in performance with a 7.5% increase in precision, a 10.3% increase in F1 score, and a 9.7% increase in accuracy compared to the CGCNN. This makes it preferred for applications that wish to screen for stable materials (usually with negative formation energy).
New materials discovery using both formation energy and synthesizability screening models
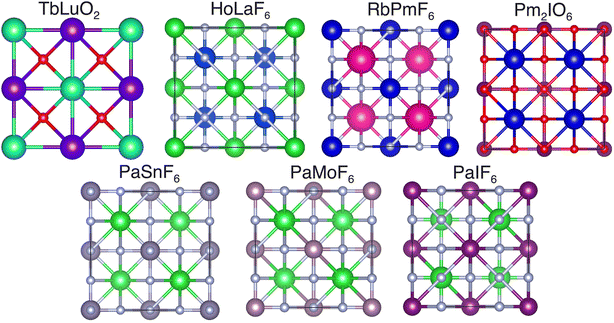
Starting with 2.5 million candidate materials, we first apply our separated TSDNN model to classify them as having positive or negative formation energies. 918![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 686 of them are predicted as having a negative formation energy. We then select 5000 of these materials with the highest prediction scores and apply our unbalanced TSDNN synthesizability model to predict their probability of being able to be synthesized. We finally select the top 1000 samples with the highest probability to be synthesizable. These samples are sent for DFT relaxation and further validation.
686 of them are predicted as having a negative formation energy. We then select 5000 of these materials with the highest prediction scores and apply our unbalanced TSDNN synthesizability model to predict their probability of being able to be synthesized. We finally select the top 1000 samples with the highest probability to be synthesizable. These samples are sent for DFT relaxation and further validation.
| Chemical formula | Space group | E form (eV per atom) |
|---|---|---|
| TbLuO2 | 225 | −3.599 |
| HoPaF6 | 216 | −3.551 |
| RbPmF6 | 216 | −3.108 |
| Pm2IO6 | 225 | −2.785 |
| PaSnF6 | 216 | −2.427 |
| PaMoF6 | 216 | −2.351 |
| PaIF6 | 216 | −2.255 |
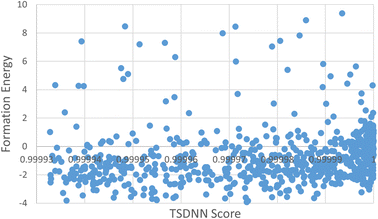
We plot the correlation between the TSDNN prediction score and the calculated formation energy of the selected materials in Fig. 7. Formation energy is not a suitable indicator for a material's synthesizability, so we do not see a strong correlation as these scores are the final predictions from our synthesizability prediction model.
Discussion
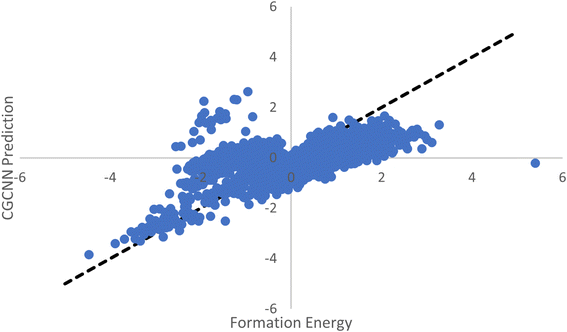
With the advent of large-scale material databases and generative machine learning models, an immense expanse of the wider inorganic material chemical design space is now possible with high throughput experiments or computation. This extensive amount of data makes it a prime target for developing machine learning models for both synthesizability and formation energy based screening. However, there is comparatively little labeled data in both cases and particularly few negative samples. Obtaining new labeled data can be costly, time-consuming, and unreliable.Previously, CGCNN-based regression models have been used to screen for stable material candidates using predicted formation energy. The issue with such models to screen for material candidates with low formation energies is the introduction of model and prediction biases due to the dataset imbalance. As shown in Fig. 3a, only 8.2% of the total MP database is comprised of materials with a formation energy greater than 0 eV. This results in ML based regression models that bias their predictions heavily toward negative formation energies with true positive samples, as shown in Fig. 8.
Here we proposed a dual crystal graph convolutional neural network-based semi-supervised learning framework for synthesizability and formation energy prediction. Comprehensive testing and validation show that our TSDNN models can successfully exploit the unlabeled data in each use case in conjunction with existing labeled data to accurately and effectively predict synthesizability and formation energies. Our TSDNN models can be paired with existing and future material generation models for efficient screening across a variety of applications, as shown with our CubicGAN. Our models' integration with generative models provides for a greatly optimized and more reliable search for new materials. Compared to the CGCNN based regression model, which misclassified a large grouping of materials as having positive formation energies due to the bias caused by the dataset imbalance, our semi-supervised TSDNN classification model reduces this bias, as it is designed with screening in mind from start. Furthermore, by using our TSDNN framework in conjunction with our CubicGAN model, we were able to use the large amount of unscreened data as unlabeled data to train our model for improved performance.
We recognize that currently the CGCNN is no longer the state-of-the-art graph neural network model for formation energy prediction with the emergence of new variants such as Megnet,27 DeeperGATGNN,14 and ALIGNN.57 Our twin network model can be easily combined with these algorithms to achieve even better performance for semi-supervised materials property prediction.
Methods
The framework for generative design of materials
We follow a generation-and-screening approach for the discovery of novel materials: first, we use generative deep learning algorithms to generate hypothetical crystal structures in a high-throughput manner with millions of candidates.8 The generated candidates will then be screened quickly using formation energy and synthesizability machine learning models. Finally, a set of top screened candidates will be verified by DFT based formation energy calculations. It should be noted that generative algorithms of materials compositions4 can also be used here to first generate and screen out top compositions that are then fed to crystal structure prediction algorithms for structure determination and follow-up DFT validation.In this work, we use our recently developed CubicGAN algorithm8 to generate 10 million hypothetical ternary cubic crystal structures of three space groups (221![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 225, and 216) which are reduced to 2.5 million unique candidate cubic structures. With such a high volume of candidates, finding stable and synthesizable ones is almost like finding a needle in a haystack. To address this challenge, we develop semi-supervised deep learning based classification models for identifying hypothetical materials candidates with negative formation energy and high synthesizability, respectively.
225, and 216) which are reduced to 2.5 million unique candidate cubic structures. With such a high volume of candidates, finding stable and synthesizable ones is almost like finding a needle in a haystack. To address this challenge, we develop semi-supervised deep learning based classification models for identifying hypothetical materials candidates with negative formation energy and high synthesizability, respectively.
General training procedure
The general training procedure of our models is as follows. The full dataset is split into a training dataset and a testing dataset, according to the requirements of the experiment. The training dataset will consist of positive samples, either ICSD entries for the TSDNN-syn or low formation energy samples for the TSDNN-fe, and unlabeled samples, which are the remaining samples after positive samples are removed. The test set, unless otherwise specified by an experiment, consists of a random subset of positive samples withheld before training. Negative samples can be added for balance before the final model is trained by sampling from the lowest average unlabeled sample scores to show that the model does not converge to only predict the positive class.Five independent models are trained under the PU learning framework, using a random subset of the unlabeled samples as negative samples to complete a labeled dataset. Each model is trained using that iteration's labeled and unlabeled sets, with an 80% training and 20% validation split for the labeled set. After each iteration has completed, the prediction scores for each unlabeled sample are averaged. The lowest of these average scores are used as negative samples in a new labeled dataset to train a sixth and final model, along with the remaining unlabeled samples. This model is used to make predictions and is evaluated using the initial test set withheld at the beginning.
The hyper-parameters of our TSDNN models are set for training as found in Table 6.
| Hyper-parameters | Value |
|---|---|
| Number of bagging iterations | 5 |
| Dataset holdout for testing | 20% |
| Holdout validation per iteration | 20% |
| Number of epochs per iteration | 100 |
| Learning rate | 0.001 |
| Momentum | 0.9 |
| Weight decay | 0 |
| Atomic feature length | 90 |
| Hidden feature length | 180 |
| Number of convolution layers | 3 |
| Number of hidden layers | 1 |
| Optimizer | SGD |
We follow the hyperparameters as specified in ref. 13 for direct comparison. Specific synthesizability dataset splitting procedures may be found in the TSDNN-syn section. Similarly, specific formation energy dataset splitting procedures may be found in the TSDNN-fe section. Each model is trained according to the general training procedure described above.
Evaluation criteria
We evaluate the TSDNN-syn models based on their true positive rate on each model's respective test set. We use a prediction score boundary of 0.5 to determine a positive or negative sample classification. This classification performance can be expressed as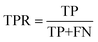 | (3) |
We evaluate the TSDNN-fe models on three metrics with variable formation energy thresholds: accuracy, precision, and F1 score. We again use a prediction score boundary of 0.5 to determine a positive or negative sample classification. The accuracy metric is shown as
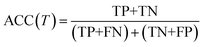 | (4) |
The precision and recall metrics can be expressed as
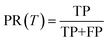 | (5) |
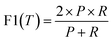 | (6) |
DFT validation of predicted candidate structures
The density functional theory (DFT) based first principle calculations were performed using the Vienna ab initio simulation package (VASP).52–55 The electron–ion interactions were treated employing the projected augmented wave (PAW) pseudopotentials where 520 eV plane-wave cutoff energy was set.58,59 The generalized gradient approximation (GGA)-based exchange-correlation functional was considered with the Perdew–Burke–Ernzerhof (PBE) method.60,61 The energy convergence criterion was set as 10−5 eV. The atomic positions were relaxed to optimize the coordinates with a force convergence criterion of 10−2 eV Å−1. Brillouin zone integration was performed for the unit cells employing the Γ-centered Monkhorst–Pack k-meshes. The formation energies (in eV per atom) of the materials were computed using eqn (7), where E[Material] is the total energy per unit formula of the material, E[Ai] is the energy of the ith atom, xi is the number of Ai atoms in the unit formula, and n is the total number of atoms in the unit formula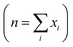 .
. | (7) |
Conclusion
Machine learning based materials property prediction faces the challenge of the lack of sufficient annotated property data and the issue of missing negative samples (non-stable materials), which are needed for building screening models for new materials discovery. To address these two issues, we propose a teacher-student twin graph neural network model (TSDNN) for materials property prediction using formation energy and synthesizability as examples. We formulate both problems as a semi-supervised binary classification problem which matches well to the real-world screening scenarios where these ML screening models are used to pick stable and synthesizable materials candidates from the big pool of hypothetical materials. Our extensive experiments show that our TSDNN models are able to significantly improve the prediction performance compared to previous methods in both synthesizability and formation energy prediction. We achieve a 92.9% true positive rate for synthesizability prediction with a much simpler model architecture and 74% prediction accuracy for formation energy screening. As further validation, we applied our models to the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 545
545![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 713 hypothetical materials generated by our CubicGAN model. Overall, we screened 918
713 hypothetical materials generated by our CubicGAN model. Overall, we screened 918![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 686 materials that were positively classified by the formation energy model with our synthesizability prediction model. We select the top 1000 of these final screened materials for DFT verification and find that 51.2% have negative formation energies. These results show that our TSDNN semi-supervised learning framework is effective for large-scale material discovery screening.
686 materials that were positively classified by the formation energy model with our synthesizability prediction model. We select the top 1000 of these final screened materials for DFT verification and find that 51.2% have negative formation energies. These results show that our TSDNN semi-supervised learning framework is effective for large-scale material discovery screening.
Data availability
The dataset of inorganic material structures are obtained from the Materials Project database for both our synthesizability prediction model and our formation energy prediction model. The source code, our results with the corresponding structures and calculations, and our pretrained models are freely available at our GitHub repository https://github.com/usccolumbia/tsdnn.Author contribution
Conceptualization, J. H.; methodology, D. G., J. H., E. S, Y. Z., and N. F.; software, D. G.; validation, E. S. and J. H.; investigation, J. H., D. G., E. S., and Y. Z.; resources, J. H.; data curation, J. H., and Y. Z.; writing–original draft preparation, D. G., J. H., and E. S.; writing–review and editing, J. H, D. G., and N. F.; visualization, D. G.; supervision, J. H.; funding acquisition, J. H.Conflicts of interest
The authors declare there are no conflicts of interest.Acknowledgements
Research reported in this work was supported in part by NSF under grants 2110033, 1940099 and 1905775. The views, perspective, and content do not necessarily represent the official views of the NSF. This work was supported in part by the South Carolina Honors College Research Program. This work was partially supported by a grant from the University of South Carolina Magellan Scholar Program.References
- A. D. Sendek, Q. Yang, E. D. Cubuk, K.-A. N Duerloo, Y. Cui and E. J. Reed, Holistic computational structure screening of more than 12000 candidates for solid lithium-ion conductor materials, Energy Environ. Sci., 2017, 10(1), 306–320 RSC.
- A. D. Sendek, Ekin D. Cubuk, E. R. Antoniuk, G. Cheon, Y. Cui and E. J. Reed, Machine learning-assisted discovery of solid li-ion conducting materials, Chem. Mater., 2018, 31(2), 342–352 CrossRef.
- C. Chen, Y. Zuo, W. Ye, X. Li, Z. Deng and S. P. Ong, A critical review of machine learning of energy materials, Adv. Energy Mater., 2020, 10(8), 1903242 CrossRef CAS.
- Y. Dan, Y. Zhao, L. Xiang, S. Li, M. Hu and J. Hu, Generative adversarial networks (gan) based efficient sampling of chemical composition space for inverse design of inorganic materials, npj Comput. Mater., 2020, 6(1), 1–7 CrossRef.
- Y. Song, E. M. D. Siriwardane, Y. Zhao and J. Hu, Computational discovery of new 2d materials using deep learning generative models, ACS Appl. Mater. Interfaces, 2021, 13(45), 53303–53313 CrossRef CAS PubMed.
- Y. Song, J. Lindsay, Y. Zhao, A. Nasiri, S.-Y. Louis, J. Ling, M. Hu and J. Hu, Machine learning based prediction of noncentrosymmetric crystal materials, Comput. Mater. Sci., 2020, 183, 109792 CrossRef CAS.
- Z. Ren, J. Noh, S. Tian, F. Oviedo, G. Xing, Q. Liang, A. Aberle, Y. Liu, Q. Li and S. Jayaveluet al., Inverse design of crystals using generalized invertible crystallographic representation, arXiv, 2020, preprint, arXiv:2005.07609.
- Y. Zhao, M. Al-Fahdi, M. Hu, M. Edirisuriya, D. Siriwardane, Y. Song, A. Nasiri and J. Hu, High-throughput discovery of novel cubic crystal materials using deep generative neural networks, Adv. Sci., 2021, 8(20), 2100566 CrossRef CAS PubMed.
- A. R. Oganov, C. J. Pickard, Q. Zhu and R. J. Needs, Structure prediction drives materials discovery, Nat. Rev. Mater., 2019, 4(5), 331–348 CrossRef.
- G. Bergerhoff, I. D. Brown and F. Allenet al., Crystallographic databases, International Union of Crystallography, Chester, 1987, vol. 360, pp. 77–95 Search PubMed.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1(1), 011002 CrossRef.
- M. Aykol, I. H. Vinay, L. Hung, S. Suram, P. Herring, C. Wolverton and J. S. Hummelshøj, Network analysis of synthesizable materials discovery, Nat. Commun., 2019, 10(1), 1–7 CrossRef CAS PubMed.
- J. Jang, G. H. Gu, J. Noh, J. Kim and Y. Jung, Structure-based synthesizability prediction of crystals using partially supervised learning, J. Am. Chem. Soc., 2020, 142(44), 18836–18843 CrossRef CAS PubMed.
- S. S. Omee, S.-Y. Louis, N. Fu, W. Lai, S. Dey, R. Dong, Q. Li and J. Hu, Scalable deeper graph neural networks for high-performance materials property prediction, arXiv, 2021, preprint, arXiv:2109.12283.
- S.-Y. Louis, Y. Zhao, A. Nasiri, X. Wang, Y. Song, F. Liu and J. Hu, Graph convolutional neural networks with global attention for improved materials property prediction, Phys. Chem. Chem. Phys., 2020, 22(32), 18141–18148 RSC.
- Md S. Islam, A. M. Nolan, S. Wang, Q. Bai and Y. Mo, A computational study of fast proton diffusion in brownmillerite sr2co2o5, Chem. Mater., 2020, 32(12), 5028–5035 CrossRef CAS.
- L. Huang and L. Chen, Practicing deep learning in materials science: An evaluation for predicting the formation energies, J. Appl. Phys., 2020, 128(12), 124901 CrossRef CAS.
- G. Peterson and J. Brgoch, Materials discovery through machine learning formation energy, J. Phys.: Energy, 2021, 3(2), 022002 CAS.
- D. Jha, L. Ward, A. Paul, W.-K. Liao, A. Choudhary, C. Wolverton and A. Agrawal, Elemnet: Deep learning the chemistry of materials from only elemental composition, Sci. Rep., 2018, 8(1), 1–13 CAS.
- D. Jha, K. Choudhary, F. Tavazza, W.-K. Liao, A. Choudhary, C. Campbell and A. Agrawal, Enhancing materials property prediction by leveraging computational and experimental data using deep transfer learning, Nat. Commun., 2019, 10(1), 1–12 CrossRef PubMed.
- D. Jha, V. Gupta, L. Ward, Z. Yang, C. Wolverton, I. Foster, W.-K. Liao, A. Choudhary and A. Agrawal, Enabling deeper learning on big data for materials informatics applications, Sci. Rep., 2021, 11(1), 1–12 CrossRef PubMed.
- Z. Zhang, L. Mu, K. Flores and R. Mishra, Machine learning formation enthalpies of intermetallics, J. Appl. Phys., 2020, 128(10), 105103 CrossRef CAS.
- R. E. A. Goodall and A. A. Lee, Predicting materials properties without crystal structure: Deep representation learning from stoichiometry, Nat. Commun., 2020, 11(1), 1–9 CrossRef PubMed.
- A. M. Krajewski, J. W. Siegel, J. Xu and Z.-K. Liu, Extensible structure-informed prediction of formation energy with improved accuracy and usability employing neural networks, arXiv, 2020, preprint, arXiv:2008.13654.
- C. J. Bartel, A. Trewartha, Q. Wang, A. Dunn, A. Jain and G. Ceder, A critical examination of compound stability predictions from machine-learned formation energies, npj Comput. Mater., 2020, 6(1), 1–11 CrossRef.
- X. Tian and J. C. Grossman, Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties, Phys. Rev. Lett., 2018, 120(14), 145301 CrossRef PubMed.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Graph networks as a universal machine learning framework for molecules and crystals, Chem. Mater., 2019, 31(9), 3564–3572 CrossRef CAS.
- V. Fung, J. Zhang, E. Juarez and B. G. Sumpter, Benchmarking graph neural networks for materials chemistry, npj Comput. Mater., 2021, 7(1), 1–8 CrossRef.
- X. Zheng, Y. Cui, Z. Liu, Y. Zhao, M. Hu and J. Hu, Evaluating explorative prediction power of machine learning algorithms for materials discovery using k-fold forward cross-validation, Comput. Mater. Sci., 2020, 171, 109203 CrossRef.
- F. T. Szczypiński, S. Bennett and K. E. Jelfs, Can we predict materials that can be synthesised?, Chem. Sci., 2021, 12(3), 830–840 RSC.
- W. Gao and C. W. Coley, The synthesizability of molecules proposed by generative models, J. Chem. Inf. Model., 2020, 60(12), 5714–5723 CrossRef CAS PubMed.
- K. Alberi, et al., The 2019 materials by design roadmap, J. Phys. D: Appl. Phys., 2019, 52(1), 013001 CrossRef PubMed.
- K. Kovnir, Predictive synthesis, Chem. Mater., 2021, 33(13), 4835–4841 CrossRef CAS.
- M. Aykol, J. H. Montoya and J. Hummelshøj, Rational solid-state synthesis routes for inorganic materials, J. Am. Chem. Soc., 2021, 143(24), 9244–9259 CrossRef CAS PubMed.
- N. Szymanski, Y. Zeng, H. Huo, C. Bartel, H. Kim and G. Ceder, Toward autonomous design and synthesis of novel inorganic materials, Mater. Horiz., 2021, 8(8), 2169–2198 RSC.
- S. A. Malik, R. E. A. Goodall and A. A. Lee, Predicting the outcomes of material syntheses with deep learning, Chem. Mater., 2021, 33(2), 616–624 CrossRef CAS.
- R. Shibukawa, S. Ishida, K. Yoshizoe, K. Wasa, K. Takasu, Y. Okuno, K. Terayama and K. Tsuda, Compret: a comprehensive recommendation framework for chemical synthesis planning with algorithmic enumeration, J. Cheminf., 2020, 12(1), 1–14 Search PubMed.
- A. Davariashtiyani, Z. Kadkhodaie and S. Kadkhodaei, Predicting synthesizability of crystalline materials via deep learning, Commun. Mater., 2021, 2(1), 115 CrossRef.
- X. J. Zhu, Semi-supervised learning literature survey, 2005 Search PubMed.
- J. E. Van Engelen and H. H. Hoos, A survey on semi-supervised learning, Mach. Learn., 2020, 109(2), 373–440 CrossRef.
- Z. Ren, R. Yeh and S. Alexander, Not all unlabeled data are equal: Learning to weight data in semi-supervised learning, Adv. Neural Inf. Process Syst., 2020, 33, 21786–21797 Search PubMed.
- Y. Ouali, C. Hudelot and M. Tami, An overview of deep semi-supervised learning, arXiv, 2020, preprint, arXiv:2006.05278.
- L. Wang, Q. Qian, Q. Zhang, J. Wang, W. Cheng and W. Yan, Classification model on big data in medical diagnosis based on semi-supervised learning, Comput. J., 2020, 65(2), 177–191 CrossRef.
- H. Huo, Z. Rong, O. Kononova, W. Sun, T. Botari, T. He, V. Tshitoyan and G. Ceder, Semi-supervised machine-learning classification of materials synthesis procedures, npj Comput. Mater., 2019, 5(1), 1–7 CrossRef.
- C. Kunselman, V. Attari, L. McClenny, U. Braga-Neto and R. Arroyave, Semi-supervised learning approaches to class assignment in ambiguous microstructures, Acta Mater., 2020, 188, 49–62 CrossRef CAS.
- H. Pham, Z. Dai, Q. Xie and V. L. Quoc, Meta pseudo labels, in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021, pp. 11557–11568 Search PubMed.
- P. Gorai, D. Gao, B. Ortiz, S. Miller, S. A. Barnett, T. Mason, L. Qin, V. Stevanović and E. S. Toberer, Te design lab: A virtual laboratory for thermoelectric material design, Comput. Mater. Sci., 2016, 112, 368–376 CrossRef.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner and G. Ceder, et al., Commentary: The materials project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1(1), 011002 CrossRef.
- F. Mordelet and J.-P. Vert, A bagging svm to learn from positive and unlabeled examples, Pattern Recognit. Lett., 2014, 37, 201–209 CrossRef.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- S. P. Ong, S. Cholia, A. Jain, M. Brafman, D. Gunter, G. Ceder and K. A. Persson, The materials application programming interface (API): A simple, flexible and efficient API for materials data based on REpresentational state transfer (REST) principles, Comput. Mater. Sci., 2015, 97, 209–215 CrossRef.
- G. Kresse and J. Hafner, ab initio , Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, ab initio , Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- J. F. G. Kresse, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- K. Momma and F. Izumi, Vesta3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44(6), 1272–1276 CrossRef CAS.
- K. Choudhary and B. DeCost, Atomistic line graph neural network for improved materials property predictions, npj Comput. Mater., 2021, 7(1), 1–8 CrossRef.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 ( Phys. Rev. Lett. , 1997 , 78 , 1396 ) CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2023 |