Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Operando characterization of rhodium catalyst degradation in hydroformylation
Martin
Gerlach
 *a,
Froze
Jameel
*a,
Froze
Jameel
 b,
Andreas
Seidel-Morgenstern
b,
Andreas
Seidel-Morgenstern
 ac,
Matthias
Stein
ac,
Matthias
Stein
 *b and
Christof
Hamel
*b and
Christof
Hamel
 a
a
aFaculty of Process and Systems Engineering, Chemical Process Engineering, Otto von Guericke University, Universitätsplatz 2, Magdeburg, Germany. E-mail: martin.gerlach@ovgu.de
bMolecular Simulations and Design Group, Max Planck Institute for Dynamics of Complex Technical Systems, Sandtorstrasse 1, 39106 Magdeburg, Germany. E-mail: matthias.stein@mpi-magdeburg.mpg.de
cPhysical and Chemical Foundations of Process Engineering, Max Planck Institute for Dynamics of Complex Technical Systems, Sandtorstrasse 1, 39106 Magdeburg, Germany
First published on 13th February 2023
Abstract
For a comprehensive understanding of catalyst stability, knowledge of deactivation processes is an important keystone in addition to activity and selectivity. The underlying mechanisms and kinetics of deactivation help to understand and control the formation of undesired byproducts, thus preventing a loss of selectivity. This work addresses catalyst deactivation in the homogeneously Rh/BiPhePhos-catalyzed hydroformylation of a long-chain olefin by hydroperoxides. Using operando FTIR spectroscopy, kinetic perturbation experiments with tert-butyl hydroperoxide were able to correlate the loss of regioselectivity in hydroformylation with the structural changes of the catalyst, providing evidence for degradation. Comparison of experimental and DFT calculated vibrational bands indicated the oxidative degradation of the diphosphite ligand and the formation of Rh carbonyl clusters. To predict a critical degradation of the ligand by hydroperoxides over time, which leads to a loss of regioselectivity, deactivation kinetics were derived and parameterized. The developed kinetic model of deactivation predicts the critical degradation of the ligand at different temperatures and concentrations of tert-butyl hydroperoxide well. It offers a model-based approach for process stabilization and optimization e.g. using ligand dosing strategies in the future.
1. Introduction
Homogeneous catalysis is the major route to produce valuable intermediates and high-quality chemical products. In green chemistry, feedstocks from sustainable sources and novel solvents are used but the persistence of catalysts over time determines strongly the overall process efficiency.1Catalyst deactivation is a less regarded aspect when designing efficient homogeneous catalytic systems.2 In this regard, the overall yield and the micro-kinetics of the process are affected by slowing down the catalytic turnover or by creating deactivated catalyst species.3,4 Thus, they can complicate the determination of intrinsic chemical processes and limit kinetic models' predictive capability, scale-up or transferability for reactor design and optimization.
Catalyst degradation may result from impurities in feedstocks and affects key performance parameters like chemo- and regioselectivity of the reaction, conversion of reactants and product yields. Those impurities that cause catalyst degradation pose a significant challenge to the control of catalytic activity on industrial scale and need to be identified. For process stabilization, efforts to exclude these impurities by pre-processing for industrial feedstocks depend on their caused deactivation. In hydroformylation on industrial scale, for example, rigorous exclusion of oxygen is difficult to achieve and as the catalyst is also applied in low concentrations traces of oxygen and peroxides may still influence catalyst stability.5 Aiming an optimal process design, pre-processing of feedstocks may be complemented by catalyst dosing strategies. Therefore, the time-dependent impact of impurities on catalyst stability in correlation to key performance parameters is needed to enable model-based catalyst dosing strategies based on deactivation kinetics.
With respect to catalyst stability, spectroscopic methods contribute significantly to the identification of inactive catalyst species and thus to the understanding of catalyst degradation mechanisms. An important spectroscopic method in this context is Fourier-transform infrared spectroscopy (FTIR) for the identification of catalytic species. If, for example, transition metal–carbonyl complexes are formed, metal–CO stretching vibrations can be used to obtain information on the catalytically active or inactive intermediates involved and rate-determining reaction steps.6 In operando spectroscopic measurements, information about detected catalytic species could be directly correlated with reaction products under realistic conditions.7 The use of operando approaches to elucidate catalyst deactivation mechanisms leading to a robust catalyst development was recently reviewed.8
Hydroformylation also known as “oxo-reaction” converts olefins into aldehydes in the presence of syngas (CO/H2) and a metal catalyst.11 The detailed reaction mechanism of hydroformylation of long-chain olefins in Fig. 1 is based on the proposed mechanism of Wilkinson and Evans.12 Possible side reactions include hydrogenation of the substrates leading to alkanes and isomerization of the terminal olefins into internal olefins. Therefore, a catalyst with high chemo- and regioselectivity is required to suppress the formation of undesired side products. Ligand-modified Rh-catalysts using bulky phosphites are known to achieve high activity and selectivity towards the desired linear aldehydes.13–23 Deviations from this metal–ligand (catalyst) specific activity and regioselectivity can be caused by structural changes of the catalyst by degradation and deactivation, respectively.
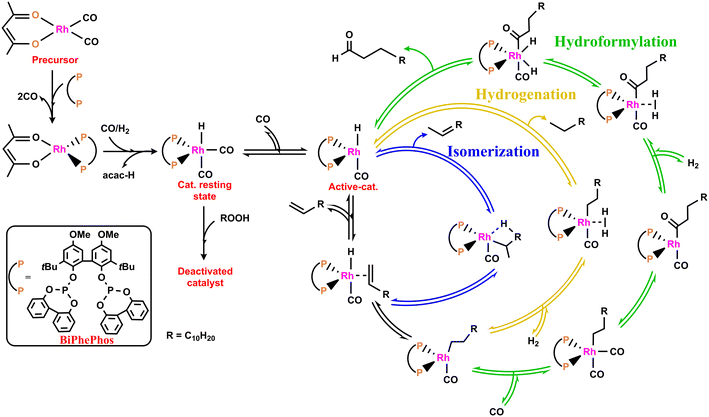 | ||
| Fig. 1 Rhodium/diphosphite-catalyzed hydroformylation of long chain olefins (green), side reactions hydrogenation to give alkanes (yellow) and isomerization to internal olefins (blue).9,10 | ||
In hydroformylation, transition metal carbonyl (M–CO) and hydride (M–H) vibrational frequencies are fingerprints for the state of the metal–ligand system since they are clearly separate from other vibrations in the reaction medium. Structural interpretations of changes in M–CO and M–H vibrations are difficult and require a thorough understanding of metal to ligand binding.
The quantum chemical calculation of carbonyl vibrational frequencies from first principles provides a powerful tool to identify such reactive intermediates. Scaling factors for vibrational carbonyl stretching frequencies were derived from a training set of 45 Rh(I) carbonyl complexes with 69 CO frequencies using the BP86 and B3LYP functionals.24 The BP86 functional was performing superior to B3LYP with a RMSE of 18 cm−1 after scaling. For the resting state of the hydroformylation catalyst, HRh(BPP)(CO)2 the agreement between the experiment was very good with deviations of only 7 and 2 cm−1.
Using both operando FTIR spectroscopic measurements25 and quantum chemical calculations,9 the mechanism of Rh/BPP-catalyzed hydroformylation of 1-decene was investigated in detail.9,25,26
Feed impurities, like intrinsic unsaturated hydroperoxides formed by autoxidation,27–29 were recently shown to negatively affect the regioselectivity of the Rh/BPP-catalyzed hydroformylation of 1-dodecene.30 Here, hydroperoxide concentrations of >0.01 to 0.26 mol% in different supplied samples significantly decreased chemo- and regioselectivity of hydroformylation during 90 min of the kinetic experiments. With respect to Rh/BPP molar ratio of 1/3.3 and a Rh concentration of 0.01 mol% (w.r.t. 1-dodecene) this resulted in an excess of hydroperoxide/BPP molar ratio of up to 8/1. Here, catalyst degradation with respect to ligand BPP was assumed based on 31P NMR of the reaction solution after the experiment.30 A time-dependent correlation of a structural change of the catalyst with key performance parameters of the reaction was missing in this study.
In another spectroscopic study of the same catalytic system, in situ FTIR spectroscopy was used to identify reactive species in the hydroformylation reaction for process monitoring.31 Deactivation processes could be detected but degraded catalytic species could not unambiguously be assigned by advanced chemometric analyses and quantum chemical calculations.25
This contribution should sensitize the interdisciplinary catalyst community for influences of hydroperoxides not only on key performance parameters but also on catalyst structure. Therefore, operando FTIR spectroscopy is used to monitor catalyst degradation in Rh/BPP-catalyzed hydroformylation of long-chain olefin 1-dodecene (Fig. 2). In particular, by perturbing the catalyzed reaction with hydroperoxides the introduced, controlled loss of chemo- and regioselectivity should be correlated with a structural change of catalyst species. The advanced interpretation of changes of FTIR bands is supported by quantum chemical calculations. These suggest an oxidation of the phosphite ligand and the formation of Rh–CO clusters. As purification of alkene feeds is a less regarded aspect,3 this study should substantiate the need for countermeasures against hydroperoxide-induced catalyst degradation by process stabilization methods.
 | ||
| Fig. 2 Rhodium/BiPhePhos-catalyzed hydroformylation of long chain olefin 1-dodecene perturbed with hydroperoxides (ROOH) to influence chemo- and regioselectivity. | ||
To support process stabilization and control a methodological alternative to upstream processing is prepared in this study. As purification of contaminated feeds is limited to a remaining amount of harmful impurities, catalyst dosing strategies are a complementary strategy to stabilize the process. Therefore, deactivation kinetics are required and will be derived to predict the timepoint of begin of critical degradation of the selective catalyst. Here, kinetic (deactivation) hydroformylation experiments are performed under consideration of a model hydroperoxide to fit the kinetic parameters. The loss of regioselectivity will be used as fingerprint for critical catalyst degradation which was validated before by operando FTIR.
2. Experimental details
2.1. Reactor setup
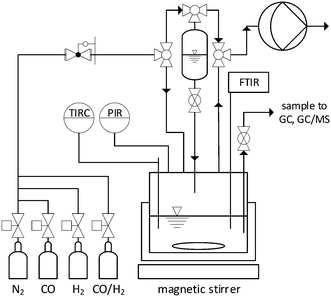
All experiments were performed in a stainless-steel reactor (316 L, Parr Instrument) with a total volume of 75 mL. The reactor was stirred via a magnetic drive with stirring fish. The reactor setup was modified with a polytetrafluoroethylene (PTFE)-coated gas cylinder for reactant dosing as well as intertization and pre-treatment. The gas supply was realized using manually controlled pressure reducers. The pressure was measured using a pressure transducer (Ashcroft Instruments GmbH, model: G2, ±1% total error range). The temperature was controlled via a heating jacket, whereby the recording and control of the temperature was carried out with a jacket thermocouple (type J, FeCuNi, ±1.5 K) in the reactor via the process control system. The reactor setup with operando FTIR is shown in Fig. 3. More information is provided in Jörke et al.262.2. Operando FTIR perturbation experiments
The influences of impurities on catalyst's structure were resolved with operando FTIR spectroscopy. This allows to detect structural changes of the catalyst (degradation/deactivation). The FTIR reactor system setup was described previously.25 The system was equipped with a silicon ATR (attenuated total reflection) probe and connected to an FTIR spectrometer (ReactIR 10, Mettler Toledo). The FTIR spectroscopic measurements were performed with a resolution of 4 cm−1 (512 scans, approx. 3 min per measurement).To study the degradation of Rh/BPP catalyst, the reactor was initially filled with a solution consisting of Rh(acac)(CO)2 (Umicore, 40.0% Rh) and ligand BiPhePhos (6,6′-[(3,3′-di-tert-butyl-5,5′-dimethoxy-[1,1′-biphenyl]-2,2′-diyl)bis(oxy)]bis(6H-dibenzo[d,f][1,3,2]dioxaphosphepine), BPP, Molisa, >99%) (Rh/BPP = 1/1.5 (molar)) in 24 mL toluene (Merck, 99.9%) at room temperature (20 °C). The transfer was performed under inert conditions using Schlenck technique and argon (Linde, 99.999%) as inert gas. Afterwards, the solution was evacuated to 50 mbar and pressurized with 1 bar syngas three times at a stirrer speed of 300 min−1. Under 1 bar syngas pressure the solution was heated within 40 min to 105 °C at a stirrer speed of 1200 min−1. For catalyst pretreatment, the solution was exposed to 5 bar syngas (CO/H2 = 1/1, Linde, CO = (50.0 ± 1.0) %) at 105 °C, over 40 min.
To investigate the influence of hydroperoxides on Rh/BPP-catalyzed hydroformylation, distilled 1-dodecene (Alfa Aesar, 97.1%) with a low hydroperoxide content of <0.01 mol% was used as the reference standard. tert-Butyl hydroperoxide (tBuOOH, Merck, 5 M solution in decane) was used as model hydroperoxide as it is commercially available in defined quality for this systematic study. Intrinsic unsaturated hydroperoxides in 1-dodecene supplied samples have varying composition of different hydroperoxides.30tBuOOH was added to distilled 1-dodecene in defined BPP/tBuOOH molar ratios prior to the kinetic experiments. In subsequent perturbations alternating pure, distilled 1-dodecene and tBuOOH were injected into the reactor to study the degradation of Rh/BPP catalyst. Therefore, the PTFE-coated gas cylinder was filled at room temperature with distilled 1-dodecene (and tBuOOH, according to perturbation). The gas cylinder was alternately evacuated (50 mbar) and purged with 1 bar syngas (CO/H2 = 1/1) for three times. Finally, the gas cylinder was pressurized with syngas at process pressure (10 bar). After completion of the 40 min catalyst pretreatment, the valve between reactor and gas cylinder was opened immediately. By pressure difference the mixture of 1-dodecene/tBuOOH was injected which initiated the hydroformylation reaction. After injection the valve was closed to prepare the gas cylinder for next perturbation and assure enough gas consumption for the next injection. The composition of the reaction solution for the various perturbations is summarized in Table 1.
| Exp. no. | Perturbation no. | Added volume | Composition (molar) | Rh conc. (mol%) | Gas/liquid volum. ratio @ 20 °C | ||||
|---|---|---|---|---|---|---|---|---|---|
| tBuOOH solution (μL) | 1D (mL) | Rh | BPP | tBuOOH | 1D | ||||
| 1 | 1 | 0 | 3 | 1 | 1.5 | 0 | 179 | 0.56 | 1.8 |
| 2 | 163 | 3 | 1 | 1.5 | 12 | 357 | 0.28 | 1.5 | |
| 2 | 1 | 0 | 3 | 1 | 1.5 | 0 | 214 | 0.47 | 1.8 |
| 2 | 0 | 3 | 1 | 1.5 | 0 | 428 | 0.23 | 1.5 | |
| 3 | 52 | 3 | 1 | 1.5 | 4.5 | 641 | 0.16 | 1.3 | |
| 4 | 100 | 3 | 1 | 1.5 | 13.5 | 855 | 0.12 | 1.1 | |
| 5 | 0 | 3 | 1 | 1.5 | 13.5 | 1068 | 0.09 | 0.9 | |
2.3. Kinetic deactivation experiments
The influence of hydroperoxide tBuOOH on the kinetics of Rh/BiPhePhos-catalyzed hydroformylation of 1-dodecene was investigated in distinct, dynamic and temperature-dependent deactivation experiments. From operando FTIR perturbation experiments key performance parameters as indicators for catalyst deactivation will be derived. These indicators will be used to determine catalyst deactivation kinetics.A thermomorphic solvent system (TMS) with decane (TCI, 99.5%) as nonpolar and N,N-dimethylformamide (DMF, VWR, 99.99%) as polar component with a 60/40 (wt%/wt%) composition was used in all experiments. Rh(acac)(CO)2 and the ligand BiPhePhos (Rh/BPP = 3.3/1) were dissolved in 12.1 mL DMF. The solution was filled into the reactor and 23.5 mL decane was added resulting in a two-phase liquid system. All steps were performed at room temperature. For inertization the two-phasic catalyst solution was evacuated (50 mbar) and purged with 1 bar syngas for three times in the reactor under stirring (300 min−1). Finally, the solution was evacuated (50 mbar). To pretreat the catalyst solution, the reactor was pressurized with syngas (20 bar) and the valve to the gas cylinder was closed. Under stirring (1200 min−1), the catalyst solution was heated to the appropriate reaction temperature and kept at this temperature for approx. 30 min. Meanwhile, the PTFE-coated gas cylinder was filled at room temperature with distilled 1-dodecene and tBuOOH and alternately evacuated (50 mbar) and purged with 1 bar syngas (CO/H2 = 1/1) for three times. Finally, the gas cylinder was pressurized with syngas at process pressure (30 bar). After completion of the 30 min catalyst pretreatment, the valve between reactor and gas cylinder was opened immediately. By pressure difference the mixture of 1-dodecene/tBuOOH was injected which initiated the hydroformylation reaction. The initial concentration of 1-dodecene at the beginning was 0.9 mol L−1 with a ratio of Rh/1-dodecene of 1/10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. The reaction conditions especially the catalyst concentration of 0.01 mol% (w.r.t. 1-dodecene) used in all kinetic deactivation experiments is comparable to current Rh-catalyzed hydroformylation processes e.g. Union Carbide/Dow (0.01–0.1 mol%) and Ruhrchemie/Rhône-Poulenc (0.001–0.1 mol%).32 The total liquid volume after injection was calculated to approx. 45 mL using component densities at 20 °C.33
000. The reaction conditions especially the catalyst concentration of 0.01 mol% (w.r.t. 1-dodecene) used in all kinetic deactivation experiments is comparable to current Rh-catalyzed hydroformylation processes e.g. Union Carbide/Dow (0.01–0.1 mol%) and Ruhrchemie/Rhône-Poulenc (0.001–0.1 mol%).32 The total liquid volume after injection was calculated to approx. 45 mL using component densities at 20 °C.33
The temperature was varied in a range from 95 °C to 115 °C. The pressure of the syngas (CO/H2 = 1/1) was kept constant at 30 bar for the duration of the experiment (semi-batch operation). At all reaction temperatures above 85 °C the TMS was one-phasic.34
The experimental design to investigate the influence of tBuOOH on the Rh/BPP-catalyzed hydroformylation of 1-dodecene is summarized in Table 2.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000)
000)
| T/°C | Composition (molar) | Number of exp. | |
|---|---|---|---|
| BPP | tBuOOH | ||
| 95 | 1 | 5 | 2 |
| 105 | 1 | 5 | 2 |
| 1 | 10 | 3 | |
| 1 | 50 | 3 | |
| 5 | 50 | 2 | |
| 115 | 1 | 5 | 3 |
2.4. Gas chromatography
Samples of the reaction mixtures (0.5 mL) were diluted with 2-propanol (1.5 mL) and analyzed using a gas chromatograph (GC, 6890 Series, Agilent) equipped with a flame ionization detector, a polar polyethylene glycol stationary phase (HP-INNOWax, 2 × 60 m, d = 250 μm, film = 0.5 μm, Agilent) and helium (Linde, 99.999%) as a carrier gas. The Inlet temperature was 250 °C and the split ratio was set to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The average carrier gas velocity was set to 15 cm s−1 in ramp flow mode. When the sample was injected, the oven was kept isothermal at 130 °C for 30 min, afterwards heated at 35 K min−1 to 200 °C for 30 min and finally heated at 35 K min−1 to 250 °C for 12 min. The samples were analyzed for the concentrations of 1-dodecene, dodecene isomers, tridecanal, aldehyde isomers and dodecane as well as for the solvents decane and DMF. Decane was used as an internal standard. Due to the lack of commercially available calibration standards, response factors of 1-dodecene and tridecanal were also used for dodecene isomers and aldehyde isomers, respectively. Reference standards with a defined composition of DMF, decane, 1-dodecene and tridecanal were analyzed before and after a measurement series to validate the analytical method. The relative standard deviation in the concentration of all analytes was found to be <3%.
1. The average carrier gas velocity was set to 15 cm s−1 in ramp flow mode. When the sample was injected, the oven was kept isothermal at 130 °C for 30 min, afterwards heated at 35 K min−1 to 200 °C for 30 min and finally heated at 35 K min−1 to 250 °C for 12 min. The samples were analyzed for the concentrations of 1-dodecene, dodecene isomers, tridecanal, aldehyde isomers and dodecane as well as for the solvents decane and DMF. Decane was used as an internal standard. Due to the lack of commercially available calibration standards, response factors of 1-dodecene and tridecanal were also used for dodecene isomers and aldehyde isomers, respectively. Reference standards with a defined composition of DMF, decane, 1-dodecene and tridecanal were analyzed before and after a measurement series to validate the analytical method. The relative standard deviation in the concentration of all analytes was found to be <3%.
2.5. Computational details
Density functional theory (DFT) calculations were performed using Turbomole V.7.5.35 All species were optimized using the BP86 (ref. 36 and 37) density functional with D3 dispersion correction38 and Becke–Johnson damping.39 This functional in combination with the Ahlrichs' triple zeta valence polarization (def2-TZVP) basis set40 was shown to provide reliable Rh–CO vibrational frequencies24,31 when compared the expensive hybrid density functionals such as B3LYP.37,41–43 All investigated chemical species were characterized as minima on the potential energy surface by absence of any imaginary frequency. A scaling factor of 1.0074 was derived for BP86 and 0.9662 for B3LYP from the training set of 45 Rh–CO complexes for the typical Rh–CO vibrational range between 1750 and 2150 cm−1.24 After scaling of the Rh–CO calculated vibrational frequencies, hybrid DFT results were of the same quality but computationally more expensive.243. Results and discussion
3.1. Reference spectrum prior to reaction
The degradation of the catalyst (metal/ligand complex) can cause a reduction in intensity of Rh–CO vibrational bands. In addition, the formation of new Rh–CO vibrational bands may occur due to degradation reactions and the formation of new catalyst complexes.The used ATR-FTIR setup offers a limited sensitivity with respect to the low concentrations of the catalyst (see Table 1) and targeted Rh–CO vibrational bands. Thus, the time-dependent spectral data presented in the following are of qualitative nature and indicate changes of major catalyst species. This qualitative information is correlated to quantifiable concentrations of reactants and products to identify easily accessible indicators of catalyst deactivation like the regioselectivity of the hydroformylation reaction.
Prior to the degradation experiments, a reference spectrum is recorded, which will be subtracted from the subsequent spectra. In the resting state, the Rh/BPP catalyst in toluene is present as hydrido dicarbonyl species e,e-HRh(CO)2(BPP) (see Fig. 1) with bis-equatorial coordination of the ligand BiPhePhos.8 Characteristic Rh–CO vibrational bands in toluene ranging from 2013 cm−1 to 2017 cm−1 and 2071 cm−1 to 2077 cm−1 have been reported in the literature.25,26,44–46 The agreement between experimental and calculated peak positions by quantum mechanics is very good.24
The reference spectrum in Fig. 4 illustrates a total of seven bands at ṽ = 1970 (α), 1991 (β), 1995 (γ), 2019 (δ), 2043 (ε), 2067 (ζ), 2077 (η) cm−1 of different intensity. In this range, Rh–H bands were expected in addition to Rh–CO vibrational bands. The bands α, β, γ, δ, ε and ζ can be attributed to the solvent toluene and signal artefacts of the FTIR.26,44–46 The remaining very weak signal η indicates the presence of the reported axial Rh–CO vibrational band of the resting state e,e-HRh(CO)2(BPP).25 This shows that under the current operating conditions, only the resting state can be characterized by FTIR since CO dissociation and reaction of the 16-electron active catalyst is fast.
In the following degradation experiments, difference spectra with respect to the reference spectrum (resting state e,e-HRh(CO)2(BPP)) are reported.
3.2. Induced degradation experiments
In subsequent perturbations alternating pure, distilled 1-dodecene and tBuOOH were injected into the reactor to study the degradation of Rh/BPP catalyst. The influence of hydroperoxides on the catalyst structure were resolved with operando FTIR spectroscopy and correlated with the loss of n-aldehyde regioselectivity. The results are illustrated in Fig. 5.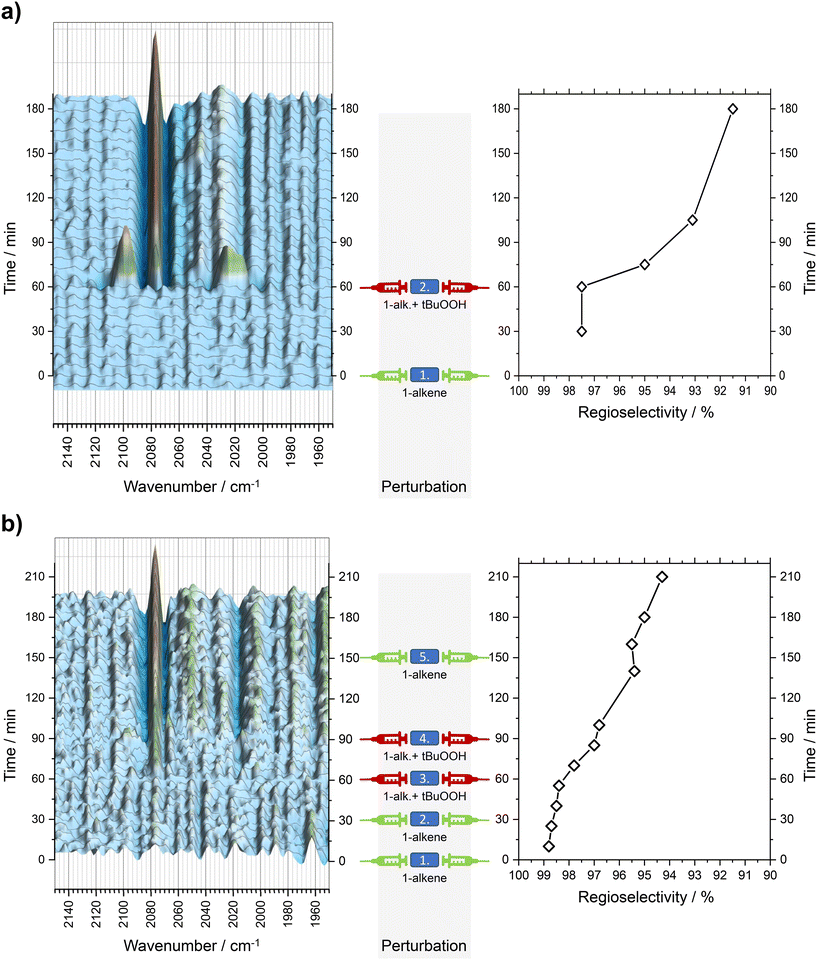 | ||
| Fig. 5 Perturbation experiments: time-dependent loss in catalytic selectivity after a single injection (a) and multiple injections (b) of tert-butyl hydroperoxide (tBuOOH) as model hydroperoxide and distillated 1-dodecene (1-alkene) into the reaction mixture. Left: FTIR difference spectra (2nd derivative w.r.t. Fig. 4). Right: Aldehyde regioselectivity. Composition after injections is given in Table 1. | ||
At t = 60 min, dosage of tBuOOH dissolved in distillated 1-dodecene shows a significant change in FTIR difference spectra and, at the same time, a loss of regioselectivity. At t = 66…72 min, an increase of intensity of bands at 2098, 2024 and 2015 cm−1 can be observed. As time progresses (t ≥ 72 min), these bands disappear and a significant new band at 2078 cm−1 appears alongside other weak bands at 2045 and 2030 cm−1. Regioselectivity is significantly reduced to 91.5% after 180 min.
Upon the first injection of tBuOOH with distillated 1-dodecene (at t = 60 min), a significant decrease in regioselectivity can be observed as described above. At the same time, the vibrational band at 2078 cm−1 increases in intensity. The band at 2016 cm−1 slightly diminishes. A second addition of tBuOOH and 1-dodecene (t = 90 min) enhances these spectral changes even more.
A final injection of distillated 1-dodecene (at t = 150 min) does not lead to further spectral changes and a recovery of the regioselectivity. This demonstrates the irreversible character of changes made to the catalyst upon hydroperoxide addition.
3.3. Spectral assignment of catalyst species
 | ||
| Fig. 6 Calculated IR-spectra of Rh/BPP catalyst in resting state and candidates for degraded species such as oxidized one-arm ligands and formation of rhodium clusters. | ||
For degraded species, the Rh/BPP catalyst with oxidized BiPhePhos derivatives are conceivable.28,47 One-arm species with a partially oxidized equatorial 2 and axial ligand 3 and the ligand-dissociated Rh(CO)4H (4) were calculated. External CO could fill the free coordination site so that one-arm complexes with equatorially or axially coordinated BiPhePhos derivatives are formed (see Fig. 6). The formation of one-arm complexes with a diphosphite ligand and Rh(acac)(CO)2 as precursor was demonstrated by van Rooy et al. by FTIR and nuclear magnetic resonance spectroscopy (NMR).45 An increase in the intensity of Rh–CO bands is due to the number of equivalent CO ligands.
New vibrational peaks appear at 1987 cm−1 in 2 and 1988 cm−1 in complex 3. The trigonal bi-pyramidal species 2 has two carbonyls and the one-armed BiPhePhos ligand in the equatorial positions, plus the hydride and CO occupying axial positions. The small peak at 1971 cm−1 corresponds to stretching vibrations of the axial hydride, and the peaks at 1987, 2023, and 2081 cm−1 refer to rhodium–carbonyl bond vibrations. Complex 3 is also a five-coordinated trigonal bipyramidal with an axial coordinated partially oxidized one-arm phosphite. Due to the change in configuration of the mono-dentate ligand, the peak for hydride bond stretch shifts to 2011 cm−1, and the peaks at 1971, 1988, and 2043 cm−1 refer to rhodium carbonyl bond stretches.
Due to the partial ligand oxidation, the bidentate ligand loses its characteristic P∩P bite angle, thus reducing the catalyst's selectivity towards the desired n-aldehydes.
When the BPP ligand is fully dissociated, complex 4 HRh(CO)4 may form which is a trigonal bipyramidal tetracarbonyl rhodium(I) hydride species with the hydride in axial position. The small peak corresponding to metal–hydride stretch is at 1994 cm−1, and the peaks referring to metal carbonyl bond stretch are at 2023, 2030, and 2109 cm−1.
Finally, the formation of Rh carbonyl clusters as dimers, tetramers or hexamers (5–7) with special focus on the 1800–2150 cm−1 wavenumber region was investigated. The irreversible formation of Rh6(CO)16 starting from Rh(acac)(CO)2 was observed by Jiao et al. using FTIR under syngas in absence of a ligand.48 Here, vibrational bands at 2077 and 1816 cm−1 were observed. The formation of these rhodium clusters (complexes 5–7) is irreversible as experimental studies have shown. No formation of (BPP)HRh(CO)2 catalytic species could be obtained upon injecting more ligand into the catalytic mixture.48 In contrast for a Rh/PPh3-catalyst, Bara-Estaún et al. were able to prove that the formation of Rh0–carbonyl clusters is reversible under H2-rich conditions.49 With the cluster formation, new bands in the 1800–1915 cm−1 range appear, which correspond to the bridging carbonyl vibrations for complexes 5 to 7. The peaks at 2033, 2056, and 2089 cm−1 in complex 5 correspond to terminal metal carbonyl bond vibrations. With the increase in the size of rhodium carbonyl clusters, there is only a minor shift in vibrational band positions but the signal at 2056 cm−1 intensifies, and the peak at 2033 cm−1 almost disappears for complex 7 (Rh6CO16).
Fig. 7 shows the spectral peak positions and the peak differences from experiment and DFT calculations. Two sets of peaks (S1 and S2) were found in the experimental results (see Fig. 5). For experimental peak group S1 (ṽS1 = 2098, 2024, 2015 cm−1), there is a difference of Δṽexp = 74 cm−1 between the first two peaks. For calculated spectra, the difference of Δṽcalc = 72 cm−1 between the peaks in complex 3 (see Fig. 7) is in good agreement with the experimental peak group difference Δṽexp for S1.
 | ||
| Fig. 7 Comparison of experimental (see Fig. 5) and calculated spectral peak positions (see Fig. 6) and spacing (Δṽ) for degraded catalyst species. | ||
It can also be seen that the peak at 2081 cm−1 (Rh–CO stretch) for complex 2 corresponds to the experimental peak at 2098 cm−1 (see Fig. 5). The experimental peak at 2024 cm−1 could be assigned to the peak at 2023 cm−1 in complex 2 and corresponds to another rhodium–carbonyl stretch. The peak appearing at 2015 cm−1 could be seen in complex 3 at 2011 cm−1, which corresponds to the rhodium axial–hydride stretch.
Hence, by comparison with DFT-calculated peak positions and peak differences it is possible that the spectrum of S1 corresponds to a mixture of partially oxidized one-arm BiPhePhos species 2 and 3. The DFT calculations give only a difference of 4 kJ mol−1 in Gibbs free energy between the mono-oxidized complexes 2 and 3. Therefore, the inter-conversion between both one-arm species is feasible.
For experimental peak group S2 (ṽS2 = 2078, 2045, 2030 cm−1), there is a difference of Δṽexp = 33 and Δṽexp = 15 cm−1 between the first and second peak, as well as the second and third peaks, respectively. For calculated spectra, differences of 33 and 34 cm−1 between the peaks in complexes 5–7 (Δṽcalc, see Fig. 7) are in good agreement with the experiment peak group difference for S2. It is suggested that S2 represents rhodium carbonyl species without the presence of the BiPhePhos ligand i.e. complexes 4–7. The quantum chemical studies suggest that the characteristic peak of S2 at 2078 cm−1 in the experimental spectra refers to a terminal Rh–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch vibration which can be found at ∼2060 cm−1 in complexes 4–7. This small difference of ∼18 cm−1 in peak position is not unusual and very sensitive to the choice of functional and basis set. The intensity of the peak increases as the cluster size increases (see Fig. 6). The difference between the second and third peaks stays almost constant for all the rhodium carbonyl clusters 5–7. However, the agreement of the peak spacings suggests that the S2 mainly comprises of complex 6, i.e., Rh4(CO)12.
O stretch vibration which can be found at ∼2060 cm−1 in complexes 4–7. This small difference of ∼18 cm−1 in peak position is not unusual and very sensitive to the choice of functional and basis set. The intensity of the peak increases as the cluster size increases (see Fig. 6). The difference between the second and third peaks stays almost constant for all the rhodium carbonyl clusters 5–7. However, the agreement of the peak spacings suggests that the S2 mainly comprises of complex 6, i.e., Rh4(CO)12.
3.4. Kinetics of catalyst deactivation
 | (1) |
 | (2) |
 | (3) |
Upon increasing the concentration of hydroperoxide tBuOOH in kinetic hydroformylation experiments, conversion of 1-dodecene is reduced from 99% to 90% after 90 min. A difference in conversion profiles is already overserved after 10 min reaction time.
The integral selectivity of hydroformylation catalyst is significantly decreased after 90 min. A direct shift of selectivity from hydroformylation towards isomerization to internal olefins of 45% is observed for experiments without hydroperoxide in comparison to high hydroperoxide concentration. For the latter, this shift of selectivity is observed earlier. Here, a significant difference in selectivity profiles is overserved after 6 min reaction time.
A similar behavior is observed for n-aldehyde regioselectivity which is reduced from 99% for experiments without hydroperoxide to less than 94% for high hydroperoxide concentrations. A significant difference in regioselectivity profiles is already overserved after 2 min reaction time.
The observed shift towards olefin isomerization may cause an increase of internal aldehydes which explains the decrease in regioselectivity. In contrast, hydroformylation of internal olefins using an active Rh/BPP-catalyst was successfully demonstrated with high regioselectivity.26,50 Thus, supported by operando FTIR experiments, catalyst degradation by hydroperoxides is evident, which is associated with a significant impact on key performance parameters.
In comparison of all key performance parameters the aldehyde regioselectivity appears to be the most time sensitive deactivation indicator. In the following, regioselectivity will be of key importance for kinetic modelling of catalyst deactivation.
As a reference of an active and selective catalyst, experiments with distilled 1-dodecene were chosen, for which a constant regioselectivity of 99% was attained throughout the kinetic experiments.
Consequently, a decrease in regioselectivity below 99% was assumed to indicate the time of critical catalyst degradation, tcrit. As diphosphites like BiPhePhos are known to undergo hydroperoxide induced oxidation reactions a ligand degradation approach was assumed.
Critical degradation was defined with respect to a BPP/Rh molar ratio, αBPP/Rh:
 | (4) |
To quantify the degradation of ligand BPP, simplified oxidations of diphosphite BPP by hydroperoxide tBuOOH were assumed as model reactions (see Fig. 9). In the first degradation reaction (D1) the non-coordinated excess ligand BiPhePhos is degraded. In a second degradation reaction (D2) the Rh-coordinated ligand BiPhePhos is degraded. Both reactions lead to a decrease in total BPP ligand concentration and thus αBPP/Rh.
As possible degradation product, a partially oxidized BPP derivative (see DFT calculations in Fig. 6) is formed due to hydroperoxide induced oxidation. Intermediate steps, such as the formation of alkyl peroxy and alkoxy radicals and derived radical reactions, were not considered.28 In addition, oxidations of the second diphosphite group of monophosphate or the Rh center, which decrease the concentration of hydroperoxides, were neglected.
Different reactions kinetics rD1 and rD2 were assumed due to the limited sterically availability of phosphite groups for the Rh-coordinated BPP ligand with respect to the free excess ligand.
Based on the model reactions for degradation, S1, and S2, two simple kinetic models of 2nd order were derived to explain the kinetics of the degradation of the free excess ligand (cfreeBPP) and of the coordinated ligand (ccoordBPP):
| rD1 = kD1(T)·cfreeBPP·ctBuOOH | (5) |
| rD2 = kD2(T)·ccoordBPP·ctBuOOH | (6) |
 | (7) |
 | (8) |
 | (9) |
| cBPP(t) = cfreeBPP(t) + ccoordBPP(t) | (10) |
 | (11) |
 | (12) |
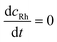 | (13) |
At the time of critical degradation tcrit, a significant loss of regioselectivity is observed and αBPP/Rh is assumed to be unity. Experimental uncertainties were considered to define tcrit. For example, for a ligand/hydroperoxide ratio of 1/5 at 105 °C, a mean time of critical degradation of ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) crit (1/5, 105 °C) = (35 ± 10) min was determined. The results of the determination of critical degradation time are illustrated in Fig. 10b.
crit (1/5, 105 °C) = (35 ± 10) min was determined. The results of the determination of critical degradation time are illustrated in Fig. 10b.
Modelling results for the time-dependent hydroperoxide-induced ligand degradation are illustrated in Fig. 11. Estimated kinetic parameters of deactivation are summarized in Table 3. The kinetic model agrees well with experimental data for varying ligand/hydroperoxide ratios as well as temperature. The times of critical degradation tcrit of the ligand BiPhePhos are in good agreement. However, for a ligand/hydroperoxide ratio of 5/50, the time of critical degradation is predicted to occur significantly earlier. This indicates the strong simplification of radical reactions underlying the degradation of the ligand. For this reason, a detailed mechanistic discussion of the kinetic parameters is omitted here, as the concept of frequency factors and activation energies should only be applied to elementary reactions.53
| Reaction | Parameter | Value | 95%-CI | Unit |
|---|---|---|---|---|
| Oxidation of free ligand (D1) | A D1 | 4.07 | 0.2% | |
| B D1 | 5.45 | 11.0% | ||
| E AD1 | 16.7 | 11.0% | kJ mol−1 | |
| Oxidation of coordinated ligand (D1) | A D2 | 1.68 | 11.3% | |
| B D2 | 6.61 | 9.1% | ||
| E AD2 | 20.2 | 9.1% | kJ mol−1 |
This simplified model provides the basis and offers the possibility in future studies on catalyst deactivation to develop and implement dosing strategies of the ligand in continuous automatized processes. For an alkene feed with a known hydroperoxide concentration, the ligand dosage rate can thus be determined in order to maintain constant selectivity and regioselectivity over the entire process duration.
4. Summary and conclusions
Catalyst deactivation, a less regarded aspect when designing efficient homogeneous catalytic systems, was investigated experimentally and computationally in this contribution for Rh/BiPhePhos-catalyzed hydroformylation of a long-chain olefin.tert-Butyl hydroperoxide as model representative for common hydroperoxide impurities in often real industrial olefin feeds was used in kinetic deactivation experiments via instructive perturbations. To monitor catalyst degradation, operando FTIR spectroscopy was applied and the interpretation of convoluted spectra was supported by quantum chemical calculations.
Applying defined hydroperoxide perturbations during hydroformylation a loss of n-aldehyde regioselectivity was accompanied by a change of the difference IR spectra. Thus, the loss of regioselectivity was identified as fingerprint for catalyst degradation. A comparison to DFT calculated IR spectra of possible candidates for degraded species revealed a good agreement with experimental spectra to identify partially oxidized one-arm derivatives of ligand BiPhePhos and rhodium carbonyl clusters. The loss of regioselectivity can be accounted to these species as result of catalyst degradation. To predict the critical degradation of ligand BiPhePhos over time that leads to a loss of regioselectivity, the kinetics of deactivation for that system were modeled for the first time. Based on selected model reactions of the oxidation of free as well as coordinated ligand, a kinetic model of deactivation could be derived and parameterized, which predicts, depending on ligand und peroxide concentration, the time of critical degradation of the ligand at different temperatures and hydroperoxide concentrations.
In conclusion, it was demonstrated that monitoring catalyst deactivation by operando FTIR is possible. Here, identification of degraded species was only feasible in combination with quantum chemical calculations. Under usual experimental conditions tracking of key performance parameters of the reaction is also suitable to identify catalyst degradation. The investigation of Rh/BiPhePhos-catalyzed hydroformylation, the regioselectivity turned out to be the most time-sensitive parameter for catalyst degradation. For a continuous process considering fluctuating hydroperoxide concentrations, a model-based dosing of the ligand BiPhePhos for process control, stabilization and optimization is possible on the basis of the derived kinetic model of deactivation.
In future, different catalytic systems with real industrial feeds in homogeneous phase should be investigated to add important knowledge of deactivation to the catalyst library. With a multi-method approach including coupled FTIR, Raman and NMR spectroscopy for advanced structure elucidation supported by quantum chemical calculations will be used to validate and refine the kinetic deactivation model. Ligand-dosing strategies should be studied in long-term experiments.
5. List of symbols
| List of symbols | ||
|---|---|---|
| Parameter | Symbol | Unit |
| Activation energy of reaction j | E A j | kJ mol−1 |
| BiPhePhos/Rh molar ratio | α BPP/Rh | — |
| Concentration | c | mol L−1 |
| Conversion | X | % |
| Frequency factor | k ∞ | L mol−1 s−1 |
| Kinetic parameters of modified Arrhenius approach | A, B | |
| n-Aldehyde regioselectivity | RSnHYFO | % |
| Reaction index | j | — |
| Reaction rate | r | mol L−1 s−1 |
| Reaction rate constant | k | L mol−1 s−1 |
| Selectivity, (chemo-) | S | % |
| Time, mean time |
t, ![[t with combining macron]](https://www.rsc.org/images/entities/i_char_0074_0304.gif) |
min |
| Time of critical degradation of the ligand | t crit | min |
| Wavenumber | ṽ | cm−1 |
| Yield | Y | % |
6. Abbreviations
| List of abbreviations | |
|---|---|
| Term | Abbreviation |
| Becke Perdew GGA functional | BP86 |
| Becke Lee–Yang–Parr hybrid functional | B3LYP |
| 1-Dodecene | 1D |
| Ahlrichs' triple zeta valence polarization basis set | def2-TZVP |
| Attenuated total reflection | ATR |
| BiPhePhos, 6,6′-[(3,3′-di-tert-butyl-5,5′-dimethoxy-[1,1′-biphenyl]-2,2′-diyl)bis(oxy)]bis-(6H-dibenzo[d,f][1,3,2]dioxaphosphepine) | BPP |
| Density functional theory | DFT |
| Diphosphite ligand | P∩P |
| First and second degradation reactions | D1, D2 |
| Fourier-transform infrared spectroscopy | FTIR |
| Infrared | IR |
| Isomerization | ISO |
| Metal carbonyl | M–CO |
| Metal hydride | M–H |
| N,N-Dimethylformamide | DMF |
| n-Aldehyde | nAld |
| n-Selective hydroformylation | nHYFO |
| Nuclear magnetic resonance spectroscopy | NMR |
| Polytetrafluoroethylene | PTFE |
| Root-mean-square error | RMSE |
| tert-Butyl hydroperoxide | tBuOOH |
| Thermomorphic solvent system | TMS |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support by the Max Planck Society for the Advancement of Science is gratefully acknowledged. Gefördert durch die Deutsche Forschungsgemeinschaft (DFG) – TRR 63 “Integrierte chemische Prozesse in flüssigen Mehrphasensystemen” (Teilprojekt A3 und A4) – 56091768. Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – TRR 63 “Integrated Chemical Processes in Liquid Multiphase Systems” (subproject A3 and A4)—56091768. This work is part of the Research Initiative “SmartProSys: Intelligent Process Systems for the Sustainable Production of Chemicals” funded by the Ministry for Science, Energy, Climate Protection and the Environment of the State of Saxony-Anhalt.Notes and references
- J.-P. Lange, Angew. Chem., Int. Ed., 2015, 54, 13186–13197, DOI:10.1002/anie.201503595.
- A. J. Martín, S. Mitchell, C. Mondelli, S. Jaydev and J. Pérez-Ramírez, Nat. Catal., 2022, 5, 854–866, DOI:10.1038/s41929-022-00842-y.
- P. W. N. M. van Leeuwen and J. C. Chadwick, Carbonylation Reactions, in Homogeneous Catalysts, ed. P. W. N. M. van Leeuwen and J. C. Chadwick, Wiley-VCH, 2011, pp. 213–278, DOI:10.1002/9783527635993.ch8.
- M. L. Clarke, Angew. Chem., Int. Ed., 2016, 55, 13377, DOI:10.1002/anie.201607967.
- D. Hess, D. Ortmann, O. Moeller, K.-D. Wiese, D. Fridag and W. Bueschken, Patent No. US7495134B2, 2009.
- O. Diebolt, P. W. N. M. van Leeuwen and P. C. J. Kamer, ACS Catal., 2012, 2, 2357–2370, DOI:10.1021/cs300471s.
- P. C. Kamer, D. Vogt and J. W. Thybaut, Contemporary catalysis: science, technology and applications, Royal Society of Chemistry, 2017, DOI:10.1016/j.focat.2017.01.048.
- K. Köhnke, N. Wessel, J. Esteban, J. Jin, A. J. Vorholt and W. Leitner, Green Chem., 2022, 24, 1951–1972, 10.1039/D1GC04383H.
- F. Jameel and M. Stein, Mol. Catal., 2021, 503, 111429, DOI:10.1016/j.mcat.2021.111429.
- G. Kiedorf, D. M. Hoang, A. Müller, A. Jörke, J. Markert, H. Arellano-Garcia, A. Seidel-Morgenstern and C. Hamel, Chem. Eng. Sci., 2014, 115, 31–48, DOI:10.1016/j.ces.2013.06.027.
- O. Roelen, German Pat., DE849548, 1938, 1952 Search PubMed.
- D. Evans, J. A. Osborn and G. Wilkinson, J. Chem. Soc. A, 1968, 3133–3142, 10.1039/J19680003133.
- E. Billig, A. G. Abatjoglou and D. R. Bryant, US4769498A, 1985.
- C. Vogl, E. Paetzold, C. Fischer and U. Kragl, J. Mol. Catal. A: Chem., 2005, 232, 41–44, DOI:10.1016/j.molcata.2005.01.019.
- A. Behr, D. Obst and B. Turkowski, J. Mol. Catal. A: Chem., 2005, 226, 215–219, DOI:10.1016/j.molcata.2004.10.030.
- K. Nozaki, N. Sakai, T. Nanno, T. Higashijima, S. Mano, T. Horiuchi and H. Takaya, J. Am. Chem. Soc., 1997, 119, 4413–4423, DOI:10.1021/ja970049d.
- P. B. Webb, M. F. Sellin, T. E. Kunene, S. Williamson, A. M. Z. Slawin and D. J. Cole-Hamilton, J. Am. Chem. Soc., 2003, 125, 15577–15588, DOI:10.1021/ja035967s.
- A. van Rooy, E. N. Orij, P. C. J. Kamer and P. W. N. M. van Leeuwen, Organometallics, 1995, 14, 34–43, DOI:10.1021/om00001a010.
- V. F. Slagt, P. C. J. Kamer, P. W. N. M. van Leeuwen and J. N. H. Reek, J. Am. Chem. Soc., 2004, 126, 1526–1536, DOI:10.1021/ja0386795.
- A. Polo, C. Claver, S. Castillon, A. Ruiz, J. C. Bayon, J. Real, C. Mealli and D. Masi, Organometallics, 1992, 11, 3525–3533, DOI:10.1021/om00059a015.
- A. Gual, C. Godard, S. Castillón and C. Claver, Tetrahedron: Asymmetry, 2010, 21, 1135–1146, DOI:10.1016/j.tetasy.2010.05.037.
- Q. Liu, L. Wu, I. Fleischer, D. Selent, R. Franke, R. Jackstell and M. Beller, Chem. – Eur. J., 2014, 20, 6888–6894, DOI:10.1002/chem.201400358.
- Y. Yuki, K. Takahashi, Y. Tanaka and K. Nozaki, J. Am. Chem. Soc., 2013, 135, 17393–17400, DOI:10.1021/ja407523j.
- E. Kohls and M. Stein, Contributions, Section of Natural, Mathematical and Biotechnical Sciences, 2017, vol. 38, pp. 43–56, DOI:10.20903/csnmbs.masa.2017.38.1.100.
- A. Jörke, A. Seidel-Morgenstern and C. Hamel, J. Mol. Catal. A: Chem., 2017, 426, 10–14, DOI:10.1016/j.molcata.2016.10.028.
- A. Jörke, T. Gaide, A. Behr, A. Vorholt, A. Seidel-Morgenstern and C. Hamel, Chem. Eng. J., 2017, 313, 382–397, DOI:10.1016/j.cej.2016.12.070.
- H. Hock and A. Neuwirth, Eur. J. Inorg. Chem., 1939, 72, 1562–1568, DOI:10.1002/cber.19390720817.
- K. Schwetlick and W. D. Habicher, Angew. Makromol. Chem., 1995, 232, 239–246, DOI:10.1002/apmc.1995.052320115.
- H. Brandl, E. Täuscher and D. Weiß, Chem. Unserer Zeit, 2016, 50, 130–139, DOI:10.1002/ciuz.201500680.
- M. Gerlach, D. Abdul Wajid, L. Hilfert, F. T. Edelmann, A. Seidel-Morgenstern and C. Hamel, Catal. Sci. Technol., 2017, 7, 1465–1469, 10.1039/C7CY00244K.
- J. M. Dreimann, E. Kohls, H. F. W. Warmeling, M. Stein, L. F. Guo, M. Garland, T. N. Dinh and A. J. Vorholt, ACS Catal., 2019, 9, 4308–4319, DOI:10.1021/acscatal.8b05066.
- G. D. Frey, J. Organomet. Chem., 2014, 754, 5–7, DOI:10.1016/j.jorganchem.2013.12.023.
- C. L. Yaws and C. Yaws, Chemical Properties Handbook: Physical, Thermodynamics, Environmental Transport, Safety & Health Related Properties for Organic &, McGraw-Hill Education, 1999 Search PubMed.
- E. Schäfer, Y. Brunsch, G. Sadowski and A. Behr, Ind. Eng. Chem. Res., 2012, 51, 10296–10306, DOI:10.1021/ie300484q.
- TURBOMOLE, V7.5 2020, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from: https://www.turbomole.com.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100, DOI:10.1103/PhysRevA.38.3098.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789, DOI:10.1103/PhysRevB.37.785.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104, DOI:10.1063/1.3382344.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465, DOI:10.1002/jcc.21759.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835, DOI:10.1063/1.467146.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652, DOI:10.1063/1.464913.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211, DOI:10.1139/p80-159.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627, DOI:10.1021/j100096a001.
- B. Moasser, W. L. Gladfelter and D. C. Roe, Organometallics, 1995, 14, 3832–3838, DOI:10.1021/om00008a034.
- A. van Rooy, P. C. J. Kamer, P. W. N. M. van Leeuwen, K. Goubitz, J. Fraanje, N. Veldman and A. L. Spek, Organometallics, 1996, 15, 835–847, DOI:10.1021/om950549k.
- D. Selent, R. Franke, C. Kubis, A. Spannenberg, W. Baumann, B. Kreidler and A. Börner, Organometallics, 2011, 30, 4509–4514, DOI:10.1021/om2000508.
- A. Börner and R. Franke, Organic Ligands, in Hydroformylation, ed. A. Börner and R. Franke, Wiley-VCH, 2016, pp. 73–266, DOI:10.1002/9783527677931.ch2.
- Y. Jiao, M. S. Torne, J. Gracia, J. W. Niemantsverdriet and P. W. N. M. van Leeuwen, Catal. Sci. Technol., 2017, 7, 1404–1414, 10.1039/C6CY01990K.
- A. Bara-Estaún, C. L. Lyall, J. P. Lowe, P. G. Pringle, P. C. J. Kamer, R. Franke and U. Hintermair, Catal. Sci. Technol., 2022, 12, 5501–5516, 10.1039/D2CY00312K.
- T. Gaide, A. Jörke, K. E. Schlipköter, C. Hamel, A. Seidel-Morgenstern, A. Behr and A. J. Vorholt, Appl. Catal., A, 2017, 532, 50–56, DOI:10.1016/j.apcata.2016.12.011.
- J. Markert, Y. Brunsch, T. Munkelt, G. Kiedorf, A. Behr, C. Hamel and A. Seidel-Morgenstern, Appl. Catal., A, 2013, 462–463, 287–295, DOI:10.1016/j.apcata.2013.04.005.
- M. Schwaab and J. C. Pinto, Chem. Eng. Sci., 2007, 62, 2750–2764, DOI:10.1016/j.ces.2007.02.020.
- A. J. Dijkstra, Eur. J. Lipid Sci. Technol., 2017, 119, 1700001, DOI:10.1002/ejlt.201700001.
| This journal is © The Royal Society of Chemistry 2023 |