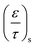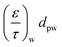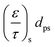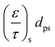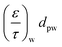Open Access Article
Open Access ArticleInvestigation of the deactivation of a washcoated monolith using a spatially resolved technique†
Yuhan
Wang
 a,
Cristina
Stere
a,
Cristina
Stere
 a,
Geoffrey
McCullough
*b,
Mingyang
Li
c and
Alexandre
Goguet
a,
Geoffrey
McCullough
*b,
Mingyang
Li
c and
Alexandre
Goguet
 *a
*a
aSchool of Chemistry and Chemical Engineering, Queen's University Belfast, Belfast, BT9 5AG, UK. E-mail: a.goguet@qub.ac.uk
bSchool of Mechanical and Aerospace Engineering, Queen's University Belfast, Belfast, BT9 5AH, UK. E-mail: g.mccullough@qub.ac.uk
cDiscipline of Chemical Engineering, Curtin University, Perth, WA 6845, Australia
First published on 9th February 2023
Abstract
A spatially resolved technique was used to investigate the impact of deactivation on the spatial distribution of the effective diffusion in an aged washcoated monolith catalyst. The technique was applied to the investigation of the reactants and products of CO oxidation inside a commercial Pd/Al2O3 monolith catalyst. The spatially distributed effective diffusivities of O2, CO and CO2 were resolved and calculated by a modified Bosanquet approach, which confirmed that the dominant diffusion regimes in the substrate and the washcoat were molecular and Knudsen respectively in the zone affected by deactivation. The technique illustrated the extent to which the deactivation, and its impact on diffusion, varied throughout the washcoat. The results presented are of relevance to the simulation of aged catalysts for automotive applications. In scenarios such as this it is common to model the reduction in catalyst activity by reducing the surface area of the precious metal, with the washcoat diffusion parameters set to their initial, non-aged values. This research quantifies the significant extent to which the diffusion parameters are affected which, when incorporated into catalyst models, will result in more accurate predictions of vehicle emissions.
Introduction
The structure of porous catalysts strongly influences the diffusion processes of gaseous species. Generally, the reactants diffuse into the porous structure to reach an active catalytic site and the products of reaction must diffuse back to the external surface of the catalyst before being transported to the bulk flow.1 This mass transfer process, which is referred to as intra-phase diffusion, is one of the key steps in heterogeneous catalytic reactions.2 When the rate of diffusion is lower than the intrinsic rate of reaction at the active sites, diffusion is considered to be the rate-controlling step and therefore significantly impacts the catalyst's performance. Further, deactivation of porous catalysts is a common challenge which can lead to the decline of the catalytic performance with time via reduction of the intra-phase diffusion rate. It is therefore important to understand and quantify the impact of deactivation on the diffusion of the reactants and products, since these are essential to the development and optimisation of catalyst design.3Deactivation can be categorised into chemical processes, thermal processes and mechanical processes. Chemical processes, including poison deposition on the catalyst's surface, can lead to deactivation by blocking access of the reactants to the active sites, and also preventing or reducing their surface diffusion.4 Thermal processes are physical processes which lead to phase changes at high temperatures and induce loss of catalytic surface and support.5 Mechanical processes include physical deposition of species from the fluid phase onto the catalytic surface and in the pores, and also include loss of catalytic material due to abrasion and crushing of the catalyst.4
Deactivation is a common issue with catalytic converters that are used to abate emissions from petrol and diesel engines.4,6 Phosphorus, zinc (Zn), calcium (Ca) and magnesium (Mg) are typical impurities present in the lubrication oils used in these engines. Small amounts of these compounds are known to present a strong deactivation effect on the performance of catalytic converters,7–9 mainly through deposition that is concentrated towards the front of the monolith.10,11 It has been reported that up to 70% of the phosphorus in the exhaust gas is deposited on the catalyst12 as an overlayer of Zn, Ca and Mg phosphates (M3(PO4)2, M = Zn, Ca or Mg), as aluminium phosphate, and even in the form of cerium phosphates within the washcoat.7,13,14 Phosphates block the pores of the washcoat by forming a film on the catalyst surface that prevents the gas molecules from reaching the catalytic active sites, and also by inducing changes in the electronic and geometric structure of the surface, thus reducing the diffusion inside of the washcoated monolith.4
In porous media such as monolith catalysts, the major reason for a decrease of activity is morphological change caused by fouling and sintering. Carbon particles are known to accumulate on the active metal and the support, with strong carbon deposition leading to the disintegration of catalyst pellets and plugging of pores and voids opening.4,15 Coke is produced by decomposition or condensation of hydrocarbon (HC) over the catalyst surface, and consists primarily of carbon and polymerised HC with high molecule weight.4 The accumulation of carbon and formation coke is greatly impacted by catalyst structure and reaction conditions. Sintering may take place when the washcoated monolith catalyst is exposed to high temperatures, which can lead to phase crystallite growth or collapse of the support and porous structure. Temperature, atmosphere, metal type, metal dispersion, promoters/impurities, support surface area and porosity are the principal factors affecting rates of sintering. Most of the study on sintering has focused on supported metals.4 Alumina (Al2O3), which is commonly used as a metal support, has been studied extensively in this regard due to the phase transformations (boehmite transforms to γ-Al2O3, δ-Al2O3, θ-Al2O3 and α-Al2O3) it undergoes as its temperature is raised.16
Heck et al.17 have presented an illustration of the impact of various deactivation mechanisms on a typical light-off curve. As shown in Fig. 1, a reduction of the number of active sites due to metal poisoning leads to a shift of the conversion curve to higher temperatures compared to the fresh catalyst. The two curves in this case have the same shape since the remaining available sites retain the same properties, thus the reaction remains under kinetic and mass transfer control for the same range of conversion as that of the fresh catalyst. Operando variations to the structure of the washcoat can occur when sintering processes take place or fouling/masking leads to pore blockage, thereby leading to an increase in the diffusional resistance. The slope change is the consequence of the diffusional rate control influence on the apparent activation energy.
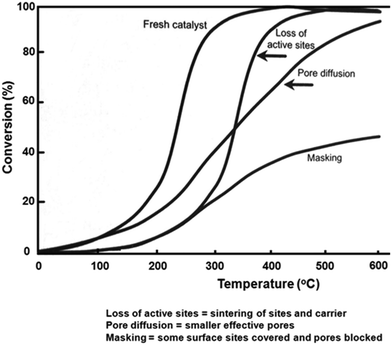 | ||
| Fig. 1 Idealised conversion versus temperature for various aging phenomena; reprinted with permission from ref. 17. | ||
In the investigation of the spatial distribution of deactivation throughout a catalyst, the spatially resolved capillary inlet mass spectrometry (SpaciMS) technique purposed by Stere18 has tremendous potential, firstly as a way of obtaining spatial information of the activity of washcoated monolith catalysts in general and, secondly, about the distributed nature of the deactivation in aged catalysts. Stere used CO oxidation as a probe reaction to investigate spatially resolved characterisation of concentration and temperature gradients along monolith catalysts. The data was obtained from a Pd/Al2O3 washcoated monolith during light-off and steady-state experiments. Recently, Wang et al.19 applied the SpaciMS technique to the investigation of methane oxidation inside a commercial monolith catalyst. The effective diffusivities of O2 and CH4 were calculated to confirm the dominant diffusion regime within the porous medium. Spatially resolved techniques have also been explored by Hofmann et al.20 to investigate the deactivation in a washcoated monolith using a combination of transmission electron microscopy and X-ray absorption/diffraction spectroscopy at various spatial scales. The inhomogeneity of the catalytic coating was demonstrated to play a critical role in the development of local deactivation. Alzahrani et al.21 used the combination of three-dimensional computational fluid dynamics (CFD) modelling and spatially resolved near-infrared tomography to investigate the local deactivation within a gas–solid packed bed reactor. The local deactivation occurred in thin layers at the exterior of the catalytic particle in contact with the flow. The intra-particle mass transfer was found to be greatly impacted by deactivation.
The present work reports on the measurement of the spatial distribution of the diffusion regimes of the reactants and products of CO oxidation in a deactivated monolith catalyst. The diffusion information within the washcoated monolith catalysts, such as the axial distribution of overall mass transfer coefficients and effective diffusivity, are depicted. The SpaciMS was used in conjunction with CO oxidation to probe the impact of deactivation on a vehicle-aged catalytic monolith to gather information regarding the location of the deactivated zone.
Experimental
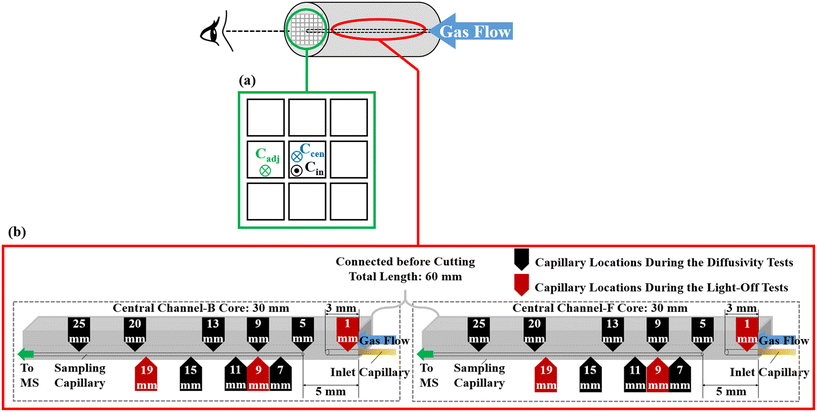
The SpaciMS apparatus used in this work is schematically depicted in Fig. 2 and has been adapted from a previous work carried out by Coney et al.22–24 The major components of the SpaciMS instrument include a mass spectrometer (MS), fused silica capillaries to collect small samples of gas at strategic locations within the monolith, a temperature interface, a z-motion drive unit to move the capillaries, a tubular split furnace and a stainless-steel reactor. A more detailed description is available in literature.25The cordierite ceramic honeycomb monolith catalyst was supplied by General Motors, and was removed from a pick-up truck after 128![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 km of real-world operation. The catalyst consisted of 55.2 g ft−3 (1.949 kg m−3) Pd supported on Al2O3, washcoated on a cordierite substrate with a channel density of 600 cells per square inch. As shown in Fig. 3, the core sample used in the present study was extracted from the central area of the full monolith brick. The extracted core sample was subsequently cut in two half parts with sample F (front core) corresponding to the inlet half, and sample B (back core) corresponding to the outlet half of the brick. The core length was ca. 30 mm, with an outer diameter of ca. 17 mm.
000 km of real-world operation. The catalyst consisted of 55.2 g ft−3 (1.949 kg m−3) Pd supported on Al2O3, washcoated on a cordierite substrate with a channel density of 600 cells per square inch. As shown in Fig. 3, the core sample used in the present study was extracted from the central area of the full monolith brick. The extracted core sample was subsequently cut in two half parts with sample F (front core) corresponding to the inlet half, and sample B (back core) corresponding to the outlet half of the brick. The core length was ca. 30 mm, with an outer diameter of ca. 17 mm.
For the mapping of spatially resolved concentration profiles, CO, O2 and CO2 were fed separately to the central channel of the monolith using an ‘inlet capillary’, and the diffusion through the washcoat and the wall were measured via the resolving of the axial concentration profiles in the inlet and adjacent channels (Fig. 4(a)). To ensure that no gaseous species fed via the inlet capillary leaked to neighbouring channels from the upstream face of the monolith core, the inlet capillary was positioned at a distance of 3 mm into the inlet channel (Fig. 4(b)). To minimise the impact of unsteady flow at the exit of the inlet capillary, which may lead to fluctuation in the MS detection, a gap of 2 mm between the sampling capillary and the inlet capillary was set up at the starting position. The sampling capillaries were moved axially with a total movement distance of 20 mm. The gas composition was analysed at seven axial positions using the MS. At each sampling position, the multi-position switch valve determined which sampling capillary was connected to the MS, and the concentrations of the gaseous species inside the inlet or adjacent channel were sequentially measured. At each of these locations the gas concentration was sampled at a rate of two measurements per second for a duration of five minutes, giving a total of 600 readings. The average and standard deviation of these 600 measurements were then recorded at each location. Axial spatial resolution scans of the monolith channel were made with a resolution of 0.5 mm. A settling time of ca. 1 min was used after moving the probes from one position to the next, to ensure that steady-state conditions were re-established and the recording was automatically paused during that time to avoid misleading fluctuations of the signal. Further details of the experimental configuration are available in the ESI.†
The flow rate of CO (10 v/v% mixture in gas cylinder), O2 (pure gas) and CO2 (pure gas) were ca. 13.1, 8.8 and 8.8 mL min−1 respectively. Argon was used as a balance gas. At the inlet, the total carrier gas Ar flow rate was ca. 2626.5 mL min−1 for the CO, O2 and CO2 diffusion tests. Since the monolith core used contained ca. 200 channels, the flow rate of the carrier gas (Ar) in each channel was ca. 13.1 mL min−1 for the diffusion test. In the central channel, the concentrations of the CO, O2 and CO2 supplied at the inlet were ca. 5, 40 and 40 v/v% respectively. The furnace temperatures employed for these tests were 25, 100 and 200 °C.
Considering the invasiveness of sampling capillary within the channel, the channel cross-sectional area was ca. 1.284 × 10−6 m2, while the capillary cross-sectional area was ca. 3.8 × 10−8 m2. Consequently, the fraction of the channel cross-sectional area occupied by the capillary was 2.96%. The sampling flowrate was ca. 10 μL min−1, while the gas flowrate within the sampling channel was 26.2 mL min−1 for CO diffusion, 21.9 mL min−1 for O2 and CO2 diffusion. The fraction of sampling flowrate in the total gas flowrate was therefore 0.038% (for CO) and 0.046% (for O2 and CO2). The invasiveness evaluation study of the sampling capillary used in this equipment was elucidated in previous work published from our group.24 Three-dimensional CFD modelling was used and showed that the insertion of the small capillaries had an extremely small impact on the flow. The results reported so far indicate that if the experimental technique is carefully designed, the invasiveness of physical probes can be minimised in order to not affect the environment of the catalyst being investigated.
In addition to the diffusion experiments, light-off experiments were also performed with the aim of measuring the variation of conversion efficiency with temperature. These tests were performed within the central channel of the F and B cores. The reaction mixture consisted of 1.0 v/v% CO, 0.525 v/v% O2 (5% stoichiometric excess of O2), 1 v/v% Kr (tracer), and balance Ar. The total flow rate was 200 mL min−1, corresponding to a volume hourly space velocity of ca. 1760 h−1. Before each test, the catalyst was pre-heated for two hours in Ar at a temperature of 150 °C (total flow rate 200 mL min−1) to achieve an isothermal temperature and to remove any residual water adsorbed on the catalyst. After the pre-treatment and cooling by the flow of Ar, the catalyst was heated at a rate of 1 °C min−1 from room temperature to 400 °C. All gases were >99.9% purity and used without further purification. Gas flow rates were regulated by Brooks Instrument mass flow controllers. As shown in Fig. 4(b), the experiments were performed with the sampling capillaries positioned at three fixed axial positions: 1, 9 and 19 mm from the front inlet of the monolith cores. As shown in Fig. 3, the MS signals were recorded using one capillary inserted in a central channel of the catalyst and the associated temperature profiles were recorded with a series of thermocouples (marked by 1 to 6 in Fig. 3), with thermocouple 1 located in the channel adjacent to the one containing the sampling capillary.
In terms of pre-treatment, all cores were exposed to 100 vol% Ar at 25, 100 and 200 °C respectively for diffusion experiments, and room temperature to 400 °C for light-off experiments for a minimum period of 40 minutes. The m/z signals of 28, 44, 32 and 36 were continuously monitored by the mass spectrometer. All masses of interest were normalized by the signal of the internal tracer (Ar) to correct for temporal variations in the detector response, and pressure/transport properties in the sampling capillary. Thus for each experiment the signals of the species of interest were corrected by the internal standard. The baseline reading was then subtracted and an average of each reading is represented as a function of axial position. Sufficiently steady mass spectrum baseline signals were deemed to occur when all recorded m/z signals exhibited change of less than 5% over a period of 15 minutes.
Results and discussion
Fig. 5 reports the concentration profiles of CO in the inlet and adjacent channels of the monolith at 25, 100 and 200 °C in the F and B core respectively (see the ESI† for O2 and CO2). Although the experimental tests for the F and B cores were carried out separately, it is worth recalling that they corresponded to one connected monolith core which had been divided into a front and a back section. The concentrations obtained in the inlet channel presented declining profiles which were the consequence of the gas diffusion from the inlet to adjacent channels through the porous channel walls. This was a consequence of the combined effect of the diffusion of gas species from the inlet channel into the adjacent channel, and further diffusion from the adjacent channel to the second adjacent channels. In the region in which the gas concentration is rising, the diffusion from the inlet channel dominated until a maximum concentration was obtained. At longer axial distances, the subsequent diffusion from the adjacent channel to the second adjacent channels took over which resulted in a progressive reduction of the concentration with axial position. The concentration profiles were temperature dependent; therefore, at identical axial positions in the inlet channel, higher concentrations were observed at lower temperatures. For the adjacent channel, the peak concentration was obtained closer to the channel inlet at the higher temperatures. For the rear part of the monolith, lower gas concentrations were observed at higher temperatures. These changing concentration profiles were consistent with gas diffusion presenting a positive temperature dependence i.e. diffusion is faster as the temperature increases.For each gaseous species, a significant change in concentration profile existed between the two monolith cores, with steeper curves inside the B core compared to the F core. A difference in the gradient of the concentration profile is indicative of a change in mass transfer e.g. pore diffusion. As previously reported, variations in the porous structure of the washcoat have a direct effect on gas diffusion.4,26 The reduction in the gradient of the curve in the F core is indicative of an alteration to the structure of the support, which can occur when sintering or fouling occurs thereby increasing diffusional resistance. The results presented here strongly support an axial gradient in the reduction in pore diffusion, which may significantly contribute to a reduction in catalyst performance. Such a variation in diffusion is consistent with other spatially resolved studies which conclude that deactivation by poisoning occurs from the front end of the catalytic converter, and evolves in a plug-like manner.27,28
Sharma et al.29 used a transport equation under the assumption of plug flow in the channels (zero radial gradients and zero axial diffusion), where the axial change of the flow rate of gas species is equal to the rate of mass transfer to the channel's surface:
 | (1) |
c g,i is the concentration of the species i in the bulk fluid (mol m−3)
c s,i is the concentration of the species i in the wall (mol m−3)
u is the linear velocity (m s−1)
r h is the channel hydraulic radius (m)
k m is the mass transfer coefficient (m s−1)
Based on the mass flux balance, the transport to the channel surface is equal to the transport between channels, and so eqn (2) can be derived:
| km(cg,i − cs,i) = koverall(cg,i,1 − cg,i,2) | (2) |
k overall is the overall mass transfer coefficient (m s−1)
c g,i,1 is the gas phase cup mixing concentration in channel 1 (inlet channel) (mol m−3)
c g,i,2 is the gas phase cup mixing concentration in channel 2 (adjacent channel) (mol m−3)
Thus eqn (1) can be rewritten as:
 | (3) |
Thus:
 | (4) |
 | (5) |
 | (6) |
c g,i(xn) is the concentration at axial position of xn (mm) in the inlet channel (mol m−3)
c g,i(0) is the inlet concentration (mol m−3)
When x = 0, cg,i,2(0) = 0
Fig. 6 summarises the calculated overall mass transfer parameters for CO, O2, and CO2 at the three temperatures explored. In order to show the evolution of the overall mass transfer coefficients as would have existed before the catalyst was separated into front and back sections, the data in Fig. 6 is plotted as though both sections were re-connected into one continuous catalyst. The x-axis therefore shows the distance from the entrance to the original monolith core, which is also the entrance to the F core. Considering eqn (6), it can be seen that the koverall value can only be calculated from the second sampling location (7 mm) onwards, since it requires knowledge of the gas concentration at the preceding sampling location. Remarkably, the combined results for all species and at all temperatures displayed an apparent continuous profile. The koverall values rose with temperature and decreased with molecular weight. The front of the F core gave further confirmation of the fact that the deactivation mainly affected the front part of the catalytic converter. If deactivation had affected the entire monolith uniformly, similar koverall values should be found in both the F and B cores. However the overall mass transfer coefficients of all gaseous species in the B core were higher than those in the F core. Moreover, with the F core, the overall mass transfer coefficients at the outlet (25 mm) were much larger than that at the front part (7 mm). Much smaller differences between the front (37 mm) and outlet (55 mm) of the B core compared to the F core also suggested that no significant change in pore diffusion had occurred in the rear section of the catalyst (Table 1 summarises the koverall values at these positions). Therefore, the average value of koverall in each position of the B core was used to determine the effective diffusivities of this core.
| Gas | F core | B core | ||
|---|---|---|---|---|
| 7 mm | 25 mm | 37 mm | 55 mm | |
| Note that the unit of koverall is m s−1. | ||||
| O2 | 0.024 | 0.036 | 0.039 | 0.043 |
| CO | 0.030 | 0.039 | 0.042 | 0.043 |
| CO2 | 0.025 | 0.031 | 0.033 | 0.035 |
From the koverall values at each position, the effective diffusivity of the different gaseous species can be calculated. Assuming that the thickness of the substrate and washcoat were uniform, eqn (7) can be used to calculate the diffusion through the wall:
 | (7) |
W is the overall wall thickness including the substrate and washcoat (m)
W s is the thickness of substrate (m)
W w is the thickness of washcoat (m)
D i,eff is the effective diffusivity through the combined substrate and washcoat layers (m2 s−1)
D i,s,eff is the effective diffusivity through the substrate thickness Ws (m2 s−1)
D i,w,eff is the effective diffusivity through the washcoat layer thickness Ww (m2 s−1)
Table 2 reports the average thicknesses of the washcoat and the substrate measured by scanning electron microscopy. This data is provided in the ESI.†
| Washcoat | 35 μm |
| Substrate | 109 μm |
Considering the combined effect of the washcoat and substrate, the overall mass transfer coefficient, or effective diffusivity, can be written as eqn (8).1,2
 | (8) |
k m1 is the external mass transfer coefficient from gas bulk to channel surface (m s−1)
k m2 is the external mass transfer coefficient from channel surface to gas bulk (m s−1)
k m can be calculated from:
 | (9) |
Sh(x) is the local Sherwood number at the position of x
D AB,M is the binary gas phase diffusivity of A and B (m2 s−1)
d h is the hydraulic diameter (m)
D AB,M was calculated through the Hirschfelder's equation (Chapman–Enskog theory)30
 | (10) |
D AB,M is the binary gas phase diffusivity of A and B (cm2 s−1)
T is the temperature (K)
M is the molar mass of species A or B (g mol−1)
p is the total pressure (atm)
σ AB is the Lennard-Jones collision diameter (Å)
Ω D is the collision integral for molecular diffusion
Once the value of the local Sherwood number, Sh(x), was known, the local mass transfer coefficient, km, can be calculated using eqn (9). Additionally,  can be calculated using eqn (8). Details regarding the method used for the calculation of local Sh(x) is available in the in previous work by Wang et al.19Fig. 7 reports the spatially resolved values of km1, km2 and
can be calculated using eqn (8). Details regarding the method used for the calculation of local Sh(x) is available in the in previous work by Wang et al.19Fig. 7 reports the spatially resolved values of km1, km2 and  for O2/Ar, CO/Ar and CO2/Ar at the various temperatures explored for the B and F cores respectively. The profile of the mass transfer parameters rose with decreasing molecular weight as expected. At the end of monolith core, especially for the B core,
for O2/Ar, CO/Ar and CO2/Ar at the various temperatures explored for the B and F cores respectively. The profile of the mass transfer parameters rose with decreasing molecular weight as expected. At the end of monolith core, especially for the B core, 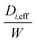 gave the largest value, i.e. where the impact of the deactivation is minimal.
gave the largest value, i.e. where the impact of the deactivation is minimal.
The monolith used in this study had a channel wall which consisted of one substrate and two washcoat layers, thus eqn (7) and (8) can be further rewritten as:
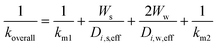 | (11) |
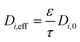 | (12) |
ε is the porosity of the material
τ is the tortuosity
D i,0 is the total diffusivity of species i (m2 s−1)
The total diffusion through the substrate or washcoat can also be expressed using the Bosanquet approach:
 | (13) |
D i,M is the molecular diffusion coefficient (m2 s−1)
D i,K is the Knudsen diffusion coefficient (m2 s−1)
Thus:
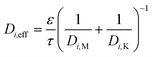 | (14) |
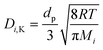 | (15) |
d p is the average pore diameter (m)
R is the universal gas constant = 8314 J kmol−1 K−1
M i is the molecular mass (g mol−1)
Due to the porosity and tortuosity being different for the substrate and the washcoat,  in eqn (8) can be fully expressed as:
in eqn (8) can be fully expressed as:
 | (16) |
The effective diffusions of O2, CO and CO2 within both the substrate and the washcoat can be derived using a modified Bosanquet approach: either molecular or Knudsen diffusion acts as the dominant diffusion regime inside the substrate or washcoat depending on the mean free path of the molecule and the pore diameter.2,29,32 Therefore, to estimate the unknown diffusion parameters and the nature of the dominant diffusion regimes inside the substrate and washcoat, a set of functions were developed and solved under four separate assumptions:
1) MM: both the diffusion within the substrate and the washcoat are in the molecular regime (eqn (17));
2) MK: the diffusion within the substrate is in the molecular regime and in the Knudsen regime within the washcoat (eqn (18));
3) KM: the diffusion within the substrate is in the Knudsen regime and in the molecular regime within the washcoat (eqn (19));
4) KK: both the diffusion within the substrate and the washcoat are in the Knudsen regime (eqn (20)).
 | (17) |
 | (18) |
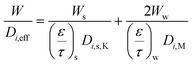 | (19) |
 | (20) |
 | (21) |
 and
and  are lumped as one number respectively and further optimised. This means that for each of the four assumptions there are two unknown numbers to determine.
are lumped as one number respectively and further optimised. This means that for each of the four assumptions there are two unknown numbers to determine.
Using the data from Fig. 7, i.e.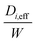 at various temperatures, the best assumptions and associated parameters could be identified through the assessment of the smallest residual sum of squared errors between the experimental and calculated values of
at various temperatures, the best assumptions and associated parameters could be identified through the assessment of the smallest residual sum of squared errors between the experimental and calculated values of  . Table 3 reports the best fitted
. Table 3 reports the best fitted  ,
,  ,
, 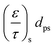 and
and  for O2, CO and CO2 employed in the four assumptions for the B core, and Fig. 8 reports the experimental and calculated
for O2, CO and CO2 employed in the four assumptions for the B core, and Fig. 8 reports the experimental and calculated  for the three gaseous species for each assumption. Table 4 reports the residual sum of squared errors of the calculated and experimental values for Fig. 8. Considering that the same diffusion assumption is applied to O2, CO and CO2, the MM assumption (molecular diffusion in the substrate and washcoat) gives the smallest deviation between the experimental data compared to the other three assumptions.
for the three gaseous species for each assumption. Table 4 reports the residual sum of squared errors of the calculated and experimental values for Fig. 8. Considering that the same diffusion assumption is applied to O2, CO and CO2, the MM assumption (molecular diffusion in the substrate and washcoat) gives the smallest deviation between the experimental data compared to the other three assumptions.
| O2 | CO2 | CO | Sum | |
|---|---|---|---|---|
| MM | 5.45 × 10−5 | 3.01 × 10−5 | 1.76 × 10−5 | 1.02 × 10−4 |
| MK | 3.47 × 10−4 | 4.30 × 10−5 | 1.07 × 10−5 | 4.01 × 10−4 |
| KM | 1.51 × 10−4 | 1.89 × 10−5 | 5.56 × 10−5 | 2.26 × 10−4 |
| KK | 5.50 × 10−4 | 1.06 × 10−4 | 8.70 × 10−5 | 7.43 × 10−4 |
Fig. S3† reports the parity plots which were used to illustrate the correlation between the experimental and calculated values of  . For the case assuming diffusion within the substrate and washcoat are in the molecular regimes (Fig. S3(a)†), the results obtained displayed little deviation of the data points from the parity line, with most points well within the ±10% window. This suggested that diffusion within the substrate and washcoat were both in the molecular regime (MM assumption).
. For the case assuming diffusion within the substrate and washcoat are in the molecular regimes (Fig. S3(a)†), the results obtained displayed little deviation of the data points from the parity line, with most points well within the ±10% window. This suggested that diffusion within the substrate and washcoat were both in the molecular regime (MM assumption).
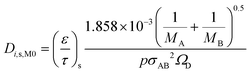
Considering that the molecular diffusion coefficients are dependent on temperature, with temperature dependence of T1.5 for both the substrate and washcoat, the following equations can be written. For the substrate:
 | (22) |
 | (23) |
 | (24) |
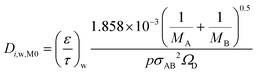 | (25) |
Table 5 summarises the calculated diffusion coefficients in the substrate (Di,s,M0) and washcoat (Di,w,M0) for O2, CO and CO2. It should be noted that the values of  and
and 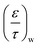 were taken from Table 3 (MM assumption).
were taken from Table 3 (MM assumption).
| Gas | Molecular diffusion coefficients (substrate) | Molecular diffusion coefficients (washcoat) |
|---|---|---|
| D i,s,M0 (m2 s−1 K−1.5) | D i,w,M0 (m2 s−1 K−1.5) | |
| O2 | 9.98 × 10−10 | 1.40 × 10−9 |
| CO | 9.87 × 10−10 | 1.38 × 10−9 |
| CO2 | 7.46 × 10−10 | 1.04 × 10−9 |
Most monolith catalysts used for automotive applications use similar cordierite-based material, therefore the effective diffusivities in such substrates would be expected to be within a similar range.29 The calculated diffusivity for O2 in the substrate at 100 and 200 °C (373.15 and 473.15 K) using eqn (22) were 7.19 × 10−6 and 1.03 × 10−5 m2 s−1 respectively. These results are comparable to the referenced values of 9.28 × 10−6 and 1.29 × 10−5 m2 s−1 (Sharma et al.29), and 1.11 × 10−5 and 1.58 × 10−5 m2 s−1 (Wang et al.19) at the same temperatures which were also measured by a spatially resolved technique. It is expected that the cordierite substrate used in both cases in essentially the same, and the agreement between these three investigations is excellent.29 Zhang et al.3 measured the effective diffusivity of CO in N2 through the washcoated monolith catalyst using a modified form of a Wicke–Kallenbach type of diffusion cell. The experiments were performed at 17 °C (290 K) and pressures between 106 and 150 kPa. The calculated diffusivity for CO in the substrate at 17 °C using eqn (22) was 4.87 × 10−6 m2 s−1. This result is in the same order of magnitude to the value of 1.00 × 10−6 m2 s−1 at the same temperatures reported by Zhang et al. For the washcoat, the calculated effective diffusivity for CO2 at 100 °C using eqn (24) was 7.50 × 10−6 m2 s−1. This result is comparable to the values of 2.26 × 10−6 m2 s−1 at the same temperature again reported by Wang et al., which was also measured using a spatially resolved technique. The calculated effective diffusivity for CO at 17 °C using eqn (24) was 6.82 × 10−6 m2 s−1. This result is in the same order of magnitude to the value of 1.5 × 10−6 m2 s−1 at the same temperatures again reported by Zhang et al.
Spatial distribution of diffusion regimes
As can be observed from Fig. 6, unlike the B core which showed a uniform nature, there is an obvious distribution of koverall in the F core. Therefore it was necessary to locally analyse the distribution of diffusion regime for each measurement position from 7 to 25 mm for the F core.The analysis procedures used for the B core were repeated at all axial point measure in the F core. To illustrate the results obtained, Table 6 reports the optimised  ,
, 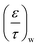 ,
,  and
and  for O2, CO and CO2 employed in four assumptions at the 9 mm position and Fig. 9 correspondingly reports the best fit for the calculated
for O2, CO and CO2 employed in four assumptions at the 9 mm position and Fig. 9 correspondingly reports the best fit for the calculated 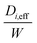 for all gaseous species for each assumption. Table 7 reports the residual sum of squared errors of the calculated and experimental value for Fig. 9. The MK assumption gave the smallest deviation between the experimental data compared to other three assumptions at this axial position.
for all gaseous species for each assumption. Table 7 reports the residual sum of squared errors of the calculated and experimental value for Fig. 9. The MK assumption gave the smallest deviation between the experimental data compared to other three assumptions at this axial position.
| O2 | CO2 | CO | Sum | |
|---|---|---|---|---|
| MM | 2.02 × 10−5 | 2.83 × 10−5 | 1.66 × 10−5 | 6.51 × 10−5 |
| MK | 1.35 × 10−6 | 7.26 × 10−6 | 3.38 × 10−6 | 1.20 × 10−5 |
| KM | 1.88 × 10−5 | 2.46 × 10−6 | 2.05 × 10−5 | 4.17 × 10−5 |
| KK | 4.78 × 10−5 | 9.79 × 10−6 | 4.07 × 10−5 | 9.82 × 10−5 |
Fig. S4† reports the parity plots which were used to illustrate the satisfactory correlation between the experimental and calculated  . At the position of 9 mm from the entrance of the F core, the assumption of diffusion within the substrate and washcoat is respectively in molecular and Knudsen diffusion regimes (Fig. S4(b)†) gave the closest results to the experimental data. Unlike the MM diffusion regime in the entire B core, this analysis suggests that the diffusion within the substrate and washcoat at the 9 mm location was in molecular and Knudsen regimes respectively (MK approach). This indicates a reduction of the pore diameter within the washcoat compared to the B core at this position, and is most likely the consequence of deactivation.
. At the position of 9 mm from the entrance of the F core, the assumption of diffusion within the substrate and washcoat is respectively in molecular and Knudsen diffusion regimes (Fig. S4(b)†) gave the closest results to the experimental data. Unlike the MM diffusion regime in the entire B core, this analysis suggests that the diffusion within the substrate and washcoat at the 9 mm location was in molecular and Knudsen regimes respectively (MK approach). This indicates a reduction of the pore diameter within the washcoat compared to the B core at this position, and is most likely the consequence of deactivation.
The same analysis procedures were used at each of the sampled positions within the F core. Table 8 summarises the spatial diffusion regime and the monolith property parameters for the entire F core. Impacted by the deactivation effects to different extents which depend on axial position, the diffusion regimes within the F core present a discrete nature. The deactivation impacts on the front part of the F core are more likely to be greater than on the exit and, compared to the substrate, the washcoat/support component is considered to be more sensitive to deactivation effects by reducing pore size, hence the Knudsen diffusion regime at the 7 mm and 9 mm locations. It should be noted that the dominant diffusion regime at the exit is the MM regime, which is coherent with the regime for the B core connected with the exit of the F core.
Using the data reported in Table 8, Fig. 10–12 report the spatial profiles of effective diffusivity for the O2, CO and CO2 in the substrate and washcoat respectively at various temperatures. For the MK regime, the equations for the effective diffusivity in the substrate are eqn (22) and (23), while for the washcoat, they are:
 | (26) |
 | (27) |
For the MM regime, the calculation of the effective diffusivity in the substrate is represented by eqn (22) and (23), and in the washcoat by eqn (24) and (25). A rise of effective diffusivity in the F core with axial position illustrates the spatially distributed nature of the deactivation and its subsequent impact on diffusion.
In the F core, the smaller diffusion coefficients compared to the B core can be explained either by fouling or sintering of the washcoat, leading to a reduction in the pore openings and thus inhibition of the gas diffusion from the inlet to adjacent channel through the washcoat. It is interesting to note that, while the effective diffusion within the substrate was less affected than that through the washcoat, a significant drop was nevertheless observed for the first 10 mm. This would tend to indicate that fouling may have been involved as a deactivation mechanism which had a stronger and deeper impact on the smaller size pores of the washcoat compared to those of the substrate.
To illustrate the satisfactory correlation between the experimental and calculated effective diffusions for O2, CO and CO2, Fig. S7† reports the parity plots between the experimentally measured values and those calculated reported in Fig. 10–12 and eqn (28). The results displayed little deviation of the data points from the parity line with most points well within the ±10% window, thus suggesting that the calculated results are close to the experimental data.
 | (28) |
Fig. 13(a) and (b) show typical gas concentration light-off profiles as a function of temperature, which was obtained at 19 mm from the inlet for the F and B core respectively. The full set of profiles obtained at 1 and 9 mm locations are provided in the ESI.† As expected, CO and O2 are gradually consumed and CO2 is formed as the temperature increases to the point that light-off is achieved and a dramatic increase in the conversion rate is obtained. Importantly, the CO is completely converted past the light-off point as expected. Fig. 13(c) and (d) summarise the CO2 concentration profiles obtained during the light-off tests for the F and B core. In all cases, the light-off temperature (T50) decreases with increasing axial position (Table 9). The axial position dependence of the T50 is consistent with its expected dependence on the amount of catalyst seen by the reacting gas i.e. at steady-state temperature, the conversion will increase with increased residence time.
 | ||
| Fig. 13 Light-off profiles for (a) F and (b) B core at 19 mm from inlet; CO2 formation vs. temperature at 1, 9 and 19 mm inside (c) F and (d) B core. | ||
| Axial position (mm) | T (°C) – F core | T (°C) – B core |
|---|---|---|
| 1 | 270 | 236 |
| 9 | 228 | 216 |
| 19 | 213 | 203 |
In the case of the F core, a more dramatic change in the shape of the light-off curves is observed between the inlet (1 mm) and middle (9 mm) part of the F core, Fig. 13(c), with much sharper profiles at 9 and 19 mm compared to the 1 mm position. This clearly indicates that much higher temperatures are required for the CO to be fully converted to CO2 at the monolith's inlet position (ca. 335 °C) compared to the middle and end-part, where the CO was fully consumed at ca. 234 °C and 220 °C respectively.
Since the catalytic activity is related to the number of active sites on the surface,17 it can be concluded that in the front region of the monolith, the loss in catalytic activity was the highest, most probably due to poison/fouling material deposition. Poisoning or fouling of the catalyst leads to changes to the active sites and/or a resistance to mass transfer between the bulk of the fluid and the surface. The consequence of such catalyst modifications will be an alteration of the apparent reaction rate constant hence the change in the profile of the light-off for 1 mm in the F core compared to the other axial positions. If poisoning/fouling material had affected the entire monolith uniformly, similar light-off temperatures and profiles would have been observed with both the F and B core. However, as shown in Fig. 13(c) and (d) and Table 9, the inlet of the B core was much more active than that of the F core. The low performance at the front part of the converter and the higher performance at the centre and rear parts of the catalyst are in agreement with other studies of the position-dependent poisoning phenomena in catalysts.34–36
A similar trend was observed for the B core, but there was less variation in the light-off temperatures from inlet to outlet. For the B core, the formation of CO2 at 1 mm started at ca. 165 °C, while with the F core it was not observed until 195 °C. The smaller difference between the temperatures at which full CO conversion was obtained at the inlet (266 °C) and outlet (ca. 209 °C) of B compared to the F core also supports the hypothesis that no significant alteration in the number of active sites had taken place in the B core.
Using the idealised conversion vs. temperature plot from Heck et al.,17 (Fig. 1), a reduced number of sites of a sintered catalyst would lead to a shift in the CO conversion curve to higher temperature compared with a fresh catalyst. The two profiles obtained in this case should be “parallel”, without any change in the slope of the curves since the remaining available sites can function as before; the reaction being under the kinetic regime. This is what is observed between the curves obtained at the 9 mm and 19 mm positions with both the B and F core, which is consistent with expectations since in the case of the 9 mm position the gas sampled has “seen” less catalyst before sampling than in the case of the 19 mm position. Conversely, the shape of the 1 mm curve differed from that of the other two, with a more shallow gradient in the mass transfer controlled region indicating a reduction in pore diffusion. There is, however, also a difference in the profile shape for the 1 mm axial position of the B core, which is unlikely to be due to sintering/pore blockages given that the middle and outlet positions of the F core were unaffected by such processes. It has been reported that when the gas flow initially enters the catalyst, the flow separates from the leading edge of the channel, resulting in the formation of turbulence flow until a laminar flow regime is established. This mass transfer effect, which increases mass transfer rate, would occur at the inlet of any core, and so there would be a contribution of such turbulence to the B core also. Given the difference in shape of the two 1 mm profiles, however, additional processes clearly occur on the F core, and this is likely to be due to pore blockages as previously discussed. This difference in activity is in agreement with the results already presented herein as well as other spatially resolved studies stating that deactivation occurs from the front end of the catalytic converter, in a plug-like manner.37–39
The results presented here are of relevance to the simulation of aged catalysts for automotive applications. In scenarios such as this it is common to model the reduction in catalyst activity by reducing the surface area of the precious metal, either as a function of location within the catalyst or, more commonly, as a uniformly distributed deactivation. The mass transfer parameters are frequently left untouched at their initial, non-aged, values. However, this research shows that deactivation of the catalyst in real-world applications results in significant changes to the mass transfer of reactants and pollutants through the washcoat, and presents values for the diffusion properties in a typical vehicle-aged catalyst. These values can readily be incorporated into catalyst models thereby providing a more accurate representation of the aged catalyst's activity and, by extension, more accurate predictions of in-service vehicle emissions.
Conclusions
An in situ spatially resolved method was developed to study the spatial impact of deactivation on the mass transfer in aged washcoated monolith cores. Axially-resolved effective diffusivity have been acquired for the reactants and products of the CO oxidation. A more accurate and comprehensive quantitative axial evolution of mass transfer coefficients was obtained from the SpaciMS analysis of monolith cores. The intra-catalyst information such as the evolution of overall mass transfer coefficients have been depicted and their values were greatly influenced by the axial position, especially for the front core, while no significant change in pore diffusion within the back core was observed. The internal mass transfer coefficients of CO, O2 and CO2 were measured at different temperatures and the resultant effective diffusivities were calculated using a modified Bosanquet approach which confirmed that the dominant diffusion regimes in the substrate and washcoat are molecular and Knudsen respectively. Further analysis of the effective diffusions quantitatively revealed the major reason of the difference of concentration profiles between the F and B cores stemmed from the reduction in diffusion within the washcoat. Furthermore, the light-off experiments were conducted to visualise the process and location of lower activity zone distributes in a plug-like manner within the washcoated monolith cores. The results presented are of relevance to the simulation of aged catalysts for automotive applications. This research quantifies the significant extent to which the diffusion parameters change when subjected to poisoning which, when incorporated into a catalyst model, will contribute to more accurate predictions of vehicle emissions.Nomenclature
Symbols and abbreviations
| c g,i | Concentration of species in the gas phase (—) |
| c p | Specific heat (J kg−1 K−1) |
| c s,i | Concentration of species in the solid wall (—) |
| D AB,M | Binary gas phase diffusivity of A and B (m2 s−1) |
| D i,0 | Total diffusivity of species i (m2 s−1) |
| D i,s,eff | Effective diffusivity of species i in substrate (m2 s−1) |
| D i,w,eff | Effective diffusivity of species i in washcoat (m2 s−1) |
| D i,eff | Effective diffusivity of species i (m2 s−1) |
| D i,K | Knudsen diffusivity of species i (m2 s−1) |
| D i,M | Molecular diffusivity of species i (m2 s−1) |
| d h | Channel hydraulic diameter (m) |
| d p | Mean pore size of porous medium (m) |
| k m | Convective mass transfer coefficient (m s−1) |
| k overall | Overall mass transfer coefficient (m s−1) |
| L | Length (m) |
| M | Molecular weight (g mol−1) |
| p | Pressure (atm) |
| r h | Channel hydraulic radius (m) |
| R | Gas constant (J kmol−1 K−1) |
| Sh | Sherwood number (—) |
| T | Temperature (K) |
| u | Linear velocity (m s−1) |
| W | Wall thickness (m) |
| ε | Porosity of the material (—) |
| σ AB | Lennard-Jones collision diameter (Å) |
| τ | Tortuosity (—) |
| Ω D | Collision integral for molecular diffusion (—) |
Abbreviations
| CFD | Computational fluid dynamics |
| HC | Hydrocarbon |
| MS | Mass spectrometer |
| SpaciMS | Spatially resolved capillary inlet mass spectroscopy |
Subscripts
| g | Gaseous phase |
| K | Knudsen diffusion |
| M | Molecular diffusion |
| s | Substrate |
| s | Solid phase |
| T | Total |
| w | Washcoat |
Conflicts of interest
There are no conflicts to declare.References
- R. E. Hayes, S. T. Kolaczkowskib, P. K. C. Li and S. Awdry, Appl. Catal., B, 2000, 25, 93–104 CrossRef CAS.
- S. T. Kolaczkowski, Catal. Today, 2003, 83, 85–95 CrossRef CAS.
- F. Zhang, R. E. Hayes and S. T. Kolaczkowski, Chem. Eng. Res. Des., 2004, 82, 481–489 CrossRef CAS.
- M. D. Argyle and C. H. Bartholomew, Catalysts, 2015, 5, 145–269 CrossRef CAS.
- S. Dey and G. C. Dhal, Mater. Today Chem., 2019, 14, 100180 CrossRef CAS.
- S. Chauhan, J. Chem. Pharm. Res., 2010, 2, 602–611 CAS.
- K. Kröger, M. Hietikko, D. Angove, D. French, U. Lassi, A. Suopanki, R. Laitinen and R. L. Keiski, Top. Catal., 2007, 42, 409–413 CrossRef.
- K. Kröger, M. Hietikko, U. Lassi, J. Ahola, K. Kallinen, R. Laitinen and R. L. Keiski, Top. Catal., 2004, 30, 469–473 CrossRef.
- J. M. Guevremont, G. Guinther, T. Jao, T. Herlihy, R. White and J. Howe, Journal of Fuels and Lubricants, 2007, 116(4), 995–1002 Search PubMed.
- P. Lanzerath, A. Guethenke, A. Massner and U. Gaertner, Catal. Today, 2009, 147, S265–S270 CrossRef CAS.
- F. M. Z. Zotin, O. da Fonseca Martins Gomes, C. H. de Oliveira, A. A. Neto and M. J. B. Cardoso, Catal. Today, 2005, 107–108, 157–167 CrossRef CAS.
- R. Beckmann, W. Engeler, E. Mueller, B. H. Engler, J. Leyrer, E. S. Lox and K. Ostgathe, SAE Tech. Pap. Ser., 1992, 922330 Search PubMed.
- M. Moldovan, R. Rauch, G. M. Morrison, M. Gómez and M. A. Palacios, Surf. Interface Anal., 2003, 35, 354–359 CrossRef CAS.
- A. Russell and W. S. Epling, Catal. Rev.: Sci. Eng., 2011, 53, 337–423 CrossRef CAS.
- P. Albers, J. Pietsch and S. F. Parker, J. Mol. Catal. A: Chem., 2001, 173, 275–286 CrossRef CAS.
- C. H. Bartholomew and R. J. Farrauto, Fundamentals of Industrial Catalytic Processes, 2nd edn, 2006 Search PubMed.
- R. M. Heck, R. Farrauto and S. T. Gulati, Chapter 5-Catalytic Air Pollution Control Commercial Technology, Catalyst Deactivation, 2009 Search PubMed.
- C. Stere, Development and application of Spaci-MS technique in the investigation of structured catalysts under real reaction conditions, Ph.D. Thesis, Queen's University Belfast, 2012 Search PubMed.
- Y. Wang, C. Coney, C. McAtee, G. McCullough and A. Goguet, Appl. Catal., A, 2022, 118608 CrossRef CAS.
- G. Hofmann, A. Rochet, S. Baier, M. Casapu, S. Ritter, F. Wilde, M. Ogurreck, F. Beckmann and G. D. Grunwaldt, J. Phys.: Conf. Ser., 2014, 499, 012017 CrossRef CAS.
- F. Alzahrani, H. Rusi, S. Assabumrungrat, D. L. A. Fernandes and F. Aiouache, Chem. Eng. J., 2019, 378, 122082 CrossRef CAS.
- C. Coney, C. Hardacre, K. Morgan, N. Artioli, A. P. E. York, P. Milington, A. Kolpin and A. Goguet, Appl. Catal., B, 2019, 258, 117918 CrossRef CAS.
- J. Stewart, R. Douglas, A. Goguet and C. Stere, Can. J. Chem. Eng., 2014, 92, 1535–1541 CrossRef CAS.
- J. Sá, C. Stere and A. Goguet, Spacims-Probing the Internal Behaviour of 3D Structured Materials, Single and two-Phase Flows on Chemical and Biomedical Engineering, 2012, pp. 3–25 Search PubMed.
- C. Coney, C. Stere, P. Millington, A. Raj, S. Wilkinson, M. Caracotsios, G. McCullough, C. Hardacre, K. Morgan, D. Thompsett and A. Goguet, Catal. Sci. Technol., 2020, 10, 1858–1874 RSC.
- N. Maguire, A. Sasegbon, A. Abdelkader, A. Goguet, C. Hardacre, K. Hellgardt, K. Morgan and S. O. Shekhtman, Chem. Eng. Sci., 2013, 87, 224–233 CrossRef CAS.
- J. Choi, W. P. Partridge, J. A. Pihl and C. S. Daw, Catal. Today, 2008, 136, 173–182 CrossRef CAS.
- T. N. Angelidis and S. A. Sklavounos, Appl. Catal., A, 1995, 133, 121–132 CrossRef CAS.
- M. Sharma and M. Dearth, Appl. Catal., B, 2016, 188, 177–188 CrossRef CAS.
- R. B. Bird, W. E. Stewart and E. N. Lightfood, Chapter 17-Diffusivity and the mechanisms of mass transport, Transport Phenomena, 2005, pp. 513–542 Search PubMed.
- N. Wakao and J. M. Smith, Chem. Eng. Sci., 1962, 17, 825–834 CrossRef CAS.
- S. Kato, H. Ozeki, H. Yamada, T. Tagawa and N. Takahashi, Chem. Eng. J., 2015, 271, 188–194 CrossRef CAS.
- J. E. Clinton, K. J. Drury, Y. Gu and M. E. Saunders, U.S. Pat., US2019161415A1, 2019 Search PubMed.
- G. C. Koltsakis and A. M. Stamatelos, Prog. Energy Combust. Sci., 1997, 23, 1–39 CrossRef CAS.
- D. E. Angove and N. W. Cant, Catal. Today, 2000, 63, 371–378 CrossRef CAS.
- A. Russell, C. Henry, N. W. Currier, A. Yezerets and W. S. Epling, Appl. Catal., A, 2011, 397(1–2), 272–284 CrossRef CAS.
- U. Lassi, Deactivation Correlations of Pd/Rh Three-way Catalysts Designed for Euro IV Emission Limits, 2003 Search PubMed.
- J. Choi, W. P. Partridge, J. A. Pihl and C. S. Daw, Catal. Today, 2008, 136, 173–182 CrossRef CAS.
- T. N. Angelidis and S. A. Sklavounos, Appl. Catal., A, 1995, 133, 121–132 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cy01961b |
| This journal is © The Royal Society of Chemistry 2023 |