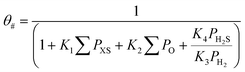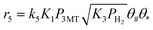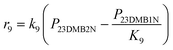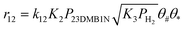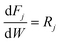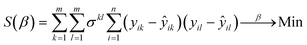High-throughput experimentation based kinetic modeling of selective hydrodesulfurization of gasoline model molecules catalyzed by CoMoS/Al₂O₃

Abstract

The selective hydrodesulfurization (HDS) of fluidized catalytic cracking gasoline still represents a challenging step to minimize hydrogen overconsumption and maintain high octane numbers. To better understand the competition between desulfurization and hydrogenation reactions, a Langmuir–Hinshelwood kinetic model is established, based on high-throughput HDS experiments of a model feedstock of 3-methyl-thiophene (3MT) and 2,3-dimethyl-but-2-ene over CoMoS/Al₂O₃ catalysts. To reduce the model's dimensionality, some key enthalpies of adsorption are determined by density functional theory (DFT) calculations. The model takes into account 16 different reactions (hydrogenation, hydrodesulfurization, isomerization) for which rate constants and adsorption constants are determined to reproduce adequately the experimental product distribution. The model is finally used to predict and discuss the impact of operating conditions (partial pressures of key reactants and temperature) on the selectivity. The selectivity is most affected by the conversion levels of the reactants, with an optimum desulfurization selectivity at approximately 30–50% 3MT conversion. Operating at low temperature (170 °C) is also favorable for the HDS selectivity.

---

Introduction

Over the last thirty years, the growing awareness of environmental constraints and tighter regulations have stimulated research into processes and catalysts for clean fuel production and reduction of pollutant emissions caused by fossil fuel combustion. Thus, numerous international legislations impose sulfur levels down to 10 ppm in gasoline for on-road vehicles.¹ Gasoline from fluidized catalytic cracking (FCC) represents 40–80 vol% in commercial fuels, but almost 85–90% of sulfur in final gasoline blends, mainly in the form of alkyl-thiophene compounds.^2,3 To comply with present regulations, FCC gasoline must be consequently post-treated, which is conventionally performed through a hydrodesulfurization (HDS) process at 200–300 °C under a hydrogen pressure of 10–30 bar. In parallel with hydrodesulfurization reactions, olefins present at 20–40 vol% in FCC gasoline undergo hydrogenation reactions (HydO), resulting in octane number decrease and H₂ overconsumption.⁴ Optimization of selectivity between hydrodesulfurization and hydrogenation at the process scale, improvement of catalyst design and fine understanding of reaction mechanisms through detailed kinetic models are therefore major research challenges in this field. Hydrodesulfurization catalysts are composed of group VI transition metal sulfide slabs (molybdenum or tungsten) supported on oxides such as transition alumina, silica or amorphous silica–alumina and promoted by group VIII elements including nickel or cobalt.^5,6 A generic structural active phase involving a CoMoS mixed site at the edges of the MoS₂ slabs describes the reactivity of such active phases as evidenced by advanced physico-chemical characterization techniques and density functional theory (DFT) simulations.^7–14 At the nanoscale, different types of active sites have been identified and correlated to catalytic HDS activities. HDS reactions may occur by two different pathways. The direct desulfurization (DDS) pathway involves C–S bond hydrogenolysis, which could be attributed to coordinatively unsaturated molybdenum sites (CUS) located at the edge sites.^7,15–17 These sulfur anion vacancies are suspected to be formed at the slab edges in the presence of H₂ at high temperature as encountered in HDS. Such vacancies have been observed by scanning tunneling microscopy (STM)¹⁸ and also highlighted by ab initio thermodynamic calculations.¹⁹ Another reaction pathway is a hydrogenation (HYD) route where C–S bond hydrogenolysis is preceded by a hydrogenation step. This pathway is supposed to be favored on the bright brims at the top of MoS₂ edges as observed in STM.^20,21 This brightness is due to a higher electron density, where electrons are situated in a dimension perpendicular to the slab edges and delocalized along the direction of the edges.^14,20 These electrons could then interact and take part in chemical bonding, which is far less favored in the case of the basal plane.¹⁰

Regarding catalytic activities, hydrogen dissociation is also an important parameter for HDS and HydO reactions and thus, the nature of hydrogenated species formed on the MoS₂ catalyst, such as sulfhydryl groups (S–H) or hydride (Mo–H), has been discussed for many years.^22–24 In particular, S–H groups were also identified by inelastic neutron spectroscopy,²⁵ while DFT calculations determined the thermodynamic stability of S–H and Mo–H groups present on the edges of MoS₂ crystallites as a function of temperature and P(H₂S)/P(H₂) conditions.^26,27 The hydrogenation was often correlated to the presence of sulfhydryl groups (S–H) at the slab edges by many experimental and theoretical studies.^24,28,29 In particular, S–H groups participate in the transfer of hydrogen atoms during hydrogenation steps and are very important in HDS reactions.³⁰

Typical molybdenum disulfide slabs present two energy-competing and stable edges commonly called the M-edge and S-edge.¹⁸ The relative free energies of both edges define the morphology of the MoS₂ slabs which may vary from triangular shapes with only the M-edge to hexagonal ones exposing both types of edges.^31,32 Slab morphology and size depend on sulforeductive conditions including temperature and H₂/H₂S partial pressures, support effects as well as on the presence of promoter atoms which may affect differently the relative edge energies.^14,32,33 Comparing the adsorption energies of 2-methylthiophene and 2,3-dimethylbutene on S- and M-edges under selective HDS conditions, Krebs et al. evidenced a competitive adsorption of sulfur compounds over olefins with a higher selectivity of the S-edge for 2-methylthiophene.^33,34 Slab morphology – i.e. S-/M-edge ratio – thus controls the selectivity of catalysts under selective HDS.^9,35 In a further study, Baubet et al.⁹ could experimentally evidence a correlation between slab morphology and catalyst selectivity for HDS and HydO reactions.

Kinetic studies on HDS of thiophenic compounds in the presence of olefins were modeled in different approaches in order to understand HDS/HydO selectivity over HDS catalysts.^36–39 A Langmuir–Hinshelwood (LH) model implying one type of active site was thus established to describe the transformation of 3-methylthiophene and 1-hexene over CoMoS/Al₂O₃ catalysts in the presence of H₂S.³⁸ Through the co-injection of H₂S, this study suggested the change of the rate-determining step depending on H₂S partial pressure. At low partial pressure of H₂S, the rate-determining steps were assumed to be the cleavage of the C–S bond for HDS of 3-methylthiophene and H transfer to the adsorbed olefin molecule for HydO of 1-hexene. At high partial pressure of H₂S, H transfer was proposed as the rate-determining step for both reactions. Other kinetic studies involving microkinetic modeling over molybdenum sulfided catalysts also suggested that the first hydrogen transfer from S–H groups to adsorbed 2-methylthiophene and 2,3-dimethyl-2-butene would be the rate determining steps in the presence or in the absence of CO as poison.^40,41 Such simple kinetic models made it also possible to correlate the HydO and HDS rates with the sulfur–metal energy of the sulfide catalysts through volcano curves, because it directly influences the optimal surface concentration of S–H species, adsorbed molecules and free sites.^41,42 A lumped kinetic model for selective HDS of a full range FCC gasoline by a LH approach was also described in the literature.⁴³ This model, containing 348 species and 444 reactions, described the product distribution as well as selectivity and octane loss. However, no rate equations were reported. Some of these previous studies proposed that the efficient HDS/HydO selectivity of the CoMoS catalyst results from an optimal competition between kinetic and thermodynamic effects: the thermodynamically more favorable adsorption of sulfur compounds should counterbalance the fast kinetics of olefin hydrogenation.^9,34,43

Nevertheless, in spite of the numerous studies previously reported, the detailed reaction mechanisms for sulfur compounds or olefins catalyzed by MoS₂ still require further investigation to gain insights into the complexity of selective HDS and assist in the development of more selective catalysts.

For this purpose, kinetic modeling based on LH formalism detailing the different elemental catalytic steps and considering the diversity of active sites involved in hydrodesulfurization and hydrogenation reactions is therefore necessary. Based on experimental data acquired by high-throughput kinetic experimentation, this work details the development of a kinetic model of 3-methylthiophene and 2,3-dimethyl-2-butene – as a model feed for FCC gasoline – based on a LH approach including a detailed reaction mechanism.

Results and discussion

Reaction network and mechanism

As explained in the introduction, HDS is believed to proceed according to the DDS and HYD routes. Scheme 1 shows the two routes as proposed by Dos Santos et al.^39,44 Both routes contain several subsequent hydrogenation and desulfurization steps all the way to 2-methylbutane. DFT studies on non-promoted model MoS₂ have suggested that the DDS route proceeds easily on the M-edge, while the HYD route is dominant on the S-edge.^28,29,45 The addition of the cobalt promoter accelerates the prehydrogenation steps on the S-edge.¹⁵ Moreover, these studies suggested that the presence of the two edges might provide an optimal configuration allowing prehydrogenation on the M-edge followed by S–C bond scission on the S-edge.

Scheme 1 Reaction network showing a direct desulfurization pathway (DDS) and a hydrogenation pathway (HYD). The products shown in dotted brackets (3MDHT and 2-methyl-butadiene) were not observed experimentally.

In our experiments, the conversion of 3MT led to the formation of 3-methyltetrahydrothiophene (3MTHT), 2-methyl-but-1-ene (2MB1N), 2-methyl-but-2-ene (2MB2N) and 2-methyl-butane (2MB), but 3-methyl-dihydrothiophene (3MDHT), 2-methyl-butadiene and thiols were not detected. Without excluding the occurrence of the DDS route for the conversion of 3MT, only the HYD route was considered in the model with direct formation of the C₅ olefins from 3MTHT, rather than through the intermediate formation of thiols.

Scheme 2 shows the reaction network for the conversion of 23DMB2N. Hydrogenation of 23DMB2N proceeds through a double bond isomerization step to yield 23DMB1N. The latter has been shown to be more reactive and has been used in the model as the reactant to be further hydrogenated into 2,3-dimethyl-butane (23DMB).⁴⁵ Skeletal isomers were also observed among the products, and it was assumed that the isomers, 33DMB1N and C6=, were formed from 23DMB1N. C6= is a hexene isomer but the exact structure could not be established. Since 23DMB2N and 23DMB1N were found in thermodynamic equilibrium, it does not matter for the mathematical model which one is involved in consecutive reactions.

Scheme 2 Reaction network for the conversion of 23DMB2N under hydro-desulfurization conditions.

C₁₂H₂₄, a product from the dimerization of 23DMB1N, was also observed experimentally. Finally, C6-methylthiophene (3MTC6) and C6-methyltetrahydrothiophene (3MTHTC6) were believed to be formed by the reaction of 3MT or 3MTHT and 23DMB1N, respectively.

Mey et al.^46,47 studied the conversion of 2-methylthiophene and 23DMB2N and reported a detailed reaction network and mechanism. The study by Dos Santos et al.⁴⁴ showed that 3MT HDS and 23DMB2N HydO were competing for the same active site. Here, we have followed this assumption to derive the corresponding rate equations. On the other hand, a separate site for hydrogen adsorption was used, which is often proposed in kinetic studies.^45,48,49 Hydrogen can adsorb dissociatively on MoS₂ active sites, through either a heterolytic or a homolytic route.^23,27,50,51 The heterolytic route involves hydrogen adsorption on both a metal (molybdenum or cobalt) and sulfur atom, whereas the homolytic route involves only sulfur atoms. Prodhomme et al.²⁷ showed that although dihydrogen may be activated heterolytically over MoS₂, the most stable configuration consists of two S–H groups. Therefore, in our kinetic model, we assume two distinct sites where only sulfur atoms correspond to the hydrogen adsorption sites (homolytic dissociative adsorption), while sulfur vacancies correspond to the sites for the adsorption of sulfur containing compounds and olefins. Sulfhydryl (S–H) groups have been shown to act as weak Brønsted acid sites^52–55 and might also be involved in isomerization reactions. The following adsorption/desorption steps were considered:

Associative adsorption for the sulfur compounds (XS):

XS + # ⇆ XS# (1)

Associative adsorption for olefins (O):

O + # ⇆ O# (2)

where # is a sulfur vacancy site. The adsorption of the alkanes was assumed to be weak and neglected in the model.

Dissociative homolytic hydrogen adsorption:

H₂ + 2* ⇆ 2H* (3)

where * is a hydrogen adsorption site (sulfur atom).

Dissociative hydrogen sulfide adsorption:

H₂S + # + 2* ⇆ S# + 2H* (4)

where # is a sulfur vacancy.

Note that S# is equivalent to a * and thus a conversion of sites can occur, which has not been considered in the model. The ratio of sulfur atoms to vacancies is believed to be very large,¹⁸ therefore, this site conversion will have a negligible effect on the number of hydrogen adsorption sites. Van Parijs and Froment³⁶ compared models with site interconversion to models with a fixed number of sites for the hydrogenolysis of thiophene over CoMoS/Al₂O₃ and found that the latter model fitted the data better. Sulfur exchange experiments show the existence of at least two different sulfur species.⁵⁶ In that light, one could argue that the species S# and * are not equivalent.

Due to the two distinct sites, two site balances are required:

θ_# + θ_XS + θ_O + θ_S = 1

θ_* + θ_H = 1

Assuming quasi-equilibrium for the above adsorption equilibria, the following expression for the free fraction of surface vacancies (θ_#) was derived:
where K_i is the adsorption equilibrium constant for step i (bar⁻¹), ∑P_XS the sum of the partial pressures of the sulfur containing components (bar), ∑P_O the sum of the partial pressures of all olefins (bar), P_H2S the partial pressure of hydrogen sulfide (bar) and P_H2 the partial pressure of hydrogen (bar).

The following expression gives the fraction of free hydrogen sites (θ_*):

The rate equations were based on the Langmuir–Hinshelwood model. The following reactions considered are listed in Table 1. Table 1 reports the reaction steps employed in the model together with the corresponding rate equations. Four isomerization reactions occur, of which two are double bond shifts (steps 7 and 9) and two skeletal rearrangements (steps 10 and 11). The experimental data show that the ratios 2MB2N/2MB1N and 23DMB2N/23DMB1N only depend on the temperature. Therefore, the double bond shifts are fast and in thermodynamic equilibrium. The rate equations for the double bond shifts are written in terms of the equilibrium constant and the active site dependence cancels out in the rate equation. In principle, these reactions can be eliminated by substituting the product in the remaining reactions by the reactant multiplied by the thermodynamic constant (K₇ and K₉ respectively). The skeletal isomerizations, on the other hand, were found not to be in thermodynamic equilibrium and it was assumed that these reactions involve the same H* sites as desulfurization and hydrogenation.⁴² As mentioned in the introduction, this means that S–H sites are assumed to act as hydrogenating species as well as Brønsted acid sites for isomerization.

Table 1 Reaction steps and their corresponding rate equations

No.	Reaction step	Rate equation
5	3MT# + 4H* → 3MTHT# + 4*
6	3MTHT# → 2MB2N + S#	r 6 = k6K1P3MTHTθ#
7	2MB2N# ⇆ 2MB1N#
8	2MB1N# + 2H* → 2MB# + 2*
9	23DMB2N# ⇆ 23DMB1N#
10	23DMB1N# ⇆ 33DMB1N#	r 10 = K2θ#(k10P23DMB1N − k−10P33DMB1N)
11	33DMB1N# ⇆ C6=#	r 11 = K2θ#(k11P23DMB1N − k−11PC6=)
12	23DMB1N# + 2H* → 23DMB# + 2*
13	33DMB1N# + 2H* → 22DMB# + 2*
14	2 23DMB1N# → C12H24# + #	r 14 = k14K^22P^223DMB1Nθ^2#
15	23DMB1N# + 3MT# → 3MT-C6# + #	r 15 = k15K1K2P3MTP23DMB1Nθ^2#
16	23DMB1N# + 3MTHT# → 3MTHT-C6# + #	r 16 = k16K1K2P3MTHTP23DMB1Nθ^2#

---

Note that the surface reactions are not elementary reaction steps, but a sequence of hydrogen additions. It was assumed that the rate limiting step in this sequence was the addition of the first hydrogen atom as proposed in some previous kinetic studies,^40,41 resulting in rate equations containing the square root of the hydrogen partial pressure in the numerator. No distinction, however, could be made between the rate limiting step being the first or second hydrogen addition, as both models fitted the data equally well by only changing the value of the hydrogen adsorption equilibrium constant. The Arrhenius and van't Hoff equations were used in a reparametrized form⁵⁷ with a reference temperature of 180 °C.

Reactor model and regression analysis

The intrinsic reaction conditions were evaluated by using the EUROKIN spreadsheet for assessment of transport limitations in gas–solid fixed beds.⁵⁸ The assessment was carried out by using the highest consumption rate of 3MT (0.4 mmol kg_cat⁻¹ s⁻¹) observed at the highest temperature of 220 °C (3MT conversion of 0.63), assuming a zero reaction order in 3MT and a heat of reaction of −92 kJ mol⁻¹. The results of the different criteria are summarized in Table S1.† The limits on these criteria are determined by a maximum allowed deviation of 5% of the reaction rate free of transport limitations.

Because of the integral reactor operation, the rate equations have been integrated numerically. A one-dimensional homogeneous plug-flow reactor model has been used, in agreement with the absence of mass and heat transfer limitations. The reactant and product molar flow rates at the reactor outlet were calculated by numerically integrating the following continuity equation:

where F_j (mol s⁻¹) is the molar flow rate for component j, W (kg) the catalyst mass and R_j (mol kg⁻¹ s⁻¹) the net consumption/production rate of component j.

The maximum likelihood parameter estimates were obtained by minimization of the objective function S(β) based on either the conversion or product yield:

where m is the number of responses (14) and n the number of experiments (26). σ^kl is the (k,l) element of the inverse covariance matrix. The (k,k) elements of this matrix were set to 1 for the reactants and inversely proportional to the yield of the products. The non-linear least-squares multi-response regression analysis was performed by means of a Levenberg–Marquardt algorithm.^59,60 After regression analysis, several statistical indicators were calculated, including the R² value, t-test, 95% confidence intervals of the parameter estimates, F-value and binary correlation coefficients. The integral method of kinetic analysis coupled with multi-response regression analysis is well described by Froment and Bischoff.⁶¹

Experimental and simulated yields

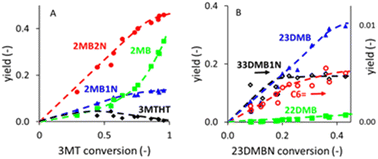
The yields of the main products obtained from 3MT or (23DM2N + 23DMB1N) conversion, shown in Fig. 1, were obtained by changing either the contact time or the temperature (200–220 °C). The yields of 3MTHT, 3MTC6 and 3MTHTC6 go through a maximum and decrease at high conversion. 2MB2N and 2MB1N olefins increase rather linearly with conversion. Although the highest conversion of 3MT amounted to 95.6%, this was not high enough to see a drop in the olefin yield, as observed by dos Santos et al.⁴⁴ The fully hydrogenated product 2MB increased exponentially. The evolution of the yields as a function of the conversion indicates the hydrogenation of 3MT into 3MTHT, which is further hydrodesulfurized into 2MB2N and 2MB1N, which are then hydrogenated into 2MB. A linear increase of the yield of all the products with the (23DMB2N + 23DMB1N) conversion is observed. Fig. 1 also shows that the selectivity is mainly dominated by the conversion level and very little by the temperature, as no specific trends for the different temperatures emerge between 200 and 220 °C. Similar observations were reported by dos Santos et al. for the conversion of 3MT⁴⁴ and for the conversion of 23DMB2N over a similar catalyst.³⁹

Fig. 1 Product distribution as a function of the conversion. A: 3MT products. B. 23DMBN products. 0.33 wt% 3MT, 10 wt% 23DMB2N over CoMo/Al₂O₃ at 15 bar, LHSV of 3 h⁻¹, H₂/feedstock ratio of 300 NL L⁻¹, 200–220 °C. The dashed lines are a guideline for the eyes.

The production of alkanes from 3MT and 23DMB2N was studied as a function of the partial pressures of 3MT and 23DMB2N, as shown in Fig. 2. The conversion of 3MT drops exponentially with increasing partial pressure of 3MT, while the 23DMB2N conversion drops initially to level off at 30% conversion at higher partial pressures of 3MT. This is due to the isomerization reaction of 23DMB2N into 23DMB1N, which is in thermodynamic equilibrium and is not affected by the inhibition by 3MT. A significant drop in the production of 2DMB as well as 23DMB was observed by increasing the partial pressure of 3MT, as shown in Fig. 2C. These results indicate a competition between 3MT and 23DMB2N for the same active sites, as also shown by Dos Santos et al.^39,44 On the other hand, the partial pressure of 23DMB2N has little effect on the conversion of both 3MT and 23DMB2N (Fig. 2B) and affects only slightly the production of the alkanes (Fig. 2D).

Fig. 2 Comparison of experimental data and model predictions for the conversions of 3MT and 23DMB2N (A and B) and the yields of 2MB and 23DMB (C and D) as a function of A and C: 3MT partial pressure, B and D: 23DMB2N partial pressure. Experiments: symbols 3MT or 2MB (black full), 23DMB2N or 23DMB (red open). Model predictions: lines 3MT or 2MB (black full), 23DMB2N or 23DMB (red dashed). 0–1.32 wt% 3MT, 10 wt% 23DMB2N over CoMo/Al₂O₃ at 15 bar, LHSV of 3 h⁻¹, H₂/feedstock ratio of 300 NL L⁻¹, 180 °C.

Fig. 2 and S1–S5† show that the model predictions for the 4 observable quantities (W/F, T, F_3MT, F_23DMB2N) are adequate for all the products when compared with experimental results. Some small deviations are observed at low flow rates of 3MT for the two pentenes 2MB2N and 2MB1N as well as the data at low temperature for C6MT and C6MTHT at the lowest contact time. A systematic deviation of the 2MB yield as a function of the 23DMB2N partial pressure is also observed (Fig. 2D), which must be toned down by the very low value of yields measured for this product.

Analysis of the kinetic parameters

Regression analysis of the 364 experimental data points was performed using rate equations r₅ through r₁₆. Preliminary regression analysis showed that strong parameter correlation occurred, especially with the adsorption constants. Therefore, the adsorption constants for all olefins in the reaction network were set at the same value (K₂, ΔH₂). Dos Santos found differences of less than 5 kJ mol⁻¹ in adsorption strength between the different olefins,³⁹ which makes the use of a single adsorption constant a reasonable assumption. To reduce the parameter correlation further, the values of the adsorption enthalpies for the 4 adsorption steps (eqn (1)–(4)) employed in the model were fixed at values calculated by DFT for adsorption on the S-edge of the CoMoS catalyst (see ESI.2† for more details and ref. 34), as given in Table 2. Several studies report weak adsorption of hydrogen over promoted molybdenum catalysts.^49,62 Therefore, the value of the adsorption entropy for the dissociative adsorption of hydrogen was fixed at −38 J mol⁻¹ K⁻¹, which corresponds to the loss of one degree of gas phase translation entropy, according to the Sackur–Tetrode equation.⁶³ This value of the hydrogen adsorption constant resulted in a calculated hydrogen coverage of ∼0.5–0.6 for all experimental conditions. Further decoupling of the adsorption constants was achieved by fixing the adsorption entropy for 3MT at −219 J mol⁻¹ K⁻¹, a value obtained from the compensation effect between the adsorption entropy and enthalpy for species adsorbing on the same site (sulfur vacancy). Using the values of the adsorption constants for 3MT and 23DMB2N at 210 °C, we were able to describe transient desorption data over a similar catalyst sample quite well, as shown in Fig. S6.† Note that changing the values of the adsorption enthalpies will directly impact the values of the other rate constants, especially the activation energies of the different steps. An example where the adsorption enthalpies for the M-edge of a CoMoS catalyst, calculated by DFT, were used as input parameters is given in the ESI† (Table S2). The model fit is, however, slightly affected in this case (+15% in residual sum of squares).

Table 2 Values of the adsorption equilibrium constants, entropies and enthalpies on the cobalt-promoted S-edge. The values with ±95% confidence intervals were estimated. All other parameters were fixed

Adsorption step	K i (bar^−1) 180 °C	ΔS^0ads^a (J mol^−1 K^−1)	ΔH^0ads (kJ mol^−1)
^aΔS^0ads = S^0ads − ΔS^0gas. ΔS^0g is the standard entropy in the gas phase at unit pressure and ΔS^0a the standard entropy in the adsorbed state at a degree of a coverage of half a monolayer and, therefore, it does not include configurational entropy.^64a DFT values reported in ref. 34 and also used in ref. 9 for XS = 2MT and O = 23DMB2N.b DFT values determined in the present study (see ESI† 2 for more detail).c Homolytic dissociation of H2 (leading to SH, SH as in eqn (3)) were calculated.d H2S dissociatively adsorbed on one vacancy and on one S, leading to two adsorbed SH species as in eqn (4) (see ESI† 2 for more detail).e Calculated from the compensation effect between the adsorption entropy and enthalpy.f Corresponds to the loss of one degree of gas phase translation entropy, according to the Sackur–Tetrode equation.^63
1 XS	1.0 × 10^4	−219^e	−134^a
2 O	(1.4 ± 0.1) × 10^2	−67 ± 19	−49^a
3 H2	0.2	−38^f	−11^b^,^c
4 H2S	(1.5 ± 0.2) × 10^5	−290 ± 36	−176^b^,^d

---

28 kinetic parameters with their 95% confidence intervals have been estimated (Tables 2 and 3) with significant statistics. The parameter correlation matrix (Table S4†) reveals strong correlations for (k₁, k₂), (k₁₀, k₋₁₀), (k₁₁, k₋₁₁) and (k₁₅, k₁₆).

Table 3 Values of the parameter estimates with their 95% confidence intervals

Step	k i (180 °C)	k −i (180°) or Ki	E a or ΔHiso (kJ mol^−1)
a Reaction enthalpy, ΔHiso (kJ mol^−1). b Activation energy for the reverse step was fixed at Ea,forward − 8 kJ mol^−1.
5	(7.1 ± 0.5) × 10^−5		162 ± 3
6	(5.5 ± 0.4) × 10^−4		181 ± 5
7		(3.6 ± 0.1) × 10^−1	−11 ± 2^a
8	(1.5 ± 0.2) × 10^−2		37 ± 6
9		(3.10 ± 0.01) × 10^−1	8 ± 1^a
10	(2.0 ± 0.2) × 10^−4	(3 ± 2) × 10^−3	73 ± 4
11	(8 ± 3) × 10^−2	(6 ± 3) × 10^−2	23 ± 5^b
12	(2.9 ± 0.1) × 10^−3		83 ± 2
13	(1.4 ± 0.1) × 10^−2		70 ± 6
14	(3 ± 2) × 10^−3		35 ± 5
15	(1.4 ± 0.1) × 10^−4		35 ± 7
16	(5.4 ± 0.4) × 10^−4		65 ± 7

---

The highest activation energy was found for the reaction converting 3MTHT into 2MB2N (6) at 181 kJ mol⁻¹, which is 19 kJ mol⁻¹ higher than the activation energy for the full hydrogenation of 3MT into 3MTHT (5). This is due to the fact that 3MTHT conversion involves the breaking of the C–S bond, while all other hydrogenation steps are double bond saturations. Sullivan and Ekerdt⁶⁵ measured an apparent activation energy of 174 kJ mol⁻¹ for tetrahydrothiophene conversion over MoS₂/SiO₂. DFT studies for HDS of thiophene over the cobalt-promoted edge of MoS₂ by Zheng et al.⁶⁶ predicted that activation energies for thiophene HYD into 1- or 2-butene range between 152 kJ mol⁻¹ and 240 kJ mol⁻¹ through the scission of the C–S bond of a dehydrogenated thiophene intermediate. DFT calculations by Moses et al.¹⁵ for the HDS reaction of thiophene over Co–Mo–S brim sites predicted that cobalt decreases the barrier for HYD while increasing the one for C–S bond scission. They found an activation energy barrier of 161 kJ mol⁻¹ for the C–S bond breaking through the HYD pathway, while a lower energy barrier of 100 kJ mol⁻¹ was found for DDS. Hence, our value of the activation energy of 181 kJ mol⁻¹ estimated for step (6) is more in line with those DFT calculations for the HYD rather than for the DDS pathway, although based on the model alone the DDS pathway cannot be excluded.

The activation energies for the hydrogenation of 2MB1N, 33DMB1N and 23DMB1N olefins into the 3 corresponding alkanes 2MB, 22DMB and 23DMB (steps 8, 12 and 13) are quite different (37, 70 and 83 kJ mol⁻¹, respectively), which reflects the trend of increasing substitution at the double bond, leading to a more difficult hydrogenation due to steric hindrance induced by the methyl substituents.^67,68 Dos Santos also measured increasing activation energies for the hydrogenation of different alkenes with increasing degree of branching, including 23DMB2N and 33DMB1N, over CoMo/Al₂O₃ with differences of up to 22 kJ mol⁻¹.³⁹

At this stage, it might be also interesting to compare the trends found for the cobalt-promoted M-edge (Table S3†). The main impact concerns the activation energies found for HydO reactions (8, 12 and 13) which are significantly higher (by 40 to 70 kJ mol⁻¹) on the M-edge than on the S-edge. Activation energies involving 3MT and 3MTHT hydrogenation (steps 5 and 6) are much less affected by about 10 kJ mol⁻¹. However, since the tested catalysts do not vary the promoter contents and its impact on the morphology of the active phase, we cannot distinguish the two models considering either S-edge or M-edge sites.

The double bond isomerization of 23DMB2N into 23DMB1N proceeds with a reaction enthalpy of 8 kJ mol⁻¹ and an entropy of 7.5 J mol⁻¹ K⁻¹, whose values are in line with the enthalpy of formation of 8.6 ± 0.2 kJ mol⁻¹ and the entropy of 11.9 ± 0.4 J mol⁻¹ K⁻¹ at 213 °C, reported by Rodgers and Wu.⁶⁹ The double bond isomerization of 2MB2N into 2MB1N proceeds with a reaction enthalpy of −11 kJ mol⁻¹. The standard reaction enthalpy for this isomerization given at the NIST webbook equals +6.3 ± 0.1 kJ mol⁻¹.⁷⁰ The value of equilibrium constant for the double bond isomerization of 2MB2N into 2MB1N at 180 °C is similar to that of 23DMB2N into 23DMB1N (0.37 vs. 0.31), predicting correctly that 2MB2N is the dominant isomer. However, the experimental ratio 2MB2N/2MB1N increases with increasing temperature, while the opposite trend is expected from the positive value of the standard isomerization enthalpy. 1-Olefins are more reactive than 2-olefins⁴⁷ and 2MB1N will be faster hydrogenated into 2MB than 2MB2N and this hydrogenation step increases with increasing temperature. However, the isomerization equilibrium is faster than the hydrogenation reaction and the ratio 2MB2N/2MB1N should still correspond to the value of equilibrium constant at the corresponding temperature.

The skeletal isomerization of 23DMB1N into 33DMB1N was found not to be in quasi-equilibrium. The rate constant for the skeletal isomerization of 23DMB1N into 33DMB1N is much lower than the subsequent hydrogenation reaction to 22DMB. The skeletal isomerization seems therefore the rate determining step for the production of 22DMB. The value of rate constant for the hydrogenation of 33DMB1N into 22DMB at 180 °C is 5 times higher than that of the hydrogenation of 23DMB1N into 23DMB, yet the ratio 23DMB/22DMB is approximately 20, due to the formation of 23DMB being directly from 23DMB1N, while the formation of 22DMB requires the slow skeletal isomerization of 23DMB1N into 33DMB1N.

Both the forward and reverse rate constants were estimated for the skeletal isomerization of 23DMB1N into C6=. Mey et al.⁴⁷ reported a detailed reaction network for the skeletal isomerization of dimethyl-butene. Iso-pentenes and hexenes can be formed from both 23DMB1N and 33DMB1N. The model did not allow discrimination between these two routes. Formation of C6= did have a significantly lower activation energy than the formation of 33DMB1N (23 vs. 73 kJ mol⁻¹), although at 180 °C the values of the forward rate constants are similar. This would imply in terms of the scheme proposed by Mey et al.⁴⁷ that the route through the protonated cyclopropane intermediate is energetically favored compared to the tertiary carbenium ion intermediate, but more sterically hindered or proceeding over different active sites.

Evolution of surface coverages

The analysis of the surface coverages as a function of the reactor length (Fig. S8†) for a 3MT conversion of 95% reveals that 3MT# and 23DMBN# are the most abundant surface species at the reactor entrance. With increasing reactor coordinate and thus increasing conversion, these surface coverages dropped rapidly. 3MTHT# is maximized right after the reactor entrance, when 3MT# starts to be consumed and it appears thus as a reaction intermediate for the HYD pathway. Conversely, the coverage of S# surface species increases and becomes predominant at the reactor outlet. The S# surface species thus result first from the desulfurization reaction of 3MTHT#, and then closer to the reactor outlet, it is determined by the equilibrium between H₂ and H₂S (step 4). The concentration of surface H* is constant over the whole catalyst bed. The fact that it does not depend on the position in the reactor (conversion) is due to the fact that under our initial hypothesis, the free sulfur sites * where H* is formed are not coupled with the # free sites where the other reactions are occurring. Thus, H* cannot be impacted by the other adsorbed species and it would depend only on H₂ partial pressure, remaining quasi-constant since hydrogen consumption is low under these operating conditions.

Exploration of other (T,p) conditions through kinetic modeling

Using the kinetic model as a predictive tool, Fig. 3 plots the model calculated consumption rate of 3MT at 180 °C versus the partial pressures of hydrogen, 3MT and H₂S. The slopes in these plots represent the calculated reaction orders with respect to the 3MT conversion. The hydrogen reaction order is positive but decreases with increasing hydrogen pressure, from 0.42 to 0.23 under the operating conditions of this study. Hence, higher hydrogen pressure increases the reaction rate considerably but has hardly an impact on the relative yields (Fig. S9C†) and thus no impact on HDS/HydO selectivity.

Fig. 3 Simulated reaction rates of 3MT (r₅, full lines) and 23DMB1N (r₁₂, dashed lines) conversion over CoMo/Al₂O at 15 bar, 180 °C as a function of the partial pressure of A: H₂, B: 3MT, and C: H₂S.

The reaction order of 3MT with respect to r₅ is close to 1 at low pressures, decreasing with increasing pressure and approaching zero at the pressures used in this study. This is due to the formation of H₂S, which saturates the sites at high partial pressure of 3MT. Borgna et al.⁴⁹ reported reaction orders of thiophene between 0.58 and 0.8 depending on the reaction temperature, in line with the values found in this study. As expected from experimental results, 3MT inhibits 23DMB1N hydrogenation (r₁₂) particularly at higher partial pressure of 3MT.

The slope of r₁₂ changes from −0.3 to −0.98 with increasing partial pressure of 3MT. This trend confirms that the thermodynamic component (relative adsorption constants and partial pressures of reactants) is able to counterbalance the intrinsic kinetic component in favor of HydO. Thus, increasing the 3MT partial pressure will enhance the HDS/HydO selectivity (Fig. S9A†).

The reaction order of H₂S decreases from approximately zero at low pressures to −0.5 at a H₂S pressure of 1 bar. Dos Santos et al.³⁸ reported an inhibiting effect of H₂S on both the hydrodesulfurization of 3MT and the hydrogenation of 1-hexene over CoMoS/Al₂O₃. Moreover, they claimed a change of the selectivity as a function of the partial pressure of H₂S. We have not varied the partial pressure of H₂S in our own experimental study, but we have compared the model simulations to the experimental data of Dos Santos et al.³⁸ under similar conditions (23DMB2N instead of 1-hexene), as shown in Fig. S10.† A similar trend as a function of the partial pressure of H₂S was found. However, the change in HDS/HydO selectivity is not due to H₂S, but due to the change in 3MT conversion. Simulations shown in the same Fig. S10† at a constant 3MT conversion of 10% show that the ratio HDS/HydO remains constant over a large range of partial pressures of H₂S.

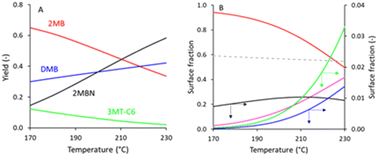
Considering the effects of temperature, Fig. 4 reveals that operating at higher temperatures lowers the extent of alkylation of sulfur components by C6 olefins but does not impact the selectivity. Fig. 5 shows the impact of the partial pressure of 3MT on the product distribution and surface species. Note that the trend is different than that presented in Fig. 2, because the data in Fig. 5 are at constant 3MT conversion (95%), instead of constant contact time. Due to the fact that the formation of 3MT-C6 and 3MTHT-C6 is more strongly impacted by sulfur inhibition (shown by the increase of θ_S in Fig. 5B) than the hydrogenation reactions, an increasing 3MT pressure leads to better selectivity.

Fig. 4 A: Product yields and B: surface coverages as a function of temperature at the reactor outlet. Black full line θ_3MT, blue dashed line θ_3MTHT, pink full line θ_{C6_olefins}, blue full line θ_{C5_olefins}, red full line θ_S, green full line θ_#, grey dotted line θ_H. P_H2 = 10 bar, P_3MT = 0.018 bar, P_23DM2BN = 0.62 bar, X_3MT = 0.95.

Fig. 5 A: Product yields and B: surface coverages at the reactor outlet as a function of the partial pressure of 3MT. Black full line θ_3MT, blue dashed line θ_3MTHT, pink full line θ_{C6_olefins}, blue full line θ_{C5_olefins}, red full line θ_S, green full line θ_#, grey dotted line θ_H. P_H2 = 10 bar, T = 180 °C, P_23DM2BN = 0.62 bar, X_3MT = 0.95.

Fig. S9† summarizes the effect of the main variables on the selectivity, expressed as the ratio HDS/HydO. Except for the effect of the catalyst mass, all simulations have been carried out at constant 3MT conversion of 95% by changing the contact time. In most cases the 23DMB2N conversion is also constant (∼50.5 ± 0.5%). The partial pressures of 3MT and 23DMB2N have a small effect on the selectivity, but no effect is found for the partial pressures of H₂ and H₂S. The effect of the temperature on the selectivity is due to a variation of the 23DMB2N conversion. It is impossible to change the temperature and keep both the conversion of 3MT and 23DMB2N constant, due to different activation energies to convert these two molecules. The largest impact on the HDS/HydO ratio results from the variation of the conversion, either of 3MT or 23DMB2N, as shown in the graph of the selectivity versus the catalyst mass (Fig. S9F†). Optimum HDS selectivity is found for 3MT conversions between 30 and 50% (at 180 °C, P = 15 bar, 0.33 wt% 3MT, 10 wt% 23DMB2N).

Experimental

Catalyst preparation

Molybdenum(VI) oxide (MoO₃, ACS Reagent ≥99.5%), cobalt(II) hydroxide (Co(OH)₂, technical grade 95%), orthophosphoric acid (85 wt% in H₂O, 99.99% trace metals basis), 2,3-dimethyl-2-butene (23DMB2N, ≥99%), 3-methylthiophene (3MT, 98%) and n-heptane were purchased from Sigma-Aldrich. Alumina (trilobe-shaped γ-Al₂O₃) was provided by Axens. Prior to tests, 23DMB2N was filtered on activated alumina to remove oxygen impurities.

The catalyst used in this work was a CoMo/γ-Al₂O₃ catalyst prepared by incipient wetness impregnation of γ-alumina. The impregnation solution was prepared by dissolution of MoO₃ and Co(OH)₂ in an aqueous solution containing H₃PO₄ by reflux at 90 °C. Following the incipient wetness impregnation of alumina with the metallic solution, an ageing step was applied for 12 h to ensure metal diffusion within the extrudates. The resulting solids were then dried at 120 °C for 24 h and finally calcined in air at 450 °C for 2 h. The final catalyst contained 13.5 wt% molybdenum, 3.2 wt% cobalt and 1.1 wt% phosphorus (according to XRF analysis), corresponding to a molybdenum surface density of 3.8 molybdenum atoms per nm² and Co/Mo and P/Mo ratios of 0.39 and 0.26 respectively. The final catalyst had a BET surface area of 200 m² g⁻¹ and a mesopore volume of 0.46 ml g⁻¹.

Catalytic tests

Catalytic tests were carried out in a Flowrence Avantium® high-throughput test unit (16 parallel reactors) with a model FCC gasoline feedstock containing 0.33 wt% of 3-methylthiophene (3MT, corresponding to 1000 wt ppm S) and 10 wt% of 2,3-dimethylbut-2-ene (23DMB2N) dissolved in n-heptane (89.7 wt%). Fixed bed reactors were loaded with 30–400 mg of catalyst. Different amounts of the catalyst were used to vary the contact time. In one series of experiments the 3MT concentration was varied between 0 and 1.32 wt%, while in another series the 23DMB2N concentration was varied between 0 and 20 wt%.

Prior to the test, the catalysts were sulfided in situ using dimethyldisulfide (4 wt%) in n-heptane (96 wt%) with the following operating conditions: a LHSV of 3 h⁻¹, a total pressure of 15 bar and a H₂/feedstock ratio of 300 NL L⁻¹. Sulfidation was carried out raising the temperature up to 350 °C by 2 °C min⁻¹ and maintaining the temperature for 2 h. After the sulfidation step, the temperature was decreased down to 180 °C and the catalysts were tested at different temperatures (180, 200, 210, 220 °C) while the total pressure and H₂/feedstock were maintained at 15 bar and 300 NL L⁻¹, respectively. Effluents were analyzed with an on-line gas chromatograph (Agilent 7890) equipped with two FID detectors using a specific configuration of DB-1 (non-polar) and Rtx-1701 (polar) columns, a heart-cutting device to ensure the absence of co-elutions, and using hydrogen as a carrier gas. Identification of products is based on the literature^38,47 and also on additional GC-MS analysis carried out at IFPEN.

Measurements of conversion and yield related to the 3MT and 23DMB2N transformations have been performed as a function of the contact time and temperature. This contact time is defined as the reverse of the weight hourly space velocity and has been varied by changing the amount of the catalyst or the reactant flow rate. The conversion and yields were calculated on a mole basis. The yields of 3MTHT, 2MB1N, 2MB2N, 2MB, 3MT-C6 and 3MTHT-C6 were calculated with respect to the 3MT conversion, while 23DMB1N, 33DMB2N, C6=, 23DMB, 22DMB and C₁₂H₂₄ were calculated with respect to the 23DMB2N conversion. HDS products consist of 2MB1N, 2MB2N and 2MB, while HydO products consist of 23DMB and 22DMB. The selectivity is expressed as the ratio of HDS/HydO.

Conclusions

The hydrodesulfurization of 3MT in the presence of 23DMB2N, as model compounds for the FCC gasoline fraction, was carried out in a high-throughput screening reactor as a function of temperature, contact time and partial pressures of 3MT and 23DMB2N at 15 bar. The kinetic data were collected under intrinsic conditions, allowing a Langmuir–Hinshelwood based modeling study. The product distribution showed that different types of reactions occurred: partial hydrogenation of 3MT, desulfurization, double bond and skeletal isomerization, hydrogenation of double carbon–carbon bonds, olefin dimerization, and reactions between sulfur containing species with olefins. 16 main reactions were included in the kinetic model. The experiments also showed an inhibition by 3MT of the hydrogenation of 23DMB2N. Homolytic dissociative adsorption of hydrogen was assumed on sulfur sites while all organic species react on free metallic sites. To reduce the number of the model's parameters, we include DFT adsorption energies of 4 key reactants adsorbed on cobalt-promoted S-edge sites: methyl-thiophene, dimethyl-butene, H₂S and H₂. The model reproduced the main experimental data adequately with physically realistic parameter values and thus allowed analysis of various intrinsic kinetic parameters. The kinetic constants of the various reactions were discussed with respect to previous experimental and theoretical data. The model confirmed the kinetic/thermodynamic balance between HDS and HydO: while olefinic compounds exhibit larger hydrogenation rate constants by two orders of magnitude, larger adsorption constants (by the same order of magnitude) of sulfur organic compounds counterbalance it. In agreement with experiments, the model recovers the inhibiting effects of 3MT on HydO. According to the model simulations, the selectivity is most affected by the conversion levels of 3MT and 23DMB2N, with an optimum desulfurization selectivity at approximately 30–50% 3MT conversion. However, this is not an option to operate a sulfur removal unit, but operating at low temperature (170 °C) is favorable for the HDS selectivity.

Beyond this fruitful comparison with high-throughput data, the kinetic model was used to predict the impact of operating conditions on HDS/HydO selectivity such as temperature and partial pressures of H₂, H₂S and 3MT. Among them, the effect of 3MT partial pressure appears to be the most critical on selectivity. We also provided an analysis of the surface coverages for the most relevant intermediates to discuss the trends.

We think that this model will help to better rationalize the observed trends and predict the impact of operating conditions in selective HDS of gasoline. Within the context of more complex feedstocks' hydrotreatment such as biomass, we hope that it may be considered as a milestone for establishing more advanced kinetic models including the transformation of oxygenated compounds.

Author contributions

Conceptualization (PR, JMS). Data curation, formal analysis, investigation (FC, EG, JMS). Methodology and project administration (PR, EG, AD, MR, YS). Data interpretation (FC, PR, JMS, YS). Validation and visualization (EG, AD, MR, YS, PR). Supervision (PR, AG, AD, MR, YS). Writing – original draft (EG, YS). Writing – review & editing (PR, EG, AD, MR, YS).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

F. Caron and E. Galand are grateful for the Ph.D. grant from IFP Energies nouvelles and support from CNRS (Centre National de la Recherche Scientifique) and IFPEN. The authors also thank Mathieu Vidalie and Amaury Donnette for catalytic data acquisition by high-throughput experimentation at IFPEN.

Notes and references

1. Official Journal of European Union, 2009, L140, 88–114,  DOI:10.3000/17252555.L_2009.140.eng.
2. J. T. Miller, W. J. Reagan, J. A. Kaduk, C. L. Marshall and A. J. Kropf, J. Catal., 2000, 193, 123–131.
3. I. V. Babich and J. A. Moulijn, Fuel, 2003, 82, 607–631.
4. S. Brunet, D. Mey, G. Pérot, C. Bouchy and F. Diehl, Appl. Catal., A, 2005, 278, 143–172.
5. Catalysis by transition metal sulphides: From molecular theory to industrial application, ed. H. Toulhoat and P. Raybaud, Ed. Technip, Paris, 2013.
6. T. A. Saleh, Trends Environ. Anal. Chem., 2020, 25, e00080.
7. H. Topsøe, B. S. Clausen and F. E. Massoth, Hydrotreating Catalysis, in Catalysis: Science and Technology, ed. J. R. Anderson and M. Boudart, Springer, Berlin Heidelberg, 1996.
8. H. Topsøe, B. S. Clausen, R. Candia, C. Wivel and S. Mørup, J. Catal., 1981, 68, 433–452.
9. B. Baubet, M. Girleanu, A.-S. Gay, A.-L. Taleb, M. Moreaud, F. Wahl, V. Delattre, E. Devers, A. Hugon, O. Ersen, P. Afanasiev and P. Raybaud, ACS Catal., 2016, 6, 1081–1092.
10. J. V. Lauritsen and F. Besenbacher, J. Catal., 2015, 328, 49–58.
11. J. Lauritsen, J. Kibsgaard, G. Olesen, P. Moses, B. Hinnemann, S. Helveg, J. Norskov, B. Clausen, H. Topsøe and E. Lægsgaard, J. Catal., 2007, 249, 220–233.
12. M. Salmeron, G. A. Somorjai, A. Wold, R. Chianelli and K. S. Liang, Chem. Phys. Lett., 1982, 90, 105–107.
13. C. Wivel, R. Candia, B. S. Clausen, S. Mørup and H. Topsøe, J. Catal., 1981, 68, 453–463.
14. H. Schweiger, P. Raybaud and H. Toulhoat, J. Catal., 2002, 212, 33–38.
15. P. G. Moses, B. Hinnemann, H. Topsøe and J. K. Nørskov, J. Catal., 2009, 268, 201–208.
16. L. S. Byskov, J. K. Nørskov, B. S. Clausen and H. Topsøe, Catal. Lett., 2000, 64, 95–99.
17. J. Lauritsen, S. Helveg, E. Lægsgaard, I. Stensgaard, B. Clausen, H. Topsøe and F. Besenbacher, J. Catal., 2001, 197, 1–5.
18. S. Helveg, J. Lauritsen, E. Lægsgaard, I. Stensgaard, J. Norskov, B. Clausen, H. Topsøe and F. Besenbacher, Phys. Rev. Lett., 2000, 84, 951–954.
19. P. Raybaud, J. Hafner, G. Kresse, S. Kasztelan and H. Toulhoat, J. Catal., 2000, 189, 129–146.
20. J. V. Lauritsen, M. Nyberg, J. K. Nørskov, B. S. Clausen, H. Topsøe, E. Lægsgaard and F. Besenbacher, J. Catal., 2004, 224, 94–106.
21. M. Daage and R. R. Chianelli, J. Catal., 1994, 149, 414–427.
22. J. Polz, H. Zeilinger, B. Müller and H. Knoezinger, J. Catal., 1989, 120, 22–28.
23. S. Kasztelan and D. Guillaume, Ind. Eng. Chem. Res., 1994, 33, 203–210.
24. M. Breysse, E. Furimsky, S. Kasztelan, M. Lacroix and G. Perot, Catal. Rev.: Sci. Eng., 2002, 44, 651–735.
25. P. Sundberg, R. B. Moyes and J. Tomkinson, Bull. Soc. Chim. Belg., 1991, 100(11–12), 967–976.
26. M. V. Bollinger, K. W. Jacobsen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 085410.
27. P.-Y. Prodhomme, P. Raybaud and H. Toulhoat, J. Catal., 2011, 280, 178–195.
28. P. G. Moses, B. Hinnemann, H. Topsøe and J. K. Nørskov, J. Catal., 2008, 260, 202–203.
29. P. Moses, B. Hinnemann, H. Topsoe and J. Norskov, J. Catal., 2007, 248, 188–203.
30. J. Barbour and K. C. Campbell, J. Chem. Soc., Chem. Commun., 1982, 1371–1372.
31. H. Schweiger, P. Raybaud, G. Kresse and H. Toulhoat, J. Catal., 2002, 207, 76–87.
32. A. S. Walton, J. V. Lauritsen, H. Topsøe and F. Besenbacher, J. Catal., 2013, 308, 306–318.
33. E. Krebs, B. Silvi and P. Raybaud, J. Chem. Theory Comput., 2009, 5, 580–593.
34. E. Krebs, B. Silvi, A. Daudin and P. Raybaud, J. Catal., 2008, 260, 276–287.
35. B. Baubet, E. Devers, A. Hugon, E. Leclerc and P. Afanasiev, Appl. Catal., A, 2014, 487, 72–81.
36. I. A. van Parijs and G. F. Froment, Ind. Eng. Chem. Prod. Res. Dev., 1986, 25, 431–436.
37. H. C. Lee and J. B. Butt, J. Catal., 1977, 49, 320–331.
38. N. Dos Santos, H. Dulot, N. Marchal and M. Vrinat, Appl. Catal., A, 2009, 352, 114–123.
39. A. S. dos Santos, PhD Thesis, Université de Poitiers, 2017.
40. F. Pelardy, A. S. dos Santos, A. Daudin, E. Devers, T. Belin and S. Brunet, Appl. Catal., B, 2017, 206, 24–34.
41. A. Daudin, A. F. Lamic, G. Pérot, S. Brunet, P. Raybaud and C. Bouchy, Catal. Today, 2008, 130, 221–230.
42. A. Daudin, S. Brunet, G. Pérot, P. Raybaud and C. Bouchy, J. Catal., 2007, 248, 111–119.
43. P. Ghosh, A. T. Andrews, R. J. Quann and T. R. Halbert, Energy Fuels, 2009, 23, 5743–5759.
44. A. S. dos Santos, E. Girard, P. Leflaive and S. Brunet, Appl. Catal., A, 2019, 570, 292–298.
45. Q. Jin, B. Chen, Z. Ren, X. Liang, N. Liu and D. Mei, Catal. Today, 2018, 312, 158–167.
46. D. Mey, PhD Thesis, Université de Poitiers, 2002.
47. D. Mey, S. Brunet, C. Canaff, F. Maugé, C. Bouchy and F. Diehl, J. Catal., 2004, 227, 436–447.
48. M. L. Vrinat, Appl. Catal., 1983, 6, 137–158.
49. A. Borgna, E. Hensen, J. van Veen and J. W. Niemantsverdriet, J. Catal., 2004, 221, 541–548.
50. C. Thomas, L. Vivier, J. L. Lemberton, S. Kasztelan and G. Pérot, J. Catal., 1997, 167, 1–11.
51. A. Travert, H. Nakamura, R. A. van Santen, S. Cristol, J.-F. Paul and E. Payen, J. Am. Chem. Soc., 2002, 124, 7084–7095.
52. N. Y. Topsøe and H. Topsøe, J. Catal., 1993, 139, 631–640.
53. F. E. Massoth and C. L. Kibby, J. Catal., 1977, 47, 300–315.
54. V. La Vopa and C. N. Satterfield, J. Catal., 1988, 110, 375–387.
55. S. Humbert, G. Izzet and P. Raybaud, J. Catal., 2016, 333, 78–93.
56. F. E. Massoth and P. Zeuthen, J. Catal., 1994, 145, 216–222.
57. R. J. Berger, E. Hugh Stitt, G. B. Marin, F. Kapteijn and J. A. Moulijn, CATTECH, 2001, 5, 36–60.
58. EUROKIN spreadsheet for assessment of transport limitations in gas-solid fixed beds, https://www.eurokin.org/wp-content/uploads/webtool/EUROKIN_fixed-bed_html.htm, (accessed June 2022).
59. D. Marquardt, J. Soc. Ind. Appl. Math., 1963, 11, 431–441.
60. K. Levenberg, Q. Appl. Math., 1944, 2, 164–168.
61. G. F. Froment, K. B. Bischoff and J. de Wilde, Chemical Reactor Analysis and Design, Wiley, 3rd edn, 2011.
62. S.-K. Ihm, S.-J. Moon and H.-J. Choi, Ind. Eng. Chem. Res., 1990, 29, 1147–1152.
63. P. Atkins, Physical Chemistry, W.H. Freeman and Company, New York, 6th edn, 2000.
64. D. H. Everett, Trans. Faraday Soc., 1950, 46, 942–957.
65. D. L. Sullivan and J. G. Ekerdt, J. Catal., 1998, 226–233.
66. M. Zheng, L. Zhao, L. Cao, C. Zhang, J. Gao and C. Xu, Mol. Catal., 2019, 467, 38–51.
67. H. Pines, The Chemistry of Catalytic Hydrocarbon Conversions, Academic Press, New York, 1981.
68. M. Toba, Y. Miki, T. Matsui, M. Harada and Y. Yoshimura, Appl. Catal., B, 2007, 542–547.
69. A. S. Rodgers and M. C. R. Wu, J. Chem. Thermodyn., 1971, 591–597.
70. NIST Chemistry WebBook, NIST Standard Reference Database 69, National Institute of Standards and Technology, 1997.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2cy02093a

---