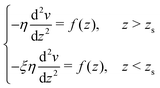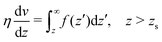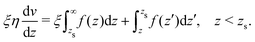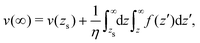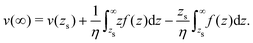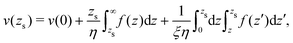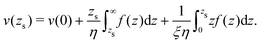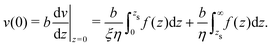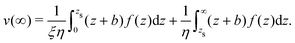Complex coupling between surface charge and thermo-osmotic phenomena
Received
30th June 2023
, Accepted 29th August 2023
First published on 29th August 2023
Abstract
Thermo-osmotic flows, generated at liquid–solid interfaces by thermal gradients, can be used to produce electric currents from waste heat on charged surfaces. The two key parameters controlling the thermo-osmotic current are the surface charge and the interfacial enthalpy excess due to liquid–solid interactions. While it has been shown that the contribution from water to the enthalpy excess can be crucial, how this contribution is affected by surface charge remained to be understood. Here, we start by discussing how thermo-osmotic flows and induced electric currents are related to the interfacial enthalpy excess. We then use molecular dynamics simulations to investigate the impact of surface charge on the interfacial enthalpy excess, for different distributions of the surface charge, and two different wetting conditions. We observe that surface charge has a strong impact on enthalpy excess, and that the dependence of enthalpy excess on surface charge depends largely on its spatial distribution. In contrast, wetting has a very small impact on the charge-enthalpy coupling. We rationalize the results with simple analytical models, and explore their consequences for thermo-osmotic phenomena. Overall, this work provides guidelines to search for systems providing optimal waste heat recovery performance.
1 Introduction
Nanofluidic systems (natural porous materials and synthetic devices where liquids are confined at the nanoscale) offer great promises to address societal challenges related to water and to energy harvesting.1–3 Liquid–solid interfaces play a critical role in such nanoscale systems, and surface effects provide efficient means to produce electricity from various thermodynamic gradients available in nature. For instance, diffusio-osmotic flows, generated at liquid–solid interfaces under a gradient of salt concentration, can be used to produce electricity from the salinity difference between sea and river water.4–6 Indeed, if the solid surface is charged, ions in the liquid reorganize to form a diffuse layer with an opposite charge in the vicinity of the surface, the electrical double layer (EDL).7–9 The advection of the EDL by the osmotic flow then generates an electric current.10–13
Similarly, thermal gradients can generate electric currents in liquids through a variety of mechanisms.14–19 Among these mechanisms, thermo-osmotic flows20,21 induced by thermal gradients could be used to produce electricity from low-grade waste heat, by advecting the charge of the EDL.22 The resulting electric current is controlled by the surface charge, which is opposite to the charge in the EDL, and by the velocity of the thermo-osmotic flow. There is an increasing effort to better understand thermo-osmotic flows, through experimental characterization23,24 and modeling.25–37 As detailed in the Theory section, for liquids, Derjaguin and collaborators developed a standard theoretical framework,13,38–40 which relates the thermo-osmotic flow velocity to the interfacial enthalpy excess, stemming from the interactions of the liquid with the solid. This framework has been extended recently to take into account liquid–solid slippage arising on low-friction surfaces,13,26,41 which can boost the flow. It has also been shown recently that, in addition to the commonly considered ion electrostatic contribution to the enthalpy excess,20,38,39 the contribution of water to the enthalpy excess could also be significant, and even dominate over the electrostatic one.22,41 While the electrostatic contribution is well described by the Poisson–Boltzmann framework42–44 (especially at low salt concentrations, at which this contribution becomes large), the water contribution to the enthalpy excess results from specific interactions with the surface and requires descriptions at the molecular level, for instance with molecular dynamics simulations.
However, previous studies have only computed the water enthalpy excess on charge neutral surfaces.41 With the ultimate goal to use thermo-osmosis to produce electricity, it is crucial to understand how surface charge modifies the interfacial enthalpy excess, and in particular its water contribution. In this article, we start by clarifying the link between the interfacial enthalpy excess and thermo-osmotic phenomena. We then present the results of molecular dynamics simulations of an aqueous electrolyte confined between parallel charged walls. We investigated the impact of surface charge density on the interfacial enthalpy excess, for different spatial distributions of the surface charge, and two different wetting conditions. We rationalized the results with simple analytical models, which can be used to evaluate the interfacial enthalpy excess in a wide variety of systems, and we explored their consequences for thermo-osmotic flows and thermo-osmotic currents.
2 Theory
The purpose of this section is to show how the enthalpy excess is related to the thermo-osmotic response. To that aim, we will briefly recall how the standard theoretical framework initially introduced by Derjaguin and collaborators13,38–40 can be extended to take into account liquid–solid slip.13,26,41 Indeed, at the nanoscale, it is known that the standard no-slip boundary condition can fail.45 The velocity jump at the liquid–solid interface is quantified by the slip length b, which is the distance inside the wall where the linear extrapolation of the liquid velocity profile reaches the wall velocity.45
We first discuss the thermo-osmotic coefficient, which quantifies the thermo-osmotic response of a liquid–solid interface to a temperature gradient parallel to the wall, and is defined by:
| | 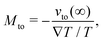 | (1) |
with
T the temperature, and
vto(∞) the thermo-osmotic velocity far from the surface;
Mto can be positive or negative, depending on the direction of the thermo-osmotic flow. The thermo-osmotic velocity profile
vto(
z) can be obtained by integrating Stokes equation, assuming a homogeneous viscosity
η (we will come back to this choice later) and taking into account slippage:
13| | 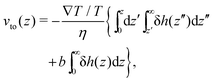 | (2) |
where
z is the distance to the wall,
b is the slip length, and δ
h(
z) is the enthalpy excess density due to interactions between the fluid and the solid; we will discuss the definition of δ
h for an electrolyte solution in the next section. The value of the velocity far from the surface is:
| | 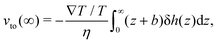 | (3) |
and the thermo-osmotic coefficient is thus expressed as:
| | 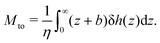 | (4) |
Defining the interfacial enthalpy excess (per unit surface):
| | 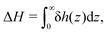 | (5) |
one can rewrite
eqn (4) as follows:
| | 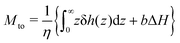 | (6) |
| | 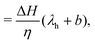 | (7) |
where we have set
| | 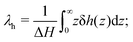 | (8) |
λh is the characteristic thickness of the layer where the liquid interacts with the wall, and hence δ
h(
z) ≠ 0. For pure water,
λh has been found to be on the order of 7 Å in previous work.
33 Generally,
λh is controlled by the range of liquid–solid interactions, therefore its value should be similar for all water–solid interfaces. Note that
λh is also the distance from the wall over which the thermo-osmotic velocity profile develops and converges to
vto(∞). As a side remark, the approach developed above for thermo-osmosis is analogous to the one used to describe electro-osmotic flows, see ref.
13,
46 and
47 and Appendix A.
Thermo-osmosis can also be used to create an electric current in the case of electrically charged surfaces.22 Indeed, in this case, the thermo-osmotic flow sets in motion the fluid and thus the EDL, which creates an electric current. One can quantify the thermo-osmotic current generated by thermo-osmosis for a planar surface surface of transverse width w by defining the thermo-osmotic conductance Kto:
| | 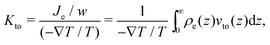 | (9) |
with
Je the thermo-electric current. When the enthalpy excess density decreases rapidly compared to the electric potential, one can consider that the thermo-osmotic velocity profile has reached its plateau value,
vto(
z) ≈
vto(∞), everywhere in the EDL. The effective Debye length is a function of the ion concentration
n0 and the surface charge density
Σ,
43 so that
λh ≪
λeff is met when
n0 < 0.1 M and
Σ < 50 mC m
−2. In that case,
Kto can be re-expressed as:
| | 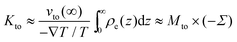 | (10) |
| | 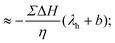 | (11) |
Kto is therefore, in this limit,
Mto scaled by the surface charge density.
Finally, let us return to the assumption of a uniform viscosity made to obtain eqn (7) and (11). Indeed, it has been shown that, near the wall, the liquid viscosity could significantly increase.25,48,49 A good approximation for the viscosity is to consider the following step function:49
| | 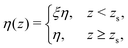 | (12) |
with
zs the position of the plane of shear
49 and
ξ ≥ 1. Using
eqn (12), one can show that the thermo-osmotic velocity far from the surface is given by (derivation provided in Appendix B):
| | 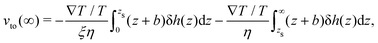 | (13) |
and the thermo-osmotic coefficient becomes:
| | 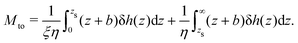 | (14) |
As expected, the thermo-osmotic coefficient is lower when considering a liquid layer near the wall with higher viscosity. The thermo-osmotic coefficient is weighted by the ratio between the two viscosities
ξ, but still remains a function of the enthalpy excess density. In the case of a stagnant liquid layer,
ξ → ∞, with
b = 0, and one obtains:
| | 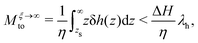 | (15) |
where
zs is now the thickness of the stagnant layer. In this case, the thermo-osmotic coefficient is significantly lower than for a uniform viscosity, since the slip length is zero and the enthalpy excess from the stagnant layer does not contribute to the osmotic flow. On the other hand, for hydrophobic surfaces, the viscosity remains constant, even near the interface,
48,49ξ = 1, and one recovers
eqn (7). Using hydrophobic surfaces seems therefore to be the optimal approach for maximizing osmotic responses.
Overall, eqn (7) and (11) highlight the key role of enthalpy excess and slip length in thermo-osmotic responses. Accordingly, to predict thermo-osmotic responses on charged surfaces, it is crucial to know how these two quantities depend on the surface charge. While the surface charge dependence of the slip length has been investigated before,50,51 less is known about the enthalpy excess, and in particular about its water contribution. In the following, we will use molecular dynamics simulations to compute ΔH as a function of the surface charge.
3 Simulation methods
3.1 System
We used the LAMMPS package52 to perform equilibrium molecular dynamics simulations of an aqueous electrolyte composed of 2000 water molecules and NaCl salt with a bulk concentration n0 ∼ 0.20 M, corresponding to a Debye length λD ∼ 7 Å, confined between two parallel walls made of four atomic layers of a fcc crystal with a lattice parameter a = 5.3496 Å (Fig. 1). Note that the standard ion electrostatic contribution to the enthalpy excess decreases with increasing salt concentration;20,38,39 for the large concentration we used in this work, the ion contribution has been shown to be negligible as compared to the one of water.41 We applied periodic boundary conditions along the x and y directions to our system of size Lx = Ly = 32.0976 Å. Water molecules were simulated using the SPC/E model,53 which employs both Lennard-Jones (LJ) and Coulombic potentials to model the atomic interactions. The LJ potential is defined by the characteristic diameter σii, and the interaction particle εii of particle i. For the ions, we used the LJ parameters given in ref. 54 along with the Lorentz–Berthelot mixing rules. For the solid atoms, we followed ref. 46: we took σss = 3.37 Å, used a close-packed density ρs = σss−3, and chose εss = 0.164 and 2.08 kcal mol−1 combined with Lorentz–Berthelot mixing rules to create, respectively, a hydrophobic and a hydrophilic surface, with contact angles of approximately 140 and 55° (as characterized in ref. 46). For the LJ interactions, we used a truncated potential with a cutoff of 9 Å and no long-range correction. For the Coulombic interactions, we used the particle–particle particle-mesh (PPPM) solver for long-range correction, with a cutoff of 10 Å and desired relative error in forces of 10−4. While we used periodic boundary conditions along the x and y directions, we used non-periodic boundary conditions in the z direction; for the PPPM solver, we treated the system as if it were periodic in z, but inserting empty volume between atom slabs and removing dipole inter-slab interactions so that slab–slab interactions are effectively turned off. The ratio of the extended dimension in z divided by the actual dimension in z was set to 3, and the actual dimension was set to 101 Å.
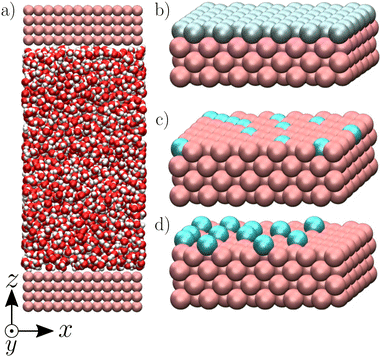 |
| | Fig. 1 Visualization of the modeled systems composed of an aqueous electrolyte solution confined between two walls (a), realized with VMD.60 The walls are charged either homogeneously (b), heterogeneously (c) or with the charge protruding from the walls to create a “defective solid” case (d) (see text for more details). | |
We studied three types of surface charge distribution. First, to represent the charge resulting from the polarization of a conductive surface (e.g. the charging of amorphous carbon electrodes in supercapacitors55–58), we considered a “homogeneous case” where we charged all surface atoms with a charge q = ΣS/Nwall, where S = LxLy is the surface of the wall and Nwall the number of atoms on the surface, which results in a surface charge density Σ (Fig. 1b). We then considered two models aimed at describing the features of surface charge on insulators, which typically arises from the dissociation of surface groups or specific adsorption of charged species, resulting in a spatially heterogeneous charge (e.g., the charge of graphene oxide/activated carbon is carried by randomly distributed protruding O− groups51,59). To capture the effect of heterogeneity, we started by studying a “heterogeneous case” where we randomly selected atoms of the surface and attributed them a charge of ±1 e (Fig. 1c) so that the surface charge density was Σ. To also capture the protruding nature of the surface charges, we finally studied a “defective case” in which randomly distributed atoms with a charge of ±1 e protrude by 2.67 Å from the surface with respect to the fcc structure of the crystal (Fig. 1d).
In all cases, both surfaces were assigned the same surface charge, and counter-ions were added to the system to keep it electrically neutral. The bottom wall was frozen and we used the top wall as a rigid piston during an equilibration phase that lasted 0.6 ns, before fixing it at its equilibrium position to set the pressure to 10 atm, following previous studies41,46 (we have checked that the density and pressure profiles had reached steady state). The equilibrium distance between the walls, reached in less than 50 ps, was d ∼ 60 Å. We fixed the temperature of the fluid at 298 K via a Nosé–Hoover thermostat with a damping time of 100 fs. The simulations lasted 10 ns with a timestep of 2 fs.
3.2 Quantities of interest
For a mixture of particles, we define the enthalpy excess density as:25| | 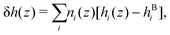 | (16) |
with i ∈ [O,H,Na,Cl] the atom type, ni the number density, hi the enthalpy per particle, and the superscript B denotes a bulk quantity, i.e. its value far from the surface, where it is homogeneous. We define the enthalpy per particle as:| | 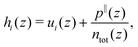 | (17) |
where ui is the internal energy per particle, 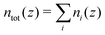 the total number density and p‖(z) the components of the virial pressure tensor parallel to the surface (pxx or pyy, which are equal). Indeed, pressure is anisotropic near the wall, and following previous studies,25,34 we consider the pressure component parallel to the surface to compute the enthalpy excess density. We can consider only the contribution of the potential energy to calculate the internal energy term. Indeed the equipartition theorem implies that the kinetic energy terms cancel out: 〈uk(z)〉 = uBk. Here attributing p‖(z)/ntot(z) to each atom amounts to evenly distribute the atomic volume regardless of the atom type.
the total number density and p‖(z) the components of the virial pressure tensor parallel to the surface (pxx or pyy, which are equal). Indeed, pressure is anisotropic near the wall, and following previous studies,25,34 we consider the pressure component parallel to the surface to compute the enthalpy excess density. We can consider only the contribution of the potential energy to calculate the internal energy term. Indeed the equipartition theorem implies that the kinetic energy terms cancel out: 〈uk(z)〉 = uBk. Here attributing p‖(z)/ntot(z) to each atom amounts to evenly distribute the atomic volume regardless of the atom type.
From the definition of the enthalpy excess density, eqn (16), δh(z) = 0 in the absence of particles, and the enthalpy per particle needs to be defined only when the density is non zero. Denoting z0 the minimum height at which fluid particles are found, eqn (16) becomes:
| | 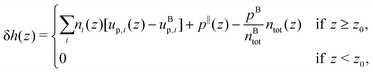 | (18) |
where we denote
pB the bulk pressure, which is isotropic, and where
up,i is the potential energy of particle type
i, which takes into account its interactions with all atom types.
We compute pressure profiles using the stress per atom approach. Indeed the virial part of the stress per atom is given by 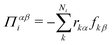 where α and β ∈ {x,y,z}, and Ni is the number of atoms of type i. With this definition,
where α and β ∈ {x,y,z}, and Ni is the number of atoms of type i. With this definition, 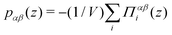 . Although it is well known that the pressure tensor is not uniquely defined for an inhomogeneous fluid near an interface,61 this is not an issue here since we will consider its integral, eqn (21), which is unambiguously defined.61
. Although it is well known that the pressure tensor is not uniquely defined for an inhomogeneous fluid near an interface,61 this is not an issue here since we will consider its integral, eqn (21), which is unambiguously defined.61
Finally, we can compute the enthalpy excess by integrating the enthalpy excess density from z0 to the middle of the channel: 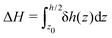 , which we decompose into three contributions: the water internal energy excess ΔUwater, the ions internal energy excess ΔUions and a pressure excess term ΔP‖:
, which we decompose into three contributions: the water internal energy excess ΔUwater, the ions internal energy excess ΔUions and a pressure excess term ΔP‖:
| | 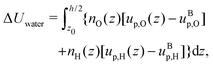 | (19) |
| | 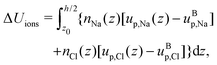 | (20) |
| | 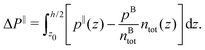 | (21) |
To estimate the thermo-osmotic and thermoelectric responses of our systems, we also computed the slip length b using non-equilibrium molecular dynamics simulations. With that regard, we moved the walls in opposite x directions with a speed Vx ∈ [10,40] m s−1 (we verified that we were in the linear response regime), generating a linear velocity profile far from the wall. The slip length can then be determined using the Navier boundary condition:22,62
| | 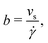 | (22) |
with
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)
the bulk shear rate and
vs the slip velocity;
vs is defined as the difference between the wall velocity and the velocity of the fluid at the hydrodynamic wall position, given by
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) h
h/2, where the hydrodynamic height
h of the liquid is given by:
63| | 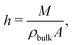 | (23) |
with
M the total mass of the fluid,
ρbulk the bulk mass density and
A the wall surface area.
We performed four independent simulations to determine the error on the calculation of ΔH. The slip length and its error were determined from measurements that fell in the linear response regime. The error bars given in the following figures correspond to a statistical error with 95% confidence level.
4 Results and discussion
4.1 Impact of surface charge density
Fig. 2 presents the enthalpy excess ΔH and its contributions as a function of the surface charge density. One can observe that ΔH varies notably with Σ, increasing significantly with the absolute value of the surface charge density. Even at the large salt concentration considered here and at large surface charges, ions do not have much impact on the enthalpy excess, because their number remains much smaller than the number of water molecules. It is actually ΔUwater and ΔP‖ which contribute the most to the enthalpy excess.
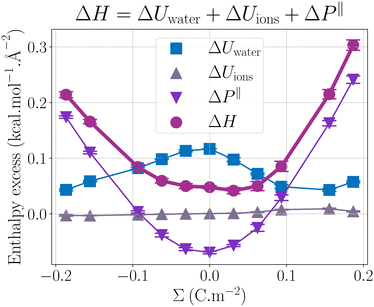 |
| | Fig. 2 Comparison of the different contributions to ΔH (mauve circles): ΔUions (grey triangles up) the contribution of the potential energy of the ions, ΔUwater (blue squares) the contribution of the water potential energy and ΔP‖ (purple triangles down) the pressure excess. | |
Let us first focus on ΔUwater. The water energy term has a parabolic form, which is relatively symmetrical with respect to the surface charge density. One can approximate this quantity using a simple dipole model. Indeed, water molecules orient themselves under the effect of the electric field created by the charged wall. In this regard the energy excess density δudpwater can be expressed as:
| | | δudpwater(z) = −〈μz〉(z)nO(z)E(z), | (24) |
with
nO the number density of oxygen atoms,
E(
z) =
Σ/
ε0εr(
z) the electrostatic field where
ε0 is the vacuum permittivity and
εr(
z) are the local relative permittivity, and 〈
μz(
z)〉 =
μ〈cos(
θ)(
z)〉 the average dipole moment along the
z axis, with 〈cos(
θ)〉 the average dipole moment orientation and
θ the angle formed by the dipole with the surface, and
μ = 1.85 D the water dipole moment. In the EDL, the electric field is weak with respect to its value at the surface (
i.e., for
z = 0) and δ
udp is negligible.
41 However, water molecules immediately at the surface experience a much stronger electric field because there are much less other water molecules to screen the field of the wall than in bulk. For those molecules, δ
udp is not negligible anymore.
We can compute 〈cos(θ)〉 from the simulation or we can compute it theoretically using Boltzmann statistics (Fig. 3b). Let P(θ) be the probability for a molecule to have an orientation angle θ, we have:
| | 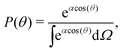 | (25) |
with
Ω the solid angle and
α =
βμE with
β = 1/
kBT. Thus,
| | 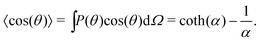 | (26) |
As stated before, water molecules at the interface experience a much less screened electric field from the charged wall. Still, the other molecules at the surface partially screen the interactions with the farther parts of the wall, which one can describe by introducing an effective relative permittivity,
εeffr. The value of
εeffr should lie between 1 and the bulk dielectric constant of SPC/E water,
εr = 71.
64,65 In the following, we will treat it as a fitting parameter. Thus, writing
E =
Σ/
ε0εeffr, one obtains:
| | 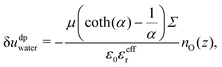 | (27) |
and so:
| | 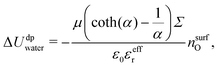 | (28) |
with
nsurfO the atomic surface density of the first layer, which can be computed from the simulations. Finally Δ
Uwater = Δ
U0water + Δ
Udpwater, where Δ
U0water is the value of Δ
Uwater for an electrically neutral surface.
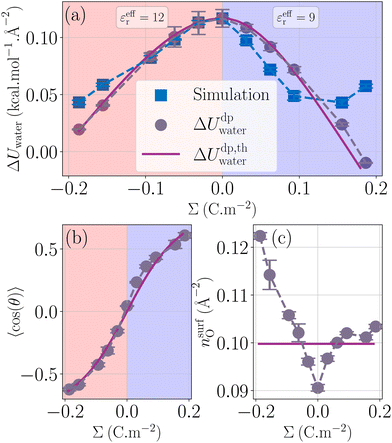 |
| | Fig. 3 Water energy contribution to the enthalpy excess (a) with the measured values ΔUwater (blue squares), the theoretical model with measured 〈cos(θ)〉 and nsurfO (grey circles), and the fully theoretical model (mauve line). The theoretical and measured orientations of water molecules near the surface (respectively mauve line and grey circles) are given in (b). The effective permittivity was set to εeffr = 12 for negatively charged surfaces, and εeffr = 9 for positively charged surfaces. The surface density of water molecules near the interface is given in (c) with the same legend as in (b). | |
Fig. 3b represents the dipole orientation, measured in the simulations, and fitted using eqn (26). We can see an asymmetry of the measured curve, where the dipole orientation follows two different patterns: for the negative surface charges, θ precisely follows its theoretical value by taking εeffr = 12. However, for the positive ones, the model is less accurate. To fit this part of the curve, we took εeffr = 9. It is not unexpected that the effective dielectric permittivity depends on the sign of the surface charge; indeed, the effective permittivity should depend on the details of the profiles of density and orientation of the water molecules around the gap between the liquid and the solid, which differ depending on the sign of the surface charge because of water's asymmetrical charge distribution.
Fig. 3c presents the atomic surface density of the first layer, measured in the simulations, and approximated by 1/σO2 ≃ 0.10 Å−2, with σO the oxygen LJ diameter. We thus have two ways of plotting the model presented (Fig. 3a): from direct measurement of 〈cos(θ)〉 and nsurfO, or from their theoretical estimates. Overall, although the asymmetry of cos(θ) and nsurfO is not sufficient to explain the asymmetry found in ΔUwater, our model describes fairly the water excess energy term.
Regarding the pressure term (Fig. 4), one way to describe it is to make an analogy between ΔP‖ and the surface tension γ. Indeed the surface tension of a liquid–solid interface can be computed by the mechanical route:66,67
| | 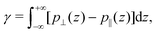 | (29) |
where
p⊥ and
p‖ are the normal and tangential components of the pressure tensor. To ensure mechanical equilibrium, it is necessary to have a constant perpendicular pressure along the channel,
p⊥(
z) =
pB⊥ =
pB‖, because pressure is isotropic in a bulk liquid. Thus, the surface tension becomes:
| | 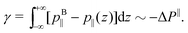 | (30) |
We will therefore try to describe the variation of Δ
P‖ with
Σ following standard electrowetting models. The variation of the surface tension with respect to the surface charge density is given by the Lippmann's equation,
68,69 which considers the energy stored in the capacitor formed by the charged surface and the EDL:
| | 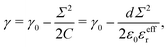 | (31) |
where
γ0 is the surface tension for a neutral surface and
C =
ε0εeffr/
d is the capacitance per unit area, with
d the capacitor thickness,
i.e. the mean distance between charges on the wall and counter-ions in the EDL. Similarly, one can define a capacitor like model to understand the variation of the pressure excess with the surface charge density:
| | 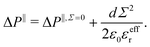 | (32) |
Once again, the relative permittivity
εeffr used in the model must be smaller than the one of bulk water due to its drop near the interface. Moreover we can see in
Fig. 3c that near the surface, water displays different structuring depending on the sign of
Σ, and so should do the relative permittivity. This allows us to fit our capacitor model with two values of the relative permittivity,
εeffr = 6 for the negative charge surfaces
εeffr = 4.5 for positive ones, see
Fig. 4. These values differ from the ones used to describe the water energy excess. This is not unexpected, because the effective permittivity involved in the potential energy model and in the capacitor model result from the averaging of different functions of the non-local heterogeneous permittivity.
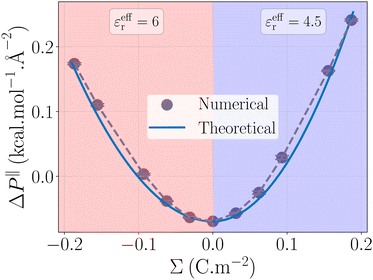 |
| | Fig. 4 Pressure term ΔP‖ as a function of the surface charge density. The value obtained from the simulations (grey points) is rationalized by a capacitor model (blue line). The effective permittivity in eqn (32) is set to εeffr = 6 for negatively charged surfaces, and εeffr = 4.5 for positively charged surfaces. | |
4.2 Effect of wetting properties
Now that we have understood the behavior of the enthalpy excess for a hydrophobic and homogeneously charged wall, let us look at the effect of wetting on the enthalpy excess. In Fig. 5c we compared the enthalpy excess calculated close to a hydrophobic and a hydrophilic surface. First we note that the hydrophobic surfaces have higher enthalpy excess, which is consistent with a previous study on thermo-osmosis that indicates that hydrophobic surfaces maximize the thermo-osmotic response.41 Secondly, for an electrically neutral surface, there is a change of sign of the enthalpy excess, indicating a change of direction of the thermo-osmotic flow, again being consistent with a previous study that reports a change of direction of the flow when changing the wetting of the system.26 On silica-based materials, which have hydrophilic surfaces, it has been shown that the surface charge density can affect the thermo-osmotic flow direction, this effect being attributed to a change of sign of the enthalpy excess,23,36 our calculations tend to confirm qualitatively the results of these studies.
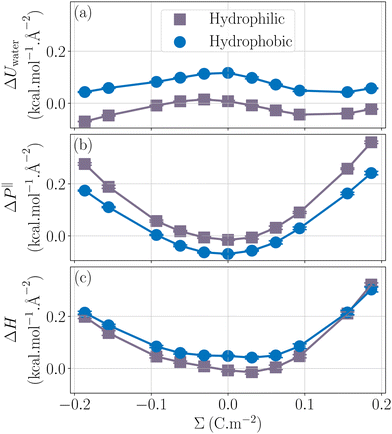 |
| | Fig. 5 Impact of wetting on the enthalpy excess. Two wettings are explored here: a hydrophobic case (blue circles) and a hydrophilic case (grey squares). The water contribution (a), the pressure term (b), as well as the total enthalpy excess (c) are represented. | |
While the enthalpy of a neutral surface largely depends on wetting, its variation with the surface charge is much less sensitive to wetting, being slightly stronger for the hydrophobic surface, see Fig. 5c. When looking at the decomposition of the enthalpy excess, it appears that ΔUwater is simply shifted and becomes smaller for hydrophilic surfaces. Water molecules are indeed more attracted to the wall in the hydrophilic case, which allows them to adopt a more favorable energy configuration thus reducing the overall internal energy (Fig. 5a). The pressure term is also shifted, and the parabola is more pronounced. One can use the capacitor model to understand this: indeed, water is more depleted on hydrophobic surfaces, resulting in a thicker capacitor, hence a stronger variation of ΔP‖ with Σ, see eqn (32). Note that we simulated two systems with very different wetting properties, and the change in capacitance remained small, so that considering that the capacitance is independent of wetting represents a good approximation.
4.3 Effect of charge distribution on the enthalpy excess
Regarding the charge distribution, one can see in Fig. 6 that it has a drastic impact on the enthalpy excess. In particular, the defective solid case differs strongly from the other two, displaying a change of sign for negatively charged surfaces. One can understand these differences by looking at the decomposition of ΔH. For ΔUwater (Fig. 6a), the dipole model, which assumes a homogeneous charge distribution, does not work for the heterogeneous and defective solid cases. Indeed, in the latter cases, each of the randomly distributed charges will only affect the surrounding water molecules, because with a heterogeneous charge distribution, a counter-ion will tend to bond to each charge, with the effect to screen the electric field. Consequently, the variation of the energy excess (per unit surface) is simply given by the energy excess induced locally by one charged site, UES, multiplied by the density of charged sites, |Σ|/e (with e the elementary charge):| | 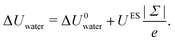 | (33) |
Because UES is controlled by the organization of water molecules around the charged sites, it takes different values depending on the sign of Σ and on the type of surface. We reported in Table 1 the values of UES obtained by linearly fitting the measured values of ΔUwater with eqn (33), see Fig. 6.
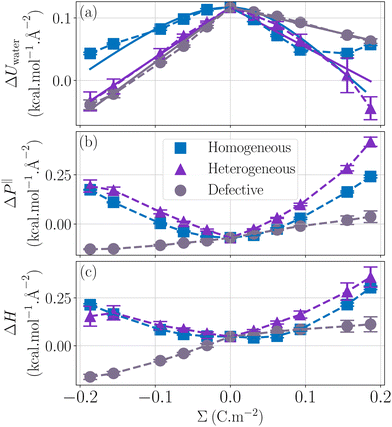 |
| | Fig. 6 Effect of the charge distribution on the enthalpy excess. For ΔUwater (a), the homogeneous case (blue squares) is described by a dipole model (blue line) while the heterogeneous (purple triangles) and the defective (grey circles) cases are described by a linear model of potential energy excess per unit charge, eqn (33), represented in full lines. For ΔP‖ (b), the homogeneous as well as the heterogeneous case can be described by a capacitor model but the model cannot describe the behavior of the defective solid. There is a change of sign of ΔH for the defective solid case, taking negative values for negatively charged surfaces (c). | |
Table 1 Water enthalpy excess per charge for different charge distributions
|
U
ES (kcal mol−1) |
Σ < 0 |
Σ > 0 |
| Heterogeneous |
−1.24 × 10−2 |
−9.8 × 10−3 |
| Defective |
−1.32 × 10−2 |
−4.3 × 10−3 |
Even though there is a quantitative difference between the three cases for ΔUwater, the differences on the total enthalpy excess come largely from ΔP‖ (Fig. 6b). For the heterogeneously charged surface, even though the charge is not evenly distributed, the capacitor model is still applicable, due to the presence of a clear gap between water molecules and the surface. However, in the presence of defects, water molecules near the surface are on the same level as charges. In this case, the thickness of the capacitor d is 0, and our model predicts that the parabolic dependence of ΔP‖ with Σ should vanish. We suggest that the small remaining drift of ΔP‖ with the surface charge, not captured by our model, originates from specific liquid-wall interactions, indirectly affected by the surface charge.
Overall, in both the homogeneous case and the heterogeneous case, ΔP‖ dominates and its convex parabola shape is reflected in the total enthalpy excess. In contrast, in the defective case, the concave shape of ΔUwater is only slightly affected by the small linear drift of ΔP‖, resulting in a drastically different shape for the total enthalpy excess.
4.4 Consequences on transport properties
Let us now look at the effect of the enthalpy excess on thermo-osmotic transport properties. To compute Mto and Kto, we used eqn (7) and (11), with λh = 7 Å and η = 0.729 mPa s, the viscosity of SPC/E water at 1 atm; it is indeed very close to the viscosity of SPC/E at 10 atm.70 We plotted the results in Fig. 7. First, one can see that the slip length decreases with the absolute value of the surface charge, but it decreases faster in both heterogeneous and defective cases.50 For the hydrophobic surface considered, the slip length is relatively small even at zero surface charge, bΣ=0 = 3.9 nm, and it decreases quickly so that b becomes smaller than λh when the absolute surface charge density exceeds 100 mC m−2 for homogeneous surfaces and 40 mC m−2 in the other cases. Thus, for relatively large surface charge densities, the thermo-osmotic and thermoelectric coefficients no longer depend on b and their variations with the surface charge are only driven by the enthalpy excess, together with the surface charge density for Kto, which explains the similarity between the homogeneous and heterogeneous cases. Regarding the defective case, the drastically different values of ΔH (see Fig. 6) are directly reflected in the transport coefficients. For low surface charges, the slip length influences the response coefficients and the homogeneous charge distribution gives the best results.
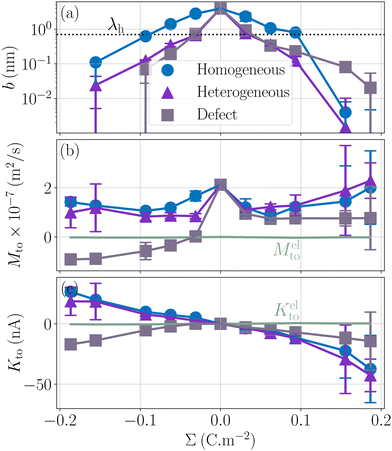 |
| | Fig. 7 Slip length and resulting transport coefficients Mto and Kto as a function of the surface charge density Σ. The slip length is relatively small for this surface, and decreases rapidly with the surface charge density, in particular in the heterogeneous and defective cases; the thickness of the interaction layer λh is shown with a dotted line for comparison (a). Corresponding thermo-osmotic coefficient (eqn (7)), along with the standard electrostatic prediction (eqn (35)) plotted in light green (b), and theoretical thermo-osmotic conductance (eqn (11)), along with the standard electrostatic prediction (eqn (36)) plotted in light green (c). | |
Let us see how these results compare to the classical theory, which only considers the electrostatic contribution of ions to the enthalpy excess density:13,41
| | 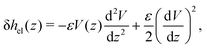 | (34) |
where
V(
z) is the electrostatic potential, which can be computed analytically using the Poisson–Boltzmann theory. In this case, the thermo-osmotic response and the thermo-osmotic conductance become:
13| | 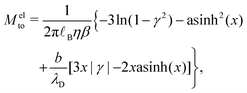 | (35) |
| | 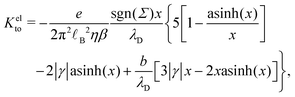 | (36) |
with
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) B
B =
βe2/(4π
ε) the Bjerrum length, where
e is the elementary charge,
x =
λD/
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) GC
GC, with
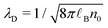
the Debye length and
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) GC
GC =
e/(2π
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) B
B|
Σ|) the Gouy–Chapman length, and
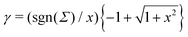
.
43
As shown in Fig. 7, for the parameters considered in this work, i.e. λD ≃ 7 Å, ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) B ≃ 8 Å, and the slip length of the homogeneous charge distribution, the classical thermo-osmotic theory predicts thermo-osmotic coefficients much lower than the ones computed with the total enthalpy excess; note however that the electrostatic contribution of ions could be larger in other range of parameters, and in particular at lower salt concentrations.41 Moreover, δhel(z) only predicts negative thermo-osmotic coefficients Mto, and predicts a thermo-osmotic conductance having the same sign as the surface charge density, which is also in strong contrast with the predictions taking into account the total enthalpy excess. Once again, this highlights the important contribution of the solvent to the enthalpy excess, which leads to a rich and complex behavior, such as the change of sign of the thermo-osmotic coefficient for protruding charges.
B ≃ 8 Å, and the slip length of the homogeneous charge distribution, the classical thermo-osmotic theory predicts thermo-osmotic coefficients much lower than the ones computed with the total enthalpy excess; note however that the electrostatic contribution of ions could be larger in other range of parameters, and in particular at lower salt concentrations.41 Moreover, δhel(z) only predicts negative thermo-osmotic coefficients Mto, and predicts a thermo-osmotic conductance having the same sign as the surface charge density, which is also in strong contrast with the predictions taking into account the total enthalpy excess. Once again, this highlights the important contribution of the solvent to the enthalpy excess, which leads to a rich and complex behavior, such as the change of sign of the thermo-osmotic coefficient for protruding charges.
5 Conclusion
In this article, we highlighted the connection between the interfacial enthalpy excess and thermo-osmotic transport; in particular, we clarified the impact of the enthalpy excess on the thermo-osmotic coefficient Mto and the thermo-osmotic conductance Kto. We then used equilibrium molecular dynamics simulations to study the effect of surface charge density and charge distribution on the enthalpy excess. We have shown that the surface charge density has a large impact on the enthalpy excess. For homogeneously charged surfaces, the enthalpy excess is enhanced by 300 to 500% for the highest surface charge densities considered. We investigated the different contributions to the enthalpy excess, and showed that it was dominated by the change of tangential pressure close to the wall, with a non-negligible correction due to the change in water internal energy. In contrast, the contribution from ions internal energy was negligible for the range of parameters used in this work. We then rationalized how the different contributions to the enthalpy excess depended on surface charge with simple analytical models.
We also studied the effect of wetting to realize that it does not significantly modify the impact of surface charge on the enthalpy excess. Nonetheless the values of the enthalpy excess are more important in the hydrophobic case, especially at small surface charges, it is thus preferable to use non-wetting surfaces to maximize the enthalpy excess. We also studied the effect of the charge distribution on the enthalpy excess. We have shown that using homogeneously or heterogeneously charged surfaces does not have a strong impact on the enthalpy excess. However, the presence of protruding defects has a great influence on it. In particular, with this charge distribution we have been able to observe a change of sign of ΔH for negative surface charges. The strong changes in the enthalpy excess are largely reflected on the thermo-osmotic transport coefficients. The standard picture, which only considers the electrostatic contribution of ions to compute the enthalpy excess, does not capture the complexity of the thermo-osmotic responses. It it thus necessary to use molecular dynamics to compute the enthalpy excess close to charged surfaces. Overall we provide a useful tool to explore a wide variety of systems and identify those promising the best thermo-osmotic performance. For example it could be interesting to study thermo-osmotic responses of new two-dimensional materials using this method.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of interest
There are no conflicts of interest to declare.
Appendices
Appendix A. Theoretical framework for the electro-osmotic velocity
The approach developed in the main text for thermo-osmosis is analogous to the one used to describe electro-osmotic flows, which are generated when an electric field E parallel to the interface is applied. In this case, the response coefficient is given by:13,46,47| | 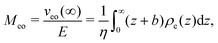 | (37) |
where veo(∞) is the electro-osmotic velocity far from the surface and ρe is the charge density. To ensure electroneutrality, 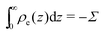 with Σ the surface charge density of the wall. Eqn (37) can then be rewritten:
with Σ the surface charge density of the wall. Eqn (37) can then be rewritten:| | 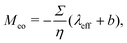 | (38) |
where 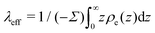 is the effective Debye length,13,43,71 which quantifies the thickness of the EDL in the non-linear Poisson–Boltzmann regime. Therefore, in the same way that one can predict the electro-osmotic flow based on the surface charge density using eqn (38), one can predict the thermo-osmotic coefficient from the enthalpy excess using eqn (7).
is the effective Debye length,13,43,71 which quantifies the thickness of the EDL in the non-linear Poisson–Boltzmann regime. Therefore, in the same way that one can predict the electro-osmotic flow based on the surface charge density using eqn (38), one can predict the thermo-osmotic coefficient from the enthalpy excess using eqn (7).
Appendix B. Derivation of the thermo-osmotic velocity with a viscosity following a step function
To derive eqn (13), we start from Stokes equation (Fig. 8):| | 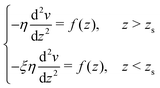 | (39) |
where f(z) is the force density generated by a thermodynamic gradient along the interface. It is equal to −δh(z)(∇T/T) for a thermal gradient. The integration of Stokes equation leads to:| | 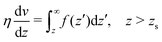 | (40) |
| | 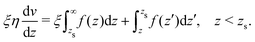 | (41) |
We integrate these equations again. From eqn (40) we get the velocity of the fluid far from the interface:| | 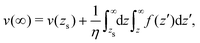 | (42) |
which we integrate by part:| | 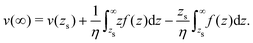 | (43) |
The velocity at the plane of shear v(zs) is determined from eqn (41):| | 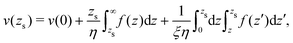 | (44) |
which simplifies by integrating by part:| | 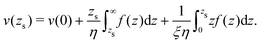 | (45) |
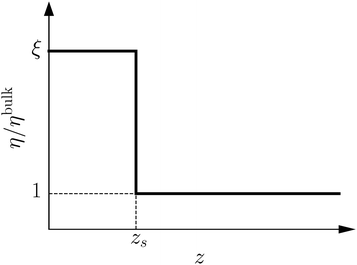 |
| | Fig. 8 Viscosity as a function of the distance to the wall in the “step” approximation. | |
The velocity of the fluid at the interface, v(0), is given by the Navier boundary condition:
| | 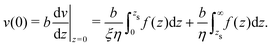 | (46) |
Finally:
| | 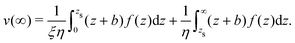 | (47) |
Substituting f(z) by −δh(z)(∇T/T), one obtains eqn (13).
Acknowledgements
The authors thank D. Pandey and S. Hardt for fruitful discussions. This work is supported by the ANR, Project ANR-21-CE50-0042-01 smoothE.
References
- R. Schoch, J. Han and P. Renaud, Rev. Mod. Phys., 2008, 80, 839–883 CrossRef CAS.
- L. Bocquet and E. Charlaix, Chem. Soc. Rev., 2010, 39, 1073–1095 RSC.
- N. Kavokine, R. R. Netz and L. Bocquet, Annu. Rev. Fluid Mech., 2021, 53, 377–410 CrossRef.
- A. Siria, M.-L. Bocquet and L. Bocquet, Nat. Rev. Chem., 2017, 1, 0091 CrossRef CAS.
- S. Marbach and L. Bocquet, Chem. Soc. Rev., 2019, 48, 3102–3144 RSC.
- L. Joly, R. H. Meißner, M. Iannuzzi and G. Tocci, ACS Nano, 2021, 15, 15249–15258 CrossRef CAS PubMed.
- D. C. Grahame, Chem. Rev., 1947, 41, 441–501 CrossRef CAS PubMed.
-
J. Israelachvili, Intermolecular and Surface Forces, Academic Press, 2011 Search PubMed.
- R. Hartkamp, A.-L. Biance, L. Fu, J.-F. Dufrêche, O. Bonhomme and L. Joly, Curr. Opin. Colloid Interface Sci., 2018, 37, 101–114 CrossRef CAS.
- J. C. Fair and J. F. Osterle, J. Chem. Phys., 1971, 54, 3307–3316 CrossRef CAS.
- A. Siria, P. Poncharal, A.-L. Biance, R. Fulcrand, X. Blase, S. T. Purcell and L. Bocquet, Nature, 2013, 494, 455–458 CrossRef CAS PubMed.
- T. Mouterde and L. Bocquet, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 148 CrossRef PubMed.
-
C. Herrero, A. Allemand, S. Merabia, A.-L. Biance and L. Joly, arXiv, 2022, preprint, arXiv:2204.13522, DOI:10.48550/arXiv.2204.13522.
- M. Bonetti, S. Nakamae, M. Roger and P. Guenoun, J. Chem. Phys., 2011, 134, 114513 CrossRef CAS PubMed.
- M. Bonetti, S. Nakamae, B. T. Huang, T. J. Salez, C. Wiertel-Gasquet and M. Roger, J. Chem. Phys., 2015, 142, 244708 CrossRef PubMed.
- M. Dietzel and S. Hardt, Phys. Rev. Lett., 2016, 116, 225901 CrossRef PubMed.
- S. Di Lecce and F. Bresme, J. Phys. Chem. B, 2018, 122, 1662–1668 CrossRef CAS PubMed.
- D. Zhao, A. Würger and X. Crispin, J. Energy Chem., 2021, 61, 88–103 CrossRef CAS.
- M. Pascual, N. Chapuis, S. Abdelghani-Idrissi, M.-C. Jullien, A. Siria and L. Bocquet, Energy Environ. Sci., 2023 10.1039/D3EE00654A.
- A. Würger, Rep. Prog. Phys., 2010, 73, 126601 CrossRef.
- V. M. Barragán and S. Kjelstrup, J. Non-Equilib. Thermodyn., 2017, 42, 217–236 Search PubMed.
- L. Fu, L. Joly and S. Merabia, Phys. Rev. Lett., 2019, 123, 138001 CrossRef CAS PubMed.
- A. P. Bregulla, A. Würger, K. Günther, M. Mertig and F. Cichos, Phys. Rev. Lett., 2016, 116, 188303 CrossRef PubMed.
- M. Fränzl and F. Cichos, Nat. Commun., 2022, 13, 656 CrossRef PubMed.
- R. Ganti, Y. Liu and D. Frenkel, Phys. Rev. Lett., 2017, 119, 038002 CrossRef PubMed.
- L. Fu, S. Merabia and L. Joly, Phys. Rev. Lett., 2017, 119, 214501 CrossRef PubMed.
- M. Dietzel and S. Hardt, J. Fluid Mech., 2017, 813, 1060–1111 CrossRef CAS.
- R. Ganti, Y. Liu and D. Frenkel, Phys. Rev. Lett., 2018, 121, 068002 CrossRef CAS PubMed.
- L. Fu, S. Merabia and L. Joly, J. Phys. Chem. Lett., 2018, 9, 2086–2092 CrossRef CAS PubMed.
- K. Proesmans and D. Frenkel, J. Chem. Phys., 2019, 151, 124109 CrossRef PubMed.
- P. Anzini, G. M. Colombo, Z. Filiberti and A. Parola, Phys. Rev. Lett., 2019, 123, 028002 CrossRef CAS PubMed.
- A. Arango-Restrepo and J. M. Rubi, Phys. Rev. Lett., 2020, 125, 045901 CrossRef CAS PubMed.
- W. Q. Chen, M. Sedighi and A. P. Jivkov, Nanoscale, 2021, 13, 1696–1716 RSC.
- P. Anzini, Z. Filiberti and A. Parola, Phys. Rev. E, 2022, 106, 024116 CrossRef CAS PubMed.
- E. Oyarzua, J. H. Walther and H. A. Zambrano, Phys. Chem. Chem. Phys., 2023, 25, 5073–5081 RSC.
- W. Q. Chen, A. P. Jivkov and M. Sedighi, ACS Appl. Mater. Interfaces, 2023, 15, 34159–34171 CrossRef CAS PubMed.
- D. Pandey and S. Hardt, J. Fluid Mech., 2023, 967, R5 CrossRef CAS.
- B. V. Derjaguin and G. P. Sidorenkov, CR Acad. Sci. URSS, 1941, 32, 622–626 Search PubMed.
-
B. V. Derjaguin, N. V. Churaev, V. M. Muller and V. Kisin, Surface forces, Springer, 1987 Search PubMed.
- J. Anderson, Annu. Rev. Fluid Mech., 1989, 21, 61–99 CrossRef.
- C. Herrero, M. De San Féliciano, S. Merabia and L. Joly, Nanoscale, 2022, 14, 626–631 RSC.
-
T. Markovich, D. Andelman and R. Podgornik, arXiv, 2016, preprint, arXiv:1603.09451, DOI:10.1201/9780429194078.
-
C. Herrero and L. Joly, arXiv, 2022, preprint, arXiv:2105.00720v2, DOI:10.48550/arXiv.2105.00720.
-
R. Blossey, The Poisson–Boltzmann Equation, Springer International Publishing, Cham, 2023 Search PubMed.
- L. Bocquet and J.-L. Barrat, Soft Matter, 2007, 3, 685–693 RSC.
- D. Huang, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2007, 98, 177801 CrossRef PubMed.
- D. M. Huang, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Langmuir, 2008, 24, 1442–1450 CrossRef CAS PubMed.
- T.-D. Li, J. Gao, R. Szoszkiewicz, U. Landman and E. Riedo, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 115415 CrossRef.
- D. J. Bonthuis and R. R. Netz, J. Phys. Chem. B, 2013, 117, 11397–11413 CrossRef CAS PubMed.
- Y. Xie, L. Fu, T. Niehaus and L. Joly, Phys. Rev. Lett., 2020, 125, 014501 CrossRef CAS PubMed.
- E. Mangaud, M.-L. Bocquet, L. Bocquet and B. Rotenberg, J. Chem. Phys., 2022, 156, 044703 CrossRef CAS PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comp. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- S. Koneshan, J. C. Rasaiah, R. M. Lynden-Bell and S. H. Lee, J. Phys. Chem. B, 1998, 102, 4193–4204 CrossRef CAS.
- C. Pean, B. Daffos, C. Merlet, B. Rotenberg, P.-L. Taberna, P. Simon and M. Salanne, J. Electrochem. Soc., 2015, 162, A5091–A5095 CrossRef CAS.
- Y. M. Liu, C. Merlet and B. Smit, ACS Cent. Sci., 2019, 5, 1813–1823 CrossRef CAS PubMed.
- N. Ganfoud, A. Sene, M. Haefele, A. Marin-Laflèche, B. Daffos, P.-L. Taberna, M. Salanne, P. Simon and B. Rotenberg, Energy Storage Mater., 2019, 21, 190–195 CrossRef.
- T. Méndez-Morales, N. Ganfoud, Z. Li, M. Haefele, B. Rotenberg and M. Salanne, Energy Storage Mater., 2019, 17, 88–92 CrossRef.
- T. Emmerich, K. S. Vasu, A. Niguès, A. Keerthi, B. Radha, A. Siria and L. Bocquet, Nat. Mater., 2022, 21, 696–702 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- K. Shi, E. R. Smith, E. E. Santiso and K. E. Gubbins, J. Chem. Phys., 2023, 158, 040901 CrossRef CAS PubMed.
- B. Cross, C. Barraud, C. Picard, L. Léger, F. Restagno and E. Charlaix, Phys. Rev. Fluids, 2018, 3, 062001 CrossRef.
- C. Herrero, T. Omori, Y. Yamaguchi and L. Joly, J. Chem. Phys., 2019, 151, 041103 CrossRef PubMed.
- M. Rami Reddy and M. Berkowitz, Chem. Phys. Lett., 1989, 155, 173–176 CrossRef.
- D. Braun, S. Boresch and O. Steinhauser, J. Chem. Phys., 2014, 140, 064107 CrossRef PubMed.
- T. Dreher, C. Lemarchand, L. Soulard, E. Bourasseau, P. Malfreyt and N. Pineau, J. Chem. Phys., 2018, 148, 034702 CrossRef CAS PubMed.
- T. Dreher, C. Lemarchand, N. Pineau, E. Bourasseau, A. Ghoufi and P. Malfreyt, J. Chem. Phys., 2019, 150, 014703 CrossRef PubMed.
-
G. Lippmann, Relations entre les phénomènes électriques et capillaires, Gauthier-Villars, 1875 Search PubMed.
- D. Kramer and J. Weissmüller, Surf. Sci., 2007, 601, 3042–3051 CrossRef CAS.
- M. A. González and J. L. F. Abascal, J. Chem. Phys., 2010, 132, 096101 CrossRef PubMed.
- L. Joly, C. Ybert, E. Trizac and L. Bocquet, J. Chem. Phys., 2006, 125, 204716 CrossRef PubMed.
Footnote |
| † Present adress: Laboratoire Charles Coulomb (L2C), Université de Montpellier, CNRS, 34095 Montpellier, France. |
|
| This journal is © the Owner Societies 2023 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Samy
Merabia
,
Samy
Merabia
 and
Laurent
Joly
and
Laurent
Joly
 *
*
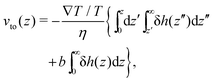
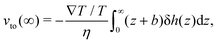
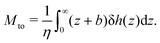
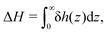
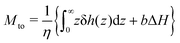
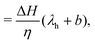
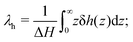
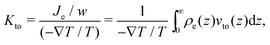
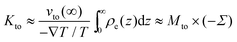
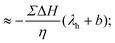
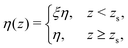
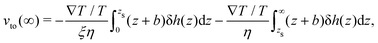
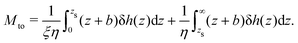
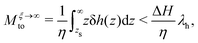

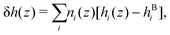
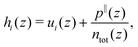
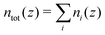 the total number density and p‖(z) the components of the virial pressure tensor parallel to the surface (pxx or pyy, which are equal). Indeed, pressure is anisotropic near the wall, and following previous studies,25,34 we consider the pressure component parallel to the surface to compute the enthalpy excess density. We can consider only the contribution of the potential energy to calculate the internal energy term. Indeed the equipartition theorem implies that the kinetic energy terms cancel out: 〈uk(z)〉 = uBk. Here attributing p‖(z)/ntot(z) to each atom amounts to evenly distribute the atomic volume regardless of the atom type.
the total number density and p‖(z) the components of the virial pressure tensor parallel to the surface (pxx or pyy, which are equal). Indeed, pressure is anisotropic near the wall, and following previous studies,25,34 we consider the pressure component parallel to the surface to compute the enthalpy excess density. We can consider only the contribution of the potential energy to calculate the internal energy term. Indeed the equipartition theorem implies that the kinetic energy terms cancel out: 〈uk(z)〉 = uBk. Here attributing p‖(z)/ntot(z) to each atom amounts to evenly distribute the atomic volume regardless of the atom type.
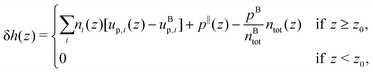
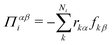 where α and β ∈ {x,y,z}, and Ni is the number of atoms of type i. With this definition,
where α and β ∈ {x,y,z}, and Ni is the number of atoms of type i. With this definition, 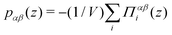 . Although it is well known that the pressure tensor is not uniquely defined for an inhomogeneous fluid near an interface,61 this is not an issue here since we will consider its integral, eqn (21), which is unambiguously defined.61
. Although it is well known that the pressure tensor is not uniquely defined for an inhomogeneous fluid near an interface,61 this is not an issue here since we will consider its integral, eqn (21), which is unambiguously defined.61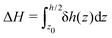 , which we decompose into three contributions: the water internal energy excess ΔUwater, the ions internal energy excess ΔUions and a pressure excess term ΔP‖:
, which we decompose into three contributions: the water internal energy excess ΔUwater, the ions internal energy excess ΔUions and a pressure excess term ΔP‖: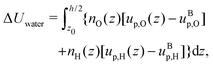
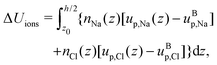
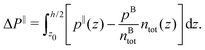
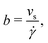
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) the bulk shear rate and vs the slip velocity; vs is defined as the difference between the wall velocity and the velocity of the fluid at the hydrodynamic wall position, given by
the bulk shear rate and vs the slip velocity; vs is defined as the difference between the wall velocity and the velocity of the fluid at the hydrodynamic wall position, given by ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) h/2, where the hydrodynamic height h of the liquid is given by:63
h/2, where the hydrodynamic height h of the liquid is given by:63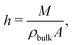

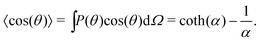
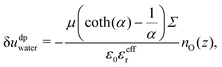
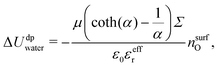
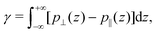
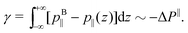
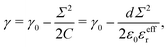
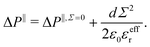

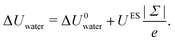


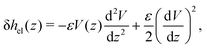
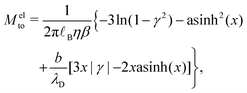
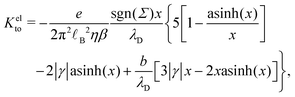
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) B = βe2/(4πε) the Bjerrum length, where e is the elementary charge, x = λD/
B = βe2/(4πε) the Bjerrum length, where e is the elementary charge, x = λD/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) GC, with
GC, with 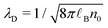 the Debye length and
the Debye length and ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) GC = e/(2π
GC = e/(2π![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) B|Σ|) the Gouy–Chapman length, and
B|Σ|) the Gouy–Chapman length, and 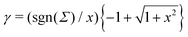 .43
.43
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) B ≃ 8 Å, and the slip length of the homogeneous charge distribution, the classical thermo-osmotic theory predicts thermo-osmotic coefficients much lower than the ones computed with the total enthalpy excess; note however that the electrostatic contribution of ions could be larger in other range of parameters, and in particular at lower salt concentrations.41 Moreover, δhel(z) only predicts negative thermo-osmotic coefficients Mto, and predicts a thermo-osmotic conductance having the same sign as the surface charge density, which is also in strong contrast with the predictions taking into account the total enthalpy excess. Once again, this highlights the important contribution of the solvent to the enthalpy excess, which leads to a rich and complex behavior, such as the change of sign of the thermo-osmotic coefficient for protruding charges.
B ≃ 8 Å, and the slip length of the homogeneous charge distribution, the classical thermo-osmotic theory predicts thermo-osmotic coefficients much lower than the ones computed with the total enthalpy excess; note however that the electrostatic contribution of ions could be larger in other range of parameters, and in particular at lower salt concentrations.41 Moreover, δhel(z) only predicts negative thermo-osmotic coefficients Mto, and predicts a thermo-osmotic conductance having the same sign as the surface charge density, which is also in strong contrast with the predictions taking into account the total enthalpy excess. Once again, this highlights the important contribution of the solvent to the enthalpy excess, which leads to a rich and complex behavior, such as the change of sign of the thermo-osmotic coefficient for protruding charges.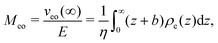
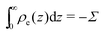 with Σ the surface charge density of the wall. Eqn (37) can then be rewritten:
with Σ the surface charge density of the wall. Eqn (37) can then be rewritten: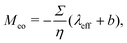
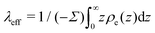 is the effective Debye length,13,43,71 which quantifies the thickness of the EDL in the non-linear Poisson–Boltzmann regime. Therefore, in the same way that one can predict the electro-osmotic flow based on the surface charge density using eqn (38), one can predict the thermo-osmotic coefficient from the enthalpy excess using eqn (7).
is the effective Debye length,13,43,71 which quantifies the thickness of the EDL in the non-linear Poisson–Boltzmann regime. Therefore, in the same way that one can predict the electro-osmotic flow based on the surface charge density using eqn (38), one can predict the thermo-osmotic coefficient from the enthalpy excess using eqn (7).