 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Data-driven tailoring of molecular dipole polarizability and frontier orbital energies in chemical compound space†
Szabolcs
Góger
 ,
Leonardo Medrano
Sandonas
,
Leonardo Medrano
Sandonas
 ,
Carolin
Müller
,
Carolin
Müller
 and
Alexandre
Tkatchenko
and
Alexandre
Tkatchenko
 *
*
Department of Physics and Materials Science, University of Luxembourg, L-1511 Luxembourg City, Luxembourg. E-mail: alexandre.tkatchenko@uni.lu
First published on 11th August 2023
Abstract
Understanding correlations – or lack thereof – between molecular properties is crucial for enabling fast and accurate molecular design strategies. In this contribution, we explore the relation between two key quantities describing the electronic structure and chemical properties of molecular systems: the energy gap between the frontier orbitals and the dipole polarizability. Based on the recently introduced QM7-X dataset, augmented with accurate molecular polarizability calculations as well as analysis of functional group compositions, we show that polarizability and HOMO–LUMO gap are uncorrelated when considering sufficiently extended subsets of the chemical compound space. The relation between these two properties is further analyzed on specific examples of molecules with similar composition as well as homooligomers. Remarkably, the freedom brought by the lack of correlation between molecular polarizability and HOMO–LUMO gap enables the design of novel materials, as we demonstrate on the example of organic photodetector candidates.
1 Introduction
Data-driven molecular design is an increasingly pursued strategy in chemical physics and computational chemistry. The search for novel molecules with tailored physicochemical properties for a given functionality is continuously motivating the development of a great variety of computer-aided molecular design approaches.1–3 The ultimate goal is to establish a feasible protocol that can be used for exploring the chemical compound space (CCS) through systematic targeting of physical properties. Physicochemical quantities, such as color, conductivity, excited state lifetime, electron affinity, ionization potential, and solubility, are commonly used in the design of molecular photosensitizers or optoelectronic devices, for instance.4–7 Given the complexity of a multi-property design task, it is essential to first have a solid grasp of the physical relationships between the various target properties.8Within this context, two fundamental quantum-mechanical (QM) electronic properties are the optical gap and the molecular dipole polarizability (α). Optical gap is an experimental property that measures the energy corresponding to the lowest observed optical transition. Many computational studies use the HOMO–LUMO gap ΔEHL (the difference between the energies of frontier molecular orbitals in the ground state) as a starting point in approximating experimental optical gaps. This approximation is widely favored due to the computational challenges associated with employing highly accurate quantum mechanical methods incorporating orbital relaxation effects (e.g. time-dependent density functional theory or multi-configurational self-consistent field methods), especially, when investigating vast areas of the CCS, macromolecules, molecular aggregates, or molecular junctions.9–11 Thus, the HOMO–LUMO gap plays a crucial role in understanding various aspects of chemical reactivity, excitation energies, and several key optical properties in these organic systems. For instance, its calculation is essential for gaining insights into optical absorption spectra, refractive indices, and conductivity.12–15 For correctness of terminology, HOMO–LUMO gap obtained from density functional calculations should be referred to as Kohn–Sham (KS) gap. Although the relations between different gaps (Kohn–Sham, fundamental, and optical) are subtle and have been discussed in detail in the literature,16,17 in this manuscript we will use the KS gap as a proxy for observable experimental properties.
The molecular dipole polarizability α (referred to simply as polarizability in the manuscript), on the other hand, describes the dipolar response of a molecule to an external electric field, becoming a key quantity for understanding intra- and intermolecular interactions (e.g. dispersion interactions, substituent and solvent effects as well as supramolecular structure formation) and for determining spectroscopic properties of molecules (Raman, Raman optical activity and sum frequency spectroscopy).18–25 These features make both polarizability and HOMO–LUMO gap essential in the derivation of structure–property/property–property relationships and, consequently, in the development of design strategies for molecules with a targeted array of QM properties for applications such as molecular dyes,26 optoelectronic devices,27 molecular junctions,28,29 heterogeneous catalysts30 and materials for non-linear optics.31,32
Various computational methods and predictive models have been developed to estimate HOMO–LUMO gaps and polarizabilities for organic molecules with different levels of tradeoff between accuracy and computational cost.33–36 Lately, it has became feasible to access a plethora of highly-accurate QM properties – including ΔEHL and α – for large swaths of the chemical compound space (CCS).37–41 Comprehensive analyses of these extensive datasets may help to understand the deeper physical picture behind the inherent property–property relationships. With this motivation, we herein perform an exhaustive investigation of the two-dimensional space defined by HOMO–LUMO gap and polarizability (i.e. (ΔEHL,α)-space) for small organic molecules with the aim to gain insights into the intrinsic relationship between these two properties. We find that while correlation might appear in homologous molecules (that is, molecules differing by a constant increment meaning that their physicochemical properties follow a general trend), if a large enough subspace of CCS is considered, HOMO–LUMO gap and polarizability are essentially uncorrelated and their 2D space is represented as a structureless “blob”. Through the analysis of diverse molecular sets, it is shown that this lack of correlation can be related to the fact that the polarizability is primarily determined by the atomic composition, while the HOMO–LUMO gap heavily depends on the arrangement of the atoms into chemical functional groups. Hence, we expect that our findings will assist the development of novel design principles in which the control of multiple electronic properties is relevant, as we finally demonstrate on the case of molecular photodetectors.
The outline of the paper is as follows: in Section 2, we review accurate and approximate models for polarizability and HOMO–LUMO gap. In Section 3, we exhaustively examine the polarizabilities (α) and HOMO–LUMO gaps (ΔEHL) of diverse molecular sets. In doing this, we have extended the QM7-X dataset41 with functional group information as well as polarizabilities calculated with the hybrid PBE0 functional. In assessing our computational setting, we tested the predictive power of this functional against coupled cluster LR-CCSD calculations, and found an overall accuracy of 1.9%. As a first order approximation to predicting polarizabilities of small organic systems, we consider a linear combination of atomic contributions in Section 3.1. In Section 3.2, we then perform PBE0 calculations of polarizability (see Section 6.1 for computational details) for homologous molecules and explore the relationship with their HOMO–LUMO gaps. A statistical analysis of the (ΔEHL,α)-space using a subset of molecules contained in QM7-X dataset is carried out in Section 3.3. Our proposed design principle is further discussed and demonstrated on the case of organic photodetectors, see Section 4. The computational methods as well as the dataset used are presented in Section 6, following the main conclusions of the manuscript in Section 5.
2 Models for polarizability and frontier orbital energy gap
Since our main focus is to have a better understanding of the relationship between polarizability and HOMO–LUMO gap in organic molecules, we first revisit different qualitative and quantitative models employed to compute them. In general, a variety of electronic structure methods can be used to calculate both of these quantities. The choice of a computational level depends on the specific target property and the necessary tradeoff between computational cost and accuracy. While calculating the HOMO–LUMO gap is feasible using various mean-field electronic structure methods, orbital relaxation effects play a significant role in determining optical properties.42 However, in computationally expensive studies such as the analysis of macromolecules or extensive datasets (e.g. QM7-X considered in this manuscript), HOMO–LUMO gap is often used as a first approximation to experimental quantities. Polarizability (α) is typically obtained from finite field, coupled perturbed Hartree–Fock or density functional perturbation theory (DFPT) calculations.33,34,43 However, these electronic structure methods need considerable computational resources when dealing with larger molecules or significant swaths of the CCS. Accordingly, we will next discuss alternative physical models, empirical correlations, and approximate methods that can be used to obtain these QM properties as well as to broaden the comprehension of property–property relationships in CCS. We will start with examining the polarizability, for which analytical models (such as the quantum Drude oscillator, or QDO) as well as empirical correlations and predictive semiempirical methods are available. After this, the models for HOMO–LUMO gap will be mentioned, before concluding the section by analyzing what is known about the correlation between these two quantities.A connection between HOMO–LUMO gap and polarizability can be anticipated starting from the perturbative expression for polarizability using the dipole moment operator ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) within second order perturbation theory as20,44
within second order perturbation theory as20,44
 | (1) |
Eqn (1) can only be analytically evaluated for simple model systems (such as the hydrogen atom or a quantum Drude oscillator). For many-electron systems, the sum can only be evaluated numerically and requires including bound-bound and bound-continuum transition dipoles.45 Modeling atoms or larger coarse-grained fragments with QDOs and solving the dipole–dipole screening equations is known to be an effective method to predict polarizability, and it is also the basis for the Many-Body Dispersion (MBD) method.46,47 Since the response properties of all atoms and molecules can be represented by QDOs by carefully setting the three parameters {charge q, frequency ω, mass μ} of the model, the analysis of the polarizability of the QDO Hamiltonian should generally be transferable to any systems. Therefore, we devote some attention to this model.
Due to selection rules of the dipole operator, only the first excited state contributes to the dipole polarizability of a QDO,44,48 making it effectively a two-state system
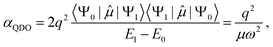 | (2) |
The idea of approximating the polarizability using an effective two-state system (so-called Unsøld approximation)44,49 is also useful for understanding qualitative trends. Within this approximation, polarizability is written using an average excitation ΔE as a fitting parameter
 | (3) |
Investigating correlations between polarizability and various molecular properties can lead to useful relationships such as the recent observation that polarizability scales with the fourth power of the characteristic size of the system.44 The correlation between polarizability and orbital energies is relevant from a theoretical standpoint, as it forms the foundation of Pearson's hard-soft acid–base (HSAB) theory.51,52 Based on recent theoretical works, we can postulate that polarizability can be expressed as a function of two factors accounting for (i) ground state geometry (e.g. van der Waals radius or molecular volume) and (ii) electronic structure (e.g. ionization energy or hardness).31,44,53–58 While these correlations provide useful conceptual insights, they have not been put to use for constructing accurate numerical predictions.
There are two types of predictive models for polarizability with lower computational burden than electronic structure calculations. Firstly, approximations for polarizability can be constructed based on the group contribution principle, which divides polarizability into atomic or bond contributions.30,59 These models can offer somewhat accurate predictions with minimal molecular information and computational effort, and we will assess such models in this work. As a second approach, machine learning (ML) models have been proposed as a cost-effective solution with improved accuracy.35 However, the training process and accuracy of the ML models are strongly dependent on the features of the dataset (e.g. chemical diversity, molecular size, number of samples) as well as on the ML method itself.
For the case of HOMO–LUMO gap, there is a well-established underlying physical principle in determining this property: it is known that the HOMO–LUMO gap of individual functional groups (called chromophores in this context) is transferable, with values documented in standard reference texts.60 These chromophores also form the foundation for both accurate ML models and earlier empirical rules for the prediction of HOMO–LUMO gaps.61,62 The HOMO–LUMO gap of a single functional group can be understood based on the molecular orbital theory, the most common version of which is the Hückel theory for conjugated systems. For instance, the inverse proportionality between the number of monomers and the HOMO–LUMO gap of polyenes is well-explained within this theory.63 In the case of non-interacting functional groups, their optical spectra are effectively independent and, consequently, the frontier energy gap of a molecule is determined by the lowest value for the constituent functional groups, making it an inherently size-independent (intensive) property.
In agreement with the analysis of the QDO model, recent studies relying on large datasets (7 k structures from the GDB-13 dataset as well as the tmQM dataset of 86 k transition metal complexes) suggest that there's no overall correlation between HOMO–LUMO gap and polarizability.64,65 Nevertheless, correlation has been observed both experimentally and computationally for different classes of structures (e.g. organic dyes and inorganic clusters26,66–68), with notable exception of smaller systems where the HOMO–LUMO transition is symmetry forbidden.24 In the following section, we explore the source of such seemingly contradictory results by showing that investigating a reduced subset of the chemical compound space can lead to correlations between quantities that are generally uncorrelated.
3 Results and discussion
3.1 First order linear atomic additive model for polarizability
To understand the correlation between polarizability and HOMO–LUMO gap, we first show that polarizability can be, up to a large degree, determined by knowing only the atomic composition (i.e. the types and the numbers of atoms present in a molecule). This analysis is done using the PBE0 polarizability values calculated for the QM7-X molecules, contrasting these quantum chemical results with a linear atomic additive method. The simplest atomic additive method (motivated by that of Bosque36) approximates the polarizability of a molecule via a linear combination of the number of each atom-types n weighted with a type-specific factor Ci, together with an intercept m | (4) |
Bosque's model was fit directly using experimental data of 426 compounds. The fitted m and Ci values for C, Cl, H, N, O, and S are listed in Table 1. Accordingly, we have here used the QM7-X dataset41 (see Section 6) to validate the accuracy and reassess the model parameters on a significantly larger swath of the CCS. In doing so, we have considered the first conformer for each entry in the QM7-X dataset; a total of ≈13 k structures. The linear regression parameters optimized on QM7-X yield the results listed in Table 1. Bosque's parameters hold up relatively well for QM7-X molecules, accounting for a correlation coefficient (R2 value) of 0.65 with a mean absolute percentage error (MAPE) of 6.11%. However, the re-fitted parameters improve the correlation coefficient to 0.72 and reduce MAPE value to 3.94%, i.e. the prediction accuracy is increased by a factor of 1.6. Note that the presence of the intercept m in eqn (4) is just an artifact of the model, since the prediction should be zero when no atoms are present. Inclusion or omission of m, however, changes neither the goodness of the regression, nor the numerical value of the atomic contributions to a meaningful degree (the mean absolute error of the linear model goes from 3.078 a.u. to 3.079 a.u.; similarly to what had also been observed in the original paper36). Therefore, we decided to include the intercept in our further analysis, to be consistent with Bosque's approach.
| Intercept | C | Cl | H | N | O | S | |
|---|---|---|---|---|---|---|---|
| Bosque | 2.14 | 10.20 | 14.60 | 1.17 | 6.95 | 3.85 | 20.20 |
| This work | 1.71 | 10.10 | 12.70 | 0.87 | 7.88 | 4.00 | 19.10 |
| No intercept | 0.00 | 10.37 | 13.00 | 0.88 | 8.11 | 4.24 | 19.37 |
A shortcoming of atomic additive methods is that the same polarizability is predicted for all structural isomers, since only the total number of each atom-types is used in the prediction. This is manifested in Fig. 1 as having a systematic error within each possible αpred value, and further demonstrated in the inset on the case of molecules with the atomic composition C6H8O – the reference polarizabilities for this chemical formula span a range of 30 a.u., but the predicted value is 73.4 a.u. for all molecules, irrespective of the chemical arrangement of the atoms. From Fig. 1, it can also be inferred that such a simple additive model will only become worse for molecules of increasing size. Indeed, a trend appears where larger molecules exhibit stronger deviations towards higher polarizabilities – a trend that an additive model is unable to describe. This can be especially the case for polymeric molecules which form long chains, whose polarizability is highly anisotropic and behaves increasingly non-additively with size.
 | ||
| Fig. 1 Performance of the atomic additive method. The linear regression parameters are fit utilizing our dataset of 13 k molecules computed at the DFT-PBE0 level of theory (subset of the QM7-X dataset,41 see Fig. S3 of ESI†). The inset shows the inherent shortcoming of the model, predicting the same polarizability for all molecules having the atomic composition C6H8O. | ||
To differentiate between structural isomers, a descriptor that accounts for different geometric properties (for example, radius of gyration) might be constructed, since polarizability is an extensive property.55,58 This extensivity is only partially captured by atomic additive methods, insofar as increasing the number of atoms in a molecule is inherently increasing the size as well. More accurate models should also differentiate between similar atoms based on their surrounding chemical environments, as it is done for example in ref. 44, where the environment is taken into account by Hirshfeld partitioning as well as in the self-consistent screening approach used in the Many-Body Dispersion (MBD) method.46,47 Therefore, while the shown first-order linear model is limited by its accuracy, it can serve as a baseline for more accurate methods involving coupling between atoms in a molecule.
To summarize, a first-order approximation to polarizability can be constructed just by using an atomic additive model without explicit knowledge of the molecular spatial arrangement or the local chemical environments. While the predictive power of such a model is rather restricted (i.e. the chemical environment of each atom is not described), its rough correlation with reference electronic-structure calculations (see Fig. 1) gives a clear evidence that a significant fraction of the polarizability is determined by just the atomic composition.
3.2 Case studies for the relation between the HOMO–LUMO gap and polarizability
Having shown that polarizability depends mainly on the atomic composition of molecules, we now turn into exploring the correlations between polarizability and HOMO–LUMO gap. In doing so, we here discuss a set of case studies of select molecules, with all calculations being done using the PBE0 functional, as described in Section 6.Experimental studies often focus on examining molecules with similar electronic structures, leading to hidden correlations between optical gap and polarizability. In our path towards the general understanding of the relationship between these QM properties, we now examine two different cases: (i) molecules having the same atom-type composition but slightly different chemical compositions and (ii) molecules with the chemical properties fixed while increasing the system size (e.g. oligomers).
As a first example, two constitutional isomers with the formula C5H8O, namely an α,β-(3-penten-2-one) and a β,γ-unsaturated enone (4-penten-2-one) is considered (see Fig. 2(a)). It is noticeable that 3-penten-2-one has a smaller gap compared to 4-penten-2-one (by 1.12 eV) because delocalization results in a greater mobility of π-electrons throughout the molecular structure. However, both molecules present a similar polarizability coming from the identical atomic composition as well as a similar total size.
 | ||
| Fig. 2 (a) Two constitution isomers, i.e. molecules with the same atomic composition but different chemical properties, showing similar polarizabilities but different HOMO–LUMO gaps. (b) HOMO–LUMO gap and polarizability of all possible linear structures having eight carbon atoms, an oxo group and a double bond between two of the carbons. The numbering of carbon atoms is shown on octane-3-one, with n representing the numbering of the carbon atom at the start of the double bond (see Fig. S5 of ESI,† for the explicit structures). The polarizability and HOMO–LUMO gap values are results of PBE0 calculations as described in Section 6.1. | ||
A second set of constitutional isomers with the formula C8H14O was constructed for molecules bearing a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (oxo-group) and C
O (oxo-group) and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C (alkene-group) on an octane backbone. These isomers are thus formed by the following substance classes: one ketene, one conjugated aldehyde, four conjugated ketones, five non-conjugated aldehydes and eight non-conjugated ketones (see Fig. 2(b) as well as Fig. S5 of ESI†). While these structures are chemically quite different, their orbital symmetries are largely similar, leading to a correlation between their polarizability and HOMO–LUMO gap. Notice, however, that the polarizabilities of the structures are all within 4% of each other, whereas the variation of HOMO–LUMO gap is about five times larger. As such, the statement that polarizability is mainly determined by the atomic composition and HOMO–LUMO gap by the chemical composition seems to hold, even though some correlation between these two quantities is observed due to the similarity of the structures.
C (alkene-group) on an octane backbone. These isomers are thus formed by the following substance classes: one ketene, one conjugated aldehyde, four conjugated ketones, five non-conjugated aldehydes and eight non-conjugated ketones (see Fig. 2(b) as well as Fig. S5 of ESI†). While these structures are chemically quite different, their orbital symmetries are largely similar, leading to a correlation between their polarizability and HOMO–LUMO gap. Notice, however, that the polarizabilities of the structures are all within 4% of each other, whereas the variation of HOMO–LUMO gap is about five times larger. As such, the statement that polarizability is mainly determined by the atomic composition and HOMO–LUMO gap by the chemical composition seems to hold, even though some correlation between these two quantities is observed due to the similarity of the structures.
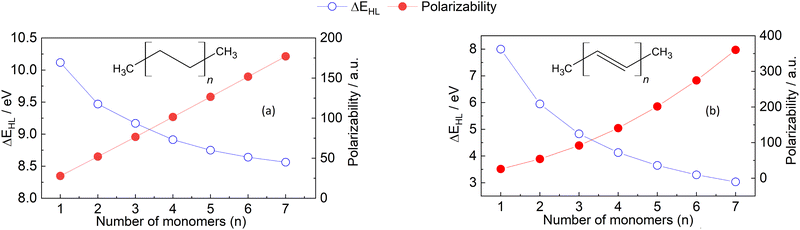 | ||
| Fig. 3 HOMO–LUMO gap (blue dots) and polarizability (red dots) of the oligomers of (a) ethylene and (b) acetylene. The calculations of both properties were carried out as described in Section 6.1. | ||
Fig. 3 shows a decreasing behaviour of HOMO–LUMO gap for oligoethylene and oligoacetylene as a function of the number of monomers n, in agreement with previous works as well as qualitative predictions from the Hückel model.63,70 Indeed, we have found that the absence of a qualitative change to the electronic structure within the ethylene oligomers leads to a relatively small HOMO–LUMO gap change going from n = 1 → 7 (≈1.5 eV) compared to the acetylene oligomers, where every monomer modifies the conjugation, producing a more significant change of ≈5.0 eV. Unlike HOMO–LUMO gap, the behavior of polarizability in the molecular chains can not be simply explained. The observation that polarizability monotonously increases with n is in line with both the principles of atomic additive models and the correlation with molecular size. However, the absolute magnitude of the polarizability values is significantly different for the two sets of oligomers, and this difference increments with increasing the number of monomers. This quantitative difference can neither be explained by atomic additive models nor correlations using molecular size, but it correlates with the reductions in HOMO–LUMO gap. Notably, not even AlphaML35 can predict this behavior: the model predicts 181 a.u. for oligoethylene and 227 a.u. for oligoacethylene in the n = 7 case, with the DFPT results being 177 a.u. and 360 a.u., respectively. The difference due to conjugation is therefore underestimated by a factor of four even when using ML methods, and this error is expected to increase with increasing the chain length. Up to now, we are not aware of any other simple polarizability estimation method that can accurately predict the values in Fig. 3. These findings provide clear evidence that further work is necessary to enhance our understanding and improve and accuracy of computational methods used for calculating polarizability, even for relatively simple molecules such as hydrocarbon oligomers.
3.3 Clustering of structures in the (ΔEHL,α)-space
To draw more general conclusions about the relationship between the properties in question, we analyse the two-dimensional (2D) property space defined by HOMO–LUMO gap and polarizability for a selected subset of QM7-X molecules8 (see Section 6.2). HOMO–LUMO gap values were taken from the dataset, while polarizability values were recalculated using the computational setup explained in Section 6.1. All previously presented examples might suggest that there is a correlation between HOMO–LUMO gap and polarizability. However, these examples considered similar molecules with respect to their functionality or chemical composition – factors that essentially determine both the HOMO–LUMO gap and polarizability. From optical spectroscopy, it is known that the optical gap is primarily determined by the functional groups in a molecule. This is reflected in characteristic optical gaps (vertical excitation energies of the lowest electronic transitions) per functional groups, e.g. the ππ* absorption of an isolated alkene-group as chromophore is between 7.51 and 6.70 eV. Since we are assuming that HOMO–LUMO gap is a good starting point in determining the optical gap of a molecule, it would be expected to find that ΔEHL values are also clustered by certain functional groups. In contrast, our analysis has shown that polarizability (α) is primarily determined by the atomic composition of a molecule. The QM7-X dataset enables us to study the (ΔEHL,α) relationship more broadly because it covers a considerable number and variety of chemical compounds.Fig. 4(a) shows the (ΔEHL,α)-space for the QM7-X molecules – indicating no direct relationship between the two quantities across the chemical compound space spanned by this dataset (R2 = 0.13). Furthermore, the role of the two main factors that determine ΔEHL (functionality) and α (atomic composition) are highlighted in Fig. 4. The panels (b) and (c) exemplarily display the distributions of ΔEHL and α for aldehydes and primary alcohols, i.e., molecules that bear one of the respective functional groups. The subplots (d) and (e) show the respective distributions for molecules with equal atomic compositions, namely with the molecular formulas C4H8O and C4H9N, respectively.
To fully explore the role of functional groups on the (ΔEHL,α) relationship, the QM7-X molecules were categorized into twelve major classes based on the functional groups they are bearing (see Section 6.2). Fig. S4 (ESI†) shows that the distribution of all detected functional groups in the dataset, confirming that ΔEHL is clustered along the chemical properties of the molecules.
Unlike ΔEHL, molecules containing aldehydes (blue) and primary alcohols (pink) exhibit polarizabilities that extend throughout the entire range of the dataset (cf.Fig. 4(b)). This finding is further reflected in the average Kolmogorov-Smirnov-metric (measuring the statistical distance between two general distributions, see Section II of ESI†) of the individual molecular classes in the (ΔEHL,α)-space, which is 0.81 and 0.40 for ΔEHL and α, respectively. Our analysis then demonstrates that functional groups primarily affect HOMO–LUMO gap rather than the polarizability, resulting in well-defined molecular clusters on the ΔEHL-axis.
In summary, we can conclude that the lack of overall correlation observed in (ΔEHL,α)-space is a consequence of two main facts: (i) the HOMO–LUMO gap is determined by the nature of the chemical composition (cf.Fig. 4c and e) and (ii) the polarizability is largely determined by the atomic composition (cf.Fig. 4b and d).
4 Case study: design of photodetectors
The possibility of an inverse correlation between the HOMO–LUMO gap and polarizability was thoroughly examined in Section 2. This specific correlation has been observed exclusively when analyzing the electronic properties of homologous series and isomers, as described in Section 3.2. However, when investigating a chemically diverse set of molecules, such as those found in QM7-X, we discovered that these two properties are essentially uncorrelated. This lack of correlation offers a flexibility in the (ΔEHL,α)-space to identify diverse molecules with a targeted pair of properties, e.g. by fixing ΔEHL, one will have a wide range of α values where we can select a molecule with desired chemical features. Now, we present how this lack of correlation can be exploited for molecular design purposes. The property data used for this analysis is from the donor–acceptor (DA) dataset,71 which was designed to enumerate promising organic photodetector candidate molecules. The DA dataset contains only molecular structures and HOMO–LUMO gap values, while the estimation of polarizability was performed using the revised Bosque model, as elucidated in Section 3.1.A common challenge in materials science is the effective design of photodetectors. These optoelectronic devices capture light and convert it to electric signal, therefore playing an important role in sensing, monitoring and optical communication. The wide range of physicochemical properties spanned by organic molecules enables various design strategies, which ultimately led to the emerging field of organic photodetectors.72,73 HOMO–LUMO gap is one of the key quantities that can be used to approximate the coupling strength of molecules with light, thereby any design strategy motivated by optics will be initially based on this property.71,74 Since the fundamental function of photodetectors is to convert light into electrical current, controlling the electrochemical behavior is also crucial. Specifically, the electrochemical work function plays a critical role in the description of organic photodetectors,75,76 as opposed to organic semiconductors, where the focus is usually on the charge carrier mobility.77 The work function ϕ of an electrode is known to change with the polarizability of the absorbed molecules as well as the surface coverage, as described by the Topping equation78 (written for a square lattice)
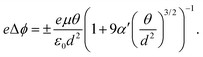 | (5) |
In the preceding sections, we have postulated that polarizability and HOMO–LUMO gap are uncorrelated if a large enough subset of the CCS is considered. This law can now be translated to the domain of organic photodetectors: since HOMO–LUMO gap and polarizability are generally independent, it should be possible to design a photodetector with a given detection peak having an arbitrary work function. Alternatively, if matching of electrochemical properties of different systems is the goal, it should be possible to design organic photodetectors with each having arbitrary optical detection windows, yet having the same effect on the work function of electrodes. To demonstrate this statement, we use a dataset generated by Xu et al.,71 who employed a self-improving Bayesian search to predict possible photodetector molecules in a large subset of CCS. The selection criterion for possible photodetectors was based on both HOMO–LUMO gap and singlet–triplet energy gap, which were evaluated from ground state DFT and TD-DFT calculations, respectively. From all predicted molecules having a donor and an acceptor site (DA structures), we have only selected those cases which have the same atom types as QM7-X molecules (see also in Table 1), leading to a total of 5311 structures. Using the atomic additive model described in Section 3.1, we have estimated the polarizabilities of the selected structures; the plot of the polarizability versus HOMO–LUMO gap is shown in the top panel of Fig. 5. Here, one can see that most structures are found in a relatively extended region having ΔEHL between 3 and 5 eV and α between 200 and 400 a.u., with the possibility to find outliers in all directions around this cluster. In particular, if a high shift in the work function is desired, there appear to be several good candidates with varying optical absorption ranges (see bottom of the graph).
 | ||
| Fig. 5 HOMO–LUMO gap and polarizability of the structures in the donor–acceptor (DA) dataset of Xu et al.71 The maximum of the HOMO–LUMO gap density (4 eV) is marked with a blue line. The four structures corresponding to the four quartiles in the predicted polarizability (within ±0.1 eV) are also shown, together with the predicted values (in a.u.). | ||
Moreover, our calculations show that the polarizability of these structures can vary by a factor of up to six for specific values of the HOMO–LUMO gap. To demonstrate this flexibility in α, Fig. 5 also shows the four molecules corresponding to the four quartiles having a HOMO–LUMO gap of 4 ± 0.1 eV, selected to correspond to the maximum density of data. For this specific HOMO–LUMO gap, polarizability changes between 149.9 a.u. and 451.1 a.u. Taking the tenfold enhancement between the polarizability of the free molecule and the absorbed α′ into account and using approximate values of μ = 4 D and d = 1.5 nm with a full surface coverage, this would mean that changes in work function could range from 0.9 eV to 1.5 eV. These variations are larger than usually achievable by modifications of a semiconductor structure or controlling the surface coverage.80,81 Therefore, our analysis shows that work function can be, for practical purposes, freely tailored, even with a very specific design requirement on HOMO–LUMO gap.
This flexibility is also relevant in the task of designing wavelength-selective detectors, which would imply hard constraint on HOMO–LUMO gap. If ΔEHL and α could not be controlled independently, then optical design restrictions would directly influence the electrochemical behavior. The decoupling of ΔEHL and α means that the wavelength of detection and the work function can be controlled independently. Fine-tuning the work functions to achieve matching on the metal–organic interface at the electrode is crucial for efficiency. Thus, with the existent “freedom of design” in (ΔEHL,α)-space, we have demonstrated that an efficient detection can be theoretically achieved for any detection wavelength. Alternatively, since the work function can be tailored to match any detection wavelength, it is also possible to design detectors for different detection ranges having equivalent electrochemical properties such as sensitivity, dark current, adhesion behavior as well as any other properties determined by the work function.
5 Conclusions
Predictive molecular design is an emerging tool in modern molecular physics and chemistry which heavily relies on the understanding of relationships between key structural and electronic properties. Identifying and explaining correlations between properties necessitates either deep physical understanding or exhaustive data analysis. Herein, we have presented a comprehensive investigation of the intricate interplay between the HOMO–LUMO gap and dipole polarizability – two central properties in designing molecules with tailored optical properties and intermolecular interactions.Despite the fact that both quantities have their root in the molecular electronic spectrum, understanding their correlation is quite complex. On one hand, the properties are essentially uncorrelated when accounting for a vast chemical space. On the other hand, when examining a small subset of the chemical compound space with similar functionalities, such as homologous series of molecules like oligomeric hydrocarbons, we show that the properties can be observed as being correlated.
To perform a data-driven analysis, we extended the QM7-X database with functional group labels and accurate polarizabilities to explain the physical cause of this phenomenon. Our results demonstrate that the atomic composition has a major role in determining polarizability, while the arrangement of these atoms into chemical functional groups dictates the HOMO–LUMO gap. The physical origin of molecular polarizability was elaborated by studying conceptual models as well as interpreted with the help of a first order linear atomic additive model. Finally, the “freedom of design” arising from the interaction of HOMO–LUMO gap and polarizability was used on the example of organic photodetectors, demonstrating that the electrochemical properties of such molecules can be freely tailored even with specific requirement on the optical properties. The theoretical insights gained from this work can give the basis for expanding the understanding of the relationship between HOMO–LUMO gap and polarizability by incorporating additional descriptors such as molecular size and electronic mobility. Additionally, the unraveled “freedom of design” could be applied to the development of new compounds with tailored optical and electronic properties for use in applications such as organic electronics, sensing or energy harvesting.
6 Computational methods
Generally, molecular design is a multi-property optimization problem and requires an exhaustive analysis of diverse structure–property and property–property relationships.1,6 In this contribution, we have opted to focus on the two-dimensional property space defined by ΔEHL and α (i.e. (ΔEHL,α)-space), as motivated in the introduction (see Section 1). To calculate the polarizability, two approaches were used: (i) the revised linear additive atomic model of Bosque (introduced in Section 3.1) was utilized for the prediction of polarizability of the organic photodetector candidates in Section 4 and (ii) density functional perturbation theory (for the case studies in Section 3.2 as well as to analyze the QM7-X molecules in Section 3.3). The HOMO–LUMO gap was always obtained from DFT calculations, either by calculating it ourselves or utilizing the values provided in the QM7-X dataset.6.1 Target molecular property space
To perform a purely data-driven study, we utilize the QM7-X dataset41 containing 42 physicochemical properties of ≈ 4.2 M (equilibrium and non-equilibrium) organic molecules with up to seven heavy (non-hydrogen) atoms (including C, O, N, S and Cl), spanning a practically important subset of CCS. Accordingly, a subset of QM7-X considering only one equilibrium constitutional isomers and stereoisomers per unique molecular graph is selected for further analysis (≈13 k molecules). In QM7-X, the molecular structures were optimized using the third-order self-consistent charge density-functional tight binding method (DFTB3)82 supplemented with a treatment of many-body dispersion/van der Waals interactions via the MBD approach.47,83 However, for our studies concerning polarizability, α was computed directly, employing density functional perturbation theory (DFPT)33 by means of the PBE084 functional as implemented in the FHI-aims code85 (version 190205). To ensure the transferability of the values, we store the molecular (mean) polarizability (denoted as α and simply referred to as polarizability in other parts of the manuscript)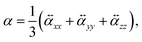 | (6) |
 | (7) |
It is known that polarizability is sensitive both to the choice of functional as well as the basis set size.25,86,87 To converge our computational setup, the respective mean polarizabilities were compared with the highly accurate values of the QM7b database.88,89 This comparison ensures an accurate assessment of the prediction error due to the following two reasons: (i) there is a large overlap between the structures in the QM7b and QM7-X databases, and (ii) QM7b provides highly accurate α values obtained at the linear-response coupled cluster singles and doubles (LR-CCSD) level of theory.35,57 Then, we computed the polarizabilities of 300 randomly selected structures of QM7b employing the same DFPT computational setup described above. We have found that the PBE0 hybrid functional using the default light basis set for all elements amended with three additional functions from the tight level predicts α with a mean average error of 1.9% and a standard deviation of 1.1% (cf. Fig. S1 of the ESI†). The accuracy of our chosen computational setup is higher than to common DFT methods, and slightly better than the 2.84% found by Hait and Head-Gordon87 for the PBE0 functional, which can be attributed to the fact that our study is concerned only with organic molecules. Polarizability anisrotropy is predicted with a mean average error of 10.2% with a standard deviation of 5.1%, which is in line with previously reported values.90,91 In general, the mean polarizability is slightly underestimated, whereas the anisotropy is almost always overestimated by PBE0.
6.2 Molecular classification: functional groups
A workflow has been implemented to identify chemical functional groups from the molecular structure in two steps: firstly, we save the Cartesian coordinates of molecules in a MDL Molfiles format using the standard implementation in Open Babel.92 Secondly, Checkmol93 is employed to detect the functional groups (204 tags) based on the connectivity tree. In total, 61 unique functional groups were detected for the subset of the ≈13 k QM7-X-molecules,41 demonstrating that the dataset covers a considerable sector of CCS (cf. Fig. S2 of the ESI†). Since Open Babel predicts valencies only based on the distance between pairs of atoms, the functional group detection scheme is prone to errors for molecules with rare functional groups. Moreover, the functional group definitions of Checkmol have significant overlaps, e.g. the molecules detected as alkylamines are also detected as primary amines. To ensure that these shortcomings do not influence our conclusions, we base our analyses only on the subset of the 14 k molecules that have certain functional groups. These groups are chosen to be chemically important, non-overlapping, and each of these categories contain at least 500 entries. The number of structures containing one of these functional groups is 9604. For the analysis in Section 3.3, only molecules containing a single functional group are considered, i.e. 1626 entries of our dataset (see Fig. S3, ESI†). Based on these constraints, the following eleven classes of molecules are identified: aldehydes, carbonitriles, dialkyl ether, enol ether, hydrazones, ketones, oximes, primary alcohols and amines, as well as secondary alcohols and amines (see labels in Fig. 4(a)).Author contributions
The work was initially conceived by SG, LMS, and AT, and designed with contributions from CM and AT. AT supervised and revised all stages of the work. All authors discussed the results and contributed to the final manuscript.Data availability
The dataset used in this work, i.e. the subset of QM7-X extended by the DFPT polarizabilities and functional group labels is available on GitHub.94Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support from the Luxembourg National Research Fund: DRIVEN (PRIDE17/12252781) under the PRIDE program as well as the INTER-FWO project MONODISP. Furthermore, the financial support from the European Research Council Executive Agency (ERCEA), Grant “101054629-FITMOL-ERC-2021-ADG” is also gratefully acknowledged. C. M. gratefully acknowledges support by the Alexander von Humboldt Foundation through a Feodor Lynen Research Fellowship.Notes and references
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Science, 2018, 361, 360–365 CrossRef CAS PubMed.
- O. A. von Lilienfeld, K.-R. Müller and A. Tkatchenko, Nat. Rev. Chem., 2020, 4, 347–358 CrossRef PubMed.
- C. Bilodeau, W. Jin, T. Jaakkola, R. Barzilay and K. F. Jensen, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1608 Search PubMed.
- C. Müller, S. Bold, M. Chavarot-Kerlidou and B. Dietzek-Ivanšić, Coord. Chem. Rev., 2022, 472, 214764 CrossRef.
- C. Kranz and M. Wächtler, Chem. Soc. Rev., 2021, 50, 1407–1437 RSC.
- Z.-J. Zhao, S. Liu, S. Zha, D. Cheng, F. Studt, G. Henkelman and J. Gong, Nat. Rev. Mater., 2019, 4, 792–804 CrossRef.
- X. Wang, G. Zhang, L. Yang, E. Sharman and J. Jiang, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1369 Search PubMed.
- L. Medrano Sandonas, J. Hoja, B. G. Ernst, A. Vazquez-Mayagoitia, R. A. DiStasio Jr and A. Tkatchenko, ChemRxiv, 2021, preprint DOI:10.26434/chemrxiv-2021-q9rc2.
- J. Roncali, Macromol. Rapid Commun., 2007, 28, 1761–1775 CrossRef CAS.
- P. M. Beaujuge and J. R. Reynolds, Chem. Rev., 2010, 110, 268–320 CrossRef CAS PubMed.
- S. Kubatkin, A. Danilov, M. Hjort, J. Cornil, J.-L. Bredas, N. Stuhr-Hansen, P. Hedegård and T. Bjørnholm, Nature, 2003, 425, 698–701 CrossRef CAS PubMed.
- A. R. Katritzky, S. Sild and M. Karelson, J. Chem. Inf. Comput. Sci., 1998, 38, 1171–1176 CrossRef CAS.
- K. Takimiya, T. Yamamoto, H. Ebata and T. Izawa, Sci. Technol. Adv. Mater., 2007, 8, 273–276 CrossRef CAS.
- S. K. S. Mazinani, R. V. Meidanshahi, J. L. Palma, P. Tarakeshwar, T. Hansen, M. A. Ratner and V. Mujica, J. Phys. Chem. C, 2016, 120, 26054–26060 CrossRef CAS.
- G. Gryn'ova, K.-H. Lin and C. Corminboeuf, J. Am. Chem. Soc., 2018, 140, 16370–16386 CrossRef PubMed.
- J.-L. Bredas, Mater. Horiz., 2014, 1, 17–19 RSC.
- T. Stein, H. Eisenberg, L. Kronik and R. Baer, Phys. Rev. Lett., 2010, 105, 266802 CrossRef PubMed.
- M. Karplus and H. J. Kolker, J. Chem. Phys., 1964, 41, 3955–3961 CrossRef CAS.
- U. Hohm, J. Phys. Chem. A, 2000, 104, 8418–8423 CrossRef.
- A. J. Stone, The Theory of Intermolecular Forces, Oxford University Press, New York, 2016 Search PubMed.
- C. Xie, A. R. Oganov, D. Dong, N. Liu, D. Li and T. T. Debela, Sci. Rep., 2015, 5, 16769 CrossRef CAS PubMed.
- D. S. Sabirov, RSC Adv., 2014, 4, 44996–45028 RSC.
- K. Kamada, M. Ueda, H. Nagao, K. Tawa, T. Sugino, Y. Shmizu and K. Ohta, J. Phys. Chem. A, 2000, 104, 4723–4734 CrossRef CAS.
- C. Pouchan, D. Bégué and D. Y. Zhang, J. Chem. Phys., 2004, 121, 4628–4634 CrossRef CAS PubMed.
- J. R. Cheeseman and M. J. Frisch, J. Chem. Theory Comput., 2011, 7, 3323–3334 CrossRef CAS PubMed.
- M. Targema, N. O. Obi-Egbedi and M. D. Adeoye, Comput. Theor. Chem., 2013, 1012, 47–53 CrossRef CAS.
- T.-D. Kim and K.-S. Lee, Macromol. Rapid Commun., 2015, 36, 943–958 CrossRef CAS PubMed.
- D. Wang, D. Fracasso, A. Nurbawono, H. V. Annadata, C. S. S. Sangeeth, L. Yuan and C. A. Nijhuis, Adv. Mater., 2015, 27, 6689–6695 CrossRef CAS PubMed.
- K. Kaasbjerg and K. Flensberg, Nano Lett., 2008, 8, 3809–3814 CrossRef CAS PubMed.
- P. Jaque and A. Toro-Labbé, J. Chem. Phys., 2002, 117, 3208–3218 CrossRef CAS.
- F. Meyers, S. R. Marder, B. M. Pierce and J. L. Bredas, J. Am. Chem. Soc., 1994, 116, 10703–10714 CrossRef CAS.
- P. Otto, Int. J. Quantum Chem., 1994, 52, 353–364 CrossRef CAS.
- H. Shang, N. Raimbault, P. Rinke, M. Scheffler, M. Rossi and C. Carbogno, New J. Phys., 2018, 20, 073040 CrossRef.
- S. P. Karna, Chem. Phys. Lett., 1993, 214, 186–192 CrossRef CAS.
- D. M. Wilkins, A. Grisafi, Y. Yang, K. U. Lao, R. A. DiStasio and M. Ceriotti, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 3401–3406 CrossRef CAS PubMed.
- R. Bosque and J. Sales, J. Chem. Inf. Comput. Sci., 2002, 42, 1154–1163 CrossRef CAS PubMed.
- S. Curtarolo, G. L. W. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, Nat. Mater., 2013, 12, 191–201 CrossRef CAS PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, Sci. Data, 2014, 1, 140022 CrossRef CAS PubMed.
- P. S. Gromski, A. B. Henson, J. M. Granda and L. Cronin, Nat. Rev. Chem., 2019, 3, 119–128 CrossRef.
- D. Gadaleta and E. Benfenati, J. Environ. Sci. Health, Part C: Environ. Health Sci., 2021, 39, 269–292 CAS.
- J. Hoja, L. M. Sandonas, B. G. Ernst, A. Vazquez-Mayagoitia, R. A. DiStasio Jr and A. Tkatchenko, Sci. Data, 2021, 8, 1–11 Search PubMed.
- C. J. Cramer, Essentials of computational chemistry: theories and models, John Wiley & Sons, West Sussex, 2013 Search PubMed.
- M. Medved’, M. Stachová, D. Jacquemin, J.-M. André and E. A. Perpete, J. Mol. Struct.: THEOCHEM, 2007, 847, 39–46 CrossRef.
- P. Szabó, S. Góger, J. Charry, M. R. Karimpour, D. V. Fedorov and A. Tkatchenko, Phys. Rev. Lett., 2022, 128, 070602 CrossRef PubMed.
- R. Buckingham, Proc. R. Soc. London, Ser. A, 1937, 160, 94–113 CAS.
- A. Mayer and P.-O. Åstrand, J. Phys. Chem. A, 2008, 112, 1277–1285 CrossRef CAS PubMed.
- A. Tkatchenko, R. A. DiStasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef PubMed.
- A. P. Jones, J. Crain, V. P. Sokhan, T. W. Whitfield and G. J. Martyna, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 144103 CrossRef.
- M. G. Sylvain and I. Csizmadia, Chem. Phys. Lett., 1987, 136, 575–582 CrossRef CAS.
- R. E. Roberts, J. Chem. Phys., 1967, 47, 1873 CrossRef CAS.
- R. G. Pearson, J. Chem. Educ., 1968, 45, 581 CrossRef CAS.
- R. G. Pearson, J. Chem. Educ., 1968, 45, 643 CrossRef CAS.
- T. Brinck, J. S. Murray and P. Politzer, J. Chem. Phys., 1993, 98, 4305–4306 CrossRef CAS.
- P. Politzer, P. Jin and J. S. Murray, J. Chem. Phys., 2002, 117, 8197–8202 CrossRef CAS.
- S. A. Blair and A. J. Thakkar, J. Chem. Phys., 2014, 141, 074306 CrossRef PubMed.
- S. Choudhary, P. Ranjan and T. Chakraborty, J. Chem. Res., 2020, 44, 227–234 CrossRef CAS.
- Y. Yang, K. U. Lao and R. A. DiStasio, Phys. Rev. Lett., 2019, 122, 026001 CrossRef CAS PubMed.
- D. V. Fedorov, M. Sadhukhan, M. Stöhr and A. Tkatchenko, Phys. Rev. Lett., 2018, 121, 183401 CrossRef CAS PubMed.
- A. J. Thakkar, AIP Conf. Proc., 2012, 1504, 586–589 CrossRef CAS.
- A. Gilbert and J. E. Baggott, Essentials of molecular photochemistry, Wiley-Blackwell, Oxford, 1991 Search PubMed.
- J. F. Joung, M. Han, J. Hwang, M. Jeong, D. H. Choi and S. Park, JACS Au, 2021, 1, 427–438 CrossRef CAS PubMed.
- R. B. Woodward, J. Am. Chem. Soc., 1941, 63, 1123–1126 CrossRef CAS.
- D. A. Bahnick, J. Chem. Educ., 1994, 71, 171 CrossRef CAS.
- D. Balcells and B. B. Skjelstad, J. Chem. Inf. Model., 2020, 60, 6135–6146 CrossRef CAS PubMed.
- G. Montavon, M. Rupp, V. Gobre, A. Vazquez-Mayagoitia, K. Hansen, A. Tkatchenko, K.-R. Müller and O. A. Von Lilienfeld, New J. Phys., 2013, 15, 095003 CrossRef CAS.
- J. Wang, M. Yang, G. Wang and J. Zhao, Chem. Phys. Lett., 2003, 367, 448–454 CrossRef CAS.
- H. Alyar, Z. Kantarci, M. Bahat and E. Kasap, J. Mol. Struct., 2007, 834–836, 516–520 CrossRef CAS.
- F. De Proft, P. W. Ayers, S. Fias and P. Geerlings, J. Chem. Phys., 2006, 125, 214101 CrossRef PubMed.
- M. A. F. Afzal, C. Cheng and J. Hachmann, J. Chem. Phys., 2018, 148, 241712 CrossRef PubMed.
- S. S. Zade and M. Bendikov, Org. Lett., 2006, 8, 5243–5246 CrossRef CAS PubMed.
- S. Xu, J. Li, P. Cai, X. Liu, B. Liu and X. Wang, J. Am. Chem. Soc., 2021, 143, 19769–19777 CrossRef CAS PubMed.
- J. L. Brédas, J. P. Calbert, D. A. da Silva Filho and J. Cornil, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5804–5809 CrossRef PubMed.
- D. Yang and D. Ma, Adv. Opt. Mater., 2019, 7, 1800522 CrossRef.
- A. K. Narsaria, J. Poater, C. Fonseca Guerra, A. W. Ehlers, K. Lammertsma and F. M. Bickelhaupt, J. Comput. Chem., 2018, 39, 2690–2696 CrossRef CAS PubMed.
- M. Castellani, S. Winkler, B. Bröker, M. Baumgarten, K. Müllen and N. Koch, Appl. Phys. A: Mater. Sci. Process., 2014, 114, 291–295 CrossRef CAS.
- X. Peng, L. Hu, F. Qin, Y. Zhou and P. K. Chu, Adv. Mater. Interfaces, 2018, 5, 1701404 CrossRef.
- C. Kunkel, C. Schober, J. T. Margraf, K. Reuter and H. Oberhofer, Chem. Mater., 2019, 31, 969–978 CrossRef CAS.
- J. Topping, Proc. R. Soc. London, Ser. A, 1927, 114, 67–72 Search PubMed.
- R. J. Maurer, V. G. Ruiz and A. Tkatchenko, J. Chem. Phys., 2015, 143, 102808 CrossRef PubMed.
- F. Widdascheck, A. A. Hauke and G. Witte, Adv. Funct. Mater., 2019, 29, 1808385 CrossRef.
- S. Naghdi, G. Sanchez-Arriaga and K. Y. Rhee, J. Alloys Compd., 2019, 805, 1117–1134 CrossRef CAS.
- G. Seifert, D. Porezag and T. Frauenheim, Int. J. Quantum Chem., 1996, 58, 185–192 CrossRef CAS.
- A. Ambrosetti, A. M. Reilly, R. A. DiStasio and A. Tkatchenko, J. Chem. Phys., 2014, 140, 18A508 CrossRef PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS.
- D. E. Woon, J. Dunning and H. Thom, J. Chem. Phys., 1994, 100, 2975–2988 CrossRef CAS.
- D. Hait and M. Head-Gordon, Phys. Chem. Chem. Phys., 2018, 20, 19800–19810 RSC.
- L. C. Blum and J.-L. Reymond, J. Am. Chem. Soc., 2009, 131, 8732 CrossRef CAS PubMed.
- M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301 CrossRef PubMed.
- C. Adamo, M. Cossi, G. Scalmani and V. Barone, Chem. Phys. Lett., 1999, 307, 265–271 CrossRef CAS.
- A. L. Hickey and C. N. Rowley, J. Phys. Chem. A, 2014, 118, 3678–3687 CrossRef CAS PubMed.
- N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, J. Cheminf., 2011, 3, 1–14 Search PubMed.
- N. Haider, Molecules, 2010, 15, 5079–5092 CrossRef PubMed.
- szgoger. (2023). szgoger/molpol: Data v1.0 (publication). Zenodo DOI:10.5281/zenodo.7650470.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02256k |
| This journal is © the Owner Societies 2023 |

