 Open Access Article
Open Access ArticleDielectric relaxation of ice in a partially crystallized poly(N-isopropylacrylamide)microgel suspension compared to other partially crystalized polymer–water mixtures†
Balachandar
Vijayakumar
ab,
Masanobu
Takatsuka
c,
Kaito
Sasaki
 de,
Rio
Kita
de,
Rio
Kita
 de,
Naoki
Shinyashiki
de,
Naoki
Shinyashiki
 *de,
Shin
Yagihara
d and
Sampathkumar
Rathnasabapathy
*de,
Shin
Yagihara
d and
Sampathkumar
Rathnasabapathy
 *a
*a
aDepartment of Physics, Sathyabama Institute of Science and Technology, Chennai-600119, India. E-mail: drrskumar@1972@gmail.com
bCentre for Nanoscience and Nanotechnology, Sathyabama Institute of Science and Technology, Chennai-600119, India
cGraduate School of Science and Technology, Tokai University, Kanagawa 259-1292, Japan
dDepartment of Physics, Tokai University, Kanagawa 259-1292, Japan. E-mail: naoki-ko@keyaki.cc.u-tokai.ac.jp
eMicro/Nano Technology Centre, Tokai University, Kanagawa 259-1292, Japan
First published on 11th August 2023
Abstract
A broadband dielectric spectroscopy study was conducted on a partially crystallized 10 wt% poly(N-isopropylacrylamide) [PNIPAM] microgel aqueous suspension to investigate the dielectric relaxation of ice in microgel suspensions. The measurements covered a frequency range of 10 mHz to 10 MHz and at temperatures ranging from 123 K to 273 K. Two distinct relaxation processes were observed at specific frequencies below the melting temperature. One is associated with the combination of the local chain motion of PNIPAM and interfacial polarization in the uncrystallized phase, while another is associated with ice. To understand the temperature-dependent behaviour of the ice relaxation process, the relaxation time of ice was compared with those observed in other frozen polymer water mixtures, including gelatin, poly-vinylpyrrolidone (PVP), and bovine serum albumin (BSA). For concentrations ≥ 10 wt%, the temperature dependence of the relaxation time of ice was found to be independent. Therefore, the study primarily focused on the 10 wt% data for easier comprehension of the ice relaxation process. It was found that the microgel and globular protein BSA had no significant effect on ice crystallization, while gelatin slowed down the crystallization process, and PVP accelerated it. To discuss the mechanism of the dielectric relaxation of ice, the trap-controlled proton transport model developed by Khamzin et al. [Chem. Phys., 2021, 541, 111040.] was employed. The model was used to discuss the dynamic heterogeneity of ice observed in this investigation, distinguishing it from the spatial heterogeneity of ice commonly discussed.
Introduction
Thermoresponsive microgels are colloidal particles composed of a cross-linked polymer network with a characteristic structure consisting of a dense core surrounded by a loose corona1,2 and exhibit volume phase transition (VPT) from a swollen to a collapsed state3 in response to temperature changes. Moreover, the internal architecture of microgels appears to be particularly favorable for successfully confining water molecules and avoiding their crystallization down to very low temperatures.4–6 This is significant for fundamental science7 because it may provide a technique to examine water properties in the so-called no man's land,8 where fascinating phenomena, such as a liquid–liquid critical point,9 should occur but for which no direct evidence exists. In addition, knowing the mechanism that leads to avoided water crystallization is important in biological systems10 for several applications ranging from the food industry11,12 to the preservation of tissues and organs.13 Ice formation during the freezing process can damage cells, tissues, and organs. Ice-inhibiting hydrogels are hydrogels designed to prevent ice crystal formation during freezing. These hydrogels confine the growth of ice crystals within their three-dimensional network and maintain a gradual osmotic shock as cryoprotectant agents permeate into cells. They incorporate ice-binding proteins or antifreeze proteins to inhibit ice growth or recrystallization. These hydrogels protect cells, tissues, and organs from damage caused by large ice crystals during cryopreservation. They can adsorb to ice surfaces, inhibit ice recrystallization, or regulate thermal properties. Certain hydrogels can regulate the thermal properties of the freezing environment, promoting slow and controlled freezing rates. By maintaining a more uniform temperature distribution, these hydrogels help prevent the formation of large ice crystals and minimize cellular damage. Furthermore, the topic of avoided crystallization in confined water is a long-standing problem in the physics of water itself.8,9,14,15 Hence, investigating the high-concentration, low-temperature region of microgel suspensions in order to better understand their interplay with solvent crystallization appears to be quite intriguing. Meanwhile, poly(N-isopropylacrylamide) (PNIPAM) microgels were proposed as a promising simplified model system16 to unravel the complex behavior of globular proteins at fluid interfaces. Hence, there has been a necessity to investigate the dynamics of water in the vicinity of the same at extremely low temperatures.Dielectric relaxation of ice has been extensively studied17–25 and found to have one dielectric loss peak. However, two different temperature dependences of the relaxation time have been observed for ice, as illustrated in Fig. 1. The first type, known as the Auty-type, follows an Arrhenius-type temperature dependence with a constant activation energy in the temperature range of 273–208 K.17 The second type, known as the Johari-type, has different activation energies in three temperature ranges: >240 K (TC1), TC1-170 K (TC2), and <TC2, with corresponding values of 53.2, 18.8, and 46.4 kJ mol−1, respectively.18 The method of ice preparation can control the relaxation times associated with these two types of relaxation. Auty-type ice is obtained through pure-water crystallization while stirring pure water at 265 K, while Johari-type ice is obtained via crystallization by lowering the temperature without stirring.19 It was interpreted that the slow growing speed of ice crystals results in a smaller impurity content of ice, giving rise to a larger relaxation time of ice with the Arrhenius temperature dependence.
 | ||
| Fig. 1 Relaxation time of ice at different temperatures quoted from ref. 17 and 18. | ||
Broadband dielectric spectroscopy (BDS) has been used to investigate the dielectric relaxations of water mixtures with different types and concentrations of solutes at sub-zero temperatures.26–42 At low temperatures, partially crystallized water mixtures exhibit highly complicated complex dielectric spectra due to the nature of ice dielectric relaxation and the intricacy of the mixtures themselves. This complexity arises because the aqueous solutions contain both an ice phase and a concentrated solution phase below the melting temperature of ice. Two categories of water mixtures were studied: partially crystalline and non-crystalline systems. Studies on partially crystallized water mixtures such as polyvinylpyrrolidone (PVP),26–29 gelatin,30,31,34,35 hyaluronic acid37 and globular proteins such as lysozyme38,39 and bovine serum albumin (BSA)32,33,39–41 were conducted using BDS. These mixtures exhibited three distinct dielectric relaxations. One is caused by ice in the ice phase, and the other two are attributed to the uncrystallized water and the combination of hydrated solute molecules and interfacial polarization in the concentrated liquid phase. The partially crystallized BSA–32 and PVP–water mixtures26 exhibited Johari-type ice, while the 10–50 wt% gelatin–water mixtures30 exhibited Auty-type ice. It is important to understand the nature of these complex dielectric spectra as partial crystallization of water can occur during cryopreservation of foods, biological tissues, and living cells. Therefore, gaining a better understanding of the spectra can aid in the preservation of these materials.41
The model based on the temperature dependence of the prevalence of the different types of defect migration described these changes in the temperature dependence of the relaxation time of the Johari-type ice.43–46 The relaxation of ice necessitates the appearance and disappearance of lattice D- and L-defects. The D-defect contains two protons located between the oxygen atoms of two neighboring water molecules, while the L-defect lacks a proton. Bjerrum proposed that these structural defects cause the ice to experience dielectric relaxation.20 The model identified two crossovers, TC1 and TC2, in the temperature dependence of the relaxation time. The temperatures where the activation energy (Ea) varies in Johari-type ice are identified as TC1 and TC2. While TC1 represents a sharp crossover, TC2 is characterized as a smooth transition between two types of Arrhenius with different activation energies (Ea). At high temperatures (T > TC1), the relaxation is driven by the diffusion of L–D orientational defects, while at intermediate temperatures (TC2 < T< TC1), the relaxation mechanism due to the ionic H3O+ and OH− defects begins to dominate.43 At low temperatures (T < TC2), the mobility of orientational defects slowed down, creating blockages for the diffusion of ionic defects,44–46 which leads to an increase in the activation energy below TC2.
We have recently investigated47 the dynamic behavior of the polymer and the water simultaneously across the volume phase transition from the dielectric relaxation spectrum of a 10 wt% PNIPAM non-ionic microgel aqueous suspension in the frequency range of 40 Hz to 50 GHz as a function of temperature ranging from 288 K to 323 K. Two distinct relaxation processes were found, one at low frequency and the other at the high frequency region of the dielectric spectra, and thought to have originated from the local chain motion of PNIPAM and the average relaxation mode of water in both the bulk solution and the microgel, respectively. Furthermore, based on the idea of two kinds of water models, the contributions of each of the two kinds of water, both free water outside the microgel and confined water within the microgel, to the high-frequency relaxation spectrum were evaluated. Despite the extensive research on PNIPAM,48–55 low temperature investigations of PNIPAM dispersions remain mostly unexplored. In this study, we used BDS to investigate the dielectric relaxation of ice of a frozen 10 wt% PNIPAM microgel aqueous suspension and compared it to other frozen polymer–water mixtures such as BSA, gelatin, and PVP of the same concentration in order to understand the mechanism of the temperature dependent dielectric relaxation behavior of ice in such partially crystallized polymer–water mixtures.
Experimental
The microgel of PNIPAM was synthesized through the free radical polymerization method, as outlined in a procedure by Balachandar et al.47 Ultrahigh purity water, with a specific resistance of 18.2 MΩ cm, was produced using a Simplicity UV machine from Merck Millipore and used as the solvent for the microgel. To analyze the behavior of the PNIPAM microgel, a BDS measurement was performed using an Alpha-A analyzer from Novocontrol on an aqueous suspension of 10 wt% of PNIPAM microgel. For the dielectric measurement, parallel gold-plated electrodes of 20 mm in diameter with a geometrical capacitance of C0 = 4.84 ± 0.05 pF and a stray capacitance of Cstray = 2.67 ± 0.07 pF were used. The quatro cryosystem from novocontrol was employed to maintain the temperature of the sample, and the suspension was stabilized for about 20 minutes with temperature changes not exceeding 0.01 K before the BDS measurement. Dielectric measurements were taken at 5 K intervals between 123 and 273 K. The temperature was then raised to the level for the subsequent measurement over the course of 10 minutes and held there for 30 minutes before the next measurement was taken. At each temperature, a dielectric measurement was taken for approximately 25 minutes.Results and discussion
The data presented in Fig. 2 shows the frequency-dependent complex permittivity spectra of a 10 wt% PNIPAM microgel aqueous suspension, measured from 10 mHz to 10 MHz at intervals of every 10 K between 123 K and 273 K during the heating processes. At a temperature of 263 K, the two relaxation processes, labeled process I and process II, are visible as two step-like increases in ε′ in the real part of the complex permittivity with decreasing frequency, and an additional increase in ε′ at lower frequencies, caused by electrode polarization (EP), and in the imaginary part ε′′, the corresponding loss peaks of EP and process II completely overlap, while process I has a loss peak around 5 kHz. These relaxation processes are associated with the relaxation process of ice19,31,41 and the local chain motion of PNIPAM microgel,26,32,42 respectively. As the temperature decreases, these relaxation processes shift to lower frequencies. From temperatures of 243 K down to 193 K, a small relaxation was observed at around 1 MHz where the high frequency tail of the loss peak of the ice process in the imaginary part, which refers to uncrystallized water.26,30,41 However, the loss peak height of this process is lower than 0.2 indicating that the strength of this process is negligible in comparison with process I with a peak height of 40–20 in the entire temperature range measured. Therefore, the small relaxation process of uncrystallized water is not considered for further discussion. | ||
| Fig. 2 Real and imaginary components of the dielectric spectra of the 10 wt% PNIPAM microgel aqueous suspension at intervals of 10 K between 123 K and 273 K. | ||
Curve fitting procedure
The experimental data for the complex permittivity of the 10 wt% PNIPAM microgel aqueous suspension reveal three main relaxation processes: Process I, II, and EP. At temperatures below 183 K, the single loss peak of Process I becomes broader due to multiple ice relaxations.31,41 At 263 K, an intermediate process (Process IIb) is observed between Processes I and II. A curve fitting procedure was employed for all the processes to understand their unique characteristics depending on the temperature. The fitting was done using the simple sum of relaxation processes given by the Cole–Cole equation and dc conductivity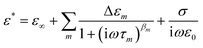 | (1) |
Fig. 4 shows the temperature dependence of the relaxation time, dielectric strength, and symmetric broadening parameter β for the ice processes of A, B, C, and D and Process II in 10 wt% PNIPAM microgel aqueous suspension obtained from the curve fitting procedure using the Cole–Cole equation (1). The dielectric strength of Process II is much larger than that of the other processes, and such large strength suggests that it is not solely due to the local chain motion of PNIPAM. Similar dielectric relaxation processes have been observed in other frozen polymer–water mixtures of PVP,26 BSA32 and gelatin.42 For the PVP–water mixtures, this process was found to be responsible for a local chain motion of PVP and/or a combination of a local chain motion of PVP and interfacial polarization, depending on the PVP concentration. Future studies will investigate the variations upon different concentrations and different cross linked microgels since the present study mainly emphasizes the mechanism of the dielectric relaxation of ice in the 10 wt% PNIPAM microgel aqueous suspension system.
Moving on to Process I, it was observed in Fig. 2 for temperatures ≤ 263 K. Above 263 K, Process I could not be detected, indicating that it is related to the formation of ice in the suspension system. As shown in Fig. 3, Process I consists of multiple relaxation processes of Ice, which are labeled as Ice A, B, C, and D in decreasing order of frequency. Ice B and Ice C contribute to Process I at temperatures ≤ 253 K. The relaxation times of Ice B and C are close and those temperature dependences are the same. Furthermore, the ratio of the strength of these two processes is almost constant and the strength of Ice B is 30–40% of that of Ice C. In addition, we cannot distinguish Ice B from Ice C in dielectric spectra shown in Fig. 2 at 183 K. This means that we need to assume Ice B and C to reproduce the experimental data, but it is impossible to say that there are two processes above 170 K (TC2). At high temperatures above 240 K (TC1), the temperature dependence of the relaxation time of the ice processes follows an Arrhenius behaviour with an activation energy (Ea) of 40–50 kJ mol−1. At TC1, the temperature dependence of the relaxation time changes, and the Ea becomes a smaller value of 15–20 kJ mol−1 in the temperature range between TC1 and TC2. At low temperatures below TC2, Ea shows a larger value of 30–40 kJ mol−1. The clear step or peak of Ice A and Ice D cannot be seen in the dielectric spectra, but these are necessary only at temperatures below TC2. The relaxation time of Ice D is close to that of Ice C and pure ice. The temperature dependence of the relaxation time of Ice D is almost the same as that of Ice C. Therefore, Ice C and D are single relaxation process and Ice D is required to describe the broadening of Ice C. In terms of the dielectric strength of the Ice relaxations, Ice C is the dominant process with larger strength for temperatures ranging from TC1 to TC2. Below TC2, the dominance of Ice C decreases, and the strength of Ice B, D, and A increases. The sum of the strength of the relaxations that make up the multiple ice relaxation increases slightly as the temperature decreases. This feature is similar to the ice relaxations observed in other frozen polymer water mixtures.18,26,32,34
Buratti et al.15 investigated the interaction between water and PNIPAM polymers, including crosslinked microgels and linear polymers, by conducting extensive differential scanning calorimetry (DSC) and dynamic light scattering (DLS) experiments. The DSC results for PNIPAM concentrations higher than 30 wt% in H2O showed two endothermic peaks at 274 K and 268–274 K. This indicated the melting of two distinct types of water, consistent with prior research.56 The peak observed at high temperatures is likely to be associated with the “free water” or bulk-like water, which has a melting point like that of the pure solvent and is relatively unaffected by concentration. In contrast, the peak detected at low temperatures is significantly influenced by the presence of the polymer, and its melting temperature tends to decrease as the concentration of PNIPAM increases, suggesting that it corresponds to crystallizing hydration water. This peak is associated with previously known freezable-bound water.56 These two types of water are present in all the samples studied, regardless of the solvent or polymer architecture. Their study specified the existence of ice with different melting points due to the spatial heterogeneity of water or ice in the aqueous solution. However, it is important to note that this is not the origin of the dynamic heterogeneity of the ice observed in the present investigation. This distinction is both challenging and intriguing.
As Fig. 4 shows, the strength of Ice B increases while that of Ice C decreases with decreasing temperature below TC2. If the dynamic heterogeneity, which includes two relaxations of Ice B and Ice C, is related to spatial heterogeneity, a change in the ratio of “bulk water ice” and “freezable-bound water ice” would be necessary. However, since the ice in the mixture is crystallized, “bulk water ice” cannot transform into “freezable-bound water ice”. Therefore, Ice B and Ice C cannot be attributed to “bulk water ice” and “freezable-bound water ice”. Hence, the dynamic heterogeneity observed in the relaxation of ice can never be interpreted to be related to the spatial heterogeneity presented by Buratti et al.15 or commonly considered.
When considering the relaxation of ice, it is essential to keep the positions of oxygen atoms fixed since ice is a crystal. The difference between “bulk water ice” and “freezable-bound water ice” is based on the local liquid water (or ice) structure, which is determined by the positions of oxygen atoms. However, the position of protons in ice is mobile, and the temperature dependence of the relaxation time of ice in the temperature ranges T > TC1, TC1> T > TC2, and TC2> T is to be interpreted based on the proton transport mechanism.44–46 Therefore, not only the relaxation time of ice but also the strength of ice relaxation must be discussed using the motion of protons, rather than the motion of oxygen atoms.
Below TC2, the strength ratio between Ice B and Ice C varies, whereas it remains constant above TC2. This implies that changes in the relaxation mechanism as a result of thermal fluctuations can influence the strength ratio even in crystal ice. In the temperature range TC1> T > TC2, ionic defects are dominant, resulting in a constant strength ratio of Ice B and Ice C. However, below TC2, the strength of Ice B increases and that of Ice C decreases due to the dominant factor changes to the blockages for the diffusion of ionic defects. The different relaxation times of Ice B and Ice C can be interpreted to be due to the difference in the potential energy depth of the traps, which control proton transport. According to the trap-controlled proton transport model44–46 the deeper potential energy results in a larger relaxation time and a higher activation energy. Based on the model, it can be interpreted that the potential energy depth of the traps related to Ice C is deeper than that of Ice B. The model also predicted that the density of traps would increase as the temperature decreased below TC2.44–46 Upon comparing this prediction to our results, we observed that the increase in the density of traps results in an increase in the strength of the relaxation of Ice B (with a shorter relaxation time) and a decrease in that of Ice C (with a longer relaxation time). This means that the shallower potential depth of the traps which brings about Ice B increases with decreasing temperature. As shown in Fig. 5, the temperature dependence of the strength of the relaxation processes of ice below TC2 depends on the solute molecular structure. The mechanism behind the observed increase in the strength of Ice B with a shorter relaxation time and a decrease in that of Ice C with a longer relaxation time is still in the veil. In order to gain a better understanding of this phenomenon, additional experiments will be necessary.
The temperature dependences of the ice processes observed in the microgel suspension system were compared with that of frozen water mixtures of gel (gelatin), linear polymer (PVP), and globular protein (BSA). Fig. 5 shows the temperature dependence of the dielectric relaxation time and strength of ice processes observed for 10 wt% PNIPAM microgel (present study), PVP,26 BSA,41 and gelatin30 water mixtures and pure ice.17–19 For partially crystallized 10 wt% PNIPAM, PVP, and BSA water mixtures, the temperature dependence of the relaxation time exhibits two or three temperature regions divided by the crossover temperatures at 240 K (TC1) and 170 K (TC2), which are the same as those of the ice relaxation observed for pure ice by Johari et al.18 and Sasaki et al.19 On the other hand, the temperature dependence of the relaxation time of ice observed in the partially crystallized 10 wt% gelatin water mixture was monotonic similar to that of the Auty type. Above TC2, two ice relaxation processes are necessary for reproducing the dielectric spectra of frozen PNIPAM and BSA water mixtures as shown in Fig. 3 at 183 K in this paper and Fig. 4 at 183 K in ref. 41 whereas the PVP and gelatin systems show only one relaxation process. This means that the ice process above TC2 is broad in the BSA and PNIPAM water mixtures.
The trap-controlled proton transport model44–46 explained the dominance of different relaxation processes observed in ice in the three different temperature regions. The presence of orientational defects at high temperatures (>TC1), ionic defects at intermediate temperatures (TC1 to TC2) and multiple traps at low temperatures (<TC2) are the main reasons for ice relaxations. According to this model, the ice relaxations in BSA and PNIPAM water mixtures have a large slope in the temperature dependence of relaxation time solely caused by the orientational defects at high temperatures (>TC1). At intermediate temperatures (TC1 > T > TC2), the temperature dependence of the relaxation time is smaller than that above TC1 because of the increase in the domination of ionic defects rather than the orientational defects. In contrast, the relaxation time of ice in PVP water mixtures shows a small slope in temperature dependence for T > TC2 even above TC1, because of the more domination of ionic defects, i.e., the relaxation time of the ice caused by ionic defects is faster than that caused by the orientational defects even above TC1. Furthermore, the relaxation times of the ice process are two orders of magnitude smaller in the PVP–water mixture and one order of magnitude smaller in the BSA and PNIPAM water mixtures than that of pure ice at temperatures below TC1 and above TC2. At temperatures (<TC2), the process of proton capture into traps begins to dominate, and the ionic relaxation mechanism weakens, resulting in a large slope in the temperature dependent relaxation time. Below TC2, the distribution of relaxation time of the ice relaxation in the BSA, PNIPAM and PVP water mixtures varies from 1 to 4 orders of magnitude. The wide distribution of apparent activation energy for the process of proton capture into traps can be attributed to variations in ice conditions within the mixtures. However, ice relaxation of gelatin water mixtures has a large slope in the temperature dependent relaxation time with more domination of the orientational defects.
It was reported that the Auty-type temperature dependent relaxation time of ice was obtained through pure–water crystallization while stirring pure water at 265 K.19 This result was interpreted as that the slower growth speed of ice excludes impurities and gives rise to a larger relaxation time of ice. The variation of the temperature dependence of relaxation time in the water mixtures of 10 wt% PNIPAM microgel, PVP, BSA, and gelatin can be interpreted consistently with ref. 19. The formation of ice in the microgel or globular protein BSA water mixtures is more closely related to the behavior of pure ice reported by Johari et al.18 and Sasaki et al.,19i.e., the presence of microgel or globular protein does not affect the relaxation time of ice significantly. This indicates that the presence of microgels or globular proteins does not appear to have a significant effect on the growth speed of ice crystallization likely due to their reduced exposure to water as a result of their condensed density in the mixtures. In contrast, gelatin may slow down the ice crystallization speed in the mixtures by creating a gel network, resulting in ice with less impurity-induced orientational defects. On the contrary, PVP seems to accelerate the growth speed of ice crystallization in the mixtures, leading to a higher concentration of impurities with ionic defects, and this causes a smaller relaxation time of ice. In summary, while PNIPAM microgels and BSA may not have a significant effect on thermal properties or controlled freezing rates, gelatin has the potential to regulate the freezing environment and promote slow freezing rates. PVP, on the other hand, can accelerate ice crystallization and may not contribute to the desired thermal properties for controlled freezing.
Conclusions
Broadband dielectric spectroscopy measurements were performed on a 10 wt% PNIPAM microgel aqueous suspension, which was partially crystallized, at frequencies ranging from 10 mHz to 10 MHz and temperatures ranging from 123–273 K. Two prominent relaxation processes were identified, Process I and Process II, at two distinct frequencies and process II was attributed to the combination of local chain motion of PNIPAM and interfacial polarization in the uncrystallized phase, while process I contributed to the relaxation of ice in the partially crystallized PNIPAM aqueous suspension. The temperature dependence of the relaxation time and strength of the ice relaxations suggests the presence of different environments of ice with different activation energies associated with different temperature ranges. The suspension system containing partially crystallized PNIPAM microgel exhibits four types of ice relaxation. The difference between the spatial heterogeneity of ice present in the Buratti et al., study15 and the dynamic heterogeneity of the ice observed in this work was clarified based on the trap-controlled proton transport model. The reason for the variation in the strength ratio between Ice B and Ice C below TC2 remains unclear. However, additional experimental results of various concentrations and solute structures of water mixtures using the model are expected to clarify this issue.The temperature dependence of the ice process observed in this system was compared to that of other frozen polymer water mixtures, including partially crystallized water mixtures with gelatin, PVP, and BSA. The trap-controlled proton transport model is used to explain the temperature-dependent dielectric relaxation behavior of ice in partially crystallized polymer water mixtures. The study found that the presence of microgel or globular protein does not have a significant impact on the structure of growing ice crystals due to their condensed density in the mixtures. In contrast, gelatin can slow down ice crystallization by creating a gel network, which results in fewer impurity-induced orientational defects. Conversely, PVP appears to accelerate ice crystal growth, resulting in a higher concentration of impurities with ionic defects. Overall, the study provides insights into the dielectric relaxation behavior of ice in the presence of microgel and other polymers. The findings suggest that the presence of these polymers can affect the relaxation behavior of ice in different ways depending on the type of polymer. This study has important implications for understanding the interaction of water and solute molecules and properties of ice in complex systems, such as biological tissues and frozen food products, which are maintained in subzero temperatures.
Author contributions
RK, NS, SY, and RS perceived and planned the research. VB and MT performed the dielectric experiments. VB and NS visualized and analyzed the data. VB, RS and NS wrote the manuscript. RK, KS and SY have contributed to its evolution to the final form. NS and RS supervised the work.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Grant-in-Aid for Scientific Research KAKENHI (22K03559). VB thanks the management of Sathyabama Institute of Science and Technology, Chennai for providing financial support.References
- A. Fernandez-Nieves, H. M. Wyss, J. Mattsson and D. A. Weitz, Microgel Suspensions: Fundamentals and Applications, Wiley-VCH, 2011 Search PubMed.
- M. Stieger, W. Richtering, J. S. Pedersen and P. Lindner, Small-angle neutron scattering study of structural changes in temperature sensitive microgel colloids, J. Chem. Phys., 2004, 120, 6197–6206 CrossRef CAS PubMed.
- R. Pelton, Poly(N-isopropylacrylamide) (PNIPAM) is never hydrophobic, J. Colloid Interface Sci., 2010, 348, 673–674 CrossRef CAS PubMed.
- F. Afroze, E. Nies and H. Berghmans, Phase transitions in the system poly(N-isopropylacrylamide)/water and swelling behaviour of the corresponding networks, J. Mol. Struct., 2000, 554, 55–68 CrossRef CAS.
- K. Van Durme, G. Van Assche and B. Van Mele, Kinetics of demixing and remixing in poly(N-isopropylacrylamide)/water studied by modulated temperature DSC, Macromolecules, 2004, 37, 9596–9605 CrossRef CAS.
- M. Zanatta, L. Tavagnacco, E. Buratti, M. Bertoldo, F. Natali, E. Chiessi, A. Orecchini and E. Zaccarelli, Evidence of a low-temperature dynamical transition in concentrated microgels, Sci. Adv., 2018, 4(9) DOI:10.1126/sciadv.aat5895.
- E. I. Tiktopulo, V. N. Uversky, V. B. Lushchik, S. I. Klenin, V. E. Bychkova and O. B. Ptitsyn, “Domain” Coil–Globule Transition in Homopolymers, Macromolecules, 1995, 28, 7519–7524 CrossRef CAS.
- O. Mishima and H. E. Stanley, Nature, 1998, 396, 329–335 CrossRef CAS.
- P. G. Debenedetti, F. Sciortino and G. H. Zerze, Second critical point in two realistic models of water, Science, 1979, 2020(369), 289–292 Search PubMed.
- C. A. Knight, Nature, 2000, 406, 249–251 CrossRef CAS PubMed.
- H. Kiani and D. W. Sun, Trends Food Sci. Technol., 2011, 22, 407–426 CrossRef CAS.
- T. Kang, Y. You and S. Jun, Food Sci. Biotechnol., 2020, 29, 303–321 CrossRef PubMed.
- R. P. Tas, V. Sampaio-Pinto, T. Wennekes, L. W. van Laake and I. K. Voets, From the freezer to the clinic, EMBO Rep., 2021, 22(3) DOI:10.15252/embr.202052162.
- P. Gallo, J. Bachler, L. E. Bove, R. Böhmer, G. Camisasca, L. E. Coronas, H. R. Corti, I. de Almeida Ribeiro, M. de Koning, G. Franzese, V. Fuentes-Landete, C. Gainaru, T. Loerting, J. M. M. de Oca, P. H. Poole, M. Rovere, F. Sciortino, C. M. Tonauer and G. A. Appignanesi, Eur. Phys. J. E: Soft Matter Biol. Phys., 2021, 44 Search PubMed.
- E. Buratti, L. Tavagnacco, M. Zanatta, E. Chiessi, S. Buoso, S. Franco, B. Ruzicka, R. Angelini, A. Orecchini, M. Bertoldo and E. Zaccarelli, The role of polymer structure on water confinement in poly(N-isopropylacrylamide) dispersions, J. Mol. Liq., 2022, 355, 118924 CrossRef CAS.
- N. Nussbaum, J. Bergfreund, J. Vialetto, L. Isa and P. Fischer, Microgels as globular protein model systems, Colloids Surf., B, 2022, 217, 112595 CrossRef CAS PubMed.
- R. P. Auty and R. H. Cole, Dielectric properties of ice and solid D2O, J. Chem. Phys., 1952, 20, 1309–1314 CrossRef CAS.
- G. P. Johari and E. Whalley, The dielectric properties of ice lh in the range 272-133 K, J. Chem. Phys., 1981, 75, 1333–1340 CrossRef CAS.
- K. Sasaki, R. Kita, N. Shinyashiki and S. Yagihara, Dielectric Relaxation Time of Ice-Ih with Different Preparation, J. Phys. Chem. B, 2016, 120, 3950–3953 CrossRef CAS PubMed.
- N. Bjerrum, Science, 1979, 1952(115), 385–390 Search PubMed.
- S. Kawada, R. G. Jin and M. Abo, Dielectric properties and 110 K anomalies in KOH- and HCl-doped ice single crystals, J. Phys. Chem. B, 1997, 101, 6223–6225 CrossRef CAS.
- O. Wörz and R. H. Cole, Dielectric properties of ice I, J. Chem. Phys., 1969, 51, 1546–1551 CrossRef.
- S. R. Gough and D. W. Davidson, Dielectric Behavior of Cubic and Hexagonal Ices at Low Temperatures, J. Chem. Phys., 1970, 52, 5442–5449 CrossRef CAS.
- S. Kawada, Dielectric Anisotropy in Ice Ih, J. Phys. Soc. Jpn., 1978, 44, 1881–1886 CrossRef CAS.
- G. P. Johari and S. J. Jones, The Orientation Polarization in Hexagonal Ice Parallel and Perpendicular to the c -axis, J. Glaciol., 1978, 21, 259–276 CrossRef CAS.
- M. Fujii, K. Sasaki, Y. Matsui, S. Inoue, R. Kita, N. Shinyashiki and S. Yagihara, Dynamics of Uncrystallized Water, Ice, and Hydrated Polymer in Partially Crystallized Poly(vinylpyrrolidone)-Water Mixtures, J. Phys. Chem. B, 2020, 124, 1521–1530 CrossRef CAS PubMed.
- S. Cerveny, S. Ouchiar, G. A. Schwartz, A. Alegria and J. Colmenero, Water dynamics in poly(vinyl pyrrolidone)-water solution before and after isothermal crystallization, J. Non-Cryst. Solids, 2010, 356, 3037–3041 CrossRef CAS.
- N. Shinyashiki, M. Shimomura, T. Ushiyama, T. Miyagawa and S. Yagihara, Dynamics of water in partially crystallized polymer/water mixtures studied by dielectric spectroscopy, J. Phys. Chem. B, 2007, 111, 10079–10087 CrossRef CAS PubMed.
- N. Shinyashiki, Y. Matsumura, N. Miura, S. Yagihara and S. Mashimo, Dielectric study of water structure in polymer solution, 1994, vol. 98.
- K. Sasaki, A. Panagopoulou, R. Kita, N. Shinyashiki, S. Yagihara, A. Kyritsis and P. Pissis, Dynamics of uncrystallized water, ice, and hydrated protein in partially crystallized gelatin-water mixtures studied by broadband dielectric spectroscopy, J. Phys. Chem. B, 2017, 121, 265–272 CrossRef CAS PubMed.
- T. Yasuda, K. Sasaki, R. Kita, N. Shinyashiki and S. Yagihara, Dielectric Relaxation of Ice in Gelatin-Water Mixtures, J. Phys. Chem. B, 2017, 121, 2896–2901 CrossRef CAS PubMed.
- N. Shinyashiki, W. Yamamoto, A. Yokoyama, T. Yoshinari, S. Yagihara, R. Kita, K. L. Ngai and S. Capaccioli, Glass Transitions in Aqueous Solutions of Protein (Bovine Serum Albumin), J. Phys. Chem. B, 2009, 113, 14448–14456 CrossRef CAS PubMed.
- A. Panagopoulou, A. Kyritsis, N. Shinyashiki and P. Pissis, Protein and water dynamics in bovine serum albumin-water mixtures over wide ranges of composition, J. Phys. Chem. B, 2012, 116, 4593–4602 CrossRef CAS PubMed.
- K. Sasaki, R. Kita, N. Shinyashiki and S. Yagihara, Glass transition of partially crystallized gelatin-water mixtures studied by broadband dielectric spectroscopy, J. Chem. Phys., 2014, 140(12), 124506 CrossRef PubMed.
- K. Sasaki, I. Popov and Y. Feldman, Water in the hydrated protein powders: Dynamic and structure, J. Chem. Phys., 2019, 150(20), 204504 CrossRef PubMed.
- M. Nakanishi and A. P. Sokolov, Protein dynamics in a broad frequency range: Dielectric spectroscopy studies, J. Non-Cryst. Solids, 2015, 407, 478–485 CrossRef CAS.
- S. Kripotou, K. Zafeiris, M. Culebras-Martínez, G. Gallego Ferrer and A. Kyritsis, Dynamics of hydration water in gelatin and hyaluronic acid hydrogels, Eur. Phys. J. E: Soft Matter Biol. Phys., 2019, 42 DOI:10.1140/epje/i2019-11871-2.
- A. Panagopoulou, A. Kyritsis, A. M. Aravantinou, D. Nanopoulos, R. S. I. Serra, J. L. Gómez Ribelles, N. Shinyashiki and P. Pissis, Glass Transition and Dynamics in Lysozyme-Water Mixtures Over Wide Ranges of Composition, Food Biophys., 2011, 6, 199–209 CrossRef.
- A. Kyritsis, A. Panagopoulou, P. Pissis, R. S. I. Serra, J. L. Gómez Ribelles and N. Shinyashiki, Water and protein dynamics in protein-water mixtures over wide range of composition, IEEE Trans. Dielectr. Electr. Insul., 2012, 19, 1239–1246 CAS.
- A. Panagopoulou, A. Kyritsis, R. Sabater, I. Serra, J. L. Gómez Ribelles, N. Shinyashiki and P. Pissis, Glass transition and dynamics in BSA-water mixtures over wide ranges of composition studied by thermal and dielectric techniques, Biochim. Biophys. Acta, Proteins Proteomics, 2011, 1814, 1984–1996 CrossRef CAS PubMed.
- T. Tsukahara, K. Sasaki, R. Kita and N. Shinyashiki, Dielectric relaxations of ice and uncrystallized water in partially crystallized bovine serum albumin-water mixtures, Phys. Chem. Chem. Phys., 2022, 24, 5803–5812 RSC.
- K. Sasaki, A. Panagopoulou, M. Miyara, K. Fujita, W. Yamamoto, P. Pissis, A. Kyritsis, R. Kita, N. Shinyashiki and S. Yagihara, AIP Conf. Proc., 2013, 1518, 288–291 CrossRef CAS.
- I. Popov, A. Puzenko, A. Khamzin and Y. Feldman, The dynamic crossover in dielectric relaxation behavior of ice Ih, Phys. Chem. Chem. Phys., 2015, 17, 1489–1497 RSC.
- I. Popov, I. Lunev, A. Khamzin, A. Greenbaum, Y. Gusev and Y. Feldman, The low-temperature dynamic crossover in the dielectric relaxation of ice Ih, Phys. Chem. Chem. Phys., 2017, 19, 28610–28620 RSC.
- A. A. Khamzin and A. I. Nasybullin, Trap-controlled proton hopping: interpretation of low-temperature dielectric relaxation of ice Ih, Phys. Chem. Chem. Phys., 2018, 20, 23142–23150 RSC.
- A. A. Khamzin, A. I. Nasybullin and A. S. Nikitin, Theoretical description of dielectric relaxation of ice with low concentration impurities, Chem. Phys., 2021, 541, 111040 CrossRef CAS.
- B. Vijayakumar, M. Takatsuka, R. Kita, N. Shinyashiki, S. Yagihara and S. Rathinasabapathy, Dynamics of the Poly(N-Isopropylacrylamide) Microgel Aqueous Suspension Investigated by Dielectric Relaxation Spectroscopy, Macromolecules, 2022, 55, 1218–1229 CrossRef CAS.
- K. Yanase, R. Buchner and T. Sato, Microscopic insights into the phase transition of poly(N-isopropylacrylamide) in aqueous media: Effects of molecular weight and polymer concentration, J. Mol. Liq., 2015, 302, 112025 CrossRef.
- M. Füllbrandt, E. Ermilova, A. Asadujjaman, R. Hölzel, F. F. Bier, R. Von Klitzing and A. Schönhals, Dynamics of linear poly(N -isopropylacrylamide) in water around the phase transition investigated by dielectric relaxation spectroscopy, J. Phys. Chem. B, 2014, 118(13), 3750–3759 CrossRef PubMed.
- S. Nakano, Y. Sato, R. Kita, N. Shinyashiki, S. Yagihara, S. Sudo and M. Yoneyama, Molecular dynamics of poly(N-isopropylacrylamide) in protic and aprotic solvents studied by dielectric relaxation spectroscopy, J. Phys. Chem. B, 2012, 116, 775–781 CrossRef CAS PubMed.
- M. Yang, C. Liu and K. Zhao, Concentration dependent phase behavior and collapse dynamics of PNIPAM microgel by dielectric relaxation, Phys. Chem. Chem. Phys., 2017, 19, 15433–15443 RSC.
- W. Su, M. Yang, K. Zhao and T. Ngai, Influence of Charged Groups on the Structure of Microgel and Volume Phase Transition by Dielectric Analysis, Macromolecules, 2016, 49, 7997–8008 CrossRef CAS.
- M. Yang, W. Su and K. Zhao, Quantification of solvent water and hydration dynamic of thermo-sensitive microgel by dielectric spectroscopy, J. Polym. Sci., Part B: Polym. Phys., 2017, 55, 1859–1864 CrossRef CAS.
- P. S. Mohanty, S. Nöjd, M. J. Bergman, G. Nägele, S. Arrese-Igor, A. Alegria, R. Roa, P. Schurtenberger and J. K. G. Dhont, Dielectric spectroscopy of ionic microgel suspensions, Soft Matter, 2016, 12, 9705–9727 RSC.
- I. Dueramae, T. Ishiyama, A. Torigaki, S. Nakano, K. Sasaki, R. Kita, N. Shinyashiki, S. Yagihara, Y. Katsumoto and M. Yoneyama, Separation of Micro-Brownian Motion and Side-group Rotational Motion for Poly(N-isopropylacrylamide) in 1,4-Dioxane Studied by Dielectric Relaxation Spectroscopy, Macromolecules, 2023, 56, 4041–4048 CrossRef CAS.
- Z. H. Ping, Q. T. Nguyen, S. M. Chen, J. Q. Zhou and Y. D. Ding, States of water in different hydrophilic polymers – DSC and FTIR studies, Polymer (Guildf), 2001, 42, 8461–8467 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02116e |
| This journal is © the Owner Societies 2023 |



