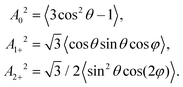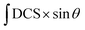Imaging rotational energy transfer: comparative stereodynamics in CO + N₂ and CO + CO inelastic scattering

Abstract

State-to-state rotational energy transfer in collisions of ground ro-vibrational state ¹³CO molecules with N₂ molecules has been studied using the crossed molecular beam method under kinematically equivalent conditions used for ¹³CO + CO rotationally inelastic scattering described in a previously published report (Sun et al., Science, 2020, 369, 307–309). The collisionally excited ¹³CO molecule products are detected by the same (1 + 1′ + 1′′) VUV (Vacuum Ultra-Violet) resonance enhanced multiphoton ionization scheme coupled with velocity map ion imaging. We present differential cross sections and scattering angle resolved rotational angular momentum alignment moments extracted from experimentally measured ¹³CO + N₂ scattering images and compare them with theoretical predictions from quasi-classical trajectories (QCT) on a newly calculated ¹³CO–N₂ potential energy surface (PES). Good agreement between experiment and theory is found, which confirms the accuracy of the ¹³CO–N₂ potential energy surface for the 1460 cm⁻¹ collision energy studied by experiment. Experimental results for ¹³CO + N₂ are compared with those for ¹³CO + CO collisions. The angle-resolved product rotational angular momentum alignment moments for the two scattering systems are very similar, which indicates that the collision induced alignment dynamics observed for both systems are dominated by a hard-shell nature. However, compared to the ¹³CO + CO measurements, the primary rainbow maximum in the DCSs for ¹³CO + N₂ is peaked consistently at more backward scattering angles and the secondary maximum becomes much less obvious, implying that the ¹³CO–N₂ PES is less anisotropic. In addition, a forward scattering component with high rotational excitation seen for ¹³CO + CO does not appear for ¹³CO–N₂ in the experiment and is not predicted by QCT theory. Some of these differences in collision dynamics behaviour can be predicted by a comparison between the properties of the PESs for the two systems. More specific behaviour is also predicted from analysis of the dependence on the relative collision geometry of ¹³CO + N₂ trajectories compared to ¹³CO + CO trajectories, which shows the special ‘do-si-do’ pathway invoked for ¹³CO + CO is not effective for ¹³CO + N₂ collisions.

---

1. Introduction

As an omnipresent gas phase molecular process, rotational energy transfer (RET) is of great interest and the subject of extensive investigations in various fields such as atmospheric, astrophysical, and combustion chemistry. Many collision systems involving small molecules have been studied in detail by experiment and theory, particularly for the NO and OH radicals, in both their ground and excited electronic states.^1,2 The essence of understanding any collision is to determine how the reagents with specific initial conditions transform into specific products. By defining the initial pre-collision conditions such as the collision energy and the internal quantum states of the molecules, the scalar and vector properties of the products after collision can be measured experimentally. Theoretically, the collisional dynamics are predicted by performing quantum or quasi-classical calculations over potential energy surfaces (PESs) of the collision complex, which describe the underlying interaction between the two collision partners. Comparisons of experimental measurements with theoretical predictions can thus test the quality of scattering theory and of potential energy surfaces, and help create and improve empirical models and approximations.

Compared to the more averaged scalar measurements such as collision rate coefficients and integral cross sections, stereodynamic measurements, especially state-to-state differential cross sections (DCSs) and/or scattering angle-resolved rotational angular momentum polarization, have proven particularly useful in providing rigorous tests of state-of-the-art theory.³ The last few decades have witnessed tremendous progress in the field of experimental study of stereodynamics in rotationally inelastic scattering; this was significantly driven by the development of the velocity map imaging (VMI)⁴ technique and its application to crossed molecular beam (CMB) experiments. The power of the CMB-VMI approach is derived from the ability to directly image the velocity vectors of scattered products independently of their position of formation onto a position-sensitive detector, thereby probing all product recoil angles simultaneously, i.e., pure angular distributions can be measured. In combination with laser-based state-selective spectroscopic probe methods (mainly resonance enhanced multiphoton ionization, (REMPI), the VMI technique yields an image that fully describes the scattering event, with the size of the image reflecting the recoil speed of scattered products into a specified channel as well as the angular distribution, yielding the state-resolved differential cross section (DCS). In addition, with appropriate choice of the REMPI spectroscopic transition and good control of the polarization of the probe laser (linearly or circularly polarized), measurement of state-to-state scattering angle-resolved rotational angular momentum alignment and orientation has become possible.^5,6 The most extensive work using the CMB-VMI approach has been performed on inelastic scattering of NO with Rare gas (abbreviated Rg) atoms by the groups of Stolte, van de Meerakker, Chandler, Brouard, and Costen.^7–17 Fully rotational state and fine-structure resolved state-to-state DCSs have been measured initially for NO(X) + Rg collision systems using hexapole state-selection for NO(X) preparation.¹² Instead of using only a hexapole filter, the group of van de Meerakker successfully utilized Stark deceleration, which manipulates neutral polar molecules based on the Stark effect to generate a compact packet of NO(X) radicals with (almost) perfect quantum state purity and very well-controlled velocity before collision. The combination of Stark deceleration and VMI detection significantly enhances the resolution of scattering images and allowed direct observation of quantum diffraction oscillations in state-to-state DCSs for inelastic scattering between Stark decelerator-selected NO(X) and He, Ne, Ar atoms.¹⁶ With the advantage of the continuous tunability of the desired velocity offered by Stark deceleration, they also pushed the collision energy of NO(X) + He collision system firstly down to the ∼20 K regime and recently to the <1 K regime,¹⁸ and gained new insight into the PESs by probing scattering resonances in the state-to-state and parity-resolved DCSs.^8,19 Imaging studies of collision-induced angular momentum polarization in NO(X) + Ar were pioneered by Chandler and Cline,^5,9 followed by Brouard and co-workers both experimentally with improved resolution⁷ and theoretically by means of various calculations.¹¹ Brouard et al. also extended detailed investigations on angular momentum polarization effects to inelastic scattering of NO(X) with other rare gas atoms such as Ne, Kr.^6,10,14 Recently, imaging of the inelastic scattering of electronically excited NO with various collision partners has been studied by Costen and co-workers, including measurements of differential cross sections and collision-induced alignment.^15,17,20

Most of the previous inelastic scattering studies have concentrated on molecule-atom inelastic scattering stereodynamics. This is because of experimental convenience and the availability of fully quantum theory. However, there are a limited number of environments where collisions between molecules and rare gas atoms are of importance in practice. By contrast, advanced studies of bimolecular inelastic scattering are much less common, and little is known about stereodynamics arising when two molecules approach each other. A molecular collision partner possesses internal degrees of freedom that allow the possibility to induce excitation of both partners (and also de-excitation of a reactant molecule that has initial rotational or vibrational population) in a scattering event. In the case of diatom-diatom inelastic scattering process, both partners may become rotationally excited after collision. Full characterization of this effect yields the so-called product-pair correlations, which provide great challenges for theory as well as experiment. Theoretically, the dimension of the PES required to describe the interaction of bimolecular collision system is increased, bringing about considerably more complexity for a numerically exact treatment, especially when the collision energy is larger than ∼700 cm⁻¹. On the experimental side, it is very challenging to prepare pure initial state molecular beams for both molecular beam sources, and it is difficult to probe correlations between two products simultaneously at the detection stage. Study of identical molecule scattering, as in our recent paper²¹ on ¹²CO + ¹³CO, is even more demanding due to the need for isotope selective REMPI. In the case of velocity map ion imaging detection used in the current work, imaging the product(s) with a specific final state result in a projection of multiple concentric Newton rings arising from excitation to a range of rotational energy levels of the molecular collision partner(s), which may overlap each other partially or fully on the detector. Up until now, only limited experimental data is available on bimolecular inelastic scattering systems and most cases studied have been collisions with H₂ or its isotopologue D₂ as the molecular colliders, such as NO(X) + (ortho-)D₂,^22–25 NO(X) + (para-)H₂,²⁴ NO(A) + D₂,²⁶ O₂ + H₂,^27,28 H₂O + H₂,²⁹ ND₃ + H₂,³⁰ CD₃ + H₂ and D₂.³¹ The choice of H₂ and D₂ as the partner molecule is favourable in that they possess relatively large rotational energy spacing and in addition their ortho or para symmetry will be conserved during collision. Jointly, these conditions, in principle, allow restriction of the number of open pair-correlated product channels and thereby simplify the complexity of both experiment and theory. Rotational excitation of H₂ or D₂ is usually not observed at the lower collision energy in the experiments mentioned above. By contrast, rotational excitation of HD (which has no ortho–para restrictions) in collision with NO at 220 cm⁻¹ collision energy has been observed,³² as discussed later in this section. Other than H₂/D₂, molecular nitrogen has been previously used as a collider in studies of inelastic scattering of diatomic and polyatomic molecules. Orr-Ewing and co-workers investigated the inelastic scattering of CD₃ with N₂ in comparison to Ar as collider; they observed evidence in the image for scattered CD₃ products with coincident rotational excitation of the unobserved N₂, but no further attempt was performed to analyse the product-pair correlation information in DCSs.³³ The group of Costen studied the state-to-state rotational energy transfer for collisions of electronically excited NO(A) with N₂ and showed that it is possible to extract stereodynamics information as a function of correlated internal energy in the products but only for coarse-grained amounts of energy transfer to N₂ rotation.³⁴ In the recent study mentioned above,³² correlated rotational excitation of NO–CO pairs at 220 cm⁻¹ collision energy was also reported.

Carbon monoxide (CO) is another benchmark molecule, along with NO, for inelastic scattering stereodynamics study in the gas-phase. As the second most abundant molecule in the universe after molecular hydrogen, CO is of extremely high astrochemical and astrophysical relevance. It is commonly used as a tracer to extract astrophysical parameters of the interstellar medium (ISM) when local thermodynamic equilibrium (LTE) can be assumed; while in the environment where the LTE approximation breaks down, successful molecular modelling of the observed CO spectra is based on accurate collision rate coefficients of CO calculated from theory, the quality of which must be tested by experiment in laboratory. Alignment-free DCSs and/or polarization dependent (PD)DCS measurements for inelastic scattering processes involving CO are shown here to offer excellent tests for theoretical calculations. In our latest study of imaging rotational energy transfer in the ¹³CO + CO system,²¹ we have shown that under the right experimental conditions velocity map imaging (VMI) can be applied to study the state-to-state inelastic scattering of identical molecules using crossed-molecular-beam methods. Polarisation dependent images for scattered ¹³CO with CO were measured experimentally and the extracted pair-correlated DCSs were compared with predictions using quasi-classical scattering theory as well as close-coupling quantum mechanical theory; new effects regarding energy partitioning and propensity rules arising with the product pair correlation have been revealed for this bimolecular collision process. The good agreement between experiment and QCT theory along with close-coupled quantum mechanics (CC QM) for the ¹³CO + CO system confirmed the reliability of the experimental approach. The most striking result of ref. 21, revealed by QCT, was the concerted face-to-face/rotation/back-to-back or ‘do-si-do’ motion taken by colliding partners which end in the same high rotational final states without changing their initial direction, i.e., exhibiting strongly forward scattering. This only occurred when the initial orientation of each molecule was such that the carbon atoms collided first, where a significant 10–20% of the collisions met this criterion. As pointed out in ref. 21, forward scattering in the CO–CO system is due to an attractive force acting after a hard repulsive collision that rotates the pair of product molecules during their separation. This concept will be further evaluated for the kinematically equivalent ¹³CO–¹²CO and ¹³CO–N₂ collisions in this paper where we now extend our CMB-VMI experimental approach to study the stereodynamics of state-to-state inelastic scattering of ¹³CO with N₂ instead of CO as the collision partner. Collisions of ¹³CO with CO and N₂ molecules appear particularly intriguing in that both collision partners have the same mass and similar chemical properties. Using the same settings for experimental conditions of molecular beams and of collision geometry, the two colliding systems will yield identical collision energies, thus identical kinematic conditions. CO and N₂ are thus in this case rather similar collision partners for the primary ¹³CO molecule, and similar collision behaviour and cross sections may be expected at first glance. Deeper insight into the dynamics for these colliding systems could be gained by observing subtle differences in their collision behaviour and cross sections. In the current report, we present and discuss the complete measurements of DCSs and alignment moments for ¹³CO + N₂ system in comparison to the full set of ¹³CO + CO data measured previously, and draw some general conclusions about the dynamics of rotational energy transfer in these kinematically equivalent colliding systems.

2. Methods

2.1 Experimental method

The CMB-VMI experimental apparatus has been described at length in ref. 21, so only the most relevant details are mentioned here. Two supersonically cooled molecular beams produced from two Nijmegen pulsed valves (NPVs)³⁵ intersected at the centre of a differentially pumped scattering chamber. Molecular beam source conditions for the ¹³CO + N₂ experiment were set the same as those of the ¹³CO + CO experiment in order to achieve nearly equivalent collision energies. A molecular beam of 5% ¹³CO seeded in Ar was formed from NPV₁ with a stagnation pressure of 1.2 bar, acting as the primary beam. The isotopologue ¹³CO was used in ¹³CO + CO scattering in order to distinguish the scattered molecular products and for ¹³CO + N₂ for a direct comparison of equal mass number ¹²C¹⁶O and ¹⁴N₂. The secondary beam was generated by the same type of pulsed valve (NPV₂) with a mixture of N₂/He of the same concentration at the same backing pressure just as the secondary molecular beam containing CO/He used previously. Both valves operated at 10 Hz and the pulse duration at the scattering center was about 50 μs. After separately being skimmed through a 1.5 mm diameter skimmer placed 3 cm downstream from the nozzle of the valve, the two molecular beams crossed each other at an estimated crossing volume of 3 × 3 × 3 mm³ with a collision angle of 70°. Using product imaging, the distance (in pixels) from the mean position of the beamspot from the ionization center, defined as the zero lab-frame velocity in the plane of the detector was measured along with the mean speeds of the molecular beams: v(¹³CO/Ar) ≈ 670 m s⁻¹, v(N₂/He) ≈ 1,660 m s⁻¹, jointly resulting in a mean collision energy of 1460 cm⁻¹ for the ¹³CO + N₂ colliding system, which is the same as that for the ¹³CO + CO system. Comparison between REMPI spectra measured for the primary beam and the corresponding simulation from Pgopher³⁶ software indicated that the rotational temperature of the rotationally cooled ¹³CO/Ar molecular beam was less than 1.5 K, giving a predominant population of ¹³CO molecules in the lowest rotational state j = 0 (more than 90%). However, this situation is different for the nitrogen molecule. ¹⁴N atom has a nuclear spin of I = 1, and the nuclear spin statistics lead to a ratio of 2 : 1 for the ortho¹⁴N₂: para¹⁴N₂ for the rotational states, where even j corresponds to ortho and odd j to para. After the rotational cooling during adiabatic expansion of the molecular beam, N₂ molecules previously populated in even j states will be redistributed mainly on the lowest even j state (j = 0), and N₂ in odd j states will fall into the lowest odd j state (j = 1), while the ratio of ortho : para will be retained. No independent measurements of the N₂ rotational distribution were made, but considering the same experimental conditions for producing the N₂ molecular beam in this experiment and the CO beam production previously, and considering the very similar rotational constants of N₂ and CO, it is reasonable to assume that the secondary beam (N₂/He) in the current experiment has a similar rotational temperature (T_rot ≈ 3 K) as the CO/He beam had. Based on the simulation with the Pgopher program for an N₂ spectrum at a rotational temperature of around 3 K, the rotational population of rotationally cooled N₂ molecular beam is estimated to be j = 0 (∼60%), j = 1 (∼32%) and higher j states (∼8%). An encounter of a N₂ molecule with a ¹³CO molecule can not only rotationally excite the ¹³CO molecule, but also induce rotation of the N₂ molecule. However, because of the fact that the nuclear spin acts as a spectator to the collision process to a high level of approximation, there is a conservation of ortho/para character of N₂ in the collision process and only Δj = even transitions are allowed.

In the experiment, single collision conditions are confirmed by monitoring the change in initial rotational population of molecules in the primary beam as a result of collision; depletion of the ¹³CO beam ground state by collision was measured to be less than 5%. The rotationally excited ¹³CO products after collision were ionized via a VUV REMPI scheme along the electronic A¹Π − X¹Σ⁺ transition using VUV radiation around 154 nm. The VUV REMPI scheme has been investigated in detail in ref. 37 and 38, therefore for experimental details we refer to the previous publications. The VUV radiation is one-photon resonant with the ¹³CO A¹Π − X¹Σ⁺ (0, 0) transition and this VUV REMPI scheme turns out to be very polarization-sensitive for measurements involving nascent CO.^37,39,40

The ionized scattered products ¹³CO⁺ were extracted by the VMI ion optics, and the three-dimensional Newton sphere, after 85 cm free flight along the time-of-flight (TOF) tube, was projected onto a two-dimensional detector consisting of chevron MCPs and a phosphor screen. The VMI voltage setting was tuned to obtain the best focusing of the ion velocity on the image detector and TOF time gating was applied to select the required mass and suppress contributions from other ionized molecules (hydrocarbons or water) in the chamber to the ion images. The ion images were captured by a charge coupled device (CCD) camera and then transferred to a laboratory computer for acquisition and averaged with DaVis software (LaVision) using an event counting mode.

Overall differential cross sections and overall alignment moments were extracted from the experimental images following the extraction procedure described by Suits et al. in ref. 39. In this procedure, two types of angular distribution components (in-plane component; out-of-plane component) were extracted from H and V polarization images by integrating over an annulus covering the two-dimensional Newton ring and over a narrow stripe through the middle of the image along the relative velocity vector. In total, four sets of angular distribution components were obtained for each final rotationally excited state j′: HIP (horizontal, in-plane), HOOP (horizontal, out-of-plane), VIP (vertical, in-plane) and VOOP (vertical, out-of-plane).³⁹ It is known that the overall detection probability function of an image depends not only on the alignment of product rotational angular momentum, but also the probe sensitivity factors which are determined by the actual experimental geometry of probe laser polarization. Solving the equations of the overall image detection probability linked to alignment moments and probe sensitivity factors result in algebraic combination of the four sets of components mentioned above, which yield the state-to-state alignment-free differential cross sections (DCSs) and the alignment moments A^{k}_q. In the current experiment, due to the large velocity difference between two incident molecular beams, the probe laser propagated at an angle of 130° with respect to the relative velocity vector of the colliding system; such experimental geometry has sensitivity to all alignment moments A^{2}₀, A^{2}₁₊ and A^{2}₂₊, and these were extracted and reported here. On the other hand, the pair-correlated differential cross sections, i.e., the rotational-state pair-correlated alignment-free moments were extracted from the radius-dependent angular distribution of the experimental images using an onion-peeling inversion method which is similar to that in ref. 41 and then summed to obtain the overall differential cross sections for comparison. Within the experimental error bar, the overall DCSs obtained from the summation of the rotational-state pair-correlated DCSs agree with the directly extracted overall DCSs, regarding the trend, shape and peak positions, etc. Since the rotational-state pair-correlated DCSs in the ¹³CO + CO inelastic scattering together with those in the ¹³CO + N₂ collisions have been described and discussed in great detail in our previous publication,²¹ we do not concentrate on pair correlation in this article and instead we compare the stereodynamics of inelastic scattering in the ¹³CO + CO and the ¹³CO + N₂ collisions based on the overall DCSs and alignment moments.

2.2 Theoretical method

For the ¹³CO–CO system the calculation of the potential energy surface and its parameterization such that it could be used in trajectory calculations followed the procedure described in detail in ref. 21. We follow the same approach for the calculation of the ¹³CO–N₂ potential energy surface in this report. The general form of the PESs for both systems is in good agreement with those presented previously for ¹²CO–¹²CO⁴² and for ¹²CO–N₂.⁴³ In short, the coupled cluster singles and doubles with perturbative triplets [CCSD(T)] approach was used as implemented in the Molpro program (2012 version).⁴⁴ The energies were corrected for basis set superposition errors (BSSE) by performing the calculations for the complex and the separate diatomic molecules in the full complex basis set. An augmented quadruple zeta (AVQZ) basis was used. For the CO–N₂ potential energy surface 3465 unique geometries were considered. These numbers are related to 21 R values and an angular grid consisting of 7 θ_A, 7 θ_B and 6 Φ values, where R is the length of the R vector pointing from the center of mass of monomer A to that of B, θ_A and θ_A are angles between the vector R and the vectors r_A and r_B pointing along the bond axis of each monomer, and Φ is the dihedral angle between the two planes defined by the vectors R and r_A, and R and r_B. The angles were chosen in such a way that the angular dependence of the interaction energy was optimally described within the spherical expansion formalism. The 21 R values chosen were 2.49, 2.5, 2.625, 2.75, 2.875, 3.0, 3.125, 3.25, 3.5, 3.75, 4.0, 4.25, 4.5, 5.0, 5.5, 6.0, 6.5, 7.0, 9.0, 15.0, 20.0 a₀. The data from the first small R value was used to set the slope at small R of the cubic spline interpolation of the spherical expansion coefficients. The slope at the largest R value was set to zero for all coefficients except for the isotropic term and the low order multipole components. The slopes of the latter components were set in accord with the proper R dependence of the energy terms (1/R⁶ for the isotropic dispersion and 1/R^(L+1) for the multipole-multipole interactions where L is sum of the multipole orders of the two diatomic molecules). For the calculation of the intermolecular interaction energy the bond lengths of the two diatomic molecules were kept fixed at their equilibrium values. Since the dynamics calculations run in 6 dimensions, the intermolecular potential was appended with two Morse oscillators with parameters chosen for optimal reproduction of the rotational levels of the dimers up to the collision energy of ∼1500 cm⁻¹ (for CO r_e = 1.128 Å, β = 2.302 Å⁻¹, D_e = 11.20 eV and for N₂r_e = 1.098 Å, β = 3.444 Å⁻¹, D_e = 9.90 eV).^45,46 The dependence of the intermolecular energy on the bond lengths of the diatomic molecules was neglected. Indirect support for this approximation was provided by trajectory calculations of CO–Ar which showed little influence of this dependence on cross sections and alignment parameters. To aid comparison of the collision dynamics of CO–CO versus CO–N₂, maps of the electrostatic moment expansions for both CO–N₂ and CO–CO are presented later in this paper.

The details of the quasi-classical trajectory calculations have been described in ref. 21 as well, hence only important points are summarized briefly here. The trajectory calculations were performed with the help of the Venus 2005 program.⁴⁷ An interface was constructed to provide energies and forces from the spherical expansion representation of the potential energy surface. Forces were derived numerically with left- and right-hand finite differences of 10⁻⁴ Å in the 4 × 3 Cartesian coordinates that were converted to the Jacobi coordinates used in the spherical expansion. The Newton equations of motion were integrated with the Velocity–Verlet scheme with a time-step of 0.02 fs. At the start of a trajectory the molecules were set apart with 8 Å between their centers of mass. The orientations and bond lengths of the diatomic molecules were randomly sampled taking care that the vibrational motion for v = 0 corresponds to the quasi-classical description and initial rotation corresponds to j = 0 or j = 1. The impact parameter range was stepped from 0 to b_max = 7 Å with 0.1 Å steps. At each impact parameter 50 000 trajectories, varying in vibrational coordinate and orientation of monomers described by v = 0, j = 0 and v = 0, j = 1 as mentioned above, were employed. A trajectory was considered finished when the R value exceeded 8 Å again. Then the coordinates and momenta of the molecules at the end of each trajectory were stored for later analysis. The collision energy was set at 1460 cm⁻¹ in all cases. With the chosen settings the energy conservation was better than 2 cm⁻¹.

The analysis consisted of the evaluation of state-to-state cross sections, pair-correlated state-to-state cross sections, state-to-state differential cross sections, pair-correlated differential cross sections and scattering angle dependent alignment moments.

(a) State-to-state cross sections (σ_j′): for final rotational state j′ values up to 30, σ_j′ was obtained by replacing the integral over impact parameter by the following sum with Δb the impact parameter step size (here equal to 0.1 Å)

where b_i refers to the ith impact parameter and P_j′(b_i) = N_j′(b_i)/N is the probability for excitation into the final rotational level j′ found as the fraction of N_j′(b_i), the number of trajectories ending up with this j′ value, out of N the total number of trajectories run at b_i. State-to-state cross sections were evaluated for each species separately. Since QCT does not conserve quantization of the vibration, trajectories were filtered out when a change in vibrational energy larger than 1% of the vibrational zero-point energy was observed. This makes N in the formula above on average 0.5% smaller than the initial value of 50 000 starting trajectories. The rotation level j′ was derived from the rotational energy E_rot = j′(j′ + 1)/2μr² with μ being the diatom reduced mass and r the instantaneous bond length. The real j′ value was rounded to the nearest integer value.

(b) Pair-correlated state-to-state cross sections (σ_j′,j′′): these are evaluated from with 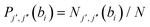and N_j′,j′′(b_i) equals the number of trajectories ending with j′ for the scattered CO product and j′′ for the scattered partner (i.e., N₂) at the ith impact parameter.

(c) State-to-state differential cross sections and pair-correlated differential cross sections. The state-to-state differential cross sections defined as σ_j′(θ) = dσ_j′/d cos θ were derived by binning the σ_j′ as function of the scattering angle θ in 40 equally spaced cosine intervals. The pair-correlated differential cross sections termed as σ_j′,j′′(θ) were derived by binning the σ_j′,j′′ of the product pair (j′, j′′) as function of the scattering angle θ.

(d) Scattering angle dependent alignment moments A^{k}_q: in accord with the experimental setup, the following alignment moments were calculated based on the formulas described in reference.⁴⁸ In each cosine interval of the scattering angle, the alignment moments were determined by the averages:

where θ is the scattering angle between the angular momentum vector j and the z-axis (parallel to the k vector) and φ is the angle between the projection of j in the k–k′ plane and the x-axis.

3. Results

Ref. 21 contains a presentation and discussion of pair-correlated scattering data for ¹³CO–CO collisions, along with a brief discussion of pair-correlated data for ¹³CO–N₂ collisions. Pair correlation is a doubly-differential cross section measurement where angular information is recorded for separate radial regions in the scattering image, which of course relies on sufficient imaging resolution. A key experimental challenge is to account for the effects of collision induced alignment when nascent molecules are probed by linearly polarized detection lasers, in order to extract alignment-free pair correlated differential scattering cross sections. The alignment information needed for this separation could be reliably obtained from ‘normal’ rotational state dependent singly (radial-angle integrated) differential cross sections which are presented in this paper along with analysis of the collision induced alignment moments for ¹³CO–N₂ and also ¹³CO–CO collisions.

Scattered ¹³CO products from inelastic scattering with N₂ were detected using a vertical and a horizontal polarized VUV probe laser via Q-branches in the 1 + 1′ + 1′′ REMPI spectra, and experimental ¹³CO⁺ velocity map images for the ¹³CO(j′) = 15, 17, 19, 22, 23 final states are presented in panel (a) of Fig. 1. These spectroscopic transitions used for detecting final states of scattered ¹³CO products are the same as those used in the ¹³CO + CO inelastic scattering experiment. Avoidance of overlap with the scattering signal due to collision with He carrier gas restricted study to states above j′ > 14, with the criteria of choosing strong Q-branch transitions free of overlap with other branches and perturbative states in the CO A-state spectrum. A Newton diagram that describes the experimental geometry is overlaid on the V-polarization image for the product final state j′ = 15, where the white arrows specify the velocity vectors of the colliders V_¹³CO and V_N2, the center of mass velocity V_CM, while the red arrow indicates the initial relative velocity vector k. All images are presented in such a way that the initial relative velocity vector k is directed horizontally, with forward scattered angles positioned at the left side of the image and small segments around forward direction are masked because of the beamspot that coincides with the lab-frame velocity of the un-scattered ¹³CO molecular beam. The beamspot is well-separated from the scattered ion signal for most of the final j′ states and the space in-between grows as j′ increases.

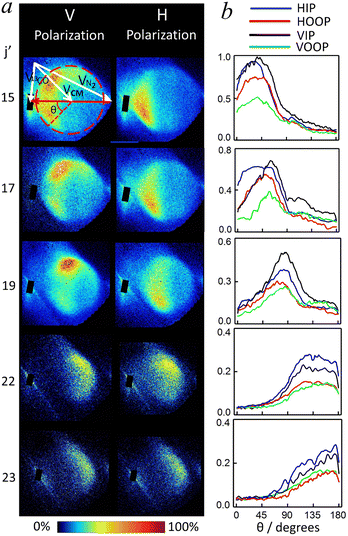Fig. 1 (a) Raw experimental velocity map images for the ¹³CO + N₂ scattering process into the j′ = 15–23 final states of ¹³CO probed using (1 + 1′ + 1′′) VUV REMPI detection of ¹³CO. Images are presented such that the relative velocity vector is directed horizontally, with forward scattered angles positioned at the left side of the image. Small masked segments near the forward direction on the images are due to the beam spots of ¹³CO molecular beam. The polarization of the resonant VUV laser is indicated by ‘V Polarization’ for E_laser perpendicular to the collision plane and ‘H Polarization’ parallel to the collision plane. The sensitivity scale for the raw images is adjusted to make the main features visible. A Newton diagram for the scattering process is overlaid on the V polarization image for the ¹³CO j′ = 15 final state, where the velocity vectors of the two colliders (V_¹³CO and V_N2), the center-of-mass velocity (V_CM) and the scattering angle (θ) are defined. The collision angle is 70° and the corresponding mean collision energy is 1460 cm⁻¹. (b) The HIP, HOOP, VIP, and VOOP distribution components extracted from these orthogonal probe polarization images by integrating selected annulus and rectangle regions upon the images as described in ref. 39.

A number of features in the raw experimental ¹³CO⁺ images can be seen directly. First of all, compared to CO + Rg inelastic scattering images we reported previously,^38–40 the measured images of ¹³CO for inelastic scattering with N₂ are much broader in the radial direction, which is attributed to the production of a range of final rotational levels of N₂. Because of the small rotational constant of the N₂ molecule, B₀(N₂) ∼ 2.0 cm⁻¹, transitions involving rotational excitation in the collision partner N₂ will cause the Newton rings for different N₂ final states to (partially) blur with each other, resulting in the ¹³CO⁺ images with a broad distribution of Newton sphere radii. This image broadening effect has also been observed in the previous experiment of ¹³CO + CO inelastic scattering. In addition, we note that the overall size of the scattering image decreases as j′(¹³CO) increases because a larger amount of collision energy is required to transfer into rotational energy with excitation to a higher final rotational state of the products. When inspecting the experimental images of the same final j′(¹³CO) state obtained from V-polarization and H-polarization laser detection, clear differences can be seen, which indicates the strong collision induced alignment of the rotational angular momentum of the scattered products. Finally, as the detected j′(¹³CO) increases, the scattering images show forward scattering behaviour moving towards sideways and backward scattering eventually, for both V- or H-polarization detection.

For each final rotationally excited state j′, four sets of angular distribution components were obtained: HIP (horizontal, in-plane), HOOP (horizontal, out-of-plane), VIP (vertical, in-plane) and VOOP (vertical, out-of-plane), as shown in the panel b) of Fig. 1, and algebraic combination of them yield the state-to-state differential cross sections (DCSs) and alignment moments A^{2}₀, A^{2}₁₊ and A^{2}₂₊. The resulting state-to-state alignment-free DCSs for scattered ¹³CO into the j′ = 15–23 final states after collision with N₂ at a mean collision energy of 1460 cm⁻¹ are shown in the top row of Fig. 2, in comparison with theoretical predictions. We note here that the ¹³CO⁺ images and alignment-free DCSs from the current experiment on ¹³CO scattering with N₂ look quite similar to those measured in the ¹³CO + CO inelastic scattering study with kinematically equivalent experimental settings: not only the image size and broadening effects, but also the angular distribution features of each image and their polarization dependence. Results for the image analysis for the state-to-state pair-correlated DCSs and alignment moments are thus expected to be similar to those for the ¹³CO + CO study. As shown in the ¹³CO + CO study described in ref. 21, analysis of the typical experimental images for the lowest detected final state of ¹³CO (j′ = 15) which have the largest image size and best resolution, yielded state-to-state pair-correlated DCSs and good agreement with theoretically predicted pair-correlation information had been observed. On the theoretical side, the weighted sum of these fully state-resolved pair-correlated DCSs over all the populated partner final CO rotational states, j′′(CO), results in the averaged DCS for a specific final ¹³CO rotational state, which show the overall preferential angular distribution of scattering as a function of j′(¹³CO) only. Similarly, the theoretical partner-state averaged alignment moments describe the overall alignment preference of rotational angular momentum of scattered ¹³CO products. In general, the overall DCSs and the overall alignment moments from the ¹³CO + CO experiment agree reasonably well with theoretical predictions. Ref. 21 contains a full discussion of impact parameter distributions and other dynamical aspects for CO–CO collisions which also apply to CO–N₂ collisions. Therefore, only the overall DCSs and alignment moments from the ¹³CO + N₂ experiment are shown here and compared to the corresponding overall data from the ¹³CO + CO system.

Fig. 2 Alignment-free differential cross sections for rotational energy transfer of ¹³CO to final states. Top row: experimental state-to-state alignment-free differential cross sections (red line) and theoretically averaged ones calculated by quasi-classical trajectory (QCT) calculations (blue line) for ¹³CO in collision with N₂ molecules. Bottom row: experimental state-to-state alignment-free differential cross sections (red line) and theoretical averaged ones calculated by quasi-classical trajectory calculations (blue line) for ¹³CO in collision with CO molecules. In the comparison between experiment and theory, the experimental results are normalized to the QCT predicted data by setting the area integration of from the experimental DCS equal to the QCT predicted DCS.

As shown in the top row of Fig. 2, there is quite good general agreement between the experimental overall alignment-free DCSs and the theoretical averaged DCSs across all the final states of ¹³CO collided with N₂. These DCSs display a gradual shift to increasingly larger scattering angles as j′(¹³CO) increases, which is consistent with the measured images in panel (a) of Fig. 1. Note that the DCSs predicted by QCT calculation go to zero in the classically forbidden region which is located at very forward scattering angles for the highest final states (j′ = 22, 23). The level of agreement between the experimentally extracted overall DCSs and the theoretically averaged DCSs for all final product states implies that the features of the ¹³CO–N₂ PES which determine the DCS are quantitatively correct within the collision energy range sampled in this experiment.

The bottom row of Fig. 2 displays the state-to-state overall DCSs for ¹³CO products scattered into the same final states together with theoretical predicted DCSs, which are taken from the ¹³CO + CO inelastic scattering work. When comparing the results of the ¹³CO + N₂ experiment and the ¹³CO + CO experiment in the context of state-to-state overall DCSs for scattered ¹³CO, it can be seen that the qualitative behaviour of the DCS is broadly similar in both overall structure aspect and absolute intensity aspect for the two collision partners. This indicates that the ¹³CO–N₂ PES and the ¹³CO–CO PES are quite similar. However, inspection reveals that the primary maximum (maxima) of the DCSs for scattered ¹³CO with N₂ collision partner appear(s) at consistently more backward scattering angles (≈15–20°) compared to the case of ¹³CO scattering with CO as collision partner. The maxima in the rotationally inelastic scattering angular distribution, to some extent, reflect the classical rotational rainbow positions, where collisions with different impact parameters result in scattering at the same final angle.

It is also apparent in Fig. 2 that for all the final states except the highest one, i.e., j′ = 23, the DCSs of scattered ¹³CO with CO collision partner clearly show a primary and secondary maximum in the DCSs, the latter of which become much less evident in the case of the ¹³CO + N₂ scattering, especially for the final state range of j′ = 17–22. Previously, such double maxima were observed as well by Lorenz et al. and McBane et al. for the CO + Ne inelastic scattering,^49,50 where the primary peak was attributed to scattering at the C end of the molecule and the secondary peak to either O-end scattering and/or supernumerary rainbows. This difference might be attributed to the different anisotropy of the collision partners with respect to the same primary collider ¹³CO. Because of the higher asymmetry of the CO molecule compared to the N₂ molecule, from a simple classical view the difference between the C-end and O-end with respect to the primary collider ¹³CO in the CO–¹³CO potential is not present in the case of N₂ with respect to ¹³CO in the N₂–¹³CO potential. In addition, ¹³CO–CO shows enhanced forward scattering at θ = 0° compared to ¹³CO–N₂, particularly for j′ = 15 products. Other details in the differences between the DCSs for ¹³CO–CO and ¹³CO–N₂ are described in the Discussion section.

Turning to the alignment moments A^{2}_q, in order to compare the collision induced rotational angular momentum polarisation in the ¹³CO + N₂ and ¹³CO + CO scattering processes clearly, experimental alignment moments for the ¹³CO + N₂ system together with the results of QCT calculations are displayed in Fig. 3. The results for the ¹³CO + CO system from ref. 21 are shown in the same format style in Fig. 4. As shown there, the QCT-predicted classical PDDCSs also go to zero in the classically forbidden region, where the alignment-free DCSs are zero. Note that the signal-to-noise ratio of the V-polarization and H-polarization experimental images are also poor in the very forward scattering regions, thus the experimental alignment moment data in the range 0–30° are discarded. When concentrating on the alignment moments results for the ¹³CO + N₂ system only, generally speaking, good agreement between experimental results and QCT calculated predictions can be seen for all the three alignment moments. For the A^{2}₀(θ) moments, even though the rapid oscillation behaviour in the very forward scattering region caused by quantum interferences cannot be predicted by QCT calculations, the amplitude and the overall shape of the QCT predicted A^{2}₀(θ) curve are well reproduced by experiment. And as the final state of scattered ¹³CO product j′ increases, both of the QCT calculated and experimental values are increasingly to the negative side. However, different from the CO + Ar, CO + He, and NO + Ar scattering studies, where the A^{2}₀(θ) moments were always found to be positive in the forward scattering region and to be at the negative limit (−1) in the backward region, the averaged A^{2}₀(θ) moments for ¹³CO scattered into such relatively high j′ states by collision with N₂ molecules still reach the negative limit but with less positive values. This reveals strong ‘Frisbee’-like rotational alignment in the backward region and less ‘propeller’-like rotational alignment in the forward region. This difference of averaged A^{2}₀(θ) moments in the current case with respect to the molecule + Rg collision cases likely comes from the difference of alignment behaviour related to the range of rotational states of the N₂ partner. The agreement between the experimental A^{2}₂₊(θ) moments and the corresponding predictions from theory is also good, not only for the amplitude and the overall shape but also in the trends with increasing j′. Even though the agreement between the experimental and theoretical A^{2}₁₊(θ) moments is not as good as those in the cases of the A^{2}₀(θ) and A^{2}₂₊(θ) moments due to the lower precision of the experimental data from the analysis procedure, the experimental shape and trend of the A^{2}₁₊(θ) moments reasonably agree with theory predictions. The overall good agreement of the theory calculations with the experimental alignment moments across all final states detected provides further evidence that the potential energy surface very accurately represents the interaction of the ¹³CO–N₂ system.

Fig. 3 Angular momentum alignment moments A^{2}_q for rotational energy transfer of ¹³CO to final states ¹³CO j′ = 15–23 in collision with N₂ molecules. Red line: overall alignment moments extracted from experimental polarization-dependent images; blue line: theoretically averaged alignment moments predicted by quasi-classical trajectory calculations. Predictions from the kinetic apse hard ellipsoid model are given by the green dashed lines.

Fig. 4 Angular momentum alignment moments A^{2}_q for rotational energy transfer of ¹³CO to final states ¹³CO j′ = 15–23 in collision with CO molecules for the purpose of comparison with the ¹³CO + N₂ system. Red line: overall alignment moments extracted from experimental polarization-dependent images; blue line: theoretically averaged alignment moments predicted by quasi-classical trajectory calculations.

For both the ¹³CO + N₂ and ¹³CO + CO systems the collision induced rotational alignment results suggest that the dominant-contribution originates from the repulsive part of the interaction potential of the colliding systems. However, only moderate and high final rotational states of the scattered products were experimentally probed here, where the hard-shell nature of the interaction is expected to mainly contribute to the collision induced alignment.

4. Discussion

The stereodynamic properties determined from differential cross sections for ¹³CO + N₂versus¹³CO + CO, as well as the model and parameters describing collision induced alignment, are similar, which is consistent with the observed behavior in state-to-state DCSs for NO(X) and NO(A) in collision with D₂ and He, where D₂ and He are kinematically similar collision partners. For our systems, however, quite large differences in the pair-correlated data for ¹³CO + N₂versus¹³CO + CO were described in ref. 21 for the forward scattering region. A significant component found there for ¹³CO + CO were products in symmetrically excited final states, i.e., j′(¹³CO) = j′′(CO) = 14, 15, 16, 17, which were not observed at all for the ¹³CO + N₂ system. Note that these differences in the two systems appear strongly in the pair-correlated doubly differential cross section data, and are less obvious in the normal, singly DCS data, in Fig. 2, which illustrates the wider scope of dynamic information provided by pair correlation measurements. In speculations about the origin of these differences particularly in forward scattering for the two systems we first consider differences in their potential energy surfaces and then show that the (miss-)use of QCT provides additional hints.

In our QCT calculations the PESs of both CO–CO and CO–N₂ are represented by a set of expansion functions, following the convention given in ref. 51. A plot of the spherical expansion analysis of the two pair potentials is shown in Fig. 5. The isotropic terms (black, full line for CO–CO, dashed line for CO–N₂) are rather similar, showing nearly the same well depth, while CO–N₂ is slightly less repulsive. The dipole–dipole term is given in red, and is of course absent for CO–N₂. The dipole quadrupole term is in blue, and the quadrupole–dipole in magenta (opposite in sign from the dipole–quadrupole term) is again absent for CO–N₂. Finally, the quadrupole-quadrupole term (green) is somewhat smaller for CO–N₂. These terms are not confined to electrostatic interactions but include also the short-range interactions with the same orientational dependence as the electrostatic multipole-multipole interactions. From Fig. 5 it is clear that considerations involving only the small dipole moment of CO and the lack thereof for N₂ are misleading since quadrupole moments play an equally or more important role in the pair potentials. Note also that the collision energy of 1460 cm⁻¹ is much higher than the equilibrium well depth of the two clusters. Short range (mainly repulsive) forces that depend strongly on the relative molecular orientations determine whether the attractive forces in the pair potential will be sampled during the collision. At 2.5 Å, for example, the least unfavourable orientation already has an energy more than twice the collision energy and other orientations are up to 35 times the collision energy. The forces calculated at the shortest distance possible should therefore also be correct.

Fig. 5 Spherical expansion of the pair potentials for CO–CO and CO–N₂ in terms of electrostatic moment interactions.

The balance and time development of repulsive and attractive forces is critical in explaining the exceptional forward scattering mechanism seen only in the ¹³CO + CO system. This is illustrated in Fig. 6, which tracks the interaction energy of a successful forward scattering with symmetric excitation (FSSE) collision at 1460 cm⁻¹ between two CO molecules that start off with an initial orientation where the two C atom ends of the molecules strike each other. At the start of the collision, a repulsive interaction of ∼150 cm⁻¹ takes place which is followed by an attractive interaction of ∼−100 cm⁻¹, corresponding to an anti-geared rotation of the molecules around each other continuing to the point where the two O-atoms reach closest approach. Symmetric excitation may be favored for efficient anti-geared motion after the initial C-end collision. This attractive force after the large rotational energy transfer (j′ ¹³CO = j′ CO = 15, RET = 2 × 462 cm⁻¹ = 924 cm⁻¹) collision results in a torque of the collision pair during separation that effectively redirects the initially sideways recoil angle towards the forward direction, as illustrated schematically in the lower panel of Fig. 6 (from ref. 21). The concept of forward scattering due to attractive forces following large rotational energy transfer was recently⁵² applied with success to other molecule-molecule collision systems.

Fig. 6 Time development traces of the interaction energy for two similar trajectories for CO–CO (ref. 21) and CO–N₂.

A remaining question is why no FSSE channel was found in the CO + N₂ system, despite the kinematic similarity with CO + CO. With QCT theory it is possible to force a CO + N₂ collision to follow the motion of a trajectory leading to FSSE in a CO + CO collision. The trajectory data of the CO–CO collision described in Fig. 2 of ref. 21, which results in the potential energy plot with the black line in Fig. 6 was used to calculate the potential interaction for the case where CO collides with N₂, given by the red line in Fig. 6. At each time step, the geometry is that of CO on CO but the potential is that for CO on N₂. The trajectory is thus in the case of CO on N₂ purely fictitious since the run is not on the own CO–N₂ potential. Still, some insight is provided: at the start of the trajectory the CO–CO and CO–N₂ potentials are rather similar. One might therefore assume that with the same initial geometry CO + N₂ would follow a similar path as CO + CO. At 250 fs there is for both systems an increasing repulsive potential. In the case of CO + CO collision this repulsion is responsible for the typical (15, 15) forward scattering behavior. Since the repulsion is approximately 3 times smaller for CO + N₂, the collisional kick is not large enough for excitation into e.g. (15, 15). In fact, only a miniscule number of CO + N₂ trajectories on the actual CO–N₂ potential energy surface (which sample all initial geometries) resulted in (15, 15) or similar high rotational excitation, and these contributed only to the primary rainbow scattering angle at ∼80 degrees.

5. Conclusion

State-to-state DCSs and scattering angle resolved alignment moments for rotational energy transfer for the ¹³CO + N₂ inelastic scattering have been measured under kinematically equivalent conditions as ¹³CO + CO scattering and compared to the corresponding results of the ¹³CO + CO system. For each scattering system, there is good agreement between experimental measurements and theoretical predictions, which confirms that the calculated PESs represent the interactions in the colliding system very well. Comparison of the observed scattering stereodynamics for collision of ¹³CO with N₂ and CO as collision partners provide extra information on the subtle differences between the two PESs. The broad similarities between the state-to-state DCSs and the qualitatively similar behaviours of the collision induced rotational alignment moments for the two collision partners indicate that the ¹³CO–N₂ PES in general has a similar form as the ¹³CO–CO PES and that the dynamics follow predictions of a hard-shell collision model. Close inspection reveals that the primary rainbow maximum in DCSs for ¹³CO in collision with N₂ appears at larger, more backward scattering angles compared to those from scattering with CO, implying that the ¹³CO–N₂ PES is less anisotropic than the ¹³CO–CO PES. This cannot be simply attributed to the dipole–dipole interaction of the ¹³CO–CO system since dipole–quadrupole and quadrupole–quadrupole interactions are important for both ¹³CO + CO and ¹³CO + N₂ and also short range repulsive forces (shape effects) play a role. The secondary maximum for scattering with N₂ is also less obvious which may result from the configurational asymmetry of a CO molecule compared to N₂. The doubly-differential product pair correlated DCS data for the two systems has previously revealed a new unexpected channel labelled forward scattering with symmetric excitation (FSSE) only for the ¹³CO + CO system. Trajectory analysis by QCT theory explained FSSE in ¹³CO + CO as a face-to-face/rotation/back-to-back or ‘do-si-do’ synchronous motion between the two colliding molecules. However, no FSSE is observed for the kinematically similar ¹³CO + N₂ system. By forcing ¹³CO + N₂ to follow the initial ¹³CO + CO trajectory of an FSSE collision using QCT, it appears that it may be difficult for ¹³CO + N₂ trajectories to reach a repulsive wall high enough to cause the deeply inelastic energy transfer.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

ZFS is supported by the National Natural Science Foundation of China (no. 22103003), Anhui Provincial Natural Science Foundation (no. 2208085Y02) and the Natural Science Research Project of Education Department of Anhui Province (no. KJ2021ZD0008). This project has moreover received funding from the University Annual Scientific Research Plan of Anhui Province (no. 2022AH010013) and the open foundation of the state key laboratory of molecular reaction dynamics in DICP, CAS (no. SKLMRD-K202204). DHP, RJAS and MCvH acknowledge the NWO-Dutch Astro-chemistry Network II project number 648.000.024, and the NWO-TOP project number 715.013.002 for support. AGS acknowledges the US National Science Foundation under award CHE-1955239. All the authors thank Prof. Gerrit C. Groenenboom and Prof. Sebastiaan Y. T. van de Meerakker (RU Nijmegen) for helpful discussions on this paper. We thank Prof. Mark Brouard (University of Oxford) for offering a program that allows the calculations of the alignment moments based on the kinematic apse model that was coded by B. Hornung.

References

1. G. Paterson, M. L. Costen and K. G. McKendrick, Int. Rev. Phys. Chem., 2012, 31, 69–109.
2. H. Chadwick, M. Brouard, T. Perkins and F. J. Aoiz, Int. Rev. Phys. Chem., 2014, 33, 79–123.
3. M. L. Costen, S. Marinakis and K. G. McKendrick, Chem. Soc. Rev., 2008, 37, 732–743.
4. A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484.
5. K. T. Lorenz, D. W. Chandler, J. W. Barr, W. W. Chen, G. L. Barnes and J. I. Cline, Science, 2001, 293, 2063–2066.
6. H. Chadwick, B. Nichols, S. D. S. Gordon, B. Hornung, E. Squires, M. Brouard, J. Kłos, M. H. Alexander, F. J. Aoiz and S. Stolte, J. Phys. Chem. Lett., 2014, 5, 3296–3301.
7. M. Brouard, H. Chadwick, C. J. Eyles, B. Hornung, B. Nichols, F. J. Aoiz, P. G. Jambrina and S. Stolte, J. Chem. Phys., 2013, 138, 104310.
8. S. N. Vogels, J. Onvlee, S. Chefdeville, A. van der Avoird, G. C. Groenenboom and S. Y. T. van de Meerakker, Science, 2015, 350, 787–790.
9. J. I. Cline, K. T. Lorenz, E. A. Wade, J. W. Barr and D. W. Chandler, J. Chem. Phys., 2001, 115, 6277–6280.
10. M. Brouard, H. Chadwick, S. D. S. Gordon, B. Hornung, B. Nichols, J. Kłos, F. J. Aoiz and S. Stolte, J. Chem. Phys., 2014, 141, 164305.
11. M. Brouard, H. Chadwick, C. J. Eyles, B. Hornung, B. Nichols, F. J. Aoiz, P. G. Jambrina, S. Stolte and M. P. de Miranda, J. Chem. Phys., 2013, 138, 104309.
12. A. Gijsbertsen, H. Linnartz, G. Rus, A. E. Wiskerke, S. Stolte, D. W. Chandler and J. Kłos, J. Chem. Phys., 2005, 123, 224305.
13. M. S. Elioff and D. W. Chandler, J. Chem. Phys., 2002, 117, 6455–6462.
14. M. Brouard, H. Chadwick, C. J. Eyles, B. Hornung, B. Nichols, J. M. Scott, F. J. Aoiz, J. Kłos, S. Stolte and X. Zhang, Mol. Phys., 2013, 111, 1759–1771.
15. T. R. Sharples, T. F. M. Luxford, D. Townsend, K. G. McKendrick and M. L. Costen, J. Chem. Phys., 2015, 143, 204301.
16. A. von Zastrow, J. Onvlee, S. N. Vogels, G. C. Groenenboom, A. van der Avoird and S. Y. T. van de Meerakker, Nat. Chem., 2014, 6, 216–221.
17. J. D. Steill, J. J. Kay, G. Paterson, T. R. Sharples, J. Kłos, M. L. Costen, K. E. Strecker, K. G. McKendrick, M. H. Alexander and D. W. Chandler, J. Phys. Chem. A, 2013, 117, 8163–8174.
18. T. de Jongh, Q. Shuai, G. L. Abma, S. Kuijpers, M. Besemer, A. van der Avoird, G. C. Groenenboom and S. Y. T. van de Meerakker, Nat. Chem., 2022, 14, 538–544.
19. T. de Jongh, M. Besemer, Q. Shuai, T. Karman, A. van der Avoird, G. C. Groenenboom and S. Y. T. van de Meerakker, Science, 2020, 368, 626–630.
20. T. F. M. Luxford, T. R. Sharples, K. G. McKendrick and M. L. Costen, J. Chem. Phys., 2016, 145, 174304.
21. Z. F. Sun, M. C. van Hemert, J. Loreau, A. van der Avoird, A. G. Suits and D. H. Parker, Science, 2020, 369, 307–309.
22. M. S. Westley, K. T. Lorenz, D. W. Chandler and P. L. Houston, J. Chem. Phys., 2001, 114, 2669–2680.
23. A. Gijsbertsen, H. Linnartz and S. Stolte, J. Chem. Phys., 2006, 125, 133112.
24. Z. Gao, S. N. Vogels, M. Besemer, T. Karman, G. C. Groenenboom, A. van der Avoird and S. Y. T. van de Meerakker, J. Phys. Chem. A, 2017, 121, 7446–7454.
25. T. de Jongh, T. Karman, S. N. Vogels, M. Besemer, J. Onvlee, A. G. Suits, J. O. F. Thompson, G. C. Groenenboom, A. van der Avoird and S. Y. T. van de Meerakker, J. Chem. Phys., 2017, 147, 013918.
26. T. F. M. Luxford, T. R. Sharples, D. Townsend, K. G. McKendrick and M. L. Costen, J. Chem. Phys., 2016, 145, 084312.
27. S. Chefdeville, Y. Kalugina, S. Y. T. van de Meerakker, C. Naulin, F. Lique and M. Costes, Science, 2013, 341, 1094–1096.
28. C. K. Bishwakarma, G. van Oevelen, R. Scheidsbach, D. H. Parker, Y. Kalugina and F. Lique, J. Chem. Phys., 2018, 149, 121101.
29. C. H. Yang, G. Sarma, D. H. Parker, J. J. ter Meulen and L. Wiesenfeld, J. Chem. Phys., 2011, 134, 204308.
30. O. Tkáč, A. K. Saha, J. Loreau, Q. L. Ma, P. J. Dagdigian, D. H. Parker, A. van der Avoird and A. J. Orr-Ewing, Mol. Phys., 2015, 113, 3925–3933.
31. O. Tkáč, Q. L. Ma, C. A. Rusher, S. J. Greaves, A. J. Orr-Ewing and P. J. Dagdigian, J. Chem. Phys., 2014, 140, 204318.
32. G. Tang, M. Besemer, J. Onvlee, T. Karman, A. van der Avoird, G. C. Groenenboom and S. Y. T. van de Meerakker, J. Chem. Phys., 2022, 156, 214304.
33. O. Tkáč, Q. L. Ma, M. Stei, A. J. Orr-Ewing and P. J. Dagdigian, J. Chem. Phys., 2015, 142, 014306.
34. T. F. M. Luxford, T. R. Sharples, K. G. McKendrick and M. L. Costen, J. Chem. Phys., 2017, 147, 013912.
35. B. Yan, P. F. H. Claus, B. G. M. van Oorschot, L. Gerritsen, A. T. J. B. Eppink, S. Y. T. van de Meerakker and D. H. Parker, Rev. Sci. Instrum., 2013, 84, 023102.
36. C. M. Western, A Program for Simulating Rotational, Vibrational and Electronic Structure, version 8.0, University of Bristol, 2014, https://pgopher.chm.bris.ac.uk.
37. Z. F. Sun, A. D. von Zastrow and D. H. Parker, J. Chem. Phys., 2017, 147, 013909.
38. L. Song, G. C. Groenenboom, A. van der Avoird, C. K. Bishwakarma, G. Sarma, D. H. Parker and A. G. Suits, J. Phys. Chem. A, 2015, 119, 12526–12537.
39. A. G. Suits, C. K. Bishwakarma, L. Song, G. C. Groenenboom, A. van der Avoird and D. H. Parker, J. Phys. Chem. A, 2015, 119, 5925–5931.
40. Z. F. Sun, C. K. Bishwakarma, L. Song, A. van der Avoird, M. C. van Hemert, A. G. Suits, G. C. McBane and D. H. Parker, Phys. Chem. Chem. Phys., 2019, 21, 9200–9211.
41. M. Brouard, S. D. S. Gordon, A. H. Boyle, C. G. Heid, B. Nichols, V. Walpole, F. J. Aoiz and S. Stolte, J. Chem. Phys., 2017, 146, 204304.
42. L. A. Surin, D. N. Fourzikov, T. F. Giesen, S. Schlemmer, G. Winnewisser, V. A. Panfilov, B. S. Dumesh, G. W. M. Vissers and A. van der Avoird, J. Phys. Chem. A, 2007, 111, 12238–12247.
43. L. A. Surin, I. V. Tarabukin, S. Schlemmer, Y. N. Kalugina and A. van der Avoird, J. Chem. Phys., 2018, 148, 044313.
44. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, WIREs Comput. Mol. Sci., 2012, 2, 242–253.
45. J. A. Coxon and P. Hajigeorgiou, J. Chem. Phys., 2004, 121, 2992–3008.
46. K. P. Huber and G. H. Herzberg, Constants of Diatomic Molecules, NIST Chemistry WebBook, NIST Standard Reference Database Number 69, 2020.
47. X. Hu, W. L. Hase and T. Pirraglia, J. Comput. Chem., 1991, 12, 1014–1024.
48. M. P. de Miranda, F. J. Aoiz, L. Banares and V. S. Rabános, J. Chem. Phys., 1999, 111, 5368–5383.
49. G. C. McBane and S. M. Cybulski, J. Chem. Phys., 1999, 110, 11734–11741.
50. K. T. Lorenz, D. W. Chandler and G. C. McBane, J. Phys. Chem. A, 2002, 106, 1144–1151.
51. M. C. van Hemert, J. Chem. Phys., 1983, 78, 2345–2354.
52. M. Besemer, G. Tang, Z. Gao, A. van der Avoird, G. C. Groenenboom, S. Y. T. van de Meerakker and T. Karman, Nat. Chem., 2022, 2022, 1–6.

---