Rate constant and branching ratio of the reaction of ethyl peroxy radicals with methyl peroxy radicals

Abstract

The cross-reaction of ethyl peroxy radicals (C₂H₅O₂) with methyl peroxy radicals (CH₃O₂) (R1) has been studied using laser photolysis coupled to time resolved detection of the two different peroxy radicals by continuous wave cavity ring down spectroscopy (cw-CRDS) in their AÖX̃ electronic transition in the near-infrared region, C₂H₅O₂ at 7602.25 cm⁻¹, and CH₃O₂ at 7488.13 cm⁻¹. This detection scheme is not completely selective for both radicals, but it is demonstrated that it has great advantages compared to the widely used, but unselective UV absorption spectroscopy. Peroxy radicals were generated from the reaction of Cl-atoms with the appropriate hydrocarbon (CH₄ and C₂H₆) in the presence of O₂, whereby Cl-atoms were generated by 351 nm photolysis of Cl₂. For different reasons detailed in the manuscript, all experiments were carried out under excess of C₂H₅O₂ over CH₃O₂. The experimental results were best reproduced by an appropriate chemical model with a rate constant for the cross-reaction of k = (3.8 ± 1.0) × 10⁻¹³ cm³ s⁻¹ and a yield for the radical channel, leading to CH₃O and C₂H₅O, of (ϕ_1a = 0.40 ± 0.20).

---

Introduction

The oxidation of volatile organic compounds (VOCs) in the troposphere is mainly driven by hydroxyl radicals (OH) and leads, after addition of O₂, to the formation of organic peroxy radicals (RO₂). The fate of these RO₂ radicals depends on the chemical composition of the environment and a detailed review on their chemistry has been given by G. Tyndall and collegues.^1,2 Briefly, in a polluted atmosphere they mainly react with nitric oxide (NO) to form alkoxy radicals or react with nitrogen dioxide (NO₂) to form peroxynitrates (RO₂NO₂). Subsequent to the reaction with NO, alkoxy radicals can react with O₂ to form hydroperoxy radicals (HO₂) together with carbonyl compounds. HO₂ further oxidises NO into NO₂ and thus regenerates OH, closing the quasi-catalytic cycle. The photolysis of the produced NO₂ leads subsequently to the formation of ozone (O₃) and is the only relevant formation path of tropospheric ozone. In clean environments with low NO_x (NO_x = NO + NO₂) concentrations, the fate of RO₂ change and their dominant loss becomes the reaction with HO₂ forming hydroperoxides ROOH and terminating the radical reaction chain. Other reaction pathways under low NO_x conditions for RO₂ radicals are either self-reaction (RO₂ + RO₂) or cross-reaction with other RO₂ (RO₂ + R′O₂)¹ or with OH radicals (RO₂ + OH).³

Methane and ethane are amongst the most abundant hydrocarbons, and their atmospheric oxidation leads to the formation of methyl peroxy (CH₃O₂) and ethyl peroxy (C₂H₅O₂) radicals. For both radicals, the kinetic and product distribution for the self-reaction has been studied numerous times (for CH₃O₂^4–12 and for C₂H₅O₂^13–26), the same is true for their reaction with HO₂ (for CH₃O₂^5,9,27–32 and for C₂H₅O₂^{13,14,20,26,30,33–35}). Their reaction with OH radicals has been the subject of a few studies (for CH₃O₂^3,36–41 and for C₂H₅O₂^42–44). The cross-reaction between both peroxy radicals has only been measured once using UV absorption spectroscopy⁴⁵ whereby the experimental details given in that paper are sparse and it is not clear how the rate constant was extracted from the absorption time profiles measured at only one wavelength where the cross sections of both radicals are very similar. As for the product distribution of this cross reaction, three pathways can be expected:

C₂H₅O₂ + CH₃O₂ → C₂H₅O + CH₃O + O₂ (R1a)

→C₂H₅OH/CH₃OH + CH₂O/CH₃CHO + O₂ (R1b)

→C₂H₅O₂CH₃ + O₂ (R1c)

whereby currently no information is available on the branching ratio between these pathways.

The investigation of this reaction is not straightforward, because secondary chemistry cannot be avoided. Both radicals will react in self-reactions, leading to analogous reaction products. The measurements are complicated, because the product of the reaction path (R1a) leads, after rapid reaction with O₂, to the formation of HO₂ radicals

CH₃O + O₂→ CH₂O + HO₂ (R2)

C₂H₅O + O₂→ CH₃CHO + HO₂ (R3)

with the HO₂ radicals reacting subsequently with both peroxy radicals:

CH₃O₂ + HO₂→ CH₃O₂H + O₂ (R4)

C₂H₅O₂ + HO₂ → C₂H₅O₂H + O₂ (R5)

The rate constants of (R4) and (R5) are faster than the rate constant of (R1), and thus the CH₃O₂ and C₂H₅O₂ decays are accelerated. Therefore, determining the rate constant k₁ from observed CH₃O₂ and C₂H₅O₂ decays depends also on the branching ratio k_1a/k₁ as well as the branching ratios for the two self-reactions used in the data treatment: for a given experimental C₂H₅O₂ or CH₃O₂ decay the retrieved rate constant k₁ will decrease with increasing branching ratio.

In this work we present a more direct measurement of the rate constant of (R1). Measurements have been carried out under an excess of C₂H₅O₂ radicals over CH₃O₂, and both radicals have been followed in their ÖX̃ electronic transition using two different wavelengths. HO₂ concentration time profiles have been measured simultaneously in a highly selective way in the 2ν₁ vibrational overtone at 6638.21 cm⁻¹.

Experimental

Experimental setup

The setup has been described in detail before^46–49 and is only briefly discussed here. The setup mainly consists of a 0.79 m long flow reactor made of stainless steel. The beam of a pulsed excimer laser (Lambda Physik LPX 202i), running at 351 nm, passed the reactor longitudinally. The flow reactor contained two identical continuous wave cavity ring-down spectroscopy (cw-CRDS) absorption paths, which were installed in a small angle with respect to the photolysis path. An overlap of the near IR-path with the photolysis beam of 0.288 m is achieved with an excimer beam width delimited to 2 cm. Both beam paths were tested for a uniform overlap with the photolysis beam before experiments. For this purpose, both cw-CRDS instruments were operated to simultaneously measure HO₂ concentrations. Deviations between HO₂ concentrations were less than 5%, demonstrating that the photolysis laser was well aligned, i.e. both light paths probed a very similar photolysed volume in the reactor. A small helium purge flow prevented the mirrors from being contaminated. Three different DFB lasers are used for the detection of the three species: HO₂: NEL NLK1E5GAAA, 6629 ± 17 cm⁻¹, on CRDS path 1, CH₃O₂: NEL NLK1B5EAAA, 7480 ± 20 cm⁻¹ on CRDS path 2, C₂H₅O₂: AOI-1312-BF-20-CW-F1-H2-N127, 7622 ± 15 cm⁻¹ on CRDS path 2. They are coupled into one of the cavities by systems of lenses and mirrors. Each probe beam passed an acousto-optic modulator (AOM, AAoptoelectronic) to rapidly turn off the 1st order beam once a threshold for light intensity at the exit of the cavity was reached, in order to measure the ring-down event. Then, the decay of light intensity was recorded and an exponential fit is applied to retrieve the ring-down time. The absorption coefficient α is derived from eqn (1).where τ is the ring-down time with an absorber present (i.e. after the photolysis pulse); τ₀ is the ring-down time with no absorber present (i.e. before the photolysis pulse); σ_A is the absorption cross section of the absorbing species A; R_L is the ratio between cavity length (79 cm) and effective absorption path (28.8 cm); c is the speed of light.

Ethyl- and methylperoxy radicals were generated by pulsed 351 nm photolysis of C₂H₆/CH₄/Cl₂/O₂ mixtures inducing the following reactions:

Cl₂ + hν_351 nm → 2 Cl (R7)

CH₄ + Cl → CH₃ + HCl (R8)

C₂H₆ + Cl → C₂H₅ + HCl (R9)

CH₃ + O₂ (+ M) → CH₃O₂ (+ M) (R10)

C₂H₅ + O₂ (+ M) → C₂H₅O₂ (+ M) (R11a)

C₂H₅ + O₂ → C₂H₄ + HO₂ (R11b)

In order to rapidly convert the different radicals (C₂H₅, CH₃, C₂H₅O and CH₃O) into peroxy or HO₂ radicals ((R2), (R3), (R10) and (R11)), all experiments have been carried out in 100 Torr O₂ (Air Liquide, Alpha Gaz 2).

C₂H₆ (Air Liquide, N35), CH₄ (Air Liquide, N45) and Cl₂ (Air Liquide, 5% in Helium) were used directly from the cylinder: a small flow was added to the mixture through a calibrated flow meter (Bronkhorst, Tylan). All experiments were carried out at 298 K.

Results and discussion

Determination of the absorption cross sections

Detecting peroxy radicals in the ÖX̃ electronic transition in the near IR region has the potential of a more selective detection for peroxy radicals compared to UV absorption spectroscopy. In order to demonstrate this, we have carried out measurements for the determination of the rate constant of the cross reaction between CH₃O₂ and C₂H₅O₂ radicals. The rate constant of this reaction was measured only once using UV absorption spectroscopy⁴⁵ whereby the experimental details given in that paper were sparse. It is not clear how the rate constant was extracted from the absorption time profiles measured only at one wavelength where the cross sections of both radicals are very similar.

The ÖX̃ transitions of peroxy radicals consist generally of peaks with a few cm⁻¹ FWHM on a rather broad background.⁵⁰ To check for the mutual selectivity of the detection for both radicals, the absorption cross sections for both radicals have been measured at three different wavelengths: at one “peak” of the ÖX̃ transitions of the CH₃O₂ radical at 7488.14 cm⁻¹ (named in the following M1, green symbols in Fig. 1), at the maximum of the transition of C₂H₅O₂ at 7596.47 cm⁻¹ (named E1, red symbols in Fig. 1) and at a “plateau” at 7602.25 cm⁻¹ (named E2, blue symbols in Fig. 1).

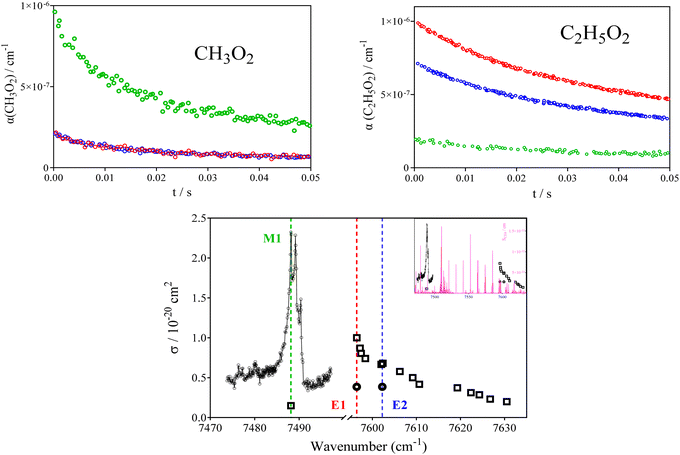Fig. 1 CH₃O₂ (upper left graph, [Cl]₀ = 4.2 × 10¹³ cm⁻³, [CH₄] = 1.9 × 10¹⁷ cm⁻³) and C₂H₅O₂ (upper right graph: [Cl]₀ = 1.0 × 10¹⁴ cm⁻³, [C₂H₆] = 4.4 × 10¹⁶ cm⁻³) profiles obtained at the three different wavelengths represented by colored vertical lines in the lower graph. Lower graph shows spectrum for both species (CH₃O₂ as circles, adapted from Farago et al.⁵¹ and C₂H₅O₂ as square adapted from Zhang et al.⁵²), main graph shows zoom on both sections with x-axis interrupted, insert shows continuous wavelength scale. Magenta lines in insert represent CH₄ spectrum from HITRAN database.⁵³

The upper graphs of Fig. 1 show for one Cl-concentration the absorption time profiles for both radicals (left: CH₃O₂, right: C₂H₅O₂) at all three wavelengths. It can be seen that both radicals still absorb at the wavelength corresponding to the transition of the counterpart radical: for both radicals the absorption at its peak is around 4 times larger than at the peak of the counterpart radical (second column Table 1). The absorption cross sections at the peak wavelengths are known from earlier works^3,51,52 and have been used here to obtain the absorption cross sections at the peak wavelength of the counterpart radical from the relative intensities in Fig. 1 type experiments (experiments using 3 different Cl-atom concentrations have been carried out). The results are summarized in Table 1 and illustrated in the lower graph of Fig. 1.

Table 1 Ratio and absorption cross sections for CH₃O₂, C₂H₅O₂ and CH₄ at three wavelengths

	Ratio (σpeak/σoff)	σ (M1)/cm^2	σ (E1)/cm^2	σ (E2)/cm^2
		7488.13 cm^−1	7596.47 cm^−1	7602.25 cm^−1
CH3O2	4.0	2.2 × 10^−20	5.5 × 10 ^−21	5.5 × 10 ^−21
C2H5O2	6.6/5.0	1.5 × 10 ^−21	1.0 × 10^−20	7.6 × 10^−21
CH4^53		1.2 × 10^−24	1.1 × 10^−23	5.0 × 10^−25
		14.6	0.55 (= 1/1.81)	0.72 (= 1/1.38)

---

It can be seen that the absorption cross sections for both radicals at the “counterpart wavelengths” (in italic in Table 1) are small (1.5 and 5.5 × 10⁻²¹ cm⁻²), but not zero, and thus complete selectivity cannot be obtained.

Determination of the rate constant

To get best selectivity for investigating the cross reaction between both radicals, C₂H₅O₂ was used for all experiments in excess over CH₃O₂ for different reasons:

• To limit the reaction of Cl-atoms with peroxy radicals: the reaction of Cl-atoms with CH₄ is much slower than the reaction of Cl-atoms with C₂H₆ (0.01 and 5.9 × 10⁻¹¹ cm³ s⁻¹ for CH₄ and C₂H₆, respectively).⁵⁴ Therefore, to even obtain identical CH₃O₂ and C₂H₅O₂ concentrations, already 580 times more CH₄ than C₂H₆ is needed. And because CH₄ is absorbing in the near IR region (the absorption cross sections for CH₄ at the three wavelengths are given in Table 1 and is shown as magenta stick spectrum⁵³ in Fig. 1), the amount of CH₄ that can be added in our experiments is limited to a few 10¹⁷ cm⁻³. If an excess of CH₃O₂ would have been chosen, only a few 10¹³ cm⁻³ C₂H₆ would need to be added to obtain comparable C₂H₅O₂ concentrations. Such low hydrocarbon concentrations would lead to Cl-atom decays too slow to avoid major complications due to the reaction of Cl-atoms with CH₃O₂ or C₂H₅O₂.

• To limit absorption of the “counterpart” radical and thus increase selectivity: the ratio of the absorption cross sections between both radicals at a given wavelength (last row of Table 1) is higher at the methyl peroxy transition: σ(CH₃O₂) is 14.6 times higher compared to σ(C₂H₅O₂) at (M1), while the inverse ratio is only 1.81 and 1.38 at (E1) and (E2), respectively. Therefore, in the example of a 10-fold (5-fold) excess of CH₃O₂ over C₂H₅O₂, the absorbance at (M1) would be more than 99% (98%) due to CH₃O₂ (i.e. excellent selectivity), but at (E1) only 15% (27%) and at (E2) only 12% (22%) of the absorbance would be due to C₂H₅O₂, respectively. In the example of a 10-fold (5-fold) excess of C₂H₅O₂ over CH₃O₂, the absorbance at (E1) would be around 95% (90%) and at (E2) 93% (87%) due to C₂H₅O₂ (i.e. still good selectivity), but now at (M1) around 59% (75%) of the signal is due to CH₃O₂ absorption.

• To maximize the importance of the cross-reaction: the self-reaction of C₂H₅O₂ is 3.5 times slower than that of CH₃O₂ (or 2 times, taking the very recent determination of the CH₃O₂ self-reaction rate constant by Onel et al.¹²), making the loss through self-reaction less important in a reaction system with excess C₂H₅O₂ compared to excess CH₃O₂.

Therefore, experiments with a 5- to 10-fold excess of C₂H₅O₂ over CH₃O₂ should lead to a good sensitivity towards the rate constant of the cross-reaction: decays at (E1) or (E2) represent nearly pure C₂H₅O₂ decays mostly governed by the self-reaction, the correction of these profiles due to CH₃O₂ absorption is very minor. Simultaneously measured profiles obtained at (M1) can now be corrected for C₂H₅O₂ absorption, and the remaining CH₃O₂ decay is mostly due to the cross reaction with C₂H₅O₂: the rate constant of the cross reaction can be extracted with good sensitivity.

Even though the absorption cross section for C₂H₅O₂ is higher on (E1) compared to (E2), all experiments have been carried out at (M1) and (E2) due to the much lower CH₄ absorption cross sections at (E2) compared to (E1): even though C₂H₅O₂ is used in excess, high CH₄ concentrations (up to 3 × 10¹⁷ cm⁻³) were still added and absorbed too much light at (E1).

Three series of experiments have been carried out, and the experimental conditions are summarized in Table 2. The initial Cl-atom concentrations (column 1) have been measured before each experiment through measuring and fitting HO₂ decays from the reaction of Cl-atoms with excess CH₃OH. C₂H₆ and CH₄ concentrations (column 2 and 3) have been obtained from flow and pressure measurements, and the initial peroxy radical concentrations (column 4 and 5) and their ratio (column 6) have then been calculated using the literature values of the rate constants for (R8) and (R9), as given in Table 3. To demonstrate the relatively good selectivity towards both radicals, the percentage of the absorbances at M1 and E2, that are due to the searched-after radical, have then been calculated using the radical concentrations and the absorption cross sections from Table 1 (column 7 and 8).

Table 2 Experimental conditions used for measuring the rate constant of the cross reaction between CH₃O₂ and C₂H₅O₂

[Cl]/10^13 cm^−3	[C2H6]/10^15 cm^−3	[CH4]/10^17 cm^−3	[C2H5O2]0/10^13 cm^−3	[CH3O2]0/10^13 cm^−3	[C2H5O2]0/[CH3O2]0	α C2H5O2 at E2 (%)	α CH3O2 at M1 (%)
8.1	2.90	2.00	7.25	0.85	8.56	92.2	63.2
11.0			9.85	1.15
13.8			12.4	1.44
7.4	2.08	2.98	5.95	1.45	4.12	85.1	78.1
10.4			8.37	2.03
12.5			10.1	2.44
7.1	1.25	2.98	5.05	2.05	2.46	77.3	85.6
9.2			6.54	2.66
11.8			8.39	3.41

---

Table 3 Reaction mechanism used to fit all experiments in this work

	Reaction	k cm^3 s^−1	Ref.
Initiation reactions
8	Cl + CH4 → CH3 + HCl	1.0 × 10^−13	54
9	Cl + C2H6 → C2H5 + HCl	5.9 × 10^−11	54
10	CH3 + O2 + M → CH3O2 + M	1.4 × 10^−13	55
11a	C2H5 + O2 + M → C2H5O2 + M	4.8 × 10^−12	56
11b	C2H5 + O2 → C2H4 + HO2	3.5 × 10^−14	This work
Peroxy radical self- and cross-reactions
1a	C2H5O2 + CH3O2 → C2H5O + CH3O + O2	1.5 × 10^−13	This work
1b	C2H5O2 + CH3O2 → stable products	2.3 × 10^−13	This work
2	CH3O + O2 → CH2O + HO2	1.92 × 10^−15	54
3	C2H5O + O2 → CH3CHO + HO2	8 × 10^−15	57
4	CH3O2 + HO2 → CH3OOH + O2	5.2 × 10^−12	52
5	C2H5O2 + HO2 → C2H5OOH + O2	6.2 × 10^−12	52
12a	2 C2H5O2 → 2 C2H5O + O2	3.2 × 10^−14	24
12b	2 C2H5O2 → stable products	7.0 × 10^−14	24
13a	2 CH3O2 → 2 CH3O + O2	1.3× 10^−13	54
13b	2 CH3O2 → stable products	2.2 × 10^−13	54
14	CH3O + HO2 → products	1.1 × 10^−10	58
15	2 HO2 → H2O2 + O2	1.7 × 10^−12	59
Secondary Cl-atom reactions
6a	Cl + C2H5O2 → ClO + C2H5O	5–8 × 10^−11	See text
6b	Cl + C2H5O2 → Products	5–8 × 10^−11	See text
16	Cl + CH3O2 → ClO + CH3O	7.5 × 10^−11	60
17	Cl + CH3O2 → Products	7.5 × 10^−11	60
18	Cl + CH2O + O2 → HCl + HO2 + CO	7.32 × 10^−11	61
19	C2H5O2/CH3O2 + ClO → C2H5O/CH3O + ClOO	1.6 × 10^−12	54
20	HO2 + ClO → O2 + HOCl	6.9 × 10^−12	62
21	ClOO (+ M) → Cl + O2 (+ M)	6.2 × 10^−13	62
22	Cl + O2 (+ M) → ClO2 (+ M)	1.6 × 10^−33	62
Other secondary chemistry
23	C2H5O + C2H5O2 → products	7 × 10^−12	This work
24	C2H5O + HO2 → products	1 × 10^−10	63
25	C2H5O2/CH3O2 → diffusion	2 s^−1	This work
26	HO2 → diffusion	3 s^−1	This work

---

Fig. 2 shows the experimental absorption time-profiles obtained at M1 and E2 for the 3 series (highest C₂H₅O₂ excess upper graph, note the different y-axis for both wavelengths, and lowest C₂H₅O₂ excess bottom graphs) as colored dots: the absorption time-profiles obtained at M1, the wavelength mostly selective to CH₃O₂, are shown in the left column, the profiles obtained at E2, mostly selective to C₂H₅O₂, are shown in the right column.

Fig. 2 Absorption-time profiles at M1 (left graphs) and E2 (right graphs) for all three series with conditions such as given in Table 2. Full lines present the simulated absorption-time profiles using the model from Table 3 and are presented as sum of absorbance due to CH₃O₂ and C₂H₅O₂, dotted lines represent the part of the absorbance due to major radical: CH₃O₂ in the left column, C₂H₅O₂ in the right column.

The profiles at both wavelengths have been simulated simultaneously using the model from Table 3, by best reproducing the signals at M1 as

α_M1 = σ_CH3O2,M1 × [CH₃O₂] + σ_C2H5O2,M1 × [C₂H₅O₂] (2)

and the signals at E2 as:

α_E2 = σ_CH3O2,E2 × [CH₃O₂] + σ_C2H5O2,E2 × [C₂H₅O₂] (3)

using the corresponding absorption cross sections such as given in Table 1. These simulations are shown as full lines. The dotted lines in each graph represent the part of the absorption that is due to the “major” radical, i.e. CH₃O₂ in the left column and C₂H₅O₂ in the right column.

The model contains, next to peroxy self-and cross reactions, also some secondary chemistry of Cl-atoms: these reactions could not completely be avoided, even though their impact is minor. Preliminary results in our laboratory indicate that the reaction of Cl-atoms with C₂H₅O₂ leads with a rate constant of around 1 × 10⁻¹⁰ cm³ s⁻¹ and a yield of 50% to formation of C₂H₅O and ClO, while no clear statement can currently be made for the fate of the other 50%. The rate constant of this reaction has also been determined by Maricq et al.⁶⁴ to be 1.6 × 10⁻¹⁰ cm³ s⁻¹, and therefore this reaction has been included into the mechanism (see Table 3) and tests have been run with the rate constant being varied between 1.0–1.6 × 10⁻¹⁰ cm³ s⁻¹, but the impact on simulated profiles and thus on the sought-after rate constant was within the noise of the experimental profiles.

Fig. 3 shows for the example of the highest C₂H₅O₂ excess (upper graphs of Fig. 2) the breakdown of the fate of the 2 peroxy radicals into the different possible reaction paths: the left graphs represent CH₃O₂, the right graphs C₂H₅O₂. The red symbols represent the fraction of the peroxy radical, which has reacted in the cross reaction (R1): it can be seen that for CH₃O₂, this reaction is the major fate for all initial radical concentrations (upper graph represent blue symbols from Fig. 2, lower graph represent green symbols from Fig. 2), while for C₂H₅O₂ this reaction is a minor loss. The major reaction path for C₂H₅O₂ is its self-reaction (black symbols), with the cross-reaction with HO₂ being the secondary contributor (blue symbols). These two pathways are very minor for CH₃O₂. For both radicals, the fraction having reacted with Cl-atoms (green symbols), is small, up to 5% for CH₃O₂ in the worst case of high initial radical concentration.

Fig. 3 Modeling results for conditions from first raw of Fig. 2 (highest excess of C₂H₅O₂). Left graph CH₃O₂, right graph C₂H₅O₂. Upper graphs are results for lowest Cl-concentration (blue symbols in Fig. 2), lower graph are results for highest Cl-concentration (green symbols in Fig. 2). Open black circles are CH₃O₂/C₂H₅O₂ concentration, blue symbols represent CH₃O₂/C₂H₅O₂ concentration having reacted through cross reaction with HO₂, black symbol represent CH₃O₂/C₂H₅O₂ concentration having reacted through self-reaction, green symbols represent CH₃O₂/C₂H₅O₂ concentration having reacted with Cl-atoms, red symbols represent CH₃O₂/C₂H₅O₂ concentration having reacted through cross reaction with C₂H₅O₂/CH₃O₂.

Determination of branching ratio

Simultaneously measured HO₂ profiles allow in principle the estimation of the branching ratio for the radical and molecular path of the cross reaction. The right graph of Fig. 4 shows the HO₂ profiles obtained for the series with the highest C₂H₅O₂/CH₃O₂ ratio. The initial fast rise of HO₂ has two origins: it is partially due to the reaction of Cl-atoms with the peroxy radicals (R6) and partially due to the small fraction of C₂H₅ radicals that form HO₂ in reaction with O₂(R11b) rather than the C₂H₅O₂ radical. The first process is taken into account in the chemical model by adding a simplified reaction schema (see Table 3), the second process has been implemented to best represent the initial HO₂ concentration and represents less than 1% of the initial C₂H₅ concentration. This observation is in excellent agreement with earlier works.^24,52,65,66 These two processes are finished within a few hundred μs, and the branching ratio of the cross reaction then influences the HO₂ concentration at longer reaction time. This is conceivable, because the HO₂ concentration at longer reaction times represents the steady-state concentration between production from peroxy self-and cross reactions and the consumption through cross reaction of HO₂ with the peroxy radicals. Best results are obtained with a branching ratio towards the radical channel of ϕ_1a = 0.40, i.e. very similar to the branching fraction of the two self-reactions, ϕ_12a = 0.32 and ϕ_13a = 0.37 for C₂H₅O₂ and CH₃O₂, respectively. To demonstrate the influence of the cross reaction on the HO₂ profiles, the full black lines in the right graph represent for the highest radical concentration the simulation with the best rate constant and a branching ratio varied by ±0.2. It can be seen that such variation of the branching ratio makes the model clearly deviating from the experimental results and therefore we estimate the uncertainty of the branching fraction from the comparison between model and experiment to be better than ±0.2.

Fig. 4 Left graph: CH₃O₂ profiles for highest C₂H₅O₂ excess: full lines represent best simulation with rate constants from Table 3 (k₁ = 3.8 × 10⁻¹³ cm³ s⁻¹), dashed lines represent a variation of k₁ of ±1.5 × 10⁻¹³ cm³ s⁻¹. Right graph: HO₂ profiles for the same experiment. Full coloured line represents best model with a radical yield of 0.4, dashed lines in the right graph show the model with k₁ varied as shown in left graph, but the branching ratio varied to best reproduce experiment (see text). The black lines show a variation of ±0.2 for the branching ratio for the highest radical concentration.

However, a major problem for estimating the branching ratio in these experiments is, that even for the self-reactions of the simplest peroxy radicals CH₃O₂ and C₂H₅O₂ there are still large uncertainty in rate constant and branching ratio. For CH₃O₂ the IUPAC recommendation⁵⁴ since many years was k₁₃ = 3.5 × 10⁻¹⁴ cm³ s⁻¹ with a branching ratio of 0.37 for the radical channel. In a very recent work, Onel et al.¹² have re-determined the rate constant and found only k₁₃ = (2.0 ± 0.9) × 10⁻¹⁴ cm³ s⁻¹, nearly 2 times slower, but they confirmed the radical yield as recommended by IUPAC. They convincingly argue that earlier experiments suffered from interferences of the fast reaction of Cl-atoms with CH₃O₂ and this would have increased the apparent rate constant. The rate constant for the self-reaction of C₂H₅O₂ radicals was also recommended by IUPAC for many years at k₁₂ = 7.6 × 10⁻¹⁴ cm³ s⁻¹ with a radical yield of 0.63, based on the measurement of stable end products. Recently, Noell et al.¹⁴ and Shamas et al.²⁴ obtained through direct radical measurements a much lower yield for the radical path and a subsequently higher rate constant (0.32 radical yield leading to k₁₂ = (1.0 ± 0.2) × 10⁻¹³ cm³ s⁻¹). A possible explanation for this disagreement could be a non-negligible yield of dimer-formation, ROOR, in the self-reaction of peroxy radicals. The decomposition of such dimer on reactor walls could lead to formation of aldehydes and thus appear as additional radical formation when measuring stable end products. The dimeric product has very recently been detected in the self-reaction of C₂H₅O₂²⁵ using advanced vacuum ultraviolet (VUV) photoionization mass spectrometry with a yield of 10 ± 5%. The dimer has also been directly detected by CIMS with a yield of 23% in the self-reaction of HOC₂H₄O₂ radicals and has been proven to decompose easily on quartz or metal surfaces.⁶⁷ But even though the cross reaction (R1) is the major HO₂ production path in the current experiments and the two self-reactions are only minor contributors, the above described uncertainties increase of course directly the uncertainty of the deduced yield in this work. Also, the HO₂ signal quality is poor in these experiments due to the absorption of high CH₄ and C₂H₆ concentrations, therefore we estimate the final uncertainty of the radical yield to be ϕ_1a = 0.40 ± 0.20. It should be noted that the uncertainty in the branching ratio has negligible influence on the determination of the rate constant: a change in radical yield for (R1) from 0.2 to 0.6 is barely visible in the modelled absorption-time profiles at both wavelengths.

To demonstrate the sensitivity of the observed absorption-time profiles to the rate constant of the cross reaction, the left graph of Fig. 4 shows the CH₃O₂ profiles of the same experiments, i.e. high excess of C₂H₅O₂. The full lines show again the model from Table 3, while the dashed lines represent a variation of k₁ = (3.8 ± 1.5) × 10⁻¹³ cm³ s⁻¹. Such variation brings the simulated profiles outside the experimental data. In these simulations, the branching ratio ϕ_1a has been adapted to best reproduce the HO₂ profiles (dashed coloured lines on the right graph): for the upper and lower limit of k₁, ϕ_1a was changed to 0.31 (for k₁ = 4.8 × 10⁻¹³ cm³ s⁻¹) and 0.54 (for k₁ = 2.8 × 10⁻¹³ cm³ s⁻¹) to best reproduce HO₂. However, this variation has no influence on the CH₃O₂ profiles as can be seen in Fig. 3 the cross reaction with HO₂ is only a minor path for CH₃O₂ and therefore a change in the branching ratio has a negligible effect on the CH₃O₂ profile. From these simulations we estimate the uncertainty of the rate constant of the cross reaction to be k₁ = (3.8 ± 1.0) × 10⁻¹³ cm³ s⁻¹.

The simulation corresponding to the lower limit of the rate constant (upper curves in Fig. 4) is close to the only published value for the cross reaction rate constant⁴⁵ (k₁ = 2.0 × 10⁻¹³ cm³ s⁻¹), and is can be seen that the observed absorption time profiles are poorly reproduced by such a model. In the work of Villenave et al.⁴⁵ no details are given on how the rate constant was obtained by solely measuring UV absorption profiles, and therefore no speculation about possible reasons for the disagreement can be proposed.

The geometric mean value rule is an empirical approach that allows for the estimation of cross-reaction rate coefficients from the self-recombination rate constants of the reacting partners⁶⁸

It has shown to work to better than 20% in the prediction of radical–radical rate coefficients for a series of hydrocarbon radicals⁶⁹ and has proven to be valid also for the cross reaction of HO₂ and DO₂ radicals.⁷⁰ When applying this rule to the cross reaction of CH₃O₂ and C₂H₅O₂ and using the values for the self-reactions from Table 3, one obtains an excellent agreement (k_{1,geometric rule} = 3.74 × 10⁻¹³ cm³ s⁻¹) with the rate constant obtained in this work. However, when using the value for the CH₃O₂ self-reaction recently obtained by Onel et al.,¹² the geometric mean rule predicts a rate constant for the cross reaction of only k₁ = 2.9 × 10⁻¹³ cm³ s⁻¹. In Fig. 5 are shown the results for both wavelength for the experiments with the lowest C₂H₅O₂ excess, using this rate constant for the cross reaction.

Fig. 5 Series of lowest C₂H₅O₂/CH₃O₂ ratio (lower raw in Fig. 3) with simulations using a rate constant for the cross reaction such as predicted by the geometric mean rule, if using data from Table 3 (full lines) and when using the recently determined rate constant for the CH₃O₂ self-reaction¹² (dashed lines).

It can be seen that this rate constant does not allow to reproduce the observed absorption-time profiles, as the decays at both wavelengths are clearly too slow. However, it has not been demonstrated that in the case of cross-reactions of peroxy radicals the geometric mean rule is a good approximation, in particular because there are no reliable determinations of the rate constants for self- and cross-reactions of peroxy radicals to validate the approach. Therefore, from the current experiments one cannot infer about the rate constant of the CH₃O₂ self-reaction. But it is clear that recent research using more selective detection methods for peroxy radicals, compared to UV absorption, have challenged long-standing results on even the simplest peroxy radicals, and more research is necessary to better understand their reactivity under low NO_x conditions.

Conclusion

The rate constant for the cross reaction of the two most simple and abundant peroxy radicals, CH₃O₂ and C₂H₅O₂, has been determined by following their concentration-time profiles in their respective ÖX̃ electronic transition. A good selectivity has been obtained by working under excess of C₂H₅O₂ and by monitoring CH₃O₂ radical at 7488.13 cm⁻¹ and C₂H₅O₂ radicals at 7602.25 cm⁻¹. A rate constant for the cross reaction of k₁ = (3.8 ± 1.0) × 10⁻¹³ cm³ s⁻¹ and a yield for the radical channel of ϕ_1a = 0.40 ± 0.20 have been obtained. The present rate constant is nearly two times faster than the only earlier value, but in excellent agreement with an estimation based on the mean geometric rule. This work shows again, that the chemistry of peroxy radicals under low NO conditions is still not well understood and more work is needed to improve the knowledge.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is a contribution to the LabEx CaPPA project funded by the French National Research Agency under contract ANR-11-LABX-0005-01 and to the CPER research project ECRIN funded by the French Ministère de l'Enseignement Supérieur et de la Recherche. The authors thank the Regional Council “Hauts-de-France” and the “European Regional Development Fund” for their financial support to these projects. The authors thank Mohamed Assali and Mirna Shamas for assistance with initial experiments. C. Z. and C. L. thanks the Chinese Scholarship Council for financial support (no. 202006340125 (C. Z.) and no. 201908140178 (C. L.)). C. F. thanks the CAS for funding through PIFI no. 2018VMA0055.

References

1. J. J. Orlando and G. S. Tyndall, Chem. Soc. Rev., 2012, 41, 6294–6317.
2. G. S. Tyndall, R. A. Cox, C. Granier, R. Lesclaux, G. K. Moortgat, M. J. Pilling, A. R. Ravishankara and T. J. Wallington, J. Geophys. Res., 2001, 106, 12157–12182.
3. C. Fittschen, Chem. Phys. Lett., 2019, 725, 102–108.
4. B. Veyret, J. C. Rayez and R. Lesclaux, J. Phys. Chem., 1982, 86, 3424–3430.
5. R. A. Cox and G. S. Tyndall, J. Chem. Soc., Faraday Trans., 1980, 76, 153–163.
6. S. P. Sander and R. T. Watson, J. Phys. Chem., 1981, 85, 2960–2964.
7. K. McAdam, B. Veyret and R. Lesclaux, Chem. Phys. Lett., 1987, 133, 39–44.
8. M. J. Kurylo and T. J. Wallington, Chem. Phys. Lett., 1987, 138, 543–547.
9. M. E. Jenkin, R. A. Cox, G. D. Hayman and L. J. Whyte, J. Chem. Soc., Faraday Trans., 1988, 84, 913–930.
10. F. G. Simon, W. Schneider and G. K. Moortgat, Int. J. Chem. Kinet., 1990, 22, 791–812.
11. P. D. Lightfoot, R. Lesclaux and B. Veyret, J. Phys. Chem., 1990, 94, 700–707.
12. L. Onel, A. Brennan, F. F. Østerstrom, E. Cooke, L. Whalley, P. W. Seakins and D. E. Heard, J. Phys. Chem. A, 2022, 126, 7639–7649.
13. F. C. Cattell, J. Cavanagh, R. A. Cox and M. E. Jenkin, J. Chem. Soc., Faraday trans. II, 1986, 82, 1999–2018.
14. A. C. Noell, L. S. Alconcel, D. J. Robichaud, M. Okumura and S. P. Sander, J. Phys. Chem. A, 2010, 114, 6983–6995.
15. H. Adachi, N. Basco and D. G. L. James, Int. J. Chem. Kinet., 1979, 11, 1211–1229.
16. C. Anastasi, D. J. Waddington and A. Woolley, J. Chem. Soc., Faraday trans. I, 1983, 79, 505–516.
17. J. Munk, P. Pagsberg, E. Ratajczak and A. Sillesen, J. Phys. Chem., 1986, 90, 2752–2757.
18. T. J. Wallington, P. Dagaut and M. J. Kurylo, J. Photochem. Photobiol., A, 1988, 42, 173–185.
19. D. Bauer, J. N. Crowley and G. K. Moortgat, J. Photochem. Photobiol., A, 1992, 65, 329–344.
20. F. F. Fenter, V. Catoire, R. Lesclaux and P. D. Lightfoot, J. Phys. Chem., 1993, 97, 3530–3538.
21. D. B. Atkinson and J. W. Hudgens, J. Phys. Chem. A, 1997, 101, 3901–3909.
22. H. Niki, P. D. Maker, C. M. Savage and L. P. Breitenbach, J. Phys. Chem., 1982, 86, 3825–3829.
23. T. J. Wallington, C. A. Gierczak, J. C. Ball and S. M. Japar, Int. J. Chem. Kinet., 1989, 21, 1077–1089.
24. M. Shamas, M. Assali, C. Zhang, X. Tang, W. Zhang, L. Pillier, C. Schoemaecker and C. Fittschen, ACS Earth Space Chem., 2022, 6, 181–188.
25. H. Yue, C. Zhang, X. Lin, Z. Wen, W. Zhang, S. Mostafa, P.-L. Luo, Z. Zhang, P. Hemberger, C. Fittschen and X. Tang, Int. J. Mol. Sci., 2023, 24, 3731.
26. Z. Wen, H. Yue, Y. Zhang, X. Lin, Z. Ma, W. Zhang, Z. Wang, C. Zhang, C. Fittschen and X. Tang, Chem. Phys. Lett., 2022, 806, 140034.
27. P. Dagaut, T. J. Wallington and M. J. Kurylo, J. Phys. Chem., 1988, 92, 3833–3836.
28. G. K. Moortgat, R. A. Cox, G. Schuster, J. P. Burrows and G. S. Tyndall, J. Chem. Soc., Faraday Trans., 1989, 85, 809–829.
29. P. D. Lightfoot, B. Veyret and R. Lesclaux, J. Phys. Chem., 1990, 94, 708–714.
30. A. A. Boyd, P.-M. Flaud, N. Daugey and R. Lesclaux, J. Phys. Chem. A, 2003, 107, 818–821.
31. M. T. Raventós-Duran, M. McGillen, C. J. Percival, P. D. Hamer and D. E. Shallcross, Int. J. Chem. Kinet., 2007, 39, 571–579.
32. P. D. Lightfoot, P. Roussel, F. Caralp and R. Lesclaux, J. Chem. Soc., Faraday Trans., 1991, 87, 3213–3220.
33. P. Dagaut, T. J. Wallington and M. J. Kurylo, J. Phys. Chem., 1988, 92, 3836–3839.
34. M. M. Maricq and J. J. Szente, J. Phys. Chem., 1994, 98, 2078–2082.
35. M. T. Raventós-Duran, C. J. Percival, M. R. McGillen, P. D. Hamer and D. E. Shallcross, Phys. Chem. Chem. Phys., 2007, 9, 4338–4348.
36. A. Bossolasco, E. P. Faragó, C. Schoemaecker and C. Fittschen, Chem. Phys. Lett., 2014, 593, 7–13.
37. C. Fittschen, L. K. Whalley and D. E. Heard, Environ. Sci. Technol., 2014, 118, 7700–7701.
38. C. Yan, S. Kocevska and L. N. Krasnoperov, J. Phys. Chem. A, 2016, 120, 6111–6121.
39. E. Assaf, B. Song, A. Tomas, C. Schoemaecker and C. Fittschen, J. Phys. Chem. A, 2016, 120, 8923–8932.
40. C. Fittschen, M. Al Ajami, S. Batut, V. Ferracci, S. Archer-Nicholls, A. T. Archibald and C. Schoemaecker, Atmos. Chem. Phys., 2019, 19, 349–362.
41. R. L. Caravan, M. A. H. Khan, J. Zádor, L. Sheps, I. O. Antonov, B. Rotavera, K. Ramasesha, K. Au, M.-W. Chen, D. Rösch, D. L. Osborn, C. Fittschen, C. Schoemaecker, M. Duncianu, A. Grira, S. Dusanter, A. Tomas, C. J. Percival, D. E. Shallcross and C. A. Taatjes, Nat. Commun., 2018, 9, 4343.
42. E. P. Faragó, C. Schoemaecker, B. Viskolcz and C. Fittschen, Chem. Phys. Lett., 2015, 619, 196–200.
43. E. Assaf, C. Schoemaecker, L. Vereecken and C. Fittschen, Int. J. Chem. Kinet., 2018, 50, 670–680.
44. E. Assaf, S. Tanaka, Y. Kajii, C. Schoemaecker and C. Fittschen, Chem. Phys. Lett., 2017, 684, 245–249.
45. E. Villenave and R. Lesclaux, J. Phys. Chem., 1996, 100, 14372–14382.
46. J. Thiebaud and C. Fittschen, Appl. Phys. B, 2006, 85, 383–389.
47. A. E. Parker, C. Jain, C. Schoemaecker, P. Szriftgiser, O. Votava and C. Fittschen, Appl. Phys. B., 2011, 103, 725–733.
48. O. Votava, M. Mašát, A. E. Parker, C. Jain and C. Fittschen, Rev. Sci. Instrum., 2012, 83, 043110.
49. E. Assaf, O. Asvany, O. Votava, S. Batut, C. Schoemaecker and C. Fittschen, J. Quant. Spectrosc. Radiat. Transfer, 2017, 201, 161–170.
50. E. N. Sharp, P. Rupper and T. A. Miller, Phys. Chem. Chem. Phys., 2008, 10, 3955–3981.
51. E. P. Faragó, B. Viskolcz, C. Schoemaecker and C. Fittschen, J. Phys. Chem. A, 2013, 117, 12802–12811.
52. C. Zhang, M. Shamas, M. Assali, X. Tang, W. Zhang, L. Pillier, C. Schoemaecker and C. Fittschen, Photonics, 2021, 8, 296.
53. L. S. Rothman, I. E. Gordon, Y. Babikov, A. Barbe, D. Chris Benner, P. F. Bernath, M. Birk, L. Bizzocchi, V. Boudon, L. R. Brown, A. Campargue, K. Chance, E. A. Cohen, L. H. Coudert, V. M. Devi, B. J. Drouin, A. Fayt, J. M. Flaud, R. R. Gamache, J. J. Harrison, J. M. Hartmann, C. Hill, J. T. Hodges, D. Jacquemart, A. Jolly, J. Lamouroux, R. J. Le Roy, G. Li, D. A. Long, O. M. Lyulin, C. J. Mackie, S. T. Massie, S. Mikhailenko, H. S. P. Müller, O. V. Naumenko, A. V. Nikitin, J. Orphal, V. Perevalov, A. Perrin, E. R. Polovtseva, C. Richard, M. A. H. Smith, E. Starikova, K. Sung, S. Tashkun, J. Tennyson, G. C. Toon, V. G. Tyuterev and G. Wagner, J. Quant. Spectrosc. Radiat. Transfer, 2013, 130, 4–50.
54. R. Atkinson, D. L. Baulch, R. A. Cox, J. N. Crowley, R. F. Hampson, R. G. Hynes, M. E. Jenkin, M. J. Rossi and J. Troe, Atmos. Chem. Phys., 2006, 6, 3625–4055.
55. R. X. Fernandes, K. Luther and J. Troe, J. Phys. Chem. A, 2006, 110, 4442–4449.
56. R. X. Fernandes, K. Luther, G. Marowsky, M. P. Rissanen, R. Timonen and J. Troe, J. Phys. Chem. A, 2015, 119, 7263–7269.
57. C. Fittschen, A. Frenzel, K. Imrik and P. Devolder, Int. J. Chem. Kinet., 1999, 31, 860–866.
58. E. Assaf, C. Schoemaecker, L. Vereecken and C. Fittschen, Phys. Chem. Chem. Phys., 2018, 20, 8707.
59. R. Atkinson, D. L. Baulch, R. A. Cox, J. N. Crowley, R. F. Hampson, R. G. Hynes, M. E. Jenkin, M. J. Rossi and J. Troe, Atmos. Chem. Phys., 2004, 4, 1461–1738.
60. V. Daele and G. Poulet, J. de Chimie Physique, 1996, 93, 1081–1099.
61. R. Atkinson, D. L. Baulch, R. A. Cox, J. N. Crowley, R. F. Hampson, R. G. Hynes, M. E. Jenkin, M. J. Rossi, J. Troe and T. J. Wallington, Atmos. Chem. Phys., 2008, 8, 4141–4496.
62. R. Atkinson, D. L. Baulch, R. A. Cox, J. N. Crowley, R. F. Hampson, R. G. Hynes, M. E. Jenkin, M. J. Rossi and J. Troe, Atmos. Chem. Phys. Discuss, 2007, 7, 981–1191.
63. E. Delbos, C. Fittschen, H. Hippler, N. Krasteva, M. Olzmann and B. Viskolcz, J. Phys. Chem. A, 2006, 110, 3238–3245.
64. M. M. Maricq, J. J. Szente, E. W. Kaiser and J. Shi, J. Phys. Chem., 1994, 98, 2083–2089.
65. E. P. Clifford, J. T. Farrell, J. D. DeSain and C. A. Taatjes, J. Phys. Chem. A, 2000, 104, 11549–11560.
66. J. D. DeSain, S. J. Klippenstein, J. A. Miller and C. A. Taatjes, J. Phys. Chem. A, 2003, 107, 4415–4427.
67. S. E. Murphy, J. D. Crounse, K. H. Møller, S. P. Rezgui, N. J. Hafeman, J. Park, H. G. Kjaergaard, B. M. Stoltz and P. O. Wennberg, Environ. Sci.: Atmos., 2023, 3, 882–893.
68. A. W. Jasper, S. J. Klippenstein and L. B. Harding, J. Phys. Chem. A, 2007, 111, 8699–8707.
69. S. J. Klippenstein, Y. Georgievskii and L. B. Harding, Phys. Chem. Chem. Phys., 2006, 8, 1133–1147.
70. M. Assali, J. Rakovsky, O. Votava and C. Fittschen, Int. J. Chem. Kinet., 2020, 52, 197–206.

---