 Open Access Article
Open Access ArticleDirect dissociative recombination of HCO+via the core-excited doublet and the lowest quartet states
Martin
Lehner
 and
Martin
Jungen
and
Martin
Jungen
 *
*
Institut für Physikalische Chemie, Universität Basel, Klingelbergstrasse 80, CH-4056 Basel, Switzerland. E-mail: martin.jungen@unibas.ch
First published on 16th June 2023
Abstract
The dissociative recombination of HCO+ up to 1 eV collision energy is studied. New calculations for several core-excited HCO states provide improved potential energy surfaces crossing the HCO+ ground state surface in the vicinity of its equilibrium geometry. Wave packet analysis leads to significantly higher contributions of the direct mechanism to the cross section for electron energy ε < 0.7 eV than according to earlier studies [Larson et al., Phys. Rev. A, 2012, 85, 042702]. The limit H + CO(a3Π) is found to be the most probable exit channel. We discuss the improved agreement of theory with the latest experiments [Hamberg et al., J. Phys. Chem., 2014, 118, 6034] resulting from combination with the most recent calculations of the indirect process [Fonseca dos Santos et al., J. Chem. Phys., 2014, 140, 164308]. For the lowest quartet surfaces some vibrational states and their population and depopulation (mediated by spin–orbit coupling) are examined.
1. Introduction
The formyl cation HCO+ is one of the most abundant polyatomic ions in interstellar clouds and planetary atmospheres. The observation of its rotational spectrum may serve as a sensitive indicator for density and hence of the star formation rate in molecular clouds. In cold clouds, where the H2 concentration is not directly measurable, the most important production and destruction reactions of HCO+ are H3+ + CO → HCO+ + H2 and HCO+ + e− → H + CO respectively. Both the H3+ and the electron concentration depend on cosmic ray ionization of H2, so the (linear) HCO+ ion tends to be a rather reliable hydrogen density marker.1Dissociative recombination (DR) mechanisms of molecular ions with free electrons are generally classified as direct2 or indirect.3 The direct mechanism is usually dominant, if the potential energy surface (PES) of a (doubly) excited dissociative state crosses the ground state surface of the ion not too far from its equilibrium geometry. The captured electron may then either be re-emitted (autoionization) or the neutral molecule dissociates along the PES. The characteristic for the indirect process is the temporary population of rovibrationally excited Rydberg states followed by predissociation or re-ionization. Both mechanisms may proceed under the same conditions; the total DR cross section can then be evaluated as the incoherent sum of the two processes.
Most theoretical studies agree that in the low electron energy limit for HCO+ (ε ≲ 0.1 eV) the indirect DR mechanism, driven by the Renner–Teller coupling of electronic and nuclear motions, is dominant.4–10 The theory of the indirect mechanism predicts some structure between 0.1 eV and 0.5 eV, drops of σ(ε) (the DR cross section as a function of the colliding energy) connected with the vibrational modes of the ion.6,9,11 However, such declines are only barely visible in the experiments,12,13 if at all. Therefore, based on an analytical model, Schneider et al.8 supposed that these drops are concealed due to a simultaneous direct DR mechanism.
A possible contribution of the direct mechanism to the DR effect has been investigated in a series of papers that have Å. Larson as a common author;14–17 the most comprehensive one is ref. 17 by Larson, Stenrup and Orel, henceforth sometimes abbreviated (LStO). In the work of Nordhorn et al.16 experimental branching ratios of DCO are compared with two-dimensional wave packet model computations for HCO. The results of the (to our knowledge) latest calculation of the total DR cross section,9 combining indirect effects with the direct contributions of (LStO), are systematically about 10% to 20% lower than the CRYRING experiment13 for 0.02 eV ≤ ε ≤ 0.2 eV.
According to the results of the quantum chemical (multi-reference configuration interaction MRCI) calculations of Larson et al.,14,15 no resonant state PES crosses the surface of HCO+(X1Σ+) near its minimum. Larson and Orel15 find the lowest vertical excitation energy for a 2Π resonant state to be 2.21 eV relative to their ionic minimum (at rCH = 2.046ao, rCO = 2.099ao). On the contrary our new MC-CEPA18 calculations show a 4Π and an ion-core-excited (‘resonant’) 2Π surface of HCO with vertical excitation energies only 0.91 eV and 1.72 eV resp. above the same (theoretical) HCO+ minimum, whose crossing seams with the HCO+ PES are for both multiplicities and both spatial symmetries (A′, A′′) partially located within the range of the ionic ground state vibrational wave function. Motivated by this observation we reexamine the possible significance of the direct mechanism to the DR cross section of HCO+. According to our findings the contributions of all open channels add up to a clearly higher cross section of direct DR than in the results of (LStO), who predicted that the energetically high exit channel O + CH(X) is absolutely dominant up to an electron energy of at least 4 eV. We find the limit H + CO(a3Π) (with the lowest possible electronic energy) to be the most probable. Our intention is to determine the dissociation rates for the direct DR processes via the lower core-excited doublet states and to explore the possible contributions of the lowest quartet states (14A′ or 14A′′).
This paper is organized as follows: In Section 2 our quantum chemical calculations of energies and couplings are explained. Some additional details will be given in a separate publication.19 The applied computational methods of wave packet dynamics (on single as well as coupled doublet and quartet surfaces) are introduced in Section 3, and the resulting DR cross sections are presented and discussed in Section 4. A discussion of the differences of our results compared to ref. 9, 15, and 17 and measurements13 is incorporated in Sections 2.4, 4.2, and 5. In Section 6 we introduce population and depopulation rates for long-lived bound vibrational states on the quartet PES, and a concise summary is found in Section 7.
The most recent theoretical papers on HCO, not dealing with DR, focus on the 12A′ and 12A′′ PES including vibrational analysis20 and photodissociation.21,22 The first excited state 12A′′ of HCO may be populated by absorption of a photon from the bent ground state 12A′. As the two states are degenerate at linear geometry (Renner–Teller coupling), the subsequent dissociation proceeds on the 12A′ ground state PES showing an oscillatory pattern of the CO rotational distribution, which has been studied experimentally and theoretically.21 In addition to the vibrational bending excitation of the 12A′′ intermediate state, its rotational excitation and C–H vibrational mode population turns out to be of great importance for the final state CO(ν,j) distribution.22 Usually a molecule (or ion) with the (ground state) PES minimum at non-bent geometry is classified as linear. Winterhoff et al.23 have calculated the bond angle expectation value for HCO+ and DCO+. Their theoretical results are compared with Coulomb Explosion Imaging experiments agreeing on non-linear average bond angles for these undoubtedly linear ions.
2. Electronic states and coupling
2.1 Potential energy surfaces
Here, and in the following sections, we presuppose that the electron in an initial (unbound) 2Π state with continuum energy ε recombines with the (linear) molecular ion HCO+ in its ground state, where (according to Cs classification) the seven orbitals 1a′ to 6a′ and 1a′′ are doubly occupied. In HCO+ 6a′ and 1a′′ are the degenerate components of 1π, whereas in linear HOC+ 1π corresponds to 5a′ and 1a′′, and the highest occupied orbital (HOMO) 6a′ is 5σ. The LUMO of the ion is always 2π (or π*; 7a′ and 2a′′). The a′′ component of 2π remains qualitatively unchanged upon bending while the a′ component is increasingly mixed with the valence orbitals of the ion core. But also in bent geometry these two components form a pair of C–O antibonding valence orbitals.In Table 1 we have collected the experimental energy data of the various adiabatic dissociation limits of some excited HCO surfaces (thereby printing in bold face the numbers of the electronic states discussed here), and also the ground levels of the neutral molecule, the ion, and of the well documented ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state. Note that these energies are not thermochemical data, in contrast to e.g. ref. 13 and 24. The main problem here was the position of the ion within the table. In order to calibrate HCO+ we combined the value of 8.14 eV for the adiabatic ionization potential IPa predicted early by Staemmler25 and observed by Dyke,26 with the value of 0.629 eV for the dissociation energy of HCO, converted by Werner et al.27 from data of ref. 28. The table shows that the 22A′, 22A′′, 14A′ and 14A′′ surfaces all adiabatically dissociate to the limit C(3P) + OH(X2Π) as well as to O(3P) + CH(X2Π), and three of them to H(1s) + CO(a3Π), whereas 22A′′ converges adiabatically to the higher limit H(1s) + CO(d3Δ). None of the four doublet or quartet surfaces considered here dissociates adiabatically to the intermediate limit H(1s) + CO(a′3Σ+) or to the lowest limit H(1s) + CO(X1Σ+). We see that all these limits are either below the minimum energy of the HCO+ ion recombining with a zero energy (ε = 0) free electron or very close above it. The CO interatomic distance of all possible CO fragment states is longer than in HCO+ (by about 10% for a3Π and nearly 25% for a′3Σ+ or d3Δ). Therefore we expect vibrational excitation upon dissociation to H + CO.
state. Note that these energies are not thermochemical data, in contrast to e.g. ref. 13 and 24. The main problem here was the position of the ion within the table. In order to calibrate HCO+ we combined the value of 8.14 eV for the adiabatic ionization potential IPa predicted early by Staemmler25 and observed by Dyke,26 with the value of 0.629 eV for the dissociation energy of HCO, converted by Werner et al.27 from data of ref. 28. The table shows that the 22A′, 22A′′, 14A′ and 14A′′ surfaces all adiabatically dissociate to the limit C(3P) + OH(X2Π) as well as to O(3P) + CH(X2Π), and three of them to H(1s) + CO(a3Π), whereas 22A′′ converges adiabatically to the higher limit H(1s) + CO(d3Δ). None of the four doublet or quartet surfaces considered here dissociates adiabatically to the intermediate limit H(1s) + CO(a′3Σ+) or to the lowest limit H(1s) + CO(X1Σ+). We see that all these limits are either below the minimum energy of the HCO+ ion recombining with a zero energy (ε = 0) free electron or very close above it. The CO interatomic distance of all possible CO fragment states is longer than in HCO+ (by about 10% for a3Π and nearly 25% for a′3Σ+ or d3Δ). Therefore we expect vibrational excitation upon dissociation to H + CO.
| Dissociation limits | E (eV) | 2A′ | 2A′′ | 4A′ | 4A′′ | E el (eV) |
|---|---|---|---|---|---|---|
| a Energy origin: the separated ground state atoms H, C, and O. b Based on the data of the Huber–Herzberg tables.29 c Electronic energies with respect to the HCO+ minimum (zero point energies ZPE subtracted). d Adiabatic ionisation potential IPa = 8.14 eV.25,26 e ZPE = 3466.1 cm−1 (0.430 eV);30 minimum of the HCO+ PES at −4.01 eV. f T o = 38695.5 cm−1 (4.798 eV), ZPE = 2521.6 cm−1 (0.313 eV).30,31 g ZPE = 2691.7 cm−1 (0.334 eV),30Doo = 0.629 eV.27,28 | ||||||
| O(X3Pg) + CH(X2Πr) | −3.465 | 1, 2, 3 | 1, 2, 3 | 1, 2, 3 | 1, 2, 3 | 0.38 |
| H(1s) + CO(d3Δi) | −3.576 | 4 | 2 | 3 | 2 | 0.36 |
| HCO+(X1Σ+)de | −3.58 | 0.00 | ||||
| H(1s) + CO(a′3Σ+) | −4.229 | 3 | 2 | −0.30 | ||
| C(X3Pg) + OH(X2Πi) | −4.392 | 1, 2, 3 | 1, 2, 3 | 1, 2, 3 | 1, 2, 3 | −0.61 |
| H(1s) + CO(a3Πr) | −5.082 | 2 | 1 | 1 | 1 | −1.18 |
| HCO(B2A′)f | −6.923 | −3.23 | ||||
| H(1s) + CO(X1Σ+) | −11.092 | 1 | −7.21 | |||
| HCO(X2A′)g | −11.721 | −8.05 | ||||
In this paper (and in the figures) we apply the appropriate system of Jacobi coordinates r,R,γ depending on the respective dissociation limit, where r denotes the inter-atomic distance in the diatom (CO, OH or CH), R is the distance from the centre of mass of the diatom to the third atom and γ = (r,R) means always a Jacobi angle, while (as in ref. 15 and 17) θ is used for bending angles (θ = 0° for linear arrangement). For the (linear) equilibrium geometry of the ion HCO+ we choose γ(H + CO) = γ(O + CH) = 0°, γ(C + OH) = 180°; the equilibrium of HOC+ is at γ(C + OH) = 0°. (Of course all possible geometries of the triatom HCO can be described by any of these Jacobi coordinate systems.)
The here studied core-excited states of (neutral) HCO are characterised by a single excitation out of the HOMO of the ion into the (now doubly occupied) LUMO components. In the linear molecule the resulting 4Π components are the lowest states of these configurations, followed by a 2Π and a 2Φ state within about 1 eV (and two further 2Π). Complementary to Table 1, Fig. 1 illustrates the paths on the lowest resonant doublet and quartet PES leading to the dissociation limits considered in this study. The lowest core-excited doublet and quartet state PES cross the zero vibration level of the ion close to the minimum of the HCO+ surface, as can be seen in Fig. 2a and b. The 14A′ and 14A′′ surfaces, with minima at bent geometries, are strictly adiabatic. Furthermore – as already conjectured by Bruna et al. (see Fig. 3 of ref. 32) – upon bending the molecule the 2A′ and 2A′′ components of the lowest resonant 2Π state are diabatically connected with the second lowest (adiabatic) PES of their symmetry (22A′ and 22A′′). With increasing bending angle they fall below the lowest quartet PES.
 | ||
| Fig. 1 Energy correlation and reaction coordinate diagram, energies in eV relative to the minimum of the ground state surface of HCO+ (red solid lines). Minimum potential energy paths for the lowest core-excited doublet (blue, purple) and the lowest quartet (green) states as functions of Jacobi coordinate R in the H + CO (blue, green), C + OH (blue) and O + CH (purple) system (solid A′, dashed A′′). All curves start at the equilibrium geometry of HCO+ (filled rectangles). The coordinate values r and γ are energy optimised with limited variation between adjacent sampling points in order to avoid irregularities. Vibrational zero point energies (dotted horizontal lines). Some calculated vibrational energies for the quartet (14A′, 14A′′) and the HCO+ (X) PES are given in Table 3, doublet vibration (22A′, 22A′′) will be discussed in a forthcoming paper19). | ||
The doublet minima have been named ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) (22A′) and
(22A′) and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) (22A′′) by Tanaka and Davidson.33 As in the region of the minima the quartets are very similar to the doublets, we propose – violating the rules of nomenclature – to call them
(22A′′) by Tanaka and Davidson.33 As in the region of the minima the quartets are very similar to the doublets, we propose – violating the rules of nomenclature – to call them ![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) (14A′) and
(14A′) and ![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) (14A′′). The characteristics of the minima are given in Table 2, and a section through their almost coinciding potential wells is shown in Fig. 2c (for the quartets see also Fig. 4 and Table 3). The bond lengths in Table 2 are about 10−1ao shorter than the corresponding results of the CI-based results of ref. 33; our Te values are up to 1 eV higher than those. Compared to more recent calculations (e.g. ref. 47) the differences of lengths are in the order of 10−2ao, of energies typically a few times 10−1 eV.
(14A′′). The characteristics of the minima are given in Table 2, and a section through their almost coinciding potential wells is shown in Fig. 2c (for the quartets see also Fig. 4 and Table 3). The bond lengths in Table 2 are about 10−1ao shorter than the corresponding results of the CI-based results of ref. 33; our Te values are up to 1 eV higher than those. Compared to more recent calculations (e.g. ref. 47) the differences of lengths are in the order of 10−2ao, of energies typically a few times 10−1 eV.
| r CO (ao) | r CH (ao) | ∢HCO (°) | T e (eV) | ||
|---|---|---|---|---|---|
| HCO+ | 11Σ+ | 2.08 | 2.06 | 180 | 8.00 |
![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) |
22A′′ | 2.69 | 2.08 | 108 | 5.04 |
![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) |
14A′ | 2.65 | 2.05 | 122 | 4.94 |
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) |
22A′ | 2.57 | 2.08 | 115 | 4.90 |
![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) |
14A′′ | 2.62 | 2.04 | 118 | 4.83 |
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) |
12A′ | 2.24 | 2.12 | 126 | 0.00 |
| E min (eV),γ | −3.060, 34° | −3.177, 36° | 0.000, 0° | −2.740, 68° | 1.633, 0° |
|---|---|---|---|---|---|
| r, R, (label) | 2.65, 3.12, ![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) |
2.62, 3.05, ![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) |
2.08, 3.25 | 1.82, 2.60, ![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) ′* ′* |
1.86 2.28* |
| ν 1 ν 2 ν 3 | 14A′ | 14A′′ | HCO+ | 14A′′ | HOC+ |
| 0 0 0 | −2.728 eV | −2.840 eV | 0.426 eV | −2.353 eV | 1.987 eV |
| 0 1 0 | 1077 | 1002 | 846 | 1133 | 250 |
| 0 0 1 | 1174 | 1226 | 2171 | 1261 | 1994 |
| 0 2 0 | 2138 | 2002 | 1622 | 2248 | 551 |
| 0 1 1 | 2234 | 2222 | 2944 | 2364 | 2223 |
| 1 0 0 | 2993 | 3081 | 3011 | 3673 | 3345 |
| 0 0 2 | 2341 | 2449 | 4111 | 2521 | 3962 |
| 0 3 0 | 3176 | 2994 | 2376 | 3337 | 880 |
| 0 0 3 | 3493 | 3646 | 3775 |
2.2 Method
All calculations of PES points are based on a version of the the multi-configuration reference coupled electron pair approximation method (MC-CEPA) by Fink and Staemmler,18 modified for applications including electronically excited states. This program processes the input of a multi-configuration reference function of Slater determinants. The orbitals – initially generated from self-consistent field (SCF) calculations (as a rule for the ionic ground state, sometimes directly for a desired configuration) – were improved by iterated medium size CI (configuration interaction) computations, separately for both A′- and A′′-symmetry. The orbitals had an expansion length of about 180 ANO (atomic natural orbitals34) Gaussians, augmented in special cases up to more than 200 and including also elements for the description of low-lying Rydberg or continuum orbitals.35 The CI consisted of roughly 104 configurations, and using transformations to natural orbitals (by diagonalizing a single-particle density matrix) the length of the constructed reference function could in most cases be restricted iteratively to a number between one and approximately a dozen determinants of the most important configurations. In order to avoid stepping down in the CEPA procedure to an unwanted solution at lower energy we have removed certain single de-excitations in the list of single and double excitations generated by this program. As a rule this was sufficient for separating core-excited configurations from the singly excited Rydberg and continuum wave functions. At a few critical points we used an auxiliary wall potential as proposed by Guérout et al.36 (details in Section 2.3) with the effect that the diffuse solutions were shifted to higher energies, while the valence states changed only negligibly. We have computed the PES for R values below 6ao; for the needs of wave packet propagation the surfaces have then been extrapolated numerically towards their correct (experimental) dissociation potentials (Table 1) up to about R = 11ao, thereby avoiding the CEPA energy error connected with the dissociation of a triple bond. For the linear minimum of the HCO+ PES we obtain −113.3927 a.u. (with frozen and non-correlated inner electron pairs 1s(C) and 1s(O)), to be compared with −113.3562 a.u. in ref. 14 and −113.1347 a.u. in ref. 15 and 17. Our calculated (electronic, adiabatic) ionization potential of HCO is 0.294 a.u. (8.00 eV, 0.05 eV less than the ZPE-corrected experimental value of Table 1).For the construction of the diabatic core-excited 2A′ and 2A′′ surfaces the reference function was restricted to all Slater determinants with 13 electrons occupying the most stable 7 orbitals, two more electrons in the components of the π* LUMO or its a′ and a′′ Cs counterparts, and iterated as explained above. Rather to the surprise of the authors this ansatz led to a very smooth (quasi)-diabatic transition from the components of the linear core-excited 2Π state embedded in the continuum to the adiabatic 2 2A′ and 2 2A′′ PES within R < 4ao, r < 2.7ao and γ < 80°, without an appropriate diabatization procedure. Outside of this area we use the adiabatic doublet surfaces. This passage is documented with three one-dimensional sections through the surfaces in the plots of Fig. 3. The diabatic doublet state Ψd surfaces (blue in the Fig. 2a and b and 3) coincide everywhere with the strictly adiabatic PES (2 2A′ and 2 2A′′) except for a region not too far from the ion equilibrium geometry, where the adiabatic (yellow in Fig. 2, black in Fig. 3) and diabatic PES split. At linear geometry (Fig. 3a) the core-excited doublet and quartet states are degenerate Π states; at r ≈ 2.4ao the adiabatic 22Π curve separates from the diabatic state. The (blue) diabatic doublet curve falls below the ion minimum for r ≥ 2.28ao (at R = 3.20ao). In C∞v symmetry the second lowest adiabatic 2A′′ corresponds to the A′′ component of 22Π, whereas the second 2A′ can be a 2Σ or the A′ component of a 2Π, depending on the order of those states at different geometries (see the crossing of 22Σ and 22Π in plot Fig. 3a). The curves in Fig. 3b show the situation for r = 2.06ao (and R = 3.20ao): the adiabatic curves 22A′, 32A′ and 42A′ turn into 12Σ, 22Σ and 22Π for γ → 0. Remarkably enough the 32A′ state features an increasing percentage of the core-excited configuration for γ ≥ 45° (and r = 2.06ao). At r = 2.06ao the core-excited A′ state stays above 22A′, but coincides with the 32A′ adiabatic state for sufficiently large γ. The seams, where the 22A′ and 22A′′ states reach the core-excited configurations, intersect the r = 2.28ao coordinate plane at γ ≈ 38° and 48° respectively (see curves in Fig. 3c).
In other words the surfaces associated with the core-excited structure are merged into the second adiabatic doublet PES of both symmetries for γ around 40° to 60° (and not too small values of r). Thus the DR process may be described by wave packets starting on the core-excited doublet surfaces at the equilibrium geometry of the ion, and subsequently propagating ‘downhill’ on the diabatic surfaces towards larger r and γ, where the (adiabatic) dissociation limits of the 22A′ and 22A′′ PES are within reach. The lowest one is H + CO(a3Π), not accessible for 2A′′ electronic symmetry (see Table 1). To sum up, the wave packets describing the dissociation process on the doublet surfaces pass through three PES regions: Resonant state, diabatic transition zone, and second adiabatic state of Cs-symmetry. As mentioned above, the multi-configuration reference function as input for the MC-CEPA program was restricted to core-excited configurations in the initial region.
The doublet system and the lowest quartet states Ψq are coupled by spin–orbit interaction. The dominant one-particle contribution of the Breit–Pauli operator HSO leads to non-vanishing matrix elements 〈4A′|HSO|2A′′〉 and 〈4A′′|HSO|2A′〉 between configurations of opposite spatial Cs-symmetry,37,38 and the wave packet may partially pass from the doublet PES over to the quartet. As mentioned in Section 2.1 both doublet surfaces fall below the coupling quartet PES for sufficiently bent geometry. Part of the energetically accessible doublet–quartet transition area is to be seen in the central parts (around γ ≈ 40°) of Fig. 2 and 3. On the other hand the spin–orbit matrix elements coupling directly the initial (doublet) continuum state to one of the dissociative quartet surfaces are expected to be very small due to the fact that the involved Slater determinants differ in more than one spatial orbital.
On the lowest 4A′ and 4A′′ PES the dissociation channels to H(1s) + CO(a3Π) as well as to C(3P) + OH(X2Π) are open for the considered initial energy range, as is documented in Table 1 and Fig. 4. The dissociation path leading to the higher limit O(3P) + CH(X2Π) after spin–orbit transition to one of the quartet surfaces was not incorporated in the present study. The 14A′ surface has only one minimum (![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) ), located at bent geometry on the HCO side (see Table 3; the groove in the left part of plot 4a shows the exit channel to C + OH with r → ∞), the 4A′′ PES has a HCO (
), located at bent geometry on the HCO side (see Table 3; the groove in the left part of plot 4a shows the exit channel to C + OH with r → ∞), the 4A′′ PES has a HCO (![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) ) as well as a HOC minimum (
) as well as a HOC minimum (![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) ′, see Section 6 for further details). The saddle point between these two minima is near −1.0 eV and rCO ≈ 2.60ao, rCH ≈ 2.35ao, and rOH ≈ 2.30ao. The relative strength of the various coupling mechanisms is discussed in the following subsection.
′, see Section 6 for further details). The saddle point between these two minima is near −1.0 eV and rCO ≈ 2.60ao, rCH ≈ 2.35ao, and rOH ≈ 2.30ao. The relative strength of the various coupling mechanisms is discussed in the following subsection.
All involved PES were calculated on a regular grid in Jacobi coordinates (15 angles γ, Δr = 0.12ao, ΔR = 0.2ao) and interpolated by three-dimensional spline functions. The density of the grid was enhanced in various critical regions (for example around the local minima).
2.3 Electronic coupling matrix elements
ΨΛc(ε) denotes the components of the initial antisymmetrized electronic wave function of the neutral unbound system (HCO+ + electron with energy ε in a continuum orbital χΛπ), where Λ abbreviates A′ or A′′. ΨΛd means the symmetry components (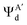 or
or  ) of the core-excited 2Π state, and Φo is the vibrational ground state wave function of the ion HCO+. The transition from the initial state ΨΛc to ΨΛd is mediated through the electronic Hamiltonian Hel,39 where the coupling matrix element
) of the core-excited 2Π state, and Φo is the vibrational ground state wave function of the ion HCO+. The transition from the initial state ΨΛc to ΨΛd is mediated through the electronic Hamiltonian Hel,39 where the coupling matrix element| VcdΛε(r,R,γ) = 〈ΨΛc(ε)|Hel|ΨΛd〉e, | (1) |
| ΩΛε(r, R, γ, t = 0) = VcdΛε(r, R, γ)·Φo(r, R, γ). | (2) |
| ΓΛε(r, R, γ) = 2π(VcdΛε(r, R, γ))2. | (3) |
As the continuum wave functions ΨΛc(ε) contribute to VcdΛ in eqn (1) only in a restricted radial and angular range around the equilibrium conformation of the ion (defined by the size of its occupied orbitals), they may be described within this region by conventional quantum chemical methods, using an auxiliary wall potential (AWP) as proposed by Guérout et al.,36 in order to obtain a locally correct description of χΛπ. The applied cubic box, centred at the positive charge centre of the HCO+ ion, with half length ρ = 11ao in the three Cartesian coordinates ξj, zero potential W = 0 inside and slope  was chosen to be large enough to not affect the slender lower bound electronic states. The box parameter b (the ‘steepness’ of the wall) then only controls the shape of the (pseudo-)continuum orbital χΛπ within the box and allows the variation of its energy. A linear combination of regular and irregular Coulomb functions fl and gl41 (with angular momentum l = 1) was fitted to the radial part of the quantum chemically calculated continuum orbitals in order to determine the energy ε of the captured electron and to energy normalize the wave functions. An additional angular momentum analysis at linear configurations confirmed the pπ character of the continuum orbitals.
was chosen to be large enough to not affect the slender lower bound electronic states. The box parameter b (the ‘steepness’ of the wall) then only controls the shape of the (pseudo-)continuum orbital χΛπ within the box and allows the variation of its energy. A linear combination of regular and irregular Coulomb functions fl and gl41 (with angular momentum l = 1) was fitted to the radial part of the quantum chemically calculated continuum orbitals in order to determine the energy ε of the captured electron and to energy normalize the wave functions. An additional angular momentum analysis at linear configurations confirmed the pπ character of the continuum orbitals.
V cdΛε was then calculated numerically at the CI level on a three-dimensional grid of (nuclear) geometries around the equilibrium conformation of the ion, applying two different orbital sets for the ε-adjusted continuum state (b > 0) and the core-excited doublet state (b = 0). The selected p-orbitals were shifted to 0.02 < ε < 0.8 eV (and in some cases 1.0 eV) by box parameters b in the range 2 × 10−8 to 9 × 10−7 a.u. ao−8. The evaluation of the matrix elements in eqn (1) involved the transformation between the two sets of orbitals and consideration of contributions from the one- and two-particle operators (i.e. one or two occupation differences of the contributing Slater determinants). As a rule increasing r or ε lets the interaction matrix element decline, whereas VcdΛε is slightly enlarged with increasing R. For low energies it is nearly ε independent; at the equilibrium of HCO+ and ε = 0.1 eV we obtain Γ = 564 cm−1. But it was found that the characteristics of VcdΛε(r, R, γ) are symmetry dependent: bending the molecule significantly increases (decreases) its value for Λ = A′ (A′′). This becomes evident if alternatively the coupling strength of the core-excited doublet states to initial continuum is characterized by the (geometry independent) expectation values
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) ε,Λ = 〈Φo(r,R,γ)2·VcdΛε(r,R,γ)〉n, ε,Λ = 〈Φo(r,R,γ)2·VcdΛε(r,R,γ)〉n, | (4) |
 while
while 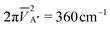 is significantly smaller due to the opposed γ-dependence of the VcdΛ.
is significantly smaller due to the opposed γ-dependence of the VcdΛ.
As mentioned in Section 2.2 the Breit–Pauli spin–orbit matrix elements VcqΛ = 〈Ψc(ε)|HSO|ΨΛq〉e, coupling electronic continuum directly to the lowest quartet states, are for both symmetries much smaller than VcdΛ, thus their contribution to the DR cross section is neglected.
2.4 Comparison with previous calculations
Larson and Orel15 show doublet potential curves for the core-excited (resonant) states as functions of rCO, rCH and the bending angle θ. While their rCO dependence agrees well with our curve for the lowest resonant 2Π state – compare the position of the core-excited doublet and quartet curves in Fig. 3b and c – the other plots exhibit distinct differences: The lowest 2A′ and 2A′′ potentials in ref. 15 are practically constant as functions of θ (for rCO = 2.08ao, rCH = 2.0ao), whereas our corresponding curves decrease monotonically up to γ≈50° and cross the HCO+ potential at γ ≈ 24° (θ ≈ 38°) and γ ≈ 33° (θ ≈ 52°) respectively (Fig. 3b). And as a function of rCH our 2Π curve falls partly below the ion surface first for rCO ≥ 2.22ao (Fig. 3c), in contrast to in ref. 15 where the lowest resonant curve intersects the ion PES at rCH ≈ 3.3ao (for rCO = 2.08ao and θ = 0°). In ref. 17 a rather crude method for obtaining three-dimensional surfaces is introduced, neglecting the fact that rCO increases on dissociation to H + CO. The dissociation limits and the electronic states of the fragments are not specified. Our results for the resonance state are lower in energy than those of (LStO), i.e. they cross the ion PES closer to its minimum.The descriptions of the applied quasidiabatization methods here and in ref. 15 sound quite similar, but they lead to different results. It seems that the quasidiabatized surfaces of (LStO) are not connected with the 22A′ (![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) ) or 22A′′ (
) or 22A′′ (![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ) states of HCO; in any case these core-excited states are never mentioned in their texts. The differences are probably due to the unlike angular comportment of the resonance state PES.
) states of HCO; in any case these core-excited states are never mentioned in their texts. The differences are probably due to the unlike angular comportment of the resonance state PES.
In contrast to our AWP approach (LStO) use the complex Kohn variational method42,43 to calculate the autoionization width Γ. They detect a considerable increase of Γ at geometries, where the ionic and resonant state PES come close. For the lowest 2Π resonant state at linear geometry with rCH = 2.0ao, rCO = 2.08ao they obtain Γ = 290 cm−1, about half our value mentioned above. But due to technical limitations concerning their program the θ-dependence of Γ was disregarded in ref. 17, which might lead to an underestimation of the (direct) DR cross section as result of too small a contribution of the core-excited 2A′ state (and by comparison too high for 2A′′).
3. Wave packet dynamics
This section is dedicated to the construction and propagation of wave packets of nuclear motion moving on the diabatized PES (introduced in Section 2.2), from the geometry of electron capture to the various dissociation limits of the adiabatic 22A′ and 22A′′ surfaces (in Section 3.1) or, after a doublet–quartet transition, to the dissociation limits of the lowest quartet surfaces (in Section 3.2). From the results DR cross sections as functions of the electron energy ε and also the (H + CO)/(C + OH) branching ratio (in Section 4.1), as well as the occupation of vibrational levels of the CO(a3Π) fragment (in Section 4.3) will be derived.3.1 Wave packet propagation on a single core-excited doublet surface
We start the exposition of our wave packet calculations with the case of motion on a single PES U(r,R,γ). The propagating wave packet ΩJM(r,R,γ,t) with rotational quantum numbers JM is expanded in an (orthonormal) Jacobi coordinate product basis set of the diatomic fragment (r) and the dissociation channel (R)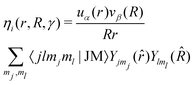 | (5) |
We may write the solution
 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, the Lanczos algorithm46 was applied (as in our previous study on predissociation of H345) to transform it into tridiagonal form in a new basis covering the range up to R ≈ 11ao, in which wave packet dynamics could be carried out efficiently. The Lanczos transformation is the most time consuming step of the procedure, but it is performed only once and greatly accelerates the propagation step for any chosen energy E. Eqn (6) was integrated numerically, using a fourth order expansion of the integrand and Δt = 10−3 fs time steps.
000, the Lanczos algorithm46 was applied (as in our previous study on predissociation of H345) to transform it into tridiagonal form in a new basis covering the range up to R ≈ 11ao, in which wave packet dynamics could be carried out efficiently. The Lanczos transformation is the most time consuming step of the procedure, but it is performed only once and greatly accelerates the propagation step for any chosen energy E. Eqn (6) was integrated numerically, using a fourth order expansion of the integrand and Δt = 10−3 fs time steps.
Unfortunately the employed Jacobi coordinates (r,R,γ), where r asymptotically is the bond length of the respective diatomic product, are not well suited for the simultaneous description of multiple dissociation limits (H + CO, C + OH, O + CH). Therefore the branching ratios could only be estimated by carrying out separate wave packet calculations in every Jacobi coordinate system. As dissociation to the respective other fragmentation channels corresponds to r → ∞, it is important to use a sufficiently extended r-basis.
Optionally an alternating propagation technique was introduced as an attempt to improve interaction of the two most important 2A′ channels in the early stages of wave packet motion. During the first 16 fs propagation was alternated every fs between the two channels H + CO and C + OH, transforming the current wave packet to the respective other Jacobi coordinate system. This periodic superposition of the wave packets, calculated in different Jacobi coordinate systems, could be restricted to the (geometrically) inner part of non-vanishing overlap of the two channels. It was damped with the time constant τ (of eqn (6)), implicating the possibility of initial amplitude exchange between channels. This procedure also increases the number of necessary integration time steps (not, of course, the real time to dissociation). The effect of the alternating propagation approach on branching ratio and cross sections will be discussed in Section 4.1.
3.2 Wave packets on coupled (doublet and quartet) surfaces
As stated in Section 2.3 the direct recombination process typically leads to a population of the core-excited doublet states. At linear configuration the matrix elements of spin–orbit interaction 〈HaSO〉 = 〈4A′′|HSO|2A′〉 and 〈HbSO〉 = 〈4A′|HSO|2A′′〉 are both approximately 50 cm−1; 〈HaSO〉 remains practically constant as a function of the Jacobi angle (see also ref. 47), whereas 〈HbSO〉 is distinctly smaller in the vicinity of the intersection of the corresponding PES (4A′, 2A′′). The pairs of surfaces to be coupled are labeled [Uad(2A′), Uaq(4A′′), and Ubd(2A′′), Ubq(4A′)], respectively. In order to carry out coupled wave packet calculations we follow the method introduced by Mead and Truhlar.48 For every point (r,R,γ) of the PES a 2 × 2 matrix of the elements (Uid and Uiq) of the two interacting states on the diagonal and 〈HiSO〉 as coupling element is diagonalized; the mixing ratio is interpreted as sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑi and cos
ϑi and cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑi of an additional (geometry-dependent) mixing angle ϑi(r,R,γ) (with i = a or b). In a second step the initial elements of Uid, Uiq and 〈HiSO〉 are replaced by
ϑi of an additional (geometry-dependent) mixing angle ϑi(r,R,γ) (with i = a or b). In a second step the initial elements of Uid, Uiq and 〈HiSO〉 are replaced byUi11(r,R,γ) = Uid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2ϑi + Uiq cos2ϑi + Uiq![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2ϑi sin2ϑi | (7) |
Ui22(r,R,γ) = Uid![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2ϑi + Uiq sin2ϑi + Uiq![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2ϑi cos2ϑi | (8) |
Ui12(r,R,γ) = (Uid − Uiq) sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑi ϑi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑi. ϑi. | (9) |
4. Direct DR cross sections
4.1 Method and results
Regardless of whether time evolution of the wave function Ωε(t) is restricted to a doublet PES or whether the quartet component of a coupled propagation is considered, the cross section for dissociative recombination may be calculated via projection of the asymptotic wave packet onto the (energy normalized) final states | (10) |
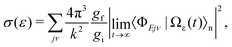 | (11) |
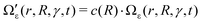 with a function c(R) prior to integration over R in eqn (11). A (real) damping function at the outermost end of the R-basis was found to be more effective to prevent disturbing wave packet reflection at the end of the basis set vβ(R) than application of an imaginary absorbing potential.
with a function c(R) prior to integration over R in eqn (11). A (real) damping function at the outermost end of the R-basis was found to be more effective to prevent disturbing wave packet reflection at the end of the basis set vβ(R) than application of an imaginary absorbing potential.
Fig. 5 shows the computed DR cross sections σ as functions of the initial energy ε of the free electron. Our computations are limited to energies between 0.02 eV and 1 eV, because energy control of the incoming electron with too low energy is difficult (see Section 2.3) and because the use of a basis (5) suited for higher energies renders the Lanczos procedure clumsy and slow. For both symmetries (A′, A′′) the sums of the squared L2-norms of the asymptotic parts  of the wave packets were calculated as a quality check. In the energy range 0 < ε < 0.9 eV the deviations of these sums from unity nowhere exceeded 0.1, and only slightly between 0.9 eV and 1.0 eV. Thus the applied technique of separately calculating the contributions to the DR cross section for every exit channel appears to be justified. In particular we may conclude that the percentage of the wave packet that remains in the vicinity of initial geometry, when treated within one of the three Jacobi coordinate systems, represents the share, which dissociates to the other two exit channels. Furthermore, the convolution function c(R) seems to be reasonably chosen. The remaining (minor) total normalization error was corrected for with energy-dependent factors (individually for both symmetries) resulting in the dashed curves in Fig. 5. As to be expected, propagation on the dissociative (diabatic) 2A′ PES is clearly the most important of all considered (direct) reaction mechanisms, and the limit H + CO (blue crosses) is more probable than C + OH (red stars) or O + CH (cyan disks). At ε = 0.15 eV the cross section ratio is σH+CO/σC+OH ≈ 2.7. Dissociation to H + CO(a) is also supported by the experiments by Adams and Babcock,51 and by Rosati et al.24 who detected CO(a3Πr) in a plasma producing HCO+ that subsequently reacts with free electrons.
of the wave packets were calculated as a quality check. In the energy range 0 < ε < 0.9 eV the deviations of these sums from unity nowhere exceeded 0.1, and only slightly between 0.9 eV and 1.0 eV. Thus the applied technique of separately calculating the contributions to the DR cross section for every exit channel appears to be justified. In particular we may conclude that the percentage of the wave packet that remains in the vicinity of initial geometry, when treated within one of the three Jacobi coordinate systems, represents the share, which dissociates to the other two exit channels. Furthermore, the convolution function c(R) seems to be reasonably chosen. The remaining (minor) total normalization error was corrected for with energy-dependent factors (individually for both symmetries) resulting in the dashed curves in Fig. 5. As to be expected, propagation on the dissociative (diabatic) 2A′ PES is clearly the most important of all considered (direct) reaction mechanisms, and the limit H + CO (blue crosses) is more probable than C + OH (red stars) or O + CH (cyan disks). At ε = 0.15 eV the cross section ratio is σH+CO/σC+OH ≈ 2.7. Dissociation to H + CO(a) is also supported by the experiments by Adams and Babcock,51 and by Rosati et al.24 who detected CO(a3Πr) in a plasma producing HCO+ that subsequently reacts with free electrons.
Typically the wave packet fraction transferred from the 2A′ to the 4A′′ surface is of the order 10−4 and its contribution (marked with black diamonds in the lower part of Fig. 5) to the cross section is very small. As mentioned in Section 2.2 the spin–orbit matrix elements coupling the initial electronic doublet (continuum) state directly to the quartet surfaces is negligibly small and is not incorporated in Fig. 5.
The solid curves in the upper plot of Fig. 5 show the effect of the alternating propagation technique between the two channels H + CO and C + OH (on the 2A′ PES, as explained at the end of Section 3.1), which led to an enlargement of the branching ratio (σH+CO/σC+OH) to about 5.3 at ε = 0.15 eV and to a slightly larger total direct cross section. And the total number of time steps Δt to reach the asymptotic region of evaluation was increased to about 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, without affecting the final translational energies in both channels. The total normalization correction was carried out analogously as outlined above. The increase of the branching ratio is associated with a weaker (final state) vibrational CO excitation (see Section 4.3), hence channel interaction during the prolonged initial propagation phase might facilitate vibrational relaxation of the wave packet.
000, without affecting the final translational energies in both channels. The total normalization correction was carried out analogously as outlined above. The increase of the branching ratio is associated with a weaker (final state) vibrational CO excitation (see Section 4.3), hence channel interaction during the prolonged initial propagation phase might facilitate vibrational relaxation of the wave packet.
4.2 Discussion
For a number of reasons the recombination process populating the 2A′′ state yields for ε < 0.5 eV (green, brown and orange curves in Fig. 5) a significantly smaller cross section than 2A′ (blue, red): The coupling matrix element to continuum is at bent geometries smaller than for 2A′, the 2A′′ PES has a higher H + CO(d3Δ) dissociation limit, and the intersection with the ionic PES is located somewhat less favorable (see Fig. 2a and b). Moreover the spin–orbit matrix element mediating the coupling to the (dissociative) 4A′ state changes sign near the doublet–quartet intersection seam, thus this quartet contribution to the cross section is even smaller than for 2A′ → 4A′′. And the low limit C + OH, accessible also for 2A′′ symmetry, requires breaking the CO bond.
is at bent geometries smaller than for 2A′, the 2A′′ PES has a higher H + CO(d3Δ) dissociation limit, and the intersection with the ionic PES is located somewhat less favorable (see Fig. 2a and b). Moreover the spin–orbit matrix element mediating the coupling to the (dissociative) 4A′ state changes sign near the doublet–quartet intersection seam, thus this quartet contribution to the cross section is even smaller than for 2A′ → 4A′′. And the low limit C + OH, accessible also for 2A′′ symmetry, requires breaking the CO bond.
The electronic energies of the dissociation limits H + CO(d3Δ) and O + CH(X) correspond quite precisely to the initial level of HCO+ including its ZPE, but are a little higher. Asymptotically at least the vibrational ground state of the diatom has to be accessible, hence the contributions of H + CO(d3Δ) and O + CH(X) to the DR cross section vanish for ε → 0. As the vibrational frequency ωe = 1172 cm−1 for CO(d3Δ) is considerably lower than ωe = 2859 cm−1 for CH(X), the consequent decrease of σ(ε) in Fig. 5 is shifted to higher energies ε in the latter case (compare the low energy end of the cyan and orange curves in Fig. 5b). The weak structure in the O + CH curves may be interpreted as follows: Around ε ≈ 0.2 eV only νCH = 0 is within reach, whereas at ε ≈ 0.55 eV νCH = 1 begins to contribute.
According to the computations of Larson et al. (LStO)17 direct DR of HCO+ proceeds (for ε < 2.5 eV) mainly via the same (lowest) 2Π resonant state as is considered in our present study. But in contradiction to our results they predict the O + CH channel to be absolutely dominant for ε < 4 eV, and their total direct cross section is clearly lower than ours up to ε ≈ 0.6 eV (see Fig. 7 in Section 5). For example they determine the direct DR cross section to be about 1.4 × 10−16 cm2 at ε = 0.15 eV, whereas our value at the same energy is 5.01 × 10−16 cm2 (or even 5.45 × 10−16 cm2 with the alternating propagation method). This discrepancy may be explained for one thing by the less advantageous intersection of their doublet (resonant) surfaces with the ionic PES, but more importantly by their weaker coupling Vcd (eqn (3)) to continuum.15 In ref. 17 the A′ and A′′ share turn out to be approximately the same size, which may be explained by the neglected dependence of Γ upon bending (see Section 2.3). In our calculations the A′ contribution is distinctly augmented by the increase of width Γ as a function of γ. According to ref. 7 (LStO) compute the direct to indirect effect ratio to be 17% at ε = 0.13 eV. And they find a minimum of the cross section resulting from the lowest 2Π resonant state at ε ≈ 0.5 eV, where our σ value is about twice as large and – in contrast to (LStO) – our total direct σ(ε) is monotonically decreasing for all examined electron energies and arrives at 10−17 cm2 near 1.0 eV.
Interestingly (LStO) state the analogous dominance of the DC + O channel for direct DR of DCO+ as in the case of HCO+. But with a simple Landau-Zener52 model allowing coupling and flux redistribution to Rydberg states they find the low energy branching ratio to completely change to approximately 85% D + CO (in accordance with the experiments at the Heidelberg TSR16). Disregarding any coupling to Rydberg states we obtain 72% H + CO(a3Π) at ε = 0.1 eV for the contribution of the direct mechanism (solid blue curve in Fig. 5).
Higher resonant states might turn out to be important for direct DR with increasing ε. In preliminary calculations we have found the lowest 2Φ to be the most promising additional state. We obtain about 6000 cm−1 as the vertical energy difference between 2Π and 2Φ at the equilibrium geometry of HCO+ and 2Φ crosses the ionic surface about 1500 cm−1 above the ZPE of the ion.
4.3 Vibrational analysis of CO(a)
For 2A′ → H + CO(a3Π) a final state vibrational analysis was carried out by projecting the r dependence of the (asymptotic) wave packet onto a set of vibrational CO wave functions. As may be seen in Fig. 6 the population of the six lowest vibrational states is quite stable as a function of ε (though the results are rather uncertain for levels higher than ν = 5 due to the limited dimension of the r-basis). In the initial transition region the core-excited 2A′ PES features a pronounced slope towards larger r (see Fig. 2a), which might in combination with the excess energy explain why even for low ε some excited vibrational states are notably populated. Except for the population of the level ν = 0 our results are in qualitative agreement with the Rosati experiment24 insofar as for the levels 1 to 4 approximately equal (not thermal) populations are predicted. For the population of the ground level however Rosati finds 45%, more than twice our value. But then our calculations do not exactly correspond to the setup of this experiment, e.g. the high vibrational ground state population might also be influenced by collisional relaxation in the flowing plasm. And of course we only cover the directly coupled contribution of the DR processes. Our restriction to total angular momentum J = 0 implies l = j (see eqn (5)). The limited diatom rotational quantum number (j ≤ 19) of the wave packet expansion might also have some influence on the calculated final state vibrational distribution.5. Comparison with experiment and with calculations including the indirect mechanism
There exist two series of experiments studying DR of HCO+: Merged beam studies by Padellec et al. from 1997 (Pa)12 and extensive CRYRING storage ring experiments by Hamberg et al. (Ha),13 published in 2014. In the energy region up to 1.5 eV the latter date from 2006 and have been reproduced and cited as ‘unpublished’ by several authors. However, above ε ≈ 0.5 eV (where part of the signal is interpreted as background) the published DR data of (Ha) do not exactly correspond to their earlier version (in particular above 0.4 eV the ‘unpublished’ data points are below the error limits postulated in ref. 13). In both studies a power function decrease of the DR cross section σ is reported, between 0.01 eV and 0.3 eV as 1.0 × ε−1.7 cm2 (Pa) or 1.3 × ε−1.3 cm2 (Ha). At energies higher than ε ≈ 0.7 eV the results of both experiments become irregular, probably because of the limitation of their sensitivity for σ < 10−16 cm2. In both papers it is explicitly stated that no DR effect could be detected above 1.0 eV (but (Ha) find resonance structures between 3 and 15 eV). At energy below 0.3 eV the cross sections measured by (Ha) are higher than those from (Pa) by a factor between 2 and 4; (Pa) report a broad peak between 0.3 and 0.8 eV, which however is absent in the results of (Ha). Based on quantum chemical calculations (Pa) believe that after electron capture the molecules dissociate to ground state H + CO, but they raise the question “how it is that CO(a3Π) molecules were seen as recombination products in the experiment of Adams and Babcock”.51 In addition a study by Nordhorn et al.16 from 2011 contributes branching ratios for the DR of DCO+ between 0 and 25 eV collisional energy (but no cross sections). (Ha) found that almost 90% of the DR events of H13 CO produce H + CO (not distinguishing ground and electronically excited CO fragments), plus rather more C + OH than O + CH.Most theoretical studies of the indirect DR process predict cross sections roughly proportional to ε−1 (caused by the k−2 prefactor in the expressions for σ) up to ε ≈ 0.1 eV and higher4–7,10 with slightly differing amplitudes. These methods only use the (spectroscopic or calculated) properties of the free HCO+ ion, and so produce smooth curves for σ(ε). The main difference lies in the value of ε (between 0.1 and 0.5 eV depending on the choice of internal degrees of freedom taken into account), where the predicted indirect cross sections fall to low values. Such drops are expected if the collision energy opens a new vibrational channel of the ion,8,11 but they could not be observed unequivocally for HCO+, where they would appear near 0.1 eV (ω2), 0.3 eV (ω3) or 0.4 eV (ω1). Therefore Schneider et al.8 ask “whether a direct process might also contribute” (and hence conceal the drop). It seems that an attempt to describe the charge distribution of the ion with higher electric multipoles7 has been given up, perhaps because a dipole field has been used instead of a quadrupole placed at the center of (positive) charge. None of the cited studies of the indirect process makes predictions about branching ratios (except assuming that dissociation leads to ground state H and CO fragments). Previous theoretical studies of the direct process culminate in the paper by Larson et al. (LStO),17 introduced in the foregoing sections.
Let us focus on the two most recent theoretical papers from 20149 and 2015,10 written by the same authors and using similar methods (the low-energy scattering matrix calculated through the variational complex Kohn method42,43), but arriving at quite different results. In the 2014 paper only the total DR cross section is documented, but it is stated that “the contribution of the direct process is only significant at energy above ∼0.1 eV”, from where on the direct (LStO) results are used (and thus the indirect part can be reconstructed). Between 0.001 eV and ∼0.07 eV the 2014 cross sections for the indirect process are about 2.5 times higher than the 2015 values. At higher ε this factor quickly increases (because the 2015 results drop at ω2, those of 2014 at ω1) up to about 0.14 eV, where the 2015 data – restricted to the indirect process – end to be documented. In both papers it is assumed that the experiments have been carried out with a mixture of 90% HCO+ and 10% HOC+, but the difference to calculations assuming pure HCO+ vanishes above 0.05 eV. Between ε = 0.005 eV and 0.1 eV the indirect DR contribution of 2015, obtained for the gas mixture, is quite close to the (Pa) experiments.
The total cross sections of the 2014 paper are the only ones that come fairly close to the CRYRING results. Up to ε ≈ 0.4 eV this is mainly due to the contribution of the indirect process, roughly parallel to the experiments and attaining about 75% of their value (below 0.3 eV proportional to ε−1.4). Near 0.4 eV the drop of the indirect DR process sets in, due to its interaction with the highest vibrational mode of HCO+, and the cross section becomes dominated by direct DR. Combination with the (LStO) results for the direct process leads to a step downwards and then to continuation with some structure at a relatively constant level just below σ ≈ 10−16 cm2 up to 1.5 eV, in contrast to the experiments decreasing to 10−17 cm2 within the same interval.
If however the calculations for the indirect process are combined with our present results for direct DR the picture changes. Fig. 7 compares our calculated cross section results for the direct process with theoretical and experimental curves reconstructed graphically from Fig. 6 of ref. 9. At ε ≈ 0.1 eV the sum of the 2014 calculations for the indirect DR mechanism and our cross section for the direct process matches well with the (Ha) experiment. Between 0.2 and 0.4 eV this sum is even higher than the (Ha) data (perhaps because the drop of the indirect process near ω3 has been neglected), but it never exceeds the upper error limit given in ref. 13. Up to ε ≈ 0.6 eV our direct mechanism cross section is distinctly larger than according to (LStO), as discussed in Section 4.2. Above 0.6 eV, in contrast to both the (LStO) calculations and the ‘unpublished’ experiments, only our regularly decreasing results for the direct (and thus total) DR match with the statement by (Ha) that “the number of DR events around 1–3 eV is close to zero”. Maybe in consequence of neglected higher resonance states our calculated curve falls somewhat too fast for ε > 0.6 eV (see the end of Section 4.2). Rather than a drop of the indirect contribution, above 0.6 eV the shape of our total DR reflects the decline of the direct process.
 | ||
| Fig. 7 Measured and calculated (total, direct, indirect) cross sections for the DR of HCO+ as functions of electron energy ε (adapted from Fig. 6 of ref. 9). Blue: CRYRING experiments;13 Red solid line: Fonseca et al. (ref. 9, total cross section); brown dot-dashed (and red solid line for ε > 0.6 eV): Larson et al. (ref. 17, direct process); green dashed: Fonseca et al. (ref. 9, indirect process, difference of the red and brown curves). Black: dashed line (and black solid line for ε > 0.6 eV): our present results (direct process); black solid line: sum of green and black dashed curves (total DR cross section). | ||
6. Population and depopulation on quartet pes
Dissociation on the quartet surfaces hardly contributes to the DR cross section (see Section 2.2). Apart from dissociation spin–orbit coupling allows for population of the vibrational states in the potential wells on the lowest quartet PES. As the lower ones of these levels – in particular those of the 4A′′ state – are situated below the lowest quartet dissociation limit, further deactivation or dissociation is possible only after a second spin changing transition. Therefore these levels – if occupied – are expected to be long lived. In the present section we shall have a closer look at these processes.The 14A′′ PES shows two minima at bent geometry (see Fig. 4), whereas there is but one pronounced potential well on the 14A′ surface. In Table 3 our calculated vibrational energies are given for the mentioned wells (![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) ,
, ![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) ,
, ![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) ′, see Section 2.1) on the quartet surfaces and for the two linear minima of the ion ground state PES. The same type of basis set expansion (see eqn (5)) as for wave packet dynamics was applied to determine vibrational frequencies. For the three quartet minima we observe a rather strong mixing of the angular and radial vibrational modes ν2 and ν3. Our vibrational energies for the
′, see Section 2.1) on the quartet surfaces and for the two linear minima of the ion ground state PES. The same type of basis set expansion (see eqn (5)) as for wave packet dynamics was applied to determine vibrational frequencies. For the three quartet minima we observe a rather strong mixing of the angular and radial vibrational modes ν2 and ν3. Our vibrational energies for the ![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) and
and ![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) minima are quite consistent with the theoretical (harmonic) frequencies found by Manaa and Yarkony.47 The same applies to the frequencies of the ions HCO+ and HOC+, if compared with the values given in the Jacox tables.30 To our knowledge for HOC+ only
minima are quite consistent with the theoretical (harmonic) frequencies found by Manaa and Yarkony.47 The same applies to the frequencies of the ions HCO+ and HOC+, if compared with the values given in the Jacox tables.30 To our knowledge for HOC+ only ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 1 has been measured, but our fundamental frequencies are also in reasonable agreement with the theoretical results of Mladenović et al.53 (predicting an unusually flat bending potential). The corresponding vibrational energies for the doublet PES and further details of the vibrational calculations will be given in a coming publication.19
1 has been measured, but our fundamental frequencies are also in reasonable agreement with the theoretical results of Mladenović et al.53 (predicting an unusually flat bending potential). The corresponding vibrational energies for the doublet PES and further details of the vibrational calculations will be given in a coming publication.19
A possible mechanism to release the excess energy of the quartet wave packet (introduced in Section 3.2) and populate a low-lying vibrational state Φvib is a dipole transition within the respective quartet state. In order to evaluate the transition dipole operator ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) between a wave packet and vibrational functions, accounting for nuclear as well as electronic contributions, the electronic dipole transition moment function was calculated at the CI level on a limited grid in the (geometrical) vicinity of the considered potential well. With Einstein's factor A of spontaneous emission a time-dependent rate is computed, which was integrated up to 36 fs, a characteristic timeframe after which the dissociation process on our coupled surfaces is essentially terminated. The wave packet energy normalization factor was omitted here, thus only relative populations of the individual vibrational levels after a (single) recombination event result. They are in the order of 10−15, depending only weakly on energy or level. Populations of the lowest five vibrational states for the two minima on the 14A′′ PES are shown in part (A) of Fig. 8 as functions of the captured electrons energy ε. It seems to be rather plausible that well
between a wave packet and vibrational functions, accounting for nuclear as well as electronic contributions, the electronic dipole transition moment function was calculated at the CI level on a limited grid in the (geometrical) vicinity of the considered potential well. With Einstein's factor A of spontaneous emission a time-dependent rate is computed, which was integrated up to 36 fs, a characteristic timeframe after which the dissociation process on our coupled surfaces is essentially terminated. The wave packet energy normalization factor was omitted here, thus only relative populations of the individual vibrational levels after a (single) recombination event result. They are in the order of 10−15, depending only weakly on energy or level. Populations of the lowest five vibrational states for the two minima on the 14A′′ PES are shown in part (A) of Fig. 8 as functions of the captured electrons energy ε. It seems to be rather plausible that well ![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) at γ ≈ 37° is more likely reached than well
at γ ≈ 37° is more likely reached than well ![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) ′ on the HOC side. Only a tiny fraction of the initial wave packet on the doublet surface reaches the quartet state, where dissociation is the absolutely dominating process. This explains the very low probability for population of a bound vibrational state. On the other hand the lifetime of these vibrational levels is expected to be very long, provided that solely radiative processes of depopulation are to be considered.
′ on the HOC side. Only a tiny fraction of the initial wave packet on the doublet surface reaches the quartet state, where dissociation is the absolutely dominating process. This explains the very low probability for population of a bound vibrational state. On the other hand the lifetime of these vibrational levels is expected to be very long, provided that solely radiative processes of depopulation are to be considered.
Our calculated depopulation rates per unit energy interval for the five lowest vibrational levels of system ![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) , w(Ek, ν1ν2ν3 → CO(X)), are depicted in part (B) of Fig. 8 as functions of the fragments translational energy Ek. The spin–orbit operator HSO leads for both the initial electronic state
, w(Ek, ν1ν2ν3 → CO(X)), are depicted in part (B) of Fig. 8 as functions of the fragments translational energy Ek. The spin–orbit operator HSO leads for both the initial electronic state  as well as the final state
as well as the final state 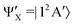 to first order expansion terms of interchanged multiplicity and spatial symmetry:38
to first order expansion terms of interchanged multiplicity and spatial symmetry:38
 | (12) |
 | (13) |
 obtained with perturbation theory, are very close to unity. In both sums only open shell configurations with three (or more) singly occupied orbitals contribute. Thus the resulting (electronic) first order transition operator
obtained with perturbation theory, are very close to unity. In both sums only open shell configurations with three (or more) singly occupied orbitals contribute. Thus the resulting (electronic) first order transition operator  is composed of two types of terms containing dipole matrix elements either between doublet or between quartet states respectively.
is composed of two types of terms containing dipole matrix elements either between doublet or between quartet states respectively.
In order to analyze the translational and vibrational energy distribution of the resulting CO(X1Σ+) fragments, energy normalized Gaussian wave packets Ων(Ek,t) were started on the  surface backwards (and upwards) from the CO levels ν, at asymptotic distance (R ≈ 9ao) with translational energy Ek. The vibrational dipole matrix elements
surface backwards (and upwards) from the CO levels ν, at asymptotic distance (R ≈ 9ao) with translational energy Ek. The vibrational dipole matrix elements  were evaluated as functions of time t, whereby the maximum of |
were evaluated as functions of time t, whereby the maximum of |![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) (t)|2 is usually reached not too far from the turning point of the wave packet. Summation over 0 ≤ νCO ≤ 4 has already been carried out for the curves in Fig. 8(B). The dashed lines show some individual νCO contributions for the initial (vibrational) ground state. As the CO(X) bond length is significantly shorter than r at the minimum of well
(t)|2 is usually reached not too far from the turning point of the wave packet. Summation over 0 ≤ νCO ≤ 4 has already been carried out for the curves in Fig. 8(B). The dashed lines show some individual νCO contributions for the initial (vibrational) ground state. As the CO(X) bond length is significantly shorter than r at the minimum of well ![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) , it is not surprising, that the final state turns out to be vibrationally hot. The rates per unit energy feature a rather broad structure with a maximum for Ek between 0.7 and 1.2 eV. Tendentially this peak is shifted towards higher Ek values with increasing initial (vibrational) excitation. The vibrational ground state of the
, it is not surprising, that the final state turns out to be vibrationally hot. The rates per unit energy feature a rather broad structure with a maximum for Ek between 0.7 and 1.2 eV. Tendentially this peak is shifted towards higher Ek values with increasing initial (vibrational) excitation. The vibrational ground state of the ![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) potential well lies about 4.2 eV above the asymptotic limit H(1s) + CO(X, νCO = 0), whereas the vertical electronic energy difference down to the ground state PES is 3.1 eV. Thus radiation is predicted in the visible and near UV, and the (radiative) lifetimes resulting after integration over Ek are in the range 8 to 36 s.
potential well lies about 4.2 eV above the asymptotic limit H(1s) + CO(X, νCO = 0), whereas the vertical electronic energy difference down to the ground state PES is 3.1 eV. Thus radiation is predicted in the visible and near UV, and the (radiative) lifetimes resulting after integration over Ek are in the range 8 to 36 s.
7. Summary
The aim of this study was to reconsider the process of direct dissociative recombination of HCO+. To this end we have calculated new electronic PES for 22A′ (![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) state), 22A′′ (
state), 22A′′ (![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) ) as well as surfaces for 14A′ (
) as well as surfaces for 14A′ (![[b with combining tilde]](https://www.rsc.org/images/entities/char_0062_0303.gif) ), 14A′′ (
), 14A′′ (![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) ) of HCO and for the ion HCO+, using a modified version of the MC-CEPA program 18 and preparing the required reference functions with iterated CI. The investigated DR mechanism involves the lowest core-excited 2Π state. The corresponding 2A′ and 2A′′ resonant state PES are merged diabatically into the
) of HCO and for the ion HCO+, using a modified version of the MC-CEPA program 18 and preparing the required reference functions with iterated CI. The investigated DR mechanism involves the lowest core-excited 2Π state. The corresponding 2A′ and 2A′′ resonant state PES are merged diabatically into the ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) and
and ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) surfaces close by their respective (bent) minima upon bending the molecule. No additional diabatization was applied to connect the region of electron capture with the PES leading to dissociation. This situation is illustrated in Fig. 2 and 3. All examined core-excited doublet and quartet PES were found to intersect the ground state surface of HCO+ within the range of the vibrational zero point energy.
surfaces close by their respective (bent) minima upon bending the molecule. No additional diabatization was applied to connect the region of electron capture with the PES leading to dissociation. This situation is illustrated in Fig. 2 and 3. All examined core-excited doublet and quartet PES were found to intersect the ground state surface of HCO+ within the range of the vibrational zero point energy.
The electronic coupling of the initial state (free electron with energy ε plus ion) to the diabatic core-excited surfaces could be treated numerically in a restricted area with aid of an auxiliary wall potential (AWP)36 allowing adjustment of ε (between 0.02 eV and 1.0 eV). We found that the coupling matrix elements increase (decrease) in value upon bending the molecule, for A′ (A′′) symmetry. At the equilibrium geometry of the ion our calculated autoionization width Γ(ε → 0) = 564 cm−1 is almost twice the value obtained by Larson et al. (LStO) in 2012.17
Wave packet propagation on the diabatic surfaces has been carried out using extended wave function basis sets and transforming the Hamiltonian of nuclear motion to tridiagonal form. We start wavepackets at the HCO+ geometry only, not from the (by ca. 2 eV higher) HOC+ minimum. We estimate that at ε = 0.15 eV dissociation to H + CO(a3Π) is by a factor 2.5 to 5 more probable than to C + OH(X2Π). The dominance of the channel H + CO decreases with increasing ε. DR cross sections are shown in Fig. 5 and 7.
Transitions from doublet to quartet surfaces mediated by spin–orbit coupling, followed by dissociation, are a possible effect. We obtain coupling matrix elements in the order of about 50 cm−1, and supported by a propagation method using coupled surfaces of the two multiplicities we predict that dissociation from 22A′′ via 14A′′ to H + CO(a3Π) is the most important pathway on a quartet surface, but its (relative) contribution to the DR cross section is only of the order of magnitude 10−4 compared to pure doublet dissociation.
Compared to the results of (LStO) our theoretical direct DR cross sections are significantly larger for ε < 0.4 eV, mainly due to the included angular dependence of autoionization width Γ (eqn (3)) and to the more favourable location of the intersection seam of the 2A′ PES with the ionic surface. At the lower end of our considered energy range (0.02 eV ≤ ε ≤ 0.2 eV) the larger contribution of the direct mechanism improves the agreement of theory and experiment. Thus the often stated dominance of the indirect process for HCO+ DR at ε ≤ 0.4 eV must be relativized. Our results support the supposition of Schneider et al.8 that the drop of σ(ε) predicted in ref. 9 is concealed by the direct DR mechanism. In other words, from the point where ε reaches the highest vibrational mode of HCO+ (3089 cm−1) the direct process becomes dominant.
In contrast to the results of (LStO) we find the (lowest accessible) H + CO(a3Π) channel to contribute most to the cross section σ for ε < 0.5 eV. This seems reasonable from a classical mechanics point of view: for low ε the wave packet tends to move in the direction of the largest excess energy. For this DR channel our theoretical final state analysis leads to a similar (non-thermal) population of vibrationally excited states as the experiments of Rosati,24 which however show a distinctly higher population of the ν = 0 level.
The low vibrational levels in the ![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) and
and ![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) ′ wells (see Table 3,
′ wells (see Table 3, ![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) ′ is a second minimum of the 14A′′ PES on the HOC side) are of special interest. They may be populated by radiative transition from the small wave packet fraction transferred to the 14A′′ state by spin–orbit interaction. Our calculations showed the population probabilities to be very small (compared to dissociation). But as the lowest quartet dissociation limits are higher than these vibrational levels, depopulation is expected to be very slow. Computation of radiative transition rates from the lowest vibrational
′ is a second minimum of the 14A′′ PES on the HOC side) are of special interest. They may be populated by radiative transition from the small wave packet fraction transferred to the 14A′′ state by spin–orbit interaction. Our calculations showed the population probabilities to be very small (compared to dissociation). But as the lowest quartet dissociation limits are higher than these vibrational levels, depopulation is expected to be very slow. Computation of radiative transition rates from the lowest vibrational ![[c with combining tilde]](https://www.rsc.org/images/entities/char_0063_0303.gif) levels to 12A′ indicate that the 14A′′ PES wells make up the best candidates for long living excited states of gaseous HCO, which might be relevant under certain astrophysical conditions.
levels to 12A′ indicate that the 14A′′ PES wells make up the best candidates for long living excited states of gaseous HCO, which might be relevant under certain astrophysical conditions.
Improved dynamics calculations including simultaneous propagation towards all three atom-diatom limits (and possibly coupling to the 2Φ and Rydberg states) might be the topic of a forthcoming paper,19 and we shall try to extend the range of collision energy ε. Time dependent calculations modelling the indirect DR process and its contribution to the branching ratios of the fragments are also desirable.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Ernst Miescher Foundation (Basel, Switzerland) for technical support. Moreover we wish to acknowledge the program development by M. Luo (spin–orbit coupling) and R. Guérout (auxiliary wall potential).Notes and references
- T. W. Hartquist, J. M. Pittard and S. A. E. G. Falle, Diffuse Matter from Star Forming Regions to Active Galaxies, 2007, ISBN 978-1-4020-5424-2 Search PubMed.
- D. R. Bates, Phys. Rev., 1950, 78, 492–493 CrossRef CAS.
- J. N. Bardsley, J. Phys. B, 1968, 1, 365–380 CrossRef.
- I. A. Mikhailov, V. Kokoouline, Å. Larson, S. Tonzani and C. H. Greene, Phys. Rev. A, 2006, 74, 032707(9) Search PubMed.
- N. Douguet, V. Kokoouline and C. H. Greene, Phys. Rev. A, 2008, 77, 064703(4) CrossRef.
- C. Jungen and S. T. Pratt, J. Chem. Phys., 2008, 129, 164311(9) Search PubMed.
- N. Douguet, V. Kokoouline and C. H. Greene, Phys. Rev. A, 2009, 80, 062712(6) CrossRef.
- I. F. Schneider, N. Pop and C. Jungen, Phys. Rev. A, 2012, 86, 062706(11) CrossRef.
- S. Fonseca dos Santos, N. Douguet, V. Kokoouline and A. E. Orel, J. Chem. Phys., 2014, 140, 164308(12) CrossRef PubMed.
- N. Douguet, S. Fonseca dos Santos, V. Kokoouline and A. E. Orel, EPJ Web Conf., 2015, 84, 07003(10) Search PubMed.
- S. T. Pratt and C. Jungen, J. Chem. Phys., 2012, 137, 174306(6) CrossRef PubMed.
- A. Le Padellec, C. Sheenan, D. Talbi and J. B. A. Mitchell, J. Phys. B, 1997, 30, 319–327 CrossRef CAS.
- M. Hamberg, et al. , J. Phys. Chem., 2014, 118, 6034–6049 CrossRef CAS PubMed.
- Å. Larson, S. Tonzani, R. Santra and C. H. Greene, J. Phys.: Conf. Ser., 2005, 4, 148–154 CrossRef.
- Å. Larson and A. E. Orel, Phys. Rev. A, 2009, 80, 062504(9) Search PubMed.
- C. Nordhorn, et al. , J. Phys.: Conf. Ser., 2011, 300, 012004(8) CrossRef.
- Å. Larson, M. Stenrup and A. E. Orel, Phys. Rev. A, 2012, 85, 042702(8) CrossRef.
- R. Fink and V. Staemmler, Theor. Chim. Acta, 1993, 87, 129 CrossRef CAS.
- M. Jungen and M. Lehner, to be published.
- Q. Chen, S. Han, X. Hu and D. Xie, Chin. J. Chem. Phys., 2022, 35, 303–310 CrossRef CAS.
- S. Han, et al. , Sci. Adv., 2019, 5, eaau0582 CrossRef PubMed.
- G. Sun, et al. , Faraday Discuss., 2022, 238, 236–248 RSC.
- G. Winterhoff, S. C. Galleguillos Kempf, P. Jensen and P. R. Bunker, J. Mol. Spec., 2018, 354, 71–82 CrossRef CAS.
- R. E. Rosati, M. P. Skrzypkowski, R. Johnsen and M. F. Golde, J. Chem. Phys., 2007, 126, 154302(8) Search PubMed.
- V. Staemmler, Theor. Chim. Acta, 1983, 64, 205–215 CrossRef CAS.
- J. M. Dyke, J. Chem. Soc., Faraday Trans., 1987, 83, 69 RSC.
- H. J. Werner, C. Bauer, P. Rosmus, H. M. Keller, M. Stumpf and R. Schinke, J. Chem. Phys., 1995, 102, 3593–3611 CrossRef CAS.
- M. C. Chuang, M. F. Foltz and C. B. Moore, J. Chem. Phys., 1987, 87, 3855 CrossRef CAS.
- K. P. Huber and G. Herzberg, Constants of Diatomic Molecules, Van Nostrand, New York, 1979 Search PubMed.
- M. E. Jacox, J. Phys. Chem. Ref. Data, 2003, 32, 1–441 CrossRef CAS.
- T. A. Cool and X. M. Song, J. Chem. Phys., 1992, 96, 8675–8683 CrossRef.
- P. J. Bruna, R. J. Buenker and S. D. Peyerimhoff, J. Mol. Struct., 1976, 32, 217–233 CrossRef CAS.
- K. Tanaka and E. R. Davidson, J. Chem. Phys., 1979, 70, 2904–2913 CrossRef CAS.
- P. O. Widmark, P. A. Malmqvist and B. O. Roos, Theoret. Chim. Acta, 1990, 77, 1007 CrossRef.
- K. Kaufmann, W. Baumeister and M. Jungen, J. Phys. B, 1989, 22, 2223–2240 CrossRef CAS.
- R. Guérout, M. Jungen and C. Jungen, J. Phys. B, 2004, 37, 3043–3055 CrossRef.
- W. Pauli, Z. Phys., 1927, 43, 601 CrossRef CAS.
- C. M. Marian, Rev. Comp. Chem., 2001, 17, 99–204 CAS.
- A. I. Florescu-Mitchell and J. B. A. Mitchell, Phys. Rep., 2006, 430, 277–374 CrossRef CAS.
- A. E. Orel, Phys. Rev. A, 2000, 62, 020701 CrossRef.
- M. J. Seaton, Comp. Phys. Commun., 1982, 25, 87 CrossRef.
- C. W. McCurdy and T. N. Rescigno, Phys. Rev. A, 1989, 39, 4487 CrossRef CAS PubMed.
- A. E. Orel, T. Rescigno and B. Lengsfield, Phys. Rev. A, 1991, 44, 4328 CrossRef CAS PubMed.
- U. Galster, Phys. Rev. A, 2010, 81, 032517 CrossRef.
- M. Lehner and M. Jungen, J. Phys. B, 2015, 48, 035101(9) CrossRef.
- C. Lanczos, J. Res. Nat. Bur. Standards B, 1950, 45, 225 Search PubMed.
- M. R. Manaa and D. R. Yarkony, J. Chem. Phys., 1994, 100, 473–480 CrossRef CAS.
- C. A. Mead and D. G. Truhlar, J. Chem. Phys., 1982, 77, 6090–6098 CrossRef CAS.
- K. C. Kulander and E. J. Heller, J. Chem. Phys., 1978, 69, 2439 CrossRef CAS.
- C. W. McCurdy and J. L. Turner, J. Chem. Phys., 1983, 78, 6773 CrossRef CAS.
- N. G. Adams and L. M. Babcock, J. Phys. Chem., 1994, 98, 4564 CrossRef CAS.
- C. Zener, Proc. R. Soc. London, 1932, A137, 696 Search PubMed.
- M. Mladenović and S. Schmatz, J. Chem. Phys., 1998, 109, 4456–4470 CrossRef.
| This journal is © the Owner Societies 2023 |






