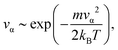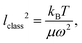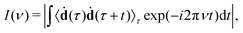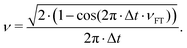Describing nuclear quantum effects in vibrational properties using molecular dynamics with Wigner sampling†
Denis S.
Tikhonov
 *a and
Yury V.
Vishnevskiy
*a and
Yury V.
Vishnevskiy
 *b
*b
aDeutsches Elektronen-Synchrotron DESY, Notkestr. 85, 22607 Hamburg, Germany. E-mail: denis.tikhonov@desy.de
b2Lehrstuhl für Anorganische Chemie und Strukturchemie, Fakultät für Chemie, Universität Bielefeld, Universitätsstr. 25, 33615 Bielefeld, Germany. E-mail: yury.vishnevskiy@uni-bielefeld.de
First published on 20th June 2023
Abstract
In this work we discuss the generally applicable Wigner sampling and introduce a new, simplified Wigner sampling method, for computationally effective modeling of molecular properties containing nuclear quantum effects and vibrational anharmonicity. For various molecular systems test calculations of (a) vibrationally averaged rotational constants, (b) vibrational IR spectra and (c) photoelectron spectra have been performed. The performance of Wigner sampling has been assessed by comparing with experimental data and with results of other theoretical models, including harmonic and VPT2 approximations. The developed simplified Wigner sampling method shows advantages in application to large and flexible molecules.
1. Introduction
Molecular dynamics (MD) is a very powerful tool for modeling molecular systems at normal and elevated temperatures T ≥ 300 K.1–3 However, the simulation of nuclear quantum effects (NQEs) is still a challenging topic in MD.1 At normal temperatures, the path-integral molecular dynamics (PIMD) approach1,4,5 is very effective for modelling equilibrium properties of molecular systems. This technique takes advantage of the exact mapping between the quantum-mechanical system and its representation as a set of N interconnected replicas (also termed as beads) with the N-times elevated temperature. Taking enough beads of this so-called ring polymer, when their respective temperature (T × N) overcomes the Debye temperature TD = hν/kB of the highest possible vibrational mode with frequency ν, the representation approaches the exact limit. The minimally required number of beads is thus estimated as . Therefore at low temperatures, this number gets very large thus diminishing the applicability of PIMD.
. Therefore at low temperatures, this number gets very large thus diminishing the applicability of PIMD.
In contrast, the most computationally inexpensive and simple vibrational model is the harmonic approximation. This approach assumes that the potential energy surface (PES) in the vicinity of the equilibrium geometry (local minimum) can be expressed with the second-order Taylor expansion. For a diatomic molecule, in which the only vibrational coordinate is the interatomic distance r, it reads as
 | (1) |
 , Vh(r) is the harmonic potential, and Wa(r) is the anharmonic correction to the harmonic potential. The quantum harmonic oscillator is one of the simplest quantum mechanical problems with a known analytical solution.6 For a molecule with reduced mass μ, the stationary vibrational states |v〉 (v = 0, 1, 2,…) have energies of Ev = ħω(v + 1/2), where
, Vh(r) is the harmonic potential, and Wa(r) is the anharmonic correction to the harmonic potential. The quantum harmonic oscillator is one of the simplest quantum mechanical problems with a known analytical solution.6 For a molecule with reduced mass μ, the stationary vibrational states |v〉 (v = 0, 1, 2,…) have energies of Ev = ħω(v + 1/2), where  is the angular vibrational harmonic frequency. The vibrationally averaged displacement 〈ξ〉 = 〈v|ξ|v〉 = 0, since the harmonic potential is symmetrical with respect to inversion of the displacement, Vh(+ξ) = Vh(−ξ). On the other hand, the vibrational amplitude l, defined as
is the angular vibrational harmonic frequency. The vibrationally averaged displacement 〈ξ〉 = 〈v|ξ|v〉 = 0, since the harmonic potential is symmetrical with respect to inversion of the displacement, Vh(+ξ) = Vh(−ξ). On the other hand, the vibrational amplitude l, defined as| l2 = 〈r2〉 − 〈r〉2 | (2) |
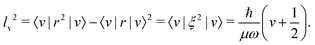 | (3) |
 | (4) |
the rotational constant may be given as6
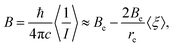 | (5) |
For bond stretching vibrations typically V3 < 0 and V2 > 0. Therefore, equilibrium rotational constants are usually larger than the respective vibrationally averaged rotational constants.
The full-dimensional quantum-mechanical treatment is the most accurate way to describe anharmonic motions of nuclei. The full solution of the vibrational Schrödinger equation is a computationally and theoretically challenging task.12,13 First, it requires extensive quantum-chemical calculations to produce the numerical potential energy surface (PES). Often these data are approximated with a suitable analytical form. Finally, it requires advanced techniques for solving multidimensional Schrödinger equations. The difficulties associated with these procedures limit the widespread usage of such methods.
The simplest quantum approach that offers anharmonic treatment of the molecular vibrations is the second-order perturbation theory, usually denoted as VPT2.14,15 In this approach, harmonic, cubic (∝V3ξ3) and semi-diagonal quartic force fields (∝V4ξ4) are taken into consideration. Since the harmonic potential is symmetric and the cubic part is antisymmetric with respect to the displacements from the equilibrium values, the perturbative first order (PT1) energy correction with the cubic force field is zero. However, the quartic semi-diagonal part of the field with the terms of the form V4,ijξi2ξj2, where i and j enumerate displacements along different modes, gives nonzero corrections at the PT1 level. The second order corrections (PT2) are thus being performed only for the cubic part of the potential. Such a procedure can be automated and is already implemented in different software packages for quantum chemistry. However, with the increasing number of atoms N in a molecule the computational cost of VPT2 increases dramatically due to the growing amount of cubic force field elements, which scales as N3. For large molecules MD simulations may become computationally more effective.13 Thus it is important to develop procedures for computation of molecular vibrational properties at low temperatures using classical MD simulations.
Wigner sampling16,17 is one of possibilities for producing initial conditions in MD simulations, that emulate the quantum harmonic ground vibrational state.18–20 In this work we combine Wigner sampling with MD simulations to provide anharmonic vibrational properties of molecules. We also propose a new simplified sampling procedure, which is based on Wigner sampling but does not require preliminary calculation of molecular Hessian.
The paper is structured as follows. First, we introduce and compare possible sampling procedures, including our simplified version of Wigner sampling, then we perform a benchmarking of vibrationally-averaged rotational constants. We demonstrate the proof-of-principle for the approach using the diatomic system of the molecular hydrogen cation. A benchmark set of five small (no more than six atoms) molecules is used to evaluate a method for calculation of rotational constants from MD trajectories. The resulting procedure is applied to another two moderately-sized molecules (20 and 62 atoms). Next, we show the application of the sampling routines for the calculation of vibrational spectra for difluoromethane. Finally, different sampling methods are applied to several systems with known experimental data. All the molecules used throughout this work are shown in Fig. 1.
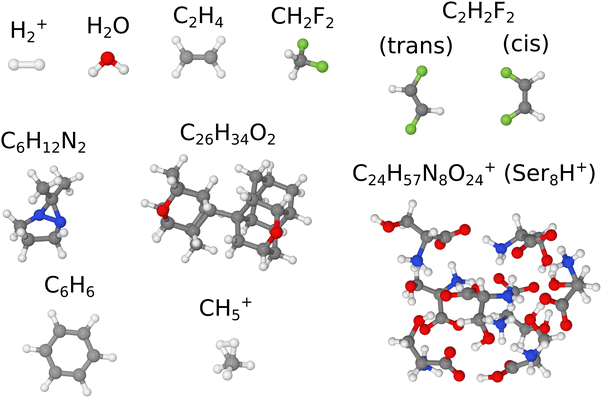 | ||
| Fig. 1 Test molecules. The standard Jmol21 coloring scheme is used for the atoms: white (H), gray (C), blue (N), red (O), and green (F). | ||
2. Theory
2.1 Maxwell–Boltzmann sampling
The classic procedure for the generation of initial conditions in MD simulations is Maxwell–Boltzmann sampling (MBS).22 Starting nuclear coordinates are defined externally, for example, they may correspond to the equilibrium molecular structure. Initial velocities of nuclei are generated from the Maxwell–Boltzmann distribution, e.g. for the temperature T the velocity να along a certain axis (α = x, y, z) of a nucleus with the mass m is distributed aswhere kB is the Boltzmann constant. This generation of the initial conditions is very effective for classical ensembles. However, we can also use MBS for crude simulation of NQEs. In simulations at elevated temperatures, pair distribution functions (PDFs) are similar to those in the classical case. The squared vibrational amplitude (eqn (2)) for the interatomic distance r in the classical harmonic approximation is:11
whereas in the quantum case it is11
 | (6) |
i.e., at half of the Debye temperature TD = hν/kB the classical PDF of the harmonic oscillator is equivalent to the PDF of the ground vibrational quantum state.
2.2 Wigner sampling
One of the currently popular sampling techniques is based on Wigner quasiprobability distributions obtained at the harmonic approximation.17,18,20,22 Let us consider the Hamiltonian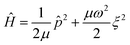 for a single vibrational mode with ξ being the displacement of the coordinate from the equilibrium position and
for a single vibrational mode with ξ being the displacement of the coordinate from the equilibrium position and ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) = −iħ∂ξ. The ground vibrational state is then given by the wavefunction
= −iħ∂ξ. The ground vibrational state is then given by the wavefunctionwhere l0 is defined in eqn (6). The corresponding Wigner quasi-probability function for the momentum p can be obtained from any given wavefunction ψ via transformation16
For the ground state of the harmonic oscillator ψ = ψ0 we get
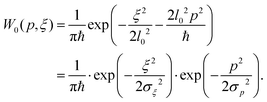 | (7) |
In the case of a polyatomic molecule, there is a mapping between independent one-dimensional vibrational modes and the Cartesian coordinates and their corresponding momentums of atoms. The linear displacement of the atoms in the Cartesian coordinates r from their equilibrium positions (re) can be related to the vector of displacements of vibrational modes ξ through the matrix of the mode shapes: 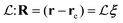 . A similar relationship connects the Cartesian momentums of the atoms P = −iħ∂R to the momentums of the independent modes p = −iħ∂ξ:
. A similar relationship connects the Cartesian momentums of the atoms P = −iħ∂R to the momentums of the independent modes p = −iħ∂ξ:  . The Wigner function for ξ and p is just a product of the one-dimensional quasi-probability distributions (eqn (7)), and it can be written as
. The Wigner function for ξ and p is just a product of the one-dimensional quasi-probability distributions (eqn (7)), and it can be written as
 and momentums
and momentums 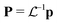 in Cartesian coordinates:
in Cartesian coordinates: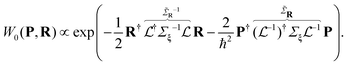 | (8) |
 is non-diagonal, unlike the initial Σξ, which indicates the correlation between atomic displacements due to the collective nature of the vibrational modes. The replacement of the variables {p,ξ} → {P, R} is unitary, since
is non-diagonal, unlike the initial Σξ, which indicates the correlation between atomic displacements due to the collective nature of the vibrational modes. The replacement of the variables {p,ξ} → {P, R} is unitary, since  . Using this distribution, it is possible to simultaneously sample both the linear displacements of the nuclei from the equilibrium geometry and nuclear velocities in polyatomic molecules.17 This and similar sampling procedures for initial conditions are called Wigner sampling (WS). If we replace l0 for each vibrational mode with the temperature-dependent lquant from eqn (6), we can also sample temperature-averaged vibrational states.
. Using this distribution, it is possible to simultaneously sample both the linear displacements of the nuclei from the equilibrium geometry and nuclear velocities in polyatomic molecules.17 This and similar sampling procedures for initial conditions are called Wigner sampling (WS). If we replace l0 for each vibrational mode with the temperature-dependent lquant from eqn (6), we can also sample temperature-averaged vibrational states.
2.3 New sampling procedure
WS requires initial optimization of the molecular structure and calculation of harmonic potential. However, we can try to construct a simplified sampling procedure similar to WS. Here we denote it as simplified Wigner sampling (SWS).Let us consider the motion of a nucleus with the mass m along the coordinate x. We will assume that at each point in time, this motion is described with a Gaussian wavepacket with width σx in the coordinate representation and the corresponding width σp in the momentum representation. In this case, the momentum p and the coordinate x should fulfill the uncertainty principle, which can be ensured by using the Wigner function similar to that in eqn (7):
 | (9) |
The construction of the Wigner distribution requires solving the quantum-mechanical problem. Alternatively, we can try to apply heuristic considerations to make a self-sustained procedure for generating such distributions. As a starting point, we need to consider that the uncertainties of the coordinate and momentum should at least fulfill the Heisenberg equality principle (σx·σp = ħ/2). This principle makes both distributions for the coordinate ρx and the momentum ρp dependent on each other: the larger the uncertainty for the momentum, the smaller it is for the coordinate, and vice versa. We can think of the uncertainty as the amount of information we have about x and p. As a guiding principle, we require the same amount of information for x and p, i.e. the uncertainty in the distributions ρx and ρp should be approximately the same.
A simple way to define a metric between distributions ρa and ρb is the Kullback–Leibler (KL) divergence23 defined as
| JKL(ρa,ρb) = JKL(ρb,ρa) = DKL(ρa||ρb) + DKL(ρb||ρa). |
In the case of the Gaussian distribution  we get24
we get24
For the case of ρx and ρp the expectation value for the displacement and the momentum are μx = μp = 0. However, we cannot compare position and momentum distributions since they have different units. To correct for that, instead of the ρx(ξ), we will consider another distribution for a new parameter
 ) and ρp is
) and ρp isDue to the relationship σx = ħ/(2σp), we can find a condition of JKL(ρX, ρp) → min as
 , which leads to
, which leads to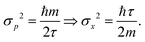 | (10) |
The sampling procedure is simple. First, we choose a reasonable τ. Next, for each coordinate (x, y, z) of all nuclei we generate a displacement and velocity according to the distribution given in eqn (9). The procedure can also be defined in terms of a multivariate quasi-distribution of all Cartesian coordinates and momentums, similar to that in eqn (8). In this case, the sampling is done on the basis of the distribution
 | (11) |
 and k enumerates all the Cartesian coordinates. This representation has two main differences compared to eqn (8). The first one is that the diagonal elements of matrix ΣR,SWS in eqn (11) are given by the parametrization from eqn (10), rather than computed from the harmonic potential. The second difference is that all the non-diagonal elements in ΣR,SWS, which carry information on the correlations between different Cartesian coordinates of atoms, are zeros. Both differences appear due to the absence of information about the shape of the local potential of nuclei in the SWS procedure, which makes it physically less justified in comparison to WS. Accordingly, SWS is expected to be less accurate, although it is not yet exactly clear how large the accuracy loss will be in different use scenarios. At the same time SWS gains an advantage, that it does not require a preliminary optimization of molecular structure and calculation of Hessian.
and k enumerates all the Cartesian coordinates. This representation has two main differences compared to eqn (8). The first one is that the diagonal elements of matrix ΣR,SWS in eqn (11) are given by the parametrization from eqn (10), rather than computed from the harmonic potential. The second difference is that all the non-diagonal elements in ΣR,SWS, which carry information on the correlations between different Cartesian coordinates of atoms, are zeros. Both differences appear due to the absence of information about the shape of the local potential of nuclei in the SWS procedure, which makes it physically less justified in comparison to WS. Accordingly, SWS is expected to be less accurate, although it is not yet exactly clear how large the accuracy loss will be in different use scenarios. At the same time SWS gains an advantage, that it does not require a preliminary optimization of molecular structure and calculation of Hessian.
A reasonable value for τ can be determined from general physical considerations. The largest displacement will be observed for the lightest nuclei, most commonly for hydrogen with the mass of 1 a.m.u. A displacement of more than 20% of the corresponding bond length will probably introduce too much energy into the system, that can even lead to a spurious fragmentation. Therefore, we require σx to be smaller than about 0.2 Å. For m = 1 a.m.u. this is achieved with τ < 13 fs. From the other side, the momentum distribution  can be thought of in terms of temperature, since for MBS σp,MB2 = mkBT, i.e. the effective temperature is defined as
can be thought of in terms of temperature, since for MBS σp,MB2 = mkBT, i.e. the effective temperature is defined as  . For velocities of nuclei Teff ≤ 5000 K can be achieved at τ > 0.8 fs. This provides a small range of reasonable values for τ, 1 ≤ τ ≤ 10 fs.
. For velocities of nuclei Teff ≤ 5000 K can be achieved at τ > 0.8 fs. This provides a small range of reasonable values for τ, 1 ≤ τ ≤ 10 fs.
Introducing temperature effects in the distribution (9) is rather straightforward. This can be done in a classical sense as the addition of the momentum δp, which is distributed according to the Maxwell–Boltzmann statistics (δp ∼ exp(−δp2/(2mkBT))). By replacing p with p + δp we need to average W(x,p) over δp, which leads to
3. Computational methods
Most of the quantum-chemical calculations have been performed using the density functional theory approximation PBE/def2-SVP25,26 (in some cases paired with D3BJ27 empirical dispersion corrections) implemented in the ORCA 5 package.28 In cases where a better agreement with experimental data was required, the composite method PBEh-3c29 has been utilized. Vibrational corrections to rotational constants within VPT230 theory were computed using the Gaussian 16 package.31 Details on methods and settings are provided in the ESI.†4. Results and discussion
4.1 A simple case of H2+
To illustrate the general idea of WS and SWS in application to molecular vibrations, we have performed calculations for a simple diatomic model, the molecular cation H2+. Here we focus on the interatomic pair distribution function, as this provides a general representation of the molecular ensemble, from which other observables can be computed. For example, the rotational constant of the diatomic molecule can be explicitly expressed via the average interatomic distance (eqn (5)).A comparison of the numerical anharmonic vibrational wavefunction with that from the harmonic approximation is shown in Fig. 2. The asymmetry of the anharmonic potential with respect to the equilibrium geometry re leads to a shift of the probability distribution into the range of larger interatomic distances r. Wigner distribution at the harmonic approximation gives symmetric probability distribution, as it is obtained from the model symmetric potential. Therefore no anharmonic shifts of the interatomic distance can be observed from the ensemble of structures sampled in this case. Although MD can be used with anharmonic PES, being a classical simulation technique, it cannot recover quantum effects (NQEs). Nevertheless, some successful examples of modified MD describing quantum properties exist in the literature.32,33 It is possible to replace the classical vibrational amplitude  with its quantum analogue in harmonic approximation.11,13,34 This substitution is justified by domination of the harmonic potential in the second moment of the interatomic distribution.
with its quantum analogue in harmonic approximation.11,13,34 This substitution is justified by domination of the harmonic potential in the second moment of the interatomic distribution.
The same logic can be transferred to WS. By default, the initial ensemble of the structures produced from the harmonic wavefunction via WS (eqn (7)) has no anharmonicity. However, the system evolves at the anharmonic PES for some time, thus allowing the classical dynamics capturing the anharmonicity to some extent. In other words, the WS procedure ensures the quantum behavior, while the anharmonicity of the PES is considered through MD. To test this, we performed a series of simulations (for details see the ESI†). Fig. 3 shows the results for the first two moments of the interatomic distribution, the averaged distance 〈r〉 and the amplitude l (eqn (2)).
 | ||
| Fig. 3 Mean internuclear distances 〈r〉 and vibrational amplitudes l (eqn (2)) for the ground vibrational state of the molecular cation H2+. Horizontal lines show the results of the harmonic (h, black line), anharmonic (anh, blue line), and MD with WS (“WS + MD”, red line). The curves show results of the MBS + MD and SWS + MD simulations at different τ = h/(kBT). | ||
The harmonic oscillator model and the pure WS result in 〈r〉h = re because the harmonic potential is symmetrical. However, MD simulations with initial conditions from WS (WS + MD) produce an average value 〈r〉WS + MD very close to that computed with the numerical ground state anharmonic wavefunction 〈r〉anh. In the case of the diatomic molecule, the SWS distribution can be exactly mapped to WS. Therefore we can get the same solution 〈r〉SWS+MD = 〈r〉WS+MD by scanning the parameter τ. The resulting curve has a single minimum at τ = 2 fs where 〈r〉SWS+MD = 〈r〉WS+MD = 〈r〉anh. Fig. 3 also shows the results from MBS + MD simulations at various temperatures, where the temperature T is mapped to τ through the Debye temperature relationship τ = ν−1 = h/(kBT). The resulting value coincides with the expected one at T around 3000 K (τ = 16 fs). The trend for MBS shows only the growth of 〈r〉 with the increase in temperature. Thus MBS requires an a priori knowledge of the appropriate temperature, in contrast to SWS + MD, where the best τ can be found in the variational procedure by minimizing the 〈r〉. The results for the amplitude l show that the harmonic value is close to those from anharmonic and WS + MD calculations. This is expected since the second moment of the internuclear distribution is dominated by the harmonic potential.11,34,35
The single minimum of 〈r〉 and l in the SWS + MD simulations suggest a similar behavior for other observables, which can be used for finding the optimal parameter τ for larger molecules. The obvious choice is an energy-related parameter, for example, the average total energy (electronic and nuclear) 〈Etot〉. The other option is the kinetic energy of nuclei (〈Ekin〉), which is often expressed in terms of temperature through the relationship 〈Ekin〉 = NfkBT/2, where Nf is the number of degrees of freedom. For example, Nf = 1 in the case of the diatomic molecule H2+. The results in Fig. 4 show that the minimum energy is reached at τ = 2 fs. Note, at this value the average distance 〈r〉 and the amplitude l are minimal, as Fig. 3 shows. The total vibrational energy Evib = 〈Etot〉 − Ee was compared to the quantum zero-point vibrational energy (ZPVE) of the system. Similar to the amplitude, ZPVE is dominated by the harmonic potential. Therefore, the harmonic and anharmonic ZPVE values are very close. There is also another consideration regarding the τ parameter. According to the equipartition theorem,36 which assumes the dominating role of the harmonic potential, the nuclear temperature can be used to guide the choice of the τ parameter in SWS. This is also confirmed by the numerical test demonstrated in Fig. 4.
4.2 Rotational constants
The accuracy of calculated vibrationally-averaged (usually B0) rotational constants is mostly determined by two factors, (a) equilibrium structure and (b) vibrational corrections Be − B0. The latter is relevant for the context of the present investigation. Thus, in the following we do not aim at reproducing the absolute values of rotational constants but benchmark only corrections Be − B0. For this, five small molecules have been chosen (see Fig. 1): water (H2O), ethylene (C2H4), difluoromethane (CH2F2), and trans and cis isomers of 1,2-difluoroethylene (C2H2F2). For each molecule the corrections Be − B0 were calculated by using Wigner sampling (in WS + MD and SWS + MD variants) and by VPT2. In our case with small semi-rigid molecules the values from VPT2 provide accurate reference values.37,38Three of the test molecules (H2O, C2H4, and CH2F2) were used to verify the position of optimal τ. Fig. 5 illustrates the effect of τ in the SWS procedure applied to these molecules. The minimal vibrational energies were in the range of 2–4 fs, very close to the optimal τ = 2 fs determined for H2+. Thus, we used this value further in our simulations. However, in general we recommend to tune τ for obtaining the most accurate results.
Computing averaged rotational constants from MD trajectories is not straightforward. In this paper we tested the following three different procedures.
• The simplest approach is the calculation of rotational constants Bα (α = a, b, c) at every time step with the following averaging of the Bα over the complete MD trajectory. This procedure is denoted as mean rotational constants (MRC).
• A more sophisticated procedure, in which the complete tensor of inertia is calculated at each MD step. The inverted tensor −1 is averaged along the trajectory, producing  . The eigenvalues of
. The eigenvalues of  are
are  , which are related to the rotational constants as
, which are related to the rotational constants as  . Since the rotation is frozen during the simulation, we may assume that the principal axes of the molecule do not deviate significantly from the initial positions. Therefore there is no need for a reorientation of the molecule with respect to the reference structure. This procedure is denoted as mean inverse inertia tensor unoriented (MIITU).
. Since the rotation is frozen during the simulation, we may assume that the principal axes of the molecule do not deviate significantly from the initial positions. Therefore there is no need for a reorientation of the molecule with respect to the reference structure. This procedure is denoted as mean inverse inertia tensor unoriented (MIITU).
• A method similar to the previous but with the orientation of all molecular frames with respect to the reference equilibrium structure. The orientation is done by minimizing the mass-weighted functional  , where i enumerates all the nuclei in the molecule, m are the masses and r are the coordinates of the nuclei, the index “e” denotes the reference equilibrium configuration of the nuclei. The minimization can be efficiently performed using the Kabsch algorithm.39 This way of computing the mean rotational constants is denoted as mean inverse inertia tensor oriented (MIITO).
, where i enumerates all the nuclei in the molecule, m are the masses and r are the coordinates of the nuclei, the index “e” denotes the reference equilibrium configuration of the nuclei. The minimization can be efficiently performed using the Kabsch algorithm.39 This way of computing the mean rotational constants is denoted as mean inverse inertia tensor oriented (MIITO).
We can consider each MD trajectory as a single measurement of the system with the resulting constants 〈A〉 = 〈Ba〉, 〈B〉 = 〈Bb〉, 〈C〉 = 〈Bc〉 obtained by either one of the MRC/MIITU/MIITO procedures. The actual result, however, requires averaging over several such MD trajectories started from different initial conditions. Therefore, the final values are the results of double averaging from multiple trajectories, defined as
where
 .
.
Using these three procedures, we have calculated the vibrational shifts of rotational constants Be,α − 〈Bα〉, which were compared with those from the standard VPT2 computations. Since the shifts are sensitive to the absolute values of rotational constants, in statistical assessments (Table 1 and Fig. 6) we used normalized quantities (Be,α − 〈B〉)/Be,α = 1 − 〈B〉/Be,α. In general, results from all tested combinations of methods for trajectory simulations (WS + MD, SWS + MD) and for calculation of rotational constants (MRC, MIITU, MIITO) correlated reasonably with reference VPT2 values. The MIITU and MIITO routines are the most physically justified, since the vibrationally-averaged rotational parameter appears from the averaging of the rotational Hamiltonian as  , where |0〉 is the ground vibrational state, and
, where |0〉 is the ground vibrational state, and ![[L with combining circumflex]](https://www.rsc.org/images/entities/b_char_004c_0302.gif) is the angular momentum operator. To quantify the performance of the methods, we have computed Pearson correlation coefficients ρ for the observed normalized rotational constant shifts from the MD trajectories and VPT2. The results are summarized in Table 1. MIITO showed the best performance among all of the routines applied, and therefore it was further used as a default procedure for the calculation of vibrationally-averaged rotational constants from MD trajectories. The resulting vibrational corrections to rotational constants are listed in Table 2. As one can see, the MD values correlate quite well with the reference values from the VPT2 model.
is the angular momentum operator. To quantify the performance of the methods, we have computed Pearson correlation coefficients ρ for the observed normalized rotational constant shifts from the MD trajectories and VPT2. The results are summarized in Table 1. MIITO showed the best performance among all of the routines applied, and therefore it was further used as a default procedure for the calculation of vibrationally-averaged rotational constants from MD trajectories. The resulting vibrational corrections to rotational constants are listed in Table 2. As one can see, the MD values correlate quite well with the reference values from the VPT2 model.
| MRC | MIITU | MIITO | |
|---|---|---|---|
| ρ(WS + MD,VPT2) | 0.77 | 0.76 | 0.80 |
| ρ(SWS + MD,VPT2) | 0.83 | 0.89 | 0.90 |
 | ||
| Fig. 6 Corrections to rotational constants Be − B0 calculated using different methods in comparison to reference values computed from cubic force fields. A solid line indicates the diagonal. | ||
| Molecule | A/B/C | B e | B e − B0 | |||
|---|---|---|---|---|---|---|
| VPT2 | VPT2 + cent. | WS + MD | SWS + MD(τ = 2 fs) | |||
| a The quantum-chemical approximation used for the simulation was PBE/def2-SVP. All values given are in m−1 (for conversion to cm−1, the values must be divided by 100). All the MD values were obtained from the MIITO routine. The uncertainties of the MD values are the ± standard errors. | ||||||
| H2O | A | 2505.328 | −31.632 | −32.781 | −12 ± 17 | −71 ± 33 |
| B | 1456.758 | 10.273 | 10.567 | 12 ± 3 | 11 ± 3 | |
| C | 921.145 | 23.594 | 24.057 | 28 ± 3 | 29 ± 4 | |
| C2H4 | A | 475.622 | 4.457 | 4.457 | 10 ± 1 | 12 ± 1 |
| B | 98.657 | 0.678 | 0.679 | 1.2 ± 0.1 | 1.8 ± 0.1 | |
| C | 81.708 | 0.821 | 0.820 | 0.9 ± 0.1 | 1.2 ± 0.1 | |
| CH2F2 | A | 164.710 | 1.710 | 1.710 | 2.5 ± 0.3 | 2.1 ± 0.4 |
| B | 34.706 | 0.206 | 0.206 | 0.28 ± 0.03 | 0.4 ± 0.1 | |
| C | 30.442 | 0.230 | 0.230 | 0.34 ± 0.03 | 0.5 ± 0.1 | |
| trans-C2H2F2 | A | 190.383 | 2.230 | 2.230 | 4.4 ± 0.3 | 9 ± 1 |
| B | 13.199 | 0.046 | 0.046 | 0.06 ± 0.01 | 0.04 ± 0.01 | |
| C | 12.343 | 0.058 | 0.058 | 0.06 ± 0.01 | 0.05 ± 0.01 | |
| cis-C2H2F2 | A | 71.606 | 0.670 | 0.670 | 1.0 ± 0.1 | 0.2 ± 0.4 |
| B | 18.895 | −0.002 | −0.003 | −0.01 ± 0.01 | 0.04 ± 0.04 | |
| C | 14.950 | 0.051 | 0.051 | 0.04 ± 0.01 | 0.12 ± 0.02 | |
| C6H12N2 | A | 12.02 | 0.12 | 0.12 | 0.16 ± 0.01 | |
| B | 5.85 | 0.06 | 0.06 | 0.10 ± 0.01 | ||
| C | 5.79 | 0.07 | 0.07 | 0.11 ± 0.01 | ||
| C26H34O2 | A | 1.3151 | 0.0126 | 0.0126 | 0.0164 ± 0.0002 | |
| B | 0.5286 | 0.0060 | 0.0060 | 0.0078 ± 0.0001 | ||
| C | 0.5281 | 0.0061 | 0.0061 | 0.0078 ± 0.0001 | ||
A very important aspect is that MD simulations with frozen out rotations cannot recover centrifugal effects. Centrifugal expansion is a few orders of magnitude smaller than the anharmonic shift (see Table 2) and is negligible in comparison to the standard errors of our MD values. Thus, even with allowed rotations the uncertainty of MD prevents its usage for calculation of this particular effect. On the other side, it is mostly dominated by the harmonic potential and therefore is well predicted in the harmonic approximation with a much smaller computational cost.14
Two additional tests of the proposed computational methods were done using the moderate-size molecular systems (see Fig. 1), 6,6-dimethyl-1,5-diazabicyclo[3.1.0]hexane (C6H12N2) and syn-conformer of 6,6′-bis(3-oxadiamantane) (C26H34O2). Both structures were previously investigated experimentally40,41 by gas electron diffraction (GED). For the latter molecule GED data were supplemented by rotational constants from microwave measurements. Results of our calculations for these two molecules are given in Table 2. The (Be − B0) values obtained by WS + MD simulations are in reasonable agreement with those from VPT2. The relative deviations are about of the same order of magnitude as for the smaller systems discussed above. Thus, WS + MD can probably be applied to larger and more complicated molecules.
4.3 Vibrational spectra
Another possible application of MD is the prediction of vibrational spectra. Here we discuss only infrared (IR) one-photon spectra. Their intensity can be computed as42where 〈ḋ(τ)ḋ(τ + t) 〉τ is the autocorrelation function (ACF) of the dipole moment time-derivative (ḋ), t the is time, and ν is the frequency. Other types of vibrational spectra, such as Raman or vibrational circular dichroism, can be computed similarly.42,43 The duration (ttot) and the time step (Δt) of ACF are the same as for the original MD trajectory. In discrete Fourier transform, the frequency resolution is determined by the trajectory duration as Δν ∝ ttot−1, while the time step determines the maximal frequency as νmax ∝ Δt−1. Generally, it is recommended to use small time steps in MD simulations, otherwise large integration steps can lead to artificial blue shifts in the high-frequency region.44 However, such shifts can be corrected using a simple replacement of Fourier-transform frequencies νFT with45
We also applied this correction throughout the work.
It is worth mentioning the practical limitations of NVE MD simulations due to the limited total number of collected frames N, determined by available computational and time resources. We calculate Nt trajectories each with Ns steps, so that the total number of frames is N = Nt·Ns. For the predefined constant N we may balance Nt and Ns but cannot increase both parameters. Smaller Ns causes lowering of the spectral resolution, because of the duration of trajectories t = Ns·Δt, where Δt is the integration time step. On the other side, smaller Nt will result in poorer phase-space sampling. To overcome this problem of NVE MD, we can try switching to NVT MD with a thermostat, in which the phase space sampling is done on-the-fly. In this case, with a similar number of computational operations it is possible to obtain fewer trajectories (smaller Nt) but with larger lengths (larger Ns) and optimal phase space sampling. However, the thermostat must not interfere too much with the dynamics of the system.13
The Andersen thermostat is the most straightforward to implement.46 The WS method relies on equilibrium molecular geometry and cannot be used for anything except for sampling of the initial conditions. SWS, on the other hand, has the same principle as MBS and thus can be used with the Andersen thermostat. Test calculations have been performed for difluoromethane CH2F2 at the PBE/def2-SVP level of theory using a combination of SWS and Andersen thermostat (abbreviated here as SWS-AT + MD). We also carried out classical constant temperature MD simulations with the Andersen thermostat applying the MBS scheme (MBS-AT + MD). Fig. 7 shows the obtained vibrational spectra in comparison to harmonic and VPT2 fundamentals. Also, for demonstrational purposes, we calculated and plotted spectra from the WS + MD and SWS + MD simulations, which were used in computation of rotational constants described above. Classical MBS introduces relatively small vibrational amplitudes. Therefore, high-frequency vibrations from MBS-AT + MD are essentially harmonic. Taking into account nuclear quantum effects in WS + MD, SWS + MD, and SWS-AT + MD simulations leads to a better agreement of the MD-based spectra with the VPT2 calculations. Short lengths of MD trajectories in the NVE MD simulations limit the frequency resolution in the WS + MD and SWS + MD simulations. The much longer SWS-AT + MD simulations show results very similar to WS + MD and SWS + MD, which is seen in the similar shapes and positions of the peaks in the spectra. However, due to the much longer duration of trajectories the spectral resolution in SWS-AT + MD exceeds by far that in WS + MD and SWS + MD. On the basis of the obtained results we can recommend the SWS-AT + MD technique for calculation of vibrational spectra.
4.4 Case studies
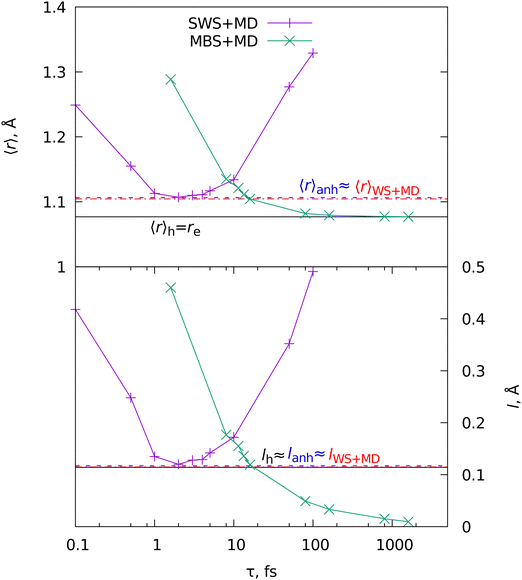
To further demonstrate the applicability of WS + MD and SWS + MD for the calculation of vibrational properties and to compare the performance of MD with harmonic and VPT2 vibrational models, we have performed three additional sets of calculations for different molecular systems. We have chosen benzene (C6H6), protonated methane cation (CH5+) and protonated serine octamer (Ser8H+, (C3H7NO3)8H+), see Fig. 1. For all of them there have been published high quality experimental and theoretical data.47–54 Benzene is an example of a simple and semi-rigid system, for which are available experimental rotational constants with respective theoretical anharmonic corrections,47,49 vibrational48 and photoelectron (PE) spectra.50 CH5+ was taken as a system with large amplitude motions (LAMs) requiring treatment beyond the localized vibrational harmonic and VPT2 approximations. Ser8H+ is used to demonstrate the increasing computational expenses of the VPT2 approach compared to MD.Furthermore, the experimental vibrational IR spectra of benzene were taken from NIST Chemistry WebBook48 and compared with those calculated in this work, see Fig. 8. The averaged IR spectra from SWS-AT + MD and WS + MD reproduce all experimental bands. MBS-AT + MD underestimates the intensity for the overtones within the 1700–2000 cm−1 range (not shown in the harmonic and VPT2 plots). It is interesting to discuss the C–H stretching region, corresponding to vibrations with the highest Debye temperature in benzene. In MBS-AT + MD the position of the corresponding peak at 3260 cm−1 is essentially the same as in the harmonic approximation (3262 cm−1). This is explained by underestimation of vibrational amplitudes in the classical MD treatment (see the discussion of eqn (4)). WS + MD results in a larger anharmonic shift with the peak maximum at 3223 cm−1. In SWS-AT + MD at both temperatures (0 and 300 K) this band is at 3185 cm−1, the closest to the experimental value at about 3058 cm−1. Notably, the MD models qualitatively correctly predict frequencies in the C–H stretching region around 3000 cm−1, whereas in the VPT2 calculation we obtained an unrealistically large anharmonic shift of 409 cm−1 for one of the modes. This VPT2 artifact probably arises from resonances, which have been discussed previously.55,56 Overall, WS and SWS demonstrate a better agreement with experimental data in comparison to other tested methods.
We also computed photoelectron spectra (PES) of benzene and compared them with the available experimental data.50 Several types of calculations were performed. First, conventional Franck–Condon factors were computed for the ground electronic states of the neutral benzene and for its cation. As a preliminary step, structure optimizations and harmonic frequency calculations were carried out for C6H6 and C6H6+. However, C6H6+ is a well-known example57,58 of the Jahn–Teller effect. Therefore, the same procedures cannot be applied to the excited electronic states of C6H6+ and only the first band of the PE spectrum could be obtained using this procedure. The WS procedure with harmonic modes has been used to account for vibrational motions. With this simplistic treatment of vibrational degrees of freedom in the harmonic approximation we computed an approximate PE spectrum, see Fig. 9. For the anharmonic treatment, trajectories from SWS-AT + MD modeling were used (see the ESI† for details). A conventional Franck-Condon computation would allow direct evaluation of the vibrational structure. However, this requires optimization of cationic excited states, which can be considerably complicated due to their strong multireference character, as in the case of benzene. Alternatively, WS and SWS can be used as the fast and simple methods for estimation of line shapes, as we demonstrate in Fig. 9. The spectra computed on the basis of MD are slightly red-shifted in the first three bands with respect to the WS-based values. This is probably due to anharmonicity.
 | ||
| Fig. 9 Experimental and modeled (see the text and ESI† for details) photoelectron spectra of benzene. ezFCS bars indicate results of the computation of Franck–Condon factors. The WS and SWS-AT + MD lines are manually shifted by 0.5 eV for a better match with the experimental peaks. | ||
| CH5++ CO2 + hν → CH4 + OCOH+, | (12) |
 | (13) |
 | ||
| Fig. 10 Experimental51 and modeled IR spectra of CH5+. Arrows indicate anharmonic VPT2 shifts. Broadening of the theoretical harmonic lines has been done by Gaussian convolution with a FWHM of 10 cm−1. | ||
To demonstrate that, we have performed two simulations, MBS-AT + MD at T = 300 K and SWS-AT + MD at T = 0 K. Since experimental spectra were obtained using a helium tag,54 we applied the intensity correction factor given in eqn (13) with the calculated helium detachment energy D = 379 cm−1. Fig. 11 shows comparison of the experimental and calculated spectra.
It is generally difficult to achieve a very good agreement between theoretical and experimental spectra for a large and complicated system such as Ser8H+. The spectra obtained here qualitatively describe intensity distribution within the ranges 1000–1800 cm−1 and 2900–3500 cm−1. There are, however, some particular deviations worth mentioning. In the experiments there were no significant signals around 2000 cm−1, whereas harmonic and SWS calculations predict some bands in this region. Only the SWS spectrum can reproduce large intensities (although with somewhat shifted frequencies) of the sharp lines at about 3350 cm−1 in the experiment, which were assigned to N–H and O–H stretchings. However, neither of our simulations showed an intense signal for another O–H stretching vibration at 3700 cm−1. Note, the same problem of very low intensity was observed in calculations performed in the original work.54 Overall, we demonstrate here the principal applicability of SWS for simulation of the vibrational spectra of large systems. At that, the accuracy in some cases may be higher than in harmonic approximation.
5. Conclusions
Wigner sampling (WS) combined with classical molecular dynamics is a powerful approach for describing nuclear quantum effects and vibrational anharmonicity at a reasonable computational cost. In this work we briefly describe the underlying theory and introduce a new procedure, denoted as simplified Wigner sampling (SWS). In contrast to WS, this procedure does not require initial calculation of Hessian. Instead, it can be controlled by a single parameter τ, whose optimal values can be found in the interval 1 ≤ τ ≤ 10 fs.To test the sampling methods a series of calculations were performed for several molecular systems. Among the modeled properties were (a) vibrational IR spectra, (b) photoelectron spectra and (c) vibrationally averaged rotational constants. For the latter, three computational procedures have been introduced and tested. The accuracy of WS and SWS has been assessed by comparing with experimental data (where available) and with results of harmonic and VPT2 anharmonic calculations. The new SWS procedure showed a promising performance taking into account its computational simplicity. Its particular advantage over the VPT2 method has been observed for the large system of the protonated serine octamer and in the cases with large amplitude motions.
List of abbreviations
| MD | Molecular dynamics |
| NQEs | Nuclear quantum effects |
| PIMD | Path-integral molecular dynamics |
| RMSD | Root-mean-square deviation |
| PES | Potential energy surface |
| VPT2 | Vibrational perturbation theory of the second order |
| PTn | Perturbation theory of the n-th order |
| MBS | Maxwell–Boltzmann sampling |
| Pair distribution function | |
| WS | Wigner sampling |
| SWS | Simplified Wigner sampling |
| MRC | Mean rotational constants |
| MIITU | Mean inverse inertia tensor (unoriented) |
| MIITO | Mean inverse inertia tensor (oriented) |
| AT | Andersen thermostat‡ |
| FWHM | Full width at half maximum |
| IR | Infrared (spectrum) |
| PE | Photoelectron (spectrum) |
| IP | Ionization potential |
Author contributions
Denis S. Tikhonov: project administration, conceptualization, data curation, investigation, software, visualization, writing – original draft. Yury V. Vishnevskiy: conceptualization, data curation, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Appendix: derivation of the heuristic damping function for the action spectroscopy
Action spectroscopy detects absorption of photons by tracing down photon-induced changes in the molecular system. For example, in the case of tag spectroscopy the molecular system is tagged by a weakly bound inert particle-like inert gas atom or nitrogen molecule. If a vibrational mode absorbs a single photon with frequency ν, the resulting energy hν is redistributed between modes, such that this leads to the detachment of the tag. Let us assume the existence of two vibrational modes in the molecule: #1, which is photoexcited, and #2 corresponding to the dissociation of the tag. We also assume that vibrations are classical and thus the total energy (kinetic plus potential) of each mode En ≥ 0 (n = 1, 2). Upon the photon absorption, the total energy of the system E = E1 + E2 increases by the photon energy hν and becomes E = hν = E1 + E2. The energy of the second mode (E2) during the redistribution process may overcome the dissociation energy (D). In this case a signal is produced and detected. We can imagine the total number of states N with the redistributed energy hν as a straight line hν = E1 + E2 (0 ≤ E1, E2 ≤ hν) in coordinates E1 − E2 (see Fig. 12) and . The number of tag-dissociating states is then a subsection of this line with D < E2 ≤ hν. If the photon energy is smaller than the dissociation energy (hν ≤ D), the removal of the tag cannot happen, and thus the number of dissociated molecules is Ndiss = 0. Otherwise, when hν > D, the number of the dissociated molecules is calculated as
. The number of tag-dissociating states is then a subsection of this line with D < E2 ≤ hν. If the photon energy is smaller than the dissociation energy (hν ≤ D), the removal of the tag cannot happen, and thus the number of dissociated molecules is Ndiss = 0. Otherwise, when hν > D, the number of the dissociated molecules is calculated as  (see Fig. 12). Thus we can find the quantum yield of the dissociation per absorbed photon with frequency ν as
(see Fig. 12). Thus we can find the quantum yield of the dissociation per absorbed photon with frequency ν asWe can approximate the final observable action spectroscopy signal as I(ν)·f(ν), where I(ν) is the absorption spectrum of the molecule and f(ν) is the quantum yield of the dissociation.
 | ||
| Fig. 12 Scheme of the heuristic derivation of the damping factor in the action-type spectroscopy. See the text for details. | ||
The general form of the damping function f(ν) from eqn (13) is given in Fig. 13. Application of this function effectively zeroes signals with energies below the threshold (hν < D). Signals above the threshold are scaled by factors, increasing with the increase of the photon energy hν.
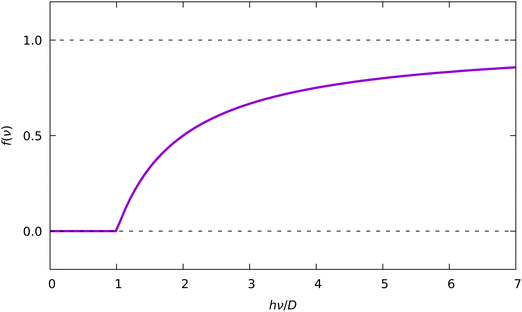 | ||
| Fig. 13 Damping function f(ν) (eqn (13)). | ||
Acknowledgements
This work has been supported by Deutsches Elektronen-Synchtrotron DESY, a member of the Helmholtz Association (HGF). Molecular dynamics calculations were enabled through the Maxwell computational resources operated at Deutsches Elektronen-Synchrotron DESY, Hamburg, Germany. YuVV is grateful to Deutsche Forschungsgemeinschaft (grant VI 713/1-3) for the support. Some of the computations were carried out at HPC facilities of the Universität zu Köln.References
- T. E. Markland and M. Ceriotti, Nuclear quantum effects enter the mainstream, Nat. Rev. Chem., 2018, 20(3), 0109, DOI:10.1038/s41570-017-0109.
- S. A. Hollingsworth and R. O. Dror, Molecular dynamics simulation for all, Neuron, 2018, 990(6), 1129–1143, DOI:10.1016/j.neuron.2018.08.011.
- R. Iftimie, P. Minary and M. E. Tuckerman, Ab initio molecular dynamics: Concepts, recent developments, and future trends, Proc. Natl. Acad. Sci. U. S. A., 2005, 1020(19), 6654–6659, DOI:10.1073/pnas.0500193102.
- D. Marx and M. Parrinello, Ab initio path integral molecular dynamics: Basic ideas, J. Chem. Phys., 1996, 1040(11), 4077–4082, DOI:10.1063/1.471221.
- S. C. Althorpe, Path-integral approximations to quantum dynamics, Eur. Phys. J. B, 2021, 940(7), 155, DOI:10.1140/epjb/s10051-021-00155-2.
- P. W. Atkins and R. S. Friedman, Molecular Quantum Mechanics, OUP, Oxford, 2011 Search PubMed.
- P. Pulay, G. Fogarasi, G. Pongor, J. E. Boggs and A. Vargha, Combination of theoretical ab initio and experimental information to obtain reliable harmonic force constants. scaled quantum mechanical (qm) force fields for glyoxal, acrolein, butadiene, formaldehyde, and ethylene, J. Am. Chem. Soc., 1983, 1050(24), 7037–7047, DOI:10.1021/ja00362a005.
- M. K. Kesharwani, B. Brauer and J. M. L. Martin, Frequency and zero-point vibrational energy scale factors for double-hybrid density functionals (and other selected methods): Can anharmonic force fields be avoided?, J. Phys. Chem. A, 2015, 1190(9), 1701–1714, DOI:10.1021/jp508422u.
- R. A. Mata and M. A. Suhm, Benchmarking quantum chemical methods: Are we heading in the right direction?, Angew. Chem., Int. Ed., 2017, 560(37), 11011–11018, DOI:10.1002/anie.201611308.
- L. D. Landau and E. M. Lifshitz, Mechanics: Volume 1 (Course of Theoretical Physics), Butterworth-Heinemann, 3rd edn, 1976 Search PubMed.
- Y. V. Vishnevskiy and D. Tikhonov, Quantum corrections to parameters of interatomic distance distributions in molecular dynamics simulations, Theor. Chem. Acc., 2016, 1350(4), 88, DOI:10.1007/s00214-016-1848-2.
- C. Qu and J. M. Bowman, Quantum approaches to vibrational dynamics and spectroscopy: is ease of interpretation sacrificed as rigor increases?, Phys. Chem. Chem. Phys., 2019, 21, 3397–3413, 10.1039/C8CP04990D.
- D. S. Tikhonov, D. I. Sharapa, J. Schwabedissen and V. V. Rybkin, Application of classical simulations for the computation of vibrational properties of free molecules, Phys. Chem. Chem. Phys., 2016, 18, 28325–28338, 10.1039/C6CP05849C.
- V. Barone, Anharmonic vibrational properties by a fully automated second-order perturbative approach, J. Chem. Phys., 2005, 1220(1), 014108, DOI:10.1063/1.1824881.
- Q. Yang, M. Mendolicchio, V. Barone and J. Bloino, Accuracy and reliability in the simulation of vibrational spectra: A comprehensive benchmark of energies and intensities issuing from generalized vibrational perturbation theory to second order (gvpt2), Frontiers in Astronomy and Space Sciences, 2021, 8 DOI:10.3389/fspas.2021.665232.
- E. Wigner, On the quantum correction for thermodynamic equilibrium, Phys. Rev., 1932, 40, 749–759, DOI:10.1103/PhysRev.40.749.
- L. Sun and W. L. Hase, Comparisons of classical and wigner sampling of transition state energy levels for quasiclassical trajectory chemical dynamics simulations, J. Chem. Phys., 2010, 1330(4), 044313, DOI:10.1063/1.3463717.
- J. P. Zobel, J. J. Nogueira and L. González, Finite-temperature wigner phase-space sampling and temperature effects on the excited-state dynamics of 2-nitronaphthalene, Phys. Chem. Chem. Phys., 2019, 21, 13906–13915, 10.1039/C8CP03273D.
- J. P. Zobel, M. Heindl, J. J. Nogueira and L. González, Vibrational sampling and solvent effects on the electronic structure of the absorption spectrum of 2-nitronaphthalene, J. Chem. Theory Comput., 2018, 140(6), 3205–3217, DOI:10.1021/acs.jctc.8b00198.
- D. Avagliano, E. Lorini and L. González, Sampling effects in quantum mechanical/molecular mechanics trajectory surface hopping non-adiabatic dynamics, Philos. Trans. R. Soc., A, 2022, 3800(2223), 20200381, DOI:10.1098/rsta.2020.0381.
- Jmol development team, Jmol: an open-source java viewer for chemical structures in 3d, https://www.jmol.org/.URLhttp://jmol.sourceforge.net/.
- M. Barbatti and K. Sen, Effects of different initial condition samplings on photodynamics and spectrum of pyrrole, Int. J. Quantum Chem., 2016, 1160(10), 762–771, DOI:10.1002/qua.25049.
- S. Kullback and R. A. Leibler, On Information and Sufficiency, Ann. Math. Stat., 1951, 220(1), 79–86, DOI:10.1214/aoms/1177729694.
- D. S. Tikhonov, Y. V. Vishnevskiy, A. N. Rykov, O. E. Grikina and L. S. Khaikin, Semi-experimental equilibrium structure of pyrazinamide from gas-phase electron diffraction. how much experimental is it?, J. Mol. Struct., 2017, 1132, 20–27, DOI:10.1016/j.molstruc.2016.05.090.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple [phys. rev. lett. 77, 3865 (1996)], Phys. Rev. Lett., 1997, 78, 1396, DOI:10.1103/PhysRevLett.78.1396.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for h to rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305, 10.1039/B508541A.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 320(7), 1456–1465, DOI:10.1002/jcc.21759.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The orca quantum chemistry program package, J. Chem. Phys., 2020, 1520(22), 224108, DOI:10.1063/5.0004608.
- S. Grimme, J. G. Brandenburg, C. Bannwarth and A. Hansen, Consistent structures and interactions by density functional theory with small atomic orbital basis sets, J. Chem. Phys., 2015, 1430(5), 054107, DOI:10.1063/1.4927476.
- V. Barone, Anharmonic vibrational properties by a fully automated second-order perturbative approach, J. Chem. Phys., 2005, 1220(1), 014108, DOI:10.1063/1.1824881.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- M. Ceriotti, G. Bussi and M. Parrinello, Nuclear quantum effects in solids using a colored-noise thermostat, Phys. Rev. Lett., 2009, 103, 030603, DOI:10.1103/PhysRevLett.103.030603.
- H. Dammak, Y. Chalopin, M. Laroche, M. Hayoun and J.-J. Greffet, Quantum thermal bath for molecular dynamics simulation, Phys. Rev. Lett., 2009, 103, 190601, DOI:10.1103/PhysRevLett.103.190601.
- V. A. Levashov, S. J. L. Billinge and M. F. Thorpe, Quantum correction to the pair distribution function, J. Comput. Chem., 2007, 280(11), 1865–1882, DOI:10.1002/jcc.20713.
- V. A. Sipachev., Diffraction measurements and equilibrium parameters, Adv. Phys. Chem., 2011, 1–14 Search PubMed.
- P. Atkins and J. Paula, Atkins' physical chemistry, Oxford University press, 2008 Search PubMed.
- N. Vogt, J. Vogt and J. Demaison, Accuracy of the rotational constants, J. Mol. Struct., 2011, 9880(1), 119–127, DOI:10.1016/j.molstruc.2010.12.040.
- S. Alessandrini, J. Gauss and C. Puzzarini, Accuracy of rotational parameters predicted by high-level quantum-chemical calculations: Case study of sulfur-containing molecules of astrochemical interest, J. Chem. Theory Comput., 2018, 140(10), 5360–5371, DOI:10.1021/acs.jctc.8b00695.
- W. Kabsch, A solution for the best rotation to relate two sets of vectors, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 320(5), 922–923, DOI:10.1107/S0567739476001873.
- Y. V. Vishnevskiy, J. Schwabedissen, A. N. Rykov, V. V. Kuznetsov and N. N. Makhova, Conformational and bonding properties of 3,3-dimethyl- and 6,6-dimethyl-1,5-diazabicyclo[3.1.0]hexane: A case study employing the monte carlo method in gas electron diffraction, J. Phys. Chem. A, 2015, 1190(44), 10871–10881, DOI:10.1021/acs.jpca.5b08228.
- A. A. Fokin, T. S. Zhuk, S. Blomeyer, C. Pérez, L. V. Chernish, A. E. Pashenko, J. Antony, Y. V. Vishnevskiy, R. J. F. Berger, S. Grimme, C. Logemann, M. Schnell, N. W. Mitzel and P. R. Schreiner, Intramolecular london dispersion interaction effects on gas-phase and solid-state structures of diamondoid dimers, J. Am. Chem. Soc., 2017, 1390(46), 16696–16707, DOI:10.1021/jacs.7b07884.
- M. Thomas, M. Brehm, R. Fligg, P. Vöhringer and B. Kirchner, Computing vibrational spectra from ab initio molecular dynamics, Phys. Chem. Chem. Phys., 2013, 15, 6608–6622, 10.1039/C3CP44302G.
- E. Ditler and S. Luber, Vibrational spectroscopy by means of first-principles molecular dynamics simulations, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12(5), e1605, DOI:10.1002/wcms.1605.
- J. Horníček, P. Kaprálová and P. Bouř, Simulations of vibrational spectra from classical trajectories: Calibration with ab initio force fields, J. Chem. Phys., 2007, 1270(8), 084502, DOI:10.1063/1.2756837.
- D. S. Tikhonov, Simple posterior frequency correction for vibrational spectra from molecular dynamics, J. Chem. Phys., 2016, 1440(17), 174108, DOI:10.1063/1.4948320.
- H. C. Andersen, Molecular dynamics simulations at constant pressure and/or temperature, J. Chem. Phys., 1980, 720(4), 2384–2393, DOI:10.1063/1.439486.
- I. Heo, J. C. Lee, B. R. Özer and T. Schultz, Structure of benzene from mass-correlated rotational Raman spectroscopy, RSC Adv., 2022, 12, 21406–21416, 10.1039/D2RA03431J.
- “Infrared Spectra” by NIST Mass Spectrometry Data Center, William E. Wallace, director, in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P.J. Linstrom and W.G. Mallard, National Institute of Standards and Technology, Gaithersburg MD, 20899, https://webbook.nist.gov/chemistry/, (retrieved January 11, 2023).
- J. Gauss and J. F. Stanton, The equilibrium structure of benzene, J. Phys. Chem. A, 2000, 1040(13), 2865–2868, DOI:10.1021/jp994408y.
- A. J. Yencha, R. I. Hall, L. Avaldi, G. Dawber, A. G. McConkey, M. A. MacDonald and G. C. King, Threshold photoelectron spectroscopy of benzene up to 26.5 ev, Can. J. Chem., 2004, 820(6), 1061–1066, DOI:10.1139/v04-057.
- O. Asvany, P. Kumar, B. Redlich, I. Hegemann, S. Schlemmer and D. Marx, Understanding the infrared spectrum of bare ch5+, Science, 2005, 3090(5738), 1219–1222, DOI:10.1126/science.1113729.
- O. Asvany, K. M. T. Yamada, S. Brünken, A. Potapov and S. Schlemmer, Experimental ground-state combination differences of ch5+, Science, 2015, 3470(6228), 1346–1349, DOI:10.1126/science.aaa3304.
- X. Huang, A. B. McCoy, J. M. Bowman, L. M. Johnson, C. Savage, F. Dong and D. J. Nesbitt, Quantum deconstruction of the infrared spectrum of ch5, Science, 2006, 3110(5757), 60–63, DOI:10.1126/science.1121166.
- V. Scutelnic, M. A. S. Perez, M. Marianski, S. Warnke, A. Gregor, U. Rothlisberger, M. T. Bowers, C. Baldauf, G. von Helden, T. R. Rizzo and J. Seo, The structure of the protonated serine octamer, J. Am. Chem. Soc., 2018, 1400(24), 7554–7560, DOI:10.1021/jacs.8b02118.
- P. E. Maslen, N. C. Handy, R. D. Amos and D. Jayatilaka, Higher analytic derivatives. IV. Anharmonic effects in the benzene spectrum, J. Chem. Phys., 1992, 970(6), 4233–4254, DOI:10.1063/1.463926.
- A. Miani, E. Cané, P. Palmieri, A. Trombetti and N. C. Handy, Experimental and theoretical anharmonicity for benzene using density functional theory, J. Chem. Phys., 2000, 1120(1), 248–259, DOI:10.1063/1.480577.
- M. L. Vidal, M. Epshtein, V. Scutelnic, Z. Yang, T. Xue, S. R. Leone, A. I. Krylov and S. Coriani, Interplay of open-shell spin-coupling and Jahn–Teller distortion in benzene radical cation probed by x-ray spectroscopy, J. Phys. Chem. A, 2020, 1240(46), 9532–9541, DOI:10.1021/acs.jpca.0c08732.
- M. Epshtein, V. Scutelnic, Z. Yang, T. Xue, M. L. Vidal, A. I. Krylov, S. Coriani and S. R. Leone, Table-top x-ray spectroscopy of benzene radical cation, J. Phys. Chem. A, 2020, 1240(46), 9524–9531, DOI:10.1021/acs.jpca.0c08736.
- D. Marx and M. Parrinello, Ch5+: The cheshire cat smiles, Science, 1999, 2840(5411), 59–61, DOI:10.1126/science.284.5411.59.
- P. Padma Kumar and M. Dominik, Understanding hydrogen scrambling and infrared spectrum of bare ch5+ based on ab initio simulations, Phys. Chem. Chem. Phys., 2006, 8, 573–586, 10.1039/B513089C.
- K. C. Thompson, D. L. Crittenden and M. J. T. Jordan, Ch5 +: Chemistryss chameleon unmasked, J. Am. Chem. Soc., 2005, 1270(13), 4954–4958, DOI:10.1021/ja0482280.
- S. D. Ivanov, O. Asvany, A. Witt, E. Hugo, G. Mathias, B. Redlich, D. Marx and S. Schlemmer, Quantum-induced symmetry breaking explains infrared spectra of ch5+ isotopologues, Nat. Chem., 2010, 20(4), 298–302, DOI:10.1038/nchem.574.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp01007d |
| ‡ X-AT with X = MBS, SWS means the same thermostat applied in a canonical fashion, and with a modified SWS sampling procedure. |
| This journal is © the Owner Societies 2023 |